Numerical model of energy dissipation and shallow-water sloshing motions in tank under different coupled excitations

Abstract

Shallow-water sloshing motions in a three-dimensional rectangular tank are investigated. The Boussinesq-type equations in terms of velocity potential and the finite-difference scheme are applied for the solutions of numerical model. Through linking the rate of decay of the wave amplitudes to the energy dissipation due to the friction at the tank walls, a linear damping term is proposed and added into the free surface boundary condition. Taking the tank under excited frequencies near the lowest natural frequency, the maximum transient wave amplitudes and steady-state wave amplitudes of sloshing motions at the tank wall are presented and verified by the experimental results given in the literature. The characteristics of sloshing motions in tank under different coupled excitations are studied. The results indicate that coupled surge-sway excitations lead to the weaker nonlinear sloshing motions in tank than the single degree of freedom excitations. The intersection of sloshing wave crest lines finally tend to the diagonal line of the tank under the coupled surge-sway excitations with different amplitudes. And the irregular free surface oscillations appear at the corners of the tank excited by the coupled surge-sway-roll-pitch-yaw harmonic motions.

1 Introduction

The phenomenon of liquid sloshing draws a great deal of attention from many researchers in the field of fluid dynamics. According to the relative filling levels in the containers, the regimes of liquid sloshing can be divided roughly into the finite water depth, intermediate water depth and shallow-water depth.

For the finite and intermediate water depth, an inviscid Finite Element Method (FEM) was used in Wu et al. [1] to simulate the sloshing motions based on the fully nonlinear wave potential theory. A time-independent Finite Difference Method (FDM) was used to simulate the liquid sloshing in a three-dimensional tank under coupled motions in Wu and Chen [2, 3] and Wu et al. [4]. When dealing with violent sloshing motions, the particle tracking methods appeared to be appropriate candidates, including Smoothed Particle Hydrodynamics (SPH) (Cao et al. [5]), Moving Particle Semi-implicit method (MPS) (Zhang and Wan [6]) and Consistent Particle Method (CPM) (Luo et al. [7] and Luo and Koh [8]). Under the framework of potential theory, the Boundary Element Method (BEM) was adopted for the sloshing motions in Ebrahimian et al. [9] and Liu et al. [10].

For the low filling ratios in tank, an ordinary differential equation was solved in Ockendon et al. [11] which represented forced water waves on the shallow-water sloshing near resonance. Asymptotic methods were used for the multiple solutions and the effects of dissipation were considered. A nonlinear, dispersion and dissipation model was developed in Lepelletier and Raichlen [12] to describe the shallow-water sloshing in two-dimensional rectangular tank. The maximum transient and steady-state wave amplitudes were compared between numerical and experimental results when the excited frequencies near the lowest resonant frequency. A two-dimensional shallow-water rectangular basin was investigated by Hill [13]. A damping coefficient based upon a boundary layer approximation was considered. The maximum transient and steady-state wave amplitudes were determined by an evolution equation using multiple-scales analysis. Amplitude response diagrams under horizontal periodic excitations demonstrated good agreement with experimental investigations. New shallow-water equations were derived in Ardakani and Bridges [14] and used to simulate the sloshing in a three-dimensional rectangular tank. The flow was assumed to be inviscid but vortical, with approximations on the vertical velocity and acceleration at the surface.

The Boussinesq-type depth-averaged equations were used in Antuono et al. [15] for the two-dimensional shallow-water sloshing in the rectangular tank. A viscosity term was added into the momentum equation to consider the dissipation due to the boundary layers and the dissipation inside the fluid bulk. The coupled sway-heave-roll motions were considered and the time histories of wave amplitudes were shown. Later the wave breaking term was added to the Boussiensq-type model in Antuono et al. [16]. The Boussinesq-type equations in terms of velocity potential was used in Su and Liu [17] for simulating two-dimensional shallow-water sloshing. The horizontal excitations were considered and the time histories of free surface elevations near the lowest resonant frequency were shown. And then the Boussinesq-type model was extended to the three dimensions in Su et al. [18]. But the energy dissipation was not considered and only simple uncoupled excitations were discussed.

The aforementioned studies about the shallow-water sloshing mostly focused on the two-dimensional wave motions near the lowest resonant frequency. In this paper, the three-dimensional Boussinesq-type model will be used for the sloshing motions in the rectangular tank. And the energy dissipation due to the friction at the tank walls will be derived. Firstly the numerical model was verified by the experimental results given by Lepelletier and Raichlen [12]. And then the sloshing motions in tanks due to different coupled excitations will be discussed. The numerical results may help to understand the complicated three-dimensional shallow-water sloshing motions.

2 Numerical model

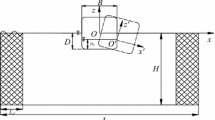
The irrotational flow of an incompressible inviscid fluid is considered and excited by a three-dimensional rectangular tank. As shown in figure 1, length of the partially filled tank is denoted by l, width b and still water depth h. A tank-fixed Cartesian coordinate system oxyz lies on the still water surface with the origin located in the middle of the tank.

Based on the potential flow theory, the velocity potential $\Phi$ in the tank satisfies the Laplace equation and the boundary conditions.

$$\begin{aligned} \nabla ^{2}\Phi&=0 \end{aligned}$$

(1)

$$\begin{aligned} \nabla \Phi \cdot \mathbf{n} =\mathbf{v} _0\cdot \mathbf{n} + \mathbf{w} \cdot [\mathbf{r} \times \mathbf{n} ]&=\mathbf{v} \cdot \mathbf{n} \end{aligned}$$

(2)

$$\begin{aligned} \eta _{t}-\mathbf{v} \cdot \nabla \eta -\Phi _{z}+\eta _{x}\Phi _{x} +\eta _{y}\Phi _{y}&=0 \end{aligned}$$

(3)

$$\begin{aligned} \Phi _{t}-\mathbf{v} \cdot \nabla \Phi +\dfrac{1}{2}\nabla \Phi \cdot \nabla \Phi +g\eta&=0 \end{aligned}$$

(4)

Here, $\mathbf{r}$ is the position vector relative to the axis of rotation. $\mathbf{n}$ denotes the outward vector normal to the tank wetted surface. g is the acceleration of gravity and $\eta$ is the free surface elevation. The symbol $\nabla$ equals to $\nabla = [\partial / \partial x, \partial / \partial y, \partial / \partial z]$.

Fig. 1

Sketch of three-dimensional rectangular tank

For the free surface boundary conditions, the temporal derivatives defined in the inertial coordinate system should be transformed into that in the tank-fixed coordinate system by the operator ($\partial / \partial t -\mathbf{v} \cdot \nabla$). The forced harmonic velocity of tank is expressed by $\mathbf{v} =\mathbf{v} _0+\mathbf{w} \times \mathbf{r} =[v_{a},v_{b},v_{c}]$, which includes the translatory velocity $\mathbf{v} _0=[v_1,v_2,v_3]$ along (x, y, z) coordinate axes and the angular velocity $\mathbf{w} =[w_1,w_2,w_3]$. The axis of rotation $w_1$ is set to $y=0$, $z=-h$ and axis of rotation $w_2$ is set to $x=0$, $z=-h$. The axis of rotation $w_3$ is located at $x=0$, $y=0$.

The velocity potential $\Phi$ is separated into two parts: $\Phi =\phi +\varphi$, a disturbance potential $\phi$ and a particular solution $\varphi$ which defines the motions of the tank. According to Su et al. [18], the particular solution can be obtained by using the Fourier series:

$$\begin{aligned} \varphi =xv_{1}+yv_{2}+zv_{3}+w_{1}\varphi _{1}+w_{2}\varphi _{2}+w_{3}\varphi _{3}. \end{aligned}$$

(5)

In addition, the velocity potential $\varphi _{1}$, $\varphi _{2}$ and $\varphi _{3}$ are shown as follows:

$$\begin{aligned} \varphi _{1}&=-z(y-b/2)+\sum _{n=1}^{\infty }\beta _{n}\cos (\gamma _{n}y) \nonumber \\&\quad \dfrac{2\sinh \gamma _{n}(z-h)}{\gamma _{n}\cosh (\gamma _{n}h)} \end{aligned}$$

(6)

$$\begin{aligned} \varphi _{2}&=-z(x-l/2)+\sum _{n=1}^{\infty }\alpha _{n}\cos (\lambda _{n}x)\nonumber \\&\quad \dfrac{2\sinh \lambda _{n}(z-h)}{\lambda _{n}\cosh (\lambda _{n}h)} \end{aligned}$$

(7)

$$\begin{aligned} \varphi _{3}&=\sum _{n=1}^{\infty }\alpha _{n}\cos (\lambda _{n}x) \dfrac{\sinh \lambda _{n}(y-b/2)}{\lambda _{n}\cosh (\lambda _{n}b/2)} \nonumber \\&\quad +\sum _{n=1}^{\infty }\beta _{n}\cos (\gamma _{n}y) \dfrac{\sinh \gamma _{n}(x-l/2)}{\gamma _{n}\cosh (\gamma _{n}l/2)}, \end{aligned}$$

(8)

where $\lambda _{n}=n\pi /l$, $\alpha _{n}=-4l/(n^2\pi ^2)$, $\gamma _{n}=n\pi /b$ and $\beta _{n}=-4b/(n^2\pi ^2)$.

If the velocity potential $\tilde{\Phi }=\Phi (x,y,\eta ,t)$ and vertical velocity $\tilde{w}=(\Phi _{z})_{z=\eta }$ are defined directly on the free surface, the Eqs. 3 and 4 can be reformed:

$$\begin{aligned} \eta _{t}&=v_{a}\eta _{x}+v_{b}\eta _{y}-\tilde{\Phi }_{x} \eta _{x}-\tilde{\Phi }_{y}\eta _{y}+(1+\eta _{x}^{2}+\eta _{y}^{2})\tilde{w} \end{aligned}$$

(9)

$$\begin{aligned} \tilde{\Phi }_{t}&=v_{a}\tilde{\Phi }_{x}+v_{b}\tilde{\Phi }_{y}+v_{c} \tilde{w}-g\eta -\dfrac{1}{2}\tilde{\Phi }^{2}_{x} -\dfrac{1}{2}\tilde{\Phi }^{2}_{y} \nonumber \\&\quad +\dfrac{1}{2}\tilde{w}^{2}(1+\eta _{x}^{2}+\eta _{y}^{2}). \end{aligned}$$

(10)

The time histories of free surface elevation $\eta (t)$ can be calculated based on the temporal derivatives $\eta _t$ and $\tilde{\Phi }_t$ when the initial values of $\tilde{\Phi }$ and $\eta$ are known. The spatial derivatives in the numerical computations are calculated by the five-points finite-difference scheme. Homogeneous Neumann boundary conditions at the side walls of tank are imposed by reflecting the finite-difference coefficients, thus all schemes are effectively centred. The vertical velocity on the free surface can be calculated by two parts $\tilde{w}=\phi _{z}+\varphi _{z}$. The derivative of particular solution can be given easily and the other part should be solved by the Boussinesq-type approach. A detailed description has been given in Su et al. [18].

The energy dissipation due to the friction at the tank walls is considered here. A linear damping term will be proposed and added to the dynamic free surface condition (Eq. 10).

3 Energy dissipation

For the three-dimensional rectangular tank without external excitations, the velocity potential satisfies the following equations based on linear potential flow theory.

$$\begin{aligned} \nabla ^2 \Phi&= 0 \end{aligned}$$

(11)

$$\begin{aligned} \nabla \Phi \cdot \mathbf {n}&= 0 \quad \text {on the tank walls}\ S_C \end{aligned}$$

(12)

$$\begin{aligned} \dfrac{\partial \Phi }{\partial t}+g\eta&= 0 \quad \dfrac{\partial \eta }{\partial t}-\dfrac{\partial \Phi }{\partial z}=0\ \text {on the free surface}\ S_F. \end{aligned}$$

(13)

When the sloshing mode n is dominant, the velocity potential can be approximately expressed by

$$\begin{aligned} \Phi _{n}=-a_{n}\phi _{n}(x,y,z)\sin (\omega _n t+\theta ), \end{aligned}$$

(14)

where $\omega _n$ is the natural frequency and $a_n$ is the amplitude. The free surface elevation $\eta _n$ can be given as follows:

$$\begin{aligned} \eta _n=a_n\dfrac{\omega _n}{g}\phi _n(x,y,z)\cos (\omega _n t+\theta ). \end{aligned}$$

(15)

The wave energy can be calculated by integrating on the free surface:

$$\begin{aligned} E=\dfrac{1}{2}\rho g a_n^2 \dfrac{\omega _n^2}{g^2}\int \int _{S_F}\phi _n^2 {\text {d}}S. \end{aligned}$$

(16)

To evaluate the dissipated energy through friction, the classical Stokes’ theory of the oscillating flat plate is used (Molin et al. [19]). The dissipated energy over one period on the tank walls is given by

$$\begin{aligned} \Delta E&=\int _{0}^{T_n}dt\int \int _{S_C}\rho V^2 \sqrt{\dfrac{\nu \omega _n}{2}}{\text {d}}S \nonumber \\&=\rho \pi \sqrt{\dfrac{\nu }{2\omega _n}}a_n^2\int \int _{S_C}\nabla \phi _n\cdot \nabla \phi _n {\text {d}}S, \end{aligned}$$

(17)

where the period $T_n=2\pi / \omega _n$ and the velocity $V=\nabla \Phi _n$. $\nu$ is the kinematic viscosity. The relative amount of dissipated energy is

$$\begin{aligned} \dfrac{\Delta E}{E}=\dfrac{2\pi g}{\omega _n^2}\sqrt{\dfrac{\nu }{2\omega _n}}\dfrac{\int \int _{S_C}\nabla \phi _n\cdot \nabla \phi _n {\text {d}}S}{\int \int _{S_F}\phi _n^2 {\text {d}}S}. \end{aligned}$$

(18)

According to the Keulegan [20], the damped amplitude $A_n$ due to the energy dissipation is given by

$$\begin{aligned} A_n=a_{n}e^{-\alpha t/T_n} \quad \text {with} \quad \alpha =\dfrac{1}{2}\dfrac{\Delta E}{E}. \end{aligned}$$

(19)

In the other hand, the linearized dynamic and kinematic free surface conditions can be reformed as follows due to the addition of a damping term $\epsilon \Phi$:

$$\begin{aligned} \dfrac{\partial \Phi }{\partial t}+g\eta +\epsilon \Phi =0 \quad \dfrac{\partial \eta }{\partial t}-\dfrac{\partial \Phi }{\partial z}=0. \end{aligned}$$

(20)

Eliminating the variable $\eta$, the free surface condition is shown:

$$\begin{aligned} \Phi _{tt}+\epsilon \Phi _t+g\Phi _z=0. \end{aligned}$$

(21)

The velocity potential of sloshing mode n can be reformed as follows:

$$\begin{aligned} \Phi _{n} = \mathfrak {R}\left\{ { - iA_{n} (\epsilon t)\phi _{n} (x,y)\frac{{\cosh \lambda _{n} (z + h)}}{{\cosh \lambda _{n} h}}e^{{ - i\omega _{n} t}} } \right\} , \end{aligned}$$

(22)

where $\omega _n^2=g\lambda _n\tanh \lambda _n h$.

Substituted into the free surface condition, the coefficient of term $\Phi _{tt}+\epsilon \Phi _t+g\Phi _z$ should be equal to zero. After eliminating the term $O(\epsilon ^2)$, the amplitude $A_n(\epsilon t)$ satisfies

$$\begin{aligned} -2\omega _n\epsilon \dot{A}_n(\epsilon t)-\omega _n\epsilon A_n(\epsilon t) = 0, \end{aligned}$$

(23)

hence

$$\begin{aligned} A_n(\epsilon t)=a_n e^{-\epsilon t/2}. \end{aligned}$$

(24)

Compared with the Eq. 19, the coefficient $\epsilon$ can be obtained:

$$\begin{aligned} \epsilon =\dfrac{2\alpha }{T_n}=\dfrac{\omega _n}{2\pi }\dfrac{\Delta E}{E}=\dfrac{g}{\omega _n}\sqrt{\dfrac{\nu }{2\omega _n}}\dfrac{\int \int _{S_C}\nabla \phi _n\cdot \nabla \phi _n {\text {d}}S}{\int \int _{S_F}\phi _n^2 {\text {d}}S}. \end{aligned}$$

(25)

The linear damping term $\epsilon \Phi$ will be added in the dynamic free surface condition.

For the rectangular tank with length l, width b and water depth h, the velocity potential $\phi _n$ should be constructed for different types of free surface profiles according to the external different harmonic excitations.

(1) The external harmonic excitations along x-axis or around y-axis. Planar sloshing waves.

$$\begin{aligned} \phi _n&=\dfrac{g}{\omega _n}\dfrac{\cosh \lambda _n(z+h)}{\cosh \lambda _n h}\cos \lambda _n \left( x+\dfrac{l}{2}\right) \end{aligned}$$

(26)

$$\begin{aligned} \epsilon&=2\omega _n\sqrt{\dfrac{\nu }{2\omega _n}}\dfrac{1}{bl}\left( l+b+b\dfrac{\lambda _n l-2\lambda _n h}{\sinh 2\lambda _n h}\right) . \end{aligned}$$

(27)

(2) The external harmonic excitations along x-axis and y-axis simultaneously in a square tank; around x-axis and y-axis simultaneously in a square tank with the same amplitudes and angular frequencies. Diagonal sloshing waves.

$$\phi _{n} = \frac{g}{{\omega _{n} }}\frac{{\cosh \lambda _{n} (z + h)}}{{\cosh \lambda _{n} h}}\left( {\cos \lambda _{n} \left( {x + \frac{l}{2}} \right) + \cos \gamma _{n} \left( {y + \frac{b}{2}} \right)} \right)$$

(28)

$$\begin{aligned} \epsilon&=2\omega _n\sqrt{\dfrac{\nu }{2\omega _n}}\dfrac{1}{bl}\left( l+b+b\dfrac{\lambda _n l-2\lambda _n h}{\sinh 2\lambda _n h}\right) \quad l=b. \end{aligned}$$

(29)

(3) The external harmonic excitations around the z-axis in a square tank ($l=b$). Swirling sloshing waves.

$$\begin{aligned} \phi _{(mn)}&=\dfrac{g}{\omega _{mn}}\dfrac{\cosh \lambda _{mn}(z+h)}{\cosh \lambda _{mn} h}\cos \lambda _m \left( x+\dfrac{l}{2}\right) \cos \gamma _n \left( y+\dfrac{b}{2}\right) \end{aligned}$$

(30)

$$\begin{aligned} \lambda _{mn}^2&=\lambda _m^2+\gamma _n^2 \quad \lambda _m=\dfrac{m\pi }{l} \quad \gamma _n=\dfrac{n\pi }{b} \end{aligned}$$

(31)

$$\begin{aligned} \omega _{mn}^2&=g\lambda _{mn}\tanh \lambda _{mn}h \end{aligned}$$

(32)

$$\begin{aligned} \epsilon&=2\omega _{mn}\sqrt{\dfrac{\nu }{2\omega _{mn}}} \dfrac{1}{bl}\left( 3l+b\dfrac{\lambda _{mn} l-2\lambda _{mn} h}{\sinh 2\lambda _{mn} h}\right) . \end{aligned}$$

(33)

4 Validation

Two rectangular tanks were constructed for the experiments in Lepelletier and Raichlen [12]. The maximum transient wave amplitudes and steady-state wave amplitudes of sloshing motions at the tank wall were measured and analyzed. The length of the first tank $l=$ 0.6095 m, width $b=$ 0.23 m and still water depth $h=$ 0.06 m is selected here for the validation. The translatory forced motions for the tank are along the x-axis and harmonic. A series of excited frequencies are selected near the lowest natural frequency $\omega _r$. Here the frequency $\omega _r$ is calculated by the linear dispersion relation. The amplitude of harmonic motions for the tank is 0.196 cm. Uniform computational points are distributed along the length of tank (31 points) and the width of tank (11 points). The time step size is 0.06 s and all the simulations have been run up to $t/T=100$ to ensure the attainment of steady-state conditions. T is the period of forcing excitation.The mode n in the particular solutions is set to 9 and the convergence has been verified in Su et al. [18].

As shown in Fig. 2 (left), the variation of maximum transient relative amplitudes are compared between the experimental data (Exp) and the numerical results (Num). The excited frequencies divided by the lowest resonant frequency are ranged from 0.9 to 1.12. The nonlinear response curves are not symmetric about $\omega /\omega _r =1$ but bend toward the right. Two discontinuities are exhibited in the response curves and the larger discontinuity (or jump) occurs around $\omega /\omega _r =1.07$ (bifurcation frequency). According to Lepelletier and Raichlen [12], the jump at the bifurcation frequency is attributed to the effects of nonlinearities and can be related to the hard spring solution of Duffing’s equation. Part of the time histories of relative free surface elevations are shown in Fig. 3 with excited frequencies $\omega /\omega _r = 1.06 \ and \ 1.08$ near the bifurcation frequency. Obviously, the wave regimes in tank are totally different for the excited frequencies larger and less than the bifurcation frequency.

The secondary jump takes place around $\omega /\omega _r =0.97$. The behavior seems to pertain only to the shallow-water tank oscillations. The experiments given by Fultz [21] on intermediate and deep water tank oscillations resulted in the response curves with only one discontinuity. The time histories of relative free surface elevations are shown in Fig. 4 with excited frequencies $\omega /\omega _r = 0.96 \ and \ 0.98$. Also the wave regimes change at the secondary jump.

The comparison between the numerical results and experimental data appears good. And the locations of the two discontinuities are correctly good. Discrepancies appear for the value of $\eta /h$ greater than 0.8 where the numerical results are less than the experiments. For larger relative wave heights, a more complete theory should be used, such as Su and Gardner [22]. According to the experiments in Lepelletier and Raichlen [12], local breaking appeared on the free surface when the excited frequency closed to the larger bifurcation frequency. But the wave breaking is not considered in the Boussinesq model. Therefore, the maximum transient relative amplitudes in the vicinity of $\omega /\omega _r =1.07$ are not shown in the Fig. 2 (left).

Fig. 2

Variation of the relative amplitudes at the tank wall with excited frequencies near the lowest resonant frequency. Left: Maximum transient wave amplitudes, right: steady-state wave amplitudes. $l$ = 0.6095 m, $b$ = 0.23 m and $h$ = 0.06 m

Fig. 3

Time histories of relative free surface elevations at different excited frequencies. Left: $\omega /\omega _r = 1.06$, right: $\omega / \omega _r =1.08$. $l$ = 0.6095 m, $b$ = 0.23 m and $h$ = 0.06 m

Fig. 4

Time histories of relative free surface elevations at different excited frequencies. Left: $\omega /\omega _r = 0.96$, right: $\omega /\omega _r =0.98$. $l$ = 0.6095 m, $b$ = 0.23 m and $h$ = 0.06 m

The comparison of steady-state relative wave amplitudes is shown in Fig. 2 (right). Due to the wave breaking, the steady-state relative wave amplitudes near $\omega /\omega _r =1.07$ are not obtained. Meanwhile, the wave amplitudes near the bifurcation frequency $\omega /\omega _r =0.97$ diminished at a much slower rate (beat pattern) and the steady-state wave amplitudes are not shown in the figure. The steady-state relative wave amplitudes and locations of bifurcation frequencies were predicted well by the numerical model. The discrepancies appear at the locations where the similar discrepancies appeared in the Fig. 2 (left).

5 Coupled excitations

Based on the Boussinesq-type numerical model with the energy dissipation term, the coupled surge-pitch excitations, coupled surge-sway-roll-pitch excitations, coupled surge-sway excitations with different amplitudes and coupled surge ($v_1$) - sway ($v_2$) - roll ($w_1$) - pitch ($w_2$) - yaw ($w_3$) excitations are calculated. For a tank under heave motion with a disturbed free surface and the vertical excitation frequency near 2$\omega _r$, the destabilizing influence of the heave motion is significant (Chen and Wu [3]). Strong nonlinear free surface oscillations lead to the numerical breaking event when the heave excitation is coupled.

5.1 Coupled surge and pitch excitations

A rectangular tank with length l = 0.5875 m, width b = 0.1 m and still water depth h = 0.03 m is considered. The uniform computational points and the time step size are the same as the settings in the Sect. 3. The amplitude of surge harmonic excitation is 0.001 m and pitch harmonic excitation is 0.001 rad. The breaking waves will appear near the tank walls for large excitation amplitudes. The excitation frequencies are ranged from 0.92 $\omega _r$ to 1.1 $\omega _r$. The relative maximum transient wave amplitudes and the steady-state wave amplitudes at the tank wall are shown in Fig. 5. The results due to the single surge excitations are denoted by o and the single pitch excitations are marked by $*$. The results due to the coupled surge and pitch excitations are plotted by $+$.

As shown in Fig. 5, the scatter diagram of relative maximum transient wave amplitudes and steady-state wave amplitudes bend towards the right side of $\omega /\omega _r =1$. The maximum transient wave amplitudes are higher than the steady-state wave amplitudes due to the initial beating phenomenon. The relative amplitudes due to the single pitch excitations are little higher than that due to the single surge excitations. Higher bifurcation frequency can also be found in the single pitch excitations. When the tank was excited by the coupled surge and pitch motions, the relative amplitudes become much lower and the bifurcation frequency is close to the lowest natural frequency.

The time histories of relative free surface elevations at the tank wall under coupled surge and pitch excitations are shown in Figs. 6, 7 and 8. For the excitation frequencies away from the lowest natural frequency (Figs. 6, 8), the envelope of the amplitude-modulated waves tend to vanish due to the energy dissipation. At the steady-state, linear standing waves in tank lead to the harmonic curves. When the excitation frequency equals to 0.98 $\omega _r$, the wave amplitudes become higher and secondary wave appear after several excitation periods. The primary and secondary waves compose the steady-state wave profiles.

Fig. 5

Variation of the relative wave amplitudes at the tank wall with the excitation frequencies near the lowest resonant frequency. Left: maximum transient wave amplitudes, right: steady-state wave amplitudes. $l$ = 0.5875 m, $b$ = 0.1 m and $h$ = 0.03 m. $*$: Pitch excitations; o: surge excitations; $+$: Coupled surge and pitch excitations

Fig. 6

Time history of relative free surface elevations at the tank wall under coupled surge and pitch excitations. Excitation frequency 0.92 $\omega _r$

Fig. 7

Time history of relative free surface elevations at the tank wall under coupled surge and pitch excitations. Excitation frequency 0.98 $\omega _r$

Fig. 8

Time history of relative free surface elevations at the tank wall under coupled surge and pitch excitations. Excitation frequency 1.06 $\omega _r$

5.2 Coupled surge-sway-roll-pitch excitations

A rectangular tank with length l = 0.5875 m, width b = 0.5875 m and still water depth h = 0.03 m is considered. Uniform computational points are distributed along the length of tank (31 points) and the width of tank (31 points). The time step size is 0.06 s and all the simulations have been run up to $t/T=100$ to ensure the attainment of steady-state conditions. The amplitudes of surge and sway harmonic excitations are both 0.001 m. Simultaneously the amplitudes of roll and pitch harmonic excitations are both 0.001 rad. The relative amplitudes at the tank corner are presented in Figs. 9 and 10 with excitation frequencies ranged from 0.92 $\omega _r$ to 1.1 $\omega _r$.

The coupled surge-sway-roll-pitch excitations in the three-dimensional tank can be divided into two parts: (a) surge-pitch excitations on the xoz plane; (b) sway-roll excitations on the yoz plane. The relative amplitudes at the tank corner due to (a) or (b) should be the same. As shown in Fig. 9, the relative maximum transient wave amplitudes at the tank corner due to the coupled surge-sway-roll-pitch excitations are compared with doubled values caused by (a). When the excitation frequencies away from the lowest natural frequency, weak nonlinear waves can be found in the tank and the principle of superposition is applicable. The red line coincide well with the blue line. With the increasing nonlinearity, the difference between the red line and the blue line gradually enlarge. The linear principle of superposition can not be applied. In Fig. 10, the relative steady-state wave amplitudes at the tank corner are compared. The principle of superposition is correct only for the excitation frequencies away from $\omega /\omega _r=1$.

Fig. 9

Relative maximum transient wave amplitudes at the tank corner due to different external excitations

Fig. 10

Relative steady-state wave amplitudes at the tank corner due to different external excitations

5.3 Coupled surge-sway excitations with different amplitudes

The rectangular tank used in the Sect. 4.2 is taken here. The frequency of both surge and sway excitations is 1.05 $\omega _r$ but the excitation amplitudes are different. The excitation amplitude of surge is 0.002 m and the excitation amplitude of sway is 0.001 m.

As shown in Figs. 11 and 12, the snapshots of free surface profiles in the tank at different times are shown. Two single-bump traveling beam waves of orthogonal direction overlay at the points of intersection marked by the arrows. Due to different excitation amplitudes, the point of intersection is not along the diagonal line of the tank at the beginning. Periodic trajectories of the point of intersection can be found by repeating the first four snapshots. When the wave motions attain to the steady-state, the point of intersection gradually close to the diagonal line of the tank. As shown in Fig. 12 middle (t = 135.24 s) and right (t = 135.66 s), two single-bump traveling waves overlay along the diagonal line of tank.

The time histories of free surface elevations at two points are compared in Fig. 13. Point A: $x=l/2$, $y=0$. Point B: $x=0$, $y=b/2$. The free surface elevations at the two points A and B can be used to explain the former phenomenon. At the beginning of the curves (Fig. 13 left), the discrepancy of wave periods can be found, which means the two single-bump traveling waves can not arrive at the tank walls at the same time. The wave periods are related to the excitation amplitudes. At the steady-state of the curves, the wave periods at the two points attain to the same (Fig. 13 right), which means the point of intersection move along the diagonal line of the tank. Different surge excitation amplitudes are discussed in Figs. 14 (0.0015 m), 15 (0.0025 m) and 16 (0.003 m). The same wave regime can be found in the figures.

Fig. 11

Numerical results for the free surface profiles in the tank at different times. Excitation frequency: $\omega /\omega _r =1.05$. Excitation amplitudes: 0.002 m (surge) and 0.001 m (sway)

Fig. 12

Numerical results for the free surface profiles in the tank at different times. Excitation frequency: $\omega /\omega _r =1.05$. Excitation amplitudes: 0.002 m (surge) and 0.001 m (sway)

Fig. 13

Time histories of relative free surface elevations at the points A and B. Excitation frequency: $\omega /\omega _r =1.05$. Excitation amplitudes: 0.002 m (surge) and 0.001 m (sway)

Fig. 14

Time histories of relative free surface elevations at the points A and B. Excitation frequency: $\omega /\omega _r =1.05$. Excitation amplitudes: 0.0015 m (surge) and 0.001 m (sway)

Fig. 15

Time histories of relative free surface elevations at the points A and B. Excitation frequency: $\omega /\omega _r =1.05$. Excitation amplitudes: 0.0025 m (surge) and 0.001 m (sway)

Fig. 16

Time histories of relative free surface elevations at the points A and B. Excitation frequency: $\omega /\omega _r =1.05$. Excitation amplitudes: 0.003 m (surge) and 0.001 m (sway)

5.4 Coupled surge-sway-roll-pitch-yaw excitations

The rectangular tank used in the Sect. 4.2 is taken here. The excitation frequency of coupled motions is 1.06 $\omega _r$. For the yaw excitation, the lowest natural frequency is calculated by $\omega _r^2=g\nu \tanh \nu h$ and $\nu =\sqrt{(\pi /l)^2+(\pi /b)^2}$, which means the first mode is applied for both directions. And the excitation amplitudes of surge and sway harmonic motions are both 0.001 m. The excitation amplitudes of roll, pitch and yaw harmonic motions are 0.001 rad. Due to the primarily swirling sloshing waves in tank, the damping term Eq. 34 was applied for the energy dissipation.

As shown in Figs. 17 and 18, five successive snapshots of free surface profiles in tank at the steady-state are arranged sequentially. Wave crest and trough alternately appear at the corners of rectangular tank due to the yaw excitation. At the diagonal corners $(x=l/2, y=b/2)$ and $(x=-l/2, y=-b/2)$, the free surface profiles are not symmetric due to the effect of coupled surge-sway-roll-pitch excitations. The time histories of relative free surface elevations at the four corners in tank are shown in Figs. 19, 20 and 21. At the two corners $(x=-l/2,y=b/2)$ and $(x=l/2,y=-b/2)$, the harmonic free surface oscillations can be found at the steady-state. But at the other two corners, the free surface oscillations are not regular due to the effect of coupled surge-sway-roll-pitch excitations.

Fig. 17

Numerical results for the free surface profiles in the tank at different times. Excitation frequency: $\omega /\omega _r =1.06$

Fig. 18

Numerical results for the free surface profiles in the tank at different times. Excitation frequency: $\omega /\omega _r =1.06$

Fig. 19

Time histories of relative free surface elevations at the corner $(x=-l/2,y=-b/2)$. Excitation frequency: $\omega /\omega _r =1.06$

Fig. 20

Time histories of relative free surface elevations at the corner $(x=-l/2,y=b/2)$. Excitation frequency: $\omega /\omega _r =1.06$

Fig. 21

Time histories of relative free surface elevations at the corners $(x=l/2,y=b/2)$ (left) and $(x=l/2,y=-b/2)$ (right). Excitation frequency: $\omega /\omega _r =1.06$

6 Conclusion

The three-dimensional shallow-water sloshing motions were studied based on the Boussinesq-type equations. The energy dissipation due to the friction at the tank walls was derived for different types of free surface profiles. According to the comparisons between the numerical results and the experimental data published in the literature, the numerical model presented good performance on simulating the shallow-water sloshing motions. The coupled surge-sway excitations leaded to the weaker nonlinear sloshing motions in tank than the single degree of freedom excitations. Due to the effects of nonlinearity, the coupled surge-sway-roll-pitch excitations can not be divided into the sum of coupled surge-pitch excitations and coupled sway-roll excitations. The intersection of sloshing wave crest lines finally tended to the diagonal line of the tank under the coupled surge-sway excitations with different amplitudes. The irregular free surface oscillations appeared at the corners of the tank excited by the coupled surge-sway-roll-pitch-yaw harmonic motions.