Abstract
Previous studies examining climate change and changes in the timing of seasons have used a fixed temperature threshold for season onset. In this study, the timing of seasons was determined using non-fixed threshold methods. Twelve new timing indices were defined to account for shifts in seasons and season onset day, thermal centroid day, and length. The Mann-Kendall test, Theil-Sen’s slope estimator, sequential Mann-Kendall test, and least square linear regression were used to assess trends. The timing indices were examined using data from two meteorological stations in Iran with 50 years of records. Spatio-temporal variations in each index over 30 years (1987–2016) were then determined for Khuzestan province in southwestern Iran. Trend analysis for several indices indicated that the timing of seasons had probably changed in the south and west of the study area, while mountainous regions showed non-significant trends. Based on the hottest and coldest 90-day periods (summer and winter, respectively), during the three decades studied, spring lengthened by 5–10 days/decade in the plain region of Khuzestan province and autumn shortened by about 5–8 days/decade. The centroid of winter occurred earlier, by 2–5 days/decade, in the plains area, while the thermal centroid of summer did not change significantly. Overall, the difference between the thermal centroid of winter and summer (Cwin-sum) in the plains area significantly decreased, by 6–8 days/decade, in the 30-year period.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Global warming caused by increasing emissions of greenhouse gases is a major concern around the world (Allen et al. 2010; Vörösmarty et al. 2000). The mean ambient air temperature of the Earth rose by approximately 0.85 °C from 1880 to 2012 (Allen and Sheridan 2016; Hartmann et al. 2013). This is reported to have caused climate change (Richardson et al. 2018), with increasing frequency of droughts, floods, and extreme weather events in many parts of the world (AghaKouchak et al. 2014; Hirabayashi et al. 2013; Knox 1993; Kundzewicz et al. 2014; Prospero and Lamb 2003). In addition, climate change has strong influences on health (McMichael et al. 2006; Patz et al. 2005; Watts et al. 2015), agriculture (Peña-Lévano et al. 2019), and water availability (Christensen et al. 2004; Haddeland et al. 2014; Piao et al. 2010). A number of metrological parameters are affected, among which temperature plays a major role in the impact of climate change (Ahmadi et al. 2018). Therefore, extensive research has been performed to determine the impact of climate change on temperature in different parts of the world (Alexander et al. 2006; Fallah-Ghalhari et al. 2019; Yin et al. 2019). Minimum, mean, and maximum daily temperature have been taken as the most important temperature characteristics in analysis of climate change (Dimri 2019; Moberg and Jones 2005; Scorzini et al. 2018; Vincent et al. 2018, 2005). In addition to minimum and maximum daily temperatures, numerous temperature indices have been introduced to monitor different characteristics of air temperature and possible changes or variations in climate (Frich et al. 2002; Kiktev et al. 2003; Qian and Lin 2004). These indices provide essential information about temperature characteristics, for example, total number of frost days, number of ice days, warm days, cold temperature percentiles, warm temperature percentiles, consecutive warm days, consecutive cold days, etc. They have been widely used to describe the magnitude, intensity, frequency, and duration of temperature changes (Erlat and Türkeş 2012; Jylhä et al. 2008; Qian and Lin 2004; Wang et al. 2013; Zhou and Ren 2011). Some studies have examined earlier onset of spring, extended summer, warm days, summer days, and warm and cold spell duration (e.g., Collazo et al. 2019; Park et al. 2018; Tong et al. 2019; Wang et al. 2017; Zhu et al. 2019). However, the timing and seasonality of temperature changes have been less well studied.
It is very important to identify variations in seasonal cycles and, in particular, extensions to the warm period, since seasonal changes can affect national energy consumption, agricultural activities, human health, the environment, and wildlife (Garonna et al. 2016; Mazaris et al. 2013; Sparks and Braslavská 2001; Tol 2009). Day-count indicators based on temperature threshold have been developed (Liu et al. 2008; Song et al. 2009; Yang et al. 2013). However, a given fixed threshold is not reasonable for all regions, since air temperature is related to geographical location of a region and a pre-determined threshold is not appropriate for specifying seasons in areas with strong climate heterogeneity (Peña-Ortiz et al. 2015). To resolve this issue, de la Franca et al. (2013) proposed that spring and winter start once the average daily temperature of a 6-day period is equal to the 25th percentile of temperature data. For summer and autumn, it is proposed that the 75th percentile of temperature data be considered (de la Franca et al. 2013) or that summer and winter be categorized as the hottest and coldest 90 days, respectively, in a long-term period (Yan et al. 2011). In the meteorological definition of the seasons, each season starts on the first day of a month that includes a solar equinox or solstice (Trenberth 1983).
The main aim of this study was to develop new indices that better address the timing and seasonal pattern of air temperature and identify possible changes. A framework based on the hottest and coldest 90 days of the year was used to explore variations in the timing of seasons, and 12 new timing indices and four temperature indices were developed. Based on these novel timing indices, a new seasonal configuration was developed to quantify timing changes in seasons without considering any set temperature threshold for seasons.
The framework and indices were tested using daily recorded temperature data (50 years, 1967–2016) from two meteorological stations, Ahvaz and Abadan, in southwestern Iran. A dataset of daily temperature for 11 other meteorological stations with at least 30 years of records (minimum 1987–2016) was then used to evaluate spatio-temporal variations in the indices in Khuzestan providence in southwestern Iran. Possible trends for each parameter were examined using parametric and non-parametric statistical tests (Mann-Kendall test, sequential Mann-Kendall test, linear regression trend, and Spearman rank correlation test). In addition, the magnitude of trends was measured using the Theil-Sen estimator and slope of linear regression methods.
2 Material and methods
2.1 Study area and dataset
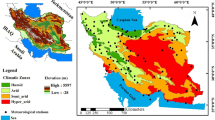
Khuzestan province in southwestern Iran (29° 57′–33° 0′ N; 47° 40′–50° 33′ E) comprises an area of 64,057 km2 (~ 4% of the total area of Iran). The geography of the province consists of plains in central and southern parts and mountainous regions in the north (Fig. 1). Land elevation ranges from 0 on the coast of the Persian Gulf to 3740 m above sea level (m a.s.l.) in the Zagros Mountains. The mountainous area has moderate weather in summer and cold weather in winter, while the central and southern plains have a warm climate. Around 20% of the total area of the province (approximately 1.3 million ha) is classified as arid, mostly in the south and southwest. During summer, daily temperatures in southwestern parts customarily exceed 45 °C. Ahvaz city, the capital of the province, is one of the hottest places in Iran, with the maximum daily temperature in the city having reached 54 °C during the past five decades.
In this study, new timing and thermal indices were developed based on 50 years (1967–2016) of daily temperature data taken from the meteorological stations in the cities of Ahvaz and Abadan (Fig. 1; Table 1). Spatial analysis of indices for Khuzestan province was based on 30-year temperature data from 11 selected meteorological stations, six of which are inside the province and the remaining five are in neighboring provinces (Fig. 1). All data were obtained through Islamic Republic of Iran Meteorological Organization (IRIMO 2017). Mean daily temperature was computed from the minimum and maximum records. Missing daily data (less than 5%) were replaced by a mean value for preceding and following days.
2.2 Timing indices
To develop the timing indices and evaluate possible seasonal thermal changes, we considered two major seasons, cold (winter) and hot (summer), defined based on the coldest and warmest 90 consecutive days, respectively. The reason for the choice of 90 days for summer and winter is that the length of the meteorological seasons is approximately 90 days. We also considered two transition seasons between the hot and cold seasons (autumn) and between the cold and hot (spring) seasons (Fig. 2). This schematic seasonal pattern was produced based on the mean daily temperature (1986–1987) at Ahvaz meteorological station (Fig. 2).
In order to determine the onset of each season and possible changes in thermal and seasonal timing, 90-day moving averages (blue curve in Fig. 2) were computed using the original daily temperature time series data (black curve in Fig. 2). In the 90-day (blue curve) moving average time series, each point represents an average of itself and 89 days ahead. Based on this curve, the coldest and warmest 90 days (minimum and maximum of the 90-day moving average) used for defining winter and summer, respectively, were selected for each year.
Based on this seasonal configuration, we developed 12 timing indices to quantify seasonal changes. These were as follows: Osum, Esum, Owin, Ewin, Lspr, Laut, Cspr, Csum, Caut, Cwin, Cwin-sum, and Cn.sum-win, as illustrated in Fig. 2.
Among these, Osum, Esum (Osum + 89), Owin, and Ewin (Owin + 89) represent the onset and end day of summer and winter, respectively. The number of days between summer and winter in each year determines the length of autumn (Laut):
Likewise, the length of spring (Lspr) is calculated as the number of days between winter and the next summer:
The thermal centroid for each season was used as another season timing parameter:
where xi is the ith day, Ai is the trapezoidal area under the temperature curve between two successive days, and n represents the number of days in each season. Based on Eq. (3), we defined centroid of summer (Csum), centroid of winter (Cwin), centroid of spring (Cspr), and centroid of autumn (Caut).
The rate of thermal change between cold (winter) and hot (summer) seasons was quantified as the slope of changing from hot to cold season (SHC) and cold to hot season (SCH):
where TOwin is the temperature of summer onset date, TEsum is the temperature of summer end date, TEwin is the temperature of winter end date, and TO(next)sum is the temperature of summer onset day in the next year.
2.3 Thermal indices
For air temperature, the mean temperature in each season was considered the thermal threshold: Tspr was defined as the average daily mean temperature between point Osum of the next year and point Ewin of the current year in two consecutive years (Fig. 2). Tsum was calculated the mean maximum 90-day moving average temperature in each year, Taut as the average daily mean temperature between points Esum and Owin in each year, and Twin as the mean minimum 90-day moving average temperature in each year. Thus, we set the mean temperature on the onset day of each season in any period as the threshold, because the seasons changed at these temperatures.
2.4 Trend analysis
We evaluated possible changes and shifts in the seasonal pattern of the new indices in the study region using several well-known parametric and non-parametric statistical tests.
2.4.1 MK and SQMK
The non-parametric Mann-Kendall (MK) test (Kendall 1975; Mann 1945) can be used to detect trends in datasets that are not distributed normally (Zhai and Feng 2009). Statistic Z in the MK test determines the significance of a trend. The null hypothesis of no trend is accepted if\( -{Z}_{1-\raisebox{1ex}{$\alpha $}\!\left/ \!\raisebox{-1ex}{$2$}\right.}\underset{\_}{<}Z\ \underset{\_}{<}\ {Z}_{1-\raisebox{1ex}{$\alpha $}\!\left/ \!\raisebox{-1ex}{$2$}\right.} \), where α is the significance level. In this study, confidence levels of 90% and 95% (α = 10% and 5%) were considered for detection of significant trends in the data. The magnitude of a trend in the time series is commonly predicted using Theil-Sen estimator (Sen 1968; Theil 1992). More details of the above methods can be found in Sayemuzzaman and Jha (2014).
The sequential Mann-Kendall (SQMK) test (Sneyers 1990) was used to specify the beginning of significant trends in the datasets. In this method, two indicators, called U(t) and U′(t), are defined based on the original time series and a retrograde series starting from the end of the original time series, respectively (Shrestha et al. 2019). Abrupt changes in the dataset are identified by plotting U(t) and U′(t), with the intersection of these two curves indicating a potential location for an abrupt change. The change becomes significant when U(t) exceeds the line associated with + 1.96 or − 1.96 for an upward or downward trend, respectively.
Before application of the MK and SQMK tests, the time series should be serially independent, since any positive serial correlation in the dataset may increase the chance of rejection of the null hypothesis of no trend (Yue and Hashino 2003). Several approaches have been introduced to remove possible serial correlation in the time series (Tabari et al. 2012; Von Storch 1999). In this study, we used the trend-free pre-whitening method (TFPW) (Yue et al. 2002).
2.4.2 LSLR
Least square linear regression (LSLR) is a parametric test used to identify the existence of linear trends in time series based on the least squares technique (Haan 1977). The significance of linear trends is examined using the Student’s t test. The statistic t is defined as follows:
where b is the estimated slope of the regression line between the variable and the time and Sb is the standard error of estimated slope. The null hypothesis of b = 0 (no trend) is rejected when \( \left|t\right|>\mathrm{t}\left(n-2,1-\raisebox{1ex}{$\alpha $}\!\left/ \!\raisebox{-1ex}{$2$}\right.\right) \) in the Student’s t distribution with n − 2 degrees of freedom, where n is the length of the time series.
2.5 Interpolation method
To determine the spatial distribution of each index over Khuzestan province, we used the ordinary Kriging estimator, which has been extensively employed in similar studies (Bhusal et al. 2018; Ozturk and Kilic 2016). We used ArcGIS 10.5 software to produce the zoning maps over the province.
3 Results
The results obtained are presented separately: (i) for the Ahvaz and Abadan stations with 50 years of daily temperature data (1967–2016) and (ii) for Khuzestan province, based on spatio-temporal analysis.
3.1 Timing and thermal indices for Ahvaz and Abadan stations
The time series for 10 of the 12 new timing indices were generated based on the 50-year recorded daily temperature from Ahvaz (Fig. 3) and Abadan (Fig. A1 in Appendix A). The trend for each index was also evaluated (Fig. 3 for Ahavaz; Fig. A1 for Abadan). Of note, the trends for Osum and Owin are identical to the trends for Esum and Ewin, respectively.
Time series of timing indices and their corresponding trends. a Length of spring (Lspr.) b Length of autumn (Laut.) c Centroid of summer (Csum.) d Centroid of winter (Cwin.) e Difference between centroid of winter and summer in a year (Cwin-sum.) f Difference between centroid of next summer and winter in two consecutive years (Cn.sum-win.) g Beginning day of summer (Osum.) h Beginning day of winter (Owin.) i Centroid of spring (Cspr.) j Centroid of autumn (Caut) (z = Mann-Kendall statistic, β = trend magnitude (Theil-Sen slope), t = Student’s t value, b = slope of linear regression)
3.1.1 Spring length (Lspr) and autumn length (Laut)
The analysis revealed that the length of spring (number of spring days, Lspr) increased significantly (95% confidence level) at both Ahvaz and Abadan stations in the period 1967–2016. According to the Theil-Sen estimator, spring lengthened by approximately 4 days/decade at Ahvaz and 2 days/decade at Abadan (Fig. 3a; Fig. A1a). Overall, the spring period lengthened by nearly 20 days at Ahvaz and 10 days at Abadan between 1967 and 2016. At Ahvaz, the average length of spring in the first decade of the study period (1967–1976) was 85.1 days, while in the last decade (2007–2016), it was 105.2 days.
Both Ahvaz and Abadan displayed significant downward trends of 3.7 and 2 days/decade, respectively, in the length of autumn (Laut) (Fig. 3b; Fig. A1b). As summer and winter were each assumed to be 90 days, we concluded that the warm seasons (spring and summer) are getting longer in the study area, while the cold seasons (autumn and winter) are getting shorter. In addition, the relative length of the four seasons changed. For example, at Ahvaz, autumn, winter, spring, and summer were 100, 90, 85, and 90 days long, respectively, in 1967–1976, but the values changed to 80, 90, 105, and 90 days in 2007–2016.
Based on the SQMK results, abrupt changes in Lspr and Laut occurred in 1999 and 2001 at Ahvaz (Fig. 4; Table 2). There was a trend for increasing Lspr during 2005–2016 (Fig. 4a). An abrupt negative trend for Laut was detected in 2001, but the trend only became significant in 2007. The critical points for the trends in Lspr and Laut approximately complied with each other. The SQMK results for Abadan station are summarized in Table 2.
3.1.2 Shift in centroid of seasons (Csum, Cwin, Cspr, Caut)
The centroid of summer (Csum) at Ahvaz and Abadan shifted forward by 10 and 5 days, respectively, while the centroid of winter (Cwin) at these stations moved backward by 7 and 5 days, respectively, during 1967–2016 (Fig. 3c, d; Fig. A1c, A1d). Thus, the hot season has been moving forward, while the period with the coldest days has been moving back, which means that the centroids of summer and winter are getting closer within years. This confirms findings in the previous section on shortening length of autumn. For Ahvaz, mean Csum occurred on July 20 (202th day of the year) in 1992–2016, whereas it occurred on July 14 (196th day) in the initial 25 years. It is worth mentioning that the positive and negative trends observed for Csum and Cwin were significant at Ahvaz and non-significant at Abadan. Significant positive trends (α = 5%) were observed for the spring centroid (Cspr), with a forward shift in Cspr at both Ahvaz and Abadan stations (Fig. 3i; Fig. A1i). At Ahvaz, the average Cspr value in early and late decades of the study period was May 6 and May 17, respectively, indicating that it had shifted by approximately 11 days. As regards the centroid of autumn (Caut), at Ahvaz, it changed from October 5 (279th day of the year) in 1967–1976 to October 9 (283th day) in 2007–2016 (Fig. 3j), which was a smaller shift than observed for Cspr. The results of the MK test also indicated a non-significant trend for Caut and a significant positive trend for Cspr in Ahvaz city (Fig. 3i, j).
The abrupt change point in Csum at Ahvaz occurred in 1983 and the positive trend exceeded the 95% confidence level in 1991 (Fig. 4d; Table 2). The centroid of winter (Cwin) did not show any clear trend until 1998, when a non-significant decreasing trend began and continued into recent years. For brevity, the SQMK results for Abadan are reported briefly in Table 2. Based on the U(t) curves (Fig. 4), Cspr experienced an abrupt change point in 2000 and the trend became significant (95% confidence level) in 2006. An obvious change point for Caut appeared in 1980 and an increasing trend with 95% confidence level began in 1990 and remained significant for about 20 years, becoming non-significant around 2010 (Fig. 4e).
3.1.3 Shift in Cwin-sum and Cn.sum-win
The differences between the centroids of winter and summer in every year (Cwin-sum) and between two successive years (Cn.sum-win) may be employed to examine the variations in the length of autumn and spring, respectively. Accordingly, Cwin-sum has experienced a significant decreasing trend, of 4 and 2 days/decade at Ahvaz and Abadan respectively (Fig. 3e; Appendix A, Fig. 1e), indicating that the centroids of summers and winters are becoming closer to one another. This may be interpreted as a declining tendency in the number of autumn days. In contrast, the centroids of summer and winter in two consecutive years are moving farther apart by approximately 2 and 1 days/decade at the Ahvaz and Abadan stations (Fig. 3f; Appendix A, Fig. 1f), indicating a rise in the number of spring days. The decreasing and increasing trend for Cwin-sum and Cn.sum-win at Ahvaz are apparent in Fig. 4 g and h, respectively.
3.1.4 Shift in the onset of summer (Osum) and winter (Owin)
The onset of summer (Osum) showed an advancing trend and Owin showed a retreating trend at both Ahvaz and Abadan (Fig. 3g, h; Fig. A1g, A1h). Based on the Theil-Sen estimator values, Osum shifted forward by around 2 days/decade and Owin shifted backward by about 1.5 days/decade at Ahvaz, while Osum shifted forward and Owin backward at a rate of 1 days/decade at Abadan. At Ahvaz, the average Osum date was May 25 in 1967–1976 and it moved to June 7 in 2007–2016. Mean Owin shifted backward from November 29 in 1967–1976 to November 23 in 2007–2016. The results of the SQMK test for Osum and Owin indicated that the point of abrupt change occurred in 1979 and 2008, respectively (Table 2). The trend in Osum became significant from 1991 at Ahvaz station. None of these indices passed the confidence level of 95% at Abadan (Table 2).
3.1.5 Thermal value and thresholds
The mean temperature in each season showed a significant positive trend at both stations (Fig. 5; Fig. A2 in Appendix A). Summer and spring experienced the greatest increasing trend in temperature, followed by winter, at both stations. According to the Theil-Sen estimator values, summer and spring became warmer by approximately 0.7 °C/decade at Ahvaz, where the average summer temperature rose significantly from 35.37 °C in 1967–1976 to 38.16 °C in 2007–2016. Mean winter temperature rose by about 0.4 and 0.5 °C/decade at Ahvaz and Abadan, respectively, while mean autumn temperature rose by 0.3 °C/decade in both cities. The Student’s t values confirmed the significant rising trend in temperature in all seasons (Fig. 5; Fig. A2), as also reported in recent literature (Ahmadi et al. 2018; Tabari et al. 2012). The abrupt change in mean daily temperature at Ahvaz occurred in 1994 for winter, 1990 for spring, 1986 for summer, and 2002 for autumn (Table 3).
Time series of thermal indices and their corresponding trends. a Mean daily temperatures of spring. b Mean daily temperatures of summer. c Mean daily temperatures of autumn. d Mean daily temperatures of winter. e Temperatures of summer onset. f Temperatures of winter onset. g Slope of change from hot to cold season SHC. h Slope of change from cold to hot season (SCH) (z = Mann-Kendall statistic, β = trend magnitude (Theil-Sen slope), t = Student’s t value, b = slope of linear regression)
The thermal threshold for the changing seasons increased significantly at both sites (Table 4). At Ahvaz, the maximum change in seasonal threshold was observed in spring (3.39 °C) and the minimum in autumn (1.61 °C), while at Abadan, the maximum change was observed in summer (2.68 °C) and the minimum in winter (1.54 °C). The maximum thresholds for all seasons occurred in the last decade (2007–2016) for both cities (Table 4). The minimum thresholds for both cities were observed in the first decade (1967–1976) for all seasons except autumn, for which the minimum thermal threshold was observed in the third (1987–1996) and second decade (1977–1986) in Ahvaz (26.53 °C) and Abadan (26.33 °C), respectively.
The temperatures of summer and winter onsets (TOsum and TOwin) have experienced significant upward trends at Ahvaz station (Fig. 5e, f), where the magnitude of thermal change for summer and winter onset was 0.08 °C/year and 0.06 °C/year, respectively. In addition, the average of TOsum in the first decade of study period was 34.05 °C, while it increased to 36.77 °C in the last decade. Considering winter onsets, the temperature average of winter onset rose from 14.45 °C in 1967–1976 to 16.66 °C in 2007–2016.
3.1.6 Shift in slope indices (SHC and SCH)
The rate of thermal change between the cold (winter) and hot (summer) seasons was quantified using the SHC and SCH indices. Interestingly, SHC displayed a strongly significant rising trend at both Ahvaz and Abadan. This indicates that not only has the denominator (Laut) in Eq. 4 followed a downward trend, but the numerator in Eq. 4 also has experienced an upward trend. The z value for SHC at Ahvaz and Abadan was 3.66 and 3.18, respectively, which was much higher than the value for the 95% confidence level, signifying highly significant differences. This indicates that the slope of temperature variations in autumn has increased in the past five decades. However, no spatial trend was observed for SCH at Ahvaz and Abadan stations. The explanation for this may be that both the numerator and denominator in Eq. 5 have experienced increasing trends, resulting in an ineffective trend for SCH. The results of the SQMK test for Ahvaz and Abadan and the magnitude of trends are summarized in Table 3. Ahvaz station experienced an abrupt change in SHC in 2000, and the change became significant in 2005.
3.2 Spatio-temporal variation in thermal and timing indices in Khuzestan province
Spatio-temporal changes in the timing indices were determined for the case of Khuzestan province (1987–2016). Based on the z values, seven of the 12 new timing indices, including Lspr, Laut, Osum, and Owin, showed a significant trend in central, southern, and southwestern parts of the province, while in the north and northeast, the trends in all indices were non-significant (Fig. 6). Overall, therefore, the mountainous area of the study region was less affected by changes in the seasons, while the trends intensified across the plains area from the mountains in the north and northeast to the coast of the Persian Gulf in the south.
In the south of the province, the length of spring (Lspr) increased by approximately 8–10 days/decade, while Laut became shorter by approximately 7–8 days/decade. Moving from south to north, the increase in Lspr and decrease in Laut declined to 2–4 days/decade (Fig. 7a, b). The centroid of summer (Csum) showed relatively non-significant upward and downward variations in almost all areas of the province (Fig. 6c). The maximum change in Csum occurred in the south, where it shifted forward by 2–3 days/decade (Fig. 7c). The centroid of winter (Cwin) moved at a rate of 3–5 day/decade in the majority of the province (Fig. 7d). Similar to Lspr, the maximum variation in Cspr occurred in the south of the province (Fig. 7i), where it moved forward by roughly 4–5 days/decade. Interestingly, the onset of winter (Owin) showed a significant trend in the whole province, shifting backward by between 3 and 5 days (Figs. 6h and 7h), which was the maximum change in southern and central zones. Onset of summer (Osum) showed non-significant negative and positive trends in northern and southern parts of the province, respectively (Fig. 6g).
Trend analysis revealed strongly increasing temperature trends in all seasons across the main parts of Khuzestan province (Fig. 8). The maximum temperature changes were generally in the south, west, and central areas. In spring, the maximum change in mean temperature occurred in the west of the province, where the temperature increased by about 0.8–1 °C/decade (Figs. 8a and 9a). There was a considerable increase in temperature in summer in all areas of the province; from east to west, the mean temperature rose by 0.15 to 1.4 °C/decade, signifying intensive temperature increases in the west (Figs. 8b and 9b). The rate of temperature increase in autumn varied from 0.4 to 0.9 °C/decade in the past three decades (Figs. 8c and 9c). In winter, almost all of the province showed a significant increasing trend in temperature, at a rate of 0.5 to 0.8 °C/decade (Figs. 8d and 9d). The change in SHC was most significant in the southwest and decreased along a transect from southwest to northeast (Fig. 8e). In contrast, the changes in SCH followed no special trend within Khuzestan province (Fig. 8f).
Spatial maps of trend magnitude (Theil-Sen slope estimator) for thermal indices in Khuzestan province in the period 1987–2016. a Spring temperature. b Summer temperature. c Winter temperature. d Autumn temperature. e Slope of change from hot to cold season (SHC). f Slope of change from cold to hot season (SCH)
Seven indices showed statistically significant trends in the plains area of the province: Lspr, Cspr, SHC, Laut,Cwin, Owin, and Cwin-sum. Significant increasing trends were observed for Lspr (5–9 day/decade), Cspr (3–5 days/decade), and SHC (days/decade) and significant decreasing trends for Laut (5–8 day/decade), Cwin (3–5 days/decade, Owin (3–4 days/decade), and Cwin-sum (6–8 days/decade).
Spatial analysis of 30-year mean ambient temperature in the seasons in Khuzestan showed that the central steppes and western plain areas had experienced the greatest changes (about 1 °C per decade).
4 Discussion
Increases in global average temperatures have been well-documented in the literature, but other characteristics of temperature, like regional and seasonal variability or timing, have been less well studied (Allen and Sheridan 2016; Rogers 2013; Trenberth 1983). Among the different thermal characteristics of climate change, timing is an important issue for many bio-climatological processes, as, e.g., earlier onset of spring/summer or delayed onset of autumn and shortening of winter can have impacts on flowering dates (Sperling et al. 2019; Woznicki et al. 2019), migratory species (Fraser et al. 2019; Helm et al. 2019; Schmaljohann 2019), and human adaptation to extreme temperature environments.
In this work, we developed a new configuration of the seasons in order to quantify changes in timing in thermal climate characteristics. We defined the seasons mainly based on the temperature (Dong et al. 2010) but used temperature data to define a new seasonal pattern. Seasonal characteristics vary from year to year or place to place. Of the four traditional seasons, there is a coldest season and a warmest season, which are called winter and summer in all climates. We used these two seasons as a benchmark for assessing changes in the timing of thermal characteristics. In our approach, in any region with any climate, the two sets of 90 consecutive days in a calendar year (representing two sets of 3 months) with the highest and lowest mean temperature are defined as summer and winter, respectively. Based on this new configuration of seasons, we defined the onset day of winter and summer for each year and assessed possible changes in the start date of each season. Based on this benchmark system, we developed two new variables for evaluating the timing characteristics of temperature in the transitions from hot to cold season (autumn) and cold to hot season (winter). To our knowledge, no previous study has considered the length of autumn and spring as a variable when assessing climate change. These transition seasons are not necessarily 3 months each, and clear criteria have to be applied to assess the length and onset day for autumn and spring, as shown here for the case study of Khuzestan province.
Threshold values for different seasons and bio-climatological processes have been widely used for exploring changes in seasons or for irrigation scheduling. For example, Klein Tank and Können (2003) used a threshold of 25 °C for summer in Europe (Klein Tank and Können 2003). In Britain, a temperature threshold of 14 °C for summer days has been considered (Kirbyshire and Bigg 2010). Zhang (1934) proposed 10 °C and 22 °C as the threshold values for winter and summer in China (Zhang 1934). Many pre-defined temperature thresholds are roughly used in the literature to calculate indices proposed by the ETCCDI team (Panda et al. 2014; Tong et al. 2019; Wang et al. 2017). As indicated above, a range of values have been defined as thresholds for summer and winter, since the onset of seasons depends on the geographical location of a region. Therefore, it is not reasonable to use a fixed threshold for determining the onset of seasons when studying the timing of seasons on larger scales. In this study, we developed a dynamic approach for defining the thermal threshold for changes in season. We recommend our seasonal configuration approach to defining the temperature threshold for different seasons as mean temperature for each season, as it was able to reveal annual or periodic changes in the case study area.
In this study, we also developed a timing index called centroid of season that can be defined for each season or any specific period. This index is based on the concept of centroid in geometry and on data on the daily temperature in each season or over the year. The centroid is a unique date or day of the year for each season in each year and can be used as a supplementary index when assessing timing changes in the thermal characteristics of climate.
5 Conclusions
We present 12 new indices for quantifying timing characteristics of air temperature, in order to gain a better understanding of the seasonal configuration. These indices deal with onset day, centroid day, and length of different seasons, and we applied them in a framework to study variations in the timing of seasons. Based on 50 years of temperature data recorded at Ahvaz city in southern Iran, 10 out of the 12 indices revealed significant trends (95% confidence level). It was found that spring (autumn) increased (decreased) by approximately 4 days/decade in the study period and that the thermal centroid of spring, summer, and autumn had shifted forward by 2, 2.2, and 0.8 days/decade, respectively, while the thermal centroid of winter had moved backward by 1.4 days/decades. The onset of the hottest 90-day period (summer) had advanced at a rate of 2 days/decade, whereas the onset of the coldest 90-day period (winter) had been delayed by 1.5 days/decade. Comparison of the difference between centroid of summers and centroid of winters revealed a significant decrease (4 days/decade). Using 30 years of temperature data, a zoning map was developed for the case of Khuzestan province in southwest Iran. This showed that south, southwest, and central areas of the province (plain region with low elevation) had generally experienced significant changes in the timing indices, while mountainous regions, mostly located in the northeast, had experienced non-significant changes.
Abbreviations
- O sum :
-
Beginning day of summer
- E sum :
-
End day of summer
- O win :
-
Beginning day of winter
- E win :
-
End day of winter
- L spr :
-
Number of spring days (length of spring)
- L aut :
-
Number of autumn days (length of autumn)
- C spr :
-
Centroid of spring
- C sum :
-
Centroid of summer
- C aut :
-
Centroid of autumn
- C win :
-
Centroid of winter
- C win-sum :
-
Difference between centroid of winter and summer in a year
- C n.sum-win :
-
Difference between centroid of next summer and winter in two consecutive years
- SHC:
-
Slope of change from hot season to cold season
- SCH:
-
Slope of change from cold season to hot season
- T aut :
-
Mean daily temperature between points Esum and Owin in a year
- T spr :
-
Mean daily mean temperature between point Osum of next year and point Ewin of current year in two consecutive years
- T sum :
-
Mean maximum 90-day moving average temperature
- T win :
-
Mean minimum 90-day moving average temperature
References
AghaKouchak A, Cheng L, Mazdiyasni O, Farahmand A (2014) Global warming and changes in risk of concurrent climate extremes: insights from the 2014 California drought. Geophys Res Lett 41:8847–8852
Ahmadi F, Nazeri Tahroudi M, Mirabbasi R, Khalili K, Jhajharia D (2018) Spatiotemporal trend and abrupt change analysis of temperature in Iran. Meteorol Appl 25:314–321
Alexander LV, Zhang X, Peterson TC, Caesar J, Gleason B, Tank AMGK, Haylock M, Collins D, Trewin B, Rahimzadeh F, Tagipour A, Kumar KR, Revadekar J, Griffiths G, Vincent L, Stephenson DB, Burn J, Aguilar E, Brunet M, Taylor M, New M, Zhai P, Rusticucci M, Vazquez-Aguirre JL (2006) Global observed changes in daily climate extremes of temperature and precipitation. J Geophys Res 111(D5) https://doi.org/10.1029/2005JD006290
Allen MJ, Sheridan SC (2016) Evaluating changes in season length, onset, and end dates across the United States (1948–2012). Int J Climatol 36:1268–1277
Allen CD et al (2010) A global overview of drought and heat-induced tree mortality reveals emerging climate change risks for forests. For Ecol Manag 259:660–684
Bhusal B, Lamichhane S, Shrestha R (2018) Mapping the soil fertility of Bisankhel catchment of Chitlang VDC and comparison of different geo-spatial interpolation techniques. J Inst Agric Anim Sci 35:95–104
Christensen NS, Wood AW, Voisin N, Lettenmaier DP, Palmer RN (2004) The effects of climate change on the hydrology and water resources of the Colorado River Basin. Clim Chang 62:337–363
Collazo S, Barrucand M, Rusticucci M (2019) Summer seasonal predictability of warm days in Argentina: statistical model approach. Theor Appl Climatol 138(3-4):1853–1876
de la Franca NL, Sánchez E, Domínguez M (2013) Changes in the onset and length of seasons from an ensemble of regional climate models over Spain for future climate conditions. Theor Appl Climatol 114:635–642
Dimri A (2019) Comparison of regional and seasonal changes and trends in daily surface temperature extremes over India and its subregions. Theor Appl Climatol 136:265–286
Dong W, Jiang Y, Yang S (2010) Response of the starting dates and the lengths of seasons in Mainland China to global warming. Clim Chang 99:81–91
Erlat E, Türkeş M (2012) Analysis of observed variability and trends in numbers of frost days in Turkey for the period 1950–2010. Int J Climatol 32:1889–1898
Fallah-Ghalhari G, Shakeri F, Dadashi-Roudbari A (2019) Impacts of climate changes on the maximum and minimum temperature in Iran. Theor Appl Climatol 138(3-4):1539–1562
Fraser KC, Shave AC, de Greef E, Siegrist J, Garroway CJ (2019) Individual variability in migration timing can explain long-term, population-level advances in a songbird. Front Ecol Evol 7:324
Frich P, Alexander LV, Della-Marta P, Gleason B, Haylock M, Tank AK, Peterson T (2002) Observed coherent changes in climatic extremes during the second half of the twentieth century. Clim Res 19:193–212
Garonna I, de Jong R, Schaepman ME (2016) Variability and evolution of global land surface phenology over the past three decades (1982–2012). Glob Chang Biol 22:1456–1468
Haan CT (1977) Statistical methods in hydrology. Iowa State University Press, Urbana-Champaign
Haddeland I et al (2014) Global water resources affected by human interventions and climate change. Proc Natl Acad Sci 111:3251–3256
Hartmann DL et al. (2013) Observations: atmosphere and surface. In: Climate change 2013: the physical science basis: Working group I contribution to the fifth assessment report of the intergovernmental panel on climate change. Cambridge University Press, pp 159-254
Helm B, Van Doren BM, Hoffmann D, Hoffmann U (2019) Evolutionary response to climate change in migratory pied flycatchers. Curr Biol 29:3714–3719. e3714
Hirabayashi Y et al (2013) Global flood risk under climate change. Nat Clim Chang 3:816
Jylhä K, Fronzek S, Tuomenvirta H, Carter TR, Ruosteenoja K (2008) Changes in frost, snow and Baltic Sea ice by the end of the twenty-first century based on climate model projections for Europe. Clim Chang 86:441–462
Kendall M (1975) Rank correlation methods, vol 8, 4th edn. Charles Griffin, San Francisco
Kiktev D, Sexton DM, Alexander L, Folland CK (2003) Comparison of modeled and observed trends in indices of daily climate extremes. J Clim 16:3560–3571
Kirbyshire A, Bigg GR (2010) Is the onset of the English summer advancing? Clim Chang 100:419–431
Klein Tank A, Können G (2003) Trends in indices of daily temperature and precipitation extremes in Europe, 1946–99. J Clim 16:3665–3680
Knox JC (1993) Large increases in flood magnitude in response to modest changes in climate. Nature 361:430
Kundzewicz ZW et al (2014) Flood risk and climate change: global and regional perspectives. Hydrol Sci J 59:1–28
Liu B, Henderson M, Xu M (2008) Spatiotemporal change in China's frost days and frost-free season, 1955–2000. J Geophys Res 113(D12) https://doi.org/10.1029/2007JD009259
Mann HB (1945) Nonparametric tests against trend. Econometrica: Journal of the Econometric Society 13:245–259
Mazaris AD, Kallimanis AS, Pantis JD, Hays GC (2013) Phenological response of sea turtles to environmental variation across a species’ northern range. Proc R Soc B Biol Sci 280:20122397
McMichael AJ, Woodruff RE, Hales S (2006) Climate change and human health: present and future risks. Lancet 367:859–869
Moberg A, Jones PD (2005) Trends in indices for extremes in daily temperature and precipitation in central and western Europe, 1901–99. Int J Climatol 25:1149–1171
Ozturk D, Kilic F (2016) Geostatistical approach for spatial interpolation of meteorological data. An Acad Bras Cienc 88:2121–2136
Panda DK, Mishra A, Kumar A, Mandal K, Thakur A, Srivastava R (2014) Spatiotemporal patterns in the mean and extreme temperature indices of India, 1971–2005. Int J Climatol 34:3585–3603
Park B-J, Kim Y-H, Min S-K, Lim E-P (2018) Anthropogenic and natural contributions to the lengthening of the summer season in the Northern Hemisphere. J Clim 31(17):6803–6819
Patz JA, Campbell-Lendrum D, Holloway T, Foley JA (2005) Impact of regional climate change on human health. Nature 438:310
Peña-Lévano LM, Taheripour F, Tyner WE (2019) Climate change interactions with agriculture, forestry sequestration, and food security. Environ Resour Econ 74:653–675
Peña-Ortiz C, Barriopedro D, García-Herrera R (2015) Multidecadal variability of the summer length in Europe. J Clim 28:5375–5388
Piao S et al (2010) The impacts of climate change on water resources and agriculture in China. Nature 467:43
Prospero JM, Lamb PJ (2003) African droughts and dust transport to the Caribbean: Climate change implications. Science 302:1024–1027
Qian W, Lin X (2004) Regional trends in recent temperature indices in China. Clim Res 27:119–134
Richardson M, Cowtan K, Millar RJ (2018) Global temperature definition affects achievement of long-term climate goals. Environ Res Lett 13:054004
Rogers JC (2013) The 20th century cooling trend over the southeastern United States. Clim Dyn 40:341–352
Sayemuzzaman M, Jha MK (2014) Seasonal and annual precipitation time series trend analysis in North Carolina, United States. Atmos Res 137:183–194
Schmaljohann H (2019) The start of migration correlates with arrival timing, and the total speed of migration increases with migration distance in migratory songbirds: a cross-continental analysis. Mov Ecol 7:25
Scorzini AR, Di Bacco M, Leopardi M (2018) Recent trends in daily temperature extremes over the central Adriatic region of Italy in a Mediterranean climatic context. Int J Climatol 38:e741–e757
Sen PK (1968) Estimates of the regression coefficient based on Kendall’s tau. J Am Stat Assoc 63:1379–1389
Shrestha S, Yao T, Adhikari TR (2019) Analysis of rainfall trends of two complex mountain river basins on the southern slopes of the Central Himalayas. Atmos Res 215:99–115
Sneyers R (1990) On the statistical analysis of series of observations, vol 415. WMO World Meteorological Organization, Geneve, p 192
Song Y, Linderholm HW, Chen D, Walther A (2009) Trends of the thermal growing season in China, 1951-2007. Int J Climatol. 30(1):33-43
Sparks T, Braslavská O (2001) The effects of temperature, altitude and latitude on the arrival and departure dates of the swallow Hirundo rustica in the Slovak Republic. Int J Biometeorol 45:212–216
Sperling O et al (2019) Predicting bloom dates by temperature mediated kinetics of carbohydrate metabolism in deciduous trees. Agric For Meteorol 276:107643
Tabari H, Talaee PH, Ezani A, Some’e BS (2012) Shift changes and monotonic trends in autocorrelated temperature series over Iran. Theor Appl Climatol 109:95–108
Theil H (1992) A rank-invariant method of linear and polynomial regression analysis. In: Raj B, Koerts J (eds) Henri Theil’s contributions to economics and econometrics: econometric theory and methodology, Dordrecht, Springer Netherlands, p 345–381. https://doi.org/10.1007/978-94-011-2546-8_20
Tol RS (2009) The economic effects of climate change. J Econ Perspect 23:29–51
Tong S, Li X, Zhang J, Bao Y, Bao Y, Na L, Si A (2019) Spatial and temporal variability in extreme temperature and precipitation events in Inner Mongolia (China) during 1960–2017. Sci Total Environ 649:75–89
Trenberth KE (1983) What are the seasons? Bull Am Meteorol Soc 64:1276–1282
Vincent LA et al (2005) Observed trends in indices of daily temperature extremes in South America 1960–2000. J Clim 18:5011–5023
Vincent L, Zhang X, Mekis É, Wan H, Bush E (2018) Changes in Canada’s climate: trends in indices based on daily temperature and precipitation data. Atmosphere-Ocean 56:332–349
Von Storch H (1999) Misuses of statistical analysis in climate research. In: Analysis of climate variability. Springer, Berlin p 11–26
Vörösmarty CJ, Green P, Salisbury J, Lammers RB (2000) Global water resources: vulnerability from climate change and population growth. Science 289:284–288
Wang B et al (2013) Changes in extreme events of temperature and precipitation over Xinjiang, Northwest China, during 1960–2009. Quat Int 298:141–151
Wang H, Pan Y, Chen Y, Ye Z (2017) Linear trend and abrupt changes of climate indices in the arid region of northwestern China. Atmos Res 196:108–118
Watts N, Adger WN, Agnolucci P, Blackstock J, Byass P, Cai W, Chaytor S, Colbourn T, Collins M, Cooper A, Cox PM, Depledge J, Drummond P, Ekins P, Galaz V, Grace D, Graham H, Grubb M, Haines A, Hamilton I, Hunter A, Jiang X, Li M, Kelman I, Liang L, Lott M, Lowe R, Luo Y, Mace G, Maslin M, Nilsson M, Oreszczyn T, Pye S, Quinn T, Svensdotter M, Venevsky S, Warner K, Xu B, Yang J, Yin Y, Yu C, Zhang Q, Gong P, Montgomery H, Costello A (2015) Health and climate change: policy responses to protect public health. Lancet 386:1861–1914
Woznicki TL, Heide OM, Sønsteby A, Måge F, Remberg SF (2019) Climate warming enhances flower formation, earliness of blooming and fruit size in plum (Prunus domestica L.) in the cool Nordic environment. Sci Hortic 257:108750
Yan Z, Xia J, Qian C, Zhou W (2011) Changes in seasonal cycle and extremes in China during the period 1960–2008. Adv Atmos Sci 28:269–283
Yang X, Tian Z, Chen B (2013) Thermal growing season trends in east China, with emphasis on urbanization effects. Int J Climatol 33(10):2402–2412
Yin Q, Wang J, Ren Z, Li J, Guo Y (2019) Mapping the increased minimum mortality temperatures in the context of global climate change. Nat Commun 10:1–8
Yue S, Hashino M (2003) temperature trends in Japan: 1900–1996. Theor Appl Climatol 75:15–27
Yue S, Pilon P, Phinney B, Cavadias G (2002) The influence of autocorrelation on the ability to detect trend in hydrological series. Hydrol Process 16:1807–1829
Zhai L, Feng Q (2009) Spatial and temporal pattern of precipitation and drought in Gansu Province, Northwest China. Nat Hazards 49:1
Zhang B (1934) The duration of four seasons in China. Acta Geograph Sin 1:29–74
Zhou Y, Ren G (2011) Change in extreme temperature event frequency over mainland China, 1961–2008. Clim Res 50:125–139
Zhu L, Ives AR, Zhang C, Guo Y, Radeloff VC (2019) Climate change causes functionally colder winters for snow cover-dependent organisms. Nat Clim Change 9(11):886–893
Acknowledgments
The authors would like to thank the Islamic Republic of Iran Meteorological Organization (IRIMO) for permission to use the daily data.
Funding
Open access funding provided by University of Oulu including Oulu University Hospital. This study was supported by Maa- ja vesitekniikan tuki Foundation (Grant No. 13-8186-16).
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher’s note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Electronic supplementary material
ESM 1
(DOCX 155 kb)
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Hekmatzadeh, A.A., Kaboli, S. & Torabi Haghighi, A. New indices for assessing changes in seasons and in timing characteristics of air temperature. Theor Appl Climatol 140, 1247–1261 (2020). https://doi.org/10.1007/s00704-020-03156-w
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00704-020-03156-w