1 Introduction

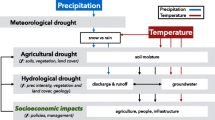
The quantification and understanding of drought characteristics is necessary for water management and planning, especially in a region like Central America where droughts occur frequently and lead to large economic and social problems. Drought-induced problems include rationing of drinking water, disruption of irrigation, negative consequences for freshwater fisheries and tourism, and energy rationing as a result of loss of hydropower (Brenes 2010). Agriculture, drinking water, and hydropower are very important for the socio-economic development and food security in the region, but they are highly vulnerable to droughts (GWP 2016). Negative effects on agriculture include disruption of the production at small and large scales, which affects food security and in turn triggers other detrimental effects for the whole society (Brenes 2010). Reduced water level in dams used for hydropower production forces countries to ration energy and to use more expensive alternative energy sources, usually based on fossil fuels. Reduced water levels in surface and subsurface water bodies increase the costs of water extraction and mean that alternative—usually more expensive—ways of providing drinking water are needed, which in turn may increase the costs of water treatment. All these negative effects, however, do not occur simultaneously. Deficits in soil moisture and, thus, effects on agriculture, are usually not observed until after a period of sustained precipitation deficits (meteorological drought), and it may take an even longer period for deficits to occur in surface and subsurface water bodies (hydrological drought). Different drought indices—or alternatively, different accumulation times of meteorological drought indices—are available to capture different types of droughts. Typically, short accumulation times are used to estimate meteorological drought (e.g. 1, 3 months), medium accumulation times are used for agricultural drought (e.g. 3, 6 months) and long for hydrological drought (e.g. 6, 12 months).

Droughts affect large parts of Central America simultaneously, and for this reason, it is important to study drought at the regional scale and identify areas with high drought risk. Knowledge of such spatiotemporal drought characteristics is necessary to support water management and planning. Peer-reviewed studies that assess the spatiotemporal characteristics of drought in Central America are scarce, though there are a few available at a local scale. Patterson (1992), for example, found that May, July and August were the months with the highest drought risk in the north-western part of Costa Rica.

The reliability of drought characterisation depends on the quality and quantity of the data used. In Central America, meteorological and hydrological observational data availability is limited at the regional scale (Portig 1965; Aguilar et al. 2005; Westerberg et al. 2014), though the situation is more serious for hydrological than for meteorological data. For this reason, a regional drought characterisation of soil moisture and/or hydrological drought in Central America cannot be done with indices requiring soil moisture or streamflow data, but it can instead be based on meteorological drought indices accumulated at different time scales. However, local studies have shown that precipitation data are often affected by substantial quality problems (Westerberg et al. 2010), and these need to be taken into account in hydro-meteorological analyses. To the authors’ best knowledge, no study has previously evaluated different meteorological datasets in terms of their suitability for drought applications in Central America, though such studies are available for other parts of the world, e.g. Iran Raziei et al. 2011) and Africa (Sylla et al. 2012). There are, however, studies that review meteorological datasets in Central America in terms of their use for climate variability studies. One example is the study by Hannah et al. (2017), who compared five historical precipitation datasets in terms of their trends and concluded that care should be taken when using only one precipitation dataset in climate variability studies in the region.

Apart from data quality, the robustness of drought characterisation depends on the choice of a suitable drought index. An important step in drought characterisation is therefore to evaluate the applicability of different drought indices in any given region. Drought is a complex phenomenon, and to find appropriate ways of evaluating a drought index using independent data is a challenging task. Several evaluations of commonly used drought indices are available in the literature, but these are often based on rather subjective set of criteria developed by experts. Keyantash and Dracup (2002) evaluated and ranked 14 drought indices in two areas of the United States (US) according to an evaluation criterion measuring aspects, such as robustness to different physical conditions and simplicity of calculation. They found that deciles and standardised precipitation index (SPI), in that order, ranked best amongst the evaluated indices. Morid et al. (2006) compared the performances of six drought indices in Iran in terms of how these captured a specific drought-spell event in 1998–2001 and found that the effective drought index (EDI) and SPI scored highest. The DI performed well, but varied very abruptly, both in space and time, between extremely wet and extremely dry conditions. Recently, more experts stress the importance of incorporating water demand in the calculation of drought indices, since this is an important factor when quantifying drought severity. For example, even though many of these studies show many advantages of the SPI compared to other indices, recent studies emphasize the importance of considering the role of temperature through evapotranspiration (i.e. potential evapotranspiration, PET) for the estimation of water deficit (Tsakiris et al. 2007; Vicente-Serrano et al. 2010). This is especially important for applications for agriculture and climate warming (Tabrizi et al. 2010; Cook et al. 2014; Asadi Zarch et al. 2014). In this study, we included the standardised precipitation and evapotranspiration index (SPEI, Vicente-Serrano et al. 2010) to compare with other indices and thereby assess the importance of temperature for drought estimation.

Considering (a) the large number of drought indices available, (b) that their suitability changes with the region of application (Mishra and Singh 2010) and (c) the key importance of droughts for water planning and management in Central America, there is a need to investigate the performance of different drought indices in the region. The aim of this study was therefore to investigate which combinations of databases and drought indices are best suited for characterising—and potentially for monitoring—droughts in Central America.

A description of the study area can be found in Section 2. Section 3 introduces the different meteorological datasets we evaluated and the hydrological data used to evaluate the different combinations of dataset and drought index. A description of the different drought indices and the analysis to assess the meteorological datasets and the drought indices is presented in Section 4. Results are presented in Section 5, discussion in Section 6 and conclusions in Section 7.

2 Study area

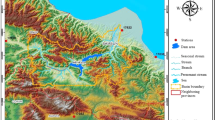
The Central-American region is the relatively narrow and mountainous strip of land that connects North and South America, located between the Caribbean Sea to the east and the Pacific Ocean to the west (Fig. 1). The interaction of the region’s high mountain range with the predominant atmospheric flow patterns plays a central role in shaping the spatial and temporal precipitation distribution. This results in two general precipitation regimes, one on the Caribbean slope and the other on the Pacific slope (Magaña et al. 1999; Rivera and Amador 2008; Amador et al. 2010). The Pacific regime is characterised by a bimodal precipitation distribution, with peaks in June and September–October and a secondary minimum during July–August (clearly visible in Fig. 2, points 10, 17 and 3). The secondary minimum is known as the mid-summer drought (MSD) or locally as “veranillo” or “canícula” and has been found to be associated with a strengthening of the trade winds during these months (Magaña et al. 1999). The dry season on the Pacific side occurs, in general, during the months of November to April, whereas there is no consistently defined dry season on the Caribbean side (Alfaro et al. 1998) (Fig. 2, point 12). Runoff is not delayed by snow storage anywhere in the region.

Fig. 1
figure 1

The Central-American region and the locations of the study points, the CIGEFI-UCR precipitation stations (1965–1990) and the GRDC hydrological stations used in this study

Full size image
Fig. 2
figure 2

Median monthly precipitation for each of the 12 months for five of the study points, for the two study periods, 1965–1985 (left column) and 1981–1990 (right column)

Full size image

Droughts in Central America are often related to inter-annual anomalies in the temporal distribution of precipitation (FAO 2012)—i.e. to an early starting date, or late ending date of the dry season or to changes in the timing of the MSD.

3 Data

The Central-American hydro-meteorological monitoring network is, in general sparser, on the less populated Caribbean Coast. The station-network density has varied significantly over time with a substantial increase around 1971 as a result of the International Hydrological Decade initiative and with a major decline at the beginning of the 2000s. We assessed four large-scale gridded meteorological datasets to calculate the indices. The quality of the different datasets was assessed against station data in 24 study points that were selected to cover the two major climatic regimes (Fig. 1). Study points 8, 12, 20, 19 and 24 in Fig. 1 have a Caribbean type of precipitation regime, while the rest of the study points have a Pacific type of regime. We evaluated the meteorological drought indices using a streamflow-based drought index at seven study points, where discharge data were available. Data are described below. Table 1 summarises the spatial and temporal characteristics of the meteorological datasets used, and Table 2 summarises the metadata for the streamflow stations.

Table 1 Spatial and temporal characteristics of the meteorological datasets
Full size table
Table 2 GRDC discharge stations used in this study and catchment areas from Westerberg et al. (2014)
Full size table

3.1 Meteorological datasets

3.1.1 CRN073

The CRN073 precipitation dataset was produced by the Centro de Ciencias de la Atmósfera de la Universidad Autónoma de México (Magaña et al. 1999, 2003). The dataset covers both the continental and the oceanic regions and was made for Central America and southern Mexico using rain gauge data for the land areas and satellite rainfall estimates over the oceans. Station data were obtained from the National Center for Atmospheric Research (NCAR) and from the Mexican and Central-American weather services. Satellite data correspond to estimates from the microwave sounding unit (Spencer 1993). Data were available for the period 1958–2000, but after evaluating the homogeneity of the dataset, it was decided that 1958–1985 was the most suitable period.

3.1.2 CIGEFI-UCR (stations)

The CIGEFI-UCR dataset consists of 154 daily rain-gauge stations with data covering the period 1958–2009. We used 1965–1990, which covered the period with the most complete data series. Completeness was defined as the maximum number of stations with ≤ 15% missing data for the whole period (while making sure that there were no large consecutive gaps). A simple quality control was applied to eliminate outliers in the data, and the resulting dataset was visually inspected. No homogenisation was applied.

3.1.3 CHIRPS

The Climate Hazards Group Infra-Red Precipitation with Station data version 2.0 (CHIRPS, Funk et al. 2014) was produced using ground-based observations, satellite observations and global climatologies. The dataset was originally developed for drought monitoring around the globe, and it is available to the near present. Its advantage with respect to the other datasets is its relatively high spatial resolution.

3.1.4 CRU

This dataset was produced by the Climatic Research Unit at the University of East Anglia. We used the precipitation and temperature data products of CRU TS3.21 (Jones and Harris 2013). The data were developed by interpolating station data to a 0.5° latitude × 0.5° longitude grid and consequently correcting the interpolated product using existing local climatology.

3.1.5 ERA-Interim

ERA-Interim (ERAI) is a global atmospheric reanalysis produced by the European Centre for Medium Range Weather Forecasts (ECMWF). ERAI covers the period from 1 January 1979 onwards and is extended forward in near real-time (www.ecmwf.int; Dee et al. 2011). ERAI is bias-corrected using data from the Global Precipitation Climatology Project (GPCP) v2.1 product (Huffman et al. 2009). We used ERAI data until 2009 since GPCP v2.1 is not available beyond 31 December of that year.

3.2 Discharge data

We used discharge data from the Global Runoff Database from the Global Runoff Data Centre (GRDC 2013), which contains 91 Central-American stations with daily and/or monthly discharge. Discharge simulations produced with the four-parameter hydrological model WASMOD (Xu 2002), driven by CRN073 data, by Westerberg et al. (2014), were used to fill gaps in the GRDC data. These gaps were few and short (see Table 2), for which we still consider the filled hydrological data to be independent from CRN073. We used seven hydrological stations (Fig. 1 and Table 2) that were selected based on their locations at non-regulated streams, their relative proximity to the meteorological stations used in this study, and that simulated data from the study of Westerberg et al. (2014) were available to fill data gaps. The discharge stations cover different time periods depending on the available data; only gaps shorter than a month were allowed so that potential uncertainties in the simulated data used for gap filling had a small effect on the index calculation (Table 2).

4 Methods

4.1 Assessment of the meteorological datasets

The ability of all the datasets to represent key features of the regional rainfall regime was first assessed by analysing how these captured the intra-annual precipitation distribution. This analysis was done at the 24 study points where we assessed the local representativeness of the large-scale datasets in comparison to station data. Differences between the datasets were assessed to see how the selection of a particular dataset could affect the drought characterisation. Since the data were available for different periods for the different datasets, we used the two periods 1965–1985 and 1981–1990, to optimise the comparison. First, visual comparisons of the median monthly intra-annual regime and the cumulative distributions were made. Then, the Spearman’s rank correlation of the monthly and annual precipitation was calculated between all dataset combinations (using the difference between the monthly values and the long-term mean monthly values to remove the effect of the annual cycle).

4.2 Drought index calculations

We used four meteorological drought indices: a variation of the deciles index (DI), SPI, SPEI and EDI. All these indices were calculated at 1-, 3-, 6-, 9- and 12-month accumulation times, to capture different drought types, i.e. meteorological, agricultural and hydrological drought. The standardised streamflow index (SSI) calculated at one-month accumulation time was used to define hydrological drought events and to evaluate the meteorological drought indices.

To calculate the indices at the n-month (n = 1, 3, 6, 9, 12) accumulation time scale, the monthly precipitation series was aggregated with an n-month moving sum, i.e. the current monthly value and the previous n − 1 monthly values. For example, at a 3-month accumulation time, data for January–February–March was used to calculate an index for the month of March. Note that it is not possible to have values for the first two months of the series, so these values are therefore not included in the calculation of the indices. In general, for accumulation times larger than one, the first n – 1 months of data in the time series are excluded since complete accumulations are not available. Accumulation times longer than 12 months were not included since reliable calculation of the indices at such time scales would require longer time series than what was available here.

4.2.1 Modified deciles index

With the deciles index (DI) (Gibbs and Maher 1967), precipitation data for each calendar month (or n-month accumulation) are ranked from lowest to highest and grouped into ten groups or deciles. The first decile contains the data that are equal or fall below the 90th exceedance percentile, the second contains data between the 90th and 80th exceedance percentiles and the third decile data between the 80th and 70th exceedance percentiles. The first, second and third deciles are used to define extreme, severe and moderate drought events, respectively. This definition can have limitations at dry locations because it can occur that more than one of the exceedance percentile values are equal to zero. We therefore included a modification and redefined the thresholds to 90th, 70th and 60th exceedance percentiles, for those cases in which the 90th was equal to the 80th exceedance percentile (and both equal to zero), and to 90th, 40th and 35th exceedance percentiles for the cases in which the 90th = 70th = 60th exceedance percentiles (i.e. with values of 0). Similar variations of the threshold values have been used in other areas with high seasonality (e.g. Fleig et al. 2006; van Huijgevoort 2012). To be able to compare the DI with the other indices, we flagged the values defined as extreme drought with a value of − 3, severe drought as − 2 and moderate drought as − 1. A similar categorisation was used by Morid et al. (2006) in a study where different drought indices were compared.

4.2.2 Standardised precipitation index

The standardised precipitation index (SPI) is calculated by first fitting precipitation data for each calendar month (or n-month accumulation) to a theoretical distribution (Mckee et al. 1993), in our study, to a gamma distribution. Since the gamma distribution is undefined for zero, only precipitation values different to zero were included in the distribution fitting. For values equal to zero, we followed the recommendation given by Stagge et al. (2015) for a n-month accumulation as

$$ \overline{p_0}=\raisebox{1ex}{${n}_{p=0}+1$}\!\left/ \!\raisebox{-1ex}{$\left(2n+1\right)$}\right. $$
(1)

where \( \overline{p_0} \) is the probability of a value equal to zero, np = 0 is the number of zeroes in the precipitation time series and n is the total number of precipitation values in the time series. The formula adjusts the probability of non-exceedance events to assure that the mean SPI is zero, thus retaining better the statistical properties of the distribution. A large number of zero precipitation events would have the effect of lowering the lowest possible SPI value so that it reaches 0 for areas without precipitation.

Finally, the probabilities are transformed to the standard normal distribution through the respective inverse cumulative distribution functions. We used the categorisation from Agnew (2000), where SPI values ≤ − 0.84 and > − 1.28 fall in the moderate drought category, SPI ≤ − 1.28 and > − 1.65 are considered to be severe drought events and SPI ≤ − 1.65 are considered to be extreme drought events, according to their probability of occurrence.

4.2.3 Effective drought index

Byun and Wilhite (1999) developed the effective drought index (EDI) to consider the effect of depletion of water resources through time. The index was initially developed at a daily time step, but Smakhtin and Hughes (2007) adapted the index to a monthly time step. Effective precipitation (EP, Eq. (2)) is used to represent water resource depletion by giving different weights to precipitation falling during m previous months and giving a higher weight to the values closest to the month of calculation (Eq. (2)):

$$ E{P}_i=\sum \limits_{n=1}^i\left[\left(\sum \limits_{m=1}^n{P}_m\right)/n\right] $$
(2)

where i is the accumulation time scale and Pm is the precipitation m months before the current month. The mean of EP, \( \overline{\mathrm{EP}} \), is then calculated for each calendar month or n-month accumulation. Byun and Wilhite (1999) recommend using the 30-year mean, but we sometimes had to use shorter periods because of limited temporal availability of some datasets (Table 1). Finally, the deviation from the mean (DEP) and the EDI is calculated as:

$$ DEP= EP-\overline{EP} $$
(3)
$$ EDI=\raisebox{1ex}{$ DEP$}\!\left/ \!\raisebox{-1ex}{${S}_{\mathrm{td}}(DEP)$}\right. $$
(4)

where Std (DEP) is the standard deviation of DEP.

4.2.4 Standardised precipitation evapotranspiration index

The standardised precipitation evapotranspiration index (SPEI) index was developed by Vicente-Serrano et al. (2010). It is calculated in the same way as that of SPI, but instead of using the time series of precipitation, it uses the monthly difference between precipitation and potential evapotranspiration (PET). This difference is fitted to a probability distribution, in our case to a log-logistic distribution. In this study, we used the SPEI package developed by Beguería and Vicente-Serrano (2013) available in R (R Development Core Team 2011) and fitted the data to the log-logistic distribution. The SPEI has been found to be sensitive to the method used for the calculation of the PET (Stagge et al. 2014; Beguería et al. 2014). The Penman-Monteith methodology has been recommended as the most suitable method (Beguería et al. 2014), but it requires meteorological variables that were not available here. We, therefore, used the Hargreaves method (Hargreaves and Samani 1985; Hargreaves and Allen 2003), which was the alternative recommendation in the study by Beguería et al. (2014) and only requires monthly maximum and minimum temperature data:

$$ ET=0.0023{R}_{\mathrm{a}}\left({T}_{\mathrm{m}}+17.8\right)\sqrt{\left({T}_{\mathrm{m}\mathrm{ax}}-{T}_{\mathrm{m}\mathrm{in}}\right)} $$

where ET is potential evapotranspiration, Tm, Tmax and Tmin are mean, maximum and minimum temperature, respectively, and Ra is net radiation at the relevant latitude.

4.2.5 Standardised streamflow index

The standardised streamflow index (SSI) is calculated in the same way as that of the SPI, but using monthly discharge instead of monthly precipitation data (Lorenzo-Lacruz et al. 2013). We fitted the monthly discharge data to a gamma distribution, which provided a good fit. The categories used for streamflow drought were the same as those for SPI and SPEI.

4.3 Comparison of the meteorological drought indices

The four meteorological drought indices were calculated using the five datasets to analyse the different combinations of drought indices and datasets and then evaluated against independent streamflow data (Section 4.4). The drought indices were calculated only for the datasets that matched their respective data requirements (Table 3). To evaluate the level of agreement between the indices, we calculated the correlation between the drought indices at the different accumulation time scales. The comparison was done in the following two ways: (1) by comparing the same drought index calculated with different datasets and (2) by comparing the different drought indices calculated with the same meteorological dataset.

Table 3 Combinations of meteorological datasets and drought indices used in the study
Full size table

4.4 Evaluation of meteorological drought indices using discharge data

To evaluate the performance of all drought indices and meteorological datasets, we compared each of these combinations against independent data, through a hydrological drought index, the SSI. By doing this comparison, we assumed a strong connection between meteorological and hydrological droughts. The latter is justified since the seven basins used here are rain-dominated and unregulated. In addition, Central-American catchments typically have a fast response where groundwater processes do not play a dominant role. The comparison was done between the SSI at 1-month accumulation time against the meteorological drought index at 1-, 3-, 6-, 9- and 12-month accumulation times. This was done since streamflow usually has a longer memory than precipitation and the highest correlation values might occur at either of these accumulation times for the different catchments. The SPI, SPEI, Deciles and EDI were compared with SSI using the correlation coefficient and the Peirce skill score (PSS; Peirce 1884). For the correlation, the actual values, both positive and negative, were used. For the PSS, a contingency table was calculated where hits (H), misses (M), false alarms (FA) and correct negatives (CN) were defined. Events with index values below the threshold − 1 were treated as drought events, for both meteorological drought indices and SSI. The PSS is defined from the contingency table as:

$$ {P}_{SS}=\frac{\left(H\times {C}_N\right)-\left({F}_A\times M\right)}{\left(H+M\right)\left({F}_A+{C}_N\right)} $$
(5)

The PSS is 1 for a perfect prediction, 0 for a random or constant (climate) prediction, whereas values below 0 denote performance worse than a random prediction. An ANOVA table was used to compare the performances of the different datasets and indices at the five accumulation times.

5 Results

5.1 Assessment of the meteorological datasets

The visual comparison of the intra-annual precipitation distribution at the 24 study points revealed that the datasets captured the bimodal intra-annual precipitation distribution for most points in the Pacific-side regime, but that the Caribbean-side regime was less well captured (Fig. 2). There were sometimes large differences between the datasets, e.g. at study points no. 10 (Fig. 2a) and no. 3 (Fig. 2d), where there was more than 100% difference in the median precipitation values. At no. 12 (Fig. 2j), the regional datasets captured a Pacific-side regime compared to the station data that has a Caribbean-side regime. This is likely caused by errors in the source data used to create the gridded datasets (e.g. too few precipitation stations being included in the compilation). Spearman’s rank correlation values at a monthly scale were between 0.45 and 0.65, with the highest average correlation between the station data and CHIRPS or CRN073 and the lowest between the station data and CRU or ERAI. The analysis at the annual scale confirmed those at the monthly scale, meaning that CHIRPS and CRN073 were good at capturing the characteristic climate of the region.

We found some inhomogeneities in the datasets. For the CRN073 data, there were large step changes in the time series for points 1 and 7 in Guatemala in 1969 and 1967, respectively. For the ERA-Interim data, there were suspiciously high peaks in November 2009 at points 17 and 19 in Costa Rica.

5.2 Comparison of the meteorological drought indices

The Spearman’s rank correlation was considerably higher when comparing the different indices calculated with the same dataset than when comparing the same index using different datasets (Tables 4 and 5). The average results when varying the drought index for all the datasets (that is, averaging the results for station data, CHIRPS, CRN, ERAI and CRU) ranged from 0.78 to 0.97 (Table 4), with the highest correlations between SPI–SPEI and Deciles–SPI. On the other hand, the results of varying the dataset and taking the average result for all drought indices resulted in lower correlation values, ranging from 0.45 to 0.57 (Table 5). Note also that the correlation values were smaller than 0.5 for CRU–ERAI and CRN–CRU. A spatial comparison of the combinations showed similar results for the spatial extent of the severe drought of 1997 (Fig. 3), which has been associated with a strong El Niño (WFP 2002). SPI, DI and SPEI calculated with the CRU dataset (Fig. 3 bottom row) agree relatively well in their representation of the spatial drought pattern, with differences mainly related to how each index classified the event. Conversely, the SPI showed a rather different spatial pattern when calculated with different datasets (Fig. 3 top row). According to the FAO (1997), the situation during this drought event was like the one depictured by SPI-3 CHIRPS, with a drought on the Pacific side of Central America and anomalous wet events on the Caribbean side. ERAI and especially CRU indicated a different situation. ERAI captured a drought over most of Central America, with a weaker wet event over the Caribbean coast of Costa Rica and most of Panama. CRU showed almost the opposite, a wet event over most of Central America, with the drought occurring only at the south of Costa Rica and Panama.

Table 4 Average correlations between the different drought indices evaluated in this study. For the correlations, the indices were calculated using the same dataset. For example, to obtain the value on the second row and first column, the average correlation of the SPI and Deciles indices was taken at the 24 study points for the five meteorological datasets. For correlations including the SPEI, the average could only be calculated with CRU and ERA-interim
Full size table
Table 5 Average of the correlations obtained from calculating the same index with different datasets. Each cell shows the average of the results for SPI, DI, EDI and SPEI (SPEI for CRU and ERA-Interim only)
Full size table
Fig. 3
figure 3

Spatial extent of drought during the period August–September–October 1997 for SPI-3 with the gridded datasets available for that year (first row) and with the CRU dataset for different drought indices (second row). Note that the SPI-3 (CRU) is repeated in the first column for comparison clarity. The colour scale represents the index value

Full size image

A visual comparison of varying different drought indices (Fig. 4a) and varying different datasets (Fig. 4b) confirms that uncertainties are larger for the latter than for the former. The differences were observed in terms of duration, timing and category of the drought events.

Fig. 4
figure 4

Drought events for Agua Caliente, Panama (no. 12), for (a) drought indices at 12-month accumulation time using CRU data and for (b) DI at 12-month accumulation time using the different meteorological datasets

Full size image

5.3 Evaluation of meteorological drought indices using discharge data

The comparison with SSI showed that the meteorological drought indices had average PSS values between 0.01 and 0.48 and average correlations between 0.08 and 0.54 (Tables 6 and 7). Note that all combinations could not be compared because of non-overlapping time periods. The highest PSS values were obtained with the meteorological indices computed at 6-month accumulation time. The highest correlation values with SSI were obtained at 3-month accumulation time for SPI, SPEI and DI and at 6-month accumulation time for EDI. In terms of datasets, the PSS and Spearman’s correlation results showed that station data performed best, followed by CRN073 and CHIRPS. CRU and ERAI were the worst performing datasets, in agreement with the results found in Section 5.2. A visual example of this is shown in Fig. 5, which shows that SPI calculated with CHIRPS agrees better with the SSI than the SPI calculated with ERAI. ERAI missed important events, such as that in 1988 in study point no. 17 (Fig. 5a) and that at the end of 1983 in study point no. 21 (Fig. 5b). ERAI also showed more false drought events, such as in those in the period 1990–1992 in study points no. 21 and 22 (Fig. 5c). Note also that SPI calculated with CHIRPS also missed drought events, such as that in the period 1983–1985 in study point no. 22 (Fig. 5c).

Table 6 Average Peirce skill score for DI at the different accumulation times and SSI-1 for the seven discharge stations
Full size table
Table 7 Average correlation of SPI at the different accumulation times and SSI-1 for the seven discharge stations
Full size table
Fig. 5
figure 5

Time series of SPI using CHIRPS and ERAI and SSI at a 3-month accumulation time period for the (a) Balsa, (b) Camarón and (c) San Francisco discharge stations

Full size image

In terms of drought index, the DI resulted, on average, in the highest PSS values followed by the EDI. The EDI resulted in the highest Spearman’s correlations, followed by the SPI and DI (which resulted in similar values). The SPEI was only calculated for the CRU and ERAI datasets, but in terms of correlation, it outperformed the EDI when using ERAI data and ranked as second best with CRU data. In terms of the best combination of drought index and dataset, the highest PSS values were obtained with the DI using station data, with an average value of 0.41 for all accumulation times, and the highest correlations were obtained with the EDI using CHIRPS data with an average value of 0.56.

The ANOVA test, calculated to compare the PSS values, showed that even though both aspects—i.e. dataset and drought index—are important for the resulting skill, the dataset selection has a higher impact, since the F values were considerably larger with respect to the datasets than for the drought indices. This pattern did not change with longer accumulation times.

6 Discussion

6.1 Quality of the meteorological datasets

We selected the datasets first based on their spatial resolution. A dataset with a resolution lower than 0.5° latitude × 0.5° longitude would have limitations in capturing the heterogeneous climate of the region. Our assessment of the local representativeness of the meteorological datasets showed that most of them captured the Pacific-side intra-annual precipitation regime described by Amador et al. (2010) and Rivera and Amador (2008), including the presence of the MSD (Magaña et al. 1999). However, the Caribbean-side regime was less well captured (Fig. 2), since the regional datasets erroneously showed a Pacific-side regime for some of the study points. This can be contributed to a combination of factors, such as our point measurement to grid cell comparison, a sparse station network on this side of the region and other errors associated with the data used to produce the gridded datasets. There were sometimes large differences between the datasets, which makes the dataset selection highly important for reliable drought characterisation. CRN073 and CHIRPS, in that order, had the highest correlation with the meteorological station data at the intra-annual time scale, as well as the best performance in comparison to the hydrological drought indices. This means that these two gridded products could be a good complement to ground-based observations for drought characterisation and drought studies in general.

Ideally, to increase the reliability of the indices, data should cover long periods of time (e.g. for SPI is recommended to have at least 30–40 years of data) (Guttman 1994; McKee et al. 1993). This ensures that a larger sample of extremes, in our case, drought events, is represented in the data and that the statistical drought models are robust. CRN073 showed good agreement with station data, and we could use 42 years of data, which makes it suitable for historical drought characterisation. However, the dataset has been discontinued since the year 2000. This is a limitation in studying droughts, especially considering that studies suggest that the frequencies of extreme precipitation events are increasing in the region (Aguilar et al. 2005; IPCC 2007). CHIRPS on the other hand covers a shorter time period but is regularly updated. In addition, its high spatial resolution allows assessing drought at the local scale. CHIRPS data has been found to be a valuable complement to station data for drought monitoring in other regions of the world (e.g. Gao et al. 2018). CRU and ERAI showed large differences in comparison with station and streamflow data, which suggests that these datasets are not suitable candidates for drought characterisation in the region.

The comparisons and evaluations between the datasets were subject to some limitations mainly related to the spatial scale and temporal coverage of the datasets. The locations of the hydrological and meteorological stations differed in some cases, and it should be remembered that the meteorological data represent point values whereas the regional datasets represent values averaged over a large grid cell. The comparison with independent discharge data strengthened the findings of the assessment of the large-scale meteorological datasets and station data (and substantiated the use of the latter as a reference for the regional datasets). This was important since the comparison with station data was limited by the possibility that some of these data had been used to compile the regional data.

6.2 The use of drought indices in Central America

The choice of dataset was more important than the selection of drought index when studying droughts in Central America. All drought indices showed good agreement when based on the same dataset. However, it should be considered that there were differences in drought duration and category. With the comparison of the drought indices, we assume that the drought categories are equivalent. We based the selection of the categories on that made by Morid et al. (2006). However, the categories for the different drought indices might not be exactly equivalent and this can be an additional source of uncertainty in the evaluation of the drought indices.

We used the SSI to evaluate the performance of the different combinations. Several studies have found that meteorological drought indices accumulated at time scales of several months can be a good approximation for hydrological droughts (Nalbantis and Tsakiris 2009; Zhai et al. 2010; Liu et al. 2012; Xuchun et al. 2016). Even though we acknowledge the limitations of this approximation, e.g. that precipitation data cannot capture natural- and human-related processes at the catchment scale (Teuling et al. 2013; Wanders et al. 2015) and droughts therefore propagate differently from catchment to catchment (Van Loon and Laaha 2015), we used a streamflow index as the best available proxy to a meteorological index. The highest agreements between SSI (1-month accumulation) and the meteorological drought indices were at 3- and 6-month accumulation times, which suggests that such configurations are most suitable for hydrological drought characterisation in the region.

We found that the best combination was EDI calculated with the CHIRPS dataset. In general, EDI and DI performed best when considering all the datasets and all accumulation times. Other studies have found the EDI to be suitable for drought assessment (e.g. Morid et al. 2006, in Iran). DI has also been recommended for drought assessment in two regions in the US (Keyantash and Dracup 2002) and is used by the Australian Bureau of meteorology for drought monitoring. The SPI, which is recommended by the World Meteorological Organisation for drought characterisation (Hayes et al. 2011), closely followed the EDI and DI, but it did not rank as the best index. The SPEI did not show an overall good performance in terms of correlation values and the PSS score. This may be more a result of the quality of the CRU and ERAI dataset than the index itself, since in the evaluation of the drought indices calculated with the same datasets, the SPEI was amongst the indices with the highest correlations with SSI. This result confirms those of the study by Vicente-Serrano et al. (2012), who assessed the performance of drought indices and reported SPEI to perform better than SPI. We still think that the use of a drought index including PET and precipitation should be considered in Central America, because of its relevance to agriculture and warming-climate studies (Tsakiris et al. 2007; Khalili et al. 2011; Cook et al. 2014; Asadi Zarch et al. 2014), especially given that scenarios show future rising temperatures for Central America (Hidalgo et al. 2013).

7 Conclusions

This study evaluated which combinations of drought index and meteorological dataset were most suitable for characterising droughts in Central America. We evaluated five meteorological datasets in terms of their ability to capture climate variability in the region. Four drought indices were calculated using the five meteorological datasets and evaluated using independent streamflow data, in the form of a hydrological drought index, the SSI. Differences between the available meteorological datasets were so substantial that the choice of dataset was more important than the choice of drought index. We found that for drought characterisation in the region, station data should be used and complemented with CRN073 and/or CHIRPS. In terms of drought index, the assessment with SSI showed that EDI and DI performed best amongst the meteorological drought indices. Even though the suitability of the SPEI was affected by the quality of CRU and ERAI, results showed that including drought indices that consider temperature might be relevant. Future drought assessments in the region should also aim at incorporating information on social dynamics (e.g. population, water use, water abstraction and policy implementation during drought events) since these may likely play an important role in how droughts evolve (Montanari et al. 2013; McMillan et al. 2016).