Characterizing uncertainties in the ESA-CCI land cover map of the epoch 2010 and their impacts on MPI-ESM climate simulations

Abstract

Limitations of mapping land surface properties and their conversion into climate model boundary conditions are major sources of uncertainty in climate simulations. In this paper, the range of the largest possible uncertainty in satellite-derived land cover (LC) map is estimated and its impact on climate simulations is quantified with the Earth System Model of the Max-Planck Institute for Meteorology utilizing prescribed sea surface temperature and sea ice. Two types of uncertainty in the LC map are addressed: (i) uncertainty due to classification algorithm of spectral reflectance into LC classes, and (ii) uncertainty due to conversion of LC classes into the climate model vegetation distribution. For forest cover, each of them is about the same order of magnitude as the uncertainty range in recent observations (∼± 700 Mha). Superposing two sources of uncertainty results in LC maps that feature the range of vegetation deviation that is about the same order of magnitude as the recent (since year 1700) forest loss due to agriculture (forest cover uncertainty range ∼± 1700 Mha). These uncertainties in vegetation distribution lead to noticeable variations in near-surface climate variables, local, regional, and global climate forcing. Temperature does not show significant uncertainty in global mean, but rather exhibits regional deviations with an opposite response to LC uncertainty that compensate each other in the global mean (e.g., albedo feedback controls temperature in boreal North America resulting in cooling (warming) with decrease (increase) of vegetation while evaporative cooling controls temperature in South America and sub-Saharan Africa resulting in cooling (warming) with increase (decrease) of vegetation). Large-scale circulation is also affected by the LC uncertainty, and consequently precipitation pattern as well. It is demonstrated that precipitation uncertainty in the monsoonal regions are about the same order of magnitude as in previous studies with idealized perturbations of vegetation. These findings indicate that the range of uncertainty in satellite-derived vegetation maps for climate models is about the same order of magnitude as the uncertainty in recent observations of forest cover or as the forest lost due to agriculture. Consequently, climate simulations have a similar range of uncertainty in variables representing near-surface climate as the observed climate change due to land use. Hence, more accurate methods are needed for mapping and converting LC properties into model vegetation in order to increase reliability of climate model simulations.

Introduction

Uncertainty is an inherent feature of complex systems (such as climate). This is also true for numerical models used to study and understand a response and sensitivity of the climate system. Uncertainties in climate system model may originate from various sources such as natural climate variability, different techniques to discretize dynamics, and physics (i.e., parameterization of sub-grid scale effects), or uncertainty in the prescribed boundary conditions (e.g., land surface characteristics at the land–atmosphere interface, or greenhouse gas and aerosol concentrations, especially if future scenarios are considered). These uncertainties are mostly due to the lack of empirical investigations or limitations of observational techniques, and they can also lead to insufficient understanding of climate processes and controversial interpretations of climate research (Curry 2011; IPCC 2014; Maslin 2013). Understanding them is crucial for the reliability of climate models to simulate present day climate as well as to determine the range of possible climate states in future projections. Therefore, it is of paramount importance to improve our understanding of processes that contribute to uncertainty in the climate model results.

One of the key sources of uncertainty in numerical simulations of carbon, energy, and momentum exchange between land and atmosphere is the uncertainty in the observed land surface properties. Either land surface properties in climate models are prescribed with static maps of vegetation or they can change in dynamic interaction with other components of the respective climate model. In both cases, the initial vegetation distribution in the model is usually derived from remote sensing products supplemented with ground observations—global land cover (LC) maps. LC represents different properties of the Earth’s surface and controls water and energy exchange, photosynthesis rates, nutrient levels, and surface roughness at the land–atmosphere interface (Sellers et al. 1997). It is identified as one of the essential climate variables needed to understand changes in carbon cycle and climate change (Feddema et al. 2005).

Numerous studies within the recent decade focused on the quantification of the impact of LC change on climate (see Mahmood et al. (2014) and references therein for a comprehensive review). There is a growing body of evidence that vegetation, especially tree cover, has an impact on terrestrial water cycle, energy balance (e.g., see Alkama and Cescatti (2016) and Duveiller et al. (2018)), and carbon cycle (e.g., see Achard et al. (2014) for the estimate of carbon losses due to changes in forest cover in tropics). However, understanding the impact of LC change on climate remains controversial and is still work in progress (e.g., for the effect of LC change on precipitation, see Bonan (2008), Ellison et al. (2012), Mahmood et al. (2014), and Sheil and Murdiyarso (2009)). At the core of the controversy lies the uncertainty in the observation of climate parameters and their internal variability, as well as uncertainty in the remote sensing–derived LC maps. Comparing several global LC maps, Congalton et al. (2014) found that the main reasons for uncertainties and inconsistencies are due to (1) different data acquisition methods (i.e., missions and sensors), (2) different map production methodologies, and (3) different classification schemes. All these factors contributed to the estimate that the total accuracy of the LC maps is below 70%.

Considering uncertainty in climate parameters such as precipitation, a recent study by Herold et al. (2016) highlights limitations in our ability to characterize not only modeled daily precipitation intensities but even observed precipitation intensities. Furthermore, it is demonstrated that the level of uncertainty in modeled precipitation is about the same order of magnitude as the uncertainty seen in observations (Herold et al. 2016, 2017; Endo et al. 2017). Shortcomings in LC and climate parameter observations result not only in the large uncertainties, but also the global LC change occurring in concert with climate change hinders progress in the attempt to understand and disentangle the impact on the climate system of both LC change as well as uncertainty in observation. Land use–land cover (LULC) change impacts in climate simulations from phase 5 of the Coupled Model Intercomparison Project (CMIP5) have been examined by Kumar et al. (2013). They found for the twentieth century climate simulations that all 15 climate models show a net increase in summer surface albedo, 11 out of 15 models show a net decrease in summer evapotranspiration, and 8 out of 15 models show a net increase in summer temperature over North America and Eurasia LULC change regions.

Closely related to the uncertainties in LC and their impact on climate change are uncertainties in ecosystem functioning. The impact of LC uncertainties on terrestrial carbon fluxes has been investigated by Quaife et al. (2008). They found that the main uncertainty in carbon flux calculations are due to incorrect conversion of LC classes into model vegetation (plant functional types—PFTs) and information loss due to aggregation of high-resolution LC data to coarser resolution used in numerical models, as well as limited accuracy of the LC map due to difficulties in discriminating some vegetation types from satellite data. These resulted in a 254 gC m^− 2 year^− 1 range of uncertainty for gross primary production (GPP) averaged over Great Britain. Vegetation GPP is also the largest terrestrial sink of atmospheric CO₂ and, hence, the vegetation distribution comprises the largest source of uncertainty in GPP estimates. In particular, the coverage rate (%) of forests was usually overestimated in previous calculations of GPP so that the global forest gross carbon dioxide uptake was overestimated as well by 5.12 ± 0.23 Pg C year^− 1 (Ma et al. 2015). Evaluating components of the global carbon cycle by the CMIP5 models, Anav et al. (2015) reported a general overestimation of photosynthesis and leaf area index and, therefore, an overestimated terrestrial carbon uptake for most of the models. Le Quéré et al. (2016) in their annual report of the global carbon budget for the last decade (2006–2015) estimated an annual uncertainty due to land-use change in carbon emission of about ± 0.5 Pg C year^− 1, while the uncertainty of terrestrial carbon uptake is ± 0.9 Pg C year^− 1.

Regardless of a clear impact of LULC change (e.g., urbanization, adoption of agriculture, irrigation, deforestation, and afforestation), to date, very little research has been done to investigate the range of uncertainty in observed LC and its impact on the near-surface climate. Recently, Hartley et al. (2017) have investigated the range of uncertainty of a newly published satellite-derived LC map and its impact on energy balance and hydrological and carbon cycle, in three land surface models (LSM). They showed that the uncertainty related to the LC observation and its conversion into LSMs’ vegetation is a key source of model uncertainty. The range of uncertainty for key model state variables indicating energy, water, and carbon cycle is comparable to the spread between models.

In this study, while we refer to our earlier work (Hartley et al. 2017), the focus is different. New aspects of LC uncertainty in comparison with observation have been pinpointed. Furthermore, the impact of LC uncertainty on the near-surface climate is investigated with the Earth System Model of the Max Planck Institute for Meteorology (MPI-ESM) using prescribed sea surface temperature and sea ice.

The LC data, as well as the conversion method of LC to vegetation for climate modeling, and MPI-ESM are described in Section 2. The range of LC uncertainty is considered and its impact on climate variables related to terrestrial water cycle (precipitation and evapotranspiration), energy budget (albedo and 2m temperatures), circulation (wind and pressure) patterns, and terrestrial carbon cycle (GPP) is examined in Section 3. Discussion and our conclusions are drawn in the final section.

Data and methods

Earth System Models (ESMs) are tools to study the complex interactions between major components of the climate system (i.e., atmosphere, hydrosphere, cryosphere, biosphere, and land surface) driven by solar radiation (see Flato (2011) for a comprehensive overview of ESMs). The aim of ESMs is to simulate the climate state of our world by solving equations representing physical and biogeochemical processes in the discrete numerical space. To solve these equations, various datasets representing initial and boundary conditions are needed. Recently in the frame of European Space Agency (ESA) Climate Change Initiative (CCI), a new global LC map representing conditions of the Earth’s surface has been published (Defourny et al. 2014). This LC map can be used to derive vegetation distribution for climate modeling. The algorithm for conversion of satellite-derived surface reflectance into LC dataset is described by Defourny et al. (2014) and its application for LSMs modeling is described by Hartley et al. (2017). The conversion of LC into PFTs used in climate models is described in Poulter et al. (2011) and Poulter et al. (2015). The estimate of the maximum plausible uncertainty range of LC observation is described by Hartley et al. (2017). In Section 2.1, the ESA-CCI-LC map is briefly described, followed by description of the cross-walking (CW) procedure (Section 2.2) that is a method to convert LC classes into PFTs, in particular for JSBACH. In Section 2.3, the land surface component—JSBACH3.1—and the atmospheric component—ECHAM6.3 of MPI-ESM1.2—are briefly described, followed by the experiment setup in Section 2.4.

ESA-CCI land cover data

The ESA-CCI-LC product (version 1.4 available at http://maps.elie.ucl.ac.be/CCI/viewer/) is derived combining remotely sensed surface reflectance and ground-truth observations at 300-m resolution (Defourny et al. 2014). The reference map examined in this study is the LC map for the epoch 2010, which is an average LC map based on the satellite data acquisition during the period 2008–2012. For each grid box at 300-m resolution, an estimate of confidence that the LC class is identified correctly is provided. This confidence can be also interpreted as a source of uncertainty (see Hartley et al. 2017, for details). To validate the data, Defourny et al. (2016) compared the CCI LC product for the 2010 epoch with the certain and homogeneous points of the GlobCover 2009 (Arino et al. 2012) validation dataset and showed overall accuracy of 73.2%. However, accuracy may differ regionally as shown, e.g., by Yang et al. (2017), who found an accuracy 71.98% for China.

The LC product complies with the United Nations Land Cover Classification Scheme (UNLCCS, Di Gregorio and Jansen 2005) and it is not directly suitable for climate modeling. Therefore, ESA-CCI-LC categorical classes need to be converted to model-specific vegetation representation. The vegetation distribution in ESMs is commonly described by PFTs. That is the classification system used to simplify the vegetation representation and group plants according to their biophysical characteristics. The conversion method of LC classes into PFTs is also called a cross-walking (CW) procedure. Within the ESA-CCI-LC project, also annual maps of continuous land cover changes at 300-m resolution were released from 1992 to 2015. The comparison of global areas of forest, cropland, and grassland conducted by Li et al. (2018) showed some differences of ESA-CCI-derived PFTs in comparison to other datasets, but ESA-CCI-LC proved to be useful for modeling studies.

Cross-walking procedure

In the frame of the ESA-CCI-LC project, a user tool and a reference cross-walking (CW) table were released to support the conversion of LC classes into PFTs. However, due to the different design and processes implemented in various climate models, differences occur in the treatment of artificial, water, ice, bare, or vegetated surfaces. Therefore, expert knowledge and additional datasets are needed to take into account associated climate model processes and the required input information for their computations. In particular, for the vegetation delineation due to climate zones and photosynthetic pathways, auxiliary datasets are needed to adapt ESA-CCI-LC for the use in climate models. For that purpose, an updated world map of the Köppen-Geiger (KG) climate classification adopted from Peel et al. (2007) is used. The photosynthetic pathway, i.e., the C4 vegetation percentage, is taken from the International Satellite Land Surface Climatology Project (ISLSCP) Initiative II (Still et al. 2009) data.

The JSBACH land surface scheme can be set to distinguish various number of PFTs. However, in this study, 12 PFTs are used that were defined in the frame of CMIP5 experiments: tropical evergreen tree, tropical deciduous tree, extra-tropical evergreen tree, extra-tropical deciduous tree, raingreen shrub, deciduous shrub, C3 grass, C4 grass, C3 pasture, C4 pasture, C3 crop, and C4 crop. Shrubs’ distributions derived from ESA-CCI-LC largely differ from the PFT distribution used in CMIP5 studies (not shown). This points out that mapping shrubs based only on spectral reflectance still remains a challenge (Hellesen and Matikainen 2013). However, this type of uncertainty depending on how many types of vegetation are present in the model is rather out of the scope of this paper and might be a subject for future studies. Therefore, we focus on major vegetation types (forest, shrubland, grassland (including savannas), and croplands) as obtained from ESA-CCI-LC and converted to the JSBACH PFTs. Figure 1 shows PFT distributions aggregated into major vegetation types used in JSBACH derived from ESA-CCI-LC.

Fig. 1

Area fraction of major vegetation types in JSBACH derived from ESA-CCI LC. Forest consists of tropical and extra-tropical evergreen trees, and tropical and extra-tropical deciduous trees. Shrubland comprises deciduous and raingreen shrub phenotypes. Grassland is diversified according to grass photosynthetic pathways (C3 and C4). Cropland includes crops and pasture, which are also divided into C3 and C4 depending on their photosynthesis processes

MPI-ESM

MPI-ESM couples the atmospheric, ocean, and land surface processes through the exchange of energy, momentum, water, carbon, and other trace gasses. In this study, the atmosphere and land components of MPI-ESM 1.2 are utilized that consist of the atmospheric general circulation model ECHAM6.3 (Stevens et al. 2013) and its land surface scheme JSBACH 3.1 (Raddatz et al. 2007; Brovkin et al. 2009). Both models have undergone several further developments since the version (ECHAM6.1/JSBACH 2.0) used for the CMIP5 experiments (Taylor et al. 2012). Several bug fixes in the ECHAM physical parameterizations led to energy conservation in the total parameterized physics and a re-calibration of the cloud processes resulted in a medium-range climate sensitivity of about 3 K. JSBACH 3.1 comprises several bug fixes, a new soil carbon model (Goll et al. 2015) and a five-layer soil hydrology scheme (Hagemann and Stacke 2014) replaced the previous bucket scheme. These five layers correspond directly to the structure used for soil temperatures and they are defined with increasing thickness (0.065, 0.254, 0.913, 2.902, and 5.7 m) down to a lower boundary at almost 10-m depth. Vegetation is represented by several PFTs in each model grid cell using a tiling approach. Here, the bare soil area fraction of a grid cell is defined implicitly as a residuum from all vegetation cover fractions, i.e., $1 - \sum f_{i}$, where $\sum f_{i}$ is the sum of area fractions of all PFTs. Various aspects of vegetation dynamics are simulated on a broad range of temporal scales, including photosynthesis/stomatal conductance, leaf phenology, carbon allocation and decomposition, and the redistribution of PFTs and deserts (Brovkin et al. 2009).

Experimental setup

In this study, five ECHAM6.3/JSBACH3.1 simulations were conducted at T63 horizontal resolution (∼1.85^∘ or ∼200 km) with 47 vertical layers in the atmosphere. They were forced by observed sea surface temperature (SST) and sea ice from the AMIP2 (Atmospheric Model Intercomparison Project 2) dataset during 1979–2009 (Taylor et al. 2000). 1979 is regarded as spin-up, so that only the period 1980–2009 is considered for the analyses. Five simulations have been performed with five different PFT maps as defined by Hartley et al. (2017). Except reference map (refLC_refCW), two maps that account for LC classification algorithm uncertainty are derived: one that minimizes vegetation (minLC_refCW) and the other that maximizes vegetation (maxLC_refCW). Two additional maps that either minimize (minLC_minCW) or maximize (maxLC_maxCW) vegetation due to CW procedure uncertainty are superimposed on maps that minimize (minLC_refCW) and maximize (maxLC_refCW) vegetation due to LC classification algorithm uncertainty. In that way with five maps, we cover the largest plausible, though not necessarily realistic, range of vegetation uncertainty. The maps are derived following the same procedure as in Hartley et al. (2017). The only difference is resolution. Offline experiments in the previous study have been conducted at 2^∘ resolution, which slightly differs from the T63 spectral resolution utilized in the present study. However, since we follow the same procedure, we also keep the same nomenclature as in the previous study (Table 1).

Table 1 Experiment names and description

Results

The present study focuses on two sources of uncertainty: (i) algorithm (Defourny et al. 2014) of converting surface reflectance into LC classes (LC mapping), and (ii) CW procedure into PFT. The range of uncertainties in PFTs map derived from ESA-CCI-LC map is quantified and compared with the range of uncertainty in forest cover observations and recent LULC change (Section 3.1). Furthermore, the impact of PFT uncertainty on MPI-ESM simulated land surface fluxes and near-surface climate is calculated (Section 3.2).

The range of PFT uncertainty

Table 2 sums the amount of the area (in Mha) covered with major vegetation types, global, and for four latitudinal zones (40 N–70 N, 10 N–40 N, 20 S–10 N, 60 S–20 S) classified by Hartley et al. (2017) as the latitudinal zones with distinctive vegetation uncertainties. Comparing these areas (Table 2 for the globe) with the area of historical LC change estimated in the literature, it turns out that the range of uncertainty is about the same order of magnitude as the historical LC change. Ramankutty and Foley (1999) estimated that approximately 1200 Mha of trees have been removed globally since 1700 up to 1992. In the simulations that minimize vegetation cover, there is 721 Mha (minLC_refCW) and 1740 Mha (minLC_minCW) less trees than in the reference experiment (refLC_refCW). In the simulations that maximize vegetation, there is 633 Mha (maxLC_refCW) and 1229 Mha (maxLC_maxCW) more trees than in the reference simulation. According to ESA-CCI-LC data for epoch 2010 used as reference LC, the area currently under farming is 2365 Mha, while Ramankutty and Foley (1999) estimated that there was 1800 Mha under farming in the year 1992. Here, it is also interesting to note the non-uniform distribution of farming area in our experiments, so that minLC_refCW simulation has the largest farming area of 2635 Mha, while maxLC_minCW has the smallest farming area (1709 Mha).

Table 2 Area in Mha, global, and for four latitudinal zones, covered with various major vegetation types for the reference and four uncertainty experiments. Grassland includes also savannas. Note that these are the largest plausible variations of vegetation, but likely not realistic. In brackets, deviations from the reference setup (refLC_refCW) are given in percentage

The range of uncertainty for forest distribution can be compared with other datasets. According to Forest Resources Assessment (FRA) reports (Keenan et al. 2015, Table 11), global forest area, for example, in the year 2000 ranges from 3870 (FRA 2000) to 4056 Mha (FRA 2015). Therefore, the quality of data used in various FRA surveys resulted with 186-Mha area of global forest uncertainty. Based on satellite data, Hansen et al. (2010) estimated global forest area of 3269 Mha, while in a later study Hansen et al. (2013) have estimated 4145 Mha. The difference between these two studies is 876 Mha, which is about the same order of magnitude as the uncertainty due to LC mapping or CW procedure in our study. In addition, the most recent studies seem to be more accurate than earlier studies, i.e., forest cover estimates from FRA 2015 are considered to be more accurate than estimates from FRA 2000 and estimates from Hansen et al. (2013) are considered to be more accurate than estimates from Hansen et al. (2010). Especially for the latter, this is due to the use of better input data (e.g., finer resolution imagery), improved methods, and different definition. Also Gross et al. (2017) report more accurate results for more recent estimates from finer resolution imagery. But comparing estimates from different studies does not necessarily provide reliable information about the reduced uncertainty of the most recent estimates. Another example to illustrate this point is the “discovery” of 400 Mha of forests in the drylands (Bastin et al. 2017). These “missing” forests are mainly (or largely) open forest (i.e., between 10 and 50% tree cover) which are considered as forests by Bastin et al. (2017) (FAO definition) but should not be considered as forests for climate simulations (predominance of shrub and grass cover).

Table 2 also shows vegetation variations due to uncertainty across the latitudinal zones. For example, the largest relative increase of forest area (81%) appears in 10 N–40 N zone for maxLC_maxCW, while the largest relative decrease (69%) appears for the minLC_minCW case in the same zone. However, the largest absolute variation occurs in the 40 N–70 N zone.

Figure 2 identifies regions where the variations in JSBACH PFT distribution occur due to the uncertainty in LC mapping algorithm (minLC_refCW and maxLC_refCW) and CW procedure (minLC_minCW and maxLC_maxCW). As already noted by Hartley et al. (2017), these variations are more pronounced for CW uncertainty than for LC mapping uncertainty. For extra-tropical evergreen trees, the largest variation in geospatial distribution of PFTs occur in Northern North America and Canada, Scandinavia, Northern Russia (from Baltic to Ural), and Southeastern China. For the extra-tropical deciduous trees, the largest variation due to uncertainty is located in Northern Russia ranging from the West Siberian Plain to the Bering Strait, in Zambezi river basin and in the South American Pampas. The most notable variation in the distribution of tropical trees is in Amazon and Congo River basins.

Fig. 2

Area deviations from the reference (refLC_refCW) simulation of major vegetation types for the four uncertainty experiments. Contours are showing absolute area changes of 10%; dashed lines indicate negative values, and full lines indicate positive values

Other notable variation appears for shrubs and herbaceous types. For example, maxLC_maxCW is characterized by the decrease in shrubs from approximately 40 N to 70 N latitude (Table 2 and Fig. 2), as well as along the northwestern border of Parana River basin in South America and in the area between the Indochina peninsula and the Yangtze River basin. This experiment is also characterized by the increase of shrubs especially along the southern and eastern coast of Australia and in some parts of sub-Saharan Africa (see green line on the shrubland panel in Fig. 2).

The global increase in the grassland area in comparison to reference case (refLC_refCW), in particular of the C3 type, characterizes all experiments. However, the most notable increase is for minLC_minCW that minimizes vegetation due to CW uncertainty (see Table 2 and red line on the grassland panel in Fig. 2).

The largest variations in croplands are in the sub-Saharan area, between 10 N and 50 N over the Eurasian continent, along the eastern coast of South America, in Central America and to the north of the Gulf of Mexico. Crops have a productivity comparable to trees, but albedo and transpiration properties are similar like grasses. Thus, variations in crops are expected to have a nonlinear feedback across the five experiments. Therefore, note that the largest increase in crops appears in minLC_refCW (cf. Cropland panels in Figs. 1 and 2 and Table 2), in particular on the southern hemisphere (SH).

MPI-ESM response to the PFT uncertainty

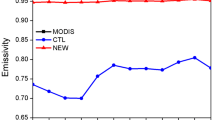
The impact of the LC uncertainty and the range of the MPI-ESM response of annual mean climate are summarized in Fig. 3 and Tables 3 and 4. Table 3 shows comparison of JSBACH offline and MPI-ESM data with observations. Though, albedo in JSBACH and MPI-ESM shows some differences in interannual variability (Fig. 3), the range of uncertainty is the same for both of them and amounts 0.024 (ranging from 0.304 to 0.280 in JSBACH and from 0.298 to 0.274 in MPI-ESM, see Table 3). GPP shows larger interannual variability in MPI-ESM simulation (Fig. 3), but uncertainty is larger for JSBACH simulations ranging from 135.917 to 173.253 Pg C year^− 1, while for MPI-ESM, GPP ranges from 134.990 to 167.492 Pg C year^− 1. ET shows larger uncertainty and interannual variability for MPI-ESM simulation. However, this is not due to coupling of surface and atmospheric processes, but due to model deficiency in the JSBACH offline version used in previous study that is resolved in a coupled setup within MPI-ESM used in the present study.

Fig. 3

MPI-ESM and JSBACH response of annual mean climate variables over land to the PFT uncertainty expressed by normalized scores of annual means for GPP, ET, Albedo, and total precipitation (TP) and 2m temperature (T2M) for MPI-ESM (filled rhombi) and offline JSBACH simulations (empty style rhombi). Overlaid boxplot shows 0.05, 0.10, 0.25, 0.5, 0.75, 0.90, and 0.95 percentiles

Table 3 Annual means for selected JSBACH and MPI-ESM variables over land for the period 1980–2009. Observations are taken from the following sources: albedo is calculated from GlobAlbedo (Muller 2013; He et al. 2014), GPP is taken from various sources in literature summarized in Anav et al. (2015), review of ET estimates is provided by Zhang et al. (2016), and terrestrial precipitation is obtained from Trenberth et al. (2007)

Comparing the values for evapotranspiration in MPI-ESM simulation (Table 3, ranging from 72748 to 77017 km³, i.e., ∼± 2000 km³ from the reference) with the estimated decrease in terrestrial evapotranspiration due to deforestation (Sterling et al. 2012, ∼3500 km³), it turns out that the range of uncertainty for certain variables is about the same order of magnitude as the estimated LULC climate change. Figure 3 shows normalized scores for annual means of various climate variables for the five experiments conducted with MPI-ESM and JSBACH offline, where the latter was taken from Hartley et al. (2017). Similar as Figure 6 in Hartley et al. (2017), the normalized scores for MPI-ESM simulations convey the same message as offline simulations. Albedo is the most impacted, equally affected by LC and CW uncertainty. It decreases with an increase in vegetation. The differences in albedo between the JSBACH offline and MPI-ESM simulations are due to differences in the prescribed WFDEI precipitation and MPI-ESM simulated precipitation which result in different snow cover in both types of simulations.

The response of GPP to the PFT uncertainty is similar for both setups, except that MPI-ESM simulations show stronger interannual variability. In both cases, GPP is much strongly affected by the CW uncertainty than by the LC mapping uncertainty. This is probably because the biggest variation in tree cover occurs for this uncertainty and trees are the largest primary producers. However, minimizing vegetation due to LC mapping uncertainty (minLC_refCW) shows a similar anomaly as in Hartley et al. (2017), i.e., it shows an increase of GPP with a reduction of vegetation. This is probably due to the largest area (2635 Mha) covered by crops in this experiment and crops have larger productivity than grasses.

In the previous version of JSBACH-offline used in Hartley et al. (2017), ET did not show much variation due to PFT uncertainty. This bug was specific to the offline version of JSBACH, but is not included in coupled setup so that the ET behavior is improved in the MPI-ESM simulations presented in this study, where ET linearly increases with increasing vegetation. As total precipitation (TP) over land and 2m air temperature (T2M) over land are prescribed in the offline simulations, they are not analyzed for JSBACH simulations but only for the MPI-ESM simulations. Here, TP increases linearly with the increase of vegetation, while T2M does not show a systematic dependence on vegetation globally, but rather regionally.

Table 4 shows global and regional (four latitudinal zones) uncertainty of five key surface climate variables in MPI-ESM. For example, global uncertainty in GPP is estimated to be ∼± 16 Pg C year^− 1. The largest zonal uncertainty from − 5 to 6.6 Pg C year^− 1 occurs in the 40 N–70 N Table (4) zone. This is also the zone featuring the largest variation in the tree distribution (from 573 to 2326 Mha, Table 2), also affecting albedo uncertainty to range from − 0.035 to 0.026. Evapotranspiration uncertainty (in 40 N–70 N zone) ranges from ∼− 926 to 995 km³ year^− 1 or from ∼− 20 to 21 mm year^− 1. All these parameters depend largely on the uncertainty in vegetation distribution, i.e., their stomatal conductance and reflective properties. Largest uncertainty in precipitation (ranging from − 1473 to 1302 km³ year^− 1 or from ∼− 51 to 45 mm year^− 1) and 2m temperature (ranging from ∼− 0.1 to 0.2 K ) are estimated in the 20 S–10 N zone.

Table 4 Deviations of uncertainty experiments (δ minLC_minCW, δ minLC_refCW, δ maxLC_refCW, δ maxLC_maxCW) from the reference experiment (refLC_refCW), for the key surface climate parameters—global and for four latitudinal zones. Compare with vegetation uncertainty in the Table 2

The box plots on Fig. 3, overlaid over annual mean scores, provide an interesting insight in the distribution of frequencies and how the simulated climate is affected by uncertainty in vegetation. For example, the median amount of precipitation for minLC_minCW lies just below the 5th percentile for maxLC_maxCW, i.e., the median amount of precipitation for the minLC_minCW experiment equals the precipitation of a very dry year in the maxLC_maxCW experiment. For ET, this difference is even more pronounced, leading to the conclusion that a median year for the minLC_minCW experiment would be a dry year in the reference (refLC_refCW) simulation, and an extremely dry in maxLC_maxCW. Positive extremes show a similar behavior. The median amount of precipitation for maxLC_maxCW lies above the 95th percentile of minLC_minCW, i.e., it has a similar amount of precipitation as the wettest year in minLC_minCW.

This redistribution of precipitation pattern indicates that PFT uncertainty has a considerable impact on large-scale phenomena, such as NAO and ENSO, and their regional implications such as monsoons and weather regimes simulated by an ESM. While studying offline LSMs, Hartley et al. (2017) could only consider land surface variables. In the present study, with MPI-ESM, we can also investigate the impact of LC uncertainties on atmospheric variables.

Figure 4 shows boreal winter (December, January, February—DJF) deviations of mean sea level pressure and 10-m winds from the reference experiment for the uncertainty experiments. Those experiments that either minimize or maximize vegetation due to CW uncertainty (minLC_minCW, and maxLC_maxCW) show a clear impact on the mid-latitude westerlies in northern hemisphere (NH) during DJF. In the minLC_minCW experiment, westerlies are strengthening while in the maxLC_maxCW experiment they are weakening. Experiments that either minimize (minLC_refCW) or maximize (maxLC_refCW) vegetation due to LC uncertainty both contribute to the formation of blocking like features, the former above the Atlantic Ocean to the north of the Great Britain, and the latter above the Central Europe. Both of them seem to have impact on increasing the Azores and Siberian high and deepening the Icelandic depression during the boreal winter. This results in intensified westerlies over the Atlantic Ocean. It is more pronounced for maxLC_refCW. These deviations in circulation pattern can be explained by an increase of surface roughness with an increase of vegetation. In addition, there are variations in the atmospheric water vapor distribution that impact the atmospheric pressure patterns and, hence, the circulation.

Fig. 4

Boreal winter (DJF) mean sea level pressure and 10-m wind deviations from the reference simulation (refLC_refCW) for the four uncertainty experiments (minLC_minCW, minLC_refCW, maxLC_refCW, and maxLC_maxCW)

Figure 5 shows the related deviations in circulation during the boreal summer (June, July, August—JJA). On the NH, only minLC_minCW shows some amplification of westerlies over the Eurasian mid-latitudes while the other simulations show negligible variation in wind speed for that area. The SH also features perturbations in circulation pattern during both seasons (Figs. 4 and 5). It is interesting to note the strengthening of the high-pressure field to the south of the African continent during the JJA season, in particular for minLC_minCW and minLC_refCW. This high-pressure field brings moist oceanic air to the Indian subcontinent and it may intensify the Indian monsoon. Hence, this demonstrates that vegetation uncertainties have a noticeable impact on the large-scale atmospheric circulation.

Fig. 5

Boreal summer (JJA) mean sea level pressure and 10-m wind deviations from the reference simulation (refLC_refCW) for the four uncertainty experiments (minLC_minCW, minLC_refCW, maxLC_refCW, and maxLC_maxCW)

The complex pattern of seasonal (DJF and JJA) variations in 2m temperature due to vegetation uncertainty as well as variations in albedo and evapotranspiration are shown in Figs. 6 and 7. Variations in temperature depend on several factors such as vegetation type, snow cover, and solar insolation related to geographic latitude. During the winter (DJF, Fig. 6), variations in NH temperature are controlled by albedo feedback and advection (Figs. 4 and 6). Variations in SH 2m temperature during winter, in particular for cases with increased vegetation (maxLC_maxCW and maxLC_refCW), are predominantly controlled by evaporative cooling. Experiments that decrease vegetation (minLC_minCW and minLC_refCW) show impact of albedo feedback and evaporative cooling on temperature. During the summer (JJA, Fig. 7), evaporative cooling takes a predominant control over 2m temperature changes, especially over North America. The albedo feedback seems to be more important for the cases that minimize vegetation (minLC_minCW and minLC_refCW).

Fig. 6

Boreal winter (DJF) mean 2m temperature differences from the reference simulation (refLC_refCW) for the four uncertainty experiments (Table 1). Overlaid contours show changes in albedo (green, −0.01 dashed line and 0.01 full line) and evapotranspiration (magenta, −5-mm/month dashed line and 5-mm/month full line)

Fig. 7

Boreal summer (JJA) mean 2m temperature differences from the reference simulation (refLCrefCW) for the four uncertainty experiments (Table 1). Overlaid contours showing changes in albedo (green, −0.01 dashed line and 0.01 full line) and evapotranspiration (magenta, −5-mm/month dashed line and 5-mm/month full line)

The impact of vegetation uncertainty on annual mean T2M and TP over land is shown in Figs. 8 and 9, respectively. Statistical significance of the annual mean (T2M and TP) deviations from refLC_refCW has been tested with a T test and with a simple standard deviation test. The latter is performed as following. Model internal variability is defined as the standard deviation of five-member ensemble performed by de Vrese and Hagemann (2016). The model setup is identical, but the simulations were started using slightly differing initial conditions. In that way, defined model internal variability is compared with the deviations of uncertainty experiments from the reference simulation. Grid points where the deviations of uncertainty experiments are larger than two standard deviations (internal variability) of the ensemble roughly coincide with the grid points showing 95% significance level according to T test. Therefore, only the former are indicated on Figs. 8 and 9. Figure 8 shows the net annual impact of seasonal variations in albedo feedback, evaporative cooling, and other factors related to PFT uncertainty, on the 2m temperature. Boreal latitudes of North America and in particular Canada exhibit cooling with decrease of vegetation (minLC_minCW and minLC_refCW) and warming with increase of vegetation (maxLC_maxCW and maxLC_refCW) indicating albedo feedback control over temperature. On the other hand, South America and sub-Saharan Africa exhibit the opposite signal, i.e., warming with decrease of vegetation and cooling with increase of vegetation in particular related to CW uncertainty (minLC_minCW and maxLC_maxCW). Therefore, this indicate evaporative cooling as dominant control over the 2m temperature for South America and sub-Saharan Africa. The Eurasian continent shows interference of both effects and the largest changes in temperature due to PFT uncertainty. The most significant warming with increasing vegetation occurs along the northeastern coast of the Eurasian continent. Seasonal variations (Figs. 6 and 7) can be even stronger. During the boreal spring (March, April, May—MAM), maxLC_maxCW shows a local warming up to 3 K along the northeastern coast of the Eurasian continent and the northwestern part of North America.

Fig. 8

Annual 2m temperature deviations from the reference simulation for the four uncertainty experiments (Table 1). Hatches indicate deviations that are larger than 2 standard deviation of 5 member ensemble internal variability

Fig. 9

Annual total land precipitation deviations from the refLC_refCW simulation for the four uncertainty experiments (Table 1). Hatches indicate deviations that are larger than 2 standard deviation of 5 member ensemble internal variability. Monsoon regions (NAM—North American, SAM—South American, NAF—North African, SAF—South African, SAS—South Asian, EAS—East Asian, and AUS—Australian) are indicated as defined by Devaraju et al. (2015) following approach of Wang and Ding (2006)

The most significant impact on precipitation (Fig. 9) appears due to CW (minLC_minCW and maxLC_maxCW) uncertainty. The major variations in precipitation occur in the Amazon, Congo, and Indonesian rainforest, but also in North America and Central Eurasia. The feedback is positive, i.e., less vegetation–less precipitation and vice versa. Figure 9 also shows monsoon rain domains as defined by Devaraju et al. (2015) following Wang and Ding (2006). Seasonal and annual mean variations of terrestrial precipitation in monsoon regions are shown in Fig. 10 The largest relative deviation of precipitation (∼± 14%) is about the same order of magnitude as in Devaraju et al. (2015), though they do not occur in the same regions. The South African domain shows ∼14% increase during the JJA season and the Australian region exhibit ∼14% decrease of precipitation during MAM season. Except for the East Asian boreal winter (DJF) monsoon, all other NH DJF monsoons (North American, North African, and South Asian) intensify with decrease of vegetation, similarly as the SH DJF monsoons (Australian, South American, and South African). During austral winter (JJA), the weakening of precipitation with decrease in vegetation is a dominant feature. However, NH monsoons are not so strongly affected as the SH monsoons by the decrease of vegetation. Experiments that maximize vegetation predominantly show intensification of DJF monsoonal precipitation, while impact on JJA monsoons is negligible.

Fig. 10

Precipitation deviations in monsoon regions (shown on Fig. 9) as an effect of vegetation distribution uncertainty.

Discussion and conclusions

In this study, the impact of LC uncertainty on climate simulations with MPI-ESM has been investigated. To our knowledge, this is the first study to estimate the impact of uncertainty in vegetation distribution based on satellite-derived LC map on ESM-simulated climate. Implications of uncertainty for remote sensing of LC have been discussed in detail by Hartley et al. (2017). Thus, in order to understand the significance of our results, we discuss them in the context of earth observations and modeling studies. Though the range of uncertainty (Hartley et al. 2017) derived from the ESA remote sensing data and the conversion into PFT might seem exaggerated, this is the largest possible range of uncertainty resulting from the superposition of these two sources of uncertainty. Each of them results in a range of vegetation coverage that is about the same order of magnitude as the uncertainty in available forest observation (Keenan et al. 2015; Hansen et al. 2010; Hansen et al. 2013). Superposing two sources of uncertainty (minLC_minCW and maxLC_maxCW) shows that the absolute value of the estimated range of vegetation differences to the reference in either direction is about the same order of magnitude as the observed forest loss due to agriculture since 1700 to 1992 (Ramankutty and Foley 1999). Therefore, perturbations of vegetation in our study are relevant for both constraining uncertainty in present day climate simulations and understanding recent climate change due to land use and to investigate possible effects of deforestation or afforestation. Propositions for constraining uncertainty from remote sensing perspective (LC mapping) and earth system modeling (CW procedure) have been discussed in depth by Hartley et al. (2017) and there is currently work in progress addressing improvements of the CW procedure. Satellite-derived PFT uncertainty is about the same order of magnitude as the observed LULC change. Therefore, simulated climate variation for some variables is about the same order of magnitude as the observed climate change due to land use.

From the modeling perspective, our results both confirm previous studies exploring vegetation–atmosphere interaction and widen our understanding of the corresponding climate uncertainty. Our experiments concur well with Bonan (2008) (indicating that tropical forests mitigate warming through evaporative cooling, but the low albedo of boreal forests is a positive climate forcing). Thus, further expand the idea that annual mean temperature of boreal North America is controlled by albedo feedback, while the annual mean temperature of South America and sub-Saharan Africa is controlled by evaporative cooling (Figs. 6, 7, and 8).

Our results considering variations in large-scale circulation and precipitation due to vegetation uncertainty have a number of similarities with previous studies exploring the impact of idealized modification of vegetation on simulated climate. For example see Swann et al. (2011) for idealized afforestation of mid-latitudes and Devaraju et al. (2015) for deforestation experiments. Both studies showed that changes in forest cover are capable of driving changes in large-scale circulation and precipitation. The precipitation variations depend on the location of vegetation variations, both Devaraju et al. (2015) and Swann et al. (2011) used idealized cases of deforestation and afforestation, respectively, while the range of our vegetation distribution is derived from uncertainty of LC observation and conversion into PFTs. Therefore, it constrains uncertainty of climate response to plausible range of model error in monsoonal precipitation estimate. However, our study does not enable us to determine the plausible range of shifts in the Intertropical Convergence Zone (ITCZ), since the ocean component is not thermodynamically interactive with the atmosphere in our model, but sea ice and SST are prescribed for all simulations. Nevertheless, prescribing SST and sea-ice conditions allows us to isolate solely the effect of vegetation variation on terrestrial near-surface climate by excluding impact of ocean thermodynamic. The impact of LC uncertainty in a fully coupled atmosphere–land–ocean system might be a subject of a follow-up study.

In summary, our analysis demonstrate that the largest plausible range of uncertainty in ESM vegetation map converted from satellite-derived LC product is about the same order of magnitude as forest loss due to agriculture in the past ∼ 300 years. Consequently, the range of uncertainty in near-surface climate is about the same order of magnitude as the observed climate change due to deforestation. Though this range of largest possible uncertainty in vegetation distribution is very likely exaggerated at the global level, it might be relevant for certain regions of the world with higher relative uncertainty (e.g., complex and heterogeneous areas, such as the mix of shrub cover, savannas, and croplands in sub-Saharan Africa, are much more difficult to map than homogeneous areas such as the Sahara). Therefore, more accurate methods of LC classification and their conversion into PFT are needed in order to increase reliability of climate model simulations and projections.