1 Introduction

The El Niño Southern Oscillation (ENSO) is the most important tropospheric mode of climate variability, affecting the climate of many parts of the globe through teleconnections. The literature refers to two main types of ENSO based on the spatial signature of sea surface temperature (SST) in the tropical Pacific Ocean (Ashok et al. 2007; Larkin and Harrison 2005; Kug et al. 2009; Hill et al. 2009). The first type of ENSO, referred to as the East Pacific (EP) type or Canonical ENSO, is dominated by the variability of SST around the EP Ocean, while the variability around the Central Pacific (CP) Ocean defines the second type of ENSO, which is named as the CP or Modoki ENSO.

There are differences in the climatic anomalies engendered by the Canonical and Modoki types of ENSO. For instance, Brown et al. (2009), Cai and Cowan (2009), and Taschetto and England (2009) described the climatic impacts of each type of ENSO on Australian rainfall, while Roy et al. (2017) and Roy and Tedeschi (2016) studied its impact on Indian Summer Monsoon. Similar studies were also performed by Weng et al. (2007, 2009) in the Pacific Rim region, Chang et al. (2008) in the South China Sea, Feng et al. (2010, 2011) on the East Asian climate and at the global scale by Ashok et al. (2007).

In the development and evolution of different ENSO type and phase, westerly wind bursts (WWBs) that develop in the tropical Pacific (western side) play a key part (Fedorov et al. 2015; Chen et al. 2015). Kao and Yu (2009) further examined the structure and evolution of the EP and CP types of ENSO and the teleconnections associated with them. Their analysis revealed that the EP type is mainly controlled by a shift in the tropical Pacific thermocline, while for the CP type, atmospheric forcing plays a more important role and it has an extratropical connection. Two mechanisms are proposed to explain the tropical-extratropical teleconnections for the CP type of ENSO: the Equatorial Ocean Advection Theory (Kug et al. 2009) and the Extra-tropical Forcing Theory (Kao and Yu 2009; Yu and Kim 2011; Yu et al. 2010). The first theory suggests that anomalous SSTs in the tropical Pacific Ocean are generated by zonal oceanic advection, while the second theory indicates that it is first excited by extra-tropical forcing in the mid-latitudes and further developed through equatorial oceanic advection. Because of their independence in structure, evolution and formation mechanism, this work focuses on different types of ENSO to explore various SST features and related oceanic teleconnection patterns.

Recent studies have found that perturbations around the North Atlantic Ocean could act as a precursor of different types of ENSO in the Pacific (Ham et al. 2013a, 2013b). One pathway to connect the North Atlantic to tropical Atlantic could be via the regional Hadley cell. A warming of SSTs in the tropical Atlantic often led a warming in the Pacific Ocean and associates an El Niño (EN) phase (Ding et al. 2012; Martin-Rey et al. 2015; Polo et al. 2014). Changes in the Walker circulation is proposed as the mechanism for explaining the links between the tropics of Atlantic and Pacific Oceans. By generating surface wind anomalies and subsidence/ascent in the central west of Pacific and inciting eastward moving Kelvin waves, it activates the required feedbacks from the ocean to trigger different ENSO phases. Thus, in combination of the effect of Hadley and Walker cell, positive/(negative) SSTs in the North Atlantic Ocean leads the development of a La Niña (LN)/(EN) event of the CP type of ENSO. North Atlantic can also directly influence Pacific without involving tropical Atlantic. That mechanism involves atmospheric Rossby wave. Anomalous SSTs in the North Atlantic develop a response of Rossby wave around the midlatitude of North Pacific and via the wind-evaporation feedback mechanism may trigger the development of ENSO conditions. All these discussion suggests that the Atlantic SST acts as a precursor of different types of ENSO in the Pacific. Hence, how SSTs in the Atlantic and tropical Pacific are coupled, in observation and models, will also be a part of this study.

A number of studies using numerical modelling and meteorological reanalyses have shown that both types of ENSO engender climatic anomalies beyond the tropics. Hurwitz et al. (2011a) found that the EP type of ENSO does not affect the extra-tropics of the Southern Hemispheric (SH) stratosphere region, while there is a causal mechanism in the CP type of ENSO. During the austral spring, the CP type of ENSO induces a planetary wave in the troposphere by increasing convective activity around the Convergence Zone of the South Pacific, which then travels upward around high latitudes of the Antarctic stratosphere and subsequently can impact on the Antarctic sea ice concentrations (Song et al. 2011) as well as surface temperatures (Schneider et al. 2012). During the austral summer, the response mainly involved high stratospheric polar temperatures (Hurwitz et al. 2011a; Zubiaurre and Calvo 2012; Hurwitz et al. 2011b). The influence of the EP ENSO is mainly noticed in the Northern Hemisphere (NH) polar region, and one mechanism is also proposed (Manzini et al. 2006; Randel et al. 2009; Garcı’a-Herrera et al., 2006). It suggested that during EN, EP-ENSO events influence the North Pacific low in the winter and subsequently increase the planetary wave forcing and reduce the strength of the polar vortex. However, there are also controversies relating to the response of the NH to both types of ENSO, CP ENSO (Graf and Zanchettin 2012; Xie et al. 2012; Hegyi and Deng 2011) and EP ENSO (Mitchell et al. 2011; Manzini et al. 2006) as models differ with observation. It is noteworthy that though CP ENSO and ENSO Modoki are the same in main features, they still differ in details; the same is also true for EP and Canonical ENSO. This study, however, focuses on main features. As discussed, ENSO extratropical connection could be an important area to explore, and this study attends those parts. It considered both polar regions (north and south) separately and also focused on Pacific Ocean alone.

Models are the most viable tool to improve our understanding on mechanisms. The latest effort among different modelling communities around the globe conducted similar experiments known as Coupled Model Inter-comparison Project 5th phase (CMIP5)1. These models can simulate ENSO-like variability, have interactive oceans and also are capable of generating inter-annual variability of SST with realistic amplitude in the location of eastern and central Pacific (Bellenger et al. 2014). Compared to CMIP3 (Coupled Model Inter-comparison Project, 3rd phase), more CMIP5 models suggest a reasonable range of ENSO of 2 to 7 years period for Canonical Phase. Research (Bellenger et al. 2014) showed that SST anomalies peaking around northern winter, as noticed in observation, are seen in nearly half of the models. Few other recent studies also analysed various aspects of ENSO in CMIP5 models. Dufresne et al. (2013) focused on one particular model IPSL-CM5 and compared CMIP5 version with CMIP3. Spectral peaks around 3–3.5 years are identified in CMIP5 version, which was only around 2.7 years for the earlier version. The feedback between the east-west SST gradient, wind speed (Bjerknes feedback) and heat (shortwave and the latent heat) flux feedback are evaluated. Their results showed that the representation of physical processes strongly influences the results. The feedback from shortwave has a key role in explaining the spread of ENSO characteristics among models (Dufresne et al. 2013; Lloyd et al. 2012). Chen et al. (2017) used anomaly composites and showed most CMIP5 models perform better for EN than LN. Also, models behave better in predicting ENSO precipitation patterns than those from temperature patterns. Kim and Yu (2012) showed that CMIP5 models simulate the observed spatial patterns of the two types of ENSO better in comparison to the CMIP3 and CMIP5 set of models significantly reduced the inter-model diversity in ENSO intensities. It is particularly obvious in the EP types of ENSO; though in terms of reproducing observed ENSO intensity, the performance of CP ENSO is better. Taschetto (2014) discussed that in terms of observed location of maximum SST anomalies and intensity during ENSO events, most models simulate realistically. Almost all CMIP5 models suggested that EN is stronger than LN. ENSO-related various teleconnections were also investigated in many recent research using observation and CMIP5 outputs (extratropical influence: Hurtitz et al. 2014; Indian Summer Monsoon (ISM): Roy and Collins 2015; Jourdain, 2013; Roy 2017; East Asian winter monsoon: Gong et al. (2014, 2015)). This study examines Canonical and Modoki ENSO phase, focusing on CMIP5 models and observation and discusses some oceanic teleconnections.

Few of the primary aims of the CMIP5 project are determining the mechanisms accountable for differences among models and assessing the reason why models indicate varied responses under similar forcing scenario. The present work tries to address those areas evaluating different ENSO spatial patterns, using CMIP5 model output. This study also identifies areas where models show high credentials and examines potential drivers for ENSO mechanism.

2 Methodology

Several indices of ENSO are introduced to represent and quantify its diversity (Capotondi et al. 2015). In the current study, only ENSO indices constructed from SSTs are considered and four different regions of the tropical Pacific Ocean are used for that purpose (Fig. 1): Region A (165° E–140° W, 10° S–10° N), the canonical region (90° W–140° W, 5° N–5° S), region B (110° W–70° W, 15° S–5° N) and region C (125° E–145° E, 10° S–20° N). Anomalies in area mean SSTs (ASST) are calculated in those four regions.

Fig. 1
figure 1

Regions of the Tropical Pacific Ocean used for defining the different types of ENSO. Latitude is shown for 20° N to 20° S, while longitude for 120° E to 290° E (70° W)

Full size image

An ENSO Modoki Index (EMI) is defined as follows (Ashok et al. 2007):

$$ \mathrm{EMI}={\mathrm{ASST}}_{\mathbf{A}}-0.5\times {\mathrm{ASST}}_{\mathbf{B}}-0.5\times {\mathrm{ASST}}_{\mathbf{C}} $$
(1)

It considers a warming of SSTs in region A (ASSTA), and a decrease in SST in regions B (ASSTB) and C (ASSTC). The different types of ENSO defined those considered various regions and also used Eq. 1 (Kao and Yu 2009; Kug et al. 2009; Ashok et al. 2007; Tedeschi et al. 2013) as follows:

  • Modoki ENSO (ENM/LNM): EMI is ± 0.7σM, where σM is the standard deviations (std) of EMI. Also, ASSTs in region A need to exceed 0.7 std.

  • Canonical ENSO (ENC/LNC): ASSTs in the Canonical region are ± 0.7σC, where σC is the std. of SSTs in that region.

  • Canonical and Modoki ENSO (ENCM/LNCM): This occurs when both the criteria defining ENSO according to the Modoki and Canonical definitions are met.

The technique of compositing is applied where the significance is tested based on hypergeometric test (Meyer 1970). Such a technique of significant testing is previously been used in other studies, e.g., Grimm (2004) and Tedeschi et al. (2013).

Previous studies have indicated that EN and LN are not the reverse mirror images of each other (Hannachi et al. 2003; Monahan and Dai 2004; An and Jin 2004). There is a difference in the duration (Okumura and Deser 2010), spatial signature (McPhaden and Zhang 2009) and also in their formation mechanism (Okumura et al. 2011; Ohba and Ueda 2009), which are not yet fully understood. For this reason, the positive and negative phases of ENSO, i.e., EN and LN, respectively, need to be examined separately through composite technique, for instance. In comparison to other commonly used techniques such as correlation and linear regression, composite techniques are more suitable to isolate EN-related features from those of LN, and hence, this technique is applied here.

The models were also categorised as either high top (H) or low top (L), to determine whether one category of models performs better over the other. Such a classification was also considered in previous studies (e.g. Hurwitz et al. 2014; Charlton-Perez et al. 2013). H tops have few model layers in the stratosphere and have upper lids up to the stratopause. H models are believed to capture polar vortex feature and hence likely equipped with better representation of polar annular modes. Amita et al. (2016) on the other hand using observational analysis discussed a connection between Southern Annular Mode (SAM) and ENSO Modoki. SAM is originated in the upper stratosphere and related to stratospheric polar vortex features. Hence, our initial task was also to examine whether ENSO Modoki features and related oceanic teleconnections are better captured for H models than L.

Roy et al. (2017) considered the period June-July-August (JJA) and analysed ENSO-ISM teleconnection. It showed that observed regional spatial patterns in different ENSO phases are not very well captured by models. ISM during JJA plays an important role to modulate global scale summer north-south Hadley circulation (Trenberth et al., 2006) and thus also has contributions on ENSO-related global scale teleconnection. Roy and Tedeschi (2016) further showed during JJA that meridional upper level wind component (V 200) is captured well by all models and those show reasonable consistencies. Surprisingly, model results largely deviate from observation, indicating that some observed teleconnection features between mid-latitude and tropics are missed by all models. That is the reason we mainly focused here on JJA to further advance ENSO-related teleconnection and ambiguities.

The SSTs were obtained from observational datasets and outputs from the CMIP5 models (Taylor et al. 2012). The observational data were obtained from the Met Office Hadley Centre Sea Ice and SST (HadISST) dataset (Rayner et al. (2003). The SST data are available monthly and globally on a 1° latitude × 1° longitude grid and a unique combination of monthly globally complete fields of sea ice concentration and SST, which is available from 1870 to date. We considered the period of 1870 to 2010. Altogether, a total of 23 CMIP5 models (those that are widely used and that also have AMIP or atmosphere only version) were selected (Table 1) with data extracted for the historical simulation during the period 1861–2005. Some models only have one ensemble member and, hence, for consistency, the first ensemble member from each of the 23 models was considered. To preserve consistency with observation, all model SST data are regrided in 1° latitude × 1° longitude grid scale.

Table 1 The CMIP5 models selected for this study, models categorised as low top (L) or high top (H)
Full size table

3 Results

The structure of the Canonical, Modoki, and the case of a combined Canonical-Modoki ENSO is investigated during composite events of both EN and LN.

3.1 SST composites during EN

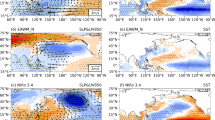
Figure 2A illustrates the structure of SSTs worldwide during various composites of EN events in observations, and the simulation of the GFDL-CM3 and MIROC5 models.

Fig. 2
figure 2figure 2

EN/LN composites showing anomalies in SSTs (°C) during JJA, comparing one typical high top (GFDL-CM3) and low top model (MIROC5) with observations (HadISST). The composite structure during ENC years (a, d, g), for ENCM years (b, e, h) and for ENM years (c, f, i). The regions with a black contour are statistically significant at the 95% confidence level. A For EN. B For LN. In A Top panel, regions of four SST criteria are marked by different coloured boxes (criteria SST I by pink, criteria SST II and III by red and criteria SST IV by green)

Full size image

Observation-HadISST

Observation suggests opposite signal outside tropics of Pacific, resembling a horseshoe pattern, which is noticed for ENC and ENCM. Different signed SST in tropical Pacific to that in Atlantic for ENCM and ENM is also detected. It also includes a region of North Atlantic around places of Greenland. A similarly signed signature around the Arabian Sea can also be marked for ENC.

CMIP5 (high top) model—GFDL-CM3

GFDL-CM3 overestimates amplitude of ENCM, ENM, while underestimates ENC. Opposite strong signature around Greenland for ENCM and ENM is not seen. Also, around tropical Atlantic, that extensive cooling pattern is missing. Horseshoe design as noticed in observation is also not present for ENC and ENCM. Signals are noted around the Southern ocean, though lacking in the observation.

CMIP5 (low top) model—MIROC5

MIROC5 overestimates all three types of EN. Pacific horseshoe pattern though present for ENC and ENCM, but is overestimated. It detects similar horseshoe pattern around north Pacific for ENM, which is not present in observation. The signal in Atlantic region for ENCM and ENM as detected in observation is missing. Also, a strong signal in the Southern Ocean is noticed.

3.2 SST composites LN: teleconnection in observations, GFDL-CM3 and MIROC5 models

Figure 2B illustrates the structure of SSTs worldwide during various composites of LN events according to observations, and the simulation of the GFDL-CM3 and MIROC5 models.

Observation-HadISST

Opposite signal outside tropics of Pacific, as horseshoe pattern, is mainly noticed for LNCM. Also different signed SSTs are observed in tropical Pacific and Atlantic (including regions of Green Land) for LNCM and LNM. In southern Pacific, beyond 45° S, some negative area is seen for LNCM.

CMIP5 (high top) model—GFDL-CM3

GFDL-CM3 overestimates amplitude of LNCM and LNM, while it underestimates LNC (like EN). Opposite signed horseshoe pattern in Pacific is noticed for LNCM and LNM, but not for LNC. Reverse signature in tropical Pacific and Atlantic (including Green Land) for LNCM and LNM is missed by model. A spurious signal is present in the Southern Ocean.

CMIP5 (low top) model-MIROC5

MIROC5 overestimates tropical Pacific signature and also fails to capture the spatial pattern of LNM. A cold region that covers the whole of the west coastal places of USA is noticed in the model for LNM, but not at all present in the observation. Opposite horseshoe pattern is also missing for LNC. Positive signature around Atlantic (including Greenland) is not captured for LNCM and LNM. Signal around Southern Pacific is a similar sign with observation for LNCM, though other signals in the Southern Ocean are spurious.

3.3 SST composites: EN and LN in the models

A visual inspection of Fig. 2A, B shows clearly that SST in different forms of El Niño phases is not exactly opposite of La Niña phases in observation, a result in agreement with previous studies (Taschetto, 2014; Chen et al. 2017). LNM and ENM, however, show different pattern in observation around Atlantic and Pacific. LNCM covers the whole of the west coast of USA but not ENCM. For LNCM and ENCM, there is also asymmetry in observation around Southern Pacific near poles; LNCM detects cold signature, which is missing for ENCM. Warming around the Arabian Sea is seen for ENC, but not for LNC. In terms of two models, GFDL-CM3, however, suggests closer match to observation than MIROC5, based on spatial pattern and magnitude. Now, if we focus on various model results from the CMIP5 output, it is noticed that most of the simulated responses of EN and LN have opposite sign as also observed by Hurwitz et al. (2014).

To discuss the results of rest of the models, we present new figures (Fig. S1 and S2), where models are separated as high top and low top and also EN and LN. To elaborate discussion using various CMIP5 models, following analyses are done. We only selected few SST criteria, to compare performances between observation and models. The focus was to test tropic-extratropic connection and to analyse Atlantic and Pacific behaviour. Former criteria were tested noting Tropical Pacific SST teleconnection with SST in three different regions: in the Pacific Ocean, SH and regions of north Atlantic near Greenland. The later criteria examined how Atlantic ocean SST acted as a precursor of tropical Pacific SST and was tested choosing two different locations of Atlantic: north Atlantic near Greenland and tropical Atlantic. Good/bad models are identified which can be used for future prediction and model evaluation purposes.

The following four SST criteria (SST-I: IV) are chosen (also marked in Fig. 2A top panel), and Table 2 is formulated based on those:

  • SST-I: Opposite signal outside tropics of Pacific resembling a horseshoe pattern mainly for LNCM and ENCM/ENC

  • SST-II: Opposite signature in tropical Pacific and Atlantic for ENM/LNM and ENCM/LNCM (extensive in tropical Atlantic)

  • SST-III: Opposite signal in north Atlantic near Greenland for (EN/LN) CM and (EN/LN) M

  • SST-IV: Spurious signature in SH beyond 45° S, significant change in model SST but not in observation. An exception, the negative signal in LNCM observation, but missing in most models

Table 2 Percentage of models satisfying various criteria of SST composites (SST-I: IV) for both El Niño (EN) and La Niña (LN) events with a further categorisation according to whether the model is high top (H) or low top (L)
Full size table

SST-I: Missing in most models. However, low tops are better than high tops, and we identified those models that agree with observation. High Top: LNCM only HadGEM2-CC; ENCM only GFDL-CM3. Low Top: LNCM-MIROC5, CSIRO-Mk3.6.0; ENCM-MIROC5, NorESM1-M, CMCC-CM, CSIRO-Mk3.6.0; ENC: MIROC5 (overestimates), CCSM4.

SST-II: Missing in almost all models. Only two low top models show for LNM are CNRM-CM5 and CMCC-CM.

SST-III: Missing in most of the models. The connection of ENSO with NH polar region through polar vortex or wave propagation is not captured well by models around Greenland area. Various studies discussed the controversies relating to connection between ENSO and NH polar region in both phases of ENSO, e.g., Modoki ENSO (Xie et al. 2012; Graf and Zanchettin 2012; Hegyi and Deng 2011) and Canonical ENSO (Mitchell et al. 2011; Manzini et al. 2006). Identified good models are low top (EN)—inmcm4, FIO-ESM; low top (LN)—GFDL-ENM2G, ACCESS1-3, bcc-csm1-1; high top (EN)—GFDL-CM3, HadGEM2-CC, MIROC-ESM; high top (LN)—no model.

SST-IV: SH beyond 45° S, significant change in SST is produced by model simulations, but not in observation, with an exception for ENCM-inmcm4, MPI-ESM-LR. SH extra-tropic connection of ENSO is not noticed in observation but captured by models. Signal around the Southern Ocean is only noticed for LNCM in observation. Such signal is also captured by 50% high top models and agrees with Hurwitz et al. (2014). They showed that ENSO-related variability around polar stratosphere in SH is best reproduced in the ‘H’ sets of models with a well-represented stratospheric features. Models in rest of SH for other ENSO phases fail to match with observation agreeing with the controversies relating to ENSO-SH teleconnection (Song et al. 2011; Hurwitz et al. 2011a; Schneider et al. 2012).

It is noteworthy that though SST signature in Atlantic is opposite to that of the tropical Pacific as observed for Modoki related phase, which is not at all the case for either ENC or LNC category. Hence, ENC and LNC in Table were kept blank for criteria SST-II and III. For criteria SST-I, opposite SST around north Pacific to that from tropical Pacific is not noticed for ENM in observation and kept blank in Table 2. For SST-I, LNC and LNM are also not very distinctly noticed and hence also not included in Table 2. The main observation from all these analyses and results presented in Table 2 are that in all four categories of SST, models are represented very poorly. SST-II is missing in almost all models. For SST-I, II and III, low tops are better, while for SST-IV, high tops are better. SST plots show that it is possible that North America and South America can have a major direct influence of Canonical and Modoki ENSO, due to the closer proximity of tropical Pacific. For SST plot, the direct impact in the Indian subcontinent is only seen for ENC in the Arabian Sea. However, this study showed weak representation of models in detecting some extratropics and circulation-related signals as captured in SST. Though tropics extra-tropics connection of ENSO in models need attention, almost all models capture tropical Pacific SST anomaly pattern reasonably well. Such analyses can be useful in improving model-generated ENSO.

Apart from those four criteria, few other points are also noticed for models as mentioned here: (i) FGOALs-s2 cannot capture the spatial pattern of ENCM, ENM, while IPSL-CM5A-MR cannot capture the spatial pattern of ENM; and (ii) for ENC, a positive signal around the Arabian Sea covering West Coast of India seen in observation is missing in almost all models with the exception—low top: BNU-ESM, FGOALS-s2, MIROC5; high top: MPI-ESM-LR.

As separating models as H or L top did not suggest substantial better performance of one set of models over the other, the subsequent analyses did not consider that separation. The results presented here are also shown not dependent on the category of models (H or L).

3.4 Atlantic vs. tropical Pacific: features of Modoki ENSO episodes

Studies suggested a connection between Pacific Niño and SST around North and tropical Atlantic (Polo et al. 2014; Martin-Rey et al. 2015; Ham et al. 2013a, 2013b). McGregor et al. (2014) even showed that the strengthening of Walker circulation and cooling of Pacific in recent days was amplified by warming in the Atlantic. Regarding mechanism, all those studies indicated about excitation of Modoki or Canonical phase of ENSO via Atlantic. To have a clearer overview, we further considered a combined situation of the Canonical and Modoki case (ENCM/LNCM). The observed SST signature in Pacific and Atlantic, opposite in nature, is most distinctive for combined Canonical and Modoki case and hence that phase was chosen here. Two specific locations in Atlantic are considered: one around North Atlantic, close to Green Land and marked as GRN (290° W, 350° W, 45° N, 80° N), and the other is in tropical Atlantic and marked as ATL (290° W, 350° W, 20° S, 20° N).

Mean value of SST around GRN and ATL region is calculated for each CMIP5 models for different ENSO phases. The mean of model ensemble is also calculated alongside observed mean SST. Those values are plotted in Fig. 3 to show Atlantic vs. tropical Pacific SST behaviour for Canonical and Modoki combined phase, (a) for ENCM and (b) for LNCM. SST around Atlantic (y-axis) is shown against tropical Pacific SST (x-axis). Top panels of Fig. 3a, b consider SST of central Pacific and bottom panel for east Pacific. The right panel is for Green Land region (GRN), a place around north Atlantic, while the left panel shows the result for tropical Atlantic (ATL).

Fig. 3
figure 3figure 3

Plot of SSTs in the tropical Atlantic vs. Pacific Ocean for various SST composites of Canonical and Modoki combined phase. a For ENCM. b For LNCM. Top panels consider SST of central Pacific (PacC) and bottom panel for east Pacific (PacE). The right panel is for the North Atlantic region in the area around Greenland (GRN), while the left panel is for tropical Atlantic (ATL)

Full size image

In each plot, a blue diamond marks observation, and model results are shown by red, while black diamond presents mean of model ensembles. The results presented are consistent with the observations of SST criteria II and III of Table 2. Interestingly, in all plots of Fig. 3, model ensemble (black) widely deviates from observation (blue). In all cases, they even show a change in sign (as seen from y-axis). Such tendency is noticed in both the phases of EN and LN, with reversed signature; for EN, observed SST is negative, though positive for LN. It indicates that model evaluation team needs to work in the area of tropical Pacific and Atlantic SST teleconnection, as all models show considerable disagreement with observation.

3.5 Tropical Pacific SSTs: high credential in models

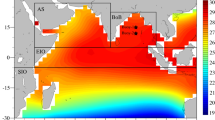
Figure 4 depicts modelled SST in tropical Pacific for Canonical and Modoki ENSO. The purpose is to identify further features of SST; those are reasonably well reproduced by models and hence need lesser attention over others. Choosing regions from east tropical Pacific (PacE) for Canonical ENSO (left) and regions of central tropical Pacific (PacC) for Modoki ENSO (right), we compare observed SST with modelled SST (Fig. 4a). LN years show negative SST, while EN indicates positive. Interestingly, all observation lies in the range of respective CMIP5 models category, with model ensemble lie closer to observation. For Canonical ENSO (left) LN, model ensemble and observation even match perfectly well and hence one shown overlaid on the other; however, for EN, it shows largest deviations. On the other hand, Modoki ENSO (right) suggests similar variation (amplitude) for both EN and LN phases. Modoki also indicate lesser mean observed SST value for both EN and LN phases than that from its respective counterpart in Canonical phase (as both have same x-axis range). Analysing spatial pattern, Roy et al. (2017) earlier discussed that in terms of sign of SST, all CMIP5 models agree with observed SST composites. Ensemble mean SST spatial pattern of 23 models is also presented (Fig. 4b), which are in agreement with tropical Pacific observed SST signature of respective category (Fig. 2). Thus, results of Fig. 4 are also in agreement with Taschetto (2014).

Fig. 4
figure 4figure 4

Observed vs. Modelled SST in tropical Pacific for Canonical and Modoki ENSO (a). For Canonical ENSO (top), regions from east tropical Pacific (PacE) are chosen, and for Modoki ENSO (bottom), it is from central tropical Pacific (PacC). In a CMIP5 models are shown by red circle, observation by blue diamond and ensemble mean of models by black diamond. b Spatial pattern of ensemble mean SST of 23 models for Canonical (left) and Modoki (right) ENSO phase, top for EN and bottom for LN

Full size image

Outside of tropical Pacific, the disagreement in SST signals could be related to combined influence among tropical atmospheric circulation as well as a change in mean state of the ocean. The branches of Walker circulation around other ocean basins and its interaction with regional Hadley circulation might be responsible factors which are again heavily modulated by the mean oceanic state. The feedback from shortwave also plays an important part in the spread of ENSO characteristics among models (Dufresne et al. 2013; Lloyd et al. 2012). To understand dynamical reasons of models’ failure to replicate ENSO-related teleconnection (on ISM), Turner and Annamalai (2012) mentioned about lack of predictability of the decadal modulation. Other studies addressed the failure from various angles; those include aerosol-based changes (Bollasina et al. 2011), circulation-based changes (Annamalai et al. 2013) and sea-surface temperatures in the Indo-Pacific (Roxy et al. 2015, among others). Those could be few potential causes of biases in CMIP5 models.

4 Discussion

Using CMIP5 simulations, this work highlights the weakness and strength of models, in general, around different oceanic sectors. Various types of ENSO are studied to test whether models agree/disagree with observations. Regarding spatial pattern, few criteria were chosen which show major disagreement between models and observations.

Compositing studies of SST were examined with models based on four chosen criteria: (i) opposite signal outside tropics of Pacific as horseshoe pattern mainly for LNCM and ENCM/ENC, (ii) opposite signature in tropical Pacific and Atlantic for ENM/LNM and ENCM/LNCM (extensive in tropical Atlantic), (iii) signal around Greenland for (EN/LN) CM and (EN/LN) M, and (iv) southern hemisphere beyond 45° S—significant change in model SST but not in observation. The exception is a negative signal for LNCM in observation, but missing in most models.

In all four categories of SST, the models poorly represent the observations, indicating that further work is required on the tropical extra-tropical teleconnections associated with ENSO. Second criteria are missing in almost all models. Separating models as high or low top do not improve the results. It is also noted that composites of SST during El Niño vary from respective La Niña features in observation, though many models fail to differentiate and generate complete opposite spatial pattern. It also suggests that for Modoki cases, the areas of Pacific Nino and Atlantic SST teleconnections and related mechanisms are very poorly represented in almost all models. To eliminate such biases could be an important step for improved ENSO projections. Apart from weaknesses, it also highlights the strengths of CMIP5 models. Models, however, well reproduce tropical Pacific SST variability in both Canonical and Modoki phase and thus indicate about improved model performances in Pacific Niño regions.

The overall study indicates areas where models, in general, need improvements. Thus, the model evaluation team will be greatly benefitted.