Abstract
Climate models project that the northern high latitudes will warm at a rate in excess of the global mean. This will pose severe problems for Arctic and sub-Arctic infrastructure dependent on maintaining low temperatures for structural integrity. This is the case for the economically important Tibbitt to Contwoyto Winter Road (TCWR)—the world’s busiest heavy haul ice road, spanning 400 km across mostly frozen lakes within the Northwest Territories of Canada. In this study, future climate scenarios are developed for the region using statistical downscaling methods. In addition, changes in lake ice thickness are projected based on historical relationships between measured ice thickness and air temperatures. These projections are used to infer the theoretical operational dates of the TCWR based on weight limits for trucks on the ice. Results across three climate models driven by four RCPs reveal a considerable warming trend over the coming decades. Projected changes in ice thickness reveal a trend towards thinner lake ice and a reduced time window when lake ice is at sufficient thickness to support trucks on the ice road, driven by increasing future temperatures. Given the uncertainties inherent in climate modelling and the resultant projections, caution should be exercised in interpreting the magnitude of these scenarios. More certain is the direction of change, with a clear trend towards winter warming that will reduce the operation time window of the TCWR. This illustrates the need for planners and policymakers to consider future changes in climate when planning annual haulage along the TCWR.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Globally averaged temperatures have increased by 0.65–1.06 °C between 1880 and 2012 (Hartmann et al. 2013), with Arctic regions warming at almost double the global rate since the 1980s (Larsen et al. 2014). This has resulted in widespread changes to the cryosphere, including a reduction in annual Arctic sea ice extent; a decrease in the average winter sea ice thickness within the Arctic basin; shrinking of almost all glaciers worldwide; accelerated ice loss from the Greenland ice sheet; a decrease in northern hemisphere snow cover extent; a decrease in lake and river ice duration; significant permafrost degradation and a decrease in the depth of seasonally frozen ground (Vaughan et al. 2013). These trends are expected to continue as global temperatures continue to rise. Climate models project a globally averaged temperature increase of 0.3–4.8 °C by the end of the twenty-first century, with a very high confidence that Arctic regions will warm most (Collins et al. 2013). This will have severe implications for socio-economic systems in northern latitudes, where much of the infrastructure, natural resources and transportation sectors have been designed around environments dominated by snow and ice (Prowse et al. 2009).
1.1 Climate impacts on northern infrastructure
The cryospheric changes impacting northern infrastructure include thawing permafrost, which is being experienced across much of the northern hemisphere (Anisimov et al. 2007). In addition to the many other negative impacts associated with increasing active layer thickness, such as contaminant and carbon release, the economy of northern countries can be profoundly affected (Instanes et al. 2005; Anisimov et al. 2007). For example, in Dawson City, Yukon, northern Canada, construction over ice-rich alluvial sediments in a permafrost zone in the 1890s (Hughes 1989) led to damaged buildings and impassable roads as ground ice thawed in subsequent decades (Prowse et al. 2009). This is also true in other regions of northern Canada, including the Northwest Territories (NWT). In the short term, it is ground disturbance and construction that causes most rapid permafrost thaw, whilst the impacts of climate change become increasingly significant over longer timescales (Prowse et al. 2009). Consideration of climate change in the design phase of the natural resource industry, including infrastructure, has become a requirement of the Canadian environmental regulatory process (Lee 2000).
Another set of cryospheric impacts of climate change that will profoundly impact the socio-economic prosperity of high-latitude regions include future changes in lake and river ice regimes. These include delayed freeze-up, advanced break-up, thinner ice and increased water temperature (Dibike et al. 2011). Borshch et al. (2001) projected that a uniform warming of 2 °C over European Russia and western Siberia would advance river ice break up by 4–10 days and delay freeze-up by 4–12 days. Prowse et al. (2002) used GCM output to project a more extreme 15- to 35-day advance in river ice break up in northern regions of Canada. Based on studies of lakes in northern Europe, a 3 °C increase in air temperature could result in a decrease of up to 100–130 days in annual ice cover duration (Burn and Hag Elnur 2002; Thompson et al. 2005). In northern Canada, changes in lake ice regimes and the natural resource industry are linked. The continued success of the natural resource industry is dependent on changing lake ice modifying the viability of ice roads (herein referred to as winter roads). The Tibbitt to Contwoyto Winter Road (TCWR)—the world’s busiest heavy haul winter road—is one such example.
1.2 The TCWR
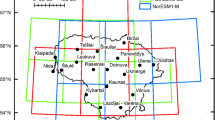
The TCWR (Fig. 1) is critical to the economy of NWT, Canada, with over $500 million of goods per year transported to service diamond mines and other industries in the region (JVMC, Joint Venture Management Committee 2015). The winter road is critical for the development of new natural resources, mainly diamonds and other high value commodities such as gold and base metals in the mineral rich Slave Geological Province (Prowse et al. 2009). Transportation of goods and services along the TCWR is vulnerable to climate change, since around 85 % is built over frozen lakes (JVMC, Joint Venture Management Committee 2015). The minimum ice thickness for hauling is 70 cm, with only very light loads travelling at this point, whilst an ice thickness of 107 cm is used as the threshold for the heaviest 42 t Super B tankers fully loaded with 50,000 l of fuel (Perrin et al. 2015). The TCWR is currently licensed and operated by the Winter Road Joint Venture (WRJV)—a private-sector partnership between BHP Billiton, Diavik Diamond Mines and Echo Bay Mines. The WRJV archives annual statistics of the usage of the winter road from 2002 to 2012 (JVMC, Joint Venture Management Committee 2015). Usage of the road has increased substantially since its construction in the early 1980s, with an all-time maximum of 10,922 truckloads travelling north on the route in 2007 to support the final phase of construction of Jericho diamond mine, making it the busiest heavy haul ice road in the world (Perrin et al. 2015). Since 2007, more modest transportation numbers have supported operation of the Ekati and Diavik diamond mines, the Lupin gold mine (currently inactive), the Snap Lake and Jericho mine developments and several other mineral exploration projects (Prowse et al. 2009), with 6551 truckloads travelling north in 2012. As shown in Fig. 2, the truckloads travelling north have had to be fitted into a shortening time window in the past decade, with the road open for 80 days in 2002 and just 58 days in 2012. Table 1 presents some additional statistics on the dates the road has opened and closed as well as the amount of truckloads and tonnage of goods transported between 2002 and 2012. Changing transportation needs (e.g. building of a mine vs. operation) is one of the reasons for variations in the seasonal duration of the TCWR operation. Climate variability and change is another reason. Changing ice stability, thickness and duration of cover associated with recent climate variability have had negative impacts on the use of the road. For example, an unusually mild and stormy winter in 2005/06 associated with an El Niño year in 2004/05 resulted in a substantially shortened winter road operation (26 days below average) and significant industry financial losses. Air temperatures and precipitation have been rising throughout the TCWR region in recent decades (Fig. 3), which may also have played a role in reducing the time window of TCWR operation from 2002 to 2012. These observed changes in climate are shown for three climate stations in the region—Hay River (60° 49’ N) in the NWT on the northern shore of Great Slave Lake, Yellowknife (62° 26’ N) in the NWT near the southern end of the road and Lupin (65° 45’ N) in Nunavut near the northern extent of the road. The temperature increases shown here are well above the global average temperature increase of 0.65–1.06 °C between 1880 and 2012 (Hartmann et al. 2013), reflecting the amplified warming at high latitudes. High transportation costs for alternative routes (e.g. air) will have a major negative influence on the feasibility of any new mining operations, and therefore it is critical for policymakers, planners and mine developers to understand how future climate variability will impact the TCWR. In this respect, high resolution climate change scenarios for the region are vital to assist with this planning.
1.3 Generating regional and local climate scenarios
A number of studies have examined the impacts of future climate change over a wide spatial area across northern Canada. Stephenson et al. (2011) used the Community Climate System Model 3.0 (CCSM3) driven by the A1B SRES emissions scenarios (Nakicenovic et al. 2000) to project future changes in transportation systems across the Arctic. Results from the study illustrate declining winter road accessibility potential on land and rising ship accessibility potential in the Arctic Ocean. This study derived results directly from a coupled atmosphere-ocean general circulation model (AOGCM or simply GCM) whilst most recent studies downscale the GCM output to a finer spatial scale for more direct relevance to the regional or local climate. Downscaling can broadly be separated into dynamical downscaling (DD)—involving the nesting of a regional model within a coarser GCM, or statistical downscaling (SD)—involving the establishment of statistical relationships between coarse GCM output and local climate (Wilby and Dawson 2007). Kiilsholm et al. (2003) used the HIRHAM regional climate model (Christensen et al. 1998; Christensen and Kuhry 2000) to simulate future climate change across all latitudes north of 65° (partly encompassing the geographical focus of this paper). The HIRHAM model is driven by the ECHAM4/OPYC3 model (Roeckner et al. 1996) and develops climate scenarios at a horizontal spatial resolution of 50 km. Plummer et al. (2006) used the Canadian Regional Climate Model (CRCM) (Laprise et al. 2003) driven by the Canadian GCM version 2 (CGCM2) (Flato and Boer 2001) develop regional climate scenarios for North America. The Mackenzie Valley and East Arctic regions (encompassing the study area of this paper) are among the regions where largest temperature increases were projected, by up to 6 °C during winter for the period 2041–60 relative to 1971–90. Precipitation is more variable between scenarios, but increases of up to 30 % for winter were projected for the East Arctic region. Mearns et al. (2013) applied 11 RCMs across North America at a spatial resolution of 0.5° × 0.5° and calculated changes in temperature and precipitation from 2041 to 2070 relative to 1971–2000. Results show temperature increases of 3.0–4.5 °C in winter and 0.5–3.5 °C in summer, with precipitation changes of 5–30 % and −5 to 25 % for the same seasons.
SD methods, meanwhile, were used by Perrin et al. (2015) to develop site-specific climate scenarios for Yellowknife in order to project changes in lake ice thickness and infer changes in the operation dates of the TCWR. This study used an ensemble monthly mean of all Coupled Model Intercomparison Project (CMIP5) climate models driven by two contrasting Representative Concentration Pathways (RCPs) to perturb observed monthly temperature values at the Yellowknife climate station. This form of SD is referred to as ‘change factor’ (CF) downscaling. CF is an established and conceptually straightforward technique for downscaling future climate projections (Arnell and Reynard 1996; Arnell 1998; Pilling and Jones 1999; Arnell et al. 2003; Diaz-Nieto and Wilby 2005). The main advantage is the simplicity and speed of calculation, whilst the main limitation is that changed baseline time series differ only in terms of their respected means, with important properties such as the range and temporal sequencing remaining unchanged (Diaz-Nieto and Wilby 2005). The other issue with the approach of Perrin et al. (2015) is that the use of a single mean ensemble of all CMIP5 climate models does not facilitate an examination of single model projections that showcase extreme temperature changes.
In this study, we apply a more sophisticated SD method that allows the mean and additional statistical properties of the observed climate to be perturbed under the guidance of three CMIP5 climate models on an individual basis, driven by four RCPs. In addition, we temporally downscale the future scenarios to a daily temporal resolution to facilitate the prediction of future lake ice thickness and ultimately inference on future TCWR operation. The SD method is a two-step process that first involves spatial downscaling of monthly GCM output to a target station using quantile mapping, and second the temporal downscaling of monthly projections to daily using a weather generator (Zhang 2005, 2012; Zhang et al. 2012). There are three potential key advantages of the approach outlined here over other SD methods. First, the method requires monthly projections, which are known to be more accurately simulated than daily projections (Maurer and Hidalgo 2007) and are often more accessible from climate modelling experiments (Chen et al. 2014). Second, use of a direct surface climate variable for downscaling the same variable (e.g. use of precipitation as a predictor for downscaling precipitation) has been shown in some cases to capture more explained variance in the predictand than other large-scale atmospheric and surface variables (Widmann et al. 2003; Schmidli et al. 2006; Chen et al. 2012; Chen et al. 2014). And third, the method is less time consuming than other SD approaches that carefully screen and shortlist a selection of predictors prior to downscaling (Mullan et al. 2012). This methodology was outlined in Zhang (2005) and has been used and extensively tested for stationary and non-stationary climates across a range of global climatic zones with satisfactory results (Zhang 2005, 2012; Zhang et al. 2012; Mullan et al. 2015).
2 Materials and methods
2.1 Datasets
Observed daily climate data for TMIN, TMAX and PPT for the three climate stations as shown in Fig. 3 and described in Table 2 was acquired from the Climate Research Division, Environment Canada (Mekis and Vincent 2011; Vincent et al. 2012). The three selected stations were the only available climate stations in the study region. Whilst observed changes in climate have been shown for all three climate stations in Fig. 3, future scenarios are developed for only one of these stations—Yellowknife. As a climate station nearest the southern extent of the TCWR, this station should be particularly appropriate in picking up the earliest signals of a changing climate for the TCWR.
In order to develop the future scenarios, the same three climatic variables as output as an ensemble mean by a set of three GCMs (GFDL-CM3, HadGEM2-AO and MIROC5) and forced by four RCPs at a monthly temporal resolution were downloaded also from the Climate Explorer site for the grid box overlying the target station. The selected climate models all participated in CMIP5—models which have all been used to develop the projections and model evaluations in the Intergovernmental Panel on Climate Change (IPCC) AR5. Climate model data for all GCMs involved a hindcast and future period, spanning the period 1861–2100. Details on the selected models are given in Table 3. The three models outlined in Table 3 were chosen specifically because (a) when examining their transient climate response (TCR), which is the change in global and annual mean surface temperature between the start of an experiment of increasing CO2 concentrations by 1 % year−1and the 20-year period centred on the time of CO2 doubling, they capture much of the spread across all CMIP5 models. The TCR range across all models is 1.1–2.6 °C, with our selected models having a TCR of 1.5, 2.0 and 2.4 °C; and (b) they are widely used models with a plethora of supporting literature on their model development and evaluation.
The RCPs replace the emissions scenarios used to drive climate model experiments from the IPCC Fourth Assessment Report. They represent four different pathways of radiative forcing up to the end of the twenty-first century, ranging from a low of 2.6 W/m2 to a high of 8.5 W/m2 (van Vuuren et al. 2011). These figures are the result of collaboration between integrated assessment modellers, climate modellers, terrestrial ecosystem modellers and emission inventory experts. Details about the RCPs are given in Table 4. Use of multiple climate models and driving RCPs in this manner allows us to characterise some of the uncertainty inherent in climate modelling, built on the premise that no single model or scenario represents a perfect projection.
In order to project estimated changes in the operational dates of the TCWR, ice thickness data for a single location in Yellowknife was downloaded from Environment Canada. The ice thickness data is approximately weekly in resolution and spans the period 1958–2012 (with a gap between 1997 and 2002). Ice thickness was measured to the nearest centimetre using either a special auger kit or a hot wire ice thickness gauge (Environment Canada 2012).
2.2 Spatial downscaling of climate model output
As shown in Table 2, climate data for Yellowknife spans the period 1943–2012. Both observed station data and GCM data were split into a 50-year calibration period (1963–2012) to develop transfer functions and a 20-year validation period (1943–1962) to assess model performance. The projected monthly climatic data (TMAX, TMIN and PPT) and observed station data for the calibration period were spatially downscaled using quantile mapping. For each calendar month, the ranked observational monthly TMAX, TMIN or PPT (Y-axis) was plotted against the ranked GCM-projected TMAX, TMIN or PPT (x-axis) using QQ-plots. A simple univariate linear function was fitted to each plot to construct transfer functions on a monthly basis. Several non-linear functions were also fitted to each plot on a monthly basis to examine if these offered any considerable improvement in fit over the linear functions, but since the difference was negligible calibration was carried out on the linear functions.
These calibrated transfer functions derived from the univariate linear regressions were then applied to the full period of the GCM data in order to construct a spatially downscaled series for each station from 1861 to 2100. The probability distributions of the downscaled series were then compared with those of the observed monthly series during the calibration period (1963–2012). As a test of model performance, probability distributions of observed, raw GCM and downscaled series were compared for the validation period (1943–1962). Finally, the downscaled series for the remainder of the century were used as the basis for considering future scenarios at Yellowknife. In all instances, the 8-month period from September–April is considered in this analysis, as these are the months of concern for the winter road in terms of formation and operation. As shown in Table 1, the months of operation tend to span January/February–March/April, with the preceding autumn and early winter months crucial in the construction of the winter road.
2.3 Temporal downscaling of climate model output
For the subsequent analysis projecting changes in lake ice thickness, it was necessary to generate daily temperature data (TMAX and TMIN) from the monthly downscaled data. This temporal downscaling was achieved using the weather generator CLIGEN (Nicks et al. 1995). CLIGEN is a stochastic weather generator that produces daily estimates of precipitation, temperature dewpoint, wind and solar radiation for a single location (Nicks et al. 1995). A first-order, two-state Markov chain is used to generate precipitation occurrence for a given day given the wet or dry status of the previous day. If a random number derived from a standard uniform distribution is lower than the conditional probability of precipitation for the previous day, a precipitation event is simulated, with a skewed normal distribution then used to generate precipitation amount for wet days (Nicks et al. 1995). For further details on CLIGEN, readers are referred to Nicks et al. (1995). CLIGEN requires monthly means and variances of TMAX and TMIN, which are then temporally disaggregated into daily series. Spatially downscaled means of TMAX and TMIN were directly used in CLIGEN as the perturbed monthly means for each of the future climate scenarios. To obtain the variances, the observed baseline daily temperature variances were multiplied by a calculated variance ratio for each month. This variance ratio was calculated as the variance of the future time slice for each scenario divided by the variance from the hindcast period, i.e. 2016–2035, 2046–2065 and 2081–2100 respectively over 1986–2005 for each modelled scenario. This method is appropriate when autocorrelation coefficients of all orders in the baseline climate are similar to those of the downscaled climate (Katz 1985). This method was used in Zhang (2005). These new parameter values were input to CLIGEN, and 20 years of daily climate data for each future scenario was then generated (2016–2035, 2046–2065 and 2081–2100). CLIGEN was tested by generating a 70-year time series based on the observed climate at Yellowknife (1943–2012) and then comparing the generated monthly means of TMIN and TMAX (shown in Appendix 1) with the observed means, as well as comparing statistics on temperature extremes between the generated and observed climate (Appendix 2). As both appendices clearly show, CLIGEN closely mirrors the mean and extreme features of observed temperatures.
2.4 Projecting future ice thicknesses
In order to project ice thickness under the guidance of future climate scenarios, it was necessary to correlate historical ice thickness measurements against historical climate data from the Yellowknife climate station. Neither TMIN nor TMAX were strongly correlated to ice thickness since a single daily value is not representative of the longer-term climatic conditions necessary for the thickening of ice. An index that is widely known to be important in ice development is freezing degree days (FDDs) as used in Perrin et al. (2015). FDDs are calculated as days with mean temperatures below 0 °C (Assel 1980). Days when mean temperatures fall below freezing therefore give a positive FDD value, whilst days when temperatures exceed freezing count as negative FDDs. The FDDs were then summed throughout the year to build up cumulative FDDs (CFDDs). Since November is typically the month when mean temperatures consistently fall below 0 °C at Yellowknife and since May is typically the month where temperatures consistently rise above freezing, the calculation of CFDDs was made starting on 1 November for the observed record. CFDDs were also calculated for each future scenario using the same approach.
CFDDs (independent variable) were then correlated against ice thickness (dependent variable). A linear fit was established (r 2 = 0.79), with the relationship statistically significant (p < 0.001). This regression equation established for the historical period was then applied to each future scenario, which enabled the prediction of ice thickness at a daily temporal resolution for each future scenario. One limitation of the linear regression was the gradual manner in which predicted ice thicknesses reduced during the late spring and early summer months compared with the more rapid decline in the measured ice thickness owing to the more rapid decline of thinner ice. In order to address this, a correction factor (CF) was applied to the predicted ice thicknesses when the mean temperature on five or more consecutive days rose above freezing. Five or more consecutive days of temperatures above 0 °C is an index that illustrates quickly deteriorating ice thickness (Perrin et al. 2015) and therefore seemed a robust basis for applying a correction factor (CF). Several CFs were tested between 0.1 and 0.9, and it was found that during late spring/early summer (16 May onwards) a CF of 0.8 resulted in the closest comparison between measured and predicted ice thickness (mean absolute relative error (ARE) of 19.2 cm) compared to a mean ARE of 27.8 cm when left uncorrected.
The final aspect of the methodology was to use these future ice thickness predictions as a basis for considering future TCWR operation dates. To achieve this, two different ice thickness thresholds were applied to the observed record and each future scenario. The first threshold was 70 cm, as this is the ice thickness required to support the lightest vehicles on the TCWR and the normal threshold required for the road to open (Perrin et al. 2015). The second threshold was 107 cm, since this is the ice thickness required to support the weight of Super B capacity trucks (Perrin et al. 2015). The first day each year the ice thickness was predicted to reach these thresholds was used as an analogue for TCWR opening date (70 cm for light vehicles and 107 cm for heavy vehicles), with the next date the ice thickness fell below each threshold used as an analogue for TCWR closing date. In this respect, the predictions made here are theoretical opening and closing dates for Yellowknife, serving as an analogue for operation dates along the TCWR. The maximum ice thickness and estimated open and close dates of the TCWR were then compared between the historical and future period.
3 Results
3.1 Validation
The correlation coefficients of a selection of univariate linear regressions between corresponding quantiles of observed station series from Yellowknife vs. a selection of three model projected series for the calibration period are shown in Table 5. With coefficients in the range 0.88–0.99, it is clear that the univariate linear regressions are appropriate as a basis for spatially downscaling GCM projected data to the observed station scale. Figures 4 and 5 compare the probability distributions of monthly observed TMIN vs. monthly projected TMIN at the native GCM grid box scale (Fig. 4) and following spatial downscaling (Fig. 5) for one GCM (GFDL-CM3) and driven by one RCP (RCP 2.6) for the calibration period. These results clearly demonstrate a much closer fit between observed and projected series following the spatial downscaling step, which is ubiquitous throughout all scenarios. As a measure of model performance, Fig. 6 shows observed, raw GCM and downscaled TMIN, TMAX and PPT for the months of October, January and April for the validation period. This illustrates that spatial downscaling generally results in a closer fit to observed series than raw GCM scenarios for the independent validation period. As a further test of model performance, Appendices 3–5 compare downscaled TMIN, TMAX and PPT respectively (for all GCMs and RCPs) with observed series for the months January–April for the observed period. These results reveal a close agreement between the observed and downscaled series, indicating that the spatial downscaling has captured a considerable portion of the variance in the observed series, therefore providing confidence in future projections.
3.2 Future scenarios
Figures 7, 8 and 9 represent future time series for TMIN, TMAX and PPT for Yellowknife for the January–April period of TCWR operation, with the same variables shown for the September–December months of TCWR development in Appendices 6–8. Represented on each chart are scenarios from three GCMs driven by four RCPs. Tables 6, 7 and 8 represent these simulated variables as relative changes for three future time periods: near twenty-first century (2016–2035), mid twenty-first century (2046–2065) and late twenty-first century (2081–2100) relative to a modelled baseline period of 1986–2005. These time slices are the same periods used in the IPCC AR5.
3.2.1 Climatic changes during the months of winter road operation
Climatic changes during the months of winter road development are discussed in the Supplementary Information. In terms of months of operation, the mid-late winter months of January and February are the coldest months of the year and therefore act as vital months in the thickening of the winter road to levels conducive to heavy haul transport. This period also sees the opening of the winter road for transport north, with the road historically opening as early as January 26 in 2002 and 2005 (Table 1). Based on monthly means from the Yellowknife station averaged over the period 1986–2005, the observed baseline TMIN is −29.2 and −26.6 °C, with a TMAX baseline of −22.0 and −17.8 °C for January and February, respectively. As was the case with the late autumn and early winter months, projected changes in temperatures during these mid-late winter months are among the highest throughout the year, with the temperature response during February being particularly pronounced. By the end of the century, mean TMIN increases of 8.8 and 8.1 °C are projected, with mean TMAX increases of 7.7 and 6.4 °C for January and February, respectively, as shown in Tables 5 and 6. Some individual scenarios project much more extreme changes, with a full TMIN range of 2.9–15.8 °C and 2.5–16.4 °C for January and February, respectively, and a full TMAX range of 2.9–14.5 °C and 2.5–12.8 °C for the same months. Despite these extreme temperature increases, the absolute temperature for both months remains well below freezing point, with TMAX in February rising highest to temperatures around −5 °C. During the same two winter months, precipitation projections also show a large increasing trend, particularly during January. The mean change for the late twenty-first century is a 0.28-mm (21 %) increase and a 0.15-mm (19 %) increase for January and February, respectively, with a full range of 8–42 % and −3–60 %, respectively. As was the case with the previous months, the more extreme precipitation rise scenarios would result in enhanced snowfall and delayed thickening of the lake ice since temperatures during these 2 months remain well below freezing for all scenarios.
The early spring months have historically been key as operational dates for the TCWR, with the road closing as late as April 16 in 2002 (Table 1). The observed baseline TMIN and TMAX for March is −21.9 and −10.8 °C, respectively, with conditions warming substantially in April with a mean TMIN of −10.9 °C and an April TMAX above freezing at 0.4 °C. Like the early autumn months, temperature projections during the spring months exhibit a less pronounced increasing trend than the winter months. The projected increase for TMIN is 5.9 and 4.9 °C by the late twenty-first century during March and April, respectively, with a full range of 2.1–10.3 °C and −0.1–8.0 °C respectively for the same months. The mean increase for the same time period for TMAX is lower than TMIN at 4.0 and 2.7 °C for March and April, respectively, with a full range of 1.9–7.3 °C and −0.7–6.7 °C respectively for the same months. Precipitation changes during these months show increases of 0.15 and 0.10 mm, respectively (both 20 %), ranging from −18 to 60 % for March and −16 to 64 %, respectively. Due to the lower temperature increases projected for March than February, highest TMAX projections for March bring temperatures to a level only marginally higher than those of February, and still below freezing at around −3 °C by the end of the century. Once again with increasing precipitation during March, the sub-zero temperatures could enable enhanced snowfall and thus reduced potential for ice road thickening but more favourable conditions than rainfall during this key month that normally sees the closure of the road. In April, warmest scenarios project TMIN rising to levels around freezing point, whilst highest scenarios for TMAX project temperatures rising to levels close to 10 °C, meaning winter road operation would clearly be unfavourable this late in the spring season.
3.2.2 Projected changes in theoretical ‘operation’ dates
As shown in Table 9, the mean projected opening and closing dates for the TCWR for the historical period (1986–2005) is from 13 January to 31 May onwards (137+ days) for the 70-cm threshold, and from 12 March–3 May (52 days) for the 107-cm threshold. The observed mean operational dates for the TCWR between 2002 and 2012 are from 30 January to 1 April (62 days). The discrepancy in the timing of the opening can be explained by both physical and socio-economic factors. In terms of the physical factors, this analysis considers the relationship between lake ice thickness at a single point in a lake in Yellowknife with air temperatures only and does not account for the fact that the TCWR also straddles land portages between frozen lakes. It is well known that under ice waves created by truck traffic can reach the land portages and erode the ice from below, resulting in thinner ice than that formed at deeper parts of the lake (JVMC, Joint Venture Management Committee 2015). This could be one of the factors delaying the opening of the TCWR. In addition, this analysis considers only climatic factors. The later opening date in reality may be related to social and economic factors (e.g. Christmas holidays) delaying construction. The projections indicate that the TCWR could theoretically be open for longer, with just over an extra month of potential to support the heaviest vehicles projected in comparison to the actual observed dates. This may relate to the fact that all haulage is completed before the road becomes unusable to the heaviest vehicles.
Table 9 also shows the projected changes to the TCWR operational dates across all three GCMs, four RCPs and three future time slices. The mean operational dates across each future period reveal a considerable shortening trend for the operational dates of the TCWR from 137+ days for light vehicles during the historical period to 131+, 117+ and 75+ days for the near, mid and late twenty-first century, respectively. In every scenario except for two (HadGEM2-AO and MIROC5, both for RCP 8.5 for the late twenty-first century), all 19 years of each scenario projected that ice thicknesses of 70 cm would be reached. For the heavy vehicle threshold of 107 cm, many future scenarios project that this ice thickness will not be reached at any time of the year. The observed number of days this threshold is exceeded is 52 days. For the near twenty-first century, the projected number is 21 days, with several scenarios projecting some years where this threshold is never met. For the mid twenty-first century, the projected number is just 5 days, with only three of the 12 future scenarios projecting any days where this threshold is met. For the late twenty-first century, just one of the 12 future scenarios projects any days where the heavy vehicle threshold is met, with the mean projected number of days across all scenarios only at two. As might be expected, the higher RCPs result in a progressively shortening time window for the TCWR, with RCP 2.6 projecting 12 operational days and RCP 8.5 projecting just four on average for the heavy vehicle threshold. The HadGEM2-AO model results in the most extreme projections, simulating six operational days across all four RCPs, compared with 8 and 12 from GFDL-CM3 and MIROC5, respectively.
4 Discussion
The amplified warming apparent in the results of this study is consistent with higher than global average warming across high-latitude regions, but tend to exhibit considerably higher mean responses when compared with the literature. As an average across all CMIP5 model simulations, mean winter warming under RCP 4.5 is 4.6 °C across high-latitude regions spanning Canada, Greenland and Iceland by the end of the century, with a full range of −0.5–8.2 °C across all 42 CMIP5 models (Flato et al. 2013). By comparison, the average winter warming across the three GCMs under RCP 4.5 in this study is 7.2 °C, which is well in excess of the CMIP5 average winter warming, but within the full CMIP5 range. One of the three downscaled scenarios forming part of this 7.2 °C average (HadGEM2-AO) projects an 8.8 °C warming under RCP 4.5, which exceeds the range across 42 CMIP5 models for high-latitude regions by 0.6 °C. Precipitation scenarios compare closely with global projections for the same high-latitude regions. As an average across all CMIP5 model simulations driven by RCP 4.5, mean winter precipitation increases by around 15 % by the end of the century, with a large range spanning −2–32 % due to enhanced precipitation in extratropical cyclones (ETCs) (Flato et al. 2013). This figure compares reasonably closely with a 22 % increase when averaged across the downscaled scenarios driven by the three GCMs used in this study under the same forcing and time period as for the scenario described above. In addition, the range across the three GCMs in this study is 13–29 %, which lies within the range projected by the CMIP5 models. The warming bias among the downscaled scenarios used in this study could arise from three main sources, each of which will now be discussed.
4.1 Choice of GCM
A useful means of comparing GCMs to a given forcing is through the TCR (defined in Section 0). The full TCR range across all CMIP5 models is 1.1–2.6 °C. The TCR of the GCMs selected here is 1.5 °C (MIROC5), 2.0 °C (GFDL-CM3) and 2.4 °C (HadGEM2-AO). It is therefore unsurprising that the magnitude of temperature projections in this study follows the TCR, with lowest warming from MIROC5 and highest warming from HadGEM2-AO. For example, under RCP 4.5 forcing for the winter months by the end of the twenty-first century, MIROC5 projects a TMIN warming of 6.2 °C, compared with 7.9 °C for GFDL-CM3 and 9.3 °C for HadGEM2-AO. The TMAX warming is 5.4, 6.2 and 8.4 °C for the same three models, respectively. The climate sensitivity and transient climate response to a given radiative forcing depends largely on the response of mixed-phase clouds to radiative forcing (Tsushima et al. 2006). The MIROC5 model tends to exhibit a lower climate sensitivity due to the development of more low clouds and an associated negative shortwave feedback (Watanabe 2010), explaining why the temperature response from this model is the lowest of the three, in keeping with its low TCR. Higher climate sensitivity and warming appears to be evident in GFDL-CM3 for the opposite reasons—positive feedback leading to increased shortwave radiation absorption associated with inadequate simulation of marine stratocumulus clouds. This results in a major warm bias over high and middle latitudes in the Northern Hemisphere primarily during northern winter (Donner et al. 2011). In the case of HadGEM2-AO, updated atmosphere and land surface parameterisation schemes have reduced a warming bias from HadGEM1, yet a warm bias remains in the Northern Hemisphere continental regions (Hardiman et al. 2011). It is thought that these warm biases are not related to the inadequate simulation of low clouds but rather in the simulation of vegetation coverage and net primary productivity (NPP) over continental regions (Hardiman et al. 2011). These differences in model parameterisation schemes appear to largely account for the differences in ECS and consequently the temperature response. Although the GCMs selected for this study were chosen to span a wide range of the TCR range across all CMIP5 models, the warm biases simulated over the study region by two of the selected GCMs may be a chief reason for the high temperature increases projected here.
4.2 Downscaling calibration
Another potential reason for the enhanced winter warming in the downscaled scenarios may originate in the calibration procedure used to spatially downscale global projections from the three GCMs to the Yellowknife climate station. Despite achieving a much closer fit to observed temperatures when moving from a comparison with raw GCM temperatures (Fig. 4) to a comparison with spatially downscaled temperatures following spatial downscaling (Fig. 5), downscaled temperatures are slightly overestimated during some months. Appendices 1– 3 also illustrate this, where modelled scenarios more frequently rise above observed temperatures than below. One of the possible reasons for the slight warming bias following spatial downscaling could arise due to the issue of non-stationarity. This is one of the major theoretical weaknesses of statistical downscaling—that statistical relationships derived for the present day will hold under future climate forcing (Busuioc et al. 1999; Solman and Nuñez 1999; von Storch et al. 2000, Wilby and Wigley 2000, Wilby et al. 2004). The relationships between GCM output and observed climate are therefore assumed to be time-invariant, yet it is well known that transfer functions may become modified under future climate forcing (Wilby et al. 2004). Non-stationary climates can also represent a problem for statistical downscaling methods in terms of calibrating models based on time series that change considerably over time. For example, downscaling models for precipitation calibrated on wetter than average periods in the observed data is likely to overestimate future precipitation (Wilby et al. 1998). If a model can closely reproduce observed precipitation for a wetter period of an observed record based on calibrating on a drier period or vice-versa, then the model can be said to successfully simulate precipitation under non-stationary climatic conditions. In Fig. 3, it is clearly visible that both TMIN and TMAX decrease during the validation period (1943–1962) compared with the general rising trend visible during the calibration period (1963–2012). The calibration of monthly models during a warmer period in the record may be one of the factors resulting in overestimated temperatures, especially when compared with the colder validation period. As shown in Appendices 1– 3, however, downscaled temperatures correspond closely with observed temperatures for the observed period, providing confidence that the downscaled scenarios are robust as a basis for projecting future changes.
4.3 Increased spatial resolution
A third possibility for the winter warming bias may arise from the increased spatial resolution offered by the spatial downscaling technique. Features of significance to the local climate (e.g. orography, local vegetation dynamics, lake ice, etc.) cannot be captured adequately due to the coarse spatial resolution of the GCMs. Owing to the comparison with a large regional area across parts of northern Canada, Greenland and Iceland, some features of significance to the climate around Yellowknife may promote an enhanced warming when compared with the wider region. An example might be the thawing of lake ice across Slave Lake that could promote positive feedback and enhanced warming. Other factors might relate to treeline and albedo. Upiter et al. (2015) show that treelines moved at a rate of 20 km year−1 associated with warming of 1–2 °C (summer chironomid inferred air temperatures at Danny’s Lake). As treelines move further north, darker surfaces lower albedo and thus may enhance warming—a feature that may be picked up more strongly on a finer spatial scale.
5 Conclusions and implications
The key conclusions and implications from this study are as follows:
-
Almost all future scenarios reveal a warming trend throughout the twenty-first century, with marginal months around the key operational months of the TCWR such as November and April experiencing projected temperatures that will exceed freezing point by the end of the twenty-first century.
-
Temperature increases are most pronounced during the vital winter months for winter road construction and operation. Despite some extreme rises in temperature, maximum temperatures are not projected to rise above freezing point during the winter months December–February. Nonetheless, rising temperatures might be insufficient to support winter road formation required for heavy haul traffic.
-
Temperature scenarios in this study reveal a winter warming bias when compared with projections from a range of 42 CMIP5 models across the wider higher-latitude regions. This may relate to the simulation of a warm bias in the high latitudes in two of the three models, or could relate to a warming bias during the calibration phase of downscaling. Alternatively, this indicates a more enhanced warming in this continental interior region than may be expected elsewhere in high northern latitudes.
-
Precipitation increases during the same winter months will negatively affect the thickening of lake ice due to the insulating effect provided by enhanced snowfall whilst temperatures remain below freezing. The impacts of snowfall, although negative, are not considered to be as deleterious for winter road development as rainfall, which will become more common during the early spring months when temperatures are projected to rise above freezing under most scenarios.
-
Projected changes to the operational dates of the TCWR reveal a narrowing time window of operation across most scenarios, with many scenarios indicating no operational dates for heaviest vehicles by the end of the twenty-first century. If such a projection were to become reality, the TCWR and other winter roads in the region would no longer be viable to support the natural resource industry in northern Canada.
-
These results illuminate the need for policymakers and planners to consider future changes in climate when planning future operations that depend on overland transportation.
-
Caution must be exercised in interpreting these results due to the many uncertainties throughout the modelling process, but this should not equate to inaction in TCWR planning as although the magnitude of changes is unclear, the direction is not.
References
Anisimov OA, Vaughan DG, Callaghan TV, Furgal C, Marchant H, Prowse TD, Vilhjálmsson H, Walsh JE (2007) Polar regions (Arctic and Antarctic). Climate Change 2007: Impacts, Adaptation and Vulnerability. Contribution of Working Group II to the Fourth Assessment Report of the Intergovernmental Panel on Climate Change. In: Parry ML, Canziani OF, Palutikof JP, van der Linden PJ, Hanson CE (eds). Cambridge University Press, Cambridge, p 653–685
Arnell NW (1998) Climate change and water resources in Britain. Clim Chang 39(1):83–110
Arnell NW, Reynard NS (1996) The effects of climate change due to global warming on river flows in Great Britain. J Hydrol 183:397–424
Arnell NW, Hudson DA, Jones RG (2003) Climate change scenarios from a regional climate model: estimating change in runoff in southern Africa. J Geophys Res 108:1–17
Assel RA (1980) Maximum freezing degree-days as a winter severity infex for the Great Lakes. Mon Weather Rev 108:1440–1445
Borshch SV, Ginzburg BM, Soldatova II (2001) Modeling the development of ice phenomena in rivers as applied to the assessment of probable changes in ice conditions at various scenarios of the future climate. Water Resources 28(2):194–200 Translated from Vodnye Resursy, 28 (2):217–223
Burn DH, Hag Elnur MA (2002) Detection of hydrologic trends and variability. J Hydrol 255:107–122
Busuioc A, von Storch H, Schnur R (1999) Verification of GCM-generated regional seasonal precipitation for current climate and of statistical downscaling estimates under changing climate conditions. J Clim 12:258–272
Chen J, Brissette FP, Leconte R (2012) Coupling statistical and dynamical methods for spatial downscaling of precipitation. Clim Chang 114:509–526
Chen J, Zhang XC, Brissette FP (2014) Assessing scale effects for statistically downscaling precipitation with GPCC model. Int J Climatol 34:708–727
Christensen JH, Kuhry P (2000) High resolution regional climate model validation and permafrost simulation for the East-European Russian Arctic. J Geophys Res 105(29):647–629 658
Christensen OB, Christensen JH, Machenhauer B, Botzet M (1998) Very-high-resolution regional climate simulations over Scandinavia, present climate. J Clim 11:3204–3229
Clarke LE, Edmonds JA, Jacoby HD, Pitcher H, Reilly JM, Richels R (2007) Scenarios of greenhouse gas emissions and atmospheric concentrations. Sub-report 2.1a of Synthesis and Assessment Product 2.1. Climate Change Science Program and the Subcommittee on Global Change Research, Washington DC
Collins M et al (2013) Long-term climate change: projections, commitments and irreversibility. In: Stocker TF, Qin D, Plattner G-K, Tignor M, Allen SK, Boschung J, Nauels A, Xia Y, Bex V, Midgley PM. (eds) Climate Change 2013: The Physical Science Basis. Contribution of Working Group I to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change. Cambridge University Press, Cambridge, United Kingdom and New York, NY, USA
Diaz-Nieto J, Wilby RL (2005) A comparison of statistical downscaling and climate change factor methods: impacts of low flows in the river Thames, United Kingdom. Clim Chang 69:245–268
Dibike Y, Prowse T, Saloranta T, Ahmed R (2011) Response of northern hemisphere lake-ice cover and lake-water thermal structure patterns to a changing climate. Hydrol Process 25:2942–2953
Donner LJ et al. (2011) The dynamical core, physical parameterizations, and basic simulation characteristics of the atmospheric component AM3 of the GFDL Global Coupled Model CM3. J Clim 24(13). doi:10.1175/2011JCLI3955.1
Environment Canada (2012) Ice Thickness Program Collection, http://www.ec.gc.ca/glaces-ice/?lang = En&n = E1B3129D-1. Accessed 2 Apr 2015
Flato G et al (2013) Evaluation of climate models. In: Stocker TF et al (eds) Climate Change 2013: the physical science basis. Contribution of Working Group I to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change. Cambridge University Press, p 741–882, doi:10.1017/CBO9781107415324.020
Flato GM, Boer GJ (2001) Warming asymmetry in climate change simulations. Geophys Res Lett 28:195–198
Fujino J, Nair R, Kainuma M, Masui T, Matsuoka Y (2006) Multigas mitigation analysis on stabilization scenarios using aim global model. Energy J Special issue 3:343–354
Hardiman SC et al (2011) Improved predictability of the troposphere using stratospheric final warnings. J Geophys Res 116. doi:10.1029/2011JD015914. issn: 0148–0227
Hartmann DL et al (2013) Observations: Atmosphere and Surface. In: Stocker TF et al (eds) Climate Change 2013: the physical science basis. Contribution of Working Group I to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change. Cambridge University Press, Cambridge, United Kingdom and New York, NY, USA
Hijioka Y, Matsuoka Y, Nishimoto H, Masui T, Kainuma M (2008) Global GHG emission scenarios under GHG concentration stabilization targets. J Glob Environ Eng 13:97–108
Hughes OL (1989) Terrain and permafrost: their influence on northern construction. In: FT F (ed) Proceedings of conference—northern hydrocarbon development in the nineties: a global perspective. Carleton University, Geotechnical Science Laboratories, Ottawa, Ontario, pp. 109–118
Instanes A, Anisimov O, Brigham L, Goering D, Khrustalev LN, Ladanyi B, Larsen JO (2005) Infrastructure: buildings, support systems, and industrial facilities. In: Arctic climate impact assessment. Cambridge University Press, Cambridge, UK, pp. 907–944
JVMC (Joint Venture Management Committee) (2015) Tibbitt to Contwoyto Winter Road Joint Venture. dev.jvtcwinterroad.ca. Accessed 24 Jan 2015
Katz RW (1985) Probabilistic models. In: Murphy AH, Katz RW (eds) Probability, statistics and decision making in the atmospheric sciences. Westview, Boulder, pp. 261–288
Kiilsholm S, Christensen JH, Dethloff K, Rinke A (2003) Net accumulation of the Greenland ice sheet: high resolution modelling of climate changes. Geophys Res Lett 30. doi:10.1029/2002GL015742
Laprise R, Caya D, Frigon A, Paquin D (2003) Current and perturbed climate as simulated by the second-generation Canadian Regional Climate Model (CRCM-II) over northwestern North America. Clim Dyn 21:405–421
Larsen JN, Anisimov OA, Constable A, Hollowed AB, Maynard N, Prestrud P, Prowse TD, Stone JMR (2014) Polar regions. In: Barros VR et al (eds) Climate Change 2014: impacts, adaptation, and vulnerability. Part B: Regional Aspects. Contribution of Working Group II to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change. Cambridge University Press, Cambridge, United Kingdom and New York, NY, USA, p 1567–1612
Lee RJ (2000) Climate Change and Environmental Assessment Part 1: review of climate change considerations in selected past environmental assessments. Canadian Environmental Assessment Agency, Research and Development Monograph Series. http://www.ceaaacee.gc.ca/015/001/005/index_e.htm
Maurer EP, Hidalgo HG (2007) Utility of daily vs. monthly large-scale climate data: an intercomparison of two statistical downscaling methods. Hydrol Earth Syst Sci Discuss 4:3413–3440
Mearns LO et al. (2013) Climate change projections of the North American Regional Climate Change Assessment Program (NARCCAP). Clim Chang 120:965–975
Mekis É, Vincent LA (2011) An overview of the second generation adjusted daily precipitation dataset for trend analysis in Canada. Atmosphere-Ocean 49(2):163–177
Mullan DJ, Chen J, Zhang X-C (2015) Validation of non-stationary precipitation series for site-specific impact assessment: comparison of two statistical downscaling techniques. Clim Dyn. doi:10.1007/s00382-015-2626-x
Mullan DJ, Fealy R, Favis-Mortlock DT (2012) Developing site-specific future temperature scenarios for Northern Ireland: addressing key issues employing a statistical downscaling approach. Int J Climatol 32(13):2007–2019
Nakicenovic N et al (2000) IPCC special report on emissions scenarios: summary for policymakers. A Special Report of Working Group III of the Intergovernmental Panel on Climate Change. Cambridge University Press, Cambridge, UK and New York
Nicks AD, Lane LJ, Gander GA (1995) Chapter 2: Weather generator. In: Flanagan DC, Nearing MA (eds) USDA − Water Erosion Prediction Project: hillslope profile and watershed model documentation. NSERL Report No. 10. USDA-ARS National Soil Erosion Research Laboratory, West Lafayette, IN
Perrin A et al (2015) Economic implications of climate change adaptations for mine access roads in Northern Canada. Northern Climate ExChange, Yukon Research Centre, Yukon College, 93 pp
Pilling C, Jones JAA (1999) High resolution climate change scenarios: implications for British runoff. Hydrol Process 13:2877–2895
Plummer DA, Caya D, Frigon A, Cote H, Giguere M, Paquin D, Biner S, Harvey R, de Elia R (2006) Climate and climate change over North America as simulated by the Canadian RCM. J Clim 19(13):3112–3132
Prowse TD, Bonsal BR, Lacroix MP (2002) Trends in river-ice breakup and related temperature controls. Paper presented at Ice in the environment. 16th IAHR international symposium on ice. 3:64–71, December 2–6, in Dunedin, New Zealand
Prowse TD, Furgal C, Chouinard R, Melling H, Milburn D, Smith SL (2009) Implications of climate change for economic development in northern Canada: energy, resource, and transportation sectors. Ambio 38:272–281
Riahi K, Grübler A, Nakicenovic N (2007) Scenarios of long-term socio-economic and environmental development under climate stabilization. Technol Forecast Soc Change 74:887–935
Roeckner E et al (1996) The atmospheric general circulation model ECHAM-4: model description and simulation of present-day climate. Max-Planck-Institut für Meteorologie Report, 218, 90
Schmidli J, Frei C, Vidale PL (2006) Downscaling from GCM precipitation: a benchmark for dynamical and statistical downscaling methods. Int J Climatol 26:679–689
Smith SJ, Wigley TML (2006) MultiGas forcing stabilization with minicam. Energy J Special issue 3:373–392
Solman S, Nuñez M (1999) Local estimates of global climate change: a statistical downscaling approach. Int J Climatol 19:835–861
Stephenson SR, Smith LC, Agnew JA (2011) Divergent long-term trajectories of human access to the Arctic. Nat Clim Chang 1:156–160
von Storch H, Hewitson B, Mearns L (2000) Review of empirical downscaling techniques. Regional climate development under global warming. Iversen T, Hoiskar BAK (eds) General Technical Report No. 4. Conf. Proceedings RegClim Spring Meeting Jevnaker, Torbjornrud, Norway, p 29–46
Thompson R, Kamenik C, Schmidt R (2005) Ulstra-sensitive alpine lakes and climate change. J Limnol 64(2):139–152
Tibbitt to Contwoyto Winter Road Joint Venture (2015) Historical winter road statistics (2002–2012), (online), available at: http://www.jvtcwinterroad.ca/facts.html. Accessed 20 jun 2015
Tsushima Y et al (2006) Importance of the mixed-phase cloud distribution in the control climate for assessing the response of clouds to carbon dioxide increase: a multi-model study. Clim Dyn 27:113–126
Upiter LM et al. (2015) Middle to late Holocene chironomid-inferred July temperatures for the central northwest territories. J Paleolimnol. doi:10.1007/s10933-014-9775-5
Vaughan DG et al (2013) Observations: cryosphere. In: Stocker TF et al (eds) Climate Change 2013: the physical science basis. Contribution of Working Group I to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change. Cambridge University Press, Cambridge, United Kingdom and New York, NY, USA
Vincent LA, Wang XL, Milewska EJ, Wan H, Yang F, Swail V (2012) A second generation of homogenized Canadian monthly surface air temperature for climate trend analysis. J Geophys Res 117:D18110. doi:10.1029/2012JD017859
van Vuuren DP et al. (2011) The representative concentration pathways: an overview. Clim Chang 109:5–31
van Vuuren DP, Eickhout B, Lucas PL, den Elzen MGJ (2006) Long-termmulti-gas scenarios to stabilise radiative forcing - exploring costs and benefits within an integrated assessment framework. Energ J 27:201–233
van Vuuren DP, Den Elzen MGJ, Lucas PL, Eickhout B, Strengers BJ, van Ruijven B, Wonink S, van Houdt R (2007) Stabilizing greenhouse gas concentrations at low levels: an assessment of reduction strategies and costs. Clim Change 81:119–159
Watanabe M (2010) Improved climate simulation by MIROC5: mean states, variability, and climate sensitivity. J Clim 23:6312–6335
Widmann M, Bretherton CS, Salathé EP Jr (2003) Statistical precipitation downscaling over the Northwestern United States using numerically simulated precipitation as a predictor. Int J Climatol 16(5):799–816 Journal of Climate 13: 1936-1950
Wilby RL, Dawson CW (2007) SDSM 4.2- A decision support tool for the assessment of regional climate change impacts, Version 4.2 User Manual. Lancaster University: Lancaster / Environment Agency of England and Wales
Wilby RL, Wigley TML (2000) Precipitation predictors for downscaling: observed and general circulation model relationships. Int J Climatol 20:641–661
Wilby RL, Charles SP, Zorita E, Timbal B, Whetton P, Mearns OL (2004) Guidelines for the use of Climate scenarios developed from statistical downscaling methods. Available at http://ipcc-ddc.cru.uea.ac.uk/guidelines/dgm_no2_v1_09_ 2004. pdf
Wilby RL, Wigley TML, Conway D, Jones PD, Hewitson BC, Main J, Wilks DS (1998) Statistical downscaling of general circulation model output: a comparison of methods. Water Resour Res 34:2995–3008
Wise M, Calvin K, Thomson A, Clarke L, Bond-Lamberty B, Sands R, Smith SJ, Janetos A, Edmonds J (2009) Implications of limiting CO2 concentrations for land use and energy. Science 324:1183–1186
Zhang X-C (2005) Spatial downscaling of global climate model output for site-specific assessment of crop production and soil erosion. Agric For Meteorol 135:215–229
Zhang X-C (2012) Verifying a temporal disaggregation method for generating daily precipitation of potentially non-stationary climate change for site-specific impact assessment. Int J Climatol 33:326–342
Zhang X-C, Chen J, Garbrecht JD, Brissette FP (2012) Evaluation of a weather generator-based method for statistically downscaling non-stationary climate scenarios for impact assessment at a point scale. Trans ASABE 55(5):1–12
Acknowledgments
The authors acknowledge financial support from Aboriginal Affairs and Northern Development Canada (AANDC) for making this study possible. We are grateful to Environment Canada for the temperature, precipitation and lake ice thickness data. Finally, we thank the contributors to the Climate Explorer site for the provision of modelled climate data used in this paper.
Author information
Authors and Affiliations
Corresponding author
Electronic supplementary material
Appendix 1
. Comparison between monthly mean values of TMIN and TMAX between the observed series at Yellowknife station (1943–2012) and a 70 year CLIGEN generated time series based on the statistics of the observed climate. (PNG 22 kb)
Appendix 2
Comparison between monthly distributional statistics of TMIN and TMAX between the observed series at Yellowknife station (1943–2012) and a 70 year CLIGEN generated time series based on the statistics of the observed climate. (DOCX 12 kb)
Appendix 3
Comparison of observed and hindcast downscaled TMIN series for Yellowknife during the months January–April. (PDF 47 kb)
Appendix 4
Comparison of observed and hindcast downscaled TMAX series for Yellowknife during the months January–April. (PDF 47 kb)
Appendix 5
Comparison of observed and hindcast downscaled PPT series for Yellowknife during the months January–April. (PDF 47 kb)
Appendix 6
Hindcast and future downscaled TMIN scenarios for Yellowknife during the months September – December. (PDF 72 kb)
Appendix 7
Hindcast and future downscaled TMAX scenarios for Yellowknife during the months September – December. (PDF 72 kb)
Appendix 8
Hindcast and future downscaled PPT scenarios for Yellowknife during the months September – December. (PDF 72 kb)
ESM 1
(DOCX 15 kb)
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Mullan, D., Swindles, G., Patterson, T. et al. Climate change and the long-term viability of the World’s busiest heavy haul ice road. Theor Appl Climatol 129, 1089–1108 (2017). https://doi.org/10.1007/s00704-016-1830-x
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00704-016-1830-x