Abstract
In powder bed based Additive Manufacturing (AM) processes like Selective Laser Melting (SLM) or Electron Beam Melting (EBM), the spatial distribution of the individual powder particles is typically unknown. Nevertheless, the distribution of particles in the heat affected zone defines the thermophysical properties of the region being processed by the heat source and therefore plays a crucial role in heat transfer processes. In this work, the spatial distribution of individual particles and their influence on the AM process is numerically investigated. Two powder bed configurations are compared: One powder bed is generated using the discrete element method (DEM) to model the coating process; the second powder bed is arranged in the BCC structure. The melting and solidification of both configurations are modelled. The predicted melt pool dimensions are compared with experimentally determined values. The results indicate that modelling the coating process is necessary to ensure accurate modelling of the heat source powder bed interaction as well as an accurate prediction of the melt pool characteristics.
Zusammenfassung
Bei Pulverbett basierten Additiven Fertigungsprozessen (AM) wie Selective Laser Melting (SLM) oder Elektron Beam Melting (EBM) ist die lokale Partikelverteilung im Pulverbett meist unbekannt. Nichts desto trotz beeinflusst die Partikelverteilung in der Wärmeeinflusszone und Prozesszone die thermophysikalischen Bedingungen signifikant und spielt eine entscheidende Rolle für die Lösung der Wärmeleitungsgleichung.
In diesem Artikel wird der Einfluss der Partikelverteilung auf den SLM Prozess mit Hilfe von Simulationen numerisch untersucht. Zur Lösung dieser Aufgabenstellung werden zwei unterschiedliche Methoden verwendet. Erstens wird der Pulverauftrag in Rahmen der diskreten Elemente Methoden (DEM) abgebildet und gelöst. Die errechneten Verteilungen dienen als Eingangsgröße für die Simulation des Schmelzprozesses beim SLM (Volume-of-fluid Methode (VOF)). In der zweiten Simulation werden das Aufschmelzen des Pulvers, die Strömung der Schmelze und das Erstarren der Schmelze in der Prozesszone simuliert.
Aus der VOF Simulation werden die charakteristischen Größen des Schmelzbades extrahiert (Breite, Tiefe) und mit experimentell ermittelten Werten verglichen.
Als Eingangsgröße für die DEM Simulation wird eine reale Partikelverteilung vermessen.
Die Ergebnisse zeigen, wie die Partikelverteilung den SLM Prozess und die finale Bauteilqualität beeinflussen.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
In powder bed based Additive Manufacturing (AM) processes, like Selective Laser Melting (SLM), a large number of variables influence the quality of the work piece [1].
Some of these variables can be set and measured directly (e.g. laser power, scanning velocity, and coater arm velocity). Some other process parameters are machine specific and can only be controlled indirectly (e.g. shielding gas velocity over the powder bed is only controlled via the volume flow rate setting of the machine). Other parameters are hard to measure or control, yet could have a significant influence on the process; the spatial distribution of the powder particles in the powder bed is a typical example for this category.
We study the influence of the powder bed characteristics (particle size distribution and spatial arrangement) on the SLM process using high fidelity models recently developed and validated [2–5]. Since the spatial arrangement of the particles in the powder bed cannot be manipulated or easily measured in a production 3D printer, the study of the impact of those parameters on the SLM process is investigated by comparing the melting behaviour of a BCC arrangement of powder particles with that of a powder bed obtained by modelling the racking process [6]. The numerically predicted melt pool characteristics are compared with experimentally observations to assess the effect of powder distribution of material behaviour.
2 Computational Models
Powder scale models are used to model the racking process as well as the laser-powder interaction to resolve powder melting and solidification.
When defining the body centred cubic lattice arrangement (BCC) of powder particles, D50 of the powder used in experiments is defined to be the powder particle diameter. The powder particles are arranged using a script and provided as input for the melt pool model.
When modelling the powder spreading process, we use discrete element methods (DEM) to study powder spreading and the distribution of powder on the processing table [7]. DEM is a Lagrangian approach where the modelled region considers the particles inside their own point of reference describing Newton’s laws of motion for conservation of momentum. Every powder particle is treated as an individual with its own properties and interacts with other particles in its vicinity.
Once the powder bed geometry is obtained, either via script or via modelling of the racking process, the particle distribution on the powder bed is provided to a computational fluid dynamics model that accounts for laser interaction with the feed stock providing more insight about the phase changes and solidification behaviour of the material [2, 8]. The momentum equations are extended using source terms to account for gravitational body forces, recoil pressure, and surface tension. The energy equation accounting for conduction (diffusion term) and convection is complemented with source terms accounting for the latent heat released or required during solidification/melting and evaporation/condensation as well as radiation.
The processing parameters used for all simulations are summarized in Table 1; they correspond to the settings chosen on an SLM 280 3D printer for specimen manufacturing.
3 Powder Characteristics and Material Properties
Throughout this effort, hot work steel 1.2367 is used for both the numerical and the experimental studies. The powder size distribution was measured using a “morphology G3” system. The measured particles are normally not perfect spheres (or, since a 2D projection is measured, circles) but shaped irregularly(compare circularity plot, shown in Figure 1). After determining the area of each particle, a circle equivalence diameter and sphere equivalent volume is calculated and is used to generate the diameter vs. volume fraction distribution for spheres matching the measured data (Figure 1). For the powder spreading models, the powder size distribution is subdivided into 9 classes (bins) (also shown in Figure 1).
Both the largest and smallest diameter classes account for less than 3% of the volume and mass fractions. If taken into account, they increase the number of particles to be modelled, thus increasing the computational effort. We therefore neglect the classes with the largest and smallest diameters in spreading simulations.
D50 (30 μm) of the measured powder size distribution is used in a body centred cubic lattice (Figure 2). The built distribution is made of two particle layers. This configuration was chosen because it enables the arrangement of the particles in the 50 µm gap estimated to be available for the particle spreading. The packing density of this manual packing is close to expected 50% packing density.
Temperature dependent material properties of hot work steel 1.2367 were gathered from data sheets, literature, and partly calculated thermodynamic databases (see Figure 3) [9, 10].
4 Results
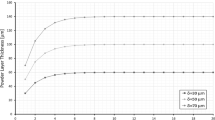
During the powder spreading process, we observe a segregation of particles leading to a different powder size distribution on the processing table as compared to the input distribution. This is in agreement with observation made for other powders [7]. Figure 4 shows the particle size distribution obtained for two different table displacements, 35 and 50 μm, and compares them the input powder size distribution. The table displacement corresponds to the gap between the coater arm lower edge and the substrate. The two largest powder classes are not present in the welding domain for both studied table displacements. The relatively large particles belonging to these classes are wiped off the platform by the coater arm. This is attributed to the mechanical filtering by the coater arm pushing larger particles that do not fit in the gap between it and the substrate.
In the case of 35 μm table displacement, some particles, slightly larger than the gap size, are observed on the processing table. These particles are compressed slightly allowing them to pass through the gap. Since the model does not account for particle crushing or compression of the particles in a partially solidified substrate, this behaviour is not expected to happen in the same manner in reality. In reality, particles larger than the gap will either be pushed away from the substrate or will interact with coater blade in some manner (e.g. crushing, denting the coater arm).
The powder packing density predicted by the spreading models is in the order of 40%. A gap size of 50 µm was chosen to model a process with a platform lowering of 30 µm with each layer and an assumed volume shrinkage of 40% from powder to fully remelted solid.
Figure 5 shows the powder distribution on the substrate as obtained from the spreading simulations. The particles are coloured by their sizes. The shaded area indicates the area to be processed by the laser during the melting simulation; the bright red spot indicates the initial laser position.
Figure 8 shows top views of the molten tracks for both the BCC powder packing as well as the numerically spread powder. In the case of the numerically spread powder, multiple layers were investigated in a numerical process that included spreading and melting several times. The BCC arrangement leads to a fairly regular shape of the melt pool and the heat affected zone. The numerically spread powder cases display irregular shapes of both the melt pool and the heat affected zone. The irregularities can be correlated with how the particles were arranged; leading to non-uniform capillary forces on both sizes of the laser track. This behaviour is in agreement with high speed camera images reported in literature [11, 12].
The corresponding shapes of the processed solidified material is presented in Figure 6. The images are coloured by vertical coordinate. It is directly visible that the BCC arrangement leads to a much smoother and regular shape of the processed material. In contrast, the numerically spread powder shows significant upper roughness that is in the order of 20 μm. The processed material dimensions were gathered for later comparison with experimental observations. The BCC melt pool dimension fluctuations are much smaller than those observed for the numerically spread powder. From the comparison of powder beds and the particle distributions, it can be seen that a uniform distribution leads to a continuous mass flow into the melt pool resulting in a more uniform melt pool geometry (Figure 7). In the case of the BCC, packing leads to a quasi-steady melt pool shape.
At the centre of the laser track, the temperature history of the material was monitored for two points: The first point was defined to be within the powder layer, close to melt surface, and the second was defined to be at the surface of the substrate.
Figure 8 compares the predicted temperature histories of the BCC powder particle arrangement with that of the numerically spread powder bed.
The temperature maxima reached in the case of numerically spread powder case (first layer) and the BCC arranged powder are very similar. The highest temperature reached on top of the powder layer is around 2200 K. The temperature peak on the substrate is reached later in the process (due to finite heat conductivity of the powder layer). At this peak the powder layer surface temperature is already below the substrate temperature (Figure 8).
At t=0.0005 s. the reheating of the powder surface due to the hot substrate can be seen as a bump in the temperature-time curve. After this event the temperature curves in the cooling process of the substrate and powder layer run parallel until the material is solidified again.
The cooling rate in vicinity of the melting point (between 1588 K and 1753 K) is around \(2\cdot 10^{5}K/s\), which is a value typical for SLM.
A gas pore is formed in the second layer of the numerically spread powder case (see Figure 9) probably due to the asymmetric particle packing on top of the first layer. Experiments show material densities in the order of 99.5%. The density of the numerically spread powder indicates high product density with very small pores, while the BCC packed powder shows no pores at all. We take this finding as an indication that the powder distribution is detrimental in the prediction of the material quality. The similarity of the temperature history for a smoother surface roughness and dense build in the case of the BCC arrangement to that of the courser surface and porous result in the case of spread powder suggests that inline monitoring of temperatures might not be indicative for these defects.
Experimental micrographs were analysed to determine the melt pool depths and widths (Figure 10). The manufactured specimens were cut in a way that the scanning vectors in the top last layer are normal to the cutting plane. After polishing and etching, the melt pool dimensions (depth and width) can be seen and measured under a microscope. The micrographs indicated a conduction like melt pool with a depth to width ratio of approximately 1 (Figure 11).
Table 2 summarizes the experimental measurements and numerically predicted melt pool widths and depths. The deviations from the reported average is also provided. The predictions of the BCC arranged particles shows larger deviations from experiments. The depth is overpredicted by approximately 14% and the width is underestimated by 26%. The numerically spread powders show much closer agreement with experiments for all studied layers. The melt pool width is underestimated in layer 1 and is about 18% below the experimental value in layer 3. The underestimated widths are possibly due to inconsistencies in the used laser profiles.
Experiments show a depth to width aspect ratio of approximately 1 indicating conduction regime melting. Numerical results show aspect ratio larger than 1 indicating keyhole effects, this is attributed to the smaller melt pool widths predicted and the corresponding increase in energy densities.
5 Conclusions and Outlook
The importance of using realistic powder bed distributions was analysed numerically by comparing a lattice arrangement with a numerically spread powder. The resulting melt pool dimensions and porosity were compared with measurements. BCC powder packing leads to uniform melt pools with overpredicted depth and porosity levels. Numerically spread powder beds shows irregular melt pool shapes that compare qualitatively well with high speed camera images. The predicted melt pool depth is comparable to measurements. The underestimated melt pool width is assumed to be related to differences in laser profiles used in experiment and numerical studies. The underestimated width leads to a high energy density leading to keyholing, which is not observed in experiments. In future work, the laser profile will be investigated in more detail in an effort to clarify the source of discrepancies. Multitrack simulations are also planned to improve numerical porosity predictions.
References
Yadroitsev, I.: Selective Laser Melting: Direct Manufacturing of 3D-Objects by Selective Laser Melting of Metal Powders, LAP Lambert Academic Publishing, 2009
Megahed, M; Mindt, H. W.; N’Dri, N; Duan, H. Z.; Desmaison, O.: Metal Additive Manufacturing Process and Residual Stress Modelling. Integrating Materials and Manufacturing Innovation, 2016, doi:10.1186/s40192-016-0047-2
Mindt, H-W; Megahed, M.; Shula, B.; Peralta, A.; Neumann, J.: Powder Bed Models – Numerical Assessment of As-Built Quality, AIAA Science and Technology Forum and Exposition, San Diego, 2016
Mindt, H.W; Megahed, M.; Shula, B; Peralta, A. D.; Neumann, J.: Powder bed models - Numerical assessment of as-built quality, AIAA , SciTech, 4-8 January 2016, San Diego, USA, 2016, pp 2016-165
Desmaison, O.; Pires, P. A.; Levesque, G.: Peralta, A.; Sundarraj, S.; Makinde, A., et al.: Influence of computational grid and deposit volume on residual stress and distortion prediction accuracy for additive manufacturing modeling, 4th World congress on integrated computational materials engineering - ICME 2017, 21-25 May 2017, Ypsilanti, Mi, USA, 2017
Mindt, H. W.; Megahed, M.; Lavery, N. P.; Homes, M. A.; Brown, S. G.: Powder bed layer characterisitcs - The overseen first order process input, 145th TMS Annual Meeting & Exhibition, Nashville, USA, 2016
Mindt, H. W.; Megahed, M.; Lavery, N. P.; Holmes, M. A.; Brown, S. G. R.: Powder bed layer charateristics: The overseen first-order process input, Metallurgical and Materials Transactions A, 47 (2016), no. 8, doi:10.1007/s11661-016-3470-2
Mindt, H. W.; Desmaison, O.; Megahed, M.; Peralta, A.; Neumann, J.: Modeling of Powder Bed Manufacturing Defects, MS&T 16, Salt Lake City, Utah, USA, 23-27 October 2016, 2016
ABRAMS PREMIUM STAHL: Datasheet 1.2367, www.premium-stahl.de (02.06.2016)
Scholtes, P. D. I. B.: Thermo-mechanisch gekoppelte Experimente zur Beurteilung der Schädigungsentwicklung an Werkzeugen zur Warmumformung, Kassel: kassel university press, 2013
Peralta, A. D.; Enright, M.; Megahed, M.; Gong, J.; Roybal, M.; Craig, J.: Towards rapid qualification of powder bed laser additively manufactured part, Integrating Materials and Manufacturing Innovation, 5 (2016), no. 8, doi:10.1186/s40192-016-0052-5
Matthews, M. J.; Guss, G.; Khairallah, S. A.; Rubenchik, A. M.; Depond, P. J.; King, W. E.: Denuda tion of metal powder layers in laser powder bed fusion processes, Acta Materialia, 114 (2016), no. 42, doi:10.1016/j.actamat.2016.05.017
Acknowledgements
This research has received funding from the German Ministry of Education and Research (BMBF) under contract no. 13N13586. The authors acknowledge the financial support of BMBF and the discussions and contributions of collaborating partners.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Zielinski, J., Vervoort, S., Mindt, HW. et al. Influence of Powder Bed Characteristics on Material Quality in Additive Manufacturing. Berg Huettenmaenn Monatsh 162, 192–198 (2017). https://doi.org/10.1007/s00501-017-0592-9
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00501-017-0592-9