Abstract
Fuzzy graphs are an individual of application tools in the area of mathematics, which permit the users to define the relative between concepts because the wildlife of fuzziness is satisfactory for any situation. They are helpful to give more exactness and suppleness to the classification as associated with the traditional models. A topological structure is a set model for graphs. The main purpose of this paper is to introduce a new kind of fuzzy topological structures in terms of fuzzy graphs called fuzzy topological graphs due to a class of fuzzy subsets, and some of their properties are investigated. Also, a new procedure to calculate the number of edges in fuzzy graphs will be defined. Further, we consider the concept of a homeomorphic between fuzzy topological graphs as a fuzzy topological property that can be used to prove the isomorphic between fuzzy graphs. Moreover, an algorithm based on the proposed operations that build some fuzzy topological graphs will be presented. Finally, we give a new method to explain the homeomorphic between some fuzzy topological graphs which will be applied in smart cities.
















Similar content being viewed by others
References
Abdul-Jabbar N, Naoom JH, Ouda EH (2009) Fuzzy dual graphs. J Al-Nahrain Univ 12(4):168–171
Akram M (2019) \(m\)-Polar fuzzy graphs, studies in fuzziness and soft computing. Springer, Berlin
Akram M, Naz S (2019) A novel decision-making approach under complex Pythagorean fuzzy environment. Math Comput Appl 24(3):73
Akram M, Luqman A (2020) Fuzzy hypergraphs and related extensions. In: Studies in fuzziness and soft computing. Springer, Berlin. https://doi.org/10.1007/978-981-15-2403-5
Akram M, Dar JM, Farooq A (2018a) Planar graphs under Pythagorean fuzzy environment. Mathematics 6(12):278
Akram M, Habib A, Ilyas F, Dar JM (2018b) Specific types of Pythagorean fuzzy graphs and application to decision-making. Math Comput Appl 23(3):42
Akram M, Bashir A, Samanta S (2020) Complex Pythagorean fuzzy planar graphs. Int J Appl Comput Math 6(58):1–27
Alshehri N, Akram M (2014) Intuitionistic fuzzy planar graphs. Discrete Dyn Nat Soc 2014:397–823
Bhattacharya P (1987) Some remarks on fuzzy graphs. Pattern Recognit Lett 6:297–302
Bhutani KR (1989) On automorphism of fuzzy graphs. Pattern Recognit Lett 9:159–162
Bondy AJ, Murty RSU (1975) Graph theory with applications. Elsevier, Amsterdam
Chang CL (1968) Fuzzy topological spaces. J Math Anal Appl 24(1):182–190
Coker D, Haydar Es A (1995) On fuzzy compactness in intuitionistic fuzzy topological spaces. J Fuzzy Math 3:899–910
Coker D (1997) An introduction to intuitionistic fuzzy topological spaces. Fuzzy Sets Syst 88(1):81–89
De Santis A, Fasano A, Mignolli N, Villa A (2014) Smart city: fact and fiction. SSRN: https://ssrn.com/abstract=2410739
El Atik A, Nasef A (2020) Some topological structures of fractals and their related graphs. Filomat 34(1):153–165
El Atik A, Nawar AS, Atef M (2020) Rough approximation models via graphs based on neighborhood systems. Granul Comput. https://doi.org/10.1007/s41066-020-00245-z
El-Naschie SM (2006) Topics in the mathematical physics of E-infinity theory. Chaos Solitons Fractals 30:656–663
Ghorai G, Pal M (2016) Some properties of \(m\)-polar fuzzy graphs. Pac Sci Rev A Nat Sci Eng 18:38–46
Jararweh Y, Otoum S, Al Ridhawi I (2020) Trustworthy and sustainable smart city services at the edge. Sustain Cities Soc 62:102394
Jiang H, Zhan J, Chen D (2018) Covering based variable precision \(({\cal{I}}, {\cal{T}})\)-fuzzy rough sets with applications to multi-attribute decision-making. IEEE Trans Fuzzy Syst. https://doi.org/10.1109/TFUZZ.2018.2883023
Harary F (1972) Graph theory, 3rd edn. Addision-Wesely, Reading
Hofer C, Kwitt R, Niethammer M, Uhl A (2017) Deep learning with topological signatures. Adv Neural Inf Process Syst 30:1634–1644
Kaufmann A (1973) Introduction a la Theorie des Sour-Ensembles Flous. Masson et Cie, Paris
Kozae AM, El Atik AA, Elrokh A, Atef M (2019) New types of graphs induced by topological spaces. J Intell Fuzzy Syst 36:5125–5134
Kramosil I, Michlek J (1975) Fuzzy metrics and statistical metric spaces. Kybernetika 11(5):336–344
Kumar H, Kumar MS, Gupta MP, Madaan J (2020) Moving towards smart cities: solutions that lead to the smart city transformation framework. Technol Forecast Soc Change 153:119281
Quijano-Sanchez L, Cantador I, Cortes-Cediel ME, Gil O (2020) Recommender systems for smart cities. Inf Syst 92:101545
Li G, Yan L, Ma Z (2019) An approach for approximate subgraph matching in fuzzy RDF graph. Fuzzy Sets Syst 376:106–126
Liu YM, Luo MK (1998) Fuzzy topology. World Scientific, Singapore
Lowen R (1976) Fuzzy topological spaces and fuzzy compactness. J Math Anal Appl 56(3):621–633
Lowen R (1977) Initial and final fuzzy topologies and the fuzzy Tychonoff theorem. J Math Anal Appl 58(1):11–21
Lum PY, Singh G, Lehman A, Ishkanov T, Vejdemo-Johansson M, Alagappan M, Carlsson J, Carlsson G (2013) Extracting insights from the shape of complex data using topology. Sci Rep 3:1236
Luqman A, Akram M, Smarandache F (2019) Complex neutrosophic hypergraphs: new social network models. Algorithms 12(11):234
Mathew S, Mordeson JN (2017) Connectivity concepts in fuzzy incidence graphs. Inf Sci 2017:326–333
Ma J, Atef M, Nada S, Nawar A (2020) Certain types of covering-based multigranulation (I;T )-fuzzy rough sets with application to decision-making. Complexity 2020:1–20. https://doi.org/10.1155/2020/6661782
Mordeson JN (1993) Fuzzy line graphs. Pattern Recognit Lett 14:381–384
Mordeson JN, Nair PS (2000) Fuzzy graphs and hypergraphs. Physica Verlag, Heidelberg
Mordeson JN, Mathew S (2019) Advanced topics in fuzzy graph theory. Springer Nature, Cham
Nagoor Gani A, Malarvizhi J (2008) Isomorphism on fuzzy graphs, world academy of science. Eng Technol 47:505–511
Naz S, Ashraf S, Akram M (2018) A novel approach to decision-making with Pythagorean fuzzy information. Mathematics 6(6):95
Nicolau M, Levine AJ, Carlsson G (2011) Topology based data analysis identifies a subgroup of breast cancers with a unique mutational profile and excellent survival. Proc Natl Acad Sci 108:72657270
Riaz M, Hashmi MR (2017) Fuzzy parameterized fuzzy soft topology with applications. Ann Fuzzy Math Inf 13(5):593–613
Riaz M, Hashmi MR (2018) Fuzzy parameterized fuzzy soft compact spaces with decision-making. Punjab UJ Math 50(2):131–145
Rosenfeld A (1971) Fuzzy groups. J Math Anal Appl 35:512–517
Rosenfeld A (1975) Fuzzy graphs. Academic Press, New York, pp 77–95
Samanta S, Pal M (2011a) Fuzzy tolerance graphs. Int J Latest Trends Math 1(2):57–67
Samanta S, Pal M (2011b) Fuzzy threshold graphs. CIIT Int J Fuzzy Syst 3(12):360–364
Samanta S, Pal M (2013) Fuzzy k-competition graphs and p-competitions fuzzy graphs. Fuzzy Inf Eng 5(2):191–204
Samanta S, Pal M (2015) Fuzzy planar graphs. IEEE Trans Fuzzy Sets Syst. https://doi.org/10.1109/TFUZZ.2014.2387875
Samanta S, Akram M, Pal M (2015) \(m\)-step fuzzy competition graphs. J Appl Math Comput 47(1):461–472
Sardiu ME, Gilmore JM, Groppe B, Florens L, Washburn MP (2017) Identification of topological network modules in perturbed protein interaction networks. Sci Rep 7:43845
Sunitha MS, Vijayakumar A (2002) Complement of fuzzy graphs. Indian J Pure Appl Math 33:1451–1464
Thirunavukarasu P, Suresh R, Viswanathan KK (2016) Energy of a complex fuzzy graph. Int J Math Sci Eng Appl 10:243–248
Vandercruysse L, Buts C, Dooms M (2020) A typology of smart city services: the case of data protection impact assessment. Cities 104:102731
Wang M, Zhou T, Wang D (2020) Tracking the evolution processes of smart cities in China by assessing performance and efficiency. Technol Soc 63:101353
Westraadt L, Calitz A (2020) A modelling framework for integrated smart city planning and management. Sustain Cities Soc 63:102444
Yaqoob N, Gulistan M, Kadry S, Wahab H (2019) Complex intuitionistic fuzzy graphs with application in cellular network provider companies. Mathematics 7(1):35
Zadeh LA (1965) Fuzzy sets. Inf Control 8:338–353
Zhan J, Sun B, Alcantud JCR (2019) Covering based multigranulation \(({mathcal I}, {mathcal T})\) -fuzzy rough set models and applications in multi-attribute group decision-making. Inf Sci 476:290–318
Zhang K, Zhan J, Wu W, Alcantud JCR (2019a) Fuzzy \(\beta \)-covering based \(({mathcal{I}}, {mathcal{T}})\)-fuzzy rough set models and applications to multi-attribute decision-making. Comput Ind Eng 128:605–621
Zhang L, Zhan J, Xu Z (2019b) Covering-based generalized IF rough sets with applications to multi-attribute decision-making. Inf Sci 478:275–302
Acknowledgements
The authors are grateful to the editor and referees for their valuable comments and suggestions.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The authors declare that they have no conflict of interest.
Human and animal rights
This article does not contain any studies with human participants or animals performed by any of the authors.
Informed consent
Informed consent was obtained from all individual participants included in the study.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendix: Proofs
Appendix: Proofs
In this section, we prove the results declared in previous sections.
Proof
(Continue proof Theorem 2) If \(\mathcal {C}_1\) and \(\mathcal {C}_2\) are two parallel classes, then there exists a bijective fuzzy function F from \(\mathcal {C}_1\) to \(\mathcal {C}_2\), i.e., \({F}:\mathcal {C}_1 \rightarrow \mathcal {C}_2\), such that \({F}(\mathcal {C}_1)=\) \(\mathcal {C}_2\), where \(\mathcal {C}_1=\) \(\{\mathcal {A}_i: i \in I\}\) and \(\mathcal {C}_2=\) \(\{{F}(\mathcal {A}_i): i \in I\}\). Then, every vertex \(v_{\mathcal {A}_i}\) in \(\mathcal {G}_1\), the graph generated by \(\mathcal {C}_1\), we have a corresponding vertex \(v_{{F}(\mathcal {A}_i)}\) in \(\mathcal {G}_2\), the fuzzy graph generated by \(C_2\). So \(\mu _{R}(v_{\mathcal {A}_i},\) \(v_{\mathcal {A}_j})=\) \(\mu _{R}(\mathcal {A}_i \cap \mathcal {A}_j)=\) \(\mu _{R}({F}(\mathcal {A}_i \cap \mathcal {A}_j))\) \(=\mu _{R}({F}(\mathcal {A}_i)\) \(\cap {F}(\mathcal {A}_j))\) \(=\mu _{R}(v_{{F}(\mathcal {A}_i)},\) \(v_{{F}(\mathcal {A}_j)})\). Also, \(\sigma _{v_{\mathcal {A}_i}}=\) \(\sigma _{v_{{F}(\mathcal {A}_i)}}\) and \(\sigma _{v_{\mathcal {A}_j}}=\) \(\sigma _{v_{{F}(\mathcal {A}_j)}}\). Thus, F is an isomorphism. \(\square \)
Proof
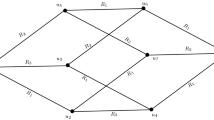
(Continue proof Theorem 3) The relation between fuzzy sets is shown in Fig. 17.
-
(i)
Let \(A \subseteq X\), \(|A| = m\) and \(|A^c| = n-m\)
$$\begin{aligned} deg\left( V_A\right)= & {} \sum R\left( V_A,V_B\right) \\&+\sum R\left( V_A,V_E\right) \\&+\sum R\left( V_A,V_L\right) \\&+\sum R\left( V_A,V_K\right) \\= & {} \sum |A \cap B|+\sum |A \cap E|\\&+\sum |(A \cap L|+\sum |A \cap K|\\= & {} \sum |B|+\sum |A|+\sum |A \cap L|.\\ \sum |B|= & {} \sum _{i=1}^{m-1} i ^mC_i\\= & {} \sum _{i=1}^{m-1} i\frac{m!}{i!(m-i)!}\\= & {} m\sum _{i=1}^{m-1} \frac{m-1)!}{(i-1)!(m-i)!}\\= & {} m\sum _{i=1}^{m-1} {}^{m-1}C_{i-1}\\= & {} m\sum _{j=0}^{m-2} \left( {}^{m-1}C_j-1\right) \\= & {} m(2^{m-1}-1), \end{aligned}$$since \(B \subseteq A\), then\( \sum |A|\) = \(m(2^{m-1} - 1 )\). But \(A \subseteq E\), then by complement \(\sum |A|\)=\(m(2^{n-m} - 1)\) and \(\sum |A \cap L|\)=\((2^{n-m} - 1)\sum _{i=1}^{m-1} i\) \(^mC_i\) \(=m(2^{n-m} - 1 )(2^{m-1} -1 )\). So \(deg(V_A)\) = \(m(2^{n-1} - 1 ) + 2m\). It follows that the number of edges of pseudographs G equals
$$\begin{aligned} |E_p(G)|= & {} \frac{1}{2}\sum _{m=1}^{n}{}^nC_mdeg(V_A)\\= & {} \frac{1}{2}\sum _{m=1}^{n}{}^nC_{m}\left( m\left( 2^{n-1} -1\right) +2m\right) \\= & {} \frac{1}{2}\sum _{m=1}^{n}{}^nC_{m} m\left( 2^{n-1} -1\right) \\&+\frac{1}{2} \sum _{m=1}^{n}{}^nC_m 2m\\= & {} n2^{n-2}\left( 2^{n-1}-1\right) \\&+\sum _{m=1}^{n}m{}^nC_m\\= & {} n2^{n-2}\left( 2^{n-1}-1\right) \\&+n\sum _{m=1}^{n}{}^{n-1}C_{m-1}\\= & {} n2^{n-2}\left( 2^{n-1}-1\right) \\&+n\sum _{j=0}^{n-1}{}^{n-1}C_j\\= & {} n2^{n-2}\left( 2^{n-1} -1\right) +n2^{n-1}. \end{aligned}$$ -
(ii)
\(deg(V_A)\) = \(m(2^{n-1} - 1 )\).
It follows that the number of edges of discrete graphs equals
$$\begin{aligned} |E_d(G)|= & {} \frac{1}{2} \sum _A deg(V_A)\\= & {} \frac{1}{2} \sum _A {}^nC_m m.\left( 2^{n-1}-1\right) \\= & {} \frac{1}{2}\left( 2^{n-1} -1\right) \sum _{m=1}^{n}m {}^nC_m\\= & {} \frac{1}{2}\left( 2^{n-1} -1\right) \sum _{m=1}^{n}m {}^nC_m\\= & {} \frac{1}{2}\left( 2^{n-1}-1 \right) \sum _{m=1}^{n} m\frac{n!}{m!(n-m)!}\\= & {} \frac{n}{2}\left( 2^{n-1}-1\right) \sum _{m=1}^{n} \frac{(n-1)!}{(m-1)!(n-m)!)}\\= & {} \frac{n}{2} \left( 2^{n-1}-1\right) \sum _{m=1}^{n} {}^{n-1}C_{m-1}\\= & {} \frac{n}{2}\left( 2^{n-1}-1\right) \sum _{j=0}^{n-1} {}^{n-1}C_j\\= & {} \frac{n}{2} \left( 2^{n-1}-1\right) 2^{n-1}\\= & {} n2^{n-2}\left( 2^{n-1}-1\right) . \end{aligned}$$ -
(iii)
\(deg (V_A) = 2^n - 2^{n-m}- 1\).
It follows that the number of edges of simple graphs G equals
$$\begin{aligned} |E_s(G)|= & {} \frac{n}{2} \sum _{m=1}^{n} {}^nC_m deg \left( V_A\right) \\= & {} \frac{1}{2}\sum _{m=1}^{n} {}^nC_m \left( 2^n-2^{n-m}-1\right) \\= & {} \frac{1}{2}\left( 2^n-1\right) \sum _{m=1}^{n} {}^nC_m\\&-\frac{1}{2}2^n \sum _{m=1}^{n} {}^nC_m 2^{-m}\\= & {} \frac{1}{2}\left( 2^n-1\right) \left( 2^{n-1}-1\right) \\&- 2^{n-1}\sum _{m=1}^{n}\left( \frac{1}{2}\right) ^m {}^nC_m\\= & {} \frac{1}{2}\left( 2^{2n}-2^{n+1}+1\right) \\&-2^{n-1}\left( \left( 1+\frac{1}{2}\right) ^n-1\right) \\= & {} \frac{1}{2}\left( \left( 2^{2n}-2.2^n +1\right) -\left( 3^n-2^n\right) \right) \\= & {} \frac{1}{2}(2^{2n}-2^n-3^n+1). \end{aligned}$$
The total degree of edges of fuzzy topological graphs can be calculated for the three different types of fuzzy graphs as follows:
[For fuzzy pseudographs:] Let \(\mathcal {B} \le \mathcal {A} \le \mathcal {E} \le X\), \(|\mathcal {A}| = m\) and \(|\mathcal {A}^c|= n-m\)
\(\forall x\in \mathcal {B}, y \in \mathcal {A}, w \in \mathcal {E}\) and \(z \in \mathcal {L}\) we have,
It follows that the total degree of edges of fuzzy pseudographs \(\mathcal {G}\) equals
[For fuzzy discrete graphs:]
\(\forall x\in \mathcal {B}, y \in \mathcal {A}, w \in \mathcal {E}\) and \(z \in \mathcal {L}\) we have,
It follows that the summation of edges of fuzzy discrete graphs \(\mathcal {G}\) equals
[For fuzzy simple graphs:] Let the number of the fuzzy subset of length \(|B|=k\), \(|A\cap E|=l\), and \(|A \cap L|=r\). Then, we have
\(\square \)
Proof
(Continue proof Theorem 4) Let \(\mathcal {G}\) be a fuzzy graph. To complete the proof, it is sufficient to prove three conditions of a fuzzy topology on \(\tau \).
-
(i)
By Definitions 3 and 7, \(\mathcal {G}\) can be represented by different classes. Suppose that the graph number of \(\mathcal {G}\) is m. Then, there exists a class, say \(\tau \), such that \(\tau \le P(\bigg \{\displaystyle \frac{a}{x_1},\) \(\frac{b}{x_2},\) \(\frac{c}{x_3}, \ldots , \frac{d}{x_m}\bigg \})\) and represents \(\mathcal {G}\). Each \(\mathcal {A}_i \in {\tau }\) represents \(v_i\) and \(X \in {\tau }\) represents the set of vertices \(V(\mathcal {G})\). So, by Definition 6, \(\mu _{R}(v_i,V(\mathcal {G}))=\) \(\mu _{R}(v_i,X)\). If \(N= \bigg \{\displaystyle \frac{a}{x_1},\) \(\frac{b}{x_2},\) \(\frac{c}{x_3}, \ldots , \frac{d}{x_m}\bigg \}\), then \(\mu _{R}(\mathcal {A} \cap X)=\) \(\mu _{R}(\mathcal {A}\cap {\mathbb {N}})=\) \(\mu _{R}(\mathcal {A})\). This means that each \(\mathcal {A} \in {\tau }\) satisfies that \(\mathcal {A} \le X\). Since every vertex in \(\mathcal {G}\) is a fuzzy graph subset of \(V(\mathcal {G})\), i.e., for every \(v_i \in V(\mathcal {G})\) the singleton \(\{v_i\} \subset V(\mathcal {G})\) and each element in \({\tau }\) is a fuzzy subset from \(X \in {\tau }\), then \(X= \bigg \{\displaystyle \frac{a}{x_1}, \frac{b}{x_2},\frac{c}{x_3}, \ldots , \frac{d}{x_m}\bigg \}\). Also, the isolated vertex \(v_0\) can be represented by \(0 \in {\tau }\).
-
(ii)
Let \(v_1, v_2, \ldots \) be an arbitrary different vertices in \(V(\mathcal {G})\) represented by \(\mathcal {A}_{v_1} ,\mathcal {A}_{v_2}, \ldots \). Since \(v_1 \vee v_2 \vee \cdots = v_{({\mathcal {A}_{v_1} \vee \mathcal {A}_{v_2} \vee \cdots })}\), then \(\mathcal {A}_{v_1} \vee \mathcal {A}_{v_2} \vee \cdots \in {\tau }\).
-
(iii)
If \(v_i\) and \(v_j\) are two different vertices in \(V(\mathcal {G})\) and represented by \(\mathcal {A}_i\) and \(\mathcal {A}_j\), respectively. Since \(v_i \wedge v_j=\) \(v_{{\mathcal {A}_i} \wedge {\mathcal {A}_j}}\), then \(\mathcal {A}_i \wedge \mathcal {A}_j \in {\tau }\). Therefore, \({\tau }\) is a fuzzy topology. \(\square \)
Proof
(Continue proof Theorem 5) Let \(\mathcal {A}_m=\) \(\{\frac{a}{x_1},\) \(\frac{b}{x_2},\ldots ,\frac{c}{x_m}\}\), \(1\le k\le m \), \(k< m < n\) and \(B_k\subseteq A_m \subseteq C_n\)
\(\forall x \in B_k, y \in A_m\) and \(z \in C_n\). The total degree of edges is \(\sum E(\mathcal {G})= \frac{1}{2}\sum \limits _{i=1}^n deg V_{\mathcal {A}_i}\). \(\square \)
Rights and permissions
About this article
Cite this article
Atef, M., El Atik, A.E.F. & Nawar, A. Fuzzy topological structures via fuzzy graphs and their applications. Soft Comput 25, 6013–6027 (2021). https://doi.org/10.1007/s00500-021-05594-8
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00500-021-05594-8