A new type of fuzzy systems using pyramid membership functions (PMFs) and approximation properties

Abstract

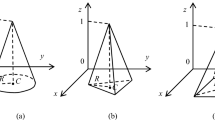
This paper focuses on improving the precision and simplifying the structure of fuzzy systems. A new type of fuzzy systems that using a proposed pyramid membership function (PMF) is constructed. The original compound of fuzzy rule antecedents is replaced by PMF. Specifically, the commonly used one-dimensional triangular membership functions are generalized to three kinds of two-dimensional PMFs. Cone fuzzy systems (CFSs) with the proposed rectangular pyramid, circular cone and triangular mesh pyramid membership functions are, respectively, given. Approximation properties of CFS, including universal approximation property and approximation accuracy, are proved theoretically. It is shown that, rectangular pyramid fuzzy system and triangular mesh pyramid fuzzy system are capable of achieving first-order and second-order accuracy, respectively. Two experimental examples are presented to demonstrate the effectiveness of CFS. Both theoretical and numerical results illustrate that CFS is capable of obtaining good accuracy.

Appendices

Appendix A: Different types of cone fuzzy systems

(1) Rectangular pyramid fuzzy system

From (23) and (9)–(12), the expressions of RPFS can be represented by:

in the domain $D_1$,

$$\begin{aligned} S(x,y)&= \frac{{({x_{i + 1}} - x)({y_{j + 1}}- {y_j})}}{{(2y +{y_{j + 1}} - 3{y_j})({x_{i + 1}} - {x_i})}}{z_{ij}} \\&\quad +\, \frac{{y - {y_j}}}{{2y +{y_{j + 1}}- 3{y_j}}}{z_{i,j + 1}}\\&\quad +\frac{{y- {y_j}}}{{2y +{y_{j + 1}}- 3{y_j}}}{z_{i + 1,j + 1}} \\ {}&\quad +\frac{{(x - {x_i})({y_{j + 1}}- {y_j})}}{{(2y + {y_{j + 1}} - 3{y_j})({x_{i + 1}} - {x_i})}}{z_{i + 1,j}}; \end{aligned}$$

in the domain $D_2$,

$$\begin{aligned} S(x,y)&= \frac{{({x_{i + 1}}- {x_i})({y_{j + 1}}- y)}}{{(2x +{x_{i + 1}}- 3{x_i})({y_{j + 1}} - {y_j})}}{z_{ij}} \\&\quad + \,\frac{{x - {x_i}}}{{2x + {x_{i+1}} - 3{x_i}}}{z_{i+1,j + 1}}\\&\quad +\, \frac{{x - {x_i}}}{{2x + {x_{i + 1}} - 3{x_i}}}{z_{i + 1,j}} \\&\quad + \,\frac{{({x_{i + 1}} - {x_i})(y - {y_j})}}{{(2x + {x_{i + 1}} - 3{x_i})({y_{j + 1}} - {y_j})}}{z_{i,j + 1}}; \end{aligned}$$

in the domain $D_3$,

$$\begin{aligned} S(x,y)&= \frac{{({y_{j + 1}} - {y_j})({x_{i + 1}} - x)}}{{( - 2y + 3{y_{j + 1}} - {y_j})({x_{i + 1}}- {x_i})}}{z_{i,j + 1}}\\&\quad +\, \frac{{{y_{j + 1}}- y}}{{ - 2y + 3{y_{j + 1}} - {y_j}}}{z_{ij}} \\&\quad +\,\frac{{{y_{j + 1}} - y}}{{ - 2y+3{y_{j + 1}}- {y_j}}}{z_{i + 1,j}}\\&\quad +\, \frac{{({y_{j + 1}} - {y_j})(x - {x_i})}}{{( - 2y +3{y_{j + 1}}- {y_j})({x_{i + 1}}- {x_i})}}{z_{i + 1,j + 1}}; \end{aligned}$$

in the domain $D_4$,

$$\begin{aligned} S(x,y)&= \frac{{({x_{i + 1}}- {x_i})({y_{j + 1}} - y)}}{{( - 2x + 3{x_{i + 1}}- {x_i})({y_{j + 1}} - {y_j})}}{z_{i + 1,j}} \\&\quad +\, \frac{{{x_{i + 1}}- x}}{{ - 2x+ 3{x_{i + 1}} - {x_i}}}{z_{ij}} \\&\quad +\, \frac{{{x_{i + 1}}- x}}{{ - 2x + 3{x_{i + 1}}- {x_i}}}{z_{i,j + 1}}\\&\quad +\, \frac{{({x_{i + 1}}- {x_i})(y - {y_j})}}{{( - 2x +{x_{i + 1}}- {x_i})({y_{j + 1}} - {y_j})}}{z_{i + 1,j + 1}}. \end{aligned}$$

(2) Circular cone fuzzy system

From (23) and (13)–(16), the general expressions of CCFS can be deduced:

In the domain $U_1$: $S(x,y)=\frac{m_1}{n_1}$, where

$$\begin{aligned} m_1&=\left( 1 - \frac{1}{h}\sqrt{{{(x - {x_i})}^2} + {{(y - {y_j})}^2}} \right) {z_{ij}}\nonumber \\&\quad +\, \left( 1 - \frac{1}{h}\sqrt{{{(x - {x_{i + 1}})}^2} + {{(y - {y_j})}^2}} \right) {z_{i + 1,j}} \nonumber \\&\quad +\,\left( 1 - \frac{1}{h}\sqrt{{{(x - {x_{i + 1}})}^2} + {{(y - {y_{j + 1}})}^2}} \right) {z_{i + 1,j + 1}}, \end{aligned}$$

(28)

$$\begin{aligned} n_1&=\left( 1 - \frac{1}{h}\sqrt{{{(x - {x_i})}^2} + {{(y - {y_j})}^2}} \right) \nonumber \\&\quad +\, \left( 1 - \frac{1}{h}\sqrt{{{(x - {x_{i + 1}})}^2} + {{(y - {y_j})}^2}} \right) \nonumber \\&\quad +\, \left( 1 - \frac{1}{h}\sqrt{{{(x - {x_{i + 1}})}^2} + {{(y - {y_{j + 1}})}^2}} \right) . \end{aligned}$$

(29)

In the domain $U_2$: $S(x,y)=\frac{m_2}{n_2}$, where

$$\begin{aligned} m_2&=\left( 1 - \frac{1}{h}\sqrt{{{(x - {x_i})}^2} + {{(y - {y_j})}^2}}\right) {z_{ij}} \nonumber \\&\quad +\, \left( 1 - \frac{1}{h}\sqrt{{{(x - {x_i})}^2} + {{(y - {y_{j + 1}})}^2}} \right) {z_{i,j + 1}} \nonumber \\&\quad +\, \left( 1 - \frac{1}{h}\sqrt{{{(x - {x_{i + 1}})}^2} + {{(y - {y_j})}^2}} \right) {z_{i + 1,j}}, \end{aligned}$$

(30)

$$\begin{aligned} n_2&=\left( 1 - \frac{1}{h}\sqrt{{{(x - {x_i})}^2} + {{(y - {y_j})}^2}} \right) \nonumber \\&\quad +\, \left( 1 - \frac{1}{h}\sqrt{{{(x - {x_i})}^2} + {{(y - {y_{j + 1}})}^2}} \right) \nonumber \\&\quad +\, \left( 1 - \frac{1}{h}\sqrt{{{(x - {x_{i + 1}})}^2} + {{(y - {y_j})}^2}} \right) . \end{aligned}$$

(31)

In the domain $U_3$: $S(x,y)=\frac{m_3}{n_3}$, where

$$\begin{aligned} m_3&=\left( 1 - \frac{1}{h}\sqrt{{{(x - {x_i})}^2} + {{(y - {y_j})}^2}} \right) {z_{ij}} \nonumber \\&\quad +\, \left( 1 - \frac{1}{h}\sqrt{{{(x - {x_i})}^2} + {{(y - {y_{j + 1}})}^2}} \right) {z_{i,j + 1}}\nonumber \\&\quad +\, \left( 1 - \frac{1}{h}\sqrt{{{(x - {x_{i + 1}})}^2} + {{(y - {y_{j + 1}})}^2}} \right) {z_{i + 1,j + 1}}, \end{aligned}$$

(32)

$$\begin{aligned} n_3&=\left( 1 - \frac{1}{h}\sqrt{{{(x - {x_i})}^2} + {{(y - {y_j})}^2}} \right) \nonumber \\&\quad +\, \left( 1 - \frac{1}{h}\sqrt{{{(x - {x_i})}^2} + {{(y - {y_{j + 1}})}^2}} \right) \nonumber \\&\quad +\, \left( 1 - \frac{1}{h}\sqrt{{{(x - {x_{i + 1}})}^2} + {{(y - {y_{j + 1}})}^2}} \right) . \end{aligned}$$

(33)

In the domain $U_4$: $S(x,y)=\frac{m_4}{n_4}$, where

$$\begin{aligned} m_4&=\left( 1 - \frac{1}{h}\sqrt{{{(x - {x_i})}^2} + {{(y - {y_{j + 1}})}^2}} \right) {z_{i,j + 1}} \nonumber \\&\quad +\, \left( 1 - \frac{1}{h}\sqrt{{{(x - {x_{i + 1}})}^2} + {{(y - {y_j})}^2}} \right) {z_{i + 1,j}}\nonumber \\&\quad +\, \left( 1 - \frac{1}{h}\sqrt{{{(x - {x_{i + 1}})}^2} + {{(y - {y_{j + 1}})}^2}} \right) {z_{i + 1,j + 1}}, \end{aligned}$$

(34)

$$\begin{aligned} n_4&=\left( 1 - \frac{1}{h}\sqrt{{{(x - {x_i})}^2} + {{(y - {y_{j + 1}})}^2}} \right) \nonumber \\&\quad +\, \left( 1 - \frac{1}{h}\sqrt{{{(x - {x_{i + 1}})}^2} + {{(y - {y_j})}^2}} \right) \nonumber \\&\quad +\, \left( 1 - \frac{1}{h}\sqrt{{{(x - {x_{i + 1}})}^2} + {{(y - {y_{j + 1}})}^2}} \right) . \end{aligned}$$

(35)

In the domain $U_5$: $S(x,y)=\frac{m_5}{n_5}$, where

$$\begin{aligned} m_5&=\left( 1 - \frac{1}{h}\sqrt{{{(x - {x_i})}^2} + {{(y - {y_j})}^2}} \right) {z_{ij}}\nonumber \\&\quad +\, \left( 1 - \frac{1}{h}\sqrt{{{(x - {x_i})}^2} + {{(y - {y_{j + 1}})}^2}} \right) {z_{i,j + 1}}\nonumber \\&\quad +\, \left( 1 - \frac{1}{h}\sqrt{{{(x - {x_{i + 1}})}^2} + {{(y - {y_j})}^2}} \right) {z_{i + 1,j}} \nonumber \\&\quad +\, \left( 1 - \frac{1}{h}\sqrt{{{(x - {x_{i + 1}})}^2} + {{(y - {y_{j + 1}})}^2}} \right) {z_{i + 1,j + 1}}, \end{aligned}$$

(36)

$$\begin{aligned} n_5&=\left( 1 - \frac{1}{h}\sqrt{{{(x - {x_i})}^2} + {{(y - {y_j})}^2}} \right) \nonumber \\&\quad +\, \left( 1 - \frac{1}{h}\sqrt{{{(x - {x_i})}^2} + {{(y - {y_{j + 1}})}^2}} \right) \nonumber \\&\quad +\, \left( 1 - \frac{1}{h}\sqrt{{{(x - {x_{i + 1}})}^2} + {{(y - {y_j})}^2}} \right) \nonumber \\&\quad +\, \left( 1 - \frac{1}{h}\sqrt{{{(x - {x_{i + 1}})}^2} + {{(y - {y_{j + 1}})}^2}} \right) . \end{aligned}$$

(37)

In the domain $V_1$:

$$\begin{aligned} S(x,y)&= \left( \left( 1 - \frac{1}{h}\sqrt{{{(x - {x_i})}^2} + {{(y - {y_j})}^2}} \right) {z_{ij}} \right. \nonumber \\&\quad \left. +\, \left( 1 - \frac{1}{h}\sqrt{{{(x - {x_{i + 1}})}^2} + {{(y - {y_j})}^2}} \right) {z_{i + 1,j}}\right) \!\Big /\nonumber \\&\quad \left( \left( 1 - \frac{1}{h}\sqrt{{{(x - {x_i})}^2} + {{(y - {y_j})}^2}} \right) \right. \nonumber \\&\quad \left. +\, \left( 1 - \frac{1}{h}\sqrt{{{(x - {x_{i + 1}})}^2} + {{(y - {y_j})}^2}} \right) \right) . \end{aligned}$$

(38)

In the domain $V_2$:

$$\begin{aligned} S(x,y)&= \left( 1 - \frac{1}{h}\sqrt{{{(x - {x_i})}^2} + {{(y - {y_j})}^2}} \right) {z_{ij}}\nonumber \\&\quad +\,\left. \left( 1 - \frac{1}{h}\sqrt{{{(x - {x_i})}^2} + {{(y - {y_{j + 1}})}^2}} \right) {z_{i,j + 1}}\right) \!\Big /\nonumber \\&\quad \left( 1 - \frac{1}{h}\sqrt{{{(x - {x_i})}^2} + {{(y - {y_j})}^2}} \right) \nonumber \\&\quad \left. + \,\left( 1 - \frac{1}{h}\sqrt{{{(x - {x_i})}^2} + {{(y - {y_{j + 1}})}^2}} \right) \right) . \end{aligned}$$

(39)

In the domain $V_3$:

$$\begin{aligned} S(x,y)&=\left( \left( 1 - \frac{1}{h}\sqrt{{{(x - {x_i})}^2} + {{(y - {y_{j + 1}})}^2}} \right) {z_{i,j + 1}}\right. \nonumber \\&\quad \left. +\, \left( 1 - \frac{1}{h}\sqrt{{{(x - {x_{i + 1}})}^2} + {{(y - {y_{j + 1}})}^2}} \right) {z_{i + 1,j + 1}}\right) \!\Big /\nonumber \\&\quad \left( \left( 1 - \frac{1}{h}\sqrt{{{(x - {x_i})}^2} + {{(y - {y_{j + 1}})}^2}} \right) \right. \nonumber \\&\quad \left. +\, \left( 1 - \frac{1}{h}\sqrt{{{(x - {x_{i + 1}})}^2} + {{(y - {y_{j + 1}})}^2}} \right) \right) . \end{aligned}$$

(40)

In the domain $V_4$:

$$\begin{aligned} S(x,y)&= \left( \left( 1 - \frac{1}{h}\sqrt{{{(x - {x_i})}^2} + {{(y - {y_j})}^2}} \right) {z_{ij}}\right. \nonumber \\&\quad \left. +\, \left( 1 - \frac{1}{h}\sqrt{{{(x - {x_{i + 1}})}^2} + {{(y - {y_{j + 1}})}^2}} \right) {z_{i + 1,j + 1}}\right) \!\Big /\nonumber \\&\quad \left( \left( 1 - \frac{1}{h}\sqrt{{{(x - {x_i})}^2} + {{(y - {y_j})}^2}}\right) \right. \nonumber \\&\quad \left. + \,\left( 1 - \frac{1}{h}\sqrt{{{(x - {x_{i + 1}})}^2} + {{(y - {y_{j + 1}})}^2}} \right) \right) . \end{aligned}$$

(41)

(3) Triangular mesh pyramid fuzzy system

From (24) and (17)–(22), the expressions of the output of a TPFS model are derived as follows:

in the domain $E_1$:

$$\begin{aligned} \begin{aligned}&S(x,y) = \left( \frac{{{x_{i + 1}}{y_{j + 1}} - {x_i}{y_{j + 1}}}}{{{m_1}}} - \frac{{{x_{i + 1}} - {x_i}}}{{{m_1}}}y\right) {z_{ij}}\\&\quad +\, \left( \frac{{{x_i}{y_{j + 1}} - {x_{i + 1}}{y_j}}}{{{m_1}}} - \frac{{{y_{j + 1}} - {y_j}}}{{{m_1}}}x - \frac{{{x_i} - {x_{i + 1}}}}{{{m_1}}}y\right) {z_{i,j + 1}}\\&\quad +\, \left( \frac{{{x_i}{y_j} - {x_i}{y_{j + 1}}}}{{{m_1}}} - \frac{{{y_j} - {y_{j + 1}}}}{{{m_1}}}x\right) {z_{i + 1,j + 1}}; \end{aligned} \end{aligned}$$

(42)

in the domain $E_2$:

$$\begin{aligned} \begin{aligned} S(x,y)&= \left( \frac{{{x_{i + 1}}{y_j} - {x_{i + 1}}{y_{j + 1}}}}{{{m_2}}} - \frac{{{y_j} - {y_{j + 1}}}}{{{m_2}}}x\right) {z_{ij}}\\&\quad +\,\left( \frac{{{x_i}{y_{j + 1}} - {x_{i + 1}}{y_j}}}{{{m_2}}} - \frac{{{y_{j + 1}} - {y_j}}}{{{m_2}}}x - \frac{{{x_i} - {x_{i + 1}}}}{{{m_2}}}y\right) {z_{i + 1,j}}\\&\quad +\, \left( \frac{{{x_{i + 1}}{y_j} - {x_i}{y_j}}}{{{m_2}}} - \frac{{{x_{i + 1}} - {x_i}}}{{{m_2}}}y\right) {z_{i + 1,j + 1}}. \end{aligned} \end{aligned}$$

(43)

Appendix B: Proofs of theorems

Proof of Theorem 3

Without losing generality, the proof is discussed on one partition of the domain D. We can now prove the theorem with the help of interpolation property of CFS.

$$\begin{aligned}&\left| S\left( x,y \right) -f\left( x,y \right) \right| \\&\quad =\left| S\left( x,y \right) -S\left( {{x}_{i}},{{y}_{j}} \right) +f\left( {{x}_{i}},{{y}_{j}} \right) -f\left( x,y \right) \right| \\&\quad \le \left| S\left( x,y \right) -S\left( {{x}_{i}},{{y}_{j}} \right) \right| +\left| f\left( {{x}_{i}},{{y}_{j}} \right) -f\left( x,y \right) \right| . \end{aligned}$$

Using Taylor expansion (Rubio 2016; Liu et al. 2016; Rubio 2015) with Lagrange remainder, there exist $({{\xi }_{1}},{{\eta }_{1}})$ and $({{\xi }_{2}},{{\eta }_{2}})$ which both belong to $\left( {{x}_{i}},{{x}_{i+1}} \right) \times \left( {{y}_{j}},{{y}_{j+1}} \right)$ such that

$$\begin{aligned}&\left| S\left( x,y \right) -f\left( x,y \right) \right| \\&\quad \le \left| \frac{\partial S}{\partial x}\left| _{({{\xi }_{1}},{{\eta }_{1}})} \right. \left( x-{{x}_{i}} \right) +\frac{\partial S}{\partial y}\left| _{({{\xi }_{1}},{{\eta }_{1}})} \right. \left( y-{{y}_{j}} \right) \right| \\&\quad \quad +\,\left| \frac{\partial f}{\partial x}\left| _{({{\xi }_{2}},{{\eta }_{2}})} \right. \left( x-{{x}_{i}} \right) +\frac{\partial f}{\partial y}\left| _{({{\xi }_{2}},{{\eta }_{2}})} \right. (y-{{y}_{j}}) \right| \\&\quad \le \left( \left| \frac{\partial S}{\partial x}\left| _{({{\xi }_{1}},{{\eta }_{1}})} \right. \right| +\left| \frac{\partial S}{\partial y}\left| _{({{\xi }_{1}},{{\eta }_{1}})} \right. \right| +\left| \frac{\partial f}{\partial x}\left| _{({{\xi }_{2}},{{\eta }_{2}})} \right. \right| \right. \\&\quad \quad \left. +\,\left| \frac{\partial f}{\partial y}\left| _{({{\xi }_{2}},{{\eta }_{2}})} \right. \right| \right) h, \end{aligned}$$

where $h=\max \{ |x-{{x}_{i}}|,|y-{{y}_{j}}| \}$.

As $\left( |\frac{\partial S}{\partial x}| _{({\xi }_{1},{\eta }_{1})}|+| \frac{\partial S}{\partial y}| _{({\xi }_{1},{\eta }_{1})}|+| \frac{\partial f}{\partial x}| _{({\xi }_{2},{\eta }_{2})} |+| \frac{\partial f}{\partial y}| _{({\xi }_{2},{\eta }_{2})} | \right)$ is a constant, when h is sufficiently small, for any $\varepsilon >0$, it is evident that the following inequality can be obtained:

$$\begin{aligned} \left| S\left( x,y \right) -f\left( x,y \right) \right| <\varepsilon \quad \forall \left( x,y \right) \in D. \end{aligned}$$

Then

$$\begin{aligned} \left\| S-f \right\| =\underset{\left( x,y \right) \in D}{\mathop {\sup }}\,\left| S\left( x,y \right) -f\left( x,y \right) \right| <\varepsilon . \end{aligned}$$

The proof is complete.$\square$

Proof of Theorem 4

The proofs of this theorem in the domains $D_1$–$D_4$ are similar, so we only discuss the case of domain $D_1$.

To utilize the property of triangular membership functions, we denote $A_i(x)$, $A_{i+1}(x)$, $B_j(y)$ and $B_{j+1}(y)$ as triangular membership functions with the peak points $x_i$, $x_{i+1}$, $y_j$ and $y_{j+1}$. For $x\in [x_i,x_{i+1}]$ and $y\in [y_j,y_{j+1}]$, we have

$$\begin{aligned} {A_i}(x)&= \frac{{{x_{i + 1}} - x}}{{{x_{i + 1}} - {x_i}}},\quad {A_{i + 1}}(x) = \frac{{x - {x_i}}}{{{x_{i + 1}} - {x_i}}},\\ {B_j}(y)&= \frac{{{y_{j + 1}} - y}}{{{y_{j + 1}} - {y_j}}}, \quad {B_{j + 1}}(y) = \frac{{y - {y_j}}}{{{y_{j + 1}} - {y_j}}}. \end{aligned}$$

For $\forall (x,y) \in [{x_i},{x_{i + 1}}] \times [{y_j},{y_{j + 1}}]$, the expression of RPFS can be rewritten as follows:

$$\begin{aligned} S(x,y)&= \frac{{{A_i}(x)}}{{1 + 2{B_{j + 1}}(y)}}{z_{ij}} + \frac{{{B_{j + 1}}(y)}}{{1 + 2{B_{j + 1}}(y)}}{z_{i,j + 1}}\\&\quad +\, \frac{{{B_{j + 1}}(y)}}{{1 + 2{B_{j + 1}}(y)}}{z_{i + 1,j + 1}} + \frac{{{A_{i + 1}}(x)}}{{1 + 2{B_{j + 1}}(y)}}{z_{i + 1,j}}. \end{aligned}$$

Let $\bar{S}(x,y)$ be defined by (3). We first estimate the following absolute difference. Note that the triangular membership functions have the properties, i.e., ${A_i}(x) + {A_{i + 1}}(x) = 1$, ${B_j}(y) + {B_{j + 1}}(y) = 1$, $A_i(x)\le 1$, $A_{i+1}(x)\le 1$, $B_j(y)\le 1$ and $B_{j+1}(y)\le 1$. It follows that

$$\begin{aligned}&\left| {S(x,y) - \bar{S}(x,y)} \right| \nonumber \\&\quad = \left| {\frac{{{A_i}(x){B_{j + 1}}(y)({B_{j + 1}}(y) - {B_j}(y))}}{{1 + 2{B_{j + 1}}(y)}}{z_{ij}}} \right. \nonumber \\&\quad \quad +\,\frac{{{B_{j + 1}}(y)({A_{i + 1}}(x) - 2{A_i}(x){B_{j + 1}}(y))}}{{1 + 2{B_{j + 1}}(y)}}{z_{i,j + 1}} \nonumber \\&\quad \quad +\, \frac{{{B_{j + 1}}(y)({A_i}(x) - 2{A_{i + 1}}(x){B_{j + 1}}(y))}}{{1 + 2{B_{j + 1}}(y)}}{z_{i + 1,j + 1}}\nonumber \\&\quad \quad \left. +\, \frac{{{A_{i + 1}}(x){B_{j + 1}}(y)({B_{j + 1}}(y) - {B_j}(y))}}{{1 + 2{B_{j + 1}}(y)}}{z_{i + 1,j}}\right| \nonumber \\&\quad = \left| {\frac{{{A_i}(x){B_{j + 1}}(y)({B_{j + 1}}(y) - {B_j}(y))}}{{1 + 2{B_{j + 1}}(y)}}({z_{ij}} - {z_{i + 1,j}})} \right. \nonumber \\&\quad \quad +\,\frac{{{B_{j + 1}}(y)({A_i}(x) - 2{A_{i + 1}}(x){B_{j + 1}}(y))}}{{1 + 2{B_{j + 1}}(y)}}({z_{i + 1,j + 1}} - {z_{i,j + 1}}) \nonumber \\&\quad \quad \left. { +\, \frac{{{B_{j + 1}}(y)({B_{j + 1}}(y) - {B_j}(y))}}{{1 + 2{B_{j + 1}}(y)}}({z_{i + 1,j}} - {z_{i,j + 1}})} \right| \nonumber \\&\quad \le \frac{1}{3}\left| {{z_{ij}} - {z_{i + 1,j}}} \right| + \frac{1}{3}\left| {{z_{i + 1,j + 1}} - {z_{i,j + 1}}} \right| \nonumber \\&\quad \quad +\, \frac{1}{3}\left| {{z_{i + 1,j}} - {z_{i,j + 1}}} \right| \nonumber \\&\quad \le \frac{1}{3}\left| {{z_{ij}} - {z_{i + 1,j}}} \right| + \frac{1}{3}\left| {{z_{i + 1,j + 1}} - {z_{i,j + 1}}} \right| \nonumber \\&\quad \quad +\, \frac{1}{3}\left| {{z_{i + 1,j}} - {z_{ij}}} \right| + \frac{1}{3}\left| {{z_{ij}} - {z_{i,j + 1}}} \right| \nonumber \\&\quad \le {\left\| {\frac{{\partial f}}{{\partial x}}} \right\| _\infty }{h_1} + \frac{1}{3}{\left\| {\frac{{\partial f}}{{\partial y}}} \right\| _\infty }{h_2}. \end{aligned}$$

(44)

According to the approximation property of $\bar{S}(x,y)$ given by Theorem 2, the difference between $\bar{S}(x,y)$ and f(x, y) can be expressed as

$$\begin{aligned}&\left| {S(x,y) - f(x,y)} \right| \\&\quad \le \left| {S(x,y) - \bar{S}(x,y)} \right| + \left| {\bar{S}(x,y) - f(x,y)} \right| \\&\quad \le \frac{1}{8}\left( {\left\| {\frac{{{\partial ^2}f}}{{\partial {x^2}}}} \right\| _\infty }{h_1}^2 +{\left\| {\frac{{{\partial ^2}f}}{{\partial {y^2}}}} \right\| _\infty }{h_2}^2\right) \\&\quad \quad +\, {\left\| {\frac{{\partial f}}{{\partial x}}} \right\| _\infty }{h_1}+ \frac{1}{3}{\left\| {\frac{{\partial f}}{{\partial y}}} \right\| _\infty }{h_2}, \end{aligned}$$

which ends the proof.$\square$

Proof of Theorem 5

Take the TPFS in $E_2$ as an example and define the error as

$$\begin{aligned} \varepsilon (x,y) = S(x,y) - f(x,y). \end{aligned}$$

Using first-order Taylor series expansion around an arbitrary point (z, w), the error expands to

$$\begin{aligned} \varepsilon (x,y)&= \varepsilon (z,w) + \frac{{\partial \varepsilon }}{{\partial x}}\left| {_{(z,w)}} \right. (x - z) \\&\quad +\, \frac{{\partial \varepsilon }}{{\partial y}}\left| {_{(z,w)}} \right. (y - w)+ r(x,y,z,w), \end{aligned}$$

where r(x, y, z, w) is the remainder term defined by

$$\begin{aligned}&r(x,y,z,w) = \frac{{{\partial ^2}\varepsilon }}{{\partial x\partial y}}\left| {_{(\xi ,\eta )}} \right. (x - z)(y - w)\nonumber \\&\quad +\, \frac{1}{2}\frac{{{\partial ^2}\varepsilon }}{{\partial {x^2}}}\left| {_{(\xi ,\eta )}} \right. {(x - z)^2} + \frac{1}{2}\frac{{{\partial ^2}\varepsilon }}{{\partial {y^2}}}\left| {_{(\xi ,\eta )}} \right. {(y - w)^2}. \end{aligned}$$

(45)

Note that S(x, y) is a linear function of two variables. It follows that

$$\begin{aligned}&\frac{{{\partial ^2}\varepsilon }}{{\partial {x^2}}}\left| {_{(\xi ,\eta )}} \right. = \frac{{{\partial ^2}f}}{{\partial {x^2}}}\left| {_{(\xi ,\eta )}} \right. ,\frac{{{\partial ^2}\varepsilon }}{{\partial {y^2}}}\left| {_{(\xi ,\eta )}} \right. = \frac{{{\partial ^2}f}}{{\partial {y^2}}}\left| {_{(\xi ,\eta )}} \right. ,\nonumber \\&\frac{{{\partial ^2}\varepsilon }}{{\partial x\partial y}}\left| {_{(\xi ,\eta )}} \right. = \frac{{{\partial ^2}f}}{{\partial x\partial y}}\left| {_{(\xi ,\eta )}} \right. . \end{aligned}$$

(46)

Substituting Eq. (46) into Eq. (45) yields

$$\begin{aligned}&r(x,y,z,w) = \frac{{{\partial ^2}f}}{{\partial x\partial y}}\left| {_{(\xi ,\eta )}} \right. (x - z)(y - w)\\&\quad +\, \frac{1}{2}\frac{{{\partial ^2}f}}{{\partial {x^2}}}\left| {_{(\xi ,\eta )}} \right. {(x - z)^2}+ \frac{1}{2}\frac{{{\partial ^2}f}}{{\partial {y^2}}}\left| {_{(\xi ,\eta )}} \right. {(y - w)^2}. \end{aligned}$$

The interpolation property of a TPFS implies that $\varepsilon (x,y)$ is equal to zero at the points $(x_i, y_j)$, $(x_{i+1}, y_j)$ and $(x_{i+1}, y_{j+1})$. It then follows that

$$\begin{aligned}&\varepsilon (z,w) + \frac{{\partial \varepsilon }}{{\partial x}}\left| {_{(z,w)}} \right. ({x_i} - z) + \frac{{\partial \varepsilon }}{{\partial y}}\left| {_{(z,w)}} \right. ({y_j} - w) \nonumber \\&\quad +\, \frac{1}{2}\frac{{{\partial ^2}f}}{{\partial {x^2}}}\left| {_{(\xi ,\eta )}} \right. {({x_i} - z)^2}+ \frac{1}{2}\frac{{{\partial ^2}f}}{{\partial {y^2}}}\left| {_{(\xi ,\eta )}} \right. {({y_j} - w)^2} \nonumber \\&\quad +\, \frac{{{\partial ^2}f}}{{\partial x\partial y}}\left| {_{(\xi ,\eta )}} \right. ({x_i} - z)({y_j} - w) = 0, \end{aligned}$$

(47)

$$\begin{aligned}&\varepsilon (z,w) + \frac{{\partial \varepsilon }}{{\partial x}}\left| {_{(z,w)}} \right. ({x_{i + 1}} - z)+\frac{{\partial \varepsilon }}{{\partial y}}\left| {_{(z,w)}} \right. ({y_j} - w) \nonumber \\&\quad +\,\frac{1}{2}\frac{{{\partial ^2}f}}{{\partial {x^2}}}\left| {_{(\xi ,\eta )}} \right. {({x_{i + 1}} - z)^2}+ \frac{1}{2}\frac{{{\partial ^2}f}}{{\partial {y^2}}}\left| {_{(\xi ,\eta )}} \right. {({y_j} - w)^2} \nonumber \\&\quad +\,\frac{{{\partial ^2}f}}{{\partial x\partial y}}\left| {_{(\xi ,\eta )}} \right. ({x_{i + 1}} - z)({y_j} - w) = 0, \end{aligned}$$

(48)

$$\begin{aligned}&\varepsilon (z,w) +\frac{{\partial \varepsilon }}{{\partial x}}\left| {_{(z,w)}} \right. ({x_{i + 1}} - z) + \frac{{\partial \varepsilon }}{{\partial y}}\left| {_{(z,w)}} \right. ({y_{j + 1}} - w) \nonumber \\&\quad +\, \frac{1}{2}\frac{{{\partial ^2}f}}{{\partial {x^2}}}\left| {_{(\xi ,\eta )}} \right. {({x_{i + 1}} - z)^2} + \frac{1}{2}\frac{{{\partial ^2}f}}{{\partial {y^2}}}\left| {_{(\xi ,\eta )}} \right. {({y_{j + 1}} - w)^2} \nonumber \\&\quad +\, \frac{{{\partial ^2}f}}{{\partial x\partial y}}\left| {_{(\xi ,\eta )}} \right. ({x_{i + 1}} - z)({y_{j + 1}}- w) = 0. \end{aligned}$$

(49)

For simplicity, the remainder terms of Eqs. (47)–(49) are denoted by $r_1$, $r_2$, $r_3$ in the following derivations. Then Eqs. (47)–(49) can be rewritten as:

$$\begin{aligned}&\varepsilon (z,w) + \frac{{\partial \varepsilon }}{{\partial x}}\left| {_{(z,w)}} \right. ({x_i} - z) +\frac{{\partial \varepsilon }}{{\partial y}}\left| {_{(z,w)}} \right. ({y_j} - w) \nonumber \\&\quad +\, {r_1}= 0, \end{aligned}$$

(50)

$$\begin{aligned}&\varepsilon (z,w) + \frac{{\partial \varepsilon }}{{\partial x}}\left| {_{(z,w)}} \right. ({x_{i + 1}} - z) + \frac{{\partial \varepsilon }}{{\partial y}}\left| {_{(z,w)}} \right. ({y_j} - w) \nonumber \\&\quad +\, {r_2} = 0, \end{aligned}$$

(51)

$$\begin{aligned}&\varepsilon (z,w) + \frac{{\partial \varepsilon }}{{\partial x}}\left| {_{(z,w)}} \right. ({x_{i + 1}} - z) + \frac{{\partial \varepsilon }}{{\partial y}}\left| {_{(z,w)}} \right. ({y_{j + 1}} - w) \nonumber \\&\quad +\, {r_3} = 0. \end{aligned}$$

(52)

Equations (5051)–(52) can be regarded as a linear system with respect to $\varepsilon (z,w)$, $\frac{{\partial \varepsilon }}{{\partial x}}\left| {_{(z,w)}} \right.$, and $\frac{{\partial \varepsilon }}{{\partial y}}\left| {_{(z,w)}} \right.$. Define the column vectors ${\varvec{\varepsilon }} = {(\varepsilon (z,w),\frac{{\partial \varepsilon }}{{\partial x}}\left| {_{(z,w)}} \right. ,\frac{{\partial \varepsilon }}{{\partial y}}\left| {_{(z,w)}} \right. )^T}$ and ${\mathbf{r}} = {( - {r_1}, - {r_2}, - {r_3})^T}$, and the coefficient matrix

$$\begin{aligned} {\mathbf{A}} = \left[ \begin{array}{lll} 1&{}\quad {x_i} - z&{}\quad {y_j} - w \\ 1&{}\quad {x_{i + 1}} - z&{}\quad {y_j} - w \\ 1&{}\quad {x_{i + 1}} - z&{}\quad {y_{j + 1}} - w \end{array} \right] . \end{aligned}$$

The linear system Eqs. (5051)–(52) can be rewritten in a compact form by

$$\begin{aligned} {\mathbf{A}}\varepsilon = {\mathbf{r}}. \end{aligned}$$

(53)

Define d and $d_1$ as follows:

$$\begin{aligned} d= & {} \left| {\mathbf{A}} \right| = {h_1}{h_2}, \\ {d_1}= & {} \left| \begin{array}{lll} - \,{r_1}&{}\quad {x_i} - z&{}\quad {y_j} - w\\ -\, {r_2}&{}\quad {x_{i + 1}} - z&{}\quad {y_j} - w\\ - \,{r_3}&{}\quad {x_{i + 1}} - z&{}\quad {y_{j + 1}} - w \\ \end{array} \right| \\= & {} - {r_1}[({x_{i + 1}} - z)({y_{j + 1}} - w) - ({x_{i + 1}} - z)({y_j} - w)] \\&+\, {r_2}[({x_i} - z)({y_{j + 1}} - w) - ({x_{i + 1}} - z)({y_j} - w)] \\&-\, {r_3}[({x_i} - z)({y_j} - w) - ({x_{i + 1}} - z)({y_j} - w)]. \end{aligned}$$

According to Cramer’s rule, it holds that $\varepsilon (z,w) = {d_1}/d$. Furthermore, it can be observed that

$$\begin{aligned} \left| {{r_1}} \right| ,\left| {{r_2}} \right| ,\left| {{r_3}} \right|&\le \frac{1}{2}{\left\| {\frac{{{\partial ^2}f}}{{\partial {x^2}}}} \right\| _\infty }{h_1}^2 +{\left\| {\frac{{{\partial ^2}f}}{{\partial x\partial y}}} \right\| _\infty }{h_1}{h_2}\\&\quad +\, \frac{1}{2}{\left\| {\frac{{{\partial ^2}f}}{{\partial {y^2}}}} \right\| _\infty }{h_2}^2, \end{aligned}$$

and

$$\begin{aligned} \left| {{d_1}} \right|\le & {} \left| { - {r_1}[({x_{i + 1}} - z)({y_{j + 1}} - w) - ({x_{i + 1}} - z)({y_j} - w)]} \right| \\&+\, \left| {{r_2}[({x_i} - z)({y_{j + 1}} - w) - ({x_{i + 1}} - z)({y_j} - w)]} \right| \\&+\, \left| { - {r_3}[({x_i} - z)({y_j} - w) - ({x_{i + 1}} - z)({y_j} - w)]} \right| \\\le & {} 2{h_1}{h_2}(\left| {{r_1}} \right| + \left| {{r_2}} \right| + \left| {{r_3}} \right| ). \end{aligned}$$

It then follows that

$$\begin{aligned} \left| {\varepsilon (z,w)} \right| \le 3{\left\| {\frac{{{\partial ^2}f}}{{\partial {x^2}}}} \right\| _\infty }{h_1}^2 +6{\left\| {\frac{{{\partial ^2}f}}{{\partial x\partial y}}} \right\| _\infty }{h_1}{h_2} + 3{\left\| {\frac{{{\partial ^2}f}}{{\partial {y^2}}}} \right\| _\infty }{h_2}^2. \end{aligned}$$

Since the point (z, w) is arbitrarily selected, it can be finally claimed that

$$\begin{aligned} {\left\| {S - f} \right\| _\infty }&\le 3{\left\| {\frac{{{\partial ^2}f}}{{\partial {x^2}}}} \right\| _\infty }{h_1}^2 + 6{\left\| {\frac{{{\partial ^2}f}}{{\partial x\partial y}}} \right\| _\infty }{h_1}{h_2} \\&\quad + \,3{\left\| {\frac{{{\partial ^2}f}}{{\partial {y^2}}}} \right\| _\infty }{h_2}^2, \end{aligned}$$

which completes the proof. $\square$