Abstract
A fundamental problem in distributed computing is the distribution of requests to a set of uniform servers without a centralized controller. Classically, such problems are modeled as static balls into bins processes, where m balls (tasks) are to be distributed among n bins (servers). In a seminal work, Azar et al. (SIAM J Comput 29(1):180–200, 1999. https://doi.org/10.1137/S0097539795288490) proposed the sequential strategy \(\textsc {Greedy}[{d}]\) for \(n=m\). Each ball queries the load of d random bins and is allocated to a least loaded of them. Azar et al.
(1999) showed that \(d=2\) yields an exponential improvement compared to \(d=1\). Berenbrink et al. (SIAM J Comput 35(6):1350–1385, 2006. https://doi.org/10.1137/S009753970444435X) extended this to \(m\gg n\), showing that for \(d=2\) the maximal load difference is independent of m (in contrast to the \(d=1\) case). We propose a new variant of an infinite balls-into-bins process. In each round an expected number of \(\lambda n\) new balls arrive and are distributed (in parallel) to the bins. Subsequently, each non-empty bin deletes one of its balls. This setting models a set of servers processing incoming requests, where clients can query a server’s current load but receive no information about parallel requests. We study the \(\textsc {Greedy}[{d}]\) distribution scheme in this setting and show a strong self-stabilizing property: for any arrival rate \(\lambda =\lambda (n)<1\), the system load is time-invariant. Moreover, for any (even super-exponential) round t, the maximum system load is (w.h.p.)  for \(d=1\) and
for \(d=1\) and  for \(d=2\). In particular, \(\textsc {Greedy}[{2}]\) has an exponentially smaller system load for high arrival rates.
for \(d=2\). In particular, \(\textsc {Greedy}[{2}]\) has an exponentially smaller system load for high arrival rates.


Similar content being viewed by others
Notes
An event \(\mathcal {E}\) occurs with high probability (w.h.p.) if
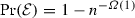 .
.The state space includes all vectors with non-increasing entries over \(\mathbb {N}^n\).
Talwar and Wieder [24] use the same potential function to analyze variants of the sequential d-Choice process without deletions. Our analysis turns out a bit more involved, since we have to consider deletions and argue over whole batches (of random size) instead of single balls.
This is easily verified by hand. Alternatively, [23, Appendix A] gives \(\sum _{i \ge 3n/4} p_i \ge \frac{1}{4} + \varepsilon '\) and the statement follows by noting that
 .
.Note that \(-\frac{1}{f\cdot n}\ge -1/e\), so that \(W_{-1}(-\frac{1}{f\cdot n})\) is well defined.
It might look tempting to use \(\varGamma \) together with Hajek’s theorem to bound the maximum system load. However, this would require (exponentially) sharper bounds on \(\varPhi \). Furthermore, it might be tempting to use the stability of \(\textsc {Greedy}[{1}] \) to prove stability of \(\textsc {Greedy}[{2}] \), however, as discussed earlier, it is not clear to achieve this, as it seems challenging to couple or majorize the processes.
References
Adler, M., Berenbrink, P., Schröder, K.: Analyzing an infinite parallel job allocation process. In: Proceedings of the 6th Annual European Symposium on Algorithms, ESA, pp. 417–428, London, UK. Springer (1998a). ISBN 3-540-64848-8. http://dl.acm.org/citation.cfm?id=647908.740138
Adler, M., Chakrabarti, S., Mitzenmacher, M., Rasmussen, L.: Parallel randomized load balancing. Random Struct. Algorithms 13(2): 159–188 (1998b). ISSN 1098-2418. https://doi.org/10.1002/(SICI)1098-2418(199809)13:2\(<\)159::AID-RSA3\(>\)3.0.CO;2-Q
Alfa, A.S.: Algorithmic analysis of the bmap/d/k system in discrete time. Adv. Appl. Probab. 35(4), 1131–1152 (2003). https://doi.org/10.1239/aap/1067436338
Azar, Y., Broder, A.Z., Karlin, A.R., Upfal, E.: Balanced allocations. SIAM J. Comput. 29(1), 180–200 (1999). https://doi.org/10.1137/S0097539795288490
Becchetti, L., Clementi, A.E.F., Natale, E., Pasquale, F., Posta, G.: Self-stabilizing repeated balls-into-bins. In: Blelloch, G.E., Agrawal, K. (eds.) Proceedings of the 27th ACM on Symposium on Parallelism in Algorithms and Architectures, SPAA 2015, Portland, OR, USA, 13–15 June 2015, pp. 332–339. ACM (2015). ISBN 978-1-4503-3588-1. https://doi.org/10.1145/2755573.2755584
Berenbrink, P., Czumaj, A., Friedetzky, T., Vvedenskaya, N.D.: Infinite parallel job allocation (extended abstract). In: Proceedings of the Twelfth Annual ACM Symposium on Parallel Algorithms and Architectures, SPAA, pp. 99–108, New York, NY, USA. ACM (2000). ISBN 1-58113-185-2. https://doi.org/10.1145/341800.341813
Berenbrink, P., Czumaj, A., Steger, A., Vöcking, B.: Balanced allocations: the heavily loaded case. SIAM J. Comput. 35(6), 1350–1385 (2006). https://doi.org/10.1137/S009753970444435X
Berenbrink, P., Czumaj, A., Englert, M., Friedetzky, T., Nagel, L.: Multiple-choice balanced allocation in (almost) parallel. In: Gupta, A., Jansen, K., Rolim, J., Servedio, R. (eds.) Approximation, Randomization, and Combinatorial Optimization. Algorithms and Techniques. Lecture Notes in Computer Science, vol. 7408, pp. 411–422. Springer, Berlin (2012). ISBN 978-3-642-32511-3. https://doi.org/10.1007/978-3-642-32512-0_35
Berenbrink, P., Khodamoradi, K., Sauerwald, T., Stauffer, A.: Balls-into-bins with nearly optimal load distribution. In: Proceedings of the Twenty-fifth Annual ACM Symposium on Parallelism in Algorithms and Architectures, SPAA, pp. 326–335, New York, NY, USA. ACM (2013). ISBN 978-1-4503-1572-2. https://doi.org/10.1145/2486159.2486191
Czumaj, A., Stemann, V.: Randomized allocation processes. In: Proceedings of the 38th Annual Symposium on Foundations of Computer Science, 1997, pp 194–203, Oct (1997). https://doi.org/10.1109/SFCS.1997.646108
Czumaj, A.: Recovery time of dynamic allocation processes. In: Proceedings of the Tenth Annual ACM Symposium on Parallel Algorithms and Architectures, SPAA, pp. 202–211, New York, NY, USA. ACM (1998). ISBN 0-89791-989-0. https://doi.org/10.1145/277651.277686
Fayolle, G., Malyshev, V.A., Menshikov, M.V.: Topics in the Constructive Theory of Countable Markov Chains. Cambridge University Press (1995). ISBN 9780521461979. https://books.google.ca/books?id=lTJltFEnnHcC
Gonnet, G.H.: Expected length of the longest probe sequence in hash code searching. J. ACM 28(2), 289–304 (1981). https://doi.org/10.1145/322248.322254. ISSN 0004-5411
Hajek, B.: Hitting-time and occupation-time bounds implied by drift analysis with applications. Adv. Appl. Probab. 14(3), 502–525 (1982)
Kamal, A.E.: Efficient solution of multiple server queues with application to the modeling of atm concentrators. In: INFOCOM. Fifteenth Annual Joint Conference of the IEEE Computer Societies. Networking the Next Generation. Proceedings IEEE, vol. 1, pp. 248–254, March (1996). https://doi.org/10.1109/INFCOM.1996.497900
Kim, N.K., Chaudhry, M.L., Yoon, B.K., Kim, K.: A complete and simple solution to a discrete-time finite-capacity BMAP/D/C queue. Appl. Math. 3, 2169 (2012)
Levin, D.A., Perres, Y.: Markov Chains and Mixing Times. American Mathematical Society, Providence (2008). ISBN 978-0-8218-4739-8
Mitzenmacher, M.: The power of two choices in randomized load balancing. IEEE Trans. Parallel Distrib. Syst. 12(10), 1094–1104 (2001). https://doi.org/10.1109/71.963420
Peres, Y., Talwar, K., Wieder, U.: The (\(1+\beta \))-choice process and weighted balls-into-bins. In: Proceedings of the 21st Annual ACM-SIAM Symposium on Discrete Algorithms (SODA), SODA, pp. 1613–1619, Philadelphia, PA, USA. Society for Industrial and Applied Mathematics (2010). ISBN 978-0-898716-98-6
Raab, M., Steger, A.: “Balls into bins”—a simple and tight analysis. In: Luby, M., Rolim, J.D.P., Serna, M.J. (eds.) Randomization and Approximation Techniques in Computer Science, Second International Workshop, RANDOM, Barcelona, Spain, 8–10 Oct 1998, Proceedings. Lecture Notes in Computer Science, vol. 1518, pp. 159–170. Springer (1998). ISBN 3-540-65142-X. https://doi.org/10.1007/3-540-49543-6_13
Sohraby, K., Ji, Z.: Spectral decomposition approach for transient analysis of multi-server discrete-time queues. In: INFOCOM. Eleventh Annual Joint Conference of the IEEE Computer and Communications Societies, IEEE, pp. 395–404. IEEE (1992)
Stemann, V.: Parallel balanced allocations. In: Proceedings of the Eighth Annual ACM Symposium on Parallel Algorithms and Architectures, SPAA, pp. 261–269, New York, NY, USA. ACM (1996). ISBN 0-89791-809-6. https://doi.org/10.1145/237502.237565
Talwar, K., Wieder, U.: Balanced allocations: a simple proof for the heavily loaded case. CoRR, abs/1310.5367 (2013). http://arxiv.org/abs/1310.5367
Talwar, K., Wieder, U.: Balanced allocations: a simple proof for the heavily loaded case. In: Esparza, J., Fraigniaud, P., Husfeldt, T., Koutsoupias, E. (eds.) Automata, Languages, and Programming. Lecture Notes in Computer Science, vol. 8572, pp. 979–990. Springer, Berlin (2014). ISBN 978-3-662-43947-0. https://doi.org/10.1007/978-3-662-43948-7_81
Funding
Petra Berenbrink is supported by the Natural Sciences and Engineering Research Council of Canada (NSERC). Peter Kling is partly supported by the Natural Sciences and Engineering Research Council of Canada (NSERC) and the Pacific Institute for the Mathematical Sciences (PIMS). Lars Nagel is supported by the German Ministry of Education and Research under Grant 01IH13004. Christopher Wastell is supported by EPSRC.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The authors declare that they have no conflict of interest.
Additional information
Petra Berenbrink and Peter Kling did some of the research while affiliated with Simon Fraser University.
A preliminary version of this paper was published in the proceedings of PODC’16.
Auxiliary Results
Auxiliary Results
The following theorem gives necessary and sufficient conditions for a Markov Chain to be positive recurrent. Roughly speaking, we want that the Markov Chain returns to a finite number of states: Given the state x of the system at some time t, we need to show that there exists some potential \(\zeta (\cdot )\) which is decreasing linearly (in \(\beta (x)\), the length of a suitably chosen period) for “most states” (first condition). For a finite number of states (set C), whose size can be a function of n but not of t, the potential is not required to decrease but the potential is required to be finite after \(\beta (x)\) time steps (second condition).
Theorem 6
(Fayolle et al. [12, Theorem 2.2.4]) A time-homogeneous irreducible aperiodic Markov chain \(\zeta \) with a countable state space \(\varOmega \) is positive recurrent if and only if there exists a positive function \(\phi (x), x\in \varOmega \), a number \(\eta > 0\), a positive integer-valued function \(\beta (x), x \in \varOmega \), and a finite set \(C \subseteq \varOmega \) such that the following inequalities hold:
-
1.
 , \(x\not \in C\)
, \(x\not \in C\) -
2.
 , \(x\in C\)
, \(x\in C\)
The following theorem gives a tail bound on a potential for which the following two properties hold: In increase in the potential has a tail bound (first condition) and whenever the potential is large, in decreases in expectation (second condition).
Theorem 7
(Simplified version of Hajek [14, Theorem 2.3]) Let \({(Y(t))}_{t \ge 0}\) be a sequence of random variables on a probability space \((\varOmega , \mathcal {F}, P)\) with respect to the filtration \({(\mathcal {F}(t))}_{t\ge 0}\). Assume the following two conditions hold:
-
(i)
(Majorization) There exists a random variable Z and a constant \(\lambda ' > 0\), such that
 for some finite D, and \((|Y({t+1}) - Y(t)| \big \vert \mathcal {F}(t)) \prec Z\) for all \(t \ge 0\); and
for some finite D, and \((|Y({t+1}) - Y(t)| \big \vert \mathcal {F}(t)) \prec Z\) for all \(t \ge 0\); and -
(ii)
(Negative Bias) There exist \(a,\varepsilon _0 > 0\), such for all t we have

Let  . Then, for all b and t we have
. Then, for all b and t we have
Proof
The statement of the theorem provided in [14] requires besides (i) and (ii) to choose constants \(\eta \), and \(\rho \) such that \(0< \rho \le \lambda '\), \(\eta < \varepsilon _0/c\) and \(\rho =1-\varepsilon _0\cdot \eta +c \eta ^2\) where  . With these requirements it then holds that for all b and t
. With these requirements it then holds that for all b and t
In the following we bound Eq. (59) by setting  . The following upper and lower bound on \(\rho \) follow.
. The following upper and lower bound on \(\rho \) follow.
-
\(\rho =1-\varepsilon _0 \cdot \eta +c \eta ^2 \le 1-\varepsilon _0 \cdot \eta + \varepsilon _0 \cdot \eta \cdot c \cdot \lambda '^2/(2D) \le 1-\varepsilon _0 \cdot \eta + \varepsilon _0 \cdot \eta /2 =1-\varepsilon _0 \cdot \eta /2 \), where we used \(c\le D/\lambda '^2\).
-
\(\rho =1-\varepsilon _0 \cdot \eta +c \eta ^2 \ge 1-\varepsilon _0 /(2\varepsilon _0) \ge 0\).
We derive, from Eq. (59) using that for any \(t\ge 0\) we have \(0\le \rho ^t\le 1\)
since \(\frac{1}{(1-\rho )}\le \frac{2 }{\varepsilon _0 \cdot \eta }\). This yields the claim. \(\square \)
Theorem 8
(Raab and Steger [20, Theorem 1]) Let M be the random variable that counts the maximum number of balls in any bin, if we throw m balls independently and uniformly at random into n bins. Then  if \(\alpha > 1\) and
if \(\alpha > 1\) and  if \(0< \alpha < 1\), where
if \(0< \alpha < 1\), where

where \(d_c\) is largest solution of \( 1 + x (\log c - \log x + 1) -c = 0\). We have \(d_1=e\) and \(d_{1.00001}= 2.7183\).
Rights and permissions
About this article
Cite this article
Berenbrink, P., Friedetzky, T., Kling, P. et al. Self-Stabilizing Balls and Bins in Batches. Algorithmica 80, 3673–3703 (2018). https://doi.org/10.1007/s00453-018-0411-z
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00453-018-0411-z





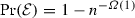 .
. .
. ,
,  ,
,  for some finite D, and
for some finite D, and 