Abstract
In the paper, two existing upgrades of the gradient damage model for the simulations of cracking in concrete are compared. The damage theory is made nonlocal via a gradient enhancement to overcome the mesh dependence of simulation results. The implicit gradient model with an averaging equation, where the internal length parameter is assumed as constant during the strain softening analysis, gives unrealistically broadened damage zones. The gradient enhancement of the scalar damage model can be improved via a function of an internal length scale, so an evolution of the gradient activity is postulated during the localization process. Two different modifications of the averaging equation and respective evolving gradient damage formulations are presented. Different activity functions are tested to see whether the formation of a too wide damage zone still occurs. Activating or localizing character of the gradient influence can be introduced and the impact of both approaches on the numerical results is shown in the paper. The aforementioned variants are implemented and examined using the benchmarks of tension in a bar and bending of a cantilever beam.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
In the paper, continuum damage mechanics [24] is employed to simulate cracking in concrete. The application of the model in a local version leads to material softening. It has been known for years, see, for example, [7], that ill-posedness of the boundary value problem (BVP) and spuriously mesh-sensitive results then occur for local models. Concrete cracking is simulated as strain localization by means of the narrowest band of finite elements allowed for the discretization, so a suitable localization limiter is needed, cf. [9]. If softening induces strain localization, then a regularization method is demanded in the concrete model. Among different higher-order theories, a gradient operator [2, 11, 18, 30] can be employed in order to ensure objectivity in numerical modelling of localization phenomena.
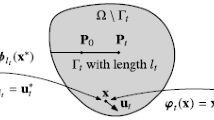
Scalar gradient-enhanced damage was firstly derived by Peerlings et al. [32] and then developed by many authors, see, for example, [1, 3, 15, 27]. The classical equilibrium problem is augmented by an extra averaging equation for a selected equivalent strain measure. This differential equation with a gradient term is converted into a weak form simultaneously with the equilibrium equation to derive the finite element (FE) formulation. The idea of regularization using gradient terms is illustrated in Fig. 1. The gradient activity is represented by a function which scales the gradient term; in other words, it influences the range of nonlocal interactions. The gradient damage model in the discretized form involves independent interpolations of the displacement and the averaged strain measure, so the BVP becomes coupled, see also [41, 42]. Since additional degrees of freedom for the averaged strain have to be included in the discretization, the model contains two mentioned above primary fields. It is also confirmed in [34] that the truly nonlocal character of the BVP is preserved if the gradient enhancement is introduced in the implicit version. General classification of strain gradient models is performed in [5, 6], and the thermodynamic background of the model is considered for example in [18, 26, 29]. Gradient damage can be employed not only in the simulations of concrete, but for example to analyse the softening and localization phenomena observed in: metals [33, 47], different composites [17, 19, 21] or even biomaterials [46].
In the gradient damage model, the zone of localization is governed by the internal length scale, not by discretization. In paper [32] this parameter is assumed to be constant; however, it can cause artificially broadened damage zones. The formation of excessively enlarged zones in damage patterns during the simulation of strain localization problems has been firstly discussed by Geers [19]. Due to the constant internal length scale in the conventional gradient damage (CGD) model, it is actually assumed that the averaging procedure remains the same for all material points during the loading history. As an effect, it provokes nonlocal mapping of the active damage zone into its expanded vicinity, which is unrealistic effect and a noticeable deficiency of the CGD model. The internal length treated as a function of the gradient activity has firstly been investigated also in [19]. In that approach, apart from the averaging equation, one more extra continuity equation for a damage measure or directly gradient activity is taken into account. It leads to a three field formulation and more additional degrees of freedom in the FE interpolation. The third interpolated field is added to ensure stable iteration process during the nonlinear analysis.
Another idea to avoid too wide damage distribution is a combination of local and nonlocal strain measures in the CGD model. It gives a so-called over-nonlocal formulation [10, 13, 16, 36, 40] or its modification [14]. However, in that approach the internal length parameter still remains constant, so it is not considered in this paper.
The model presented in [19, 20] can be modified according to [39], where the internal length function is set in the denominator in the averaging equation and two primary fields are maintained in the formulation. In this paper, it will be called the SVS gradient damage model. Acronym SVSGD is based on names of the authors of [39]. In that paper, the gradient activity linearly increases with the equivalent strain. Another averaging equation with evolving length scale is proposed in [35, 43]. The damage zone is controlled via a reduction of the nonlocal interaction. In this paper, it will be called the PS gradient damage model (abbreviation PSGD). Originally in [35, 43] the gradient activity exponentially decreases with damage and the model has been named by Poh and Sun the localizing gradient damage. Comparison of CGD and PSGD models is broadly discussed in [38]. Moreover, different methods of mesh adaptation using the PSGD model are shown in [37]. A detailed examination of damage formulations with constant or variable internal lengths in the example of one-dimensional tensile bar is carefully studied in [23].
In the paper, a description of gradient damage with evolving internal length scale is presented. Based on the CGD model, derivation of FE formulations for the SVSGD [39] and PSGD [35, 43] models is described in detail in Sect. 2 in order to correctly build in-house code in the FEAP package [44]. Different functions of gradient activity are illustrated in Sect. 3. The implemented models are examined in Sects. 4 and 5 by the test of a bar with imperfection under one-dimensional tension and the benchmark of a cantilever beam under in-plane bending, respectively. Final conclusions are summarized in Sect. 6. Small strains are assumed. Voigt’s notation (also called matrix–vector notation) is used.
2 Finite element formulations and their linearization
2.1 Basic equations for scalar damage
The scalar damage model [24] is considered in the paper, where one damage measure \(\omega \) depends on the damage history parameter \(\kappa ^\mathrm {d}\). The damage growth function can be defined for instance using the exponential relation [28]:
where \(\kappa _\mathrm {o}\) is the damage threshold, \(\alpha \) is connected with the presence of residual stress when the material stiffness is lost and \(\eta \) sets the rate at which damage increases and decides whether the quasi-brittle material is more or less ductile. This function resembles the exponential character of uniaxial softening in the experiment of the tensile fracture in concrete, see [22]. The strain equivalence is postulated [25], and a loading function \(F^\mathrm {d}\) is described in the strain space:
where \({\tilde{\epsilon }}\) is an equivalent strain measure as a function of the strain tensor \(\varvec{\epsilon }\). For example, it can be determined as the modified von Mises definition [45]:
where \(I_1^{\varvec{\epsilon }}\) and \(J_2^{\varvec{\epsilon }}\) are the first and second strain invariants, respectively, k is the ratio of compressive strength \(f'_{c}\) and tensile strength \(f'_{t}\), \(\nu \) is Poisson’s ratio.
If the standard elasto-damage model is applied, then the stress tensor \(\varvec{\sigma }\) is related to the effective stress \({\hat{\varvec{\sigma }}}\) as follows:
where \(\varvec{{D}}\) is the elastic stiffness matrix. Loading/unloading (Kuhn–Tucker) conditions are imposed. The stress rate \({\dot{\varvec{\sigma }}}\) can be derived from Eq. (4):
where the rate of damage \({\dot{\omega }}\) is evaluated as:
where:
The above derivatives can be denoted in the following way:
Finally, the rate constitutive relation is expressed as:
The kinematic and equilibrium equations at the material point level are standard. A geometrically linear problem is considered.
2.2 Conventional gradient damage (CGD)
It is known that the local approach for the damage model gives in the softening regime a spurious dependency of the results on the density of the mesh and also on the direction of mesh lines. The problem can be overcome using different regularization techniques, and in this paper higher-order gradients are applied. A so-called implicit gradient enhancement [19, 32] is employed; hence, an averaging equation with a gradient scaling factor is adopted:
For a domain \(\mathcal {B}\), the natural boundary condition is postulated \(\mathcal {N}^\mathrm {T}\nabla {\bar{\epsilon }} = 0\) on \(\partial \mathcal {B}\), where \(\mathcal {N}\) is the outward normal to the surface of domain \(\mathcal {B}\). Equation (10) leads to a two-field formulation with independent interpolations of displacements \(\varvec{{u}}\) and averaged strain measure \({\bar{\epsilon }}\). In the conventional gradient damage model, the parameter \(\varphi > 0\) remains constant and corresponds to the internal length parameter \( l \) in the following way [4]:
In the loading function (2), the local equivalent strain \({\tilde{\epsilon }}\) is replaced by the averaged strain \({\bar{\epsilon }}\):
This type of enhancement is formally equivalent with the nonlocal approach, cf. [9, 34]. The model can be coupled with hardening plasticity defined for the undamaged skeleton of the material and then \(\varvec{\epsilon }\) in Eq. (4) is substituted by \(\varvec{\epsilon }^\mathrm {e}= \varvec{\epsilon }- \varvec{\epsilon }^\mathrm {p}\), where \(\varvec{\epsilon }^\mathrm {p}\) is the plastic strain tensor. Further derivation, i.e. discretization, linearization as well as detailed algorithm for gradient damage plasticity can be found in [12, 31]. Moreover, it is possible to incorporate a crack-closing projection operator in this constitutive model, see, for example, [48]. The two aspects of the model are not discussed, because they are out of the scope of the paper.
2.3 SVS gradient damage (SVSGD)
It is possible to introduce a variable \(\varphi \) which is a function of the gradient activity as first shown in [19]. Originally, nodal values of continuous damage or strain-based gradient activity variable have been interpolated additionally in the transient gradient damage model [19, 20]. As mentioned in the introduction—this approach leads to a three-field formulation. If in the averaging equation (10) all terms are divided by \(\varphi \) [39]:
then only two primary fields can be preserved similarly to the original version of this model [32]. The weak form, discretization and linearization are derived below for this modification of the model.
The weak form of equilibrium equation is written multiplying it by a variation of displacement field \(\delta \varvec{{u}}\) and integrating over \(\mathcal {B}\). After that, Green’s formula and the natural boundary condition are introduced, so the final form is as follows:
where \(\varvec{{b}}\) is the body force vector and \(\varvec{{t}}\) denotes tractions. In an analogical way, Eq. (13) is transformed into a weak form using a variation of averaged strain \(\delta {\bar{\epsilon }}\):
A two-field formulation emerges when independent interpolations of displacements \(\varvec{{u}}\) and of the averaged strain measure \({\bar{\epsilon }}\) are employed in the semi-discrete linear system as follows:
where \(\varvec{{N}}\) and \(\varvec{{h}}\) contain suitable shape functions. The secondary fields \(\varvec{\epsilon }\) and \(\nabla {\bar{\epsilon }}\) can be calculated as:
where \(\varvec{{B}}= \varvec{{L}}\, \varvec{{N}}\) and \(\varvec{{g}}^\mathrm {T}= \nabla \varvec{{h}}^\mathrm {T}\). Matrix \(\varvec{{L}}\) consists of differential operators. The variations are, respectively, interpolated. Equations (14) and (15) in a discretized form are as follows:
Identities (18) and (19) must hold for any admissible \(\delta \varvec{{a}}\) and \(\delta \varvec{{e}}\). Finally, they can be rephrased into the residual form:
Tractions and body forces do not depend on deformation.
The BVP is linearized so that equilibrium is obtained at (pseudo-)time step \(t + \Delta t\) in subsequent iteration \(i+1\) based on previous iteration i using a correction as follows:
In the further consideration, the subscript \(t+\Delta t\) is skipped. The update is performed at nodal points for the primary fields:
and also at integration points for the secondary fields:
The residual \(R_{\varvec{\sigma }}\) in Eq. (20) is decomposed according to:
The increment \(\mathrm {d}R_{\varvec{\sigma }}\) depends on two primary fields:
The constitutive equation (9) can be written in the incremental form:
where the following relations are introduced:
The increment \(\mathrm {d}\varvec{\sigma }\) in Eq. (27) is substituted into the equation for out-of-balance forces as follows:
The relation below is obtained after the transfer of the first three integrals to the right-hand side and rewriting the equation in a matrix form:
where the definitions of the submatrices and the right-hand side vectors are:
The residuum in Eq. (21) is obtained in this way:
where
The increments at integration points are also considered for the equivalent strain \({\tilde{\epsilon }}\) and the gradient activity function \(\varphi \):
The increment of the equivalent strain can be given as:
In general, it is admitted that the gradient activity \(\varphi \) can be linked with the equivalent strain \({\tilde{\epsilon }}\) and/or damage \(\omega \), i.e. \(\varphi = \varphi ({\tilde{\epsilon }}, \omega ) = \varphi (\varvec{\epsilon }, {\bar{\epsilon }})\); hence, the increment of the gradient activity is:
Additionally, the following notation is introduced:
Substituting discretization, \(\mathrm {d}\varphi \) is written as:
Similarly to Eq. (25), the increment \(\mathrm {d}R_\mathrm{{SVS}}\) is expressed in the following way:
Now \(\mathrm {d}R_\mathrm{{SVS}}\) is derived as:
Using Eqs. (37) and (44), the residuum in Eq. (36) is transformed into the matrix form:
The matrices and vectors in this equation are:
Finally, this gradient damage formulation can be assembled as a coupled matrix problem:
Actually, it should be pointed out that in practice function \(\varphi \) can depend either on equivalent strain \({\tilde{\epsilon }}\) or damage \(\omega \). This means that if \(\varphi = \varphi ({\tilde{\epsilon }})\) then in Eq. (52) \(\varvec{{K}}_{ea}^\mathrm{{SVS}} \ne \mathbf {0}\) and \(\varvec{{K}}_{ee}^\mathrm{{SVS}} = \mathbf {0}\), and if \(\varphi = \varphi (\omega )\) then \(\varvec{{K}}_{ea}^\mathrm{{SVS}} = \mathbf {0}\) and \(\varvec{{K}}_{ee}^\mathrm{{SVS}} \ne \mathbf {0}\).
The incremental nodal displacements \(\mathrm {d}\varvec{{a}}\) and the incremental averaged strain \(\mathrm {d}\varvec{{e}}\) are solved for in each step. The standard Newton–Raphson method is employed to search for equilibrium after iterations in succeeding steps.
2.4 PS gradient damage (PSGD)
In this approach, the system of kinematic, constitutive and equilibrium equations is exact as for the CGD and SVSGD models presented in the previous subsections. Again, the scalar damage model with one measure \(\omega \) is assumed. The weak form, discretization and linearization of equilibrium equation are identical to the one described in Sect. 2.3; thus, Eq. (20) and the coupled problem are still employed in the computations.
The averaging equation for the PS gradient damage model is redefined according to [35, 43]:
Similarly to Eq. (13), function \(\varphi \) is associated with the gradient activity and theoretically can depend on equivalent strain \({\tilde{\epsilon }}\) and/or damage \(\omega \). In [35, 43] it is a function of material degradation, i.e. \(\varphi = \varphi (\omega )\). Eq. (53) is multiplied by a variation of the averaged strain \(\delta {\bar{\epsilon }}\) and integrated by parts in order to obtain the weak form (after using Green’s formula and homogeneous natural boundary condition):
Further derivation of averaging equation to the matrix form is analogical as in the previous subsection. Two fields are again interpolated: displacements \(\varvec{{u}}\) and averaged strain measure \({\bar{\epsilon }}\), see Eqs. (16) and (17). The averaging equation is expressed as follows:
The above equation holds for any admissible \(\delta \varvec{{e}}\) and can be written in the residual form:
Linearization is introduced for the averaging equation which is reformulated into a residuum in such manner:
The residual for the iteration i is:
Generalizing the definition of the gradient activity \(\varphi \), it can be a two-field function, i.e. \(\varphi = \varphi ({\tilde{\epsilon }}, \omega ) = \varphi (\varvec{{a}}, \varvec{{e}})\), so that \(\mathrm {d}R_\mathrm{{PS}}\) is equal to:
Taking into account the relations in Eqs. (39)–(42), the increment \(\mathrm {d}R_\mathrm{{PS}}\) from Eq. (59) is rewritten as:
Finally, the residuum in Eq. (57) is converted into the matrix equation:
The above matrices and vectors are defined as:
Similarly to the proposal in the previous subsection for the SVS gradient damage model, here function \(\varphi \) can be governed by equivalent strain \({\tilde{\epsilon }}\) and then \(\varvec{{K}}_{ea}^\mathrm{{PS}} \ne \mathbf {0}\) and \(\varvec{{K}}_{ee}^\mathrm{{PS}} = \mathbf {0}\), or by damage \(\omega \) and then \(\varvec{{K}}_{ea}^\mathrm{{PS}} = \mathbf {0}\) and \(\varvec{{K}}_{ee}^\mathrm{{PS}} \ne \mathbf {0}\). Again, the standard Newton–Raphson method is used.
3 Functions of gradient activity
Function \(\varphi \), which is responsible for the character of the gradient activity, can be defined in different ways.
For the CGD model [32], the gradient activity remains constant during the loading process:
The definition of \(\varphi _0\) is introduced for the computations included in this paper, where the parameter \(c_{\max }\) is correlated to the internal length scale \( l \) as presented in Eq. (11) [4].
In [39] it is assumed that function \(\varphi \) is increasing and equivalent strain \({\tilde{\epsilon }}\) decides about the development of the damage zone in this manner:
where \(c_0\) is the initial length scale squared, \(c_{\max }\)—the maximum internal length scale squared, \({\tilde{\epsilon }}_{\max }\)—the equivalent strain level at which \(c_{\max }\) is reached, and n—the exponent of function \(\varphi _1\) which is called the intensity of the gradient activity. It is also assumed that \(c_0 > 0\), but reasonably small to preclude extensive nonlocal effects at the initial step, cf. [39]. The condition \(c_{\max } > c_0\) seems to be obvious, but it should be written here for completeness. Figure 2 illustrates a linear-constant character of this function (intensity \(n=1.0\)) depending on parameter \({\tilde{\epsilon }}_{\max }\). Diagrams of \(\varphi _1({\tilde{\epsilon }})\) shown in Fig. 3 are performed for different rates of intensity n, while \({\tilde{\epsilon }}_{\max } = 0.0015\) remains the same. All parameters are compatible with the data applied in the test presented further in Sect. 4.3. The gradient activity function in Eq. (69) represents progressively growing interactions in the material microstructure. Hence, \(\varphi _1({\tilde{\epsilon }})\) has an activating character. The derivative of \(\varphi _1\) with respect to \({\tilde{\epsilon }}\) is:
A next idea suggested in [35, 43] is that the gradient activity \(\varphi \) is reduced together with the damage growth; hence, function \(\varphi _2\) and its derivative with respect to \(\omega \) are as follows:
where R is the minimum (residual) level of interaction between microprocesses within the localization band, \(c_{\max }\) and n can be determined as in previous definitions. If \(R=1\), then \(\varphi _2(\omega ) = c_{\max }\) and the CGD model is restored. If \(R=0\) and \(\varphi _2(\omega \rightarrow 0) \rightarrow 0\), then local damage starts to manifest, so for positive \(R \approx 0\) small interactions between microcracks in the fully damaged region are present, see also [43]. Hence, the character of this function is localizing due to a decreasing of the gradient activity. Figure 4 presents diagrams of \(\varphi _2(\omega )\), where intensity n is equal to 3.0 and the level of residual interaction R changes from 0.05 to 0.2. These parameters are also in accordance with the data used in the test of the tensile bar with imperfection, see Sect. 4.4.
In this paper, alternative definitions are also decisively verified. For example, function \(\varphi (\omega )\) and its corresponding derivative can be connected respectively with cosine and sine functions:
Again, for \(R=1\) the CGD model is retrieved. On the other hand, for \(R \approx 0\) the model behaves as almost local in a fully damaged area. The character of function \(\varphi _3\) is decreasing, similarly to \(\varphi _2\). Functions \(\varphi _2(\omega )\) and \(\varphi _3(\omega )\) are compared in Fig. 5, where parameter \(R=0.05\) remains unchanged and the rate of the gradient activity is different because of changed values of intensity n. Again, these parameters are employed in the test described in Sect. 4.4.
If parameters \(c_0\) and \(c_{\max }\) are swapped in function \(\varphi _1\), then the gradient activity can also descend, but now together with the increase of the equivalent strain \({\tilde{\epsilon }}\):
The range of the applicability and the usefulness of the four above functions are discussed in the next section.
4 Test of tensile bar with imperfection
4.1 Specification of test
The simulation of uniaxial tension for a bar with assumed imperfection in the middle is one of the most basic and typical tests in physically nonlinear mechanics. Strain localization is triggered in a zone where the specimen is assumed to be made from a weaker material. Therefore, it can be observed how a considered material model behaves, e.g. whether it is characterized by mesh objectivity or not. For instance, this test was used for the gradient plasticity model [11, 30] or the CGD model [32] just to confirm the presence and the effectiveness of regularization using the gradient enhancement.
The scheme of the test is depicted in Fig. 6. The configuration with two-dimensional finite elements (FEs) is computed; however, uniaxial tension without any effects in the second direction is taken into account. The length of the bar is \(L = 100\) mm, while the length of the imperfection zone, which is here rather a weakened zone, is \(L_{\mathrm {imp}} = 10\) mm. The elastic constants are Young’s modulus \(E = 20{,}000\) MPa and Poisson’s ratio \(\nu = 0.0\). According to the data in [11] the uniaxial tensile strength \(f'_t = 2\) MPa, but in the damage theory initial threshold \(\kappa _\mathrm {o}\) is needed. It is calculated as the quotient of the tensile strength and Young’s modulus, so \(\kappa _\mathrm {o}= f'_t / E = 0.0001\). The reduction of the damage threshold by 10 % is introduced in the zone between \(x=45\) mm and 55 mm. Alternatively, it is also possible to reduce the cross section, but here the width and the thickness equal 5 mm in the whole bar. Plane stress is assumed. After reaching the peak load, the damage growth law with the exponential softening relation given in Eq. (1) is selected. The parameters are \(\alpha = 0.99\) and \(\eta = 400\) or optionally \(\eta = 100\) for the PSGD model. The value of \(c_{\max } = 18\) \(\hbox {mm}^2\) is intentionally enlarged. The internal length scale is constant for the CGD model, but \(c_{\max }\) denotes either the final or the initial value of \(\varphi \) for the considered models. It is known that the internal length parameter is connected with the microstructure of the material. For quasi-brittle materials like concrete, this value has been associated with the maximum aggregate size, see [8]. Here, it corresponds to \( l = 6\) mm, according to Eq. (11). It should be emphasized that for the CGD model the width of the expected smeared crack band can be estimated as \(2 \pi \, l = 6.28 \, l = 37.7\) mm, see also [4]. In fact, it covers the entire imperfection zone with an excess, but for SVSGD and PSGD models the aforementioned estimates are no longer valid, because the gradient activity becomes function \(\varphi \) and changes during the loading process. The detailed data for all cases computed in this subsection are listed in Table 1. Their order is consistent with the description of the results.
In the paper, only FEs with quadratic interpolation of displacements \(\varvec{{a}}\) and linear interpolation of averaged strain \(\varvec{{e}}\) are employed. This type of interpolation is optimal, since possible oscillations in the distribution of secondary fields as for example stress variables vanish. However, other \(C^{0}\)-continuous shape functions are sufficient for the approximated fields as shown in [41, 42]. Along the specimen, three mesh densities are adopted. Starting from 80 FEs, each next mesh is doubled in the horizontal direction, thus three discretizations with 80/160/320 FEs are tested. Mesh convergence study is performed for each model presented in the paper. Despite the fact that the exponential softening is taken into account, the arc length control is used in order to assure more stable computations. The loading process is divided into equal incremental steps for further legible illustration of the evolution of selected variables. Apart from the evolution, the axial stress \(\sigma _x\) as the function of the horizontal displacement on the right end of the bar, as shown in Fig. 6, is also monitored. The value of \(\sigma _x\) is measured as the force divided by the area of the bar cross section. The value of the displacement u(L) is actually the elongation of the bar.
4.2 Results for constant gradient activity
First, the solution for the conventional gradient damage (CGD) model is presented. The parameter \(\varphi _0 = c_{\max } = 18\) \(\hbox {mm}^2\) remains constant during the loading process. Figure 7 shows that the stress–displacement diagrams overlap for the considered cases CGD-80, CGD-160 and CGD-320, i.e. for the meshes with 80, 160 and 320 FEs. It is visible that these results are free from spurious mesh sensitivity and the regularization is effective. This effect is also confirmed in Fig. 8, where the final distribution of damage \(\omega \) for the CGD model is shown in a grey scale. The highest values of damage \(\omega \) are marked by black colour. The evolution of averaged strain \({\bar{\epsilon }}\) for case CGD-320 is depicted in Fig. 9a. The averaged strain grows in the middle of the bar. It should be additionally noticed that in every picture where evolving profiles are drawn, on the horizontal plane in the range of \(x = 45 \div 55\) mm along the evolution axis the zone of imperfection is marked by grey colour. It is plotted for better visibility of imaged surfaces for selected variables. A corresponding response is observed for the damage evolution given in Fig. 9b, but now the problem of unexpected and too wide distribution of \(\omega \) occurs. It spuriously spreads over more than half of the length of the bar. Although mesh convergence is very well reproduced, the zone of active damage is significantly broadened in comparison to the averaged strain distribution.
Stress–displacement diagrams for conventional gradient damage (CGD) model—mesh sensitivity study. Diagram acronyms explained in text and Table 1
4.3 Results for increasing gradient activity
A next portion of the results is made for the SVS gradient damage (SVSGD) model, but the PSGD model, where function \(\varphi _1({\tilde{\epsilon }})\) is used, is also presented here for one case. It should be emphasized that for this function the gradient activity at first increases and later becomes constant, regardless of the used model. Figure 10 depicts the stress–elongation diagram for cases SVS-80, SVS-160, SVS-320 and CGD-320 for comparison. As for the CGD model, these three cases correspond to the three applied discretizations. The paths run the same way, but the peak is slightly lower than for the case CGD-320. It is connected with the fact that the gradient activity develops together with the loading process and for more advanced stage of softening, i.e. when \(u(L) \approx 0.03\) mm, they start to coincide and later retain a similar character. Mesh sensitivity study is also illustrated in Fig. 11 where the final distribution of damage \(\omega \) is illustrated. Apart from mesh objectivity, it can also be seen that the damage zone is much narrower in comparison to the distribution for the CGD model. The evolution of averaged strain measure \({\bar{\epsilon }}\) for the SVSGD model and 320 FEs is shown in Fig. 12a. It is noticeable that the width of the zone where averaged strains are active is thinner than in the case of the CGD model, cf. Fig. 9a. A similar effect is visible if the damage distribution is analysed, see Fig. 12b. In fact, for advanced states damage occupies less than half of the bar, cf. Fig. 9b. For the SVSGD model, the gradient activity function \(\varphi _1({\tilde{\epsilon }})\) increases from initial \(c_0 = 0.05\) \(\hbox {mm}^2\) to final \(c_{\max } = 18\) \(\hbox {mm}^2\) when \({\tilde{\epsilon }}_{\max }\) reaches 0.0015, i.e. \(15 \, \kappa _\mathrm {o}\). For \(n=1\) this growth is linear. Figure 12c presents the evolution of the gradient activity for SVS-320, which grows in the localized zone as well as in its close neighbourhood.
In Fig. 13 there are the stress–displacement diagrams for cases SVS-80-k0005, SVS-80-k001, SVS-80 and additionally PS1-80. Now only the mesh with 80 FEs is employed. This comparison shows the influence of gradient activity on the solution for different values of the limit equivalent strain \({\tilde{\epsilon }}_{\max }\). The applied functions \(\varphi _1({\tilde{\epsilon }})\) are presented in Fig. 2. In case SVS-80-k0005: \({\tilde{\epsilon }}_{\max } = 0.0005 = 5 \, \kappa _\mathrm {o}\), for SVS-80-k001: \({\tilde{\epsilon }}_{\max } = 0.001 = 10 \, \kappa _\mathrm {o}\) and case SVS-80 is as for case SVS-320. The peak loads for the diagrams of the SVSGD model in Fig. 13 become higher when the value of the limiting equivalent strain \({\tilde{\epsilon }}_{\max }\) gets smaller. It is clear that the model approaches to the standard gradient damage when \({\tilde{\epsilon }}_{\max }\) is diminished. For case PS1-80 the same parameters as for SVS-80 are adopted, so \({\tilde{\epsilon }}_{\max } = 0.0015 = 15 \, \kappa _\mathrm {o}\), but here the PS gradient damage model is applied instead of the SVSGD model. Hence, matrix \(\varvec{{K}}_{ea}^\mathrm{{PS}}\) is activated in the system of equations, in a similar fashion as the incorporation of \(\varvec{{K}}_{ea}^\mathrm{{SVS}}\) in the SVSGD model, cf. Eqs. (52) and (61). The solution for PS1-80 gives a slightly lower softening diagram in comparison to SVS-80. The damage evolution for cases SVS-80-k0005, SVS-80-k001 and PS1-80 is illustrated in Fig. 14. The zone of damage \(\omega \) becomes wider with simultaneously decreasing value of \({\tilde{\epsilon }}_{\max }\), see in turn Figs. 12b, 14b, a. Summarizing, an optimal value of the maximum equivalent strain \({\tilde{\epsilon }}_{\max }\) should be possibly large. On the other hand, the danger of instabilities together with oscillations or even divergence of the computations can appear. It is possible if the rate of increase of \(\varphi _1\) is too small. Damage distributions at the final instant for cases SVS-80, PS1-80 and additionally for CGD-80 are compared in Fig. 15. It is seen that \(\omega \) for case PS1-80 tends to a broader active zone than for SVS-80. It is also confirmed when the evolution given in Fig. 14c for PS1-80 and in Fig. 12b for SVS-320 is considered. It means that the application of \(\varphi _1({\tilde{\epsilon }})\) in the PSGD model is possible and can be accepted, but it does not work in a more effective way than the SVSGD model to reduce the width of the active damage zone stronger.
The next comparison concerns the character of function \(\varphi _1({\tilde{\epsilon }})\). Figure 3 explains that the power n in Eq. (69) decides how the gradient activity increases to \(c_{\max }\). As mentioned before, a linear growth is given for intensity \(n=1.0\), so its rate is constant. If \(n = 0.5\) in \(\varphi _1({\tilde{\epsilon }})\), then the increase of the gradient activity is fast at the beginning of the loading process and slows down later. For \(n = 2.0\) a quadratic character of \(\varphi _1({\tilde{\epsilon }})\) is set; therefore, the effect of the gradient activity accelerates with the development of localization. The stress–elongation diagrams in Fig. 16 are prepared for the above cases, namely for: SVS-80-n05—intensity \(n = 0.5\), SVS-80—intensity \(n=1.0\), and SVS-80-n2—intensity \(n = 2.0\). Again, the discretization with 80 FEs is applied. It can be seen that the distinction between cases SVS-80-n05 and SVS-80 is almost negligible. The diagram for case SVS-80-n2 differs from the others. A problem with numerical instabilities occurs for it just after the onset of damage. Similar issues have also been observed in [19] for the so-called failure-based transient–gradient damage formulation. As mentioned in the previous paragraph if an increase of the gradient activity is too slow and strain softening arises rather as a local phenomenon, instabilities during the computations can happen. Figure 17 shows the damage evolution for cases SVS-80-n05 and SVS-80-n2. If intensity n is equal to 0.5, then the developing damage zone is wider than for case SVS-320, cf. Fig. 12b. On the other hand, in case SVS-80-n2 damage \(\omega \) evolves in a quite promising way, but due to possible numerical instabilities it is not further taken into account.
4.4 Results for decreasing gradient activity
In this subsection, cases, where the gradient activity is reduced during the loading process, are analysed. The computations are performed mainly using function \(\varphi _2(\omega )\) and the PS gradient damage (PSGD) model, but other available options are also taken into account in order to show the outcome of employment of different functions (see Sect. 3) and models.
Now the presentation is divided into two parts—according to two different values of parameter \(\eta \) defined in Eq. (1). The first part includes the numerical analysis for the PSGD model with \(\eta = 400\) as for CGD and SVSGD models. Figure 18 depicts the stress–extension diagrams for three cases: PS-80-E, PS-160-E and PS-320-E. The diagram CGD-320 is recalled for comparison. As previously, 80, 160 or 320 FEs are used. Next, parameters \(R=0.05\) and \(n=3.0\) are introduced for function \(\varphi _2(\omega )\) defined in Eq. (71) in the PSGD model. It is clearly visible that for this model, in spite of identical \(\alpha =0.99\) and \(\eta =400\) as for CGD and SVSGD models and the same \(c_{\max } = 18.0\) \(\hbox {mm}^2\), the slope of equilibrium paths drastically differs in the softening phase in comparison to the solution for the previous models. After the localization progress, a similar level of the residual stress \(\sigma _x\) is attained four times faster for the PSGD model than for the CGD model. For instance, values of \(\sigma _x\) when \(u(L) = 0.04\) mm for PSGD and when final \(u(L) > 0.15\) mm for CGD are close. It should be mentioned that the diagrams for the PSGD model overlap. Mesh objectivity is also noticeable for the subsequent presented results. Moreover, it is visible in Fig. 19 that the zone of damage \(\omega \rightarrow 1.0\) marked by the black colour is much narrower than for the previous models. Figure 20a illustrates the averaged strain evolution for case PS-320-E. Again, the zone of nonzero strains is much thinner than for the previous models, but the maximum value in the peak is more or less doubled. Corresponding profiles of damage evolution are given in Fig. 20b. In fact, for the cases considered here with \(\eta = 400\) the localization zone is the narrowest one among all the results presented in this numerical example. However, it seems that the range of the support for the damage band is similar to the SVSGD model (cf. Figs. 20b and 12b). In other words, nonzero damage appears in a similar region, but its intensity via its shape is essentially different. The curves for the PSGD model look like a bell-shaped function, while for the SVSGD model those curves rather have a cup-shaped form. It is known that for the SVSGD and PSGD models the character of the gradient activity is different. In the PSGD model, \(\varphi _2(\omega )\) governs the solution and it can be even said that this function creates an inverted image of damage evolution, as shown in Fig. 20c. The range of values changes from \(c_{\max } = 18\) \(\hbox {mm}^2\) to almost zero according to the definition of residual interactions determined by the parameter R.
The stress–displacement diagrams in Fig. 21 depict the solution influenced by various minimum levels of interaction between microcracks in the vicinity of strain localization. The 80 FEs mesh is applied. The parameters for exponential softening are as previously: \(\alpha = 0.99\) and \(\eta = 400\). The power n for function \(\varphi _2(\omega )\) equals 3.0. The following cases are compared: PS-80-E-R02 where \(R=0.2\), PS-80-E-R01 for \(R = 0.1\) and PS-80-E for \(R = 0.05\). The slope of softening branches presented in Fig. 21 changes for different R. The smaller the value of this parameter is the more localized response occurs using the PSGD model. Figure 20b, 22a, b shows the damage evolution depending on the minimum interaction level. The damaged zone becomes wider and wider for larger R.
Next, the results for the PSGD model with \(\eta = 100\) are discussed. The fourfold decrease in the value of this parameter causes the response to be more ductile using the exponential damage growth law. Parameters \(\alpha = 0.99\), \(R=0.05\), \(n=3.0\) and \(c_{\max } = 18.0\) \(\hbox {mm}^2\) are maintained. The stress–elongation diagrams given in Fig. 23 are plotted for three cases of FE discretization: PS-80–80 elements, PS-160–160 elements and PS-320–320 elements. It is visible that the differences in the diagrams are negligible. The case CGD-320 is recalled to show that the equilibrium paths for the PSGD model are able to replicate the diagram for the CGD model by controlling the parameter \(\eta \). The change of \(\eta \) results in a somewhat broader zone of damage \(\omega \), cf. the distributions in Fig. 24 with the ones depicted in Fig. 19 for \(\eta = 400\). Furthermore, mesh objectivity is noticed again. The averaged strain evolution plot in Fig. 25a is similar to the case where \(\eta = 400\) in the PSGD model. However, the maximum averaged strain measure reaches 0.06 for \(\eta = 100\). The damage evolution in Fig. 25b exhibits a slightly broader damage zone in comparison to these demonstrated in Fig. 20b, but the issue of artificially wide damaged zone is overcome, cf. also Fig. 9b. For completeness, the evolution of gradient activity function \(\varphi _2(\omega )\) is depicted in Fig. 25c for case PS-320 and it demonstrates that the so-called localizing process, i.e. the effect of vanishing interactions, is present in the middle, but the zone of gradient activity is slightly wider in comparison to the case where \(\eta = 400\).
The rate of decrease of the gradient activity for this benchmark is verified in Figs. 26 and 27. The mesh is divided into 80 FEs. The data are the same apart from intensity n which is varied. The case PS-80 is taken from the previous analysis. For the case PS-80-n1, the power n equals 1.0, for the case PS-80-n5—\(n=5.0\). Function \(\varphi _2(\omega )\) with different intensities of the decreasing effect is shown in Fig. 5. Additionally, the case SVS2-80 is taken into account. The same parameters as for PS-80 are adopted, i.e. \(R = 0.05\) and \(n = 3.0\), but now the SVSGD model is combined with function \(\varphi _2(\omega )\), so as a consequence \(\varvec{{K}}_{ee}^\mathrm{{SVS}}\) is nonzero in the coupled matrix problem in a similar way as the presence of \(\varvec{{K}}_{ee}^\mathrm{{PS}}\) in the formulation of the PSGD model, cf. Eqs. (52) and (61). The diagrams in Fig. 26 indicate that for this test the intensity n almost does not influence the equilibrium paths—they differ only in the initial phase of material softening. On the other hand, the influence in the damage evolution is observable. The support of the damage zone narrows with increasing value of n, see Figs. 27a, 25b and 27b. The damage evolution for the case SVS2-80 in Fig. 27c looks rather like for the case PS-80-n1 than for the case PS-320. It means that a combination of the SVSGD model with the localized gradient activity defined by function \(\varphi _2(\omega )\) is possible, but not optimal. The above remark is also confirmed in Fig. 28, where damage distributions for the final stage are confronted. The case CGD-80 should be treated as a reference. It is observed that damage \(\omega \) is larger than 0.99 is in the same part inside the weakened zone for each considered case, i.e. PS-80-E, PS-80 and SVS2-80. On the other hand, among those three cases, the widest distribution is obtained for SVS2-80.
Damage evolution—alternative gradient activity functions: a PSGD model, \(\varphi _3(\omega )\), b PSGD model, \(\varphi _4({\tilde{\epsilon }})\) and c SVSGD model, \(\varphi _4({\tilde{\epsilon }})\). Acronyms explained in text and Table 1
The last part of this subsection is devoted to the brief presentation of the results where alternative gradient activity functions are used, namely \(\varphi _3(\omega )\) and \(\varphi _4({\tilde{\epsilon }})\). Both of them also have a decreasing character. Figure 29 presents the stress–extension diagrams. In the case PS3-80, cosine function \(\varphi _3(\omega )\) with \(R = 0.05\) and \(n = 1.0\) is adopted, see Fig. 5. For cases PS4-80 and SVS4-80, linear-constant function \(\varphi _4({\tilde{\epsilon }})\) is determined via initial \(c_{\max } = 18\) \(\hbox {mm}^2\), then decreasing until residual \(c_0 = 0.2\) \(\hbox {mm}^2\) for \({\tilde{\epsilon }}_{\max } = 0.0015\) and further constant small \(c_0\) is held. This function has a localized character opposite to \(\varphi _1({\tilde{\epsilon }})\). In Fig. 29 the diagram for PS3-80 is comparable with the case PS-80-n1, but the damage zone in the evolution plotted in Fig. 30a significantly broadens at the bottom, cf. Fig. 27a. The usage of that function is possible and gives better response than for the CGD model, but the ability to reproduce a relatively thin damaged region is questionable. Hence, a good selection of the gradient activity function can be crucial for the effectiveness of the solution. This aspect is briefly discussed in the next subsection. Finally, diagrams for PS4-80 and SVS4-80 show unstable equilibrium paths, despite the fact that the arc length method is applied in the computations. Material degradation demonstrated in Figs. 30b, c evolves as much wider even in confrontation with the CGD model. Function \(\varphi _4({\tilde{\epsilon }})\) is inacceptable in both (SVSGD and PSGD) models.
4.5 Summary of test
Summarizing the test of the bar with imperfection defined by the weakened zone, the CGD model produces damage distribution with unrealistically broad crack band in the middle.
The selection of the gradient activity function influences significantly in the width and the shape of the damage distribution. Focusing on the results for the PSGD model for which all the functions have been employed, Fig. 31 shows damage \(\omega \) along the bar for the final state. The following cases are chosen: CGD-80—\(\varphi _0 = c_{\max }\), PS1-80—\(\varphi _1({\tilde{\epsilon }})\), PS-80—\(\varphi _2(\omega )\), PS3-80—\(\varphi _3(\omega )\) and PS4-80—\(\varphi _4({\tilde{\epsilon }})\). Functions of gradient activity are discussed in Sect. 3. It is seen that the results for cases CGD-80 and PS4-80 are the worst, because the zone of damage is too broad. The other cases could be adopted; however, the range of the support on axis x along the bar for damage distribution (\(0 < \omega \le 0.2\)) is very wide for case PS3-80. This range is similar to case CGD-80, where \(\varphi _0\) is constant. It follows from the slow decrease of the gradient activity at the beginning of the degradation process in the bar. The onset of the damage growth for cases PS1-80 and PS-80 is the same, i.e. it starts in the range \(x \in [32.0, 68.0]\) mm, but the shape is different. The profile of \(\omega \) for \(\varphi _1({\tilde{\epsilon }})\) reminds a cup upside-down (see also the results for the SVSGD model), while the profile of \(\omega \) for \(\varphi _2(\omega )\) is rather bell-shaped. The most efficient response is obtained for PS-80. Moreover, because function \(\varphi _2(\omega )\) has the decreasing (localizing) character, it seems to be more adequate to simulate cracking phenomena in concrete than \(\varphi _1({\tilde{\epsilon }})\).
Generally, the problem of too wide damage zone is overcome using both SVSGD or PSGD models. The comparisons presented in this section confirm that it is preferred to use the PSGD model with function \(\varphi _2(\omega )\). However, the SVSGD model with function \(\varphi _1({\tilde{\epsilon }})\) is also considered in the example presented in Sect. 5 for completeness of the study.
5 Numerical analysis of bending in cantilever beam
5.1 Data setup
The benchmark of a cantilever beam is now analysed to show not only different efficiency in regularization of the models, but also to verify whether a good representation of damage distribution is reproduced. The vertical force is exerted along the left edge under deformation control of all vertical degrees of freedom. The clamped edge on the right is fully constrained. Hence, the cracked area is expected at the bottom on this side. The employed FE mesh B with boundary conditions is depicted in Fig. 32. Furthermore, the dimensions of the domain are also given. The thickness of the beam is 50 mm. Two or three additional discretizations are used to study mesh sensitivity. All meshes are refined near the constrained edge, where damage is expected. The part of the domain with coarse mesh A or fine mesh C is illustrated further with the results. Moreover, additional more refined mesh D is also used in two cases for the PSGD model. As in the previous test quadratic interpolation of the displacements \(\varvec{{u}}\) and linear interpolation of the averaged strain measure \({\bar{\epsilon }}\) is used and \(2 \times 2\) Gauss integration is adopted. The dimensions of the smallest FE, total number of nodes and total number of FEs for the applied meshes are as follows: mesh A—5 mm \(\times \) 6.25 mm, 635 nodes, 192 FEs, mesh B—2.5 mm \(\times \) 2.5 mm, 2443 nodes, 780 FEs and mesh C—1.25 mm \(\times \) 1.25 mm, 9371 nodes, 3060 FEs. The characteristics of additionally refined mesh D are: smallest element size 0.625 mm \(\times \) 0.625 mm, 34389 nodes and 11340 FEs.
The elastic constants are the same for each model: Young’s modulus \(E = 40{,}000\) N/\(\hbox {mm}^2\) and Poisson’s ratio \(\nu = 0.0\). The following common data for gradient damage are employed: when the degradation process starts threshold \(\kappa _\mathrm {o}\) is 0.000075 (tensile strength of concrete \(f'_t = 3\) MPa), equivalent strain measure \({\tilde{\epsilon }}\) is determined by modified von Mises in Eq. (3) with ratio \(k = 10\), the (maximum) internal length parameter corresponding to \(c_{\max } = 8\) \(\hbox {mm}^2\) and the exponential relation given in Eq. (1) is taken into account to describe the damage growth. Parameters \(\alpha = 0.92\) and \(\eta = 300\) for exponential softening have been primarily adjusted in [31]. The simulation of four-point bending test for the notched beam using the gradient damage–plasticity model has been compared there with the experiment [22]. Next, these values of \(\alpha \) and \(\eta \) have been inherited for the computations performed in [48] to present the crack closing effect in the cantilever beam under reversed loading. Moreover, they have also been used in [39] for the notched beam benchmark in four-point bending in order to address the SVS gradient damage (SVSGD) model. More material model data are given when the results are presented for individual models. It should only be emphasized here, based on the previous test for the bar with imperfection, that the rate of damage growth for the PS gradient damage (PSGD) model should be reduced, so \(\eta = 75\) is introduced.
5.2 Discussion of results
The results of this test for the local damage model, where the constitutive relation is determined only by Eq. (9) without any regularization within the material model description, can be found in [48]. Spuriously mesh-sensitive damage patterns as well as different load-carrying capacities for each discretization are shown there.
For the CGD model, no additional data are required—all the needed parameters are specified above. Function \(\varphi _0\) is actually defined as constant, see Eq. (68). The solution obtained for this model is depicted in Fig. 33. It is visible that the equilibrium paths in Fig. 33a are almost identical for each mesh. Crack patterns in Fig. 33b–d represented by damage \(\omega \) exhibit that the same region is marked for the degraded material, but the issue of too wide spread distribution of this variable is noticed. The gradient enhancement guarantees the response which is not sensitive to the discretization; nevertheless, the constant internal length scale parameter in the CGD model involves the spurious damage growth during the loading process.
The application of the SVSGD model demands the selection of the following extra parameters: initial length scale squared \(c_0 = 0.05\) \(\hbox {mm}^2\), equivalent strain \({\tilde{\epsilon }}_{\max } = 0.0015 = 20 \, \kappa _\mathrm {o}\) where function \(\varphi _1 ({\tilde{\epsilon }})\) is changed from linear to constant and intensity \(n=1.0\). The load–displacement diagrams in Fig. 34a almost overlap and their character is similar to the one presented for the CGD model, but now the maximum value of P is slightly smaller. Damage distributions for mesh A, B and C look the same, see Fig. 34b–d. The solution for the SVSGD model is mesh-objective. The most intensive damage zones (black colour) are narrower in comparison to the zone in the contour plots for the CGD model. Barely visible grey region at the bottom can be connected with the presence of excessive ductility effects in the simulated material model. It was mentioned that in this model the gradient activity has the increasing character. Function \(\varphi _1 ({\tilde{\epsilon }})\) activates the gradient terms inside and nearby the localization zone and it makes the incremental-iterative computations for the SVSGD model as stable as for the CGD model. However, as concluded in [35], the interaction should rather decrease with the damage evolution progress, so the physical interpretation and the range of applicability for quasi-brittle materials like concrete can be questioned. More results of similar calculations for a four-point bending beam are reported in [39].
The mesh sensitivity study for the cantilever beam using the PSGD model is divided into two parts. In this model, for function \(\varphi _2\) which decreases with damage \(\omega \), two parameters have to be set: the minimum level R of nonlocal interactions within the localization zone and power n as the degree of the decreasing intensity of gradient activity. It is also recalled that now parameter \(\eta \) equals 75, i.e. four times less than for CGD and SVSGD models. Figure 35 presents the solution for \(R=0.1\) and \(n=1.0\). After the peak the load–displacement diagram for mesh A differs from the others. The paths for meshes B and C almost coincide. However, damage patterns for all discretizations have exactly the same character, cf. Fig. 35b–d. Hence, mesh-independent results are observed although mesh A is coarse and produces a stiffer response; compare as well the maximum load for the models—here \(P > 2000\) N. The employed parameters \(R = 0.1\) and \(n=1.0\) in the PSGD model give as one of the results a quite slim zone for \(\omega \approx 1\), but for lower and lower levels of damage plot this distribution becomes even more spread than for the CGD model. The reason is that in this case the localizing character of the PSGD model is weaker. If R becomes ten times smaller for example, i.e. equals 0.01, then after the peak equilibrium paths for meshes A, B and C run differently, see Fig. 36a. It does not mean that mesh dependence occurs, since it is observed that load–displacement diagrams for mesh C and the finest mesh D are close to each other. Notice that damage zones shown in Fig. 36b, c as well as Fig. 37a, b (both plots are enlarged) are similar. The question is how strongly the applied mesh should be densified. All results for two dimensional problems using the so-called localizing gradient damage model in the literature, see, for example, [35, 38, 43], are obtained with the discretization of thousands FEs or using additional mesh adaptivity during the nonlinear analysis, cf. [37]. Hence, meshes A and B can be not enough to obtain overlapped diagrams. It is demonstrated that for the PSGD model with assumed small level of residual interaction R a quite dense discretization should be employed. Figure 38a shows the load–displacement diagrams, where \(R = 0.01\) is kept and n is raised to 5.0. Identical tendency as in Fig. 36a is observed, but now the peak of P is lower. The larger value of power n accelerates the decrease of the gradient activity interaction between microcracks during the loading process. It seems to be more physical in the modelling of strain localization. Moreover, the effect of spreading for damage patterns illustrated in Figs. 38b, c and 39 disappears. The most degraded zone is much thinner than for the CGD model, so the issue with spuriously too broad band of damage in gradient-enhanced damage models is reduced using the PSGD model. However, it should be noted that during the computations the quadratic convergence can be lost due to many overlapping nonlinear effects.
In this paragraph the comparison of the results for the cantilever beam benchmark using the models discussed in the paper is performed. Mesh C is only applied. The load–displacement diagrams gathered in Fig. 40 are compared for the cases for which the damage distributions are presented in Figs. 33d, 34d, 35d, 37a and additionally for the case where \(\eta = 75\) is used for the CGD model. This last case is represented by the damage pattern in Fig. 42a. It is seen that for \(\eta = 75\) the response for the CGD model is very ductile and the localized band is extremely broadened. The diagrams for CGD and SVSGD models with \(\eta = 300\) are comparable. On the other hand, the solution for the PSGD model is strongly dependent on parameter R which is responsible for the final level of decreasing function \(\varphi _2(\omega )\), i.e. it governs how the gradient activity interacts in the model. Figure 41 in turn illustrates the influence of intensity n in the PSGD model. Of course, peaks and the progress of softening are quite different, but finally all diagrams coincide. In the last comparison, attention is focused on parameter \(\eta \) defined for the PSGD model. The equilibrium paths are shown in Fig. 43 together with the diagram for the CGD model and \(\eta =300\) as a reference solution. Corresponding damage distributions are depicted in Figs. 42b–d and 39a. It has been expected that the smaller \(\eta \) is the more ductile behaviour is observed. Hence, the value of this parameter should be as large as possible to simulate quasi-brittle materials using the PSGD model.
6 Conclusions
The gradient-enhanced damage models with a constant or evolving gradient influence are discussed in the paper. The issue of spuriously wide zone for damage using the conventional gradient damage (CGD) model is shown. Two alternative formulations with an increasing or decreasing gradient activity function are implemented by the author in the FEAP package [44]. There are: the SVS gradient damage (SVSGD) model based on [39] and the PS gradient damage (PSGD) model based on [35, 43]. The PSGD model has been also called the localizing gradient damage model in the literature, see, for example, [23, 35, 37]. The efficiency of regularization for used models is assessed. Different options of gradient activity functions are examined. The models are compared in two tests, namely the tensile bar with imperfection and the cantilever beam under in-plane bending.
While an uncontrolled damage zone in the CGD model is observed, two concepts of gradient activity with an evolving length scale parameter are considered. Activating or localizing character of the evolution can be adopted. With reference to [35, 39], a generalization of both models is derived in Eqs. (52) and (61). The gradient activity function can now be determined by equivalent strain or damage in both models. It is possible to use a function with localizing character for the SVSGD model and use a function with activating character for the PSGD model. However, increasing gradient activity in the function of the equivalent strain measure is preferred for the SVSGD model as in [39]. It is also confirmed that the function proposed originally in [35], where the damage growth causes a decrease of nonlocality, is favourable for the PSGD model.
In the formulation, the interpolation of a third extra independent field for gradient activity as in [19] is unnecessary. Therefore, the numerical framework is similar to the CGD model and, as a consequence, limited modifications in the code are required. The Newton–Raphson algorithm converges easier for the SVSGD model than for the PSGD model.
A parametric study of the models with different gradient activity functions is performed. Despite the fact that the results for the SVSGD model are correct, a physical motivation to employ an increasing gradient activity seems to be inadequate for quasi-brittle materials. The PSGD model provides a more suitable interpretation when the gradient activity function decreases together with the degradation progress. In fact, proper selection of the gradient activity function is crucial.
When the SVSGD model is applied, the achievement of the maximum internal length scale squared should be delayed as much as possible. However, then numerical instabilities or even divergence of the computations can occur. The PSGD model is also sensitive to its parameters, especially to the rate of the damage growth determined by parameter \(\eta \) and the minimum level of interaction between microprocesses within the localization band determined by parameter R. Both parameters are able to change completely the response of the material model. It is suggested to apply a possibly large value for \(\eta \) and a possibly small value for R. On the other hand, as for the SVSGD model numerical divergence can appear in the analysis, so both parameters should be carefully selected. It should also be indicated that for the PSGD model, when low residual interaction R is applied, a refined mesh with thousands of finite elements is suggested to ensure a fully mesh-independent solution. The third parameter for the PSGD model which is called the intensity does not modify the solution so strongly as those two previous ones. Summarizing, both approaches are able to overcome the issue of excessively broadening damage region in the simulations of concrete cracking, but the values of model parameters should be fitted with caution.
References
Abu Al-Rub, R.K., Voyiadjis, G.Z.: Gradient-enhanced coupled plasticity-anisotropic damage model for concrete fracture: computational aspects and applications. Int. J. Damage Mech. 18(2), 115–154 (2009). https://doi.org/10.1177/1056789508097541
Aifantis, E.C.: On the microstructural origin of certain inelastic models. J. Eng. Mater. Technol. 106(4), 326–330 (1984). https://doi.org/10.1115/1.3225725
Alessi, R., Marigo, J.J., Vidoli, S.: Gradient damage models coupled with plasticity: variational formulation and main properties. Mech. Mater. 80, 351–367 (2015). https://doi.org/10.1016/j.mechmat.2013.12.005
Askes, H., Pamin, J., de Borst, R.: Dispersion analysis and element-free Galerkin solutions of second- and fourth-order gradient-enhanced damage models. Int. J. Numer. Methods Eng. 49, 811–832 (2000). https://doi.org/10.1002/1097-0207(20001030)49:6<811::AID-NME985>3.0.CO;2-9
Askes, H., Sluys, L.J.: A classification of higher-order strain-gradient models in damage mechanics. Arch. Appl. Mech. 73(5–6), 448–465 (2003). https://doi.org/10.1007/s00419-003-0296-3
Askes, H., Suiker, A.S.J., Sluys, L.J.: A classification of higher-order strain-gradient models-linear analysis. Arch. Appl. Mech. 72(2–3), 171–188 (2002). https://doi.org/10.1007/s00419-002-0202-4
Bažant, Z.P.: Instability, ductility, and size effect in strain-softening concrete. ASCE J. Eng. Mech. Div. 102(2), 331–344 (1976)
Bažant, Z.P., Pijaudier-Cabot, G.: Nonlocal continuum damage, localization instability and convergence. ASME J. Appl. Mech. 55, 287–293 (1988). https://doi.org/10.1115/1.3173674
Belytschko, T., Lasry, D.: A study of localization limiters for strain-softening in statics and dynamics. Comput. Struct. 33(3), 707–715 (1989). https://doi.org/10.1016/0045-7949(89)90244-7
Bobiński, J., Tejchman, J.: Modelling of strain localization in quasi-brittle materials with nonlocal continuum models. In: Meschke, G., et al. (eds.) Proceedings of EURO-C 2006 International Conference on Computational Modelling of Concrete Structures, pp. 301–307. Taylor & Francis, London (2006)
de Borst, R., Mühlhaus, H.B.: Gradient-dependent plasticity: formulation and algorithmic aspects. Int. J. Numer. Methods Eng. 35, 521–539 (1992). https://doi.org/10.1002/nme.1620350307
de Borst, R., Pamin, J., Geers, M.G.D.: On coupled gradient-dependent plasticity and damage theories with a view to localization analysis. Eur. J. Mech. A/Solids 18(6), 939–962 (1999). https://doi.org/10.1016/S0997-7538(99)00114-X
Brinkgreve, R.B.J.: Geomaterial models and numerical analysis of softening. Ph.D. dissertation, Delft University of Technology, Delft (1994). http://resolver.tudelft.nl/uuid:6738de62-4dde-45b0-b3bd-3635504767c2
Bui, Q.: Initiation of damage with implicit gradient-enhanced damage models. Int. J. Solids Struct. 47(18–19), 2425–2435 (2010). https://doi.org/10.1016/j.ijsolstr.2010.05.003
Comi, C.: Computational modelling of gradient-enhanced damage in quasi-brittle materials. Mech. Cohes. Frict. Mater. 4(1), 17–36 (1999). https://doi.org/10.1002/(SICI)1099-1484(199901)4:1<17::AID-CFM55>3.0.CO;2-6
Di Luzio, G., Bažant, Z.P.: Spectral analysis of localization in nonlocal and over-nonlocal materials with softening plasticity or damage. Int. J. Solids Struct. 42(23), 6071–6100 (2005). https://doi.org/10.1016/j.ijsolstr.2005.03.038
Dimitrijevic, B.J., Aifantis, K.E., Hackl, K.: The influence of particle size and spacing on the fragmentation of nanocomposite anodes for Li batteries. J. Power Sources 206, 343–343 (2012). https://doi.org/10.1016/j.jpowsour.2012.01.065
Forest, S.: Micromorphic approach for gradient elasticity, viscoplasticity, and damage. ASCE J. Eng. Mech. 135(3), 117–131 (2009). https://doi.org/10.1061/(ASCE)0733-9399(2009)135:3(117)
Geers, M.G.D.: Experimental analysis and computational modelling of damage and fracture. Ph.D. dissertation, Eindhoven University of Technology, Eindhoven (1997). https://doi.org/10.6100/IR477352
Geers, M.G.D., de Borst, R., Brekelmans, W.A.M., Peerlings, R.H.J.: Strain-based transient-gradient damage model for failure analyses. Comput. Methods Appl. Mech. Eng. 160(1–2), 133–153 (1998). https://doi.org/10.1016/S0045-7825(98)80011-X
Geers, M.G.D., de Borst, R.D., Brekelmans, W.A.M., Peerlings, R.H.J.: Validation and internal length scale determination for a gradient damage model: application to short glass-fibre-reinforced polypropylene. Int. J. Solids Struct. 36(17), 2557–2583 (1999). https://doi.org/10.1016/S0020-7683(98)00123-1
Hordijk, D.A.: Local approach to fatigue of concrete. Ph.D. dissertation, Delft University of Technology, Delft (1991). http://resolver.tudelft.nl/uuid:fa87147b-8201-47ed-83d7-b812b09c5fbb
Jirásek, M.: Regularized continuum damage formulations acting as localization limiters. In: Meschke, G., et al. (eds.) Proceedings of EURO-C 2018 International Conference on Computational Modelling of Concrete Structures, pp. 25–41. CRC Press, London (2018). https://www.taylorfrancis.com/books/e/9781315182964/chapters/10.1201/9781315182964-3
Kachanov, L.M.: Time of rupture process under creep conditions. Izd. Akad. Nauk SSSR Otd. Tekh. Nauk 8, 26–31 (1958) (in Russian)
Lemaitre, J.: Evaluation of dissipation and damage in metals. In: Proceedings of ICM, vol. 1. Kyoto, Japan (1971)
Liebe, T., Steinmann, P., Benallal, A.: Theoretical and computational aspects of a thermodynamically consistent framework for geometrically linear gradient damage. Comput. Methods Appl. Mech. Eng. 190, 6555–6576 (2001). https://doi.org/10.1016/S0045-7825(01)00250-X
Mahnken, R., Kuhl, E.: Parameter identification of gradient enhanced damage models with the finite element method. Eur. J. Mech. A/Solids 18, 819–835 (1999). https://doi.org/10.1016/S0997-7538(99)00127-8
Mazars, J., Pijaudier-Cabot, G.: Continuum damage theory—application to concrete. ASCE J. Eng. Mech. 115(2), 345–365 (1989). https://doi.org/10.1061/(ASCE)0733-9399(1989)115:2(345)
Mühlich, U., Zybell, L., Hütter, G., Kuna, M.: A first-order strain gradient damage model for simulating quasi-brittle failure in porous elastic solids. Arch. Appl. Mech. 83, 955–967 (2013). https://doi.org/10.1007/s00419-013-0729-6
Pamin, J.: Gradient-dependent plasticity in numerical simulation of localization phenomena. Ph.D. dissertation, Delft University of Technology, Delft (1994). http://resolver.tudelft.nl/uuid:f69c526b-bfa3-4dfc-9e92-b76e1ff16fdd
Pamin, J., de Borst, R.: Stiffness degradation in gradient-dependent coupled damage-plasticity. Arch. Mech. 51(3–4), 419–446 (1999). http://am.ippt.pan.pl/index.php/am/article/view/v51p419
Peerlings, R.H.J., de Borst, R., Brekelmans, W.A.M., de Vree, J.H.P.: Gradient-enhanced damage for quasi-brittle materials. Int. J. Numer. Methods Eng. 39(19), 3391–3403 (1996). https://doi.org/10.1002/(SICI)1097-0207(19961015)39:19<3391::AID-NME7>3.0.CO;2-D
Peerlings, R.H.J., Brekelmans, W.A.M., de Borst, R., Geers, M.G.D.: Gradient-enhanced damage modelling of high-cycle fatigue. Int. J. Numer. Methods Eng. 49(12), 1547–1569 (2000). https://doi.org/10.1002/1097-0207(20001230)49:12<1547::AID-NME16>3.0.CO;2-D
Peerlings, R.H.J., Geers, M.G.D., de Borst, R., Brekelmans, W.A.M.: A critical comparison of nonlocal and gradient-enhanced softening continua. Int. J. Solids Struct. 38(44–45), 7723–7746 (2001). https://doi.org/10.1016/S0020-7683(01)00087-7
Poh, L.H., Sun, G.: Localizing gradient damage model with decreasing interaction. Int. J. Numer. Methods Eng. 110(6), 503–522 (2017). https://doi.org/10.1002/nme.5364
Poh, L.H., Swaddiwudhipong, S.: Over-nonlocal gradient enhanced plastic-damage model for concrete. Int. J. Solids Struct. 46(25–26), 4369–4378 (2009). https://doi.org/10.1016/j.ijsolstr.2009.08.025
Sarkar, S., Singh, I., Mishra, B.: Adaptive mesh refinement schemes for the localizing gradient damage method based on biquadratic-bilinear coupled-field elements. Eng. Fract. Mech. 223, 106790 (2020). https://doi.org/10.1016/j.engfracmech.2019.106790
Sarkar, S., Singh, I., Mishra, B., Shedbale, A., Poh, L.: A comparative study and ABAQUS implementation of conventional and localizing gradient enhanced damage models. Finite Elem. Anal. Des. 160, 1–31 (2019). https://doi.org/10.1016/j.finel.2019.04.001
Saroukhani, S., Vafadari, R., Simone, A.: A simplified implementation of a gradient-enhanced damage model with transient length scale effects. Comput. Mech. 51(6), 899–909 (2013). https://doi.org/10.1007/s00466-012-0769-8
Schreter, M., Neuner, M., Hofstetter, G.: Evaluation of the implicit gradient-enhanced regularization of a damage-plasticity rock model. Appl. Sci. 8(6), 1004 (2008). https://doi.org/10.3390/app8061004
Simone, A., Askes, H., Peerlings, R.H.J., Sluys, L.J.: Interpolation requirements for implicit gradient-enhanced continuum damage models. Commun. Numer. Methods Eng. 19, 563–572 (2003). https://doi.org/10.1002/cnm.597
Simone, A., Askes, H., Peerlings, R.H.J., Sluys, L.J.: Corrigendum “Interpolation requirements for implicit gradient-enhanced continuum damage models”. Commun. Numer. Methods Eng. 20, 163–165 (2004). https://doi.org/10.1002/cnm.663
Sun, G.: Localizing gradient damage models for the fracture of quasi-brittle materials. Ph.D. dissertation, National University of Singapore, Kent Ridge, Singapore (2017). https://scholarbank.nus.edu.sg/handle/10635/138662
Taylor, R.: FEAP: A Finite Element Analysis Program, Version 7.4, User manual. University of California at Berkeley, Berkeley (2001)
de Vree, J.H.P., Brekelmans, W.A.M., van Gils, M.A.J.: Comparison of nonlocal approaches in continuum damage mechanics. Comput. Struct. 55(4), 581–588 (1995). https://doi.org/10.1016/0045-7949(94)00501-S
Waffenschmidt, T., Polindara, C., Menzel, A., Sergio, B.: A gradient-enhanced large-deformation continuum damage model for fibre-reinforced materials. Comput. Methods Appl. Mech. Eng. 268, 801–842 (2014). https://doi.org/10.1016/j.cma.2013.10.013
Wcisło, B., Pamin, J., Kowalczyk-Gajewska, K.: Gradient-enhanced damage model for large deformations of elastic-plastic materials. Arch. Mech. 65(5), 407–428 (2013). https://am.ippt.pan.pl/am/article/view/v65p407
Wosatko, A., Genikomsou, A., Pamin, J., Polak, M.A., Winnicki, A.: Examination of two regularized damage-plasticity models for concrete with regard to crack closing. Eng. Fract. Mech. 194, 190–211 (2018). https://doi.org/10.1016/j.engfracmech.2018.03.002
Acknowledgements
Valuable support of Prof. Jerzy Pamin from Cracow University of Technology is gratefully acknowledged.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Wosatko, A. Comparison of evolving gradient damage formulations with different activity functions. Arch Appl Mech 91, 597–627 (2021). https://doi.org/10.1007/s00419-021-01889-2
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00419-021-01889-2