1 Introduction

Curved beams are integral components widely used in aerospace, mechanical, and civil engineering structures such as circular truss antenna. Therefore, their thermomechanical analysis has always been of interest to engineers [1,2,3,4,5,6,7,8,9,10,11,12,13,14,15]. Structural responses of curved beams strongly depend on their curvatures, particularly for open curved beams. Accurate information about thermal deformations, strains, and stresses is necessary for adequate serviceability, stability, and strength limit state designs of curved beams under various types of temperature fields. However, the thermoelastic analysis of curved beams under temperature field appears to have attracted only a limited amount of research.

As mentioned, circular truss antenna has been used in the space exploring for many years. The circular truss antenna system consists of an astrovehicle, a truss antenna, and a solar wing. The extended truss antennas are widely used in many space missions, such as deep space exploration, land remote sensing, weather forecasting, and ocean detection. With the further improvement in the work requirements, the truss antenna is designed to be foldable and deployable structures with the large apertures and the components are flexible. Since most of the components in the truss antenna system are lightweight and have high-flexibility structures, the system may have the low stiffness and the large deformations under any external excitation such as thermal loading which can adversely impact its performance and reliability [1]. Furthermore, a beam is a structural element that has been studied for many years and widely used in various engineering fields across the length scale. In many large-scale structures, beams are used as horizontal structures to carry vertical loads, such as keels in ship structures and girders in bridge structures. Also, for microstructures, curved beams are used to construct architected metamaterials for energy trapping owing to their bistability [2]. For these reasons, investigation of the nonlinear thermal modeling of the curved beam may assist to predict more accurately the performance of this type of practical curved-shape structures. Asgari et al. [3] focused on investigating nonlinear, thermo-elastic responses of pin-ended circular shallow arches made of functionally graded materials (FGMs) under uniform temperature rise. It was found that employing FGMs can increase the critical buckling temperature of shallow arches, even for thin beams. Bateni and Eslami [4] carried out an analysis of nonlinear stability behavior of functionally graded, circular shallow arches under a uniform radial pressure. Based on their conclusion, elasticity modulus distribution patterns through the thickness of the shallow arches play a dominant role in changing the stability behavior of the structure. Also, it was shown that instability modes of shallow arches subjected to a uniform radial pressure with simply supported boundary conditions are more active than the other types of boundary conditions. Stanciulescu [5] researched to elucidate dynamic snap-through reaction of curved beams under thermomechanical loads using a three-dimensional finite element analysis. A non-trivial configuration of the curved beam was identified at a critical temperature below which the curved beam will no longer experience snap-through instability under any magnitude of applied quasi-static load. A third-order efficient layerwise theory (ELWT) has been developed by Yaqoob Yasin et al. [6] to assess static deflections, stresses, and natural frequencies of laminated composite and sandwich curved beams. Outcomes indicated that at the same number of degrees of freedom, the accuracy of results estimated by the ELWT is more than that of equivalent single-layer theories. Keybolahi et al. [7] investigated dynamic buckling of a shallow arch subjected to transient thermal loading in which a surface was kept at the reference temperature, while the other surface was exposed to thermal shock. It was verified that rapid surface heating of shallow arches may cause dynamic snap-through type of motion. Higher-order shear deformation theory was implemented and used by Polit et al. [8] to examine the elastic stability responses of thick, functionally graded, porous, nanocomposite curved beams reinforced by graphene platelets. Based on their observations, dispersion and concentration of GPLs are two dominant factors that significantly influence the curved beam stiffness. Additionally, it was also seen that weight and dispersion patterns of GPLs and porosities have a particular importance in the stress distribution in the thickness direction of curved beams. Hodges [10] investigated the in-plane deformation of isotropic rings and shallow arches with rectangular section by implementing a nonlinear theory based on the total potential energy principle. Kiani and Eslami [14] obtained a closed-form solution for the nonlinear equilibrium and stability equations derived according to the Euler–Bernoulli beam theory for exploring the buckling behavior of beams made of FGMs under various types of thermal loading, namely uniform, linear, and nonlinear temperature rise. By considering different cases of thermal loading and boundary conditions, it was concluded that buckling temperature of fully ceramic beams is higher than FGM ones.

In recent decades, due to the advancement of manufacturing processes, various types of microscopically structured materials have been produced ranging from microporous zeolite ceramics to macroporous polymers, and their applications have been expanded from biological implants to energy technologies. There are many reasons which motivate a large number of scientists across the world to conduct theoretical and experimental research to shed light on the influence of porosities on various engineering structures made of FGMs. One of the most significant motivations is to reduce the impact of porosities on the material strength [16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31]. Thanh et al. [17] presented a novel research to investigate the size-dependent effects on the thermal stability of FGM micro-plates with three types of porosity dispersion patterns, including even, uneven, and logarithmic uneven. Results indicated that the critical buckling temperature of porous models is higher than the perfect, nonporous, FGM microplates. Also, it was concluded that the uniform porosity model has the best thermal resistance among the three types of porosity dispersion patterns. Khaneh Masjedi et al. [18] have studied the influence of various loading conditions and different porosity distributions on the large deflection of functionally graded porous beams utilizing a geometrically exact beam model along with fully intrinsic formulation for the first time. It was found that the method brings some advantages, such as computational efficiency and results accuracy. Jouneghani et al. [19] have conducted a research in order to explore the effect of hygro-thermo-mechanical loadings on the nonlinear bending behavior of functionally graded porous nonbeams by applying Eringen’s nonlocal theory. The numerical results demonstrated that some parameters, including moisture concentration, power-law index, and porosity volume fraction, are of great importance in the maximum deflection of beams because the existence of porosities and moistures can remarkably affect the material characteristics and ultimately results in varying bending stiffness through the thickness direction of the structure. Research on thermal buckling and free vibration of a temperature-dependent, functionally graded circular plate with internal porosities exposed to nonlinear thermal load was performed by Shojaeefard et al. [20]. The outcomes revealed that by increasing the temperature, porosities influence more substantially the free vibration of hinged circular plates compared to the other types of boundary conditions. Jalali and Heshmati [21] carried out a vibration analysis of tapered circular plates with radially graded porosity by applying a pseudospectral method. It was observed that FG external solid porosity distribution gives the highest frequency for all values of porosity parameters. Chen et al. [22] presented a numerical solution for buckling and static bending of shear deformable functionally graded beams with different types of boundary conditions in which the material properties, particularly elasticity modulus, vary through the thickness due to the various assumptions of porosity distributions. The influence of different porosity distributions on the buckling performance and bending resistance was highlighted in the results. Accordingly, uniform porosity distribution offers a higher buckling capacity and better bending resistance in comparison with asymmetric patterns. Akbas [23] performed a finite element analysis to evaluate the nonlinear static deflection of functionally graded porous beams in thermal environment. Because of the existence of porosities in nanoscale of FGMs possibly occurring during fabrication procedure, and subjecting to thermal loads, material properties are defined as a function of temperature and spatial coordinates. By using an analytical method with enough potential to satisfy different types of boundary conditions, Barati [24] succeeded in solving the nonlinear equations of motion obtained from Hamilton’s principle to investigate the free vibration of functionally graded piezoelectric plates with various porosity distributions. Shahsavari [25] introduced a novel, quasi-3D, hyperbolic theory by which free vibration equations of functionally graded porous plates resting on elastic foundation were solved. It was deduced that by considering the elastic foundation as a determining factor, the highest frequency of FG porous plate with various types of porosity distribution is achieved for even porosity pattern, which means that this type of distribution can provide a better plate stiffness compared with the other patterns, including uneven and logarithmic uneven. Cong et al. [26] also proposed an analytical approach based on higher-order shear deformation plate theory in order to identify thermomechanical stability behavior of functionally graded porous plates resting on elastic foundations. Comprehensive parametric studies indicated that the even porosity distribution offers higher critical buckling load than uneven porosity patterns, when the plate is subjected to compressive loads. Additionally, it can be inferred from the results that the effect of porosity volume fraction on the postbuckling response of plates with an even porosity distribution is more substantial than that with an uneven pattern. Nguyen [27] adopted an efficient polygonal finite element method in conjunction with quadratic serendipity shape functions to assess static and dynamic stability responses of functionally graded plates with various porosity dispersions, namely even and uneven. Hieu and Van Tung [28] developed an effective analytical approach to examine the thermal instability responses of composite cylindrical shells enhanced by carbon nanotubes and subjected to various types of mechanical and thermal loadings. A numerical analysis was conducted by Bahranifard et al. [29] in order to explore the influence of the graphene platelet weight and distributions on the thermoelastic in-plane behavior of composite curved beams reinforced by GPL.

There are many reasons which have motivated the authors to do this research. One of the most important of which is that linear analysis of curved beams leads to an over-estimation of antisymmetric bifurcation buckling loads, caused by geometric nonlinearity. Therefore, it is required to apply nonlinear methods in order to have an accurate prediction about the nonlinear behavior of this type of structure which has a common application in many fields of engineering, particularly in aerospace and biomaterial engineering. Moreover, these days FGMs are widely used in several engineering applications and porosities have been taken into consideration as one of the drawbacks which may occur during the fabrication process. The porosities significantly affect thermo-mechanical properties of the FGM; therefore, conducting a complete study to evaluate the effect of the porosity on the thermal postbuckling behavior of one of the common engineering structures, curved beam, is of great value which is done in this paper for the first time.

The work presented in this paper aims to highlight the influence of different porosity dispersion patterns on the nonlinear radial deflection of FG porous curved beams exposed to some variety of temperature rise functions. For this purpose, nonlinear governing equations are derived based on the first-order shear deformation theory (FSDT) along with the nonlinear Green strains. The nonlinear governing equations are solved by the aid of the Rayleigh–Ritz method conjugated with the Newton–Raphson method. A detailed parametric study is conducted to examine the effects of volume fraction and distribution of porosities, geometrical parameters, and boundary conditions on the in-plane thermoelastic characteristics of the FG porous curved beams. Due to the absence of similar results in the literature, this paper is filling a gap in the state-of-the-art knowledge of FG porous structures essential to the design of FG porous curved beams under thermal loadings.

2 Material properties

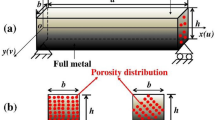
Consider a curved beam made of FG porous materials in which mechanical and thermal properties vary across the thickness direction, where the bottom surface of the curved beam is assumed to be made of full metal; on the other hand, the composition of the top surface is pure ceramic. One of the targets of the current study is to investigate the role of porosity dispersion in stability responses of curved beams. For this purpose, imperfect FGM with three types of porosity dispersions are taken into consideration, including even, uneven, and logarithmic uneven dispersion presented in Fig. 1. As a consequence, the associated Young’s modulus \(E\), shear modulus \(G\), Poisson’s ratio \(\nu\), and thermal expansion coefficient \(\alpha\) can be extracted based on the modified rule of mixture in the following forms [17]:

$$\begin{gathered} {\text{even}}\,{\text{porosity}}\,{\text{dispersion}} \hfill \\ \left\{ \begin{gathered} E\left( {z,T} \right) = \left( {E_{c} \left( T \right) - E_{m} \left( T \right)} \right)\left( {\frac{1}{2} + \frac{z}{h}} \right)^{n} + E_{m} \left( T \right) - \frac{\xi }{2}\left( {E_{c} \left( T \right) + E_{m} \left( T \right)} \right) \hfill \\ \nu \left( {z,T} \right) = \left( {\nu_{c} (T) - \nu_{m} \left( T \right)} \right)\left( {\frac{1}{2} + \frac{z}{h}} \right)^{n} + \nu_{m} \left( T \right) - \frac{\xi }{2}\left( {\nu_{c} \left( T \right) + \nu_{m} \left( T \right)} \right) \hfill \\ \alpha \left( {z,T} \right) = \left( {\alpha_{c} \left( T \right) - \alpha_{m} \left( T \right)} \right)\left( {\frac{1}{2} + \frac{z}{h}} \right)^{n} + \alpha_{m} \left( T \right) - \frac{\xi }{2}\left( {\alpha_{c} \left( T \right) + \alpha_{m} \left( T \right)} \right) \hfill \\ G\left( {z,T} \right) = \frac{{E\left( {z,T} \right)}}{{2\left( {1 + \nu \left( {z,T} \right)} \right)}} \hfill \\ \end{gathered} \right. \hfill \\ \end{gathered}$$
(1)
$$\begin{gathered} {\text{uneven}}\,{\text{porosity}}\,{\text{dispersion}} \hfill \\ \left\{ \begin{gathered} E\left( {z,T} \right) = \left( {E_{c} \left( T \right) - E_{m} \left( T \right)} \right)\left( {\frac{1}{2} + \frac{z}{h}} \right)^{n} + E_{m} \left( T \right) - \frac{\xi }{2}\left( {1 - \frac{2\left| z \right|}{h}} \right)\left( {E_{c} \left( T \right) + E_{m} \left( T \right)} \right) \hfill \\ \nu \left( {z,T} \right) = \left( {\nu_{c} \left( T \right) - \nu_{m} \left( T \right)} \right)\left( {\frac{1}{2} + \frac{z}{h}} \right)^{n} + \nu_{m} \left( T \right) - \frac{\xi }{2}\left( {1 - \frac{2\left| z \right|}{h}} \right)\left( {\nu_{c} \left( T \right) + \nu_{m} \left( T \right)} \right) \hfill \\ \alpha \left( {z,T} \right) = \left( {\alpha_{c} \left( T \right) - \alpha_{m} \left( T \right)} \right)\left( {\frac{1}{2} + \frac{z}{h}} \right)^{n} + \alpha_{m} \left( T \right) - \frac{\xi }{2}\left( {1 - \frac{2\left| z \right|}{h}} \right)\left( {\alpha_{c} \left( T \right) + \alpha_{m} \left( T \right)} \right) \hfill \\ G\left( {z,T} \right) = \frac{{E\left( {z,T} \right)}}{{2\left( {1 + \nu \left( {z,T} \right)} \right)}} \hfill \\ \end{gathered} \right. \hfill \\ \end{gathered}$$
$$\begin{gathered} {\text{Logarithmic}}\,{\text{uneven}}\,{\text{porosity}}\,{\text{dispersion}} \hfill \\ \left\{ \begin{gathered} E\left( {z,T} \right) = \left( {E_{c} \left( T \right) - E_{m} \left( T \right)} \right)\left( {\frac{1}{2} + \frac{z}{h}} \right)^{n} + E_{m} \left( T \right) - \log \left( {1 + \frac{\xi }{2}} \right)\left( {1 - \frac{2\left| z \right|}{h}} \right)\left( {E_{c} \left( T \right) + E_{m} \left( T \right)} \right) \hfill \\ \nu \left( {z,T} \right) = \left( {\nu_{c} \left( T \right) - \nu_{m} \left( T \right)} \right)\left( {\frac{1}{2} + \frac{z}{h}} \right)^{n} + \nu_{m} \left( T \right) - \log \left( {1 + \frac{\xi }{2}} \right)\left( {1 - \frac{2\left| z \right|}{h}} \right)\left( {\nu_{c} \left( T \right) + \nu_{m} \left( T \right)} \right) \hfill \\ \alpha \left( {z,T} \right) = \left( {\alpha_{c} \left( T \right) - \alpha_{m} \left( T \right)} \right)\left( {\frac{1}{2} + \frac{z}{h}} \right)^{n} + \alpha_{m} \left( T \right) - \log \left( {1 + \frac{\xi }{2}} \right)\left( {1 - \frac{2\left| z \right|}{h}} \right)\left( {\alpha_{c} \left( T \right) + \alpha_{m} \left( T \right)} \right) \hfill \\ G(z,T) = \frac{{E\left( {z,T} \right)}}{{2\left( {1 + \nu \left( {z,T} \right)} \right)}} \hfill \\ \end{gathered} \right. \hfill \\ \end{gathered}.$$

where the subscripts \(m\) and \(c\) represent the properties of metal and ceramic constituents, respectively. Temperature dependency of the material properties is assumed to follow the Touloukian model as [32]:

$$p\left( T \right) = p_{0} \left( {p_{ - 1} T^{ - 1} + 1 + p_{1} T^{1} + p_{2} T^{2} + p_{3} T^{3} } \right)$$
(2)

in which T is the temperature measured in Kelvin and pi’s (i =  − 1, 0, 1, 2, 3) are constants and unique to each constituent.

Fig. 1
figure 1

Porosity dispersion through the thickness of FG porous curved beam

Full size image

As shown in the above equations, variation of the material properties through the z-direction depends on the value of \(n\) defined as the power-law index. Also, \(\xi\) is introduced as the porosity volume fraction (porosity parameter), and \(\xi = 0\) means that we have a perfect, nonporous, FGM curved beam. Figure 2 illustrates the variation of thermal expansion coefficient and Young’s modulus through the thickness direction of the curved beams, where \(\xi = 0.5,\,n = 2\). Accordingly, Young’s modulus and thermal expansion coefficient of the uneven and logarithmic uneven patterns coincide with the perfect FGM at the bottom and top surfaces of the curved beam, which are pure metal and ceramic, respectively. Generally, these two mechanical parameters related to all three imperfect models are lower than that of the perfect FGM because of the porosity existence.

Fig. 2
figure 2

Material properties variation through the thickness direction of FG porous curved beam: a thermal expansion coefficient b Young’s modulus

Full size image

2.1 Types of thermal loading

Three types of temperature fields are assumed to highlight the influence of temperature rise on the stability responses of the FG porous curved beam, two of which vary through the z-direction of the curved beam.

2.2 Uniform temperature rise

This type of temperature change is defined as a constant factor independent of thickness direction and is written in the following form [17]:

$$\Delta T = T - T_{i}$$
(3)

in which \(T\) and \(T_{i}\) denote the current and initial reference temperatures of the structure, respectively.

2.3 Linear and nonlinear temperature rise

The most pivotal step in developing a linear and nonlinear temperature rise equation through the thickness direction of the FG porous curved beam is to define appropriate thermal boundary conditions at both transverse sides of the curved beam by which the heat conduction equation can be solved in this direction. For this purpose, in the current research, \(T_{m}\) and \(T_{c}\) are assumed as the temperatures of the metal-rich and ceramic-rich surfaces of the curved beam, respectively. If the thickness of the related structure is thin enough, the temperature distribution is approximated as a linear function of thickness coordinate z as [17]:

$$T\left( z \right) = T_{m} + r\Delta T_{cm}.$$
(4)

Besides, a nonlinear function for the nonlinear temperature rise depending on the thickness of the FG porous curved beam can be taken as follows [17]:

$$T\left( z \right) = T_{m} + r\Delta T_{cm} \left( {{\raise0.7ex\hbox{${\sum\limits_{i = 0}^{\infty } {\left( {\frac{{r^{ni} k_{mc}^{i} }}{ni + 1}} \right)} }$} \!\mathord{\left/ {\vphantom {{\sum\limits_{i = 0}^{\infty } {\left( {\frac{{r^{ni} k_{mc}^{i} }}{ni + 1}} \right)} } {\sum\limits_{i = 0}^{\infty } {\left( {\frac{{k_{mc}^{i} }}{ni + 1}} \right)} }}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${\sum\limits_{i = 0}^{\infty } {\left( {\frac{{k_{mc}^{i} }}{ni + 1}} \right)} }$}}} \right)$$
(5)

where \(r = \left( {\frac{1}{2} + \frac{z}{h}} \right)\), \(\Delta T_{cm} = T_{c} - T_{m}\), \(k_{mc} = \frac{{k_{m} - k_{c} }}{{k_{m} }}\), \(k_{c}\) and \(k_{m}\) are the thermal conductivity of ceramic and metal, respectively.

3 Governing equations

3.1 Kinematic assumptions

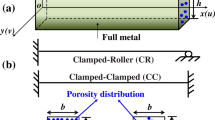
Consider an FG porous curved beam of rectangular cross section \(b \times h\) and constant radius of curvature,\(R\), exposed to various types of thermal loadings, namely uniform, linear, and nonlinear temperature rise. The subtending angle of the curved beam is set equal to \(2\theta\); hence the length of curved beam is \(2R\theta\). Schematic of the curved beam and the coordinates system is depicted in Fig. 3, in which \(\theta ,\,y\) and \(z\) denote the coordinates of circumferential, through-the-width, and through-the-thickness directions, respectively. In this research, deformations through the width are ignored due to assumption that the curved beam only deforms in the \(\theta - z\) plane [7].

Fig. 3
figure 3

Schematic of FG porous curved beam subjected to various types of thermal loadings

Full size image

To capture the effect of shear deformations in the \(z\) direction, the first-order shear deformation theory is used to develop governing equations of the FG porous curved beam. Regarding the FSDT, displacement components on a generic point of the FG porous curved beam can be expressed as [33]:

$$\begin{gathered} u\left( {\theta ,z} \right) = u_{0} \left( \theta \right) + z\varphi \left( \theta \right) \hfill \\ w\left( {\theta ,z} \right) = w_{0} \left( \theta \right) \hfill \\ \end{gathered}.$$
(6)

In the above equations, \(u_{0}\) and \(w_{0}\) stand for displacements at the mid-surface of the curved beam through the circumferential and the thickness directions, respectively, \(\varphi\) represents the cross section rotation of the curved beam in the plane of its curvature.

3.2 Nonlinear strain–displacement equations

According to the Green strains and the FSDT, the strain–displacement relations for the curved beam are given as follows [32]:

$$\begin{gathered} \varepsilon_{\theta \theta } = \frac{1}{R}\frac{\partial u}{{\partial \theta }} - \frac{w}{R} + \frac{1}{{2R^{2} }}\left[ {\left( {\frac{\partial u}{{\partial \theta }}} \right)^{2} + \left( {\frac{\partial w}{{\partial \theta }}} \right)^{2} } \right] \hfill \\ \gamma_{\theta z} = \frac{\partial u}{{\partial z}} + \frac{1}{R}\frac{\partial w}{{\partial \theta }} \hfill \\ \end{gathered}$$
(7)

where \(\varepsilon {}_{\theta \theta }\) represents the circumferential normal strain and \(\gamma_{\theta z}\) denotes the shear strain component. The first assumption which is usually considered by the researches to do any analysis on the beam and curved beam structures is that these types of structures can be treated as one-dimensional problems which means that the displacement fields are functions of just one coordinate\(\theta\), because of the small ratio of the width/thickness compared to the length/thickness. Moreover, the strains associated with the displacement fields can be computed using the nonlinear strain–displacements based on the Green–Lagrange theory. However, by implying the small strain assumption, a large number of nonlinear terms of the displacement are negligible. It is important to note that in postbuckling analysis of structures, because of the nonlinear out-of-plane displacement of the structure, the rotation of transverse normal \(\left( {{\raise0.7ex\hbox{${\partial W}$} \!\mathord{\left/ {\vphantom {{\partial W} {\partial \theta }}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${\partial \theta }$}}} \right)\) is moderate and cannot be negligible. Accordingly, in this paper, due to the inherent geometric nonlinearity of the curved beam and nonlinear radial displacement which may happen by rising the temperature, both nonlinear strain–displacement terms of Green’s theory \(\left( {{\raise0.7ex\hbox{${\partial W}$} \!\mathord{\left/ {\vphantom {{\partial W} {\partial \theta }}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${\partial \theta }$}}} \right)^{2} ,\left( {{\raise0.7ex\hbox{${\partial u}$} \!\mathord{\left/ {\vphantom {{\partial u} {\partial \theta }}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${\partial \theta }$}}} \right)^{2}\) are considered to predict more accurately the thermal postbuckling behavior of the FG porous curved beams [33].

3.3 Constitutive equations

In a plane stress state, the stress–strain relation of the FG porous curved beam in thermal environments can be expressed as follows [32]:

$$\begin{gathered} \sigma_{\theta \theta } = E\left( {z,T} \right)\left( {\varepsilon_{\theta \theta } \left( {z,T} \right) - \alpha_{\theta \theta } \left( {z,T} \right)\left( {T - T_{0} } \right)} \right) \hfill \\ \tau_{\theta z} = G\left( {z,T} \right)\gamma_{\theta z} \hfill \\ \end{gathered}$$
(8)

in which \(T\) and \(T_{0}\) are the elevated temperature and the reference temperature, respectively. Equations (6) and (7) are combined to give the circumferential normal stress in terms of the middle surface displacements as follows:

$$\begin{gathered} \sigma_{\theta \theta } = E\left( {z,T} \right)\left( {\left( {\frac{1}{R}\frac{\partial u}{{\partial \theta }} - \frac{w}{R} + \frac{1}{{2R^{2} }}\left[ {\left( {\frac{\partial u}{{\partial \theta }}} \right)^{2} + \left( {\frac{\partial w}{{\partial \theta }}} \right)^{2} } \right]} \right) - \alpha_{\theta \theta } \left( {T - T_{0} } \right)} \right) \hfill \\ \tau_{\theta z} = G\left( {z,T} \right)\left( {\frac{\partial u}{{\partial z}} + \frac{1}{R}\frac{\partial w}{{\partial \theta }}} \right) \hfill \\ \end{gathered}.$$
(9)

3.4 Stress resultants

According to the FSDT, the stress resultants related to the stress components are obtained through the following equations [32]:

$$\left( {N_{\theta \theta } ,\,M_{\theta \theta ,} \,Q_{\theta z} } \right) = \int\limits_{{{\raise0.7ex\hbox{${ - h}$} \!\mathord{\left/ {\vphantom {{ - h} 2}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$2$}}}}^{{{\raise0.7ex\hbox{$h$} \!\mathord{\left/ {\vphantom {h 2}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$2$}}}} {\left( {\sigma_{\theta \theta } ,\,z\sigma {}_{\theta \theta },\,\gamma_{\theta z} } \right)} \,{\text{d}}z\, .$$
(10)

Stress resultants can be extracted in terms of mid-plane displacements by substituting Eq. (9) into Eq. (10) as follows [32]:

$$\left\{ \begin{gathered} N_{{\theta \theta }} \hfill \\ M_{{\theta \theta }} \hfill \\ Q_{{z\theta }} \hfill \\ \end{gathered} \right\} = \left[ {\begin{array}{*{20}c} {A_{{11}} } & {B_{{11}} } & 0 \\ {B_{{11}} } & {D_{{11}} } & 0 \\ 0 & 0 & {A_{{44}} } \\ \end{array} } \right]\left\{ \begin{gathered} \frac{1}{R}\left( {\frac{{\partial u_{0} }}{{\partial \theta }} - w_{0} } \right) + \frac{1}{{2R^{2} }}\left( {\frac{{\partial w_{0} }}{{\partial \theta }}} \right)^{2} \hfill \\ \frac{1}{R}\left( {\frac{{\partial \varphi }}{{\partial \theta }}} \right) \hfill \\ \,\frac{1}{R}\left( {\frac{{\partial W}}{{\partial \theta }}} \right) + \varphi \hfill \\ \end{gathered} \right\} - \left\{ \begin{gathered} N^{T} \hfill \\ M^{T} \hfill \\ \;0 \hfill \\ \end{gathered} \right\}$$
(11)

In the above equations, the constant coefficients \(A_{11}\),\(B_{11}\), and \(D_{11}\) are stretching, bending–stretching, and bending stiffness, respectively, given by:

$$\left( {A_{11} ,B_{11} ,D_{11} } \right) = \int\limits_{{{\raise0.7ex\hbox{${ - h}$} \!\mathord{\left/ {\vphantom {{ - h} 2}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$2$}}}}^{{{\raise0.7ex\hbox{$h$} \!\mathord{\left/ {\vphantom {h 2}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$2$}}}} {E\left( {z,T} \right)\left( {1,z,z^{2} } \right){\text{d}}z}$$
$$A_{44} = \int\limits_{{{\raise0.7ex\hbox{${ - h}$} \!\mathord{\left/ {\vphantom {{ - h} 2}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$2$}}}}^{{{\raise0.7ex\hbox{$h$} \!\mathord{\left/ {\vphantom {h 2}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$2$}}}} {\frac{{E\left( {z,T} \right)}}{{2\left( {1 + \nu \left( {z,T} \right)} \right)}}\,} {\text{d}}z.$$
(12)

Moreover, \(N^{T}\) and \(M^{T}\) are introduced as thermal force and thermal moment resultants, which are calculated using the following relations:

$$\left( {N^{T} ,M^{T} } \right) = \int\limits_{{{\raise0.7ex\hbox{${ - h}$} \!\mathord{\left/ {\vphantom {{ - h} 2}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$2$}}}}^{{{\raise0.7ex\hbox{$h$} \!\mathord{\left/ {\vphantom {h 2}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$2$}}}} {\left( {1,z} \right)E\left( {z,T} \right)\alpha \left( {z,T} \right)\left( {T - T_{0} } \right)\,{\text{d}}z}.$$
(13)

3.5 Stability equations

The equilibrium equations of FG porous curved beams subjected to thermal loading can be developed in accordance with the stationary potential energy. The total potential energy can be written as [33]:

$$\Pi = U$$
(14)

where \(U\) is the total strain energy of FG porous curved beam which can be calculated through the following equation [33]:

$$U = R\int\limits_{ - \phi }^{\phi } {\int\limits_{{{{ - h} \mathord{\left/ {\vphantom {{ - h} 2}} \right. \kern-\nulldelimiterspace} 2}}}^{{{h \mathord{\left/ {\vphantom {h 2}} \right. \kern-\nulldelimiterspace} 2}}} {\left( {\sigma_{\theta \theta } \varepsilon_{\theta \theta } + K_{s} \tau_{\theta z} \gamma_{\theta z} } \right)} } \,{\text{d}}z\,{\text{d}}\theta$$
(15)

in which \(K_{s}\) is the shear correction factor of the FSDT and is set \(K_{s} = \frac{5}{{6 - \nu_{12} }}\).

At this stage, the Ritz method with polynomial admissible functions is adopted to approximate the dependency of the displacement fields to space. As known, expansion through the Ritz method only depends on the essential type of boundary conditions [33]. Evaluating the influence of boundary conditions on the nonlinear in-plane deflection of the FG porous curved beam is one of the targets of the current work. Therefore, various types of boundary conditions such as immovable, simply supported (S) or immovable, clamped (C) are assumed at both ends of the curved beam as case studies. The mathematical expressions for these classes of edge supports can be defined as follows:

$$\begin{gathered} S:\quad u_{0} = w_{0} = M_{\theta \theta } = 0 \hfill \\ C:\quad u_{0} = w_{0} = \phi = 0 \hfill \\ \end{gathered}.$$
(16)

The displacement field components can be separated as:

$$\left\{ \begin{gathered} u_{0} \left( \theta \right) \hfill \\ w_{0} \left( \theta \right) \hfill \\ \varphi \left( \theta \right) \hfill \\ \end{gathered} \right\} = \sum\limits_{m = 1}^{M} {\left[ {\begin{array}{*{20}c} {N_{m}^{u} \left( \theta \right)} & 0 & 0 \\ 0 & {N_{m}^{w} \left( \theta \right)} & 0 \\ 0 & 0 & {N_{m}^{\varphi } \left( \theta \right)} \\ \end{array} } \right]} \left\{ \begin{gathered} U_{m} \hfill \\ W_{m} \hfill \\ \Phi_{m} \hfill \\ \end{gathered} \right\}.$$
(17)

The above admissible functions for three types of edge supports, namely simply supported–simply supported (S–S), clamped–simply supported (C–S), and clamped–clamped are presented in Table 1. These functions are implemented based on the types of boundary conditions defined in Eq. (16). Emphasis is placed on the sufficient terms of series expansion that should be taken into account to assure the convergence of the results.

Table 1 Appropriate Ritz shape functions associated with the boundary conditions
Full size table

After determination of the total potential energy using Eqs. (14–15), by substituting the energy into the following formulation,

$$\frac{\partial \Pi }{{\partial \chi_{j} }} = 0$$
(18)

the nonlinear governing equations can be derived [34]. In Eq. (18), \(\chi\) is the vector of unknowns, \(\chi = \left\{ {\begin{array}{*{20}c} {U_{m}^{\left( j \right)} ,} & {W_{m}^{\left( j \right)} ,} & {\Phi_{m}^{\left( j \right)} } \\ \end{array} } \right\}\). Equation (18) leads to the following matrix representation of the equilibrium equations:

$$\left[ {{\rm K}\left( {\chi ,T} \right)} \right]\left\{ \chi \right\} = \left\{ {F\left( T \right)} \right\}.$$
(19)

Due to initial curvature of the FG porous curved beam, the force vector \(\left\{ {F\left( T \right)} \right\}\) is presented, and the problem is of the nonlinear bending type, whose stable equilibrium paths can be traced by employing the Newton–Raphson iterative procedure.

4 Numerical results

A series of steps is followed for the investigation of the nonlinear in-plane behaviors of an FG porous curved beam subjected to various fields of temperature rise. First, comparative studies are demonstrated for some cases available in the literature, to endorse the accuracy and efficiency of the outlined solution procedures. Afterward, comprehensive parametric studies examine the effect of volume fraction and dispersion of porosity, geometrical parameters, as well as boundary conditions on the in-plane response of the FG porous curved beams.

After validating the results derived by implementing the proposed method, novel numerical results are given for the case of FG porous curved beam in thermal environment made of SUS304/Si3N4FGM. According to this assumption, development of the numerical results is performed. The coefficients for these constituents are given in Table 1.

Table 2 Temperature-dependent coefficients for SUS304 and Si3N4 [32]
Full size table

4.1 Comparative studies

This comparative study is devoted to an FG porous square plate with a length-to-thickness ratio, \({\raise0.7ex\hbox{$L$} \!\mathord{\left/ {\vphantom {L h}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$h$}} = 100\) and simply supported boundary condition at four edges, which is exposed to a linear and nonlinear temperature rise. Figures 4, 5, and 6 indicate the effect of porosity dispersion patterns on the load–deflection behavior of the FG porous micro-plate in comparison with a perfect FGM micro-plate. The results reveal that an increase in the temperature variation results in an increase in non-dimensional central deflection. Another conclusion that can be inferred from these figures is that for all porosity patterns, the central deflection of the porous micro-plate under a linear temperature rise is higher than that of nonlinear temperature rise [17]. A brief review of these figures reveals the accuracy of the outlined method with a maximum discrepancy less than 1%.

Fig. 4
figure 4

Temperature–displacement curves of SSSS FG porous micro-plate with even porosity distribution: a linear temperature rise, b nonlinear temperature rise

Full size image
Fig. 5
figure 5

Temperature–displacement curves of SSSS FG porous micro-plate with linear uneven porosity distribution: a linear temperature rise, b nonlinear temperature rise

Full size image
Fig. 6
figure 6

Temperature–displacement curves of SSSS FG porous micro-plate with logarithmic uneven porosity distribution: a linear temperature rise, b nonlinear temperature rise

Full size image

4.2 Parametric studies

Figures 7, 8, and 9 reveal the influence of porosity dispersions, volume fraction, and temperature distribution on the thermal equilibrium paths of the FG porous curved beam. As can be seen from all these figures, non-dimensional radial deflection at the crown of the FG porous curved beam increases due to the increase in temperature variation. Moreover, these figures imply that without concerning the porosity dispersion patterns, non-dimensional radial deflection of the curved beam exposed to uniform temperature rise is higher than that of linear and nonlinear ones. Furthermore, it is found that, in contrast to the temperature variation, increases in porosity volume fraction decrease the non-dimensional radial deflection of the FG porous curved beam.

Fig. 7
figure 7

The effect of porosity volume fraction and temperature rise fields on the equilibrium paths of FG porous curved beam with even porosity dispersion: a uniform temperature rise, b linear temperature rise, c nonlinear temperature rise

Full size image
Fig. 8
figure 8

The effect of porosity volume fraction and temperature rise fields on the equilibrium paths of FG porous curved beam with linear uneven porosity dispersion: a uniform temperature rise, b linear temperature rise, c nonlinear temperature rise

Full size image
Fig. 9
figure 9

The effect of porosity volume fraction and temperature rise fields on the equilibrium paths of FG porous curved beam with logarithmic uneven porosity dispersion: a uniform temperature rise, b linear temperature rise, c nonlinear temperature rise

Full size image

Figure 10 aims to highlight more effectively the influence of the porosity dispersion patterns on the nonlinear thermoelastic response of the FG porous curved beam. As this figure displays, for various types of temperature rise fields, the non-dimensional radial deflection of the curved beam with length-to-thickness ratio \({\raise0.7ex\hbox{${2R\theta }$} \!\mathord{\left/ {\vphantom {{2R\theta } h}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$h$}} = 40\), subtending angle \(2\theta = 20\), and even porosity dispersion is lower than that of uneven and logarithmic uneven patterns. It means that even porosity distribution can offer higher thermal resistance to FG porous curved beams. The reason of such observation can be explored through the thermal moments, which are generated along the curved beam span.

Fig. 10
figure 10

The effect of porosity dispersion and temperature rise fields on the equilibrium paths of FG porous curved beam: a uniform temperature rise, b linear temperature rise, c nonlinear temperature rise

Full size image

At this section, it should be pointed out the main target of Figs. 7, 8, 9, and 10 is to investigate the thermal postbuckling behavior of the FG porous curved beams subjected to nonlinear temperature rise. In the buckling analysis, the load–deflection path may consist of two important parts which are related to the prebuckling and postbuckling sections named primary equilibrium path and secondary equilibrium path. In flat structures such as plates, the load–deflection curve has both linear primary equilibrium paths which continue up to the bifurcation point and after that point the nonlinear secondary equilibrium path initiates, but in some structures which have an initially geometrical nonlinearity imperfection such as curved beams the load–deflection path does not experience any bifurcation points and we have only one equilibrium path [35].

The total thermal bending moment of the curved beams through the span is illustrated in Fig. 11 for the case of the linear temperature rise. It can be concluded from Fig. 11 that porosity dispersion has a strong impact on the total bending moment of the curved beam, and among all the cases, the even porosity dispersion has the minimum thermal bending moment. Moreover, it is worth noting that due to the non-symmetrical distribution of material properties with respect to the mid-surface of the curved beam, an extra thermal bending moment is generated along the span of the curved beam because of stretching–bending coupling.

Fig. 11
figure 11

The influence of the porosity dispersion on the total bending moment through the curved beam span

Full size image

Figure 12 shows a more detailed view of the effect of porosity dispersion and subtending angle on the maximum central stress at the top and bottom surfaces of the FG porous curved beam. It can be inferred from this figure that the stress level of both top and bottom surfaces of the FG porous curved beam with logarithmic uneven dispersion is significantly more than that with even porosity patterns. For example, for the case of the logarithmic uneven porosity dispersion, if the subtending angle is set \(60^{ \circ }\), the bottom central stress of the curved beam is approximately five times more than that with even porosity patterns.

Fig. 12
figure 12

The effect of the porosity dispersion and subtending angle on the maximum stress of the curved beam: a top surface, b bottom surface

Full size image

To address the effect of the subtending angle on the maximum radial displacement of the curved beam, the variation of the maximum lateral deflection versus the subtending angle is demonstrated in Fig. 13, for three types of porosity dispersions and perfect FGM. It can be observed from this figure that the influence of the porosity dispersion on the radial displacement of the curved beam is insignificant when the subtending angle \(2\theta\) is more than \(70^{ \circ }\). Besides, it is found that the subtending angle has a remarkable influence on the radial displacement of the curved beam. An increase in the subtending angle of the curved beam leads to a dramatic reduction in the maximum lateral displacement.

Fig. 13
figure 13

The influence of the porosity dispersion and the subtending angle on the maximum radial displacement of the curved beam

Full size image

For instance, for the case of logarithmic uneven porosity distribution, increasing the subtending angle from \(0^{ \circ }\) to \(70^{0}\) leads to a decrease of about 89% in the maximum lateral deflection of the curved beam. It should be noted that to convert the curved beam into straight beam, the subtending angle should be set zero. Of special interest of this figure is that when subtending angle is equal to zero, for all the imperfect cases (logarithmic uneven, linear uneven, and even) and the perfect FGM beam, the structure experiences a temperature–deformation path rather than primary–secondary equilibrium path in the framework of buckling and postbuckling responses. This reflects the fact that there is an extra thermal moment prior to the buckling stage due to the non-symmetric material stiffness distribution across the thickness of the FGM structures as shown in Fig. 14.

Fig. 14
figure 14

The influence of the porosity dispersion and subtending angle on the total bending moment at the crown of the FG porous curved beam

Full size image

Figure 15 illustrates the effect of porosity dispersion on in-plane behavior of the FG porous curved beam, variation of the axial displacement along the span of the curved beam at top, bottom, and middle surfaces. The numerical data show that the axial displacement vanishes at the mid-span of the FG porous curved beam for all types of porosity dispersions because of the symmetric loading condition and boundary conditions. Furthermore, it is revealed that dispersion of porosities has a remarkable influence on the axial displacement of the curved beam at the top, bottom, and middle surfaces. Another point which can be seen in this figure is that the in-plane response of the FG porous curved beam with logarithmic uneven dispersion is similar to the perfect FGM curved beam, while the results related to the even porosity pattern has a considerable difference than the perfect FGM curved beam.

Fig. 15
figure 15

The influence of the porosity dispersion on the in-plane displacement through the curved beam span: a top surface, b middle surface, c bottom surface

Full size image

Figure 16 demonstrates the effect of boundary conditions on the thermal equilibrium paths of the FG porous curved beam with logarithmic uneven and even porosity dispersions considered as the worst and the best cases in terms of thermal resistance, respectively. It is found that implementing different boundary conditions does not noticeably change the thermal stability of the curved beam with various porosity patterns. Besides, this figure implies that the non-dimensional central deflection of the FG porous curved beam with clamped–simply supported boundary condition is slightly higher than that of other types of conditions. This can also be concluded from Fig. 17, which indicates the out-of-plane displacement variation of the FG porous curved beam along its span. Figure 17 also shows that in contrast to the symmetric boundary conditions, the maximum deflection of the curved beam with asymmetric boundary condition (C-S) occurs at an off-center point.

Fig. 16
figure 16

The influence of the porosity dispersion and boundary condition on the equilibrium paths of the FG porous curved beam subjected to linear temperature rise

Full size image
Fig. 17
figure 17

Out-of-plane displacement of the FG porous curved beam under various boundary conditions: a even porosity dispersion; b logarithmic uneven porosity dispersion

Full size image

5 Conclusion

This contribution discussed the in-plane stability of the FG porous curved beam under various types of thermal loading. The stability equations were established in accordance with the Green–Lagrange-type, nonlinear kinematics within the framework of the first-order, shear deformation theory. The nonlinear governing equations were solved using the Rayleigh–Ritz method along with Newton–Raphson method. A detailed parametric study was conducted to shed light into the effect of volume fraction and dispersion of porosities, geometrical parameters, and boundary conditions on the in-plane thermoelastic characteristics of the FG porous curved beam. The numerical results elaborate on the fact that designers need to be careful about the following points:

  • Among different types of porosity dispersion patterns, the thermal stability response of the even porosity dispersion is better than that of other distributions because of the higher thermal resistance of the even porosity dispersion.

  • The radial and axial displacements of the FG porous curved beam strongly depend on the dispersion of porosities through the thickness.

  • The influence of the porosity dispersion on the radial displacement of the curved beam is insignificant for the subtending angle higher than \(120^{ \circ }\). Besides, the maximum radial displacement decreases substantially with increasing the subtending angle of the curved beams.

  • The stress level and porosity dispersion can be completely altered through the concept of functionally graded materials, and these parameters can be efficiently controlled by selecting an appropriate porosity dispersion.

  • Along with the porosity dispersion, porosity volume fraction can be taken into consideration as another significant factor in thermal stability responses of the FG porous curved beams.