1 Introduction

As the composite materials play important role in the industrial applications [11], the strong adhesion between the laminated layers is essential and must remain reliable even at high strains and high stresses [15]. Presence and propagation of a delamination in lightweight composite materials [35, 38] can significantly decrease the load bearing capability of the structure [7, 26, 28], modify the dynamic properties [6, 20, 27, 39, 40], and furthermore, they can easily lead to sudden and catastrophic failure of the brittle mechanical system. Thus, the description [22, 36] and the avoidance [10, 59] of an interlaminar failure, which may take place because of low-velocity impact [5, 24], blast loading [32, 37], manufacturing defects [16,17,18] and free edge effects [13], are inevitable from engineering point of view.

Fig. 1
figure 1

Beam elements with different delamination position over the beam thickness

Full size image

The application of the linear elastic fracture mechanics is one possibility to characterise the interlaminar fracture resistance of conventional high performance composites with inherent brittleness [8, 9]. The critical value of the energy release rate \(G_c\), which can be considered as a material property, is suitable to characterise the strength of an interface layer between two elastic plies [19]. Like any other material parameters, mechanical tests must be carried out to be determined. In the case of fracture mechanical investigation, as linear elastic fracture mechanics works only if the location, size and shape of the crack are known, the experiments must be carried out on different type of pre-cracked specimens including mode-I [23], mode-II [8], mixed-mode I/II [58], mode-III [14, 25], mixed-mode I/III [1], mixed-mode II/III [43, 50] and mixed-mode I/II/III [57] fracture conditions. Finally, these experiments must be evaluated based on very simple mechanical structures where the delamination zone is known a priori, such as delaminated beam and plate structures.

To increase the accuracy of the evaluation techniques and to capture more precisely the complex fracture mechanical behaviour of these mechanical systems, the researchers have been inspired to introduce novel, higher-order beam and plate theories [33, 53, 54]. The first-order shear deformable beam theory (FSDT) assumes independent rotation around the bending axes [46]. As a next step, the second-order shear deformable theory (SSDT) describes the in-plane displacement as a quadratic function in terms of the through-thickness coordinate. The third-order shear deformable theory (TSDT) captures the longitudinal displacement in the form of cubic function [12]. And finally but not least, in order to satisfy dynamic boundary conditions at the top and bottom surfaces of the beam, Reddy’s third-order shear deformable theory is also developed [41, 47].

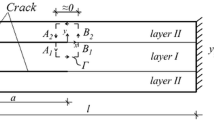
In the following, to analyse a delaminated composite beam under mixed-mode I/II fracture conditions, the basic idea of higher-order beam theories is utilised with the semi-layerwise approach [51]. The concept of the proposed description can be seen in Fig. 1. where beam elements with an artificial delamination are depicted. To perform fracture mechanical investigation, the J-integral with zero-area path is applied [42, 50]. Moreover, a partitioning method is proposed to determine the mode-I and mode-II in-plane fracture modes without any semi-analytical considerations [29]. Finally, the obtained results of the mode partitioning are compared to previously published evaluation methods in the literature [4, 21, 34, 56].

Applications already exist in the literature which uses the J-integral to evaluate delaminated composite beams [3, 30, 44] under pure mode-I or pure mode-II fracture conditions. The effect of reinforcement direction and delamination length on the energy release rate have already been investigated in numerous studies, but J-integral- based mode mixity evaluation, which undeniably requires complicated mechanical models, has not been extensively studied.

It is important to note that the methods described herein are only suitable for describing brittle composite materials. If the brittle carbon or glass fibres are protected by more damage tolerant resin system, the application of the linear elastic fracture mechanics is no longer appropriate. The nonlinear fracture process zone and the growth of multiple cracks at small scale should also be considered [55].

Fig. 2
figure 2

Cross section and the assumed deformation of the undelaminated portion in the \(X{-}Z\) plane (a) and distributions of the transverse shear strain by different theories (b) using 2ESLs

Full size image

2 Mechanical model: the method of two equivalent single layers (ESLs)

A delaminated beam with an arbitrary stacking sequence including orthotropic or transversely isotropic plies is depicted in Fig. 2. As it is illustrated by this figure, different mathematical models must be applied to capture the displacement field of the cracked and uncracked portion separately [50]. Firstly, to describe the undelaminated portion, the membrane displacement field must remain continuous along the thickness coordinate. While in the case of the delaminated portion, the presence of the delamination splits the functions into separated displacement fields resulting in two individual sub-laminates [48]. To handle this phenomenon properly, each and every sub-laminate is modelled as an equivalent single layer (ESL). This method is the so-called semi-layerwise technique, which has already been introduced and used in numerous studies to describe delaminated composite plates under mixed-mode II/III fracture conditions [45]. Furthermore, the displacement field can be expressed by using the above-mentioned higher-order polynomials to increase the accuracy in terms of shear stress distribution:

$$\begin{aligned} \begin{aligned} u_{(i)}(x,z^{(i)})&=u_0(x)+u_{0i}(x)+\theta _{i}(x)z^{(i)}+\phi _{i}(x)[z^{(i)}]^2+\lambda _{i}(x)[z^{(i)}]^3, \\ w_{(i)}(x)&=w_{(i)}(x), \end{aligned} \end{aligned}$$
(1)

where i denotes the index of actual ESL, \(z^{(i)}\) is the local thickness coordinate of the ith ESL and always coincides with the local midplane, \(u_0\) is the global, \(u_{0i}\) is the local membrane displacement, \(\theta \) denotes the rotation of the cross section about the Y axes, \(\phi \) means the second-order, and \(\lambda \) expresses the third-order polynomial terms. Moreover, \(w_{(i)}\) represents the separate transverse deflection functions. The displacement field of FSDT and SSDT can be obtained by substituting \(\phi =0\) and \(\lambda =0\) into the Eq. (1), respectively. In the case of the undelaminated part, the kinematic continuity between ESLs can be imposed by the system of exact kinematic conditions [50].

Based on the above assumed displacement fields, the nonzero terms of the strain field become

$$\begin{aligned} \varepsilon _{x(i)}=\frac{\partial u_{(i)}}{\partial x}, \quad \gamma _{xz(i)}=\frac{\partial u_{(i)}}{\partial z^{(i)}}+\frac{\partial w_{(i)}}{\partial x}, \end{aligned}$$
(2)

where \(\varepsilon _{x(i)}\) is the normal strain of the ith ESL in the X-direction, and \(\gamma _{xz(i)}\) is the shear strain of the ith layer in the \(X{-}Z\) plane. The in-plane strains can be decomposed into constant, linear and higher-order terms with respect to the through-thickness coordinate:

$$\begin{aligned} \varepsilon _{x(i)}=\varepsilon _{x(i)}^{(0)}+z^{(i)}\cdot \varepsilon _{x(i)}^{(1)}+[z^{(i)}]^2\cdot \varepsilon _{x(i)}^{(2)}+[z^{(i)}]^3\cdot \varepsilon _{z(i)}^{(3)}, \end{aligned}$$
(3)

and:

$$\begin{aligned} \gamma _{xz(i)}=\gamma _{xz(i)}^{(0)}+z^{(i)}\cdot \gamma _{xz(i)}^{(1)}+[z^{(i)}]^2\cdot \gamma _{xz(i)}^{(2)}. \end{aligned}$$
(4)

By applying the constitutive equation of orthotropic materials the stress resultants can be introduced for each ESL:

$$\begin{aligned} \left( \begin{array}{c} N_x\\ M_x\\ L_x\\ P_x\\ \end{array} \right) _{(i)}=\int \limits _{0}^{b} \int \limits _{-t_i/2}^{t_i/2} \sigma _{x} \left( \begin{array}{c} 1\\ z\\ z^2\\ z^3\\ \end{array}\right) _{(i)} \mathrm{d}z^{(i)}\mathrm{d}y, \end{aligned}$$
(5)

and:

$$\begin{aligned} \left( \begin{array}{c} Q_{x}\\ R_{x}\\ S_{x}\\ \end{array} \right) _{(i)}=\int \limits _{0}^{b} \int \limits _{-t_i/2}^{t_i/2} \tau _{xz} \left( \begin{array}{c} 1\\ z\\ z^2\\ \end{array}\right) _{(i)} \mathrm{d}z^{(i)}\mathrm{d}y, \end{aligned}$$
(6)

where \(N_{x(i)}\) defines the normal force, \(M_{x(i)}\) denotes the bending moment, \(Q_{x(i)}\) is the transverse shear force, and \(L_{x(i)}\), \(P_{x(i)}\), \(R_{x(i)}\), \(S_{x(i)}\) are the higher-order stress resultants [41, 50]. By using the through-thickness coordinate dependence and the presented constitutive law, the relationship between the strain field and the stress resultants can be formulated as:

$$\begin{aligned} \left( \begin{array}{c} N_x\\ M_x\\ L_x\\ P_x\\ \end{array} \right) _{(i)}= \begin{bmatrix} A_{11}&\quad B_{11}&\quad D_{11}&\quad E_{11}\\ B_{11}&\quad D_{11}&\quad E_{11}&\quad F_{11}\\ D_{11}&\quad E_{11}&\quad F_{11}&\quad G_{11}\\ E_{11}&\quad F_{11}&\quad G_{11}&\quad H_{11}\\ \end{bmatrix} _{(i)} \left( \begin{array}{c} \varepsilon ^{(0)}\\ \varepsilon ^{(1)}\\ \varepsilon ^{(2)}\\ \varepsilon ^{(3)}\\ \end{array}\right) _{(i)}, \end{aligned}$$
(7)

and

$$\begin{aligned} \left( \begin{array}{c} Q_{x}\\ R_{x}\\ S_{x}\\ \end{array} \right) _{(i)}= \begin{bmatrix} A_{55}&\quad B_{55}&\quad D_{55} \\ B_{55}&\quad D_{55}&\quad E_{55} \\ D_{55}&\quad E_{55}&\quad F_{55} \\ \end{bmatrix} _{(i)} \left( \begin{array}{c} \gamma _{xz}^{(0)}\\ \gamma _{xz}^{(1)}\\ \gamma _{xz}^{(2)}\\ \end{array}\right) _{(i)}, \end{aligned}$$
(8)

where \(A_{pp(i)}\) denotes the extensional, \(B_{pp(i)}\) represents the coupling, \(D_{pp(i)}\) is the bending, \(E_{pp(i)}\), \(F_{pp(i)}\), \(G_{pp(i)}\) and \(H_{pp(i)}\) are the higher-order stiffnesses. These terms can be calculated by [41, 49]:

$$\begin{aligned} \begin{aligned}&(A_{pp},B_{pp},D_{pp},E_{pp},F_{pp},G_{pp},H_{pp})_{(i)} \\&\quad =\sum _{m=1}^{N_{l(i)}} \int \limits _{0}^{b} \int \limits _{z_m^{(i)}}^{z_{m+1}^{(i)}} \overline{C}_{pp(i)}^{(m)}(1,z,z^2,z^3,z^4,z^5,z^6)^{(i)}\mathrm{d}z^{(i)}\mathrm{d}y, \,\, p=1 \,\, \text {or} \,\,5, \end{aligned} \end{aligned}$$
(9)

where \(N_{l(i)}\) is the number of orthotropic layers within the actual ith ESL, b defines the width of the beam, \(z^{i}_{m}\) and \(z^{i}_{m+1}\) are the local bottom and top coordinates of the mth layer in the ith ESL [49]. Furthermore, \(\overline{\varvec{C}}_{(i)}^{(m)}\) is the stiffness matrix of the mth layer within the ith ESL expressed as:

$$\begin{aligned} \left( \begin{array}{c} \sigma _x\\ \tau _{xz}\\ \end{array} \right) _{(i)} =\begin{bmatrix} \overline{C}_{11}&\quad 0 \\ 0&\quad \overline{C}_{55} \\ \end{bmatrix} _{(i)}^{(m)} \left( \begin{array}{c} \varepsilon _x\\ \gamma _{xz}\\ \end{array}\right) _{(i)} =\begin{bmatrix} E_{11}/(1-\nu _{21}\nu _{12})&\quad 0 \\ 0&\quad G_{13} \\ \end{bmatrix} _{(i)}^{(m)} \left( \begin{array}{c} \varepsilon _x\\ \gamma _{xz}\\ \end{array}\right) _{(i)}. \end{aligned}$$
(10)

2.1 Description of the undelaminated portion

In order to impose the continuity between two ESLs, the following condition can be formulated [50]:

$$\begin{aligned} (u_{(1)},w_{(1)}) \Big |_{z^{(1)}=t_1/2}=(u_{(2)},w_{(2)}) \Big |_{z^{(2)}=-t_2/2}, \end{aligned}$$
(11)

which imposes the displacement continuity and the identity of the transverse deflections. The second condition defines the position of the global reference plane:

$$\begin{aligned} u_{(1)}\Big |_{z^{(1)}=t_2/2}-u_0(x)=0, \end{aligned}$$
(12)

with respect to ESL1. As a first step, to develop semi-layerwise model only for FSDT solution, these equations are already enough. However, it is reasonable to increase the accuracy of the model further by using SSDT and TSDT. Thus, the shear strain continuity at the interface plane, referring to Fig. 2, can be also imposed:

$$\begin{aligned} \gamma _{xz(1)}\Big |_{z^{(1)}=t_1/2}=\gamma _{xz(2)}\Big |_{z^{(2)}=-t_{2}/2}\,. \end{aligned}$$
(13)

Furthermore, in accordance with the basic concept of Reddy-TSDT theory, even the traction-free boundary condition can be imposed on the bottom and top surfaces of the beam:

$$\begin{aligned} \gamma _{xz(1)}\Big |_{z^{(1)}=-t_1/2}=\gamma _{xz(2)}\Big |_{z^{(2)}=t_{2}/2}=0 \,. \end{aligned}$$
(14)

Finally, by taking into account the previously discussed conditions, in each and every case the in-pane displacement functions can be expressed in the following invariant form:

$$\begin{aligned} \begin{aligned} u_{(i)}&=u_{0}+\Big ( K_{ij}^{(0)} + K_{ij}^{(1)}z^{(i)} + K_{ij}^{(2)}[z^{(i)}]^2 + K_{ij}^{(3)}[z^{(i)}]^3 \Big )\psi _{j}, \\ w_{(i)}&=w(x), \end{aligned} \end{aligned}$$
(15)

where the \(K_{ij}\) matrices depend on the actual ESL thicknesses and the order of the applied theory, i refers to the ESL number, the summation index j defines the component in \(\psi _{j}\) primary parameter vector, and w(x) expresses the transverse deflection of the beam [49].

2.1.1 Reddy’s third-order beam theory

Using the above-mentioned exact kinematic conditions by Eqs. (11)–(14), 5 unknown displacement parameters can be eliminated from the original 10 parameters. The secondary parameters are: \(u_{0i}\), \(\phi _{i}\) for \(i=1..2\) and \(\theta _{2}\). The unknown terms and the vector of primary parameters become:

$$\begin{aligned} u_{0}, \quad w, \quad \varvec{\psi _{p}}=\Big ( \theta _1 \,\, \lambda _1 \,\, \lambda _2 \,\, \frac{\partial w}{\partial x} \Big )^\mathrm{{T}}. \end{aligned}$$
(16)

The nonzero elements of the \(K_{ij}^{(0)}\),\(K_{ij}^{(1)}\),\(K_{ij}^{(2)}\) and \(K_{ij}^{(3)}\) matrices in Eq. (15) can be found in Appendix  A.1.1. It is important to highlight, by the application of the Reddy’s third-order beam theory, the first derivate of the deflection becomes also a primary parameter. Later on we will see that it results much more complicated differential equation with respect to the transverse deflection than the other higher-order theories.

2.1.2 Third-order beam theory

Using again the above discussed exact kinematic conditions [(referring to Eqs. (11)–(13)], apart from the traction-free condition, 3 unknown displacement parameters can be eliminated from the original 10 parameters. The secondary parameters are: \(u_{0i}\) for \(i=1..2\) and \(\lambda _{1}\). The unknown terms and the vector of primary parameters are:

$$\begin{aligned} u_{0}, \quad w, \quad \varvec{\psi _{p}}=\Big ( \theta _1 \,\, \theta _2 \,\, \phi _1 \,\, \phi _2 \,\, \lambda _2 \Big )^\mathrm{{T}}. \end{aligned}$$
(17)

The nonzero elements of the \(K_{ij}^{(0)}\),\(K_{ij}^{(1)}\),\(K_{ij}^{(2)}\) and \(K_{ij}^{(3)}\) matrices in Eq. (15) are defined in Appendix A.2.1.

2.1.3 Second-order beam theory

In the case of SSDT, 3 unknown displacement parameters can be eliminated from the original 8 parameters by using Eqs. (11)–(13). The secondary parameters are: \(u_{0i}\) for \(i=1..2\) and \(\phi _{1}\). The unknown terms and the vector of primary parameters become

$$\begin{aligned} u_{0}, \quad w, \quad \varvec{\psi _{p}}=\Big ( \theta _1 \,\, \theta _2 \,\, \phi _1 \Big )^\mathrm{{T}}. \end{aligned}$$
(18)

Obviously, \(K_{ij}^{(3)}=0\) in this case. The elements of the \(K_{ij}^{(0)}\),\(K_{ij}^{(1)}\) and \(K_{ij}^{(2)}\) matrices in Eq. (15) are specified by Appendix A.3.1.

2.1.4 First-order beam theory

As it was previously discussed, in the case of FSDT theory, only the continuity conditions by Eqs. (11)–(12) continuity can be imposed, meaning that 2 unknown displacement parameters are eliminated from the original 6 parameters. These secondary parameters are: \(u_{0(i)}\) for \(i=1,2\). The vector of primary parameters becomes

$$\begin{aligned} u_{0}, \quad w, \quad \varvec{\psi _{p}}=\Big ( \theta _1 \,\, \theta _2 \Big )^\mathrm{{T}}. \end{aligned}$$
(19)

Using FSDT theory \(K_{ij}^{(3)}=K_{ij}^{(2)}=0\), the elements of the \(K_{ij}^{(0)}\) and \(K_{ij}^{(1)}\) matrices in Eq. (15) can be found in Appendix A.4.1.

2.1.5 Equilibrium equations

The equilibrium equations of the undelaminated beam can be deduced from the virtual work principle [41], by setting the sum of coefficients for the virtual membrane displacement \(\delta u_0\):

$$\begin{aligned} \delta u_0 : \, \sum _{i=1}^{2} \Bigg (\frac{\partial N_{x(i)}}{\partial x}\Bigg )=0,\,\, \,\, {\left\{ \begin{array}{ll} {\text {Reddy }} \\ {\text {TSDT }} \\ {\text {SSDT }} \\ {\text {FSDT }} \end{array}\right. } \end{aligned}$$
(20)

the primary parameters \(\delta \psi _j\):

$$\begin{aligned} \begin{aligned}&\delta \psi _{j} : \, \sum _{i=1}^{2}\left( K_{ij}^{(0)} \frac{\partial N_{x(i)}}{\partial x} + K_{ij}^{(1)} \frac{\partial M_{x(i)}}{\partial x} + K_{ij}^{(2)} \frac{\partial L_{x(i)}}{\partial x} + K_{ij}^{(3)} \frac{\partial P_{x(i)}}{\partial x} - K_{ij}^{(1)} Q_{x(i)} \right. \\&\quad \left. -\,2K_{ij}^{(2)} R_{x(i)} - 3K_{ij}^{(3)} S_{x(i)}\right) =0, \,\, {\left\{ \begin{array}{ll} {\text {Reddy: }} &{}j=1..3, \\ {\text {TSDT }}: &{}j=1..5, \\ {\text {SSDT }}: &{}j=1..3, \\ {\text {FSDT }}: &{}j=1..2, \end{array}\right. } \end{aligned} \end{aligned}$$
(21)

and the deflection \(\delta w\):

$$\begin{aligned}&\delta w : \, \sum _{i=1}^{2} \left( -K_{i4}^{(0)} \frac{\partial ^2 N_{x(i)}}{\partial x^2} -K_{i4}^{(1)} \frac{\partial ^2 M_{x(i)}}{\partial x^2}-K_{i4}^{(2)} \frac{\partial ^2 L_{x(i)}}{\partial x^2}-K_{i4}^{(3)} \frac{\partial ^2 P_{x(i)}}{\partial x^2} \right. \nonumber \\&\quad \left. + \,K_{i4}^{(1)} \frac{\partial Q_{x(i)}}{\partial x} + 2K_{i4}^{(2)} \frac{\partial R_{x(i)}}{\partial x}+ 3K_{i4}^{(3)} \frac{\partial S_{x(i)}}{\partial x} \right) +q=0, \,\, {\left\{ \begin{array}{ll} {\text {Reddy, }} \end{array}\right. } \end{aligned}$$
(22)
$$\begin{aligned}&\delta w : \, \sum _{i=1}^{2} \Bigg ( \frac{\partial Q_{x(i)}}{\partial x} \Bigg ) + q=0 ,\,\, {\left\{ \begin{array}{ll} {\text {TSDT }} \\ {\text {SSDT }} \\ {\text {FSDT }} \end{array}\right. } \end{aligned}$$
(23)

to zero. It is worth giving attention to Eq. (22) where the application of Reddy’s third-order theory results a more complex equilibrium equation [41] compared to the other theories.

2.2 Description of the delaminated portion

As it was previously discussed, the presence of a delamination divides the beam into a top and a bottom sub-laminates. Thus, diverse mathematical functions are applied to the top and bottom parts:

$$\begin{aligned} \begin{aligned} u_{(1)}&=u_{0b}+\Big ( K_{1j}^{(0)} + K_{1j}^{(1)}z^{(1)} + K_{1j}^{(2)}[z^{(1)}]^2 + K_{1j}^{(3)}[z^{(1)}]^3 \Big )\psi _{j}, \\ u_{(2)}&=u_{0t}+\Big ( K_{2j}^{(0)} + K_{2j}^{(1)}z^{(2)} + K_{2j}^{(2)}[z^{(2)}]^2 + K_{2j}^{(3)}[z^{(2)}]^3 \Big )\psi _{j}, \\ w_{(1)}&=w_b(x), \\ w_{(2)}&=w_t(x), \end{aligned} \end{aligned}$$
(24)

where notations are exactly the same as they were in Eq. (15). Although in this context, \(u_{0b}\) and \(u_{0t}\) express the global membrane displacement of the bottom and top sub-laminates, local membrane displacement parameters are not defined, and finally but not least \(w_b\) describes the transverse deflection of the bottom beam and \(w_t\) represents the deflection of the top beam [49].

2.2.1 Reddy’s third-order beam theory

According to Reddy’s third-order beam theory, the top and bottom beams are traction-free at their top and bottom boundaries, as well. But based on our computational experience, if these conditions are strictly imposed, we always get inconsistent and over-constrained shear strain distribution around the delamination tip. In order to avoid this phenomenon in this paper, the traction-free conditions are only imposed at the top boundary of the top sub-laminate and at the bottom boundary of the bottom sub-laminate. Referring to Fig. 2 and Eq. (13), 2 unknown displacement parameters can be eliminated from the original 10 parameters. The secondary parameters are: \(\phi _{i}\) for \(i=1..2\). The unknown terms and the vector of primary parameters become:

(25)

where circles denote the auto-continuity parameters. The role of these parameters will be important when the displacement continuity between the delaminated and undelaminated portions is discussed. The nonzero elements of the matrices \(K_{ij}^{(0)}\), \(K_{ij}^{(1)}\), \(K_{ij}^{(2)}\) and \(K_{ij}^{(3)}\) in Eq. (24) can be found in Appendix A.1.2. Similarly to the case of undelaminated portion, the derivative of the deflections become also primary parameters which results more complex differential equations in terms of the transverse deflections.

2.2.2 Third-order beam theory

Since no other condition can be imposed, the primary parameters become:

(26)

where circle denotes the above-mentioned auto-continuity parameter [50]. The corresponding \(K_{ij}^{(0)}\), \(K_{ij}^{(1)}\), \(K_{ij}^{(2)}\) and \(K_{ij}^{(3)}\) matrices in Eq. (24) can be found in Appendix  A.2.2.

2.2.3 Second-order beam theory

No other condition can be imposed against the displacement field in the case of SSDT, as well. We only have primary parameters:

(27)

and \(K_{ij}^{(3)}=0\). The nonzero elements of the \(K_{ij}^{(0)}\), \(K_{ij}^{(1)}\) and \(K_{ij}^{(2)}\) matrices in Eq. (24) are given in Appendix A.3.2.

2.2.4 First-order beam theory

In the case of FSDT, the primary parameters are:

$$\begin{aligned} u_{0b}, \quad u_{0t}, \quad w_b, \quad w_t, \quad \varvec{\psi _{p}}=\Big ( \theta _1 \,\, \theta _2 \Big )^\mathrm{{T}} \end{aligned}$$
(28)

The elements of the \(K_{ij}^{(0)}\) and \(K_{ij}^{(1)}\) matrices in Eq. (24) can be found in Appendix A.4.2. By using this theory, there is no need to define auto-continuity parameter and \(K_{ij}^{(3)}=K_{ij}^{(2)}=0\).

2.2.5 Equilibrium equations

Using the principle of virtual work, it is possible to determine the equilibrium equations of the delaminated part also, by setting the sum of coefficients for the virtual membrane displacements \(\delta u_{0b}\) and \(\delta u_{0t}\):

$$\begin{aligned} \delta u_{0b} : \, \frac{\partial N_{x(1)}}{\partial x} =0, \delta u_{0t} : \, \frac{\partial N_{x(2)}}{\partial x} =0, \, \, {\left\{ \begin{array}{ll} {\text {Reddy }} \\ {\text {TSDT }} \\ {\text {SSDT }} \\ {\text {FSDT }} \end{array}\right. } \end{aligned}$$
(29)

the primary parameters \(\delta \psi _j\):

$$\begin{aligned} \delta \psi _{j}&: K_{ij}^{(0)} \frac{\partial N_{x(i)}}{\partial x} + K_{ij}^{(1)} \frac{\partial M_{x(i)}}{\partial x} + K_{ij}^{(2)} \frac{\partial L_{x(i)}}{\partial x} + K_{ij}^{(3)} \frac{\partial P_{x(i)}}{\partial x} - K_{ij}^{(1)} Q_{x(i)} \nonumber \\&\quad -2K_{ij}^{(2)} R_{x(i)} - 3K_{ij}^{(3)} S_{x(i)} =0, \, {\left\{ \begin{array}{ll} {\text {Reddy: }} &{}j=1,2,4,5 \\ {\text {TSDT: }} &{}j=1..6, \,{\text {Bot. }}: i=1,\\ {\text {SSDT: }} &{}j=1..4, \,{\text {Top. }}: i=2, \\ {\text {FSDT: }} &{}j=1..2, \\ \end{array}\right. } \end{aligned}$$
(30)

and the transverse deflection terms \(\delta w_b\) and \(\delta w_t\):

$$\begin{aligned} \delta w_b&: -\,K_{13}^{(0)} \frac{\partial ^2 N_{x(1)}}{\partial x^2} -K_{13}^{(1)} \frac{\partial ^2 M_{x(1)}}{\partial x^2}-K_{13}^{(2)} \frac{\partial ^2 L_{x(1)}}{\partial x^2}-K_{13}^{(3)} \frac{\partial ^2 P_{x(1)}}{\partial x^2} \nonumber \\&\quad +\,K_{13}^{(1)} \frac{\partial Q_{x(1)}}{\partial x} + 2K_{13}^{(2)} \frac{\partial R_{x(1)}}{\partial x}+ 3K_{13}^{(3)} \frac{\partial S_{x(1)}}{\partial x} +q_b=0,\, {\left\{ \begin{array}{ll} {\text {Reddy,}} \end{array}\right. } \end{aligned}$$
(31)
$$\begin{aligned} \delta w_t&: -\,K_{26}^{(0)} \frac{\partial ^2 N_{x(2)}}{\partial x^2} -K_{26}^{(1)} \frac{\partial ^2 M_{x(2)}}{\partial x^2}-K_{26}^{(2)} \frac{\partial ^2 L_{x(2)}}{\partial x^2}-K_{26}^{(3)} \frac{\partial ^2 P_{x(2)}}{\partial x^2}\nonumber \\&\quad +\,K_{26}^{(1)} \frac{\partial Q_{x(2)}}{\partial x} + 2K_{26}^{(2)} \frac{\partial R_{x(2)}}{\partial x}+ 3K_{26}^{(3)} \frac{\partial S_{x(2)}}{\partial x} +q_t=0,\, {\left\{ \begin{array}{ll} {\text {Reddy,}} \end{array}\right. } \end{aligned}$$
(32)
$$\begin{aligned} \delta w_b&: \frac{\partial Q_{x(1)}}{\partial x} + q_b=0, \, \delta w_t : \, \frac{\partial Q_{x(2)}}{\partial x} + q_t=0 \,\, {\left\{ \begin{array}{ll} {\text {TSDT }} \\ {\text {SSDT }} \\ {\text {FSDT }} \end{array}\right. } \end{aligned}$$
(33)

to zero. As we can see, the application of Reddy’s third-order theory results much more complex equilibrium equations in terms of the transverse deflections than the other higher-order theories [41].

Fig. 3
figure 3

Built-in configuration of a delaminated beam with orthotropic plies

Full size image
Table 1 Elastic properties of the composite layers
Full size table

3 Example: built-in configuration of a delaminated beam

As an example a built-in beam with asymmetric delamination is considered. The geometry of the structure is depicted by Fig. 3, where l denotes the total length, a represents the length of the delamination, b is the beam width and 2h is the total thickness of the beam with \([\pm 30/0_2/\pm 30/\overline{0}]_S\) lay-up. The corresponding thicknesses of the sub-laminates are denoted by \(t_1\) and \(t_2\). The material properties of the transversely isotropic and cross-ply layers are given by Table 1 [49, 52]. The structure of the ELSs in each and every case is determined according to Fig. 1.

3.1 Continuity conditions of the displacement field

The continuity conditions between the regions can be imposed by using the discussed primary parameters. The conditions for the components of the membrane displacement and the transverse deflection can be ensured by:

$$\begin{aligned}&\Big ( u_{0}+\sum _{j=1}^{q_\mathrm{{undel}}} K_{1j}^{(0)}\psi _j\Big |_{x=-0}^{(\mathrm{undel})} \Big )= u_{0b} \Big |_{x=+0}^{(\mathrm{del})}, w\Big |_{x=-0}^{(\mathrm{undel})}=w_b\Big |_{x=+0}^{(\mathrm{del})}, \end{aligned}$$
(34)
$$\begin{aligned}&\Big (u_{0}+\sum _{j=1}^{q_\mathrm{{undel}}} K_{2j}^{(0)}\psi _j\Big |_{x=-0}^{(\mathrm{undel})}\Big )= u_{0t} \Big |_{x=+0}^{(\mathrm{del})}, w\Big |_{x=-0}^{(\mathrm{undel})}=w_t\Big |_{x=+0}^{(\mathrm{del})}, \end{aligned}$$
(35)

where \(q_\mathrm{{undel}}\) is the number of the primary parameters in \(\varvec{\psi _{p}}\) vector. Independently of the order of the applied theory, these equations always represent four conditions. The continuity of the first-, second-, and third-order terms in the displacement functions can be specified through the element of the primary parameter vectors by connecting the first-order terms with first-order, the second-order terms with second-order, the third-order with the third-order terms and the deflection derivatives with the corresponding deflection derivatives. These represent \(q_\mathrm{{undel}}\) number of conditions between the undelaminated and delaminated portions. For the Reddy’s TSDT theory, by referring to Eqs. (16) and (25), these conditions can be formulated as:

$$\begin{aligned} \Big ( \theta _1 \,\, \lambda _1 \,\, \lambda _2 \Big )\Big |_{x=-0}^{(\mathrm{undel})}= \Big ( \theta _1 \,\, \lambda _1 \,\, \lambda _2 \Big )\Big |_{x=+0}^{(\mathrm{del})}, \end{aligned}$$
(36)

and

$$\begin{aligned} \Big ( \frac{\partial w}{\partial x} \Big )\Big |_{x=-0}^{(\mathrm{undel})}=\Big ( \frac{\partial w_b}{\partial x} \Big )\Big |_{x=0}^{(\mathrm{del})}. \end{aligned}$$
(37)

As the number of parameters in the \(\varvec{\psi _{p}}\) vector for the undelaminated and delaminated parts is generally not equal to each other, i.e.: \(q_\mathrm{{del}} \ne q_\mathrm{{undel}}\), the continuity of the remaining terms cannot be expressed directly. The remaining \(\theta _2\) and \(\frac{\partial w_t}{\partial x}\) terms in the primary parameter vector of the delaminated part, which are indicated by circles in Eq. (25), can be defined as auto-continuity parameters [50]. According to the theorem of auto-continuity, the continuity of these terms can be ensured by using only the primary parameters of the undelaminated part. The equations can be written as:

$$\begin{aligned} \theta _2\Big |_{x=+0}^{(\mathrm{del})}=\sum _{j=2}^{q_\mathrm{{undel}}} K_{2j}^{(1)}\psi _j\Big |_{x=-0}^{(\mathrm{undel})} =\Big (\theta _1+ \frac{3}{4}t_1^2 \lambda _1 - \frac{3}{4}t_2^2 \lambda _2 \Big )\Big |_{x=-0}^{(\mathrm{undel})}, \end{aligned}$$
(38)

and

$$\begin{aligned} \Big ( \frac{\partial w}{\partial x} \Big )\Big |_{x=-0}^{(\mathrm{undel})}=\Big ( \frac{\partial w_t}{\partial x} \Big )\Big |_{x=0}^{(\mathrm{del})}, \end{aligned}$$
(39)

representing \(q_\mathrm{{undel}}+2=4+2=6\) for Reddy’s TSDT. Regarding TSDT, the situation is exactly the same. The inequality, by referring to Eqs. (17) and (26), can be handled in a similar way:

$$\begin{aligned} \Big ( \theta _1 \,\, \theta _2 \,\, \phi _1 \,\, \phi _2 \,\, \lambda _2 \Big )\Big |_{x=-0}^{(\mathrm{undel})}= \Big (\theta _1 \,\, \theta _2 \,\, \phi _1 \,\, \phi _2 \,\, \lambda _2 \Big )\Big |_{x=+0}^{(\mathrm{del})}, \end{aligned}$$
(40)

and

$$\begin{aligned} \lambda _1\Big |_{x=+0}^{(\mathrm{del})}=\sum _{j=1}^{q_\mathrm{{undel}}} K_{1j}^{(3)}\psi _j\Big |_{x=-0}^{(\mathrm{undel})} =\frac{4}{3} \Big ( \frac{\theta _2-\theta _1-t_2 \phi _2+t_1 \phi _1+t_2^2 \lambda _2}{t_1^2} \Big )\Big |_{x=+0}^{(\mathrm{del})}, \end{aligned}$$
(41)

meaning \(q_\mathrm{{undel}}+1=5+1=6\) number of conditions. In connection with SSDT, referring to Eqs. (18) and (27), the continuity can be written as:

$$\begin{aligned} \Big ( \theta _1 \,\, \theta _2 \,\, \phi _1 \Big )\Big |_{x=-0}^{(\mathrm{undel})}= \Big (\theta _1 \,\, \theta _2 \,\, \phi _1 \Big )\Big |_{x=+0}^{(\mathrm{del})}, \end{aligned}$$
(42)

and

$$\begin{aligned} \phi _2\Big |_{x=+0}^{(\mathrm{del})}=\sum _{j=1}^{q_\mathrm{{undel}}} K_{2j}^{(2)}\psi _j\Big |_{x=-0}^{(\mathrm{undel})} = \Big ( \frac{-\theta _1+\theta _2-t_1\phi _1}{t_2}\Big )\Big |_{x=-0}^{(\mathrm{undel})}, \end{aligned}$$
(43)

representing \(q_\mathrm{{undel}}+1=3+1=4\) conditions. Fortunately, in connection with FSDT, by referring to Eqs. (19) and (28), the number of terms in the primary parameter vector for undelaminated and delaminated portions are equal to each other \(q_\mathrm{{del}} = q_\mathrm{{undel}}\). No further auto-continuity condition is required to be imposed. It can be expressed easily by:

$$\begin{aligned} \Big ( \theta _1 \,\, \theta _2 \Big )\Big |_{x=-0}^{(\mathrm{undel})}= \Big ( \theta _1 \,\, \theta _2 \Big )\Big |_{x=+0}^{(\mathrm{del})}, \end{aligned}$$
(44)

meaning \(q_\mathrm{{del}} = q_\mathrm{{undel}}=2\) conditions [50].

Fig. 4
figure 4

Continuity of the stress resultants at the delamination tip

Full size image

3.2 Continuity conditions of the stress resultants

As a result of arbitrary external forces, \(Q_{x(i)}\), \(R_{x(i)}\), \(S_{x(i)}\)\(N_{x(i)}\), \(M_{x(i)}\), \(L_{x(i)}\) and \(P_{x(i)}\) unknown stress resultants take place at the left end of the delaminated portion in each ESL. These stress resultants and their derivatives are transferred between the portions resulting equivalent normal force, equivalent shear force and equivalent bending moments on the right hand side of the undelaminated portion. The basic concept of the idea is depicted by Fig. 4, where the same arrows are used to sign \(R_{x(i)}\), \(S_{x(i)}\), and \(L_{x(i)}\), \(P_{x(i)}\). The form of the equations can be read out from the presented equilibrium equations [49]. Thus, the continuity of the normal forces, which means one condition for each theory, can be formulated as:

$$\begin{aligned} {\hat{N}}_{x}^{(\mathrm{undel})}:=\sum _{i=1}^{2} \left. \Bigg ( N_{x(i)} \Bigg ) \right| ^{(\mathrm{undel})}_{x=-0} = \left. \Bigg ( N_{x(1)} +N_{x(2)} \Bigg ) \right| ^{(\mathrm{del})}_{x=+0} ,\,\, {\left\{ \begin{array}{ll} {\text {Reddy, }} \\ {\text {TSDT, }} \\ {\text {SSDT, }} \\ {\text {FSDT, }} \end{array}\right. } \end{aligned}$$
(45)

where \({\hat{N}}_{x}^{(\mathrm{undel})}\) represents the equivalent normal force. The next conditions between the portions are the continuity of the equivalent bending moments. These continuity conditions can be formulated as:

$$\begin{aligned} \begin{aligned} {\hat{M}}_{x(j)}^{(\mathrm{undel})}:=&\sum _{i=1}^{2} \Big ( \varvec{K}_{ij}^{(\mathrm{undel})}\Big )^T \cdot \left. \left( \begin{array}{*{20}c} N_{x(i)}\\ M_{x(i)}\\ L_{x(i)}\\ P_{x(i)}\\ \end{array} \right) \right| _{x=-0}^{(\mathrm{undel})} \\ =&\sum _{i=1}^{2} \Big ( \varvec{K}_{ij}^{(\mathrm{undel})}\Big )^T \cdot \left. \left( \begin{array}{*{20}c} N_{x(i)}\\ M_{x(i)}\\ L_{x(i)}\\ P_{x(i)}\\ \end{array} \right) \right| _{x=+0}^{(\mathrm{del})} ,\,\, {\left\{ \begin{array}{ll} {\text {Reddy: }} &{}j=1..4, \\ {\text {TSDT: }} &{}j=1..5, \\ {\text {SSDT: }} &{}j=1..3, \\ {\text {FSDT: }} &{}j=1..2, \end{array}\right. } \end{aligned} \end{aligned}$$
(46)

where \(\varvec{K}_{ij}^{(\mathrm{undel})}\) collects the \(K_{ij}\) matrix elements of the undelaminated part:

$$\begin{aligned} \Big ( \varvec{K}_{ij}^{(\mathrm{undel})}\Big )^T=\Big ( K_{ij}^{(0)} \,\, K_{ij}^{(1)} \,\, K_{ij}^{(2)} \,\, K_{ij}^{(3)} \Big )\Big |^{(\mathrm{undel})}, \end{aligned}$$
(47)

and \({\hat{M}}_{x(j)}^{(\mathrm{undel})}\) denotes the equivalent bending moments imposing four conditions for the Reddy’s TSDT, five for the TSDT, three for the SSDT and two for the FSDT. It is worth giving attention to Reddy’s TSDT where we obtained an additional bending continuity condition in terms of the deflection derivative (Reddy: \(j=4\)), referring to Eqs. (16) and (22). Finally, the shear force continuity of the problem can be imposed for Reddy’s TSDT as:

$$\begin{aligned} \begin{aligned} {\hat{Q}}_{x}^{(\mathrm{undel})}&:=\sum _{i=1}^{2} \Big ( \varvec{K}_{i4}^{(\mathrm{undel})}\Big )^T \cdot \left. \left( \begin{array}{*{20}c} -\frac{\partial N_{x(i)}}{\partial x}\\ -\frac{\partial M_{x(i)}}{\partial x}+ Q_{x(i)} \\ -\frac{\partial L_{x(i)}}{\partial x}+2 R_{x(i)}\\ -\frac{\partial P_{x(i)}}{\partial x}+3 S_{x(i)}\\ \end{array} \right) \right| _{x=-0}^{(\mathrm{undel})} \\&= \sum _{i=1}^{2} \Big ( \varvec{K}_{i4}^{(\mathrm{undel})}\Big )^T \cdot \left. \left( \begin{array}{*{20}c} -\frac{\partial N_{x(i)}}{\partial x}\\ -\frac{\partial M_{x(i)}}{\partial x}+ Q_{x(i)} \\ -\frac{\partial L_{x(i)}}{\partial x}+2 R_{x(i)}\\ -\frac{\partial P_{x(i)}}{\partial x}+3 S_{x(i)}\\ \end{array} \right) \right| _{x=+0}^{(\mathrm{del})} ,\,\, {\left\{ \begin{array}{ll} {\text {Reddy, }} \end{array}\right. } \end{aligned} \end{aligned}$$
(48)

and for the other theories:

$$\begin{aligned} {\hat{Q}}_{x}^{(\mathrm{undel})}:=\sum _{i=1}^{2} \left. \Bigg ( Q_{x(i)} \Bigg ) \right| ^{(\mathrm{undel})}_{x=-0} = \left. \Bigg ( Q_{x(1)} +Q_{x(2)} \Bigg ) \right| ^{(\mathrm{del})}_{x=+0} ,\,\, {\left\{ \begin{array}{ll} {\text {TSDT, }} \\ {\text {SSDT, }} \\ {\text {FSDT, }} \end{array}\right. } \end{aligned}$$
(49)

resulting one more condition for each case.

3.3 Boundary conditions

In order to impose built-in boundary condition at the left end of the undelaminated part the displacement field must be zero. This condition can be easily prescribed by using the primary parameters:

$$\begin{aligned} u_{0}|_{x=-l+a}^{(\mathrm{undel})}=0, \qquad w\Big |_{x=-l+a}^{(\mathrm{undel})}=0, \qquad \varvec{\psi _{p}} \Big |_{x=-l+a}^{(\mathrm{undel})}=\varvec{0}. \end{aligned}$$
(50)

The external forces acting on the right hand side of the sub-laminates can be considered as equivalent stress resultants in accordance with Eqs. (29)–(30) and (31)–(33). In the lack of external forces in the axial direction, two boundary conditions can be imposed for each theory:

$$\begin{aligned} \left. \Bigg ( N_{x(1)} \Bigg ) \right| ^{(\mathrm{del})}_{x=-l+a} =0, \qquad \left. \Bigg ( N_{x(2)} \Bigg ) \right| ^{(\mathrm{del})}_{x=-l+a}=0, \,\, {\left\{ \begin{array}{ll} {\text {Reddy, }} \\ {\text {TSDT, }} \\ {\text {SSDT, }} \\ {\text {FSDT. }} \end{array}\right. } \end{aligned}$$
(51)

In the lack of external bending moments, the caused equivalent bending moments can be formulated as:

$$\begin{aligned} \Big ( \varvec{K}_{ij}^{(\mathrm{del})}\Big )^T \cdot \left. \left( \begin{array}{*{20}c} N_{x(i)}\\ M_{x(i)}\\ L_{x(i)}\\ P_{x(i)}\\ \end{array} \right) \right| _{x=-l+a}^{(\mathrm{del})} =0 \,\, {\left\{ \begin{array}{ll} {\text {Reddy: }} &{}j=1..6, \\ {\text {TSDT: }} &{}j=1..6, \,\,{\text {Bot. }}: i=1,\\ {\text {SSDT: }} &{}j=1..4, \,\,{\text {Top. }}: i=2, \\ {\text {FSDT: }} &{}j=1..2, \\ \end{array}\right. } \end{aligned}$$
(52)

where \(\varvec{K}_{ij}^{(\mathrm{del})}\) arranges the \(K_{ij}\) matrix elements of the delaminated part:

$$\begin{aligned} \Big ( \varvec{K}_{ij}^{(\mathrm{del})}\Big )^T=\Big ( K_{ij}^{(0)} \,\, K_{ij}^{(1)} \,\, K_{ij}^{(2)} \,\, K_{ij}^{(3)} \Big )\Big |^{(\mathrm{del})}. \end{aligned}$$
(53)

And finally, according to Fig. 3, the top and bottom parts of the delaminated regions are subjected to \(F_\mathrm{t}\) and \(F_\mathrm{b}\) forces, causing the following two boundary conditions for the Reddy’s TSDT:

$$\begin{aligned}&\Big ( \varvec{K}_{13}^{(\mathrm{del})}\Big )^T \cdot \left. \left( \begin{array}{*{20}c} -\frac{\partial N_{x(1)}}{\partial x}\\ -\frac{\partial M_{x(1)}}{\partial x}+ Q_{xz(1)} \\ -\frac{\partial L_{x(1)}}{\partial x}+2 R_{xz(1)}\\ -\frac{\partial P_{x(1)}}{\partial x}+3 S_{xz(1)}\\ \end{array} \right) \right| _{x=-l+a}^{(\mathrm{del})} =F_\mathrm{b}, \,\, {\left\{ \begin{array}{ll} {\text {Reddy, }} \end{array}\right. } \end{aligned}$$
(54)
$$\begin{aligned}&\Big ( \varvec{K}_{26}^{(\mathrm{del})}\Big )^T \cdot \left. \left( \begin{array}{*{20}c} -\frac{\partial N_{x(2)}}{\partial x}\\ -\frac{\partial M_{x(2)}}{\partial x}+ Q_{xz(2))} \\ -\frac{\partial L_{x(2)}}{\partial x}+2 R_{xz(2)}\\ -\frac{\partial P_{x(2)}}{\partial x}+3 S_{xz(2)}\\ \end{array} \right) \right| _{x=-l+a}^{(\mathrm{del})} =F_\mathrm{t}, \,\, {\left\{ \begin{array}{ll} {\text {Reddy, }} \end{array}\right. } \end{aligned}$$
(55)

and causing two boundary conditions for the other theories:

$$\begin{aligned} \left. \Bigg ( Q_{x(1)} \Bigg ) \right| ^{(\mathrm{del})}_{x=-l+a} =F_\mathrm{b}, \qquad \left. \Bigg ( Q_{x(2)} \Bigg ) \right| ^{(\mathrm{del})}_{x=-l+a}=F_\mathrm{t}, \,\, {\left\{ \begin{array}{ll} {\text {TSDT, }} \\ {\text {SSDT, }} \\ {\text {FSDT. }} \end{array}\right. } \end{aligned}$$
(56)

4 Displacements and stress distributions

Two different delamination scenarios are considered in this section in order to investigate the performance of the higher-order shear deformable theories. In each end every case, according to the presented Fig. 1, the analysis is carried out based on the novel semi-layerwise beam models. Moreover, to verify the obtained analytical results finite element (FE) analyses with the so- called virtual crack closure technique (FE-VCCT) are carried out [31], as well.

Fig. 5
figure 5

Distribution of the u displacement at the delamination tip cross section (a) and comparison of the deflection along the beam (b), “Case I”, \(F_\mathrm{t}= 10\) N and \(F_\mathrm{b}=-10\) N

Full size image
Fig. 6
figure 6

Distribution of the \(\sigma _x\) normal stresses (a) and the \(\tau _{xz}\) shear stresses at the delamination tip cross section (b), “Case I”, \(F_\mathrm{t}=10\) N and \(F_\mathrm{b}= -10\) N.

Full size image
Fig. 7
figure 7

Distribution of the u displacement at the delamination tip cross section (a) and comparison of the deflection along the beam (b), “Case II”, \(F_\mathrm{t}= 10\) N and \(F_\mathrm{b}=-10\) N

Full size image
Fig. 8
figure 8

Distribution of the \(\sigma _x\) normal stresses (a) and the \(\tau _{xz}\) shear stresses at the delamination tip cross section (b), “Case II”, \(F_\mathrm{t}= 10\) N and \(F_\mathrm{b}= -10\) N

Full size image

Regarding “Case I” delamination scenario, when the top and bottom sub-laminates are subjected to \(F_\mathrm{t}=10\) N and \(F_\mathrm{b}=-10\) N external forces, the u in-plane displacement fields and the w deflections are depicted by Fig. 5. As we can see, by using any kind of higher-order theories, the results show good agreement with the finite element solution in connection with u in-plane displacement field. In terms of the w deflections the agreement between the numerical and the analytical results is also quite good. The application of the higher-order beam theories results only a bit smaller function values than the FEA solution. As it is also illustrated by the highlighted part of the figure, the contribution of the higher-order theories to the deflection becomes smaller and smaller by increasing the order of theory. Thus, the deflection improvement of the SSDT, TSDT and Reddy’s TSDT compared with the FSDT is negligible. From this point of view, application of the higher-order theories is not necessary. In order to present the essence of the higher-order beam theories, Fig. 6 depicts further results regarding the \(\sigma _x\) normal and \(\tau _{xz}\) shear stresses. The stresses are provided at the delamination tip, separately at the undelaminated \(X=+0\) [mm] and the delaminated \(X=-0\) [mm] portions. As we can see, certain stress discontinuities take place at the crack tip which result different \(\sigma _x\) normal and \(\tau _{xz}\) shear stress distributions on the sides. Based on Fig. 6a, apart from the singular nature of the numerical solution, \(\sigma _x\) normal stresses are in good agreement with each other. Although, if we take a look at the delaminated part, the Reddy’s TSDT solution shows a little perturbation. It can only be explained by the rigorously imposed traction-free conditions. The application of the higher-order beam theories becomes quite important only if the \(\tau _{xz}\) shear stresses are investigated. Based on Fig. 6b, by increasing the order of the solutions, the \(\tau _{xz}\) shear stress can be described with a more and more accurate way. If the exact description of the \(\tau _{xz}\) shear stress at the crack tip is important, the application of higher-order theories becomes inevitable. It is worth giving attention to \(\tau _{xz}\) shear stress distribution which is obtained by the Reddy’s TSDT. As it was discussed previously, it is already able to satisfy the traction-free boundary conditions all along the top and bottom surfaces of the beam. Although, it is important to emphasise, it cannot satisfy the boundary conditions at the bottom surface of the top sub-laminate and at the top surface of the bottom sub-laminate. According to our computational experience, if these conditions had been strictly imposed it would have resulted in over-constrained shear strain distribution around the crack tip.

In the case of “Case II” scenario the structure is also loaded by \(F_\mathrm{t}=10\) N and \(F_\mathrm{b}=-10\) N external forces (Figs. 7, 8). Quite similarly to the “Case I” scenario, if only the deflection function is taken into account, the application of SSDT and TSDT theories would not be important. Nevertheless, if the knowledge of \(\tau _{xz}\) shear stress distribution represents key role of the fracture mechanical investigation, the application of the higher-order theories is unavoidable. Although, if we investigate the delaminated portion of the structure, the perturbation caused by the Reddy’s TSDT solution is no longer negligible. Unfortunately, the traction-free condition can significantly disturb the \(\sigma _x\) normal stress distribution.

Fig. 9
figure 9

Defintion of the J-integral for plane problems (a). The application of the J-integral for semi-layerwise model using zero-area concept and the inevitable extension (b). The opening (Mode-I) and the sliding (Mode-II) fracture modes (c)

Full size image

5 J-integral

In order to perform in-plane fracture mechanical investigation the so-called J-integral can be applied [42]. Based on the basic definition, considering any arbitrary counterclockwise C contour around the crack tip, the J-integral can be formulated as:

$$\begin{aligned} J=\int \limits _{C} \Bigg \{ U n_1-\sigma _{ij}n_j\frac{\partial u_i}{\partial x_1} \Bigg \} \mathrm{d}s, \end{aligned}$$
(57)

where U is the strain energy density, \(\sigma _{ij}\) are the components of the stress tensors, \(u_i\) means the displacement vector components, \(\mathrm{d}s\) is the length increment along the contour and \(n_i\) represents the components of the outward unit vector in the given (\(X_1-X_2\)) Cartesian coordinate system. The basic concept is depicted by Fig. 9a. Moreover, considering only linear elastic fracture mechanics, the fundamental property of this integral is the following [2]:

$$\begin{aligned} J=G_\mathrm{T}, \end{aligned}$$
(58)

where \(G_\mathrm{T}\) denotes the total energy release rate and J represents the value of the contour integral. Regarding delaminated beams, and based on the discussed semi-layerwise approach, the J-integral can be calculated as a zero-area path integral. The idea is depicted by Fig. 9b, where the \(\varvec{n}\) unit vector always remains parallel to the X-axis. Finally, taking into consideration the actual coordinate system (\(X_1= - X\) and \(X_2=z^{(i)}\)) and the actual number of ESLs, the total value of the energy release rate becomes

$$\begin{aligned} \begin{aligned} G_\mathrm{T} =&\sum _{i=1}^{2} \int \limits _{-t_{i}/2}^{t_{i}/2} \left. \left( - \frac{1}{2} \sigma _{x(i)} \varepsilon _{x(i)} + \tau _{xz(i)} \left( \frac{1}{2} \gamma _{xz(i)} - \frac{\partial w_{(i)}}{\partial x} \right) \right) \right| ^{(\mathrm{undel})}_{x=-0} \mathrm{d}z^{(i)} \\&+ \sum _{i=1}^{2} \int \limits _{-t_{i}/2}^{t_{i}/2} \left. \left( \frac{1}{2} \sigma _{x(i)} \varepsilon _{x(i)} - \tau _{xz(i)} \left( \frac{1}{2} \gamma _{xz(i)} - \frac{\partial w_{(i)}}{\partial x} \right) \right) \right| ^{(\mathrm{del})}_{x=+0} \mathrm{d}z^{(i)}. \end{aligned} \end{aligned}$$
(59)
Fig. 10
figure 10

Linear function transformation of the \(\sigma _{x}\) function (a) and the obtained symmetrical and asymmetrical function components of the field (b) for “Case I”

Full size image

5.1 Mode partitioning

Many models were developed in the literature to perform mode partitioning in beam-type fracture specimens, but generally these evaluation strategies, apart from the Suo–Hutchinson method [21], apply semi-analytical considerations [34] or arbitrary assumptions to make the separation feasible [4, 56]. Fortunately, the application of the J-integral makes these type of considerations absolutely avoidable and provides a methodical separation technique. For this purpose, we only have to separate the strain and stress fields into symmetrical and asymmetrical function components with respect to the delamination plane:

$$\begin{aligned} f_{(\mathrm{sym})}=\frac{f(+z_d)+f(-z_d)}{2}, f_{(\mathrm{ant})}=\frac{f(+z_d)-f(-z_d)}{2}, \end{aligned}$$
(60)

where the \((\mathrm{sym})\) and \((\mathrm{ant})\) subscripts indicate the symmetrical and asymmetrical function components, respectively [29]. To make it understandable, Fig. 10 represents an example based on a previously calculated stress distribution function (TSDT solution of “Case I”). Finally, knowing the symmetrical and asymmetrical function components of the field quantities [29], the mode-I fracture mode becomes

$$\begin{aligned} \begin{aligned} G_{\mathrm{I}}=&\int \limits _{-t}^{+t} \left. \left( - \frac{1}{2} \sigma _{x(\mathrm{sym})} \varepsilon _{x(\mathrm{sym})} + \tau _{xz(\mathrm{ant})} \left( \frac{1}{2} \gamma _{xz(\mathrm{ant})} - \frac{\partial w_{(\mathrm{ant})}}{\partial x} \right) \right) \right| ^{(\mathrm{undel})}_{x=-0} \mathrm{d}z_d \\&+ \int \limits _{-t}^{+t} \left. \left( \frac{1}{2} \sigma _{x(\mathrm{sym})} \varepsilon _{x(\mathrm{sym})} - \tau _{xz(\mathrm{ant})} \left( \frac{1}{2} \gamma _{xz(\mathrm{ant})} - \frac{\partial w_{(\mathrm{ant})}}{\partial x} \right) \right) \right| ^{(\mathrm{del})}_{x=+0} \mathrm{d}z_d, \end{aligned} \end{aligned}$$
(61)

and the mode-II fracture mode can be calculated as:

$$\begin{aligned} \begin{aligned} G_{\mathrm{II}}=&\int \limits _{-t}^{+t} \left. \left( - \frac{1}{2} \sigma _{x(\mathrm{ant})} \varepsilon _{x(\mathrm{ant})} + \tau _{xz(\mathrm{sym})} \left( \frac{1}{2} \gamma _{xz(\mathrm{sym})} - \frac{\partial w_{(\mathrm{sym})}}{\partial x} \right) \right) \right| ^{(\mathrm{undel})}_{x=-0} \mathrm{d}z_d \\&+ \int \limits _{-t}^{+t} \left. \left( \frac{1}{2} \sigma _{x(\mathrm{ant})} \varepsilon _{x(\mathrm{ant})} - \tau _{xz(\mathrm{sym})} \left( \frac{1}{2} \gamma _{xz(\mathrm{sym})} - \frac{\partial w_{(\mathrm{sym})}}{\partial x} \right) \right) \right| ^{(\mathrm{del})}_{x=+0} \mathrm{d}z_d. \end{aligned} \end{aligned}$$
(62)

First of all, to verify the proposed evaluation technique, the mode mixity of a symmetrically delaminated beam with unidirectional composite layers has to be investigated. The geometry of the beam is exactly the same as it is depicted by Fig. 3, but in this test problem the ESLs consist of transversely isotropic layers. The results, referring to Fig. 11, need no further explanations. Comparing to other solutions from the literature [4, 21, 34, 56], the developed higher-order evaluation techniques predict the mode mixity quite well .

Fig. 11
figure 11

Mode mixity of symmetrically delaminated transversely isotropic composite beam under different loading scenarios using analytical (a) and numerical (b) solutions, \(a/l=1/3\), \(2h=4.5\hbox { mm}\)

Full size image
Fig. 12
figure 12

Mode mixity of different loading scenarios with different evaluation techniques. The delamination is located between 0 and \(\pm 30\) layers, \(a/l=1/3\), \(b=20\hbox { mm}\), \(2h=4.5\hbox { mm}\)

Full size image

For “Case I” delamination scenario, the obtained results are depicted by Fig. 12. As can be seen, under different external loadings the FSDT, SSDT and TSDT solutions give results quite close to each other and the Euler–Bernoulli-based evaluation techniques. Furthermore, the agreement with the numerical FEA-VCCT solution is also quite good. Although, the application of Reddy’s TSDT significantly decreases the ratio of the mode-I energy release rate. The difference can only be explained by the rigorously imposed traction-free boundary condition. The caused \(\sigma _x\) perturbation, referring to Fig. 6, is no longer insignificant and it certainly disturbs the ratio of the symmetrical and asymmetrical function components, as well.

Figure 13 gives result of the mode mixity evaluations for “Case II”. In general, we can state that the FSDT, SSDT and TSDT are located between the Williams’ curvature based and the Reddy’s TSDT solutions. The FSDT and the Luo-Tong theory predict almost the same mode mixity values as the FEM-VCCT. Unfortunately, as in the delamination scenario discussed above, the application of Reddy’s TSDT significantly decreases the ratio of the mode-I energy release rate, which can only be attributable to the \(\sigma _x\) perturbation in Fig. 8.

6 Conclusion

To analyse brittle interlaminar fracture in composite structures under mixed-mode I/II fracture conditions first-, second-, third- and Reddy’s third-order shear deformable theories were discussed in this paper with two ESLs. The displacement continuity between the ESLs was described and imposed by using the system of exact kinematic conditions. Using Reddy’s TSDT theory, the traction-free boundary condition was also imposed along the top and bottom surfaces of the beam. As an example, a built-in configuration with different delamination scenario subjected to different external loads was presented. To solve the higher-order beam problems, the corresponding continuity and boundary conditions were discussed. Based on the obtained results, the mechanical fields at the delamination tip were provided and compared to each other. As a next step, to calculate the \(G_\mathrm{T}\) total energy release rate and to perform in-plane mode mixity analysis, the J-integral with zero-area path was introduced. By using symmetric and asymmetric decomposition of the mechanical fields, a well-ordered evaluation technique was proposed.

Fig. 13
figure 13

Mode mixity of different loading scenarios with different evaluation techniques. The delamination is located between 0 and 0 layers, \(a/l=1/3\), \(b=20\) mm, \(2h=4.5\) mm

Full size image

The results of different higher-order theories, apart form the Reddy’s TSDT, were close to each other and the Luo-Tong solution. Furthermore, these evaluation methods gave results between the Williams’ curvature based and the Bruno-Greco solutions, which defined the most extreme mode ratios. Unfortunately, regarding Reddy’s TSDT it was not true. The rigorously imposed traction-free condition significantly decreased the ratio of mode-I energy release rate and it significantly disturbed the \(\sigma _x\) normal stress distribution in the thinner sub-laminate.

Nevertheless, this paper is the first attempt to perform mode separation by combining the higher-order theories with the J-integral. The next step could be the semi-layerwise approach- based finite element development and the consideration of the transverse stretch modelling [52].