Abstract
We show that Dedekind, in his proof of the principle of definition by mathematical recursion, used implicitly both the concept of an inductive cone from an inductive system of sets and that of the inductive limit of an inductive system of sets. Moreover, we show that in Dedekind’s work on the foundations of mathematics one can also find specific occurrences of various profound mathematical ideas in the fields of universal algebra, category theory, the theory of primitive recursive mappings, and set theory, which undoubtedly point towards the mathematics of twentieth and twenty-first centuries.
Similar content being viewed by others
Change history
07 February 2018
The original version of this article unfortunately contained a mistake: The equation on page 34 was incorrect. The corrected equation is given below.
Notes
We refer the reader to Sect. 3 for the equivalence between the Dedekind–Peano algebra axioms and Lawvere’s Axiom 3 (Lawvere 1964, p. 1507). In this respect, it seems pertinent to point that the aforementioned principle laid the groundwork, through the derived principle of primitive recursion with parameters and the generalized composition of mappings, for Kurt Gödel to obtain, at the beginning of the 1930s, the set of all primitive recursive mappings in his work on the incompleteness of certain mathematical theories (Gödel 1931).
For clearness here and in the following theorem (126) I have especially mentioned condition \(\mathrm {I}\), although properly it is a consequence of \(\mathrm {II}\) and \(\mathrm {III}\).
References
Albers, D.J., and G.L. Alexanderson (eds.). 2008. Mathematical people, 2nd ed. Wellesley, MA: A. K. Peters Ltd.
Alexandroff, P. 1928. Untersuchungen über Gestalt und Lage abgeschlossneser Mengen. Annals of Mathmatics 2 (30): 101–187.
Aristotle, 1984. The complete works of Aristotle. (The Revised Oxford Translation), vol. 2, ed. J. Barnes. Princeton, NJ: Princeton University Press.
Baer, R. 1937. Abelian fields and duality of Abelian groups. American Journal of Mathematics 59: 869–888.
Birkhoff, G. 1933. On the combination of subalgebras. Proceedings of the Cambridge Philosophical Society 29: 441–464.
Birkhoff, G. 1934. Note on the paper “On the combination of subalgebras.”. Proceedings of the Cambridge Philosophical Society 30: 200.
Birkhoff, G. 1935. On the structure of abstract algebras. Proceedings of the Cambridge Philosophical Society 31: 433–454.
Birkhoff, G. 1987. Selected papers on algebra and topology. Boston: Birkhäuser Boston Inc.
Büchi, J.R. 1989. Finite automata, their algebras and grammars. Towards a theory of formal expressions. Edited and with a preface by Dirk Siefkes. New York: Springer-Verlag.
Cantor, G. 1955. Contributions to the founding of the theory of transfinite numbers. Translated, and provided with an introduction and notes, by Philip E. B. Jourdain. New York: Dover Publications, Inc.
Dedekind, R. 1888. Was sind und was sollen die Zahlen? Braunschweig: Friedr. Vieweg & Sohn. (English trans: R. Dedekind). Essays on the theory of numbers. I: Continuity and irrational numbers. II: The nature and meaning of numbers. (Authorized trans: Wooster Woodruff Beman), Dover, New York, 1963. Beman’s translation has been extensively revised by William Ewald in (Ewald, 1996, pp. 787–833).
Dedekind, R. 1930–1932. Gessammelte mathematische Werke. Herausgegeben von Robert Fricke, Emmy Noether, Øystein Ore. Vols. I–III. Braunschweig: Friedr. Vieweg & Sohn.
de Vries, J. 1993. Elements of topological dynamics. Mathematics and its applications, vol. 257. Dordrecht: Kluwer Academic Publishers Group.
Dieudonné, J. 1989. A History of algebraic and differential topology 1900–1960. Boston, Basel: Birkhäuser.
Dugac, P. 1976. Richard Dedekind et les fondements des mathématiques (avec de nombreux textes inédites). Préface de Jean Dieudonné. Collection des Travaux de l’Académie Internationale d’Histoire des Sciences No. 24. L’Histoire des Sciences, Textes et Études. Paris: Librairie Philosophique J. Vrin.
Ewald, W. 1996. From Kant to Hilbert: A source book in the foundations of mathematics. Vol. II. Ed. William Ewald. Oxford Science Publications. New York: The Clarendon Press, Oxford University Press.
Frege, G. 1879. Begriffsschrift, Eine der arithmetischen nachgebildete Formelsprache des reinen Denkens. Halle: Verlag von L. Nebert.
Frege, G. 1966. Grundgesetze der Arithmetik. Band I, II. Hildesheim: Georg Olms Verlagsbuchhandlung.
Freudenthal, H. 1937. Entwicklungen von Räumen und ihren Gruppen. Compositio Mathematica 4: 145–234.
Gödel, K. 1931. Über formal unentscheidbare Sätze der Principia Mathematica und verwandter Systeme, I. Monatshefte für Mathematik und Physik 38: 173–198.
Gray, J. 2000. Linear differential equations and group theory from Riemann to Poincaré, 2nd ed. Boston: Birkhäuser Boston Inc.
Grassmann, H. 1861. Lehrbuch der Arithmetik für höhere Lehranstalten. Berlin: Verlag von T. C. F. Enslin (Adolph Enslin).
Grothendieck, A. 1971. Revêtements étales et groupe fondamental (SGA1), éd. par A. Grothendieck, Lecture notes in mathematics, No. 224. Berlin, New York: Springer.
Heck Jr., R.G. 2012. Reading Frege’s Grundgesetze. Oxford: The Clarendon Press, Oxford University Press.
Herbrand, J. 1933. Théorie arithmétique des corps de nombres de degré infini II. Mathematische Annalen 108: 699–717.
Hilbert, D. 1931. Die Grundlegun der elementaren Zahlenlehre. Mathematische Annalen 104: 485–494.
Hocking, J.G., and G.S. Young. 1988. Topology, 2nd ed. New York: Dover Publications Inc.
Krömer, R. 2010. From Cantor to Sheaves: The development of the concepts of direct and inverse limits—A case study on shifts in mathematical methodology in the prehistory of category theory. In Symposium on the philosophy of the logic of sheaves, October 19–21. 2010. Universidad del Valle, Cali, Colombia.
Kurosh, A.G. 1935. Kombinatorischer Aufbau der bikompakten topologischen Räume. Compositio Mathematica 2: 471–476.
Lawvere, F.W. 1964. An elementary theory of the category of sets. Proceedings of National Academy of Sciences USA 52: 1506–1511.
Lipschitz, R. 1986. Briefwechsel mit Cantor, Dedekind, Helmholtz, Kronecker, Weierstrass und anderen. Ed. Winfried Scharlau. Dokumente zur Geschichte der Mathematik, 2. Freiburg: Friedr. Vieweg & Sohn, Braunschweig; Deutsche Mathematiker Vereinigung.
MacLane, S. 1970. Hamiltonian mechanics and geometry. American Mathematical Monthly 77: 570–586.
MacLane, S., and G. Birkhoff. 1988. Algebra, 3rd ed. New York: Chelsea Publishing Co.
Manes, E.G. 1976. Algebraic theories, vol. 26., Graduate texts in mathematics New York, Heidelberg: Springer.
Manes, E.G., and M.A. Arbib. 1986. Algebraic approaches to program semantics., Texts and monographs in computer science, AKM series in theoretical computer science New York: Springer.
Minkowski, H. 1905. Peter Gustav Lejeune Dirichlet und seine Bedeutung für die heutige Mathematik. Jahresber. Deutsch. Math.-Verein. 14: 149–163.
Peano, I. 1889. Arithmetices principia, nova methodo exposita. Turin: Fratres Bocca. (English trans: G. Peano). The principles of arithmetic, presented by a new method. (Trans: Jean van Heijenoort in van Heijenoort) (1967, pp. 83–97).
Peirce, C.S. 1881. On the logic of number. American Journal of Mathematics 4: 85–95.
Pontrjagin, L. 1931. Über den algebraischen Inhalt topologischer Dualitätssätze. Mathematische Annalen 105: 165–205.
Pontrjagin, L. 1934. Sur les groupes topologiques compacts et le cinquième problème de Hilbert. Comptes rendus de l’Académie des Sciences Paris 198: 238–240.
Raussen, M., and Chr Skau. 2004. Interview with Michael Atiyah and Isadore Singer. Newsletter of the European Mathematical Society 53: 24–30.
Russell, B. 1903. The principles of mathematics, vol. 1. Cambridge: Cambridge University Press.
Sancho Guimerá, J.B. 1959. Teoría de cuerpos algebraicos con ley de composición conmutativa. Revista Matemática Hispano-Americana, \(4.^{a}\) Serie 19: 18–39.
Smith, H.J.S. 1875. On the integration of discontinuous functions. Proceedings of the London Mathematical Society 6: 140–153.
van der Waerden, B.L. 1975. On the sources of my book Moderne Algebra. Historia Mathematica 2: 31–40.
van Heijenoort, J. (ed.). 1967. From Frege to Gödel. A source book in mathematical logic, 1879–1931. Cambridge, MA: Harvard University Press.
Weber, H. 1891/92. Leopold Kronecker. Jahresber. Deutsch. Math.-Verein 2: 5–31.
Weil, A. 1975. L’intégration dans les groupes topologiques et ses applications. Hermann: Deuxième édition.
Zermelo, E. 1967. A new proof of the possibility of a well-ordering. In From Frege to Gödel. A source book in mathematical logic, 1879–1931, ed. J. van Heijenoort, 183–198. Cambridge, MA: Harvard University Press.
Zermelo, E. 2010. Ernst Zermelo: Collected Works/Gesammelte Werke. Vol. I/Band I. Set Theory, Miscellanea/Mengenlehre, Varia. Ed. Heinz-Dieter Ebbinghaus, Craig G. Fraser and Akihiro Kanamori. Schriften der Mathematisch-Naturwissenschaftlichen Klasse der Heidelberger Akademie der Wissenschaften [Publications of the Mathematics and Natural Sciences Section of Heidelberg Academy of Sciences], 21. Berlin: Springer.
Acknowledgements
We would like to thank all who helped us by reading parts of the manuscript and suggesting mathematical improvements: Enric Cosme, Emily Riehl, Roberto Rubio, Sergiu Rudeanu, and Rafael Sivera. Our thanks are further due to our dear friend José García Roca—example of intelligence, goodness, and integrity—for correcting the English and suggesting improvements. And also for his tireless encouragement and invaluable continued moral support. Moreover, we are greatly indebted to the reviewer for his helpful comments and important stylistic suggestions.
Author information
Authors and Affiliations
Corresponding author
Additional information
Communicated by Jeremy Gray.
The original version of this article was revised: The equation on page 34 was incorrect. The equation was corrected in the article.
Appendix A: A many-sorted algebraic model of the theory of primitive recursive mappings
Appendix A: A many-sorted algebraic model of the theory of primitive recursive mappings
We next provide—in the algebraic spirit of Dedekind—a new model, based on many-sorted universal algebra, of the theory of primitive recursive mappings which will allow us to diagrammatically prove that the three basic mathematical operations, addition, multiplication, and exponentiation, defined by Dedekind in \(\S \S \) 11–13 of Dedekind (1888), are primitive recursive. We remark that the just-mentioned many-sorted algebraic model, appropriately modified, can be used to supply many-sorted algebraic models of the theories of general recursive mappings and of recursive partial mappings. Moreover, the subalgebra generating operators associated with these models make the notion of relative recursiveness, in each case, natural.
Since the set of all primitive recursive mappings will be the union of the underlying many-sorted set of the smallest many-sorted subalgebra of a convenient many-sorted algebra, we begin by defining the many-sorted signature of the many-sorted algebra at issue. Note that in what follows \(\mathbb {N}^{\star }\) stands for the underlying set of the free monoid on \(\mathbb {N}\), that \(\curlywedge \) is the binary operation of concatenation on \(\mathbb {N}^{\star }\), and that \(\lambda \) denotes the empty word on \(\mathbb {N}\). Moreover, given sets A, B, and C, and mappings  and
and  , we denote by \(\left<f,g\right>\) the unique mapping from C to \(A\times B\) such that \(\mathrm {pr}_{A}\circ \left<f,g\right> = f\) and \(\mathrm {pr}_{B}\circ \left<f,g\right> = g\), where \(\mathrm {pr}_{A}\) is the canonical projection from \(A\times B\) to A and \(\mathrm {pr}_{B}\) the canonical projection from \(A\times B\) to B.
, we denote by \(\left<f,g\right>\) the unique mapping from C to \(A\times B\) such that \(\mathrm {pr}_{A}\circ \left<f,g\right> = f\) and \(\mathrm {pr}_{B}\circ \left<f,g\right> = g\), where \(\mathrm {pr}_{A}\) is the canonical projection from \(A\times B\) to A and \(\mathrm {pr}_{B}\) the canonical projection from \(A\times B\) to B.
Definition
We denote by \(\varvec{{\varSigma }}^{\mathrm {pr}}\) the \(\mathbb {N}\)-sorted signature, for the primitive recursive mappings, whose (w, n)-th coordinate, where \((w,n)\in \mathbb {N}^{\star }\times \mathbb {N}\), is defined as follows:
Definition
We denote by  the many-sorted \(\varvec{{\varSigma }}^{\mathrm {pr}}\)-algebra whose underlying \(\mathbb {N}\)-sorted set,
the many-sorted \(\varvec{{\varSigma }}^{\mathrm {pr}}\)-algebra whose underlying \(\mathbb {N}\)-sorted set,  , is \((\mathrm {Hom}(\mathbb {N}^{n},\mathbb {N}))_{n\in \mathbb {N}}\), so its n-th coordinate is the set of all mappings from \(\mathbb {N}^{n}\) to \(\mathbb {N}\), and where the structural operations are the following:
, is \((\mathrm {Hom}(\mathbb {N}^{n},\mathbb {N}))_{n\in \mathbb {N}}\), so its n-th coordinate is the set of all mappings from \(\mathbb {N}^{n}\) to \(\mathbb {N}\), and where the structural operations are the following:
-
1.
\(\kappa _{0,0}\), the 0-ary constant mapping determined by 0, which is the mapping from \(\mathbb {N}^{0}\) to \(\mathbb {N}\) that sends the unique element of \(\mathbb {N}^{0}\) to 0.
-
2.
\(\mathrm {sc}\), the successor mapping.
-
3.
\(\mathrm {pr}_{1,0}\), the identity mapping at \(\mathbb {N}\).
-
4.
For every \(n\ge 2\) and every \(i\in n\), \(\mathrm {pr}_{n,i}\), the i-th canonical projection from \(\mathbb {N}^{n}\) to \(\mathbb {N}\).
-
5.
For every \(m\in \mathbb {N}-1\) and every \(n\in \mathbb {N}\), \({\varOmega }_{\mathrm {C}}^{m,n}\), the operator of (generalized) composition of arity \((m)\curlywedge (n\mid i\in m)\) and co-arity n, which is the mapping from \(\mathrm {Hom}(\mathbb {N}^{m},\mathbb {N})\times (\mathrm {Hom}(\mathbb {N}^{n},\mathbb {N}))^{m}\) to \(\mathrm {Hom}(\mathbb {N}^{n},\mathbb {N})\) that sends a pair \((f,(g_{i})_{i\in m})\) in \(\mathrm {Hom}(\mathbb {N}^{m},\mathbb {N})\times (\mathrm {Hom}(\mathbb {N}^{n},\mathbb {N}))^{m}\) to the mapping \({\varOmega }_{\mathrm {C}}^{m,n}(f,(g_{i})_{i\in m})\) from \(\mathbb {N}^{n}\) to \(\mathbb {N}\) obtained by composing \(\left<g_{i}\right>_{i\in m}\) and f, where \(\left<g_{i}\right>_{i\in m}\) is the unique mapping from \(\mathbb {N}^{n}\) to \(\mathbb {N}^{m}\) such that, for every \(i\in m\), \(g_{i} = \mathrm {pr}_{m,i}\circ \left<g_{i}\right>_{i\in m}\).
-
6.
For every \(m\in \mathbb {N}\), \({\varOmega }_{\mathrm {R}}^{m}\), the operator of primitive recursion (also known as the parameterized operation of primitive recursion) of arity \((m)\curlywedge (m+2)\) and co-arity \(m+1\), which is the mapping from \(\mathrm {Hom}(\mathbb {N}^{m},\mathbb {N})\times \mathrm {Hom}(\mathbb {N}^{m+2},\mathbb {N})\) to \(\mathrm {Hom}(\mathbb {N}^{m+1},\mathbb {N})\) that sends a pair (f, g) in \(\mathrm {Hom}(\mathbb {N}^{m},\mathbb {N})\times \mathrm {Hom}(\mathbb {N}^{m+2},\mathbb {N})\) to the mapping \({\varOmega }_{\mathrm {R}}^{m}(f,g)\) from \(\mathbb {N}^{m+1}\) to \(\mathbb {N}\) obtained from f and g by primitive recursion. Let us recall that, for every \(m\in \mathbb {N}\), if
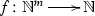 and
and 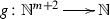 , then, from the principle of definition by mathematical recursion, it follows immediately that there exists a unique mapping
, then, from the principle of definition by mathematical recursion, it follows immediately that there exists a unique mapping 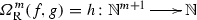 such that the following diagram:
such that the following diagram: 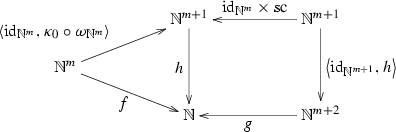
commutes (where \(\omega _{\mathbb {N}^{m}}\) is the unique mapping from \(\mathbb {N}^{m}\) to \(1 = \{0\}\) and \(\kappa _{0}\) the mapping from 1 to \(\mathbb {N}\) that sends 0 to 0), i.e., such that:
-
(a)
\(\forall a\in \mathbb {N}^{m}\,(h(a,0) = f(a)).\)
-
(b)
\(\forall a\in \mathbb {N}^{m}\,\,\forall n\in \mathbb {N}\,(h(a,\mathrm {sc}(n)) = g(a,n,h(a,n))).\)
-
(a)
In the above definition, we have identified the set \(\mathrm {Hom}(\mathbb {N}^{1},\mathbb {N})\) with the set \(\mathrm {End}(\mathbb {N})\), of all endomorphisms of the set \(\mathbb {N}\). Moreover, to simplify the notation, no distinction has been made between the symbols of operation and their realizations on the \(\mathbb {N}\)-sorted set \((\mathrm {Hom}(\mathbb {N}^{n},\mathbb {N}))_{n\in \mathbb {N}}\).
Since it will be used below to define the set of all primitive recursive mappings, we will next recall under what conditions an \(\mathbb {N}\)-sorted subset of the underlying \(\mathbb {N}\)-sorted set  of
of  is a subalgebra of the many-sorted \(\varvec{{\varSigma }}^{\mathrm {pr}}\)-algebra
is a subalgebra of the many-sorted \(\varvec{{\varSigma }}^{\mathrm {pr}}\)-algebra  .
.
Definition
An \(\mathbb {N}\)-sorted subset \(\mathcal {F}=(\mathcal {F}_{n})_{n\in \mathbb {N}}\) of the underlying \(\mathbb {N}\)-sorted set  of
of  is a subalgebra of
is a subalgebra of  exactly if it satisfies the following conditions:
exactly if it satisfies the following conditions:
-
1.
\(\kappa _{0,0}\in \mathcal {F}_{0}\).
-
2.
\(\mathrm {sc}\in \mathcal {F}_{1}\).
-
3.
\(\mathrm {pr}_{1,0}\in \mathcal {F}_{1}\).
-
4.
For every \(n\ge 2\) and every \(i\in n\), \(\mathrm {pr}_{n,i}\in \mathcal {F}_{n}\).
-
5.
For every \(m\in \mathbb {N}-1\), every \(n\in \mathbb {N}\), every \(f\in \mathcal {F}_{m}\), and every \((g_{i})_{i\in m}\in (\mathcal {F}_{n})^{m}\), \({\varOmega }_{\mathrm {C}}^{m,n}(f,(g_{i})_{i\in m})\in \mathcal {F}_{n}\).
-
6.
For every \(m\in \mathbb {N}\), every \(f\in \mathcal {F}_{m}\), and every \(g\in \mathcal {F}_{m+2}\), \({\varOmega }_{\mathrm {R}}^{m}(f,g)\in \mathcal {F}_{m+1}\).
We denote by  the set of all subalgebras of the many-sorted \(\varvec{{\varSigma }}^{\mathrm {pr}}\)-algebra
the set of all subalgebras of the many-sorted \(\varvec{{\varSigma }}^{\mathrm {pr}}\)-algebra  .
.
We next state the fundamental properties of the set of all subalgebras of  .
.
Proposition
The set  , of all subalgebra of the many-sorted \(\varvec{{\varSigma }}^{\mathrm {pr}}\)-algebra
, of all subalgebra of the many-sorted \(\varvec{{\varSigma }}^{\mathrm {pr}}\)-algebra  , is an algebraic closure system on
, is an algebraic closure system on  , i.e.,
, i.e.,  satisfies the following conditions:
satisfies the following conditions:
-
1.
\((\mathrm {Hom}(\mathbb {N}^{n},\mathbb {N}))_{n\in \mathbb {N}}\) is a subalgebra de
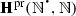 .
. -
2.
If \((\mathcal {F}^{i})_{i\in I}\) is a nonempty family of subalgebras of
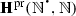 , then \(\bigcap _{i\in I}\mathcal {F}^{i}\) is a subalgebra of
, then \(\bigcap _{i\in I}\mathcal {F}^{i}\) is a subalgebra of 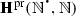 .
. -
3.
If \((\mathcal {F}^{i})_{i\in I}\) is a nonempty family of subalgebras of
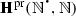 , and if, for every \(i,j\in I\), there exist \(k\in I\) such that \(\mathcal {F}^{i}\cup \mathcal {F}^{j}\subseteq \mathcal {F}^{k}\), then \(\bigcup _{i\in I}\mathcal {F}^{i}\) is a subalgebra of
, and if, for every \(i,j\in I\), there exist \(k\in I\) such that \(\mathcal {F}^{i}\cup \mathcal {F}^{j}\subseteq \mathcal {F}^{k}\), then \(\bigcup _{i\in I}\mathcal {F}^{i}\) is a subalgebra of 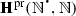 .
.
From the algebraic closure system  on
on  we obtain the algebraic closure operator \(\mathrm {Sg}_{\mathrm {pr}}\) on
we obtain the algebraic closure operator \(\mathrm {Sg}_{\mathrm {pr}}\) on  induced by it, as stated in the following corollary.
induced by it, as stated in the following corollary.
Corollary
For the many-sorted \(\varvec{{\varSigma }}^{\mathrm {pr}}\)-algebra  , the endomorphism \(\mathrm {Sg}_{\mathrm {pr}}\) of the set
, the endomorphism \(\mathrm {Sg}_{\mathrm {pr}}\) of the set  , of all \(\mathbb {N}\)-sorted subsets of
, of all \(\mathbb {N}\)-sorted subsets of  , defined as:
, defined as:

has the following properties:
-
1.
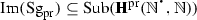 , i.e., for every
, i.e., for every 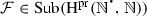 , \(\mathrm {Sg}_{\mathrm {pr}}(\mathcal {F})\) is a subalgebra of
, \(\mathrm {Sg}_{\mathrm {pr}}(\mathcal {F})\) is a subalgebra of 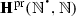 .
. -
2.
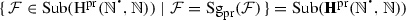 , i.e., the fixed points of \(\mathrm {Sg}_{\mathrm {pr}}\) are exactly the subalgebras of
, i.e., the fixed points of \(\mathrm {Sg}_{\mathrm {pr}}\) are exactly the subalgebras of 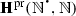 .
. -
3.
\(\mathrm {Sg}_{\mathrm {pr}}\) is extensive, i.e., for every
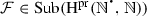 , it happens that \(\mathcal {F}\subseteq \mathrm {Sg}_{\mathrm {pr}}(\mathcal {F})\).
, it happens that \(\mathcal {F}\subseteq \mathrm {Sg}_{\mathrm {pr}}(\mathcal {F})\). -
4.
\(\mathrm {Sg}_{\mathrm {pr}}\) is isotone, i.e., for every
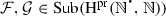 , if \(\mathcal {F}\subseteq \mathcal {G}\), then \(\mathrm {Sg}_{\mathrm {pr}}(\mathcal {F})\subseteq \mathrm {Sg}_{\mathrm {pr}}(\mathcal {G})\).
, if \(\mathcal {F}\subseteq \mathcal {G}\), then \(\mathrm {Sg}_{\mathrm {pr}}(\mathcal {F})\subseteq \mathrm {Sg}_{\mathrm {pr}}(\mathcal {G})\). -
5.
\(\mathrm {Sg}_{\mathrm {pr}}\) is idempotent, i.e., for every
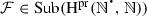 , it happens that \(\mathrm {Sg}_{\mathrm {pr}}(\mathcal {F}) = \mathrm {Sg}_{\mathrm {pr}}(\mathrm {Sg}_{\mathrm {pr}}(\mathcal {F}))\).
, it happens that \(\mathrm {Sg}_{\mathrm {pr}}(\mathcal {F}) = \mathrm {Sg}_{\mathrm {pr}}(\mathrm {Sg}_{\mathrm {pr}}(\mathcal {F}))\). -
6.
\(\mathrm {Sg}_{\mathrm {pr}}\) is algebraic, i.e., for every nonempty family \((\mathcal {F}^{i})_{i\in I}\) in
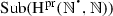 , if, for every \(i,j\in I\), there exists a \(k\in I\) such that \(\mathcal {F}^{i}\cup \mathcal {F}^{j}\subseteq \mathcal {F}^{k}\), then \(\mathrm {Sg}_{\mathrm {pr}}(\bigcup _{i\in I}\mathcal {F}^{i}) = \bigcup _{i\in I}\mathrm {Sg}_{\mathrm {pr}}(\mathcal {F}^{i})\).
, if, for every \(i,j\in I\), there exists a \(k\in I\) such that \(\mathcal {F}^{i}\cup \mathcal {F}^{j}\subseteq \mathcal {F}^{k}\), then \(\mathrm {Sg}_{\mathrm {pr}}(\bigcup _{i\in I}\mathcal {F}^{i}) = \bigcup _{i\in I}\mathrm {Sg}_{\mathrm {pr}}(\mathcal {F}^{i})\).
Thus, for any  , \(\mathrm {Sg}_{\mathrm {pr}}(\mathcal {F})\) is the smallest subalgebra of
, \(\mathrm {Sg}_{\mathrm {pr}}(\mathcal {F})\) is the smallest subalgebra of  that includes \(\mathcal {F}\). \(\mathrm {Sg}_{\mathrm {pr}}(\mathcal {F})\) is called the subalgebra of
that includes \(\mathcal {F}\). \(\mathrm {Sg}_{\mathrm {pr}}(\mathcal {F})\) is called the subalgebra of  generated by \(\mathcal {F}\) and \(\mathrm {Sg}_{\mathrm {pr}}\) the subalgebra generating operator on
generated by \(\mathcal {F}\) and \(\mathrm {Sg}_{\mathrm {pr}}\) the subalgebra generating operator on  .
.
Definition
Let \(\mathcal {F} = (\mathcal {F}_{n})_{n\in \mathbb {N}}\) be a countable \(\mathbb {N}\)-sorted subset of  , i.e., an \(\mathbb {N}\)-sorted subset of
, i.e., an \(\mathbb {N}\)-sorted subset of  such that \(\mathrm {card}(\coprod \mathcal {F})\le \aleph _{0}\). Then we call the mappings in \(\bigcup \mathrm {Sg}_{\mathrm {pr}}(\mathcal {F})\), the union of the subalgebra of
such that \(\mathrm {card}(\coprod \mathcal {F})\le \aleph _{0}\). Then we call the mappings in \(\bigcup \mathrm {Sg}_{\mathrm {pr}}(\mathcal {F})\), the union of the subalgebra of  generated by \(\mathcal {F}\), the \(\mathcal {F}\)-primitive recursive mappings or the primitive recursive mappings relative to \(\mathcal {F}\), and, to shorten the notation, we will write \(\mathrm {PRM}(\mathcal {F})\) instead of \(\bigcup \mathrm {Sg}_{\mathrm {pr}}(\mathcal {F})\). In particular, the set of all primitive recursive mappings, denoted by \(\mathrm {PRM}\), is \(\bigcup \mathrm {Sg}_{\mathrm {pr}}((\varnothing )_{n\in \mathbb {N}})\), the union of the subalgebra of
generated by \(\mathcal {F}\), the \(\mathcal {F}\)-primitive recursive mappings or the primitive recursive mappings relative to \(\mathcal {F}\), and, to shorten the notation, we will write \(\mathrm {PRM}(\mathcal {F})\) instead of \(\bigcup \mathrm {Sg}_{\mathrm {pr}}(\mathcal {F})\). In particular, the set of all primitive recursive mappings, denoted by \(\mathrm {PRM}\), is \(\bigcup \mathrm {Sg}_{\mathrm {pr}}((\varnothing )_{n\in \mathbb {N}})\), the union of the subalgebra of  generated by the \(\mathbb {N}\)-sorted set \((\varnothing )_{n\in \mathbb {N}}\) (which is constantly empty).
generated by the \(\mathbb {N}\)-sorted set \((\varnothing )_{n\in \mathbb {N}}\) (which is constantly empty).
We next provide, for a countable \(\mathbb {N}\)-sorted subset \(\mathcal {F}\) of  , a constructive characterization of \(\mathrm {PRM}(\mathcal {F})\) (which is also valid when \(\mathcal {F}\) is arbitrary).
, a constructive characterization of \(\mathrm {PRM}(\mathcal {F})\) (which is also valid when \(\mathcal {F}\) is arbitrary).
Proposition
Let \(\mathcal {F} = (\mathcal {F}_{n})_{n\in \mathbb {N}}\) be an \(\mathbb {N}\)-sorted subset of  such that \(\mathrm {card}(\coprod \mathcal {F})\le \aleph _{0}\) and \(f\in \bigcup _{n\in \mathbb {N}}\mathrm {Hom}(\mathbb {N}^{n},\mathbb {N})\). Then \(f\in \mathrm {PRM}(\mathcal {F})\) if, and only if, there exists a formative construction for f relative to \(\varvec{{\varSigma }}^{\mathrm {pr}}\) and \(\mathcal {F}\), i.e., if, and only if, there exists a \(p\in \mathbb {N}-1\) and a family \((f_{i})_{i\in p}\) in \(\bigcup _{n\in \mathbb {N}}\mathrm {Hom}(\mathbb {N}^{n},\mathbb {N})\) such that \(f = f_{p-1}\) and, for every \(i\in p\), it happens that:
such that \(\mathrm {card}(\coprod \mathcal {F})\le \aleph _{0}\) and \(f\in \bigcup _{n\in \mathbb {N}}\mathrm {Hom}(\mathbb {N}^{n},\mathbb {N})\). Then \(f\in \mathrm {PRM}(\mathcal {F})\) if, and only if, there exists a formative construction for f relative to \(\varvec{{\varSigma }}^{\mathrm {pr}}\) and \(\mathcal {F}\), i.e., if, and only if, there exists a \(p\in \mathbb {N}-1\) and a family \((f_{i})_{i\in p}\) in \(\bigcup _{n\in \mathbb {N}}\mathrm {Hom}(\mathbb {N}^{n},\mathbb {N})\) such that \(f = f_{p-1}\) and, for every \(i\in p\), it happens that:
-
1.
\(f_{i}\in \mathcal {F}_{n}\), for some \(n\in \mathbb {N}\), or
-
2.
\(f_{i} = \kappa _{0,0}\), or
-
3.
\(f_{i} = \mathrm {sc}\), or
-
4.
\(f_{i} = \mathrm {pr}_{1,0}\), or
-
5.
\(f_{i} = \mathrm {pr}_{n,j}\), for some \(n\ge 2\) and some \(j\in n\), or
-
6.
\(f_{i}\) is \(m+1\)-ary and \(f_{i} = {\varOmega }_{\mathrm {R}}^{m}(f_{j},f_{k})\), for a j and a \(k\in i\) such that \(f_{j}\) is m-ary and \(f_{k}\) is \(m+2\)-ary, or
-
7.
\(f_{i}\) is n-ary and \(f_{i} = {\varOmega }_{\mathrm {C}}^{m,n}(f_{j},(f_{k_{\alpha }})_{\alpha \in m})\), for an \(m\in \mathbb {N}-1\), a \(j\in i\) and a family \((k_{\alpha })_{\alpha \in m}\in i^{m}\) such that \(f_{j}\) is m-ary and, for every \(\alpha \in m\), \(f_{k_{\alpha }}\) is n-ary.
Proof
Let \(\mathcal {L}\) denote the \(\mathbb {N}\)-sorted subset of  whose n-th coordinate, \(\mathcal {L}_{n}\), for \(n\in \mathbb {N}\), has as elements all mappings \(f\in \mathrm {Hom}(\mathbb {N}^{n},\mathbb {N})\) for which there exists a formative construction for f relative to \(\varvec{{\varSigma }}^{\mathrm {pr}}\) and \(\mathcal {F}\). Since \(\mathrm {PRM}(\mathcal {F})\) is the union of the underlying \(\mathbb {N}\)-sorted set of the least subalgebra of
whose n-th coordinate, \(\mathcal {L}_{n}\), for \(n\in \mathbb {N}\), has as elements all mappings \(f\in \mathrm {Hom}(\mathbb {N}^{n},\mathbb {N})\) for which there exists a formative construction for f relative to \(\varvec{{\varSigma }}^{\mathrm {pr}}\) and \(\mathcal {F}\). Since \(\mathrm {PRM}(\mathcal {F})\) is the union of the underlying \(\mathbb {N}\)-sorted set of the least subalgebra of  that contains \(\mathcal {F}\), to show that \(\mathrm {PRM}(\mathcal {F})\subseteq \bigcup _{n\in \mathbb {N}}\mathcal {L}_{n}\) it suffices to verify that \(\mathcal {L}\) contains \(\mathcal {F}\) and that \(\mathcal {L}\) is a subalgebra of
that contains \(\mathcal {F}\), to show that \(\mathrm {PRM}(\mathcal {F})\subseteq \bigcup _{n\in \mathbb {N}}\mathcal {L}_{n}\) it suffices to verify that \(\mathcal {L}\) contains \(\mathcal {F}\) and that \(\mathcal {L}\) is a subalgebra of  . \(\square \)
. \(\square \)
We have that \(\mathcal {F}\subseteq \mathcal {L}\), since, for \(n\in \mathbb {N}\) and \(f\in \mathcal {F}_{n}\), the family \((f_{i})_{i\in 1}\) with \(f_{0} = f\), is a formative construction for f. It is obvious that \(\kappa _{0,0}\in \mathcal {L}_{0}\), that \(\mathrm {sc}\) and \(\mathrm {pr}_{1,0}\in \mathcal {L}_{1}\) and that, for every \(n\ge 2\) and every \(j\in n\), \(\mathrm {pr}_{n,j}\in \mathcal {L}_{n}\). Moreover, given an \(m\in \mathbb {N}-1\), an \(n\in \mathbb {N}\), an \(f\in \mathcal {L}_{m}\), and an m-indexed family \((g_{j})_{j\in m}\) in \(\mathcal {L}_{n}\), then, by virtue of the definition of \(\mathcal {L}\), there exists a formative construction \((f_{i})_{i\in n_{f}}\) for f and, for every \(j\in m\), there exists a formative construction \((f_{j,i})_{i\in n_{j}}\) for \(g_{j}\). Since it may be helpful for the sake of understanding, let us represent the situation just described by the following figure:
Then, for \(n = n_{f}+\left( \sum _{j\in m}n_{j}\right) +1\) and taking as \((h_{i})_{i\in n}\) the family of mappings whose last term is \({\varOmega }_{\mathrm {C}}^{m,n}(f,(g_{j})_{j\in m})\) and being the other terms those formed by the terms of the previous figure, going from left to right and from top to bottom, we have that \((h_{i})_{i\in n}\) is a formative construction for \({\varOmega }_{\mathrm {C}}^{m,n}(f,(g_{j})_{j\in m})\). Hence \({\varOmega }_{\mathrm {C}}^{m,n}(f,(g_{j})_{j\in m})\in \mathcal {L}_{n}\). In the same way one proves that \(\mathcal {L}\) is closed under \({\varOmega }_{\mathrm {R}}^{m}\). Therefore \(\mathcal {L}\) is a subalgebra of  . From all this we conclude that \(\mathrm {PRM}(\mathcal {F}) \subseteq \bigcup _{n\in \mathbb {N}}\mathcal {L}_{n}\).
. From all this we conclude that \(\mathrm {PRM}(\mathcal {F}) \subseteq \bigcup _{n\in \mathbb {N}}\mathcal {L}_{n}\).
We next show, by induction limited to an initial segment of \(\mathbb {N}\), that \(\bigcup _{n\in \mathbb {N}}\mathcal {L}_{n}\) is a subset of \(\mathrm {PRM}(\mathcal {F})\).
Let \(n\in \mathbb {N}\) and \(f\in \mathcal {L}_{n}\). Then, by definition, there exists a \(p\in \mathbb {N}-1\) and a family \((f_{i})_{i\in p}\) in \(\bigcup _{n\in \mathbb {N}}\mathrm {Hom}(\mathbb {N}^{n},\mathbb {N})\) such that \(f = f_{p-1}\) and, for every \(i\in p\), we have that \(f_{i}\in \mathcal {F}_{n}\), for some \(n\in \mathbb {N}\), or \(f_{i} = \kappa _{0,0}\), or \(f_{i} = \mathrm {sc}\), or \(f_{i} = \mathrm {pr}_{1,0}\), or \(f_{i} = \mathrm {pr}_{n,j}\), for some \(n\ge 2\) and some \(j\in n\), or \(f_{i}\) is \(m+1\)-ary and \(f_{i} = {\varOmega }_{\mathrm {R}}^{m}(f_{j},f_{k})\), for a j and a \(k\in i\) such that \(f_{j}\) is m-ary and \(f_{k}\) is \(m+2\)-ary, or \(f_{i}\) is n-ary and \(f_{i} = {\varOmega }_{\mathrm {C}}^{m,n}(f_{j},(f_{k_{\alpha }})_{\alpha \in m})\), for an \(m\in \mathbb {N}-1\), a \(j\in i\) and a family \((k_{\alpha })_{\alpha \in m}\in i^{m}\) such that \(f_{j}\) is m-ary and, for every \(\alpha \in m\), \(f_{k_{\alpha }}\) is n-ary.
Now we will prove, by induction on \(i\in p\), that \(f = f_{p-1}\in \mathrm {PRM}(\mathcal {F})\). For \(i = 0\), \(f_{0}\in \mathrm {PRM}(\mathcal {F})\), because, in this case, \(f_{0}\) either belongs to \(\mathcal {F}_{n}\), for some \(n\in \mathbb {N}\), or is of the form \(\kappa _{0,0}\), or \(\mathrm {sc}\), or \(\mathrm {pr}_{1,0}\), or \(\mathrm {pr}_{n,j}\), for some \(n\ge 2\) and some \(j\in n\), and then \(f_{0}\in \mathrm {PRM}(\mathcal {F})\), because \(\mathrm {PRM}(\mathcal {F})\) is the union of the underlying \(\mathbb {N}\)-sorted set of the least subalgebra of  that contains \(\mathcal {F}\). Let \(k\in p\) and let us suppose that, for every \(i\in k\), \(f_{i}\in \mathrm {PRM}(\mathcal {F})\). Then, by definition, \(f_{k}\in \mathcal {F}_{n}\), for some \(n\in \mathbb {N}\), or \(f_{k} = \kappa _{0,0}\), or \(f_{k} = \mathrm {sc}\), or \(f_{k} = \mathrm {pr}_{1,0}\), or \(f_{k} = \mathrm {pr}_{n,j}\), for some \(n\ge 2\) and some \(j\in n\), or \(f_{k}\) is \(m+1\)-ary and \(f_{k} = {\varOmega }_{\mathrm {R}}^{m}(f_{u},f_{v})\), for a u and a \(v\in k\) such that \(f_{u}\) is m-ary and \(f_{v}\) is \(m+2\)-ary, or \(f_{k}\) is n-ary and \(f_{k} = {\varOmega }_{\mathrm {C}}^{m,n}(f_{j},(f_{k_{\alpha }})_{\alpha \in m})\), for an \(m\in \mathbb {N}-1\), a \(j\in k\) and a family \((k_{\alpha } )_{\alpha \in m}\in k^{m}\) such that \(f_{j}\) is m-ary and, for every \(\alpha \in m\), \(f_{k_{\alpha }}\) is n-ary. It is evident that in the first five cases \(f_{k}\in \mathrm {PRM}(\mathcal {F})\). In the last two cases too \(f_{k}\in \mathrm {PRM}(\mathcal {F})\), because being, by hypothesis, \(f_{0},\dots ,f_{k-1}\in \mathrm {PRM}(\mathcal {F})\), also \(f_{u}\), \(f_{v}\) and \(f_{k_{0}},\dots ,f_{k_{m-1}}\in \mathrm {PRM}(\mathcal {F})\), hence, since \(\mathrm {PRM}(\mathcal {F})\) is the union of the underlying \(\mathbb {N}\)-sorted set of the least subalgebra of
that contains \(\mathcal {F}\). Let \(k\in p\) and let us suppose that, for every \(i\in k\), \(f_{i}\in \mathrm {PRM}(\mathcal {F})\). Then, by definition, \(f_{k}\in \mathcal {F}_{n}\), for some \(n\in \mathbb {N}\), or \(f_{k} = \kappa _{0,0}\), or \(f_{k} = \mathrm {sc}\), or \(f_{k} = \mathrm {pr}_{1,0}\), or \(f_{k} = \mathrm {pr}_{n,j}\), for some \(n\ge 2\) and some \(j\in n\), or \(f_{k}\) is \(m+1\)-ary and \(f_{k} = {\varOmega }_{\mathrm {R}}^{m}(f_{u},f_{v})\), for a u and a \(v\in k\) such that \(f_{u}\) is m-ary and \(f_{v}\) is \(m+2\)-ary, or \(f_{k}\) is n-ary and \(f_{k} = {\varOmega }_{\mathrm {C}}^{m,n}(f_{j},(f_{k_{\alpha }})_{\alpha \in m})\), for an \(m\in \mathbb {N}-1\), a \(j\in k\) and a family \((k_{\alpha } )_{\alpha \in m}\in k^{m}\) such that \(f_{j}\) is m-ary and, for every \(\alpha \in m\), \(f_{k_{\alpha }}\) is n-ary. It is evident that in the first five cases \(f_{k}\in \mathrm {PRM}(\mathcal {F})\). In the last two cases too \(f_{k}\in \mathrm {PRM}(\mathcal {F})\), because being, by hypothesis, \(f_{0},\dots ,f_{k-1}\in \mathrm {PRM}(\mathcal {F})\), also \(f_{u}\), \(f_{v}\) and \(f_{k_{0}},\dots ,f_{k_{m-1}}\in \mathrm {PRM}(\mathcal {F})\), hence, since \(\mathrm {PRM}(\mathcal {F})\) is the union of the underlying \(\mathbb {N}\)-sorted set of the least subalgebra of  that contains \(\mathcal {F}\), \(f_{k} = {\varOmega }_{\mathrm {R}}^{m}(f_{u},f_{v})\in \mathrm {PRM}(\mathcal {F})\) and \(f_{k} = {\varOmega }_{\mathrm {C}}^{m,n}(f_{j},(f_{k_{\alpha }})_{\alpha \in m})\in \mathrm {PRM}(\mathcal {F})\). Therefore, for every \(k\in p\), \(f_{k}\in \mathrm {PRM}(\mathcal {F})\). Hence, for \(k = p-1\), \(f = f_{p-1}\in \mathrm {PRM}(\mathcal {F})\). From this it follows that \(\bigcup _{n\in \mathbb {N}}\mathcal {L}_{n}\subseteq \mathrm {PRM}(\mathcal {F})\). Hereby completing our proof.
that contains \(\mathcal {F}\), \(f_{k} = {\varOmega }_{\mathrm {R}}^{m}(f_{u},f_{v})\in \mathrm {PRM}(\mathcal {F})\) and \(f_{k} = {\varOmega }_{\mathrm {C}}^{m,n}(f_{j},(f_{k_{\alpha }})_{\alpha \in m})\in \mathrm {PRM}(\mathcal {F})\). Therefore, for every \(k\in p\), \(f_{k}\in \mathrm {PRM}(\mathcal {F})\). Hence, for \(k = p-1\), \(f = f_{p-1}\in \mathrm {PRM}(\mathcal {F})\). From this it follows that \(\bigcup _{n\in \mathbb {N}}\mathcal {L}_{n}\subseteq \mathrm {PRM}(\mathcal {F})\). Hereby completing our proof.
From the above proposition, for \(\mathcal {F} = (\varnothing )_{n\in \mathbb {N}}\) one obtains, immediately, a constructive characterization of the set \(\mathrm {PRM}\).
Corollary
Let f be an element of \(\bigcup _{n\in \mathbb {N}}\mathrm {Hom}(\mathbb {N}^{n},\mathbb {N})\). Then \(f\in \mathrm {PRM}\) if, and only if, there exists a \(p\in \mathbb {N}-1\) and a family \((f_{i})_{i\in p}\) in \(\bigcup _{n\in \mathbb {N}}\mathrm {Hom}(\mathbb {N}^{n},\mathbb {N})\) such that \(f = f_{p-1}\) and, for every \(i\in p\), it happens that:
-
1.
\(f_{i} = \kappa _{0,0}\), or
-
2.
\(f_{i} = \mathrm {sc}\), or
-
3.
\(f_{i} = \mathrm {pr}_{1,0}\), or
-
4.
\(f_{i} = \mathrm {pr}_{n,j}\), for some \(n\ge 2\) and some \(j\in n\), or
-
5.
\(f_{i}\) is \(m+1\)-ary and \(f_{i} = {\varOmega }_{\mathrm {R}}^{m}(f_{j},f_{k})\), for a j and a \(k\in i\) such that \(f_{j}\) is m-ary and \(f_{k}\) is \(m+2\)-ary, or
-
6.
\(f_{i}\) is n-ary and \(f_{i} = {\varOmega }_{\mathrm {C}}^{m,n}(f_{j},(f_{k_{\alpha }})_{\alpha \in m})\), for an \(m\in \mathbb {N}-1\), a \(j\in i\) and a family \((k_{\alpha })_{\alpha \in m}\in i^{m}\) such that \(f_{j}\) is m-ary and, for every \(\alpha \in p\), \(f_{k_{\alpha }}\) is n-ary.
Since it will be used afterwards, to prove that the multiplication and exponentiation are primitive recursive mappings, we notice that, for every \(n\in \mathbb {N}\) and every \(k\in \mathbb {N}\), the constant mapping  , which sends every element of \(\mathbb {N}^{n}\) to k, is a primitive recursive mapping.
, which sends every element of \(\mathbb {N}^{n}\) to k, is a primitive recursive mapping.
Proposition
The addition  , defined as:
, defined as:
is a primitive recursive mapping.
Proof
This is so because \(+ = {\varOmega }_{\mathrm {R}}^{1}(\mathrm {pr}_{1,0},{\varOmega }_{\mathrm {C}}^{1,3}(\mathrm {sc},(\mathrm {pr}_{3,2})))\), or in a diagrammatic manner:

where \({\varOmega }_{\mathrm {C}}^{1,3}(\mathrm {sc},(\mathrm {pr}_{3,2}))\) is the mapping from \(\mathbb {N}^{3}\) to \(\mathbb {N}\) obtained as:

\(\square \)
Proposition
The multiplication  , defined as:
, defined as:
is a primitive recursive mapping.
Proof
This is so because \(\cdot = {\varOmega }_{\mathrm {R}}^{1}(\kappa _{1,0}, {\varOmega }_{\mathrm {C}}^{2,3}(+,(\mathrm {pr}_{3,2},\mathrm {pr}_{3,0})))\), or in a diagrammatic manner:

where \({\varOmega }_{\mathrm {C}}^{2,3}(+,(\mathrm {pr}_{3,2},\mathrm {pr}_{3,0}))\) is the mapping from \(\mathbb {N}^{3}\) to \(\mathbb {N}\) obtained as:

\(\square \)
Proposition
The exponentiation  , defined as:
, defined as:
is a primitive recursive mapping.
Proof
This is so because \(\mathrm {exp} = {\varOmega }_{\mathrm {R}}^{1}(\kappa _{1,1}, {\varOmega }_{\mathrm {C}}^{2,3}(\cdot ,(\mathrm {pr}_{3,2},\mathrm {pr}_{3,0})))\), or in a diagrammatic manner:

where \({\varOmega }_{\mathrm {C}}^{2,3}(\cdot ,(\mathrm {pr}_{3,2},\mathrm {pr}_{3,0}))\) is the mapping from \(\mathbb {N}^{3}\) to \(\mathbb {N}\) obtained as:

\(\square \)
Rights and permissions
About this article
Cite this article
Climent Vidal, J., Soliveres Tur, J. The modernity of Dedekind’s anticipations contained in What are numbers and what are they good for?. Arch. Hist. Exact Sci. 72, 99–141 (2018). https://doi.org/10.1007/s00407-018-0202-6
Received:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00407-018-0202-6





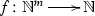 and
and 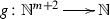 , then, from the principle of definition by mathematical recursion, it follows immediately that there exists a unique mapping
, then, from the principle of definition by mathematical recursion, it follows immediately that there exists a unique mapping 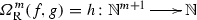 such that the following diagram:
such that the following diagram: 
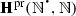 .
.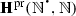 , then
, then 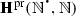 .
.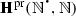 , and if, for every
, and if, for every 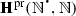 .
.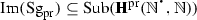 , i.e., for every
, i.e., for every 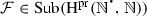 ,
, 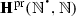 .
.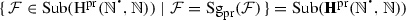 , i.e., the fixed points of
, i.e., the fixed points of 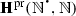 .
.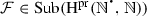 , it happens that
, it happens that 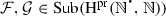 , if
, if 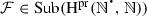 , it happens that
, it happens that 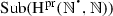 , if, for every
, if, for every