Abstract
Interannual to decadal variability in the Pacific Ocean is a prominent feature of Earth’s climate system, with global teleconnections. Recent studies have identified Pacific decadal variability as a major driver of periods of rapid and slower global mean surface air temperature change. Here, we use an eddy-permitting global ocean model to investigate the role of the observed 1992–2011 trade wind intensification and concurrent trends in surface atmospheric variables over the Pacific associated with the negative phase of the Interdecadal Pacific Oscillation (IPO) in driving ocean circulation and heat content changes. We find a strengthening of the Equatorial Undercurrent (EUC) in response to strengthened winds, which brings cooler water to the surface of the eastern Pacific and an increase in the Pacific shallow overturning cells (PSOC), which in turn drives additional heat into the subsurface western Pacific. The wind acceleration also results in an increase in the strength and subsequent heat transport of the Indonesian throughflow (ITF), which transports some of the additional heat from the western Pacific into the Indian Ocean. The circulation changes result in warming of the subsurface western Pacific, cooling of the upper eastern Pacific Ocean and warming of the subsurface Indian Ocean, with an overall increase in Indo-Pacific heat content. Further experiments impose a symmetric reversal of the atmospheric state to examine how the ocean would behave if the winds (and other atmospheric variables) were to revert to their initial state. This mimics a return to the neutral phase of the IPO, characterised by a weakening of the Pacific trade winds. In response we find a slowdown of the EUC and the PSOC, which results in a return to climatological SST conditions in the western and eastern Pacific. The ITF also slows towards its original strength. However, the subsurface temperature, heat content and ITF responses are not symmetric due to an overall increase in the surface heat flux into the ocean associated with the cooler surface of the Pacific. There may also be irreversible heat transport across the thermocline via diapycnal mixing, further contributing to this asymmetry. The net result of the experiment is that the Indo-Pacific subsurface ocean is warmer than it was in its initial state.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Decadal variability in the Pacific is largely associated with the Interdecadal Pacific Oscillation (IPO), first defined by Power et al. (1999) and Folland et al. (1999). This mode is strongly correlated with the Pacific Decadal Oscillation (PDO) (Mantua et al. 1997), which relates to a SST dipole in the North Pacific (Han et al. 2014). The negative phase of the IPO is characterised by eastern Pacific cooling and northwest and southwest Pacific warming and a strengthening of the equatorial trade winds over the Pacific Ocean (Folland et al. 1999). The climate of the last century, as measured by global mean surface air temperature (SAT), is modulated by the IPO on decadal timescales (Meehl et al. 2009; Kosaka and Xie 2013; Trenberth and Fasullo 2013; Meehl et al. 2013; England et al. 2014; Maher et al. 2014; Dai et al. 2015; Steinman et al. 2015; Roberts et al. 2015; Yao et al. 2016; Kosaka and Xie 2016; Meehl et al. 2016b; Middlemas and Clement 2016).
The Pacific shallow overturning circulation (PSOC) can be largely understood by investigating subtropical cells (STC), which connect tropical upwelling areas to subtropical subduction (Liu 1994; McCreary and Lu 1994). These cells provide a connection between subtropical wind changes and tropical SSTs (Farneti et al. 2014b). Modulation of the STC by mid-latitude winds may help to explain low frequency changes in tropical SST (Farneti et al. 2014a). Using an single ocean model forced with CORE IAF.v2 interannually varying atmospheric forcing since 1948, Farneti et al. (2014a) were able to reproduce observed changes in STC transport, convergence and tropical Pacific SST anomalies when run at multiple resolutions. They found that STC strengthening is associated with equatorial Pacific cooling, and weakening with equatorial Pacific warming and demonstrated that STC variability is a major driver of Pacific decadal variability. The importance of the STC in low frequency SST anomaly modulation has also been demonstrated in the CMIP5 models (Song et al. 2014).
Farneti et al. (2014a) also simulated a decrease in the STC up until the late 1990s, consistent with the observational results of McPhaden and Zhang (2002) based on hydrographic sections. Weakened STC driven by a weakening of the Hadley Circulation and an associated weakened sub-tropical wind stress is shown to result in a reduction in the transport of cooler subtropical water into the tropics and an increase in the surface temperature of the tropics (Farneti et al. 2014b). Farneti et al. (2014a, b) emphasise the role of subtropical wind trends as dominant drivers of STC changes, however, another study by Nonaka et al. (2002) found that equatorial SST anomalies on decadal timescales are equally influenced by tropical and subtropical wind trends. McPhaden and Zhang (2004) also found an increase in the STCs, beginning in the late 1990s. This spin up is consistent with the postulation by England et al. (2014) that a negative IPO associated with a spin-up of the STC drove heat from the surface to subsurface ocean during the period 1992–2012.
There has been an increase in the Walker circulation and the associated Pacific trade winds since 1992 (L’Heureux et al. 2013; England et al. 2014), with the strongest acceleration observed over the period 2003–2012 (Saenko et al. 2016). While we would not expect the phase of decadal variability to be the same in unforced climate models as in observations, the CMIP5 models are not able to reproduce any 20 year periods with a wind intensification that matches the observed increase over the 1992–2011 period (England et al. 2014). It is unclear whether the strengthening of the trade winds is purely related to internal Pacific variability (and that the models are underestimating the strength of multi-decadal variability; e.g. Han et al. 2014; Kociuba and Power 2015) or whether the strengthening is affected by external forcing such as the recent warming in the Atlantic Ocean (McGregor et al. 2014; Kucharski et al. 2016; Li et al. 2016; Chikamoto et al. 2016; Kajtar et al. 2017) or enhanced tropical Indian Ocean warming (Luo et al. 2012; Han et al. 2014; Hamlington et al. 2014; Mochizuki et al. 2016).
It has been suggested that the recent wind increase and concurrent negative IPO phase was at least partially responsible for the slowdown in the warming of SAT that occured over the period 2001–2014 (Kosaka and Xie 2013; England et al. 2014). England et al. (2014) emphasise the role of the negative IPO and associated STC changes in the drawdown of heat into the subsurface tropical Pacific Ocean, which acts to cool the surface, thereby reducing global SAT. An observational study by Nieves et al. (2015) supports this result. They examine three different observational products and three different reanalysis datasets and suggest that a cooling at the ocean surface was compensated for by warming at 100–300 m in the western Pacific and Indian Oceans over the period 2003–2012. Recent modelling by Lee et al. (2015) suggests that the Indian Ocean also played an important role in storing the heat during this period. They found an increase in heat content in the upper 700 m of the Indian Ocean over the period 2003–2012. Their study suggests that over the course of the recent hiatus, OHC in the Pacific initially increased, however the additional heat was subsequently transported into the subsurface Indian Ocean due to an increase in the Indonesian throughflow (ITF) transport. They argue that the increase in ITF transport is due to an anomalous pressure gradient between the west Pacific and east Indian Ocean associated with stronger Pacific trade winds.
The motivation of this study is to better understand the response of ocean circulation and heat content in the Indo-Pacific region to Pacific atmospheric variability, particularly over the period considered by England et al. (2014). Here, a high-resolution eddy-permitting ocean model is used to investigate the role of the Pacific wind intensification and other associated atmospheric state changes in driving subsurface heat content and circulation trends (IPO\(^{-}\) experiment). A recent paper predicts an imminent transition toward a positive IPO (Meehl et al. 2016a), indeed, the Pacific Decadal Oscialltion (highly correlated with the IPO) has been in a positive phase since late 2014 (NOAA 2017b) in combination with a weakening of the trade winds between late 2014 to early 2016 (NOAA 2017a). Given the possibility of a phase change, we investigate how the ocean would respond to a symmetric reversal in the atmospheric forcing back to the IPO neutral state (IPO\(^{neut}\) experiment). Further details of the model experimental design can be found in Sect. 2. Results are presented and discussed in Sects. 3–5. Finally in Sect. 6 we summarise and conclude the main findings of this study.
2 Methods
2.1 Model description
The model used in this study is the eddy-permitting Modular Ocean Model 5 (MOM5). This is a global ocean and sea ice model based on the Geophysical Fluid Dynamics Laboratory (GFDL) CM2.5 coupled climate model (Delworth et al. 2012). This model is integrated on a 1/4 degree Mercator grid, which has displaced poles over northern Canada and Russia (Delworth et al. 2012) and has 50 depth levels in a z* coordinate system. The model is forced by prescribing the surface atmospheric state, which is converted to ocean surface fluxes using bulk formulae (Spence et al. 2014).
The model does not have an eddy parameterisation, but does include a sub-mesoscale mixed layer eddy parameterisation (Fox-Kemper et al. 2011). It uses a third order finite difference advection scheme, namely the piecewise parabolic method (PPM) (Delworth et al. 2012). There is no explicit lateral diffusion and no background vertical diffusion. The K-profile parameterisation (KPP) vertical mixing scheme is used (Large et al. 1994), as is a coastal mixing scheme from Lee et al. (2006) and an internal tide mixing scheme from Simmons et al. (2004). The model has low viscosity with a Smagorinsky biharmoinc formulation used with prescribed background viscosity (Griffies and Hallberg 2000).
This model was initially spun up for 200 years subject to a repeating CORE normal year forcing (CNYF) (Large and Yeager 2004). The CNYF contains synoptic variability and has been derived from 43 years of atmospheric data to present one nominal normal year, representative of El Niño Southern Oscillation neutral conditions, with no major anomalies associated with other modes of climate variability. The CNYF specifies annual mean runoff, monthly varying precipitation, daily varying radiative fluxes and 6 h varying meteorological fields (Griffies et al. 2009).
The prescribed atmospheric fields used to force the model in each experiment are: specific humidity, northerly and easterly wind speed, temperature at 10 m, longwave radiation, shortwave radiation, precipitation and sea level pressure (examples are shown in Fig. 1a–c). The model uses this information in conjunction with the internally calculated SST to compute air-sea heat fluxes via bulk formulae. Heat fluxes in the model depend on windspeed, SAT, SST, specific humidity, longwave radiation (both upward and downward) and downward shortwave radiation.
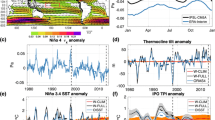
ERA-interim reanalysis trends over the period 1992–2011 for: a specific humidity (kg/kg/year), b easterly wind velocity (m/s/year), c SAT (\(^{\circ }\)C/year) and d surface flux from the IPO\(^{-}\) experiment. The dashed region indicates the outline of the Pacific only region, where input trends are reduced over four grid points using the scaling \(\sin (x)\), where x ranges from zero to \(\pi /2\) with increments of \(\pi /10\)
2.2 Experimental design
A perturbation trend experiment is designed to examine the role of the recent observed trade wind intensification and concurrent trends in atmospheric fields in the Pacific on subsurface heat content, ocean temperatures and circulation. Here, an ocean only model is used so that we can control the overlying atmospheric forcing applied. The atmospheric forcing consists of repeating CNYF fields with linearly increasing anomalies (over a 20 year period) superimposed over the Pacific basin. The anomalies are based on the observed IPO negative trends in surface variables calculated from ERA-interim (Fig. 1a–c; 1992–2011) (Balsamo et al. 2012). Repeating CNYF fields are used outside the Pacific basin. This results in an idealized transition towards a negative IPO (IPO\(^{-}\) experiment). This period was chosen to match the study by England et al. (2014), which was flagged as a period of unprecedented strengthening of the trade winds, corresponding to a time of transition from a positive phase of the IPO through to a negative phase. The dashed region in Fig. 1 indicates the outline of the Pacific only region, where input trends are reduced over four grid points using the scaling \(\sin (x)\), where x ranges from zero to \(\pi /2\) with increments of \(\pi /10\).
Meehl et al. (2016a) predict a imminent transition to a positive IPO, which agrees well with the observed weakening of the trade winds between late 2014 and early 2016 (NOAA 2017a). The IPO\(^{neut}\) experiment extends the IPO\(^{-}\) experiment for a further the 20 years over the period of 2012–2031, to investigate possible changes associated with the return to a neutral IPO. Specifically, the experiment is run with exactly the opposite atmospheric trends used in the original experiment only now applied to the atmospheric state taken at the end of the IPO\(^{-}\) experiment. As such the atmospheric surface forcing returns to CNYF by the end of 2031.
Two additional sensitivity experiments are also carried out for the IPO\(^{-}\) experiment. In the first, forcing changes associated with the wind speed trends in isolation are only applied in the Pacific region to isolate the wind driven changes from the other atmospheric driven changes (i.e. no change is made to SAT or other atmospheric variables). This experiment is somewhat unrealistic, as the system in the tropics is highly coupled and any change in winds will also be accompanied by changes in SST, SAT, sea level pressure, humidity, and so on. While SAT is fixed, wind changes alone can result in heat flux changes. The second sensitivity experiment applies ERA-Interim atmospheric trends globally, in order to identify the additional effect on the ocean of extra-Pacific atmospheric field changes.
A control experiment with only CNYF global input fields is run in parallel to the transient experiments. Models are known to exhibit spurious long term trends or drift, which are largely independent of variability and forcing, especially in the deep ocean (Sen Gupta et al. 2013). We find that while there is some drift in the control run, it is considerably smaller than the forced trends.
2.3 Transport and heat calculations
As identified by Lee et al. (2015), the ITF is important in the transfer of heat from the Pacific to the Indian Ocean, motivating the ITF calculations in this study. ITF volume and heat transport are calculated along 114.9\({^{\circ }}\)E as in England and Huang (2005). ITF volume transport is calculated as
where \(y_{0}\) is \(-\,22.5{^{\circ }}\) latitude, \(y_{1}\) is \(-\,8.5{^{\circ }}\) latitude, \(-\,H\) is the ocean depth and \(\eta\) is the ocean surface. ITF heat transport is given as
where \(\rho\) is density (1035.0 kg m\(^{-3}\)), \(c_{p}\) is specific heat capacity at constant pressure (3992.1.0 J \({^{\circ }}\text {C}^{-1}\,\text {kg}^{-1})\), \(\theta\) is temperature and \(\theta _{r}\) is the reference temperature taken as 3.4 \({^{\circ }}\)C as in England and Huang (2005) and Vranes et al. (2002) (this is the spatially averaged observed temperature between Australia and Antarctica).
In this study we are also interested in OHC in order to evaluate the total heat storage changes in each ocean basin over the experiment. OHC anomalies are calculated as:
where \(y_{0}\) \(y_{1}\) \(x_{0}\) and \(x_{1}\) are the latitude and longitude bounds of the region of interest. \(\rho\) is density (1035.0 kg m\(^{-3}\)), \(c_{p}\) is specific heat capacity at constant pressure (3992.1 J \({^{\circ }}\text {C}^{-1}\,\text {kg}^{-1})\), both as specified for heat transport within the model, \(\theta _{r}\) is again a reference temperature, only here it is taken as the annual 3-D control experiment temperature, chosen to show the increase in heat content in comparison to the unforced scenario.
3 IPO\(^{-}\) experiment
3.1 Comparison with observed temperature trends
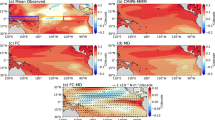
The IPO\(^{-}\) simulation reproduces a negative IPO-like pattern with east Pacific cooling and west Pacific warming as found in the observations, however, the magnitude of the pattern is smaller than observed, with trends which are too strong in the southern extratropics (Fig. 2). To examine subsurface trends we only consider trends after 2003, when the observational uncertainly is considerably reduced due to the introduction of Argo [as demonstrated by the uncertainty fields from Levitus et al. (2012)] (Fig. 3b). The simulated trends are broadly similar to those found in the observations (Fig. 3a), however, the eastern Pacific cooling in the thermocline is underestimated, and the western Pacific subsurface warming extends too far into the central Pacific and does not reach the surface in the far western Pacific. While our study considers a linear increase in the winds over the period 1992–2011, observations show that the wind trend is not linear with the strongest trend found post 2003 (Saenko et al. 2016). This could be a factor in the weaker simulated cooling found in this comparison. The underestimated Eastern Pacific cooling may also be due to difficulties of the model in representing turbulent vertical mixing, an important element of the upper-ocean heat budget in this region. Here, the mixing processes in and above the thermocline are not well parameterised in many models due to their complexity and fine vertical structure (Moum et al. 2013).
Temperature trends over the period 1992–2011 (\({^{\circ }}\)C/year) for: a observed SST from HadISST (Rayner et al. 2003), b IPO\(^{-}\) experiment SST. Dashed lines indicate the outline of the forced Pacific region
Longitude versus depth section of the temperature trend averaged between 5\({^{\circ }}\)N and 5\({^{\circ }}\)S (\({^{\circ }}\)C/year). Shown over the Argo period 2003–2011 for a observations similar to Nieves et al. (2015) (Levitus et al. 2012) and b model results. Mean temperature contours (\({^{\circ }}\)C) are overlaid
3.2 Response of the ocean circulation
Tropical and extratropical Pacific wind driven changes have been shown to modify subsurface temperatures by modifying the strength of the PSOC and changing the magnitude of the transport of heat from the surface into the subsurface western Pacific Ocean (Farneti et al. 2014a; England et al. 2014). The PSOC are cells that reach a few 100 m in depth and extend from the subtropics to the equator as part of the Pacific Meridional Overturning Circulation as shown in Fig. 4. Water subducts primarily in the eastern subtropics and flows equatorward at thermocline depths. At the equator water enters the EUC either in the interior or via western boundary currents and moves eastward and shoals, finally upwelling in the eastern basin, the return flow is largely in the Ekman layer (Liu 1994; McCreary and Lu 1994). As in England et al. (2014), we consider the PSOC, rather than the STC as this metric captures both tropical and subtropical circulation.
Circulation changes in response to the idealised IPO\(^{-}\) and IPO\(^{neut}\) forcing. Pacific shallow overturning circulation (PSOC) (100\({^{\circ }}\)E–60\({^{\circ }}\)W) is shown in contours for the control with colour overlay of: a mean from the control experiment (Sv), b average of the trends between 1992–2011 and 2012–2031, c trend over 1992–2011 (Sv/year) and d trend over 2012–2031 (Sv/year). The PSOC are calculated as the meridional overturning circulation in the Pacific basin as in Farneti et al. (2014a). The trend in eastward velocity [m/s/year; representative of the equatorial undercurrent (EUC)] is shown for: e 1992–2012 and f 2012–2031, with the mean velocity contours overlaid for each experiment. Transport (Sv) is shown for: g EUC (found by integrating the transport between 10\({^{\circ }}\)S and 10\({^{\circ }}\)N in the top 450 m for 160\({^{\circ }}\)W and 160\({^{\circ }}\)E) and h PSOC transport (defined as maximum transport of PSOC) for both the Northern and Southern Hemisphere components
The PSOC accelerates in response to the imposed changes in the atmospheric fields in the IPO\(^{-}\) experiment (Fig. 4c, h). This acceleration shows an intensification relative to the control experiment, which extends much deeper south of the equator than north. The largest changes are seen between 15\({^{\circ }}\)S and 15\({^{\circ }}\)N, with the strongest trends found straddling the Equator around depths of 50–100 m. Between the equator and 10\({^{\circ }}\)S negative anomalies extend to much greater depths (approx. 500 m), clearly indicating an acceleration of the PSOC. The location and depth of these changes are similar to those described by Farneti et al. (2014a), who also use the same MOM ocean-only model forced by an interannually varying dataset (CORE IAF.v2) to investigate the PSOC. The sign of the trends in their study are the opposite to those obtained here as they examine changes over a transition to a positive IPO period. Associated with the increase of the PSOC we also see an increase in the EUC (Fig. 4e, g), which brings cooler subsurface water to the upper eastern Pacific (Fig. 2b).
The 20 \({^{\circ }}\)C isotherm (which is a good proxy for the thermocline in the model, i.e. maximum vertical temperature gradient), deepens in the western Pacific and shoals in the east (Fig. 5a). The importance of the wind in modifying thermocline depth and subsurface temperatures over recent decades has been examined by Han et al. (2006). Changes in thermocline depth in addition to changes in the PSOC and EUC could influence the subsurface ocean temperature structure. Han et al. (2006) focused on thermocline changes driven primarily by a trade wind weakening between the 1960s and 1990s, (i.e. similar in direction to the future experiment discussed later in our study). They find that weakening equatorial wind stress results in increased upward Ekman pumping, a shoaling of the thermocline and resultant cooling in the upper thermocline in the central and eastern Pacific. The temperature response relies on the fact that a small vertical displacement of the thermocline can result in large subsurface changes in temperature. The response shown in Fig. 5a is consistent with this study, however for an acceleration of the wind fields. Warming in the western Pacific would also deepen the 20 \({^{\circ }}\)C isotherm, so it is not straightforward to delineate between warming and wind-driven thermocline deepening.
Lee et al. (2015) suggested an important role for the ITF in transporting heat from the western Pacific to the Indian Ocean during the recent hiatus. On interannual timescales, changes in equatorial winds can modulate the ITF transport, with estimates of the ITF transport as low as 5.6 Sv during the 1997 El Niño and as high as 16.9 Sv during the 2007 La Niña (Susanto and Song 2015). We find that over the period 1992–2011, the volume transport increases by approximately 3 Sv (35%) and heat transport increases by approximately 0.4 PW (47%, Fig. 6a, b). Interestingly while the ITF in our model is too low (8.5 Sv) in comparison to observations (15 Sv, Sprintall et al. 2009; Gordon et al. 2010) and simulates only two thirds of the magnitude of heat transport as in the model used by Lee et al. (2015), the heat transport increases by about 20% more in our study compared to the increase seen by Lee et al. (2015).
The increased ITF flow can be clearly seen in the upper 100 m of the water column (Fig. 6d). Weaker increases are simulated in the 100–300 m depth range (figure not shown) with little change in the circulation at greater depths. Given that the ITF is a baroclinic, surface intensified current, we expect the largest changes would be seen at the surface, where the flow field is already the strongest. Figure 6d shows that in the model the ITF intensification occurs through both the Timor Straight and the Lombok Straight at around 8\({^{\circ }}\)S. We also find an intensification further north (around 2\({^{\circ }}\)) in both the Massaker strait and the Lifamatola strait.
Annual ITF transport. a Volume transport (Sv) through 114.9\({^{\circ }}\)E, b heat transport (PW) through 114.9\({^{\circ }}\), c section used for ITF transport calculation overlaid on mean sea surface temperature in the control experiment. The main straits through which the ITF flows are marked by black circles. d Temperature trends (\({^{\circ }}\)C/year) in the ITF region over the period 1992–2011 (IPO\(^{-}\) experiment), overlaid with vectors of ocean velocity trends (m/s/year) in the 0–100 m layer
3.3 Interior temperature trends
In this section we present temperature trends that result from a strengthening of the PSOC, EUC and dynamic wind induced changes in the thermocline depth (20 \({^{\circ }}\)C isotherm). The strongest signal is a warming in the thermocline in the western Pacific between 100 and 300 m near the equator (Figs. 7b, 8a), which is found deeper with the deepening thermocline at higher latitudes (Fig. 9a). At higher latitudes the maximum warming is located further eastwards (Fig. 7a–c) and extends from the surface (where isotherms in the equatorial thermocline outcrop, Fig. 9a) particularly in the Southern Hemisphere. This is suggestive of extra heat being sequestered into the outcropping thermocline in the eastern subtropics. In the eastern Pacific there is a cooling, that is again strongest in the thermocline (although a cooling signal extends to the surface, Fig. 8a). In the Indian Ocean there is warming associated with the increase in the ITF (Figs. 7, 8a, 9). However, the Western Pacific warming trend is about four times stronger than the Indian Ocean warming. The Indian Ocean warms in the 100–300 m layer from about 30\({^{\circ }}\)S to 25\({^{\circ }}\)N (Fig. 9c) with warming extending to 600 m between 10\({^{\circ }}\)S and 30\({^{\circ }}\)S. This warming is asymmetric, with the region south of the equator warming to much greater depths than in the north, consistent with the known pathways of the ITF (van Sebille et al. 2014). Trends are considerably weaker at greater depths (below 500 m; Fig. 7d). The lack of surface warming in the Indian Ocean is found to be due to a increase in the heat flux from ocean to atmosphere in this region and is also due to the experimental design where the surface variables are held constant over this region.
Longitude versus depth section of the temperature trend averaged between 5\({^{\circ }}\)N and 5\({^{\circ }}\)S (\({^{\circ }}\)C/year). Model results for a IPO\(^{-}\) experiment (1992–2011), b IPO\(^{neut}\) experiment (2012–2031) and c average of panel (a, b). Mean temperature contours (\({^{\circ }}\)C) are overlaid
Latitude versus depth sections of temperature trends (\({^{\circ }}\)C/year) with mean temperature contours overlaid in the IPO\(^{-}\) experiment for a Western Pacific (115\({^{\circ }}\)E–160\({^{\circ }}\)W), b Eastern Pacific (160\({^{\circ }}\)W–60\({^{\circ }}\)W) and c the Indian Ocean (80\({^{\circ }}\)E–115\({^{\circ }}\)E)
3.4 Ocean heat content and heat transport
To determine whether the temperature trends discussed above are related to changes in OHC in the Indo-Pacific or whether they are purely due to a redistribution of heat within the ocean, OHC changes are examined for each ocean basin (Fig. 10). Over the course of the simulation there is a net heat gain in the ocean, which is approximately equal to the cumulative surface heat flux into the ocean, indicating a closed heat budget (Fig. 10a).
Almost all of the OHC increase (92%) occurs in the Pacific and Indian Oceans, with the Atlantic losing a small amount of heat between 1992 and 2011 (2%) and the Southern Ocean gaining a small amount of heat (10% of the global gain) (Fig. 10a). There is a discrepancy between the total OHC changes and the cumulative surface flux in the Pacific, indicating that heat is being transported out of this region by the ITF into the Indian Ocean, which then loses heat to the atmosphere (Fig. 11). Lee et al. (2015) find a net decrease in OHC in the Pacific region during the hiatus. In contrast our simulation indicates that the heat content in the Pacific continues to rise over the 20 year period along with the Indian Ocean. Overall, the experiment suggests that heat primarily enters the ocean in the eastern Pacific (Fig. 11a). This additional heat is then redistributed to the western Pacific and Indian Oceans via an acceleration of the PSOC, EUC and the ITF as summarised in Fig. 11b. The reason for no significant heat transport out of the southern boundary in the Indian Ocean, is that the 20 year timescale for wind acceleration is not sufficient to pump water into the interior Western Pacific, through the Indonesian throughflow, and then into the subtropical south Indian Ocean gyre, and out of the southern boundary. Instead, in approximately equal proportions, the heat accumulates in the Indian Ocean, and is also lost back to the atmosphere north of the southern boundary.
When we compare simulated OHC to multiple observational products (Fig. 10b) we see an overall agreement. There are discrepancies between the observational products, which become much smaller post-2003 coinciding with the introduction of Argo floats. The model shows a faster rate of OHC increase over the last four years of the experiment compared to the observational products. This discrepancy could be caused by the lack of interannual variability in the model runs or due to the assumption of a linear increase in wind stress over the period 1992–2011.
a Full depth ocean heat content anomalies and cumulative surface heat flux (10\(^{22}\) J) relative to the control experiment in each ocean basin. b 0–700m global ocean heat content anomalies in both the model and observations (relative to 1992). The basins are defined as: Western Pacific (115\({^{\circ }}\)E–160\({^{\circ }}\)W), Eastern Pacific (160\({^{\circ }}\)W–60\({^{\circ }}\)W), Indian (80\({^{\circ }}\)E–115\({^{\circ }}\)E), Atlantic (60\({^{\circ }}\)W–30\({^{\circ }}\)E) all from 40.5\({^{\circ }}\)S to 65\({^{\circ }}\)N and the Southern Ocean as all longitudes from 90\({^{\circ }}\)S to 40.5\({^{\circ }}\)S
a Cumulative surface heat flux (red into and blue out of the ocean) and cumulative OHC (black) shown as the mean value over the IPO\(^{-}\) experiment for each individual ocean basin (10\(^{22}\) J). The basins are defined as: Pacific (115\({^{\circ }}\)E–60\({^{\circ }}\)W), Indian (80\({^{\circ }}\)E–115\({^{\circ }}\)E), Atlantic (60\({^{\circ }}\)W–30\({^{\circ }}\)E) all from 40.5\({^{\circ }}\)S to 65\({^{\circ }}\)N, the Southern Ocean as all longitudes south of 40.5\({^{\circ }}\)S and the North High-Latitudes as all longitudes north of 65\({^{\circ }}\)N. The implied heat transport between basins is shown in the black arrows and boxes (also in units of 10\(^{22}\) J). Values are overlaid on a map of the mean depth integrated OHC anomalies. b Schematic illustrating the temperature trends (\({^{\circ }}\)C/year) over the period 1992–2011 and the circulation response responsible
4 IPO\(^{neut}\) experiment
To investigate how the ocean would respond to the return to neutral conditions we examine a scenario where the prescribed atmospheric state changes are symmetrically reversed over the subsequent 20 years (2012–2031) such that the atmosphere returns to the 1992 state at the end of 2031. In response to the reversal of the atmospheric fields, there is warming in the eastern Pacific, strong cooling between 100 and 300 m (Figs. 8b, 12b) in the western Pacific and weak cooling extending from 100 to 500m depth south of the equator in the Indian Ocean (Figs. 8b, c, 12b). The resulting Pacific surface trend pattern resembles a transition towards a more positive IPO state (Fig. 12a). These temperature changes are consistent with a weakening of the ITF (Fig. 6a–d), a weakening of the PSOC (Fig. 4d) and a reversal of the thermocline trends (Fig. 5b).
Given non-linearities in the climate system it is interesting to examine whether the response to a symmetric reversal in the atmospheric state results in a symmetric ocean response. This can be seen by averaging the 1992–2011 and 2011–2031 temperature trends (Fig. 8c) and in the cumulative surface flux and OHC displayed in Table 1. Above the thermocline, the trends over the 1992–2011 period are almost exactly matched by opposing trends in the IPO\(^{neut}\) experiment (i.e. the mean is close to zero; Fig. 8c). However, in both the equatorial Pacific and Indian Oceans, there is a residual warming within and below the thermocline to depths of around 400 m (or greater in the Indian Ocean). In the Pacific the residual warming is intensified in the thermocline. This demonstrates that the west Pacific and Indian Oceans cool less than they warmed over the IPO\(^{-}\) experiment and that the eastern Pacific warms more than it cooled between 1992 and 2011. The lack of return to the initial state of the Pacific by the end of the experiment may be caused by asymmetric changes in ITF heat transport into the Indian Ocean (not the wind-driven component, but the component dependent on slower internal baroclinic adjustments) as well as irreversible mixing below the thermocline. Both these responses are slower time-scale adjustments, which involve interior temperature and density adjustments, unlike the fast and symmetric PSOC response that is almost exclusively wind-driven. We note that we have only simulated half of the IPO cycle to investigate the changes associated with the trade wind strengthening and weakening back to neutral state. A full IPO cycle through the positive phase may result in a symmetric OHC response, although we believe that the mixing of heat below the thermocline is not reversible.
In the Western Pacific Ocean, even after the atmospheric fields reverse, the OHC continues to increase for a further two years before it eventually begins to decrease (Fig. 10a). In the western Pacific, the reversal of the OHC increase is also delayed by 2 years (Fig. 10a), with OHC anomalies of \(8.7 \times 10^{22}\) J at the beginning of the reversal and \(1.4\times 10^{22}\) J at the end of the experiment. Unlike in the west, the eastern Pacific begins to gain heat immediately after the reversal at a much greater rate (approximately 7.5\(\times\) faster over the first 4 years following the reversal) than it lost heat in the IPO\(^{-}\) experiment. Here, both the transport of warm water via the EUC from the Western Pacific and the PSOC weakening result in a decrease in the transport of warm water out of the eastern Pacific. In addition the relatively cool initial state of the surface allows additional heat flux into the region, resulting in an overall increase in the warming in the region. Even after the wind reversal, the Indian Ocean shows a continued increase in heat for about 5 years until around 2017, when the region begins to cool. This is due to the continued transport of warm water accumulated in the western Pacific (that remains above its initial strength for most of the simulation) by the ITF (Fig. 6).
Both the Indian and Pacific Oceans accumulate heat over the combined period 1992–2031 (Table 1), with the heat accumulation primarily occurring in the Pacific (70%). Here, the overall heat content increase in the Indo-Pacific is \(12.1 \times 10^{22}\) J just before the reversal (92% of the global gain) and \(6.8\times 10^{22}\) J at the end of the experiment (81% of the global gain). This suggests that if the wind trend were to reverse, the heat content of the Indo-Pacific would not return to its original state. The extra heat in the ocean is due to a net heat flux into the ocean over both experiments as shown in Fig. 10a. As previously mentioned we propose that the transport of heat from the Pacific into the Indian Ocean and mixing of heat below the thermocline cause this asymmetry. The lags found before a reversal in heat content can be explained by the lag in the reversal of the air-sea cumulative heat fluxes (Fig. 10a). The cumulative heat flux continues to increase for two years after the reversal in atmospheric trends, then it is another 4 years before the heat flux begins to decrease. Here, the heat flux anomalies are driven not only by the atmospheric state, but also by the oceanic surface state i.e. the heat flux continues to increase after the reversal in the atmospheric state because the ocean surface is much cooler, causing heat to continue to be moved from the atmospheric boundary layer into the ocean. In this case, given that the ITF heat transport stays above initial values for most of the experiment, heat can only be released from the atmosphere, stay in the Indian Ocean or be transported via ocean circulation out of this region.
The response of the ITF to the wind trend reversal is also asymmetric (Fig. 6a–d). In particular the ITF volume transport initially decreases faster than it increased over the IPO\(^{-}\) experiment, while the decrease slows over the last 4–5 years of the simulation. The ITF transport is below initial values at the end of the experiment. Despite the lack of interannual variability in the forcing there is still some large internally generated variability in the ITF transport. Our results demonstrate that the ITF change is not purely driven by the applied trends in the surface winds, but is also affected by buoyancy changes similar to the density-driven flow mechanism described by Sen Gupta et al. (2016); only in our study for shallower density gradients across the sills of the Indonesian archipelago. The ITF heat transport also initially decreases faster than it increased over the IPO\(^{-}\) experiment, with heat transport decreasing to below initial values around 4–5 years before the end of the experiment, and continuing to decrease until the end of the experiment. As with the volume transport the ITF transport is below initial values at the end of the experiment.
In contrast to the ITF, the decrease in PSOC strength over the course of the IPO\(^{neut}\) experiment is largely symmetric with regard to the changes in wind forcing (Fig. 4d, h), with the weakening trend almost exactly equal and opposite to the strengthening trend over the historical experiment. Here, the PSOC are primarily wind driven features of the Pacific overturning circulation. However, even with a symmetric reversal in the meridional circulation the movement of heat will change as the temperature distribution within the Pacific has changed. The trend in the 20 \({^{\circ }}\)C isotherm (proxy for thermocline depth) shows a deepening/shoaling of the thermocline in the west/east in the IPO\(^{neut}\) experiment (Fig. 5b), however, the response is not symmetric, with the thermocline remaining deeper across most of the Pacific, particularly south of the equator at the end of the experiment (Fig. 5c). The EUC decreases in strength over the period 2012–2031 in comparison to 1992–2012 (Fig. 4f, g). Like the PSOC, the response is relatively symmetric (Fig. 4g).
5 IPO\(^{-}\) sensitivity experiments
5.1 Wind-only Pacific experiment
In order to isolate the importance of changes in Pacific winds from other surface changes an additional experiment is carried out where only trends in surface winds are applied in the Pacific region i.e. SAT, specific humidity etc. were unchanged relative to the control simulation with any changes in the air-sea heat flux are only related to changes in the surface winds. Much of the dynamical changes to the circulation (ITF, PSOC and EUC) are reproduced, as are the changes in the 20 \({^{\circ }}\)C isotherm (figure not shown). The primary difference is in the surface Pacific where the observed SST response is further underestimated because SAT is fixed at its initial value. As a result the accumulation of heat in the Pacific is only 72% of the value found in the IPO\(^{-}\) experiment. Importantly the Indian Ocean response is largely unchanged. The near identical change in the ITF transport in comparison to the IPO\(^{-}\) experiment suggests that the ITF change is largely a dynamical response to the wind. While Lee et al. (2015) find that surface fluxes in both the Indian and Pacific regions are needed to correctly reproduce the recent hiatus, our analysis suggests that changes in the Pacific winds are sufficient to drive heat into the Indian Ocean.
5.2 Globally forced experiment
A second sensitivity experiment, which includes global trends in all atmospheric fields is used to assess the importance of wind and climatological forcing changes outside of the Pacific domain. The results from the experiment show minimal differences in the upper 1000 m in the tropical Pacific region which are confined to depths of 200–400 m outside of 20\({^{\circ }}\)S and 10\({^{\circ }}\)N in the Pacific. Differences between the two experiments only occur south of 10\({^{\circ }}\)S in the Indian Ocean, with some additional cooling seen in this region at the surface. In the Northern Pacific, Southern Ocean and Atlantic, larger temperature trend differences are found. These results demonstrate that there is very little response within the Indo-Pacific region driven by the atmospheric field changes outside the Pacific; instead local Pacific forcing dominates the trends both inside the Pacific Ocean and importantly also within the Indian Ocean.
We find that even in the globally forced sensitivity experiment there are only small Atlantic Ocean heat content trends. This conflicts with the findings of Chen and Tung (2014) who argue for an Atlantic role in the early 2000s hiatus. They suggest that salinity changes in the sub-polar North Atlantic result in an increase in deep convection and heat uptake during the recent hiatus, however, we do not see an increase in heat uptake in the global experiment, despite forcing by ERA-interim estimated climate trends over the global oceans. Our results are however supported by the observational study of Nieves et al. (2015) who find that the Atlantic is not a major driver of increased ocean heat uptake.
6 Summary and conclusions
This study applies linear trends in all atmospheric fields over the period 1992–2011 in the Pacific region to isolate the role of Pacific atmospheric forcing, especially the acceleration of the trade winds, in driving Pacific temperature, circulation and OHC changes. We confirm the results of lower resolution studies by showing warming in the subsurface western Pacific, cooling surface eastern Pacific and warming in the subsurface Indian Ocean associated with an acceleration of the PSOC and ITF. This result compares well with observed temperature trends over the period 2003–2011, in the post-Argo observing era. Sensitivity experiments show that trends in the atmospheric Pacific winds in isolation can explain most of the the subsurface Indian Ocean response, suggesting that the recent Indian Ocean heat content trends are primarily driven by the Pacific wind trends. We suggest that the atmospheric trends during the recent hiatus could cause both the Indian and Pacific Oceans to gain heat.
A symmetric reversal of the atmospheric fields back to their original state shows that the heat content changes are not fully reversible, with the Indo-Pacific having a net increase in heat over the course of the combined experiments. While the PSOC response is largely symmetrical with respect to the reversal of the atmospheric state, there is a clear asymmetry in the heat flux associated with the ITF and in the surface heat fluxes. Additionally heat redistributed to the subsurface Pacific Ocean is partially mixed below the thermocline, a process which is not reversible. As such a return to a neutral IPO phase will not result in a complete reversal in the ocean heat content changes, even if the reversal in atmospheric forcing were perfectly symmetric.
Change history
18 May 2018
Patients with the feeling of a congested nose not always suffer from an anatomical obstruction but might just have a low trigeminal sensibility, which prevents them from perceiving the nasal airstream. We examined whether intermittent trigeminal stimulation increases sensitivity of the nasal trigeminal nerve and whether this effect is accompanied by subjective improvement of nasal breathing.
References
Balsamo G et al (2012) Era-interim/land: a global land-surface reanalysis based on era-interim meteorological forcing. Shinfield Park, Reading, p 25
Chen X, Tung K-K (2014) Varying planetary heat sink led to global-warming slowdown and acceleration. Science 345:897–903
Chikamoto Y, Mochizuki T, Timmermann A, Kimoto M, Watanabe M (2016) Potential tropical Atlantic impacts on Pacific ecadal climate trends. Geophys Res Lett 43:7143–7151
Dai A, Fyfe JC, Xie S-P, Dai X (2015) Decadal modulation of global surface temperature by internal climate variability. Nat Clim Change 5:555–559
Delworth TL et al (2012) Simulated climate and climate change in the GFDL CM2.5 high-resolution coupled climate model. J Clim 25:2755–2781
England MH, Huang F (2005) On the interannual variability of the Indonesian throughflow and its linkage with ENSO. J Clim 18:1435–1444
England MH et al (2014) Intensified Pacific Ocean wind-driven circulation during the ongoing warming hiatus. Nat Clim Change 4:222–227
Farneti R, Dwivedi S, Kucharski F, Molteni F, Griffies SM (2014a) On Pacific subtropical cell variability over the second half of the twentieth century. J Clim 27:7102–7112
Farneti R, Molteni F, Kucharski F (2014b) Pacific interdecadal variability driven by tropical–extratropical interactions. Clim Dyn 42:3337–3355
Folland CK, Parker DE, Colman A (1999) Large scale modes of ocean surface temperature since the late nineteenth century. In: Navarra A (ed) Beyond El Nino: decade 1 and interdecade 1 climate variability. Springer, Berlin, pp 73–102
Fox-Kemper B et al (2011) Parameterization of mixed layer eddies. III: Implementation and impact in global ocean climate simulations. Ocean Model 39:61–78
Gordon A et al (2010) The Indonesian throughflow during 2004–2006 as observed by the INSTANT program. Dyn Atmos Oceans 50(2):115–128
Griffies SM, Hallberg RW (2000) Biharmonic friction with a Smagorinsky-like viscosity for use in large-scale eddy-permitting ocean models. Mon Weather Rev 128:2935–2946
Griffies SM et al (2009) Coordinated ocean-ice reference experiments (COREs). Ocean Model 26:1–46
Hamlington B, Strassburg M, Leben R, Han W, Nerem R, Kim K (2014) Uncovering an anthropogenic sea-level rise signal in the Pacific Ocean. Nat Clim Change 4:782–785
Han W, Meehl G, Hu A (2006) Interpretation of tropical thermocline cooling in the Indian and Pacific oceans during recent decades. Geophys Res Lett. doi:10.1029/2006GL027 982
Han W et al (2014) Intensification of decadal and multi-decadal sea level variability in the western tropical Pacific during recent decades. Clim Dyn 43:1357–1379
Kajtar J, Santoso A, McGregor S, England MH, Baillie Z (2017) Model under-representation of decadal Pacific trade wind trends and its link to tropical Atlantic bias. Clim Dyn 48:2173–2190
Kociuba G, Power S (2015) Inability of CMIP5 models to simulate recent strengthening of the Walker circulation: implications for projections. J Clim 28:20–35
Kosaka Y, Xie S-P (2013) Recent global-warming hiatus tied to equatorial Pacific surface cooling. Nature 501(7467):403–407
Kosaka Y, Xie S-P (2016) The tropical Pacific as a key pacemaker of the variable rates of global warming. Nat Geosci 9:669–674
Kucharski F et al (2016) Atlantic forcing of Pacific decadal variability. Clim Dyn 46:2337–2351
Large WG, McWilliams JC, Doney SC (1994) Oceanic vertical mixing: a review and a model with a nonlocal boundary layer parameterization. Rev Geophys 32:363–403
Large WG, Yeager SG (2004) Diurnal to decadal global forcing for ocean and sea-ice models: the data sets and flux climatologies. NCAR Technical Note NCAR/TN-460+STR. doi:10.5065/D6KK98Q6
Lee H-C, Rosati A, Spelman MJ (2006) Barotropic tidal mixing effects in a coupled climate model: oceanic conditions in the North Atlantic. Ocean Model 11:467–477
Lee S-K, Park W, Baringer MO, Gordon AL, Huber B, Liu Y (2015) Pacific origin of the abrupt increase in Indian Ocean heat content during the warming hiatus. Nat Geosci 8:445–450
Levitus S et al (2012) World ocean heat content and thermosteric sea level change (0–2000 m), 1955–2010. Geophys Res Lett. doi:10.1029/2012GL051106
L’Heureux ML, Lee S, Lyon B (2013) Recent multidecadal strengthening of the Walker circulation across the tropical Pacific. Nat Clim Change 3:571–576
Li X, Xie S-P, Gille S, Yoo C (2016) Atlantic-induced pan-tropical climate change over the past three decades. Nat Clim Change 6:275–279
Liu Z (1994) A simple model of the mass exchange between the subtropical and tropical ocean. J Phys Oceanogr 24:1153–1165
Luo J, Sasaki W, Masumoto Y (2012) Indian Ocean warming modulates Pacific climate change. In: Proceedings of the National Academy of Sciences, vol 109, no. 46, pp 18,701–18,706
Maher N, Gupta AS, England MH (2014) Drivers of decadal hiatus periods in the 20th and 21st centuries. Geophys Res Lett 41:5978–5986
Mantua NJ, Hare SR, Zhang Y, Wallace JM, Francis RC (1997) A Pacific Interdecadal Climate Oscillation with impacts on salmon production. Bull Am Meteorol Soc 78:1069–1079
McCreary JP, Lu P (1994) Interaction between the subtropical and equatorial ocean circulations: the subtropical cell. J Phys Oceanogr 24:466–497
McGregor S, Timmermann A, Stuecker M, England M, Merrifield M, Jin F-F, Chikamoto Y (2014) Recent Walker circulation strengthening and Pacific cooling amplified by Atlantic warming. Nat Clim Change 4:888–892
McPhaden MJ, Zhang D (2002) Slowdown of the meridional overturning circulation in the upper Pacific Ocean. Nature 415:603–608
McPhaden MJ, Zhang D (2004) Pacific Ocean circulation rebounds. Geophys Res Lett. doi:10.1029/2004GL020 727
Meehl G, Hu A, Arblaster J, Fasullo J, Trenberth KE (2013) Externally forced and internally generated decadal climate variability associated with the Interdecadal Pacific Oscillation. J Clim 26:7298–7310
Meehl G, Hu A, Teng H (2016a) Initialized decadal prediction for transition to positive phase of the Interdecadal Pacific Oscillation. Nat Commun. doi:10.1038/ncomms11718
Meehl GA, Hu A, Santer BD (2009) The mid-1970s climate shift in the Pacific and the relative roles of forced versus inherent decadal variability. J Clim 22:780–792
Meehl GA, Hu A, Santer BD, Xie S-P (2016b) Contribution of the Interdecadal Pacific Oscillation to twentieth-century global surface temperature trends. Nat Clim Change. doi:10.1038/NCLIMATE3107
Middlemas E, Clement A (2016) Spatial patterns and frequency of unforced decadal-scale changes in global mean surface temperature in climate models. J Clim 29:6245–6257
Mochizuki T, Kimoto M, Watanabe M, Chikamoto Y, Ishii M (2016) Interbasin effects of the Indian Ocean on Pacific decadal climate change. Geophys Res Lett 43:7168–7175
Moum J, Perlin A, Nash J, McPhaden MJ (2013) Seasonal sea surface cooling in the equatorial Pacific cold tongue controlled by ocean mixing. Nature 500:64–67
Nieves V, Willis JK, Patzert WC (2015) Recent hiatus caused by decadal shift in Indo-Pacific heating. Science 349(6247):532–535
NOAA (2017a) Monthly atmospheric and SST indicies. http://www.cpc.ncep.noaa.gov/data/indicies/
NOAA (2017b) Pacific decadal oscillation (PDO). http://www.ncdc.noaa.gov/teleconnections/pdo/
Nonaka M, Xie S-P, McCreary J (2002) Decadal variations in the subtropical cells and equatorial pacific SST. Geophys Res Lett 29(7):1116–1120
Power S, Casey T, Folland C, Colman A, Mehta V (1999) Inter-decadal modulation of the impact of ENSO on Australia. Clim Dyn 15:319–324
Rayner NA, Parker DE, Horton EB, Folland CK, Alexander LV, Rowell DP, Kent EC, Kaplan A (2003) Global analyses of sea surface temperature, sea ice, and night marine air temperature since the late nineteenth century. J Geophys Res. doi:10.1029/2002JD002670
Roberts C, Palmer M, McNeali D, Collins M (2015) Quantifying the likelihood of a continued global warming hiatus. Nat Clim Change. doi:10.1038/nclimate2531
Saenko OA, Swart NC, England MH (2016) Influence of tropical wind on global temperature from months to decades. Clim Dyn 47:2193–2203
Sen Gupta A, Jourdain NC, Brown JN, Monselesan D (2013) Climate drift in the CMIP5 models. J Clim 26(21):8597–8615
Sen Gupta A, McGregor S, van Sebille E, Ganachaud A, Brown JN, Santoso A (2016) Future changes to the Indonesian Throughflow and Pacific circulation: the differing role of wind and deep circulation changes. Geophys Res Lett. doi:10.1002/2016GL067 757
Simmons HL, Jayne SR, Laurent LCS, Weaver AJ (2004) Tidally driven mixing in a numerical model of the ocean general circulation. Ocean Model 6:245–263
Song Y, Yu Y, Lin P (2014) The hiatus and accelerated warming decades in CMIP5 simulations. Adv Atmos Sci 31:1316–1330
Spence P, Griffies SM, England MH, Hogg AM, Saenko OA, Jourdain NC (2014) Rapid subsurface warming and circulation changes of Antarctic coastal waters by poleward shifting winds. Geophys Res Lett 41:4601–4610
Sprintall J, Wijffels S, Molcard R, Jaya I (2009) Direct estimate of the Indonesian Through-flow entering the Indian Ocean: 2004–2006. J Geophys Res. doi:10.1029/2008JC005 257
Steinman BA, Mann ME, Miller SK (2015) Atlantic and Pacific multidecadal oscillations and Northern Hemisphere temperatures. Science 347(6225):988–991
Susanto R, Song Y (2015) Indonesian throughflow proxy from satellite altimeters andgravimeters. Geophys Res Lett 120:2844–2855
Trenberth KE, Fasullo JT (2013) An apparant hiatus in global warming? Earth’s Future 1(1):19–32
van Sebille E, Sprintall J, Schwarzkopf FU, Sen Gupta A, Santoso A, England M, Biastoch A, Boning C (2014) Pacific-to-Indian Ocean connectivity: tasman leakage, Indonesian Throughflow, and the role of ENSO. J Geophys Res Oceans 119(2):1365–1382
Vranes K, Gordon AL, Field A (2002) The heat transport of the Indonesian Throughflow and implications for the Indian Ocean heat budget. Deep Sea Res 49B:1391–1410
Yao S-L, Huanf G, Wu R-G, Qu X (2016) The global warming hiatus—a natural product of interactions of a secular warming trend and a multi-decadal oscillation. Theoret Appl Climatol 123:349–360
Acknowledgements
Open access funding provided by Max Planck Society. This work was supported by the Australian Research Council (ARC) including the ARC Centre of Excellence in Climate System Science, and an award under the Merit Allocation Scheme on the NCI National Facility at the ANU, Canberra. We would like to thank Ryan Holmes for his input and advice on the transport calculations. We would also like to thank the two anonymous reviewers for their helpful comments. This work was funded by Grant number FL100100214.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The authors declare that they have no conflict of interest.
Additional information
The original version of this article was revised: The original published manuscript had an error in the units of many figures. All figures with the incorrect units per 20 years have been corrected to per year. We note that for Fig. 5 the units of per 20 years were originally correct and have not been changed.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Maher, N., England, M.H., Gupta, A.S. et al. Role of Pacific trade winds in driving ocean temperatures during the recent slowdown and projections under a wind trend reversal. Clim Dyn 51, 321–336 (2018). https://doi.org/10.1007/s00382-017-3923-3
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00382-017-3923-3