An ensemble climate projection for Africa

Abstract

The Met Office Hadley Centre’s PRECIS regional climate modelling system has been used to generate a five member ensemble of climate projections for Africa over the 50 km resolution Coordinated Regional climate Downscaling Experiment-Africa domain. The ensemble comprises the downscaling of a subset of the Hadley Centre’s perturbed physics global climate model (GCM) ensemble chosen to exclude ensemble members unable to represent the African climate realistically and then to capture the spread in outcomes from the projections of the remaining models. The PRECIS simulations were run from December 1949 to December 2100. The regional climate model (RCM) ensemble captures the annual cycle of temperatures well both for Africa as a whole and the sub-regions. It slightly overestimates precipitation over Africa as a whole and captures the annual cycle of rainfall for most of the African regions. The RCM ensemble substantially improve the patterns and magnitude of precipitation simulation compared to their driving GCM which is particularly noticeable in the Sahel for both the magnitude and timing of the wet season. Present-day simulations of the RCM ensemble are more similar to each other than those of the driving GCM ensemble which indicates that their climatologies are influenced significantly by the RCM formulation and less so by their driving GCMs. Consistent with this, the spread and magnitudes of the large-scale responses of the RCMs are often different than the driving GCMs and arguably more credible given the improved performance of the RCM. This also suggests that local climate forcing will be a significant driver of the regional response to climate change over Africa.

Introduction

Global climate models (GCMs) are physically-based models of the important components of the climate system and are the main tools for generating projections of how climate may change in the future. GCM projections may be adequate up to a few hundred kilometres or so, however they capture neither the local detail nor the local forcing, both of which can be important for regional climate as well as for impact assessments at national and regional levels. A widely applied and flexible method for capturing these local forcings and detail is to use a higher resolution regional climate model (RCM) driven at the edges of its domain of application by boundary conditions from a GCM (Giorgi 2007).

RCMs are also physically based models incorporating representations of the important processes of the climate system and resolve, at higher resolution, the processes, interactions and feedbacks between the climate system components over their domain of application. RCMs simulate dynamical flow, radiative and convective processes, clouds and precipitation, the land surface and the deep soil and the fluxes of heat and moisture between all these components are all represented in the RCM. With a few notable exceptions (e.g. Döscher et al. 2002; Artale et al. 2010; Ratnam et al. 2008) RCMs do not model oceans explicitly as this would substantially increase the computing cost yet, in many cases, would make little difference to the projections over land where most impact assessments are conducted. More information on the RCM configuration used in this study is given in Sect. 2.

It has long been recognised that a single model projection whilst often providing a plausible representation of climate gives no indication of the range of outcomes which are required when trying to assess the risks or opportunities of future climate change and how to respond to them. For this a range of projected future climate changes is required, preferably with some assessment of their trustworthiness. There are a number of ways in which an ensemble of climate projections can be generated and here we have here adopted a perturbed physics ensemble (PPE) approach. A PPE enables modelling uncertainties to be sampled systematically by perturbing uncertain parameters in a climate model (Collins et al. 2006).

The Met Office Hadley Centre has run a large PPE as part of a project entitled. Quantifying Uncertainties in Model Projections (QUMP) based on the HadCM3 global model (Gordon et al. 2000; Pope et al. 2000; Collins et al. 2001). This ensemble, some members of which were downscaled over Europe, was used as the basis of the UK Climate Projections 2009 (Murphy et al. 2009). The UKCP09 projections were generated to help inform adaptation options in the UK. However, data from the subset of GCMs downscaled are also available globally and in this paper we describe how these have been used to develop a set of policy-relevant climate scenarios for Africa.

The experimental set-up for the regional model simulations is described in Sect. 2, including an account of some adjustments made to ancillary files in order to improve the representation of the African great lakes in the model. The method and subsequent selection of ensemble members for Africa is given in Sect. 2.2. Section 4 investigates how well the RCM results are able to reproduce the current climate and Sect. 5 presents the precipitation changes projected by the model by the 2080s over the domain. In Sect. 6 we summarise the model set-up, performance and projections.

Description of models, observations and experimental design

GCMS

The individual members of the QUMP ensemble are referred to as HadCM3Q0–16, where HadCM3Q0 is the unperturbed member (the parameters values are the same as those used by the standard HadCM3 GCM) and the perturbed members Q1–16 are numbered according to the value of their global climate sensitivity, thus Q1 has the lowest global average temperature response to a given increase in atmospheric $\hbox {CO}_2$, and Q16 the highest. From here on, these models are referred to simply as Q0–Q16. To downscale a GCM ensemble of this size with an RCM would be highly resource intensive. We therefore employ a method outlined in McSweeney et al. (2012) to sample from the ensemble in order to select a subset which represents a similar range of outcomes as the full ensemble.

RCMs

The regional configuration of the Met Office Hadley Centre Climate model, HadRM3P (Jones et al. 2004), was run for the period from December 1949 to December 2100 for whole of Africa using the domain defined by the Coordinated Regional climate Downscaling Experiment (CORDEX) project (Giorgi et al. 2009). The HadRM3P configuration for these simulations has a resolution of 50 km, with 19 vertical atmospheric levels and includes MOSES 2.2 (Met Office Surface Exchange Scheme version 2.2), a tiled land surface scheme (Essery et al. 2001) with 4 soil levels. The chosen global QUMP ensemble members, which were selected using the methodology outlined in Sect. 2.5, provide the boundary conditions for the RCM simulations. In all of the ensemble members the SRES A1B scenario (Nakicenovic et al. 2000) is used to represent future emissions; this scenario contains no mitigation and represents only one of several possible futures considered in the 4th assessment report of the IPCC (Meehl et al. 2007b).

Observations

Validating models’ simulations against observations can be a challenging exercise in Africa. Data coverage is generally sparse and the observational record often show significant discontinuity in times. While there is no simple solution to this lack of data we tried to address the issue by looking at a number datasets which use different techniques and data sources. The observed datasets used are detailed Table 1.

Table 1 Observational datasets used for validation of regional model simulations for Africa

The African Great Lakes

The African Great Lakes are an important feature of Africa and are crucial in representing the climate of the region. In HadRM3P and MOSES2.2 there is no specific lake model and therefore the model makes certain assumptions when the lakes are set to be inland water or sea points. A limitation of this particular configuration of the regional model is that lakes are assumed to be at sea level, and lake surface temperatures are interpolated from the nearest sea point. This results in a warm bias in the lake surface temperatures, and subsequently excessive evaporation. In order to alleviate the problem in these simulations, two actions are taken; first the Great Lakes are set to land points in the domain orography which means that they are at the correct height above sea level, but are maintained as water by the land-sea mask. Secondly, the lake surface temperatures in the SST ancillary files must be corrected from the values that were interpolated from sea points, using lake surface temperature observations.

We use the (night-time) climatological lake mean temperatures for each month for Lake Nyasa (Malawi), Tanganyiki and Victoria from the ARCLake project v1.1.2 (MacCallum and Merchant 2010, 2011), covering the period 1995–2009. The biases in the ancillaries are calculated from the difference between the observed annual temperature cycle and the model annual temperature cycle over a baseline period (1961–1990) for the unperturbed QUMP run (Q0), rounded to the nearest 0.5 K. These biases are then applied to each model run over their entire time period, which assumes all model runs have a common bias. This process is illustrated in Fig. 1; the black curve shows the annual cycle of observations and the yellow curve shows the annual cycle of the original Q0 ancillary. Once bias corrected to the observations (light-blue), the model ancillary is much closer to the observed ARCLake mean temperatures. As an example, the uncorrected (red) and corrected (dark-blue) annual cycle from another model run (Q2) is also included, illustrating that the correction derived for Q0 also improves the lake surface temperatures in this model run. A key assumption made here is that the bias correction applied will remain relevant into the future, i.e. that the difference between the true lake mean temperatures (as provided by ARCLake) and the temperatures interpolated from the nearest sea point will remain the same in a future climate. However, given that the bias between the model ancillaries and the lake mean temperatures from ARCLake is large, almost 3° in some cases, the application of the bias correction is necessary to ensure that the current and near future climate is represented correctly.

Fig. 1

The annual variation of the ARCLake observations (black); the original lake surface temperature ancillaries for two of the model ensemble members (red and yellow); and the lake surface temperature ancillaries after bias corrected to observations (blue and light blue)

Selection of driving GCM runs

In order to reduce the computational requirements, only a sub-set of the 17-member QUMP ensemble was downscaled from the global models. To identify the most informative selection we adopt the procedure outlined in McSweeney et al. (2012).

First we eliminate the ensemble members that perform poorly in simulating the key features of the current African regional climate.

Once this operation is completed we select, from those remaining, the sub-set that best captures the range of responses in temperature and precipitation simulated by the 17 QUMP ensemble members.

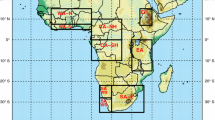
In order to select the most appropriate sample the broad range of climatic regimes that occur across Africa must be considered. For this reason, as well as validating the QUMP ensemble projections against temperature and precipitation data for the whole of Africa, we also present results for nine geographical sub-regions that were chosen to represent the different climatic regimes across Africa. The climatic regions are shown in Fig. 2.

Fig. 2

Regions selected for validating QUMP ensemble members across different climatic regions of Africa. Moving left to right along each row, the panels show: Africa, Northern Africa, West Sahel, Central Sahel, East Sahel, Western Tropical Africa, Horn of Africa, Southern Africa, and Kenya

The coordinates that have been used to define the Africa region and the other climatic sub-regions are illustrated in Fig. 2 and given in Table 2.

Table 2 The Western longitude (W), Eastern longitude (E), Northern latitude (N) and Southern latitude (S) of the sub-regions

Validation of the African climate simulations

To validate the performance of the models, we compared the observed and simulated annual cycles of temperature and precipitation ( Fig. 3, and the geographical patterns of precipitation and 850 hpa winds in the simulations to those in observed datasets for the period 1961–1990 (not shown). The annual cycle of temperature for the whole of Africa suggests that the models capture the seasonal cycle of temperature realistically, although the majority slightly over-estimate temperatures between May and September (Fig. 3, top left).

Most models also capture the different seasonal cycles of temperature in the sub-regions although for some there is a greater spread in the simulations (e.g. Southern Africa in October), Model Q16 tends to be consistently the warmest model, and lies apart from the other models, and Q4 the coolest. The temperatures for Central Sahel, Fig. 4 (top left) and East Sahel, Fig. 4 (middle left) are generally under-estimated by most of the models for the period between April and June. In general the ensemble captures the annual cycle of rainfall for many of the regions of Africa shown here (Fig. 3, right column), however again there are differences in spread between ensemble members for different regions.

The simulations capture the main rainy season in the Sahelian regions in JAS, although the rainy season begins 2–3 months too early in most of the models for Central and East Sahel, and the range of magnitudes of wet-season rainfall is large. Rainfall in the western Tropical region arrives in the correct seasons, but is systematically too large, to a varying degree depending on the particular ensemble member. The simulations of precipitation for some of the sub-regions do not compare that well with observations, for example the northern Africa region seasonal cycle is not captured at all (Fig. 3, middle right) and though the two wet seasons observed in Kenya (Fig. 5, bottom right) are simulated by the ensemble, the first [March, April, May, (MAM)] is under-estimated by all of the ensemble members and the second [September, October, November (SON)] is over-estimated by some.

However, modelling the climate of Africa is a challenge, as highlighted in the IPCC 4th assessment (Solomon et al. 2007) , which noted excess rainfall over southern Africa of over 20 % on average in 90 % of the GCMs assessed and a tendency for the Inter-Tropical Convergence zone to be displaced towards to equator. In addition, several of the GCMs had no representation of the West African Monsoon at all (Meehl et al. 2007b). Also, given that the amounts of precipitation that occur in some of these sub-regions is very small it is helpful to compare the geographical patterns of precipitation with observations.

For the seasons June, July, August and September (JJAS) and December, January, February (DJF) the large scale patterns are generally captured by all the ensemble members (Figs. 4, 5) however many over-estimate the magnitude over central southern Africa particularly during DJF. In Fig. 4 the lower sensitivity models (Q1–Q5) tend to match the magnitude of the observed DJF precipitation climatology more closely than the higher sensitivity models (Q15 and Q16). The timings, and geographical location of wet periods and regions, however, are realistic.

Fig. 3

The annual variation of temperature over land (left) and precipitation (right) for Africa, North Africa and West Sahel. The black line shows the observed values (CRU 3.0 and CMAP) while the coloured lines show the model outcomes. The plots for all the regions of Africa used in the analysis can be found in the supplementary information

Figures 4 and 5 show the precipitation for Africa for the seasons JJAS and DJF respectively. The large scale patterns are generally captured by all the ensemble members, however many over-estimate the magnitude of the precipitation over central southern Africa particularly during DJF. In Fig. 5 the lower sensitivity models (Q1–Q5) tend to match the magnitude of the observed DJF precipitation climatology more closely than the higher sensitivity models (Q15 and Q16). The timings, and geographical location of wet periods and regions, however, are realistic.

Fig. 4

Comparison of observed (top left) and simulated precipitation (all other boxes) for Africa during JJAS. The observations were averaged over the period 1979–1998 (and were regridded to the QUMP grid) and the simulation data over the period 1961–1990

Fig. 5

Comparison of observed (top left) and simulated precipitation (all other boxes) for Africa during DJF. The observations were averaged over the period 1979–1998 (and were regridded to the QUMP grid) and the simulation data over the period 1961–1990

The circulation simulated by the model at 850 hPa has been compared with ERA40 (Uppala et al. 2005). As with the precipitation maps the models generally reproduce prevailing circulation patterns, including the direction of the trade winds (both north-east and south-east) (see supplementary information for more details). During JJAS the region of higher wind-speeds over the Horn of Africa (referred to as the ‘Somali Jet’) are also captured. However there is some variation between the ensemble members in the magnitude of the Somali Jet, with Q2, Q3, Q6 and Q7 matching the observations more closely than the other ensemble members. The direction of the DJF trade winds are also captured in most of the ensemble members e.g. Q8, Q9, Q11 and Q13; however the magnitude of the winds over the Sahel and southern Africa are slightly over-estimated in most of the ensemble members. Of all the ensemble members Q3 is the closest match to the observed climatology for the magnitude of DJF wind-speed. The near-surface temperature and sea surface temperature patterns (not shown here) in general compare well with the CRU observations and HadISST datasets respectively. However some of the ensemble members, particularly the higher sensitivity ones (Q9–Q16) do overestimate the temperatures in regions where temperatures are high. The mean sea level pressure patterns (also not shown) for the ensemble members also compare well with observations. Our validation of the 17 models shows that while all the models capture the broad seasonal and geographical pattern in key climate features, the range in magnitudes of features such as seasonal rainfalls, and the realism of those magnitudes, varies from across the models. However, it is not straightforward to identify a subset of models that perform better or worse across the whole region—models that do least well in some regions tend to be the most realistic in another. Our approach, therefore, is to select the sub-set based mainly on representing the spread of future climate outcomes across the regions. When making this decision, however, we take into account the shortcomings of some of the models. For example, where two models project similar characteristics of change in the future, we can use the validation information to choose to include the better performing model. On this basis Q1, Q3, Q4, and Q16 were discarded and not considered further in this analysis because the seasonal cycle of both precipitation and temperature do not compare as well with observations as other ensembles in the largest number of regions. In the following analysis we consider the spread of models with respect to temperature and precipitation changes to make the final selection of ensemble members (see Sect. 2.5.2).

Choosing a selection to represent the spread in QUMP outcomes

The final selection of ensemble members for Africa involves identifying the models which represent the range of the full ensemble in their change in precipitation ($\varDelta P$) and temperature ($\varDelta T$) for Africa and the key climatic sub-regions (see Table 2) for the A1B scenario between the 1970s and the 2080s. We average over 30 year time periods centred on these decades, in order to partially compensate for natural climate variability. This analysis takes the form of scatter plots which are shown for each region and season in Figs. 6, 7 and 8. There is no particular model that consistently shows the largest change in precipitation for all regions throughout the year e.g. for Kenya in DJF (Fig. 8, top) the largest change in precipitation is seen in Q14 but this model is not always the wettest model for the other seasons for this region; for example, Q14 is close to the ensemble mean for Kenya in JJA (Fig. 8, 3rd row). Q14 is also one of the driest models for some sub-regions, for example, some seasons (MAM, JJA, SON) in the West Sahel (Fig. 6 3rd column). On this basis the extremes of the ensemble distribution are classified in terms of which models consistently have the largest positive or negative change in precipitation across all the sub-regions and seasons. Therefore using this scoring system Q9 represents one of the wettest and Q0 represents one of the driest models in the range of the ensemble (but this does not mean these are the wettest and driest models in all sub-regions and seasons).

Temperature

Although the models are numbered 1–16 according to their global temperature response, regional responses will vary. Temperature response is more consistent across the regions and the seasons than the precipitation response, with, as expected, the higher response models tending to capture the warmer end of the range (Q13, Q14, and Q16 tend to have the largest temperature response across the regions and seasons) while the lower-response models, tend to indicate smaller temperature responses (Q1, Q2, Q3 tend to be coolest). Therefore on the basis that, of the lower response models, Q1 and Q3 do not validate as well as Q2 (and Q0 which also has a low regional temperature response) Q0 and Q2 are selected to represent the colder end of the range. At the warmer end of the range, Q16 has already been discounted on the basis of validation results, thus Q13 and Q14 are selected to represent this part of the range.

Rainfall

There is no particular ensemble member that consistently shows the largest change in precipitation for all regions throughout the year e.g. for Kenya in winter (DJF) the largest change in precipitation is seen in Q14 but this model does not then feature as the wettest model for the other seasons for this region; for example, Q14 is close to the ensemble mean for southern Africa and one of the driest models for western tropical Africa. On this basis the extremes of the ensemble distribution are classified in terms of which models consistently have the largest positive or negative change in precipitation across all the sub-regions and seasons. Therefore using this scoring system Q9 captures the wettest and Q0 captures the driest end of the ensemble range (but this does not mean these are the wettest and driest models in all sub-regions and seasons). On the basis of this analysis we conclude that a sample which reproduces important characteristics of current the African and Kenyan climates and represents the spread in projected outcomes produced by the QUMP ensemble consists of the following models: Q0, Q2, Q9, Q13 and Q14.

Fig. 6

Plots for the QUMP ensemble showing projected change in precipitation versus change in the temperature for all Africa, North Africa and West Sahel. The panels show the spread in projected outcomes during DJF, MAM, JJA, SON and annual (ANN). The data point labels (Q#) identify the models and the red data points indicate the selected sample. The box and whisker symbols that appear on the two axis of each individual plot represent the median, the inter-quartile difference and the absolute range of the ensemble along that dimension. Black box and whisker refer to QUMP while blue has been used for the CMIP3 ensemble

Fig. 7

Plots for the QUMP ensemble showing projected change in precipitation versus change in the temperature for East Sahel, Western tropical Africa and the Horn of Africa. The panels show the spread in projected outcomes during DJF, MAM, JJA, SON and annual (ANN). The data point labels (Q#) identify the models and the red data points indicate the selected sample. The box and whisker symbols that appear on the two axis of each individual plot represent the median, the inter-quartile difference and the absolute range of the ensemble along that dimension. Black box and whisker refer to QUMP while blue has been used for the CMIP3 ensemble

Fig. 8

Plots for the QUMP ensemble showing projected change in precipitation versus change in the temperature for southern Africa and East of Lake Victoria. The panels show the spread in projected outcomes during DJF, MAM, JJA, SON and annual (ANN). The data point labels (Q#) identify the models and the red data points indicate the selected sample. The box and whisker symbols that appear on the two axis of each individual plot represent the median, the inter-quartile difference and the absolute range of the ensemble along that dimension. Black box and whisker refer to QUMP while blue has been used for the CMIP3 ensemble

Table 3 Full run name of the regional model simulaitons, the name that was used to refer to these simulaitons in the text and the member of the QUMP ensemble member that has been used to drive them

Comparison between QUMP and CMIP3

As discussed in Sect. 1, QUMP is a perturbed-physics ensemble based on a single GCM. In order to investigate whether the projections from the QUMP ensemble represent the full range of climate futures, according to current knowledge, it is useful to examine it in the context of a multi-model ensemble such as CMIP3 (Meehl et al. 2007a). Figures 6, 7 and 8 show both temperature and precipitation response of each ensemble member and its comparison with CMIP3 ensemble. In general, the spread of the projected temperature changes are of a comparable size, but with the QUMP distribution shifted to slightly higher values. The temperature projections in QUMP therefore do not sample the lower values of temperature changes sufficiently. This may be due to the generally high climate sensitivity of HadCM3 family of models. The two sets of projected precipitation changes show even greater disagreement. In the majority of regions and seasons, the range of CMIP3 projections is significantly outside the range of QUMP projections, e.g. East Sahel in JJA, where QUMP predicts wetter conditions across the ensemble, while the CMIP3 projections include both wetter and drier climates. Note also that, in many cases, the QUMP projections are outside the range of CMIP3 projections (e.g. West Sahel in JJA), indicating the importance of considering both MME and PPE ensembles.

Validation of RCM results

The RCM ensemble in general captures the annual cycle of temperatures well both for Africa as a whole and the sub-regions (Fig. 9).

The performance of HadRM3P has been evaluated in the context of several papers analysing the performance of multiple RCMs driven by the quasi-observed ERA-Interim reanalyses as part of the CORDEX programme. This has shown that it simulates the precipitation well over Africa (Nikulin et al. 2012) and its performance is compares well with other RCMs (Kim et al. 2014) including at regional level (e.g. over West Africa, Gbobaniyi et al. 2014). In all regions, the RCM ensemble fits the observations better than the QUMP ensemble and the spread has been reduced, which is consistent with the selection criteria for the driving QUMP members, since we discarded those that were a poorer fit. In general, N1 is the coolest and N2 is the warmest ensemble member. The RCM ensemble has a cold bias May–September in the East Sahel and West Sahel regions, which appears to be inherited from the driving QUMP members. One feature that emerges more clearly in the RCM ensemble than the QUMP ensemble is that, while the GCM ensemble generally has a warm bias in Kenya with respect to observations, it has a cold bias during OND, during the second of the two rainy seasons (the short rains).

The RCM ensemble shows a substantial improvement over the QUMP ensemble in many regions (Fig. 9), in reproducing the seasonal cycle of precipitation (the plots for the other regions are available in the supplementary information) This is particularly noticeable in the Sahelian regions, where the RCM reproduces both the magnitude and timing of the wet season better. The magnitude of the peak in the East Sahel region (not shown) is still over estimated in the model and the wet season in the model is still early compared to observations, but to a much lesser extent than in the GCMs. In general, the RCM ensemble overestimates precipitation over Africa as a whole (Fig. 9, top right). In some regions, this positive bias is particularly pronounced, e.g. Western Tropical Africa April–June, the Horn of Africa October–December and Kenya October–December. The case of Kenya is particularly interesting, since there is an accompanying dry bias in the March-May rainy season (the long rains) with the result that the model maximum occurs during the earlier rainy season. This is in contrast to the observations which show the greater proportion of precipitation occurring in the later rainy season. This is possibly linked to the warm bias in the model in the long rains and the cold bias in the model during the short rains.

Figures 10 and 11 show the geographical patterns of precipitation in the RCM ensemble for JJAS and DJF respectively. CPC-FEWS (Love et al. 2004) observations (averaged over 1982–2012) are also shown. Whilst this is a quite different time-period from the one that has been used in the analysis of climate model outputs, the high-resolution of the dataset can provide a useful benchmark for evaluation the regional model simulations.

The RCM ensemble is better at reproducing the JJAS precipitation (Fig. 10) than the QUMP ensemble. Both the magnitudes and spatial patterns are well represented in comparison with QUMP, although some features, such as the observed peak in precipitation over the Cameroon highlands, are still not captured by the RCM ensemble.

As discussed in Sect. 2.5, the QUMP ensemble represented the spatial patterns of DJF rainfall well, but overestimated its magnitude over central Southern Africa. The RCM ensemble performs significantly better over land—it reproduces both the spatial pattern and the magnitude well, as illustrated in Fig. 11.

The RCM has introduced a larger positive bias in precipitation over the Western Indian Ocean in DJF, consistently over the ensemble. Lake Victoria and Lake Malawi are visible in Fig. 11 in the model results (and, to a much lesser extent, in the observations). We have investigated the case of Lake Victoria in detail and found the precipitation in the short rains to be significantly over-estimated over Lake Victoria in the RCMs both with respect to the CMAP data and CPC-FEWS data shown here and CRU and GPCP (not shown). As it is explained in a separate paper (Williams et al. 2014) this issue appears to be very localised to the lake itself and therefore of little relevance to the land outside the Lake Victoria basin.

Finally, comparison of RCM winds at 850 hPa (supplementary material) with those in the GCM simulations shows, as expected, they follow closely those of the driving GCMs. Thus, as with the GCMs, these compare well with observations but it also demonstrates consistency of the large-scale circulation in the RCMs with their driving GCMs.

Fig. 9

The annual variation of temperature over land (left) and precipitation (right) for Africa, North Africa and West Sahel. The black line shows the observed values (CRU 3.0 and CMAP) while the coloured lines show the model outcomes

Fig. 10

Comparison of observed and simulated precipitation in the RCM for Africa during JJAS. The CPC-FEWS observations were averaged over the period 1983–2012 and the simulation data over the period 1961–1990

Fig. 11

Comparison of observed and simulated precipitation in the RCM for Africa during DJF. The CPC-FEWS observations were averaged over the period 1983–2012 and the simulation data over the period 1961–1990

RCM projections for the A1B scenario

Figure 13 shows the spatial patterns of the projected changes in African precipitation over the RCM ensemble. In general, the RCM ensemble projects an increase in precipitation over central Africa, which is particularly pronounced in N2 and N3 see Table 3. There is also a general decrease across the ensemble over the West half of the Western Sahel region in JJA, accompanied by a band of increase on the coast further south. This is particularly interesting in the context of the CMIP3 results, which showed a robust decrease in precipitation in this region (see e.g. figure 8 in Buontempo et al. 2010). In the RCM runs, this decrease over the Western Sahel in JJA is accompanied by a band of increase on the coast further south. In three of the five runs, there is also a decrease in this season in the Gulf of Guinea. This band-like structure points to a change in the West African Monsoon system, which, as noted above, is a system which current climate models find very difficult to model. There is also a decrease in precipitation over Lake Victoria, particularly from March through to November. However, as we noted earlier, there was also a strong positive precipitation bias over the lake, which needs to be further understood before interpreting the precipitation projection in this location and which has been addressed in a separate publication (Williams et al. 2014).

Figure 12, compares the RCM projections to those in their driving GCMs and the QUMP ensemble as a whole. Generally, the projected temperature changes are very similar but the projected precipitation changes can show substantial differences. The All Africa precipitation changes (Fig. 12, left column) in DJF and JJA for N2 are very different from those projected Q9. In Southern Africa RCM ensemble members project less drying than their driving GCMs and in Central and East Sahel, the JJA precipitation in the RCM is projected to increase more. Similarly, in the West Sahel, RCM precipitation is projected to increase more (or decrease less) compared to the driving GCMs.

Fig. 12

Plots for the RCM ensemble (green, N#) and QUMP ensemble (black and red, Q#) showing projected change in precipitation versus change in the temperature for all Africa, North Africa and West Sahel. The panels show the spread in projected outcomes during DJF, MAM, JJA, SON and annual (ANN). The red data points indicate the sub-set of QUMP chosen to drive the RCM. The box and whisker symbols that appear on the two axis of each individual plot represent the median, the inter-quartile difference and the absolute range of the ensemble along that dimension. Black box and whisker refer to QUMP while green has been used for the RCM ensemble

Fig. 13

Plots for the RCM ensemble showing projected change in precipitation. Each row represents an ensemble member and each column represents a season. From left to right these are DJF, MAM, JJA and SON

Discussion

The results presented here highlight two important aspects of the simulations. On one hand the ensemble of regional model simulations show a smaller bias for present day than the corresponding GCM simulations (Figs. 10, 11) over the African continent. On the other hand the climate change response in the RCMs appears to be different, and for many regions narrower in spread, than that of the driving GCM ensemble (Fig. 12). A similar conclusion can be reached by comparing Figs. 13 and 14.

Fig. 14

Plots for the GCM ensemble showing projected change in precipitation. Each row represents an ensemble member and each column represents a season. From left to right these are DJF, MAM, JJA and SON

We hypothesise that there are three factors which explain this behaviour. The first is that a single RCM is used for downscaling whereas the driving GCMs have different formulations (i.e. they use a range of parameter values). The second is that the climate of Africa, at least as simulated in the models, is significantly influenced by (the representation of) local/regional processes within Africa. The third is that the GCM circulations over the oceanic regions are very similar and similarly for their future simulations (not shown). The evidence for the second statement comes from the similarity of RCM simulations of current climate and the much larger range from the GCMs.

Similar GCM circulations over the oceanic regions would be expected, as seen, to result in similar behaviour in the RCM simulations of current climate. In the case of the GCMs themselves, their simulations of current climate differ which must result from their different formulations, i.e. despite similar circulations over the adjacent oceanic regions their differing representation of local and regional physical processes over Africa leads to different simulations.

This behaviour of the various models’ simulations of current climate would also explain why the RCM projections of future climate tend to have both a narrower spread and an offset range as compared to those of the driving GCMs.

The boundary conditions from the GCM future simulations will involve perturbations to the temperature, humidity and wind inputs. The former two will involve increases, of a lesser or greater extent depending mainly on the climate sensitivity of the GCM. These would tend to induce similar responses in the various RCM projections but, as with their simulations of the current climate, differing responses over Africa in the GCMs.

There are several interesting questions raised by these results. One is whether similar behaviour would be seen using an RCM over a smaller domain, i.e. only part of Africa. The large size of the domain used in these experiments gives the RCM more freedom to develop its own climatology than a smaller domain would have allowed.

A second is whether any judgement can be made about the credibility of the RCM as opposed to the GCM projections. Given the improved simulation of current climate of the RCM, is it not unreasonable to argue that it is better able to downscale the large-scale climate change from the GCMs into credible future climates over Africa.

This would imply that more confidence can be put in the ranges of downscaled projections as credible representations of the regional implications of climate change over Africa. This is in addition to the downscaled projections generating projections at a scale more suitable for impact and adaptation studies.

Summary

This paper outlines climate model simulations which have been performed over the CORDEX domain using the RCM, HadRM3P with the MOSES2.2 tiled land-surface scheme. The runs span from December 1949 to December 2100. It should be noted that the SRES A1B scenario was used to represent future emissions; this scenario contains no mitigation and represents only one of several possible futures considered in the 4th assessment report of the IPCC. The lateral boundary data for the five simulations were taken from a subset of the Hadley Centres QUMP PPE. Members of the QUMP ensemble were selected in order to capture the spread in outcomes produced by the full ensemble, whilst excluding any members that do not represent the African climate realistically. In this way, we effectively sample the uncertainty due to parameter estimation in the boundary data. Additional uncertainty due to parameter estimation in the RCM and differences in model formulation (both in the regional and driving climate models) are not sampled. Particular attention has been paid to the treatment of the African Great Lakes. Since the configuration of the regional model did not contain a lake model, the lake surface temperatures must be prescribed as a boundary condition. In these simulations the lake surface temperatures were derived by interpolating SSTs from adjacent sea grid-boxes which were then bias-corrected using lake surface observations from the ARCLake project.

The model results show a significant improvement both in the representation of the current spatial distribution of precipitation over the African continent and in the seasonal cycle, as compared to the QUMP ensemble. We analyse the projections for the 2080s for each model run for each of the four seasons in both the RCM and in the driving GCMs. The results indicate that the spread in the climate change in the regional model simulations is narrower than in the driving GCM for most of the sub-regions. We speculate that this behaviour underscores the importance of local processes for determining African climate and its response to global climate change.

The outputs of the RCM simulations used in this study have been submitted to British Atmospheric Data Centre (http://badc.nerc.ac.uk). The dataset is publicly available and free of charge for any bona fide research purposes.