Abstract
Driving data and physical parametrizations can significantly impact the performance of regional dynamical atmospheric models in reproducing hydrometeorologically relevant variables. Our study addresses the water budget sensitivity of the Weather Research and Forecasting Model System WRF (WRF-ARW) with respect to two cumulus parametrizations (Kain–Fritsch, Betts–Miller–Janjić), two global driving reanalyses (ECMWF ERA-INTERIM and NCAR/NCEP NNRP), time variant and invariant sea surface temperature and optional gridded nudging. The skill of global and downscaled models is evaluated against different gridded observations for precipitation, 2 m-temperature, evapotranspiration, and against measured discharge time-series on a monthly basis. Multi-year spatial deviation patterns and basin aggregated time series are examined for four globally distributed regions with different climatic characteristics: Siberia, Northern and Western Africa, the Central Australian Plane, and the Amazonian tropics. The simulations cover the period from 2003 to 2006 with a horizontal mesh of 30 km. The results suggest a high sensitivity of the physical parametrizations and the driving data on the water budgets of the regional atmospheric simulations. While the global reanalyses tend to underestimate 2 m-temperature by 0.2–2 K, the regional simulations are typically 0.5–3 K warmer than observed. Many configurations show difficulties in reproducing the water budget terms, e.g. with long-term mean precipitation biases of 150 mm month−1 and higher. Nevertheless, with the water budget analysis viable setups can be deduced for all four study regions.
Similar content being viewed by others
1 Introduction
The awareness of currently observed and future expected variations of climate, land-use, and demography leads to an increased need for information about water availability. Such information can be advantageously derived by regional climate models (RCMs). The central question is, how well do RCMs correspond to observations, and what is their performance in describing the regional water cycle.
A rising number of RCM applications with the Weather Research and Forecasting Model (WRF) (Skamarock and Klemp 2008) were carried out for different climatic regions worldwide for this purpose. The analysis of the performance of such models is important also for applications of numerical weather prediction (NWP), climate simulations, or seasonal prediction. Most of the longer-term regional atmospheric downscaling studies with WRF analyze the skill of their simulations with respect to near-surface air temperature and precipitation (see e.g. Heikkilä et al. 2011; Chotamonsak et al. 2011). Our study aims at a comprehensive analysis of the impact of the model configuration of WRF on the simulated water budget of continental scale hydrological basins, covering different climatic regions of the Earth.
Until recently, the lack of trans-regional evapotranspiration observations impeded a comprehensive analysis of the regional model’s water cycle. With the Global Land surface Evaporation: the Amsterdam Method GLEAM (Miralles et al. 2011), a newly available global evapotranspiration product, in combination with gridded precipitation observations, it is now possible to evaluate the atmospheric water budget of a regional atmospheric simulation. GLEAM uses remote sensing data to obtain a physically based computation of the monthly actual evapotranspiration according to the model of Priestley and Taylor (1972).
For the WRF model, the sensitivity of driving data and physics parametrization for the water and energy budgets has been addressed by several studies: Flaounas et al. (2010) found that the type of planetary boundary and convective parametrization scheme affects precipitation amounts and patterns in a simulation for the the West African Monsoon. A study by Borge et al. (2008) investigated viable setups of WRF for the Iberian peninsula. A more general work by Kim and Hong (2010) comes to the conclusion that differences in modeled sea air interaction can considerably affect the water budgets of regional atmospheric models. Heikkilä et al. (2011) examined the skill of 30 and 10 km downscaling with WRF for the Scandinavian region. The higher resolution simulations further improved the quality of the downscaling. A study by Berg et al. (2013) and Wagner et al. (2013) comparing different RCMs for Germany found that by dynamical downscaling, precipitation biases of the global circulation model (GCM) typically propagate to the RCM results. However, they state that the examined RCMs are able to add value to the precipitation intensity distributions with respect to the GCMs. Miguez-Macho et al. (2004) pointed out that dynamic downscaling models can develop unrealistic circulation patterns if only the lateral boundaries are considered for global input. By applying a nudging term to the model’s prognostic equations, important large-scale features can be preserved within the dynamic downscaling process.
In our study we investigate the sensitivity and performance of different configurations for the dynamic downscaling model WRF-ARW (Advanced Research WRF) with respect to the water budget of long-term simulations for continental scale hydrological basins of 2–5 million km2 extent. The analysis is based on a monthly time-scale and covers four years from 2003 to 2006. The sensitivity analysis encompasses (1) two different global driving models, (2) two alternative convective parametrization schemes, (3) gridded nudging, and (4) time-variant and invariant sea-surface temperature (SST). Four globally distributed study regions are selected to cover different climatic conditions. The results of the regional atmospheric downscaling and the respective fields of the global driving models are evaluated with a range of independent global observation data sets for (1) precipitation, (2) ground level temperature, (3) evapotranspiration, and basin discharge.
2 Methods and data
For regional simulations exceeding the time range of a classical weather forecast, the different terms of the water budget need to match with observations to ensure physical consistency. However, changing the models’ configurations does often result in significant repartitioning of the simulated fluxes of the hydrological cycle. In our study, we evaluate different configurations of the WRF-ARW model with globally available observations of precipitation (P), actual evapotranspiration (E a ), and ground-level air temperature (T2). In order to account for the immanent uncertainties resulting from the processing and interpolation of station data, we incorporate multiple data-sets for P and T2. Moreover, to include also the uncertainty of the boundary conditions for the dynamical downscaling, two global atmospheric reanalysis products are employed for driving the regional simulations. In the following, the examined configurations of the WRF-ARW model are specified and the data-sets used for the evaluation comparison are expounded.
2.1 WRF-ARW model sensitivity
The Weather Forecast and Research modeling system WRF addresses the simulation of atmospheric dynamics including the exchange with the land surface on a scale much smaller than depicted by global atmospheric models. The most notable features in WRF-ARW are the terrain following mass (η) coordinate and the 3rd order Runge Kutta integration scheme. The model describes the atmosphere in a fully compressible, non-hydrostatic, and mass conserving way (Skamarock and Klemp 2008).
WRF is a community project with many institutions contributing their specific models and parametrizations of the various physical compartments involved in dynamical atmospheric simulations. With WRF-ARW 3.1 more than 100,000 combinations of the available physical schemes are theoretically possible (microphysics: 11, LW-radiation: 4, SW-radiation: 3, surface-layer: 4, planetary boundary layer (PBL): 8, cumulus: 5, land-surface model: 5) but of course not all of them add up. Within the limits of the available computational resources, a number of specific combinations with emphasis on the water budget sensitivity were realized above a basic configuration of the WRF model.
2.1.1 Basic model configuration
For this study, version 3.1 of the regional atmospheric model WRF-ARW (Skamarock and Klemp 2008) is applied. A summary of the selected model configuration and the variations in the setup is given in Table 1. The spatial resolution for downscaling is chosen with 30 km × 30 km. The vertical coordinate is decomposed into 40 layers with specific refinement at the near surface and the PBL. A single nest approach is used i.e. the global driving reanalyses are directly scaled-down to the final resolution. The output is stored every 6 h (00, 06, 12, 18 UTC) and monthly fields are therefrom derived. The simulations cover the years 2003–2006 plus a spin-up of 2 years (2001–2002) to account for the soil moisture equilibrium. For the Siberia domain, the spin-up period starts after the snow has melted in May 2001. To remain consistent with the global model driving, the soil moisture information for initialization is taken from the respective reanalyses. Nevertheless, it is assumed that after the spin-up period, the state of the soil moisture memory is completely equilibrated with respect to the lateral boundary conditions.
The basic selection of the physical schemes is based on the findings of Borge et al. (2008), and on the recommendations of Skamarock et al. (2008) and Wang et al. (2009). In terms of the microphysics, the WSM5 (WRF single moment 5-class) scheme is selected. It features a detailed representation of phase transition processes among vapor, rain, snow, cloud ice, and cloud water (Hong et al. 2004). The rapid radiative transfer model (RRTM, Mlawer et al. 1997) and the Goddard shortwave scheme (Chou and Suarez 1994) are used to represent the longwave and shortwave radiation processes with high spectral detail, respectively. For specific humidity, the range among different radiation parametrizations is only little (Borge et al. 2008). While Flaounas et al. (2010) recommends the Mellor–Yamada–Janjić (MYJ) PBL scheme but also the Yonsai University model (YSU Hong et al. 2006) for West-Africa, Borge et al. (2008) concludes with a recommendation for YSU for the Iberian peninsula. Because of the different climatic regions that examined for our study, the YSU model is favored for the PBL physics in conjunction with the MM5 surface layer scheme. For the land surface model (LSM) the Noah model (Chen and Dudhia 2001) is chosen. With its 4 soil layers, it corresponds best with the soil model of the global driving data and it outperforms the other available schemes in terms of the near surface moisture mixing ratio (Borge et al. 2008). Moreover, in its WRF-Hydro version (Gochis et al. 2013), increased attention is paid to lateral surface and subsurface hydrological processes.
2.1.2 Model boundary conditions
Two main types of driving data are available for dynamical downscaling with the WRF-ARW model. Global analysis products like the European Centre for Medium-Range Weather Forecasts’ (ECMWF) Operational Analysis or the Final Analysis of the National Center of Environmental Prediction (NCEP) with a short cutoff time for ingested observations are intended for near real-time applications. Moreover, the assimilation procedures and model physics are changed at irregular intervals. Reanalyses are more consistent in both respects by relying on a longer lag time for data collection and typically with a time invariant setup.
To account for uncertainties emerging from differences in the lateral boundary conditions of the RCM, two global reanalysis products are used to drive the downscaling model. The selected products comprise ERA INTERIM (Uppala et al. 2008) from ECMWF and the NCAR/NCEP Reanalysis Project (NNRP, Kalnay et al. 1996). Table 2 lists the main properties of the two products. The more recent reanalyses CFSR and MERRA are not examined here as their performance with respect to the global and regional water budgets is unsatisfactory (Lorenz and Kunstmann 2012). Despite their different spatial resolutions, both reanalyses are downscaled using a single nest approach. According to the studies of Beck et al. (2004) and Denis et al. (2003) a resolution jump by a factor of up to 10–12 between GCM and RCM is justifiable without a deterioration in the skill of the downscaling. In our study, the jump in resolution is 7 for the NNRP driving and 2.6 for ERA-INTERIM.
2.1.3 Model physics alternations
Within the available range of computational resources, several physical options that typically have a large impact on the water budget of the regional simulations, are examined.
The spatio-temporal distribution of convective precipitation depicts a major source of uncertainty in current regional atmospheric models (e.g. Liu and Wang 2011). Therefore, the two parametrizations of Kain–Fritsch (Kain 2004), and Betts–Miller–Janjić (Baldwin et al. 2002; Janjić 2000) are compared in combination with the non-convective contribution from the WSM5 microphysics scheme with respect to the spatial distribution and the total amount of generated precipitation. An overview of the underlying concepts in the two convective schemes is given in Wang and Seaman (1997).
Moreover, the outcome of regional atmospheric simulations with respect to the water budget can be very sensitive to the applied lateral boundary conditions. By a nudging towards the global driving data, it is possible to improve the model skill, e.g. with respect to precipitation or near-surface temperature (Miguez-Macho et al. 2004). Two common approaches are typically used with dynamical downscaling models. For gridded nudging, the prognostic equations for wind, temperature and moisture are directly relaxed towards the state of the global driving model. The nudging strength is given by a factor. With spectral nudging a transformation of the variables into the frequency domain is performed and only certain wavelengths are updated to consider for the large scale patterns of the global model. Nevertheless, nudging does not always imply an improvement for regional simulations. Alexandru et al. (2009) found that using large scale spectral nudging can also have some negative side effects, e.g. for predicted precipitation maximums. Bowden et al. (2012) compared gridded and spectral nudging techniques in WRF for Northern America and came to the conclusion that a clear implication to prefer one of these methods above the other cannot be made. Since this study has a distinct focus on the water budget and moisture nudging is not available with the spectral nudging option, the sensitivity of gridded nudging in combination with the Kain–Fritsch cumulus scheme is examined. Gridded nudging is applied for the model layers above the PBL for wind, temperature, and moisture fields with a uniform factor of 0.0003. The gridded nudging option is referred to as four dimensional data assimilation (FDDA).
Furthermore, the sensitivity of the sea surface temperature (SST) lower boundary condition of WRF is analyzed. cSST refers to a constant SST setup where the SST is kept in its initial condition throughout the simulation. The simulations tagged with vSST use 6-hourly SST data from their respective global driving reanalyses. vSST also includes monthly updates of the 2-dimensional albedo and vegetation fraction fields whereas for cSST table values are used for an climatological interpolation. The cSST configuration depicts fictive conditions to assess the sensitivity of the lower boundary conditions. Thus, this option is only applied in combination with the KF convective scheme, however for both global driving models.
It would be of further interest to test additional model configurations of the RCM with respect to the water budgets. However, it was not feasible in this study as it had required an significant additional allocation of computational resources. Altogether, for the 4 study regions, the two global drivings, and the alteration of 4 physics schemes, 32 simulations are performed for the years 2001–2006 (including spin-up), summing up to a total of 192 simulated years. In total, the 4 model domains contain ≈12,900 horizontal grid cells.
2.2 Evaluation datasets
The skill of both global reanalyses and regional downscaling is evaluated with the following globally available data-sets for temperature, precipitation, evapotranspiration, and discharge. To account for the uncertainties of the observations the modeled fields are compared to a range of temperature and precipitation products. Unless differently mentioned the gridded data is available on a 0.5° × 0.5° grid.
2.2.1 Temperature observations
For the validation of the near surface air temperature of global reanalyses and dynamical downscaling, two different gridded global products are selected:
-
CRUTEMP 3.00 of Climatic Research Unit, University of East Anglia (CRU, Brohan et al. 2006)
-
Temperature data set released by the University of Delaware (Matsuura and Willmot 2009a)
In the following, the acronyms CRUT and DELT will be used for reference. Both products are based on quality checked station observations. The monthly fields of CRUTEMP rely on homogenized, quality-checked observations from 4,349 stations. In this study a further processed version of CRUTEMP with higher spatial resolution is used. The monthly means are provided by the British Atmospheric Data Centre (BADC, Jones and Harris 2008). The University of Delaware provides a gridded time series of terrestrial air temperature, starting from 1900. The number of considered stations lies between 1,600 and 12,200, where the higher count refers to the more recent dates. One fraction of the station data comes from the Global Historical Climatology Network (GHCN, Peterson and Vose 1997). This input has a very high quality that is equivalent to CRUT. In contrast to CRUT, the Delaware product is extended with additional observations (Matsuura and Willmot 2009a).
2.2.2 Precipitation observations
In contrast to the measurement of air temperature, the quantification of precipitation is connected with significantly higher uncertainty because of its highly variable distribution in time and space. Hence, for evaluating the atmospheric models, a total of four different gridded data sets are selected to represent the underlying uncertainties of these global observations. The following products are incorporated:
-
Global Precipitation Climatology Centre (GPCC, version 4) (Schneider et al. 2008),
-
Climate Research Unit, University of East Anglia (CRUP, version 3),
-
University of Delaware (DELP) (Matsuura and Willmot 2009b), and
-
Global Precipitation Climatology Project (GPCP) (Adler et al. 2003).
The Global Precipitation Climatology Centre is part of the World Climate Research Program (WCRP). For the study, the Full Data Reanalysis Product (Version 4) is used. While for the period from 1989 to 2001 the data base counts more than 30,000 stations, this number decreases from about 20,000 in 2003 to only 10,000 in the year 2008. The CRUP data-set relies on the same processing as the CRUT product. It covers the years 1901–2006 (BADC, Jones and Harris 2008). DELP is based on the GHCN database, complemented by additionally available station data. It comprehends the time span from 1900 to 2008. In total 4,800–22,000 station time series were incorporated. GPCP inputs also to the WCRP but differs significantly from GPCC by utilizing microwave and infrared space borne observations techniques in addition to ground station measurements. Thus, compared to the precipitation products described before, it is the only fully globally available data set as it covers not only the land masses but the oceans. GPCP is provided at 2.5° × 2.5°. The data is available for the period 1979 to present. The global number of included ground stations lies between 6,500 and 7,000 (Adler et al. 2003). For the use in this study, the the original data of GPCP is bi-linearly interpolated to 0.5° × 0.5° using a conservative algorithm.
2.2.3 Evapotranspiration data from GLEAM
The Global Land surface Evaporation the Amsterdam Methodology GLEAM (Miralles et al. 2011) applies the radiation driven evaporation model of Priestley and Taylor (1972). The physically observed variables consist of microwave derived soil moisture, land surface temperature, and vegetation density. An additional analytical model is used to account for canopy interception loss. GLEAM distinguishes and parametrizes three different land-surface properties: bare soil, short vegetation, and tall canopy. Global maps of evapotranspiration from land-surface (without water bodies) are available with a daily resolution on a 0.25° × 0.25° mesh. In a monthly averages comparison with 43 FLUXNET stations, GLEAM shows reasonable coherence (r = 0.9) with a small global bias of −5 % (Miralles et al. 2011). Because GLEAM doesn’t depict a direct measurement, the product is considered for comparison with the atmospheric models but not for validation.
Modeled fields of actual evapotranspiration are available for the ERA-INTERIM reanalysis. NNRP provides only potential evaporation which cannot be compared with GLEAM.
2.2.4 Discharge and runoff
If available, discharge data from the Global Runoff Data Centre (GRDC) is used to evaluate the simulated runoff in global and downscaled reanalyses for the hydrological basins. Of course, the comparison of basin aggregated runoff with gauge measurements cannot account for the time lag caused by lateral transport but the long term bias gives valuable information on the closure of the water budget for the considered region.
2.3 Model evaluation
For evaluation, the 2003–2006 monthly averages of the global and downscaled reanalyses are compared with the above described gridded observation data sets. For temperature and precipitation the deviation patterns with respect to CRUT and GPCC are visualized with maps. In addition, basin aggregated time-series of temperature, precipitation, evapotranspiration, and if applicable runoff are shown and bias and RMSE are the measures considered for the performance analysis.
The comparison of two methods for spatial averaging of the WRF fields shows that for (1) averaging with a basin mask of 30 km resolution and (2) regridding by conservative interpolation to the 0.5° × 0.5° grid of the global observations with subsequent averaging, the differences remain below 1 % for the monthly basin averages. Hence, the fields of the regional atmospheric model are regridded to 0.5° × 0.5° for the spatial deviation plots and the basin averaged time series are derived therefrom. Some of resolved features of the regional model may disappear due to the interpolation. But as seen from the comparison this is not significant for the monthly based basin analysis.
2.4 Atmospheric water budget analysis
The consideration of the atmospheric moisture budget provides an additional means for the evaluation of P − E a for global and regional models. The spatially averaged water budget of the atmosphere relates to the terrestrial water balance in the following way
with \(\langle \rangle\) denoting spatial averaging. dW/dt describes variations in the moisture content of the atmospheric column. \(\nabla \cdot {\bf Q}\) depicts the net balance of horizontal moisture flux for a specified region. E a and P are actual evapotranspiration and precipitation, respectively.
The first term in Eq. 1 refers to the temporal variation of water vapor in the atmospheric column. A direct transition between varying air masses can yield larger changes for W. However, for monthly or longer averaging periods, the storage fluctuations cancel out and can therefore be neglected (Peixoto and Oort 1992; Rasmusson 1977).
The divergence term of Eq. 1 is computed from the vertical integral of the horizontal moisture flux
with air pressure p (Pa) from the land surface to the top of the atmospheric model, the gravitational acceleration g (m s−2), the horizontal wind vector \(\varvec{\nu}_h\) (m s−1), and the specific humidity q (kg kg−1). For WRF p top is defined with 50 hPa. The NNRP data contains moisture information until 275 hPa and ERA INTERIM reaches to 0.1 hPa. The different model ceiling heights are not problematic for the computation of the vertical integral since the majority of moisture is concentrated within the lower regions of the atmosphere (Rasmusson 1977).
3 Study regions
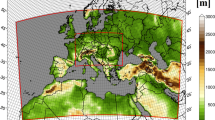
The study comprises four climatological and hydrographical regions. The respective domains of the regional atmospheric model and the contained hydrological basins are illustrated in Fig. 1.
The arctic winterly cold climate is represented by the Siberia domain, combining the two river catchments of Yenissei and Lena with a total area of around 5 × 106 km2. The Africa domain covers different climatic zones ranging from desert in the North to tropics and monsoon influenced conditions on the Western and the Central continent. For this study we analyze the water budgets of the Sahara desert, the Niger basin and the Lake Chad catchment. The Australian continent is completely surrounded by the ocean and has very steep climatic gradients from the coast to the center. The Central Australian Plane is considered for the water budget analysis. The tropical climate domain of the Amazon region shows very strong variations of the annual water cycle.
4 Results
4.1 Siberia domain
Precipitation The upper panel in Fig. 2 depicts the deviation patterns for the 2003–2006 mean precipitation in relation to GPCC. Over the Siberia domain, the GPCC station network is densely distributed south of 50°N but rather coarsely towards the north. The comparison with CRUP and DELP shows significant deviations where both products suggest lower annual sums by an average of 200–300 mm. As distinct from CRUP and DELP, GPCP is much closer to the observations of GPCC with random fluctuations of up to ±100 mm year−1.
The global reanalysis fields of INTERIM and NNRP contain visible differences in their spatial patterns. With respect to GPCC, INTERIM suggests increased precipitation values for the upper basins of Lena and Yenisei. The high values that GPCC observes for the northwestern parts of the domain is not resembled by neither of the models. Altogether, with respect to the spatial pattern, INTERIM agrees better with CRUP than with any other observation data set. NNRP tends to overestimate the precipitation amount for the river catchments by 100–300 mm year−1. This bias is larger than the internal variability among the gridded precipitation observations.
For the dynamical downscaling of the two global reanalyses, at first appearance, all realizations show very similar deviations from GPCC. Along the eastern coastline, wetter conditions are obtained with the regional simulations. For the combined catchments of Lena and Yenisei, less prominent deviations are experienced with respect to GPCC. Concerning the different configurations of the regional atmospheric model, the strongest effect is seen for the SST switch. NR cSST+KF and EI cSST+KF lead to dryer conditions along the eastern coastline. The NNRP driven simulation is stronger affected than the one driven by INTERIM. However, for 2004 (not shown), also EI cSST+KF yields wetter conditions than seen from the observations. Thus, the SST option can result in both dryer and wetter conditions. In general, it affects mainly the southeastern sea-adjacent region of the domain, but also parts of the basins of Lena and Yenisei.
For the mountainous regions in the southern part of the domain, all regional simulations conclude with wetter conditions than observed by the global data sets. In general, the EI runs are dryer in the southwest than the corresponding NR runs. The regional simulations yield precipitation patterns that are better related to CRUP and DELP than to GPCC and GPCP. From the above findings, the validity of GPCC and GPCP could be challenged for the mid to north-western part of the domain.
Figure 3a shows the monthly precipitation basin average time series for the gridded observations (blue filled area depicts range among GPCC, DELP, CRUP, GPCP), the global reanalyses and the WRF simulations for the combined river catchments of Lena and Yenisei. The corresponding bias and RMSE values are given in Table 3. The comparison reveals reasonable performance for the global INTERIM reanalysis. Summer peaks are slightly overestimated, leading to a long-term (2003–2006) bias of ≈5–10 mm month−1. NNRP also resembles the seasonality reasonably but contains a large positive bias that ranges from 10 to 50 mm month−1 between winter and summer.
While the WRF simulations tend to cut off the observed peak in summer rainfall, for the spring periods slight overestimation is obtained. As can be seen from Table 3, the bias for most the regional simulations stays within the range of uncertainty of the gridded observations. With constant lower boundary conditions (initialized in May 2001), WRF yields increased precipitation for the summer season. During fall and early winter, GPCC is very well resembled by each of the regional model runs. Gridded nudging (+FDDA) does not yield improvement compared to the vSST+KF mode.
With respect to the precipitation bias, the global reanalyses can be improved by the downscaling. If the RMSE is considered the picture becomes more diverse. INTERIM yields lower values for P than the respective WRF simulations. Contrarily, the WRF results with NNRP driving lead to an decrease of the RMSE values.
2 m temperature The lower panel of Fig. 2 gives the deviations for T2 with respect to the 2003–2006 mean temperature of CRUT. A significant warm bias is experienced for all the WRF model runs (Table 3). In contrast, the global fields seem to be more closely related to CRUT. Despite of the bias, the spatial deviation patterns are very similar for the regional and the global fields. Between the center and the west of the domain, the models suggest a larger temperature gradient than it is observed with CRUT.
By looking at the time series (Fig. 3b), it is found that the deviations do not persist over the whole annual cycle. The largest differences with the regional simulations occur at the extremes of summer and winter with up to +10 K. The transition periods lying inbetween are reasonably resembled. Systematic deviation is also seen for the global reanalyses. NNRP underestimates spring temperatures with up to 4° and during winter a bias of +5 K is observed. INTERIM contains a similar seasonal bias dependence. However, the deviations are smaller than for NNRP. During summer a peak bias of 0.5 K is observed. In winter this value increases up to 2.5 K. In general, it can be stated that INTERIM performs best for both the spatial deviations and the basin aggregated time-series.
The issue of large positive temperature biases in WRF for the polar region was also addressed by the Polar WRF (PWRF) community. Two separate effects might be responsible for winter and summer overestimation of the near surface temperature in WRF. For the summer it seems that an underestimation of evaporation from melting ponds and small tundra lakes causes a shift of the Bowen ratio towards an increase of latent heat flux (Hines et al. 2010). This assumption corresponds with the observed deviation of modeled and observed evapotranspiration of Fig. 2c where the regional simulations yield substantial lower rates for the summer months. Moreover it is reported that WRF has difficulties to correctly represent the strong winter inversions of the polar regions. Additionally, for the Noah-LSM the depiction of snow and ice is modestly realized (Hines et al. 2010).
Evapotranspiration Fig. 3c depicts the basin averaged time series for evapotranspiration (no data is available for NNRP). For the winter period, where evapotranspiration is usually close to zero, the range between the different models is small. Larger deviation is seen from May to September. In the comparison with GLEAM only ERA-INTERIM agrees with the annual value distribution. The regional simulations tend to underestimate during summer which is likely related to an unrealistic description of the surface moisture characteristics.
Atmospheric water budget In Fig. 3d the modeled atmospheric moisture budgets \((-\nabla\cdot{\bf Q})\) are compared to the range of the precipitation observations minus GLEAM (blue area). For the winter months, global and regional simulations lie within the bounds. All models suggest a lower net evapotranspiration for May and June. The peak outlet of moisture seen for the observations in July are resembled closely by the NR vSST+KF setup. The atmospheric moisture budget of ERA-INTERIM (i.e. the global reanalysis that showed a good agreement for precipitation and evapotranspiration) yields also increased rates. NNRP resembles the negative peaks of 2003 and 2004 but shows a time lag of one to two months. However, the effect cannot be found for the respective NNRP driven dynamical downscaling results.
Aggregated runoff versus gauge discharge The bias numbers shown in the rightmost column of Table 3 reveal a moderate to strong underestimation of runoff for the regional downscaling. The magnitude seems to be rather connected to the model configuration than to the driving data. Due to the comparatively high precipitation amount for the EI and NR cSST+KF simulations, more runoff is generated which in turn reduces the bias with respect to the observations. The global INTERIM reanalysis yields an unbiased times series for runoff but with a RMSE of ≈20 mm month−1. NNRP has its maximum runoff in winter and minimum rates in summer and therefore, the NNRP product does not qualify for any comparison.
Skill of the downscaling For the Siberia study region it is concluded that by dynamical downscaling, the positive bias and the RMSE for precipitation of the global NNRP reanalysis can be reduced. Contrarily, the downscaling of the global INTERIM reanalysis does not lead to an improvement. All regional simulations show difficulties in simulating the peak values of summer precipitation. The cSST option leads to the worst downscaling performance regardless of the driving used.
In terms of temperature, WRF yields strong deviations of up to +8 K. These deviations occur regardless of the tested model configuration, follow a certain periodicity with a maximum every summer and winter and are connected to the above mentioned shortcomings in WRF to simulate winter inversion and summer evapotranspiration.
Altogether, it is difficult to isolate a particular configuration of the regional model that outperforms all others. In terms of time-series correlation, INTERIM driving leads to a small improvement (r = 0.7) as compared to NR (r = 0.63). Nevertheless, for P, E a , and T2, the time series of the global INTERIM reanalysis fits the observations considerably better than any of the tested regional simulations for the Siberia domain do.
4.2 North Africa domain
Precipitation The top panel of Fig. 4 illustrates the deviations of 2003–2006 mean precipitation with respect to GPCC. The GPCC station network reveals large gaps for the arid regions between 15°N and 30°N. Over the Sahara desert, the absolute differences among the gridded observations are comparatively small. GPCP shows 25–100 mm year−1 higher values in the eastern part. CRUP suggests dryer conditions with an order of 25–100 mm year−1. Towards the south, the deviations become more distinct. Especially along the southwestern coastline, differences of ±500 mm year−1 are found. For the central humid region (5°N, 30°E), CRUP, DELP, and GPCP are up to 500 mm year−1 dryer than the GPCC reference product.
The deviation patterns are clearly biased for the global reanalyses. Both, NNRP and INTERIM simulate dryer conditions for the desert and the Sahel zone. For the basins of Niger and Chad, annual precipitation is up to 500 mm year−1 lower than observed by GPCC. For the southwestern coastal regions and for the Kongo basin rainfall is vastly overestimated. The deviations occur over large areas and reach 1,500 mm year−1 and above, at some locations. NNRP appears to be dryer within the Kongo region.
The results for the regional downscaling are provided in the first two rows of Fig. 4. Because of problems of WRF with the numerical stability, no runs with time invariant SST could be computed with ERA-INTERIM driving. At a first glance, all simulations share similar distinctive features. The 15° N line divides an area of strong deviations in the south (blue colors) and an area of moderate deviations in the north (green colors). Remarkably lower values are obtained for the eastern equatorial regions. All vSST+KF simulations result in a wet bias. For the Sahara, over large areas, the values are 25–300 mm year−1 higher than observed by GPCC. South of 15° N, 1, 000–2, 000 mm year−1 overestimation is obtained. Over the Kongo river basin the values are further exceeded. Enabling the gridded nudging option (FDDA) leads to a further increase in annual precipitation amounts. For vSST+KF and vSST+KF+FDDA, the resulting conditions are a bit dryer when NNRP driving is used with the regional model.
With NNRP and ERA-INTERIM model driving, the vSST+BMJ configuration leads to more reasonable results if compared to GPCC, especially for the Sahara and the Lake Chad basin. At many locations, the deviations lie within a range of ±25 mm year−1. In the western part, a slight dry tendency is experienced. Furthermore, compared to vSST+EI, smaller overestimation is also seen, e.g. for the basins of Chad, Niger, and Kongo. Compared to EI vSST+BMJ, NR vSST+BMJ shows lower precipitation amounts for nearly the complete modeling domain. A substantial decrease is seen over the basins of Chad and Kongo and also partly for the Niger.
The analysis of precipitation patterns shows clearly that the Betts–Miller–Janjić cumulus parametrization is better suited for the African study region. With Kain–Fritsch, a tremendous overestimation is experienced for the Central regions and the tropical zone. Gridded nudging (FDDA) further increases the wet bias. Thus, vSST+BMJ with NNRP driving is seen to be the most reasonable tested configuration of the regional model for the domain. The deviation patterns for the global reanalyses and the downscaling share similar structures.
2 m temperature The deviation patterns for 2 m-temperature are depicted in the lower panel of Fig. 4. For the global reanalyses, a cold bias tendency can be recognized. NNRP is about 2 K below the CRUT observations. For INTERIM the picture is more mixed. A slight positive bias is seen for the northern and eastern regions. Towards the south, the field converges towards NNRP.
The WRF simulations result in a warm bias for most of the domain area. Lower values are obtained for West Africa’s southern coastline and in the East. Differences in the regional model parametrization alter the strength of the bias. However, no significant changes are seen in the spatial patterns. For the Sahara basin, the NR vSST+KF configuration leads to an accordance with the mean value of CRUT. Surprisingly, when gridded nudging is applied (vSST+KF+FDDA), the bias values show an additional increment, especially over the northwestern continent. With the vSST+BMJ setup, the zone where temperature is overestimated by 4 K or more, moves towards the south. Thus, from the perspective of bias, the BMJ cumulus parametrization does not outperform the other tested configurations as it is seen for precipitation. But, as the comparison shows, precipitation and near surface air temperature have no connection in their spatial deviation patterns. Therefore, the BMJ configuration still seems to be the better choice with respect to the water budgets.
In the following, the water budget comparisons are presented for the Sahara, the Chad, and the Niger basin.
4.2.1 Sahara basin
Precipitation Figure 5a depicts the basin averaged time series (2003–2006) for the Sahara basin. The global reanalyses resemble the seasonality of the GPCC observations but underestimate rainfall by 50–75 %. In contrast, the regional simulations tend to overestimate precipitation during the summer period (May–August). EI vSST+BMJ, NR vSST+BMJ, and NR cSST+KF yield the best coherence with the gridded observations. All vSST+KF simulations have much higher standard deviation values, caused by a strong overestimation of the Sahara summer rainfall. Table 4 gives the values for mean bias and RMSE. The best performance for the bias of the regional model is obtained with the BMJ configuration (≈2.5 mm month−1). All vSST+KF simulations reveal a positive bias between 5 and 10 mm. Global INTERIM stays in the same range but with reversed sign. With ≈− 5 mm month−1, NNRP is close to predicting zero precipitation for the region. The analysis of the RMSE identifies NR cSST+KF as the best performing configuration of the regional model for P followed by NR vSST+BMJ.
2 m temperature The basin averaged time series for temperature (Fig. 5b) are a lot more uniform than it was obtained for the precipitation comparison. NNRP is the only product that constantly underestimates. As listed in Table 4, NNRP has a negative bias of about 1.75 K. INTERIM follows the observations and is only slightly warmer during the summer months. The regional simulations return a warm bias with all tested configurations. For the NNRP driven simulations, the deviation ranges between 1° and 2.7° with respect to CRUT. For the downscaling of ERA-INTERIM, a warm bias of 1–1.5 K is calculated. NR cSST+KF gives the warmest configuration of the regional model with a warm bias of about 2.5 K. Altogether, with respect to the RMSE, the best performance for T2 is obtained with global INTERIM and regional NR vSST+KF.
Evapotranspiration The plot of time series of simulated evapotranspiration versus GLEAM (Fig. 5c) is very similar to that of precipitation. The WRF simulations that overestimated precipitation are likewise doing the same for evapotranspiration. The highest rates are obtained for EI vSST+KF+FDDA, EI vSST+KF, and NR vSST+KF+FDDA with 12.2–13.4 mm month−1. The BMJ configurations of the regional model and NR vSST+KF agree reasonably with the GLEAM product (−1.5 to −2.3 mm month−1). NR cSST+KF and the global INTERIM reanalysis show a stronger dry tendency of around −3.2 mm month−1. NR vSST+BMJ yields the best RMSE value. For January–May in 2004 and 2005, the GLEAM product differs considerably from the global and regional models and might thus be erroneous for that specific periods in that region.
Atmospheric water budget For the atmospheric water budget, the time series of the simulations are not distinctively grouped (Fig. 5d). Positive deviation from the observations occurs mainly during summer time. Again, as already seen for P and E a , the vSST+KF+FDDA and the vSST+KF configurations of WRF are the most differing ones while the BMJ cumulus parametrization runs are much closer to the observations.
For an ephemeral basin, the average discharge is zero (because of no water leaving the outer boundaries) and hence \(\nabla \cdot {\bf Q}\) equals the terrestrial water storage variation. For the 2003–2006 mean the storage variations and hence \(\nabla \cdot {\bf Q}\) should be close to zero.
Contrarily, the regional simulations yield to values of 5–10 mm month−1. Only NR vSST+BMJ (3.1 mm month−1) and the global reanalysis of ERA-INTERIM (2.3 mm month−1) are close to being leveled out. NNRP gives a considerable negative bias (−8.5 mm month−1). This may explain the general underestimation of precipitation here.
Skill of the downscaling When driven by NNRP and by using the vSST+BMJ configuration, the WRF model outperforms its global counterpart. The dry and cold bias of the global reanalysis can be improved. The cSST option leads to slightly better estimates of P but likewise a strong temperature bias is introduced. Similar results are obtained when driving the regional model with INTERIM fields. However, with this set up, slightly wetter conditions are seen.
4.2.2 Lake Chad basin
Precipitation For the Chad basin, the intra-annual distribution of rainfall yields a dry period in winter and a maximum in August. The comparison of modeled and observed precipitation (Fig. 6a) reveals similar characteristics to what is found for the Sahara basin. For the basin averaged precipitation, the observation products for GPCC, GPCP, CRUP, and DELP span a small range (cyan ribbon). The seasonal patterns are well resembled by the global reanalyses and the regional simulations. Differences occur mainly for the amplitudes.
Both global reanalyses suggest lower precipitation values than observed. INTERIM and NNRP have a dry bias of −7 to −9 and −10 to −12 mm month−1, respectively (Table 5). The NR vSST+BMJ configuration of WRF yields the lowest bias and RMSE while the other regional simulations overestimate the rainfall. With vSST+KF and vSST+KF+FDDA the summer values are vastly exceeded by 100–150 . With respect to rainfall, with 20–23 mm month−1 overestimation, vSST+BMJ is the best performing configuration with EI driving. NR cSST+KF is similar to EI vSST+BMJ. As already mentioned, EI cSST+KF could not be analyzed because of numerical stability problems with WRF. Similar to the findings for the Sahara basin, NR driving results in less precipitation than the respective EI simulation.
2 m temperature Time series for temperature are depicted in Fig. 6b. For the Chad basin, different results are mainly found for the temperature minimum around January. While for some months, the regional simulations are 3–4 K too warm, the global reanalyses are 1–2.5 K below the observations (Table 5). NNRP has a cold bias throughout the year. With 2.6–3 K, the highest temperature deviation for the regional simulations is obtained with the NR cSST+KF setup. Apart from that, the BMJ configurations (EI and NR) return the warmest conditions, with an overestimation for all seasons. KF and KF+FDDA are very close to the observations during the summer periods.
Evapotranspiration As with the Sahara basin, the evaluation with GLEAM shows deviation structures similar to that for precipitation (Fig. 6c). The time series of INTERIM almost completely follows the reference data, with a very small bias of 1.5 mm month−1 and a RMSE of 2.6 mm month−1 (Table 5). All the regional simulations overestimate E a during summertime and underestimate the winter rates. The closest coherence is obtained with the NR vSST+BMJ configuration of WRF with a bias of 1.3 mm month−1. However, the small bias is a result from the compensation of overestimated summer and underestimated winter rates which becomes reflected in the higher RMSE value of 8.3 mm month−1.
Atmospheric water budget For the atmospheric water budget (Fig. 6d), the INTERIM reanalysis and the regional models are able to reproduce the seasonality P − E a . The summer rates for NNRP appear shifted in phase. INTERIM is too dry for the summer peaks and the winter months. Compared to the reference data all regional simulations except for NR vSST+BMJ overestimate the budget. However, NR vSST+BMJ tends to cut off the peaks during summer.
Skill of the downscaling For the Chad basin it is concluded that the performance of the KF cumulus scheme in WRF is inadequate. With BMJ the monthly rainfall time series fit better to the gridded observations. In contrast to Siberia, the application of alternative global driving has an important impact on the water balance of the regional model. Moreover, the global reanalyses reveal a considerable dry bias for P and the atmospheric water budget.
In terms of 2 m-temperature, KF and KF+FDDA outperform the BMJ cumulus scheme. However, with regard to precipitation, KF cannot be considered as reasonable, especially for the summer months, where large precipitation overestimation contradicts the good fit for temperature.
For the Chad basin, the regional model simulations add substantial skill to their global driving reanalyses. The NNRP driven downscaling agrees better with the global observations of precipitation, but only if the vSST+BMJ configuration is applied. The downscaling leads to a significant reduction of the dry bias of the global reanalysis. However, the global cold bias of around −2 K is turned into a warm bias of similar size.
4.2.3 Niger basin
Precipitation The regime for the basin aggregated precipitation observations of the Niger (Fig. 7a) share the same seasonality with that of the Chad basin. However, for the Niger, the annual peak values are about 75–100 % increased.
For the global reanalyses, a general dry bias is observed (INTERIM −7 to −14 and NNRP −13 to −20 mm month−1). NNRP underestimates P in particular for the spring and early summer periods. All regional simulations exceed the observed curves. Table 6 lists the respective bias amounts. As with the Chad basin, the strongest deviations are obtained with the vSST+KF and vSST+KF+FDDA configuration of the regional model. In terms of phase correlation, all simulations show a reasonable performance (r > 0.9). With vSST+BMJ, maximum coefficients of 0.98 are obtained. NR cSST+KF shows reasonable performance with respect to P but has a large bias for temperature (see below).
Altogether, the BMJ cumulus scheme outperforms the KF method for both global driving models. For the regional simulations, the best performance is seen with the NR vSST+BMJ configuration. While NNRP is topped by its regional counterpart, no skill could be added for the basin aggregated P to INTERIM by dynamical downscaling with WRF.
2 m temperature As illustrated in Fig. 7b, all regional simulations yield a warm bias. The highest deviation is seen for NR cSST+KF with ≈ 2.7 K. vSST+KF and vSST+KF+FDDA result in a mean overestimation of 0.5–0.8 K. As already observed for the Chad basin, the BMJ scheme leads to higher temperatures than the KF scheme.
In terms of the global reanalyses, INTERIM shows the best coherence with CRUT and DELT (r > 0.99) while NNRP is less correlated (R ≈ 0.95). The preeminence of INTERIM is further corroborated by the bias and RMSE results listed in Table 6. NNRP suggest more than 2 K colder conditions than observed. INTERIM contains also a cold bias but it amounts only ≈0.2 K.
Evapotranspiration The evaluation for E a is given in Fig. 7c. The results appear in the same line as for the Sahara and Lake Chad basins. For the spring to summer period, large overestimation is observed for all regional simulations except for NR cSST+KF. The latter configuration resembles the GLEAM data-set closely with some underestimation for late spring. For the winter, the downscaling leads to a slight underestimation but also with NR cSST+KF performing better than the other configurations. Moreover, INTERIM agrees well with the GLEAM data with some overestimation during winter.
Atmospheric water budget INTERIM and NR vSST+BMJ depict also the best achieved realizations of the atmospheric water budget analysis (Fig. 7d). NNRP contains a significant phase shift with respect to the reference data. For 2003 and 2006 INTERIM is significantly dryer than observed. The best coherence is obtained with the NR vSST+BMJ configuration of WRF. With NR cSST+KF the atmospheric water budget is overestimated for the summer months.
Aggregated runoff versus gauge discharge The comparison of 2003–2005 mean modeled surface runoff with the mean observed stream-flow (right column of Table 6) yields good agreement for both of the global reanalyses. With the regional simulations the resulting bias is between 45 and 64 mm month−1. Again, the best performing downscaling is NR vSST+BMJ with 23 mm month−1 of deviation. It seems that for the vSST+BMJ configuration the overestimated precipitation is mostly converted to runoff with only a small contribution to the evapotranspiration bias.
Skill of the downscaling For the Niger basin, the downscaling does not result in a clear improvement of the global reanalyses. Besides the temperature overestimation that was also seen in a similar range for the Sahara and the Chad basin, the precipitation is overestimated. Large bias values are especially observed for the monsoon period. In general, NNRP driven simulations fit better to the global observational data sets. However, the global NNRP reanalysis contains a remarkable dry and cold bias that is about the negative amount of the overestimation by the regional model. By taking P, E a , and T2 into account, the best realization with the regional model could be achieved with the NR vSST+BMJ configuration.
4.2.4 Summary Africa domain: performance of regionalization
Altogether, it can be stated that INTERIM performs best in the comparison of the global reanalyses. For the regional simulations, NR vSST+BMJ is the configuration that agrees best with the observations of P and T2. For the Sahara and the Chad basin, with this setup of the regional model, the global driving reanalysis is clearly outperformed. The INTERIM driven WRF simulations yield a serious wet bias for the rainy periods. In general it is found that precipitation is strongly overestimated for the tropical and monsoonal regions during the rainy season.
4.3 Australian domain
Precipitation In the upper panel of Fig. 8 the 2003–2006 deviations for precipitation are presented for the Australian domain. The station network of GPCC is comparatively dense for the eastern and southwestern regions. Like for the North Africa domain, large gaps exist for the deserts regions in the center of the continent. Compared to GPCC, CRUP shows a dry bias for large areas. East of 120°E and in the eastern coastal regions, the values are lowered by 100–200 mm year−1. DELP agrees for the most part with GPCC. Many areas lie within the ±25 mm year−1 range. Stronger deviations are seen along the eastern coastline and around 20°S 130°E. GPCP returns wetter conditions for most parts of Australia. Especially along the coastline, the observations exceed those of GPCC by up to 300 mm year−1.
The global reanalysis fields contain a visible dry bias. NNRP returns 100–400 mm year−1 decreased amounts of precipitation over large extents. In INTERIM the regions of significant negative deviation are concentrated over the north and at some narrow regions along the coasts. All maps in Fig. 8 contain a spot at the same position in the north where precipitation is more than 300 mm year−1 below that of GPCC. This is likely to be a shortcoming of the GPCC observations. The sparse station density in this region corroborates this assumption.
In summary, it can be stated that for the arid inland locations, the relative uncertainties based on the different observational data are between 30 and 50 %. GPCP seems to overestimate precipitation for the coastal regions and the fields from the global reanalysis models are clearly biased towards dryer conditions.
For the different regional model configurations a similar southwest to northeast gradient is obtained. Along the eastern and northeastern coast the values of GPCC are exceeded by 1,500 mm year−1 and more. The strongest overestimation is seen for NR vSST+KF+FDDA and EI vSST+KF. When gridded nudging is activated and INTERIM driving is used (EI vSST+KF+FDDA), the areas with 500–1,500 mm year−1 exceeding become considerably smaller. With the BMJ cumulus parametrization, precipitation along the northern coast is better represented with NNRP driving, but along the latitude of 120°E a new maximum is produced. The feature also remains when ERA INTERIM boundary conditions are used.
Independent from the applied driving data, only for the outermost southwestern part of Australia, the precipitation results from the regional model agree well with the global observation fields. The analysis of precipitation patterns reveals that the regional model has structural problems in resembling the observed annual patterns. Virtually all of the high rainfall rates are obtained during the southern summer months from November–January (Fig. 9a). This effect is captured with both model drivings. However, the deviation strength depends on the physical configuration of WRF. The largest exceedance lies outside of the defined study area. Hence, for the aggregated time series the average deviations will possibly wrongly remain within reasonable boundaries. The dryer regions in the south and southwest should compensate for a certain amount of the overestimation that is obtained for the northern part.
Although suffering from a seasonal overestimation for the Central Australian basin, with the EI vSST+KF+FDDA configuration, the most reasonable results are obtained in terms of the bias and RMSE (see Table 7). NR vSST+BMJ in turn gives the best performance for the temporal correlation with GPCC (r = 0.84).
2 m temperature The north to south deviation gradient obtained from WRF precipitation is not found for the temperature field. The results of the regional simulations exhibit a very uniform spatial distribution for all three configurations of the regional model. The 2003–2006 mean deviation fields are shown in the lower panel of Fig. 8. For all regional simulations, except for the easternmost regions, a warm bias of 0.5–3.5 K is found. Values of 0.5–1.5 K are obtained for most of the coastal regions. The Central Australian plane is about 3 K warmer than suggested by the observations of CRUT on average, but also gives areas where the temperature is 4–5 K higher than suggested by CRUT. For both model drivings, no changes are seen when the gridded nudging option is activated. Also with the vSST+BMJ configurations, the general deviation patterns remain similar to those of vSST+KF.
The comparison for the time series of the Central Australian basin is shown in Fig. 9b. All regional simulations exhibit similar skill for the temperature. The seasonal signal is also well observed. Compared to the observational data sets, the seasonal amplitude is too small for the results of the regional model. This is caused by the overestimation of temperature during southern hemisphere winter of up to 5.5 K. Apart from NR cSST+KF, the summer values and the peak in January are better resembled for all considered configurations of WRF. Nevertheless, a warm tendency of 1–2 K is experienced for these periods. Typical values for the annual bias lie between 2.7 and 3.6 K for the regional time series and the global data of CRUT and DELT. The bias and RMSE values are printed in Table 7. NR cSST+KF returns a seasonal amplitude similar to the references. However, the bias values are relatively high for all months, ranging from 3 to 5 K. Thus, the NR cSST+KF configuration has to be rejected in terms of reasonableness.
For the global reanalyses, INTERIM exhibits a warm bias in the central to western part of Australia, the overall pattern is mainly captured. NNRP contains a more distinct cold bias, ranging from −0.5 to −3 K Similar, to the results from the regional simulation, the temperature deviations are not in coherence with those of precipitation.
The analysis of the basin time series shows a very good match between the global observations and INTERIM. Small deviations between 0.5 and 1 K exist only for the warmest summer months, not including NNRP. With respect to CRUT, the amplitude is 2–3 K larger. In winter, a cold bias of about 2 K is experienced. During summer, NNRP is around 1 K warmer than CRUT. The mean annual deviation lies around −0.3 K, in the opposite direction to INTERIM.
Evapotranspiration The time series for E a are plotted in Fig. 9c. In general, all models are in good agreement with the GLEAM data. Stronger deviation is experienced for the regional simulations during the austral summer and fall. Interestingly, NR cSST+KF, which has a strong warm bias in temperature, fits very well to GLEAM. Moreover, INTERIM resembles the reference data closely. Also the bias and RMSE values listed in Table 7 reflect the good coherence.
Atmospheric water budget As a consequence of the good simulation skill for E a and the problems with P, the regional simulations resemble the atmospheric water budget poorly. If the monsoon period is overlooked, the vSST+BMJ runs yield reasonable agreement with the reference. However, INTERIM performs well for the whole study period. Contrarily, NNRP contains large negative spikes during southern winter time.
Skill of the downscaling Similar to the findings for the Siberia and the North Africa domain, the performance of the regional model is not constant with time. The warm bias in temperature varies typically from 1 to 4 K within a year. Precipitation is strongly overestimated for the Australian summer. Remarkably, the temperature bias reaches its minimum for those periods. During fall and especially for the years 2003–2004, the WRF simulations improve the dry bias of the global reanalyses.
It seems that from ocean evaporation, too much water is introduced into the regional atmospheric model during these specific months. The ocean boundary is problematic in terms of the water budget as it provides an infinite source. The analysis shows, that the regional model returns unrealistic water fluxes for the summer months for the northern Australian domain. Thus, independent of the chosen configuration, the global fields cannot be outperformed by the regional downscaling approach for these periods.
4.4 Amazon domain
Precipitation The 2003–2006 precipitation deviations for the Amazon domain are displayed in Fig. 10. The station network density for GPCC is rather sparse and uniformly distributed over the study region.
Compared to GPCC, CRUP is 30–40 % wetter in the northern part of the domain (Orinoco region), and 30–50 % dryer over the amazon catchment. DELP suggest a higher amount of precipitation for the central regions but dryer conditions towards the east. GPCP is wetter at the southeast and up to 2,000 mm year−1 dryer in the west. In general, all three products are dryer than GPCC over the Andes.
The global reanalysis fields of NNRP and INTERIM show stronger deviation amounts than the gridded observations. INTERIM contains spots with three times elevated rainfall but also regions with strongly decreased annual sums. NNRP stays in the same range, albeit the spatial distribution differs slightly from INTERIM.
The results for the regional downscaling exhibit remarkable deviations for the different model runs. vSST+KF leads to a strong overestimation for the whole domain, except for the west and the northwestern coastal region. Here, the deviations remain within the uncertainty range of the global data sets. For vSST+KF and cSST+KF, NR driving produces less rainfall than EI. The enabling of gridded nudging (FDDA) results in globally reduced precipitation. With this configuration, the values of EI are shifted towards the uncertainty range of the global data sets, whereas by using NR model driving, an underestimation of 50–100 % with respect to GPCC is experienced.
Figure 11a shows the catchment averaged precipitation time series. As already indicated by the spatial analysis, except for EI vSST+KF+FDDA, significant biases of up to 225 mm month−1 are experienced for the regional simulations. With a precipitation bias of −3.5 to 26 mm month−1 and a RMSE of 22.5–35.1 mm month−1 (Table 8), EI vSST+KF+FDDA produces reasonable results in terms of basin-averaged time series within the uncertainty range of the evaluation data sets. Besides gridded nudging, the BMJ cumulus scheme outperforms KF with regard to the spatial deviation patterns but the bias is still large. The strong deviation of the NR vSST+KF+FDDA configuration seems not to be a problem of the regional model but might be caused by deficiencies in the NNRP driving data for that region.
2 m temperature The comparison of global fields with CRUT (Fig. 10, lower panel) yields colder conditions for the modeled variables. For the Andean mountains, both reanalyses are warmer than the observations. For the basin average, INTERIM underestimates temperature by 0.5–1 K and NNRP yields a cold bias of 1–3 K (Fig. 11b).
The deviation patterns of the annual 2-m temperature of the regional simulations relate well to the results of the precipitation analysis. EI vSST+KF and NR vSST+KF lead to an overestimation of up to 3 K, except for the mountainous regions where CRUT suggests colder values. The large negative bias in rainfall obtained from NR vSST+KF+FDDA goes along with a 5–8 K overestimation in temperature. While the vSST+KF simulations are very similar, with constant SST strong deviations are experienced depending on the driving data used. No temperature maps are shown for cSST because EI cSST+KF is very close to EI vSST+KF and NR cSST+KF has resembling spatial patterns with NR vSST+KF+FDDA although the maximum is shifted towards the East. The vSST+BMJ run is almost identical to vSST+KF but yields an increased bias for T2. With respect to the RMSE the vSST+BMJ configurations return the best match for the basin aggregated time-series of T2. If the bias is also included, EI vSST+KF+FDDA can be labeled as the best of the tested configurations.
Evapotranspiration The time series for E a are depicted in Fig. 11c. Only two realizations resemble the GLEAM data with reasonable coherence. INTERIM provides agreeable seasonality and amplitude but yields a negative time shift of several months. The bias is low with 3.6 mm month−1. The downscaling with INTERIM driving and gridded nudging option EI vSST+KF+FDDA corresponds well with GLEAM with a bias of −2.8 mm month−1 (Table 8) and improves also the RMSE. With NNRP driving and nudging, E a is significantly underestimated. All other tested configurations of the regional model lead to a positive bias of around 15–60 mm month−1.
Atmospheric water budget As visualized in Fig. (11d), most of the results are out of the range of P − E a . While NNRP is dryer than the reference data, INTERIM and EI vSST+KF+FDDA are in good agreement. All other configurations of the regional model lead to significant overestimation.
Aggregated runoff versus gauge discharge For the runoff, the bias of −45 mm month−1 for EI vSST+KF+FDDA goes along with the precipitation underestimated by −26 mm month−1 (Table 8). With the 2003–2006 average, INTERIM matches the observation. NNRP is too dry by around −19 mm month−1.
Skill of the downscaling As with the tropical regions of Northern Australia and Africa, the regional simulations tend to massively overestimate the precipitation amount of the rainy season. Thus, most of the regional model setups show a worse performance compared to their global driving reanalyses. However, with gridded nudging a significant improvement is seen for the ERA-INTERIM driven WRF run. Besides a slight dry bias, the regional model is able to add value to the respective global reanalysis in terms P and E a . The representation of the 2 m-temperature is significantly improved and the cold bias of the global reanalysis is clearly outperformed. Although reasonable results can be obtained with the gridded nudging setup of WRF, conceptually, this configuration is not ideal for this regional water budget study as it suppresses the development of individual patterns and physical conditions independent from the global driving data.
5 Discussion
The skill of the regional atmospheric model in representing the water budgets of continental scale hydrological basins is affected by different factors. Thus, for every study domain, the configurations of the regional atmospheric model WRF-ARW need to be individually adapted. A general configuration that fits well to all of the test regions cannot be identified. In the following, the issue of regional model configuration is examined from different viewpoints.
Impact of global driving data Two different sets of global atmospheric reanalyses are dynamically downscaled with the regional atmospheric model WRF. The evaluation for the global fields reveals important differences between the two products of ECMWF ERA-INTERIM and NCAR/NCEP NNRP. Besides the differences in horizontal and vertical model resolution, remarkable deviations are obtained for the spatial patterns of modeled and observed monthly fields of 2-m temperature and precipitation.
It cannot be stated that one of the two used reanalyses is superior for driving the WRF model. While for the Siberia domain it is found that INTERIM driving resembles the observed best, NNRP input seems to be the better choice for the North Africa domain as the INTERIM driven simulations tend to overestimate precipitation and thus the storage input. For Australia, with NNRP a good performance is seen, but also with INTERIM reasonable results are achieved. Regarding the Amazon domain, only INTERIM driving in combination with gridded nudging returns realistic water budgets.
The suitability of a certain regional model driving seems to be additionally related to the climatological properties of the considered regional model domain. For the regions tested in this study, NCAR/NCEP NNRP is preferable for the dry and hot conditions of the Sahara and the Central Australian basin. ECMWF ERA-INTERIM gives more appropriate results for the polar climate of the Siberia domain. For the transition zones between desert and tropical characteristics, an individual validation against observations (e.g. precipitation) is necessary for a ranking of the two driving scenarios. Under tropical conditions, INTERIM driving tends to overestimate convective precipitation. For the Amazon basin, this could be corrected by gridded nudging.
To summarize, it can be stated that the results of the regional downscaling are strongly affected by the chosen driving conditions. The validation with global, gridded observations indicates that none of the boundary fields can be taken as a global optimum. An individual selection depending on the region is necessary.
Impact of regional model configuration The WRF modeling system contains numerous selectable parametrizations for different physical compartments. Some of these modules can be chosen by logical reasons like the ability to represent the physical processes with sufficient detail. However, for some of the compartments no favorable configuration can be assessed.
The parametrization of convective motion and precipitation generation becomes necessary for horizontal model resolutions larger than (3−5 km)2. The Kain–Fritsch (KF) scheme tends to overestimate convective precipitation for the warm and moist conditions of the Amazon, the African, and the Australian model domain. Large discrepancies between simulations and observations are obtained during the rainy and monsoon periods over the Amazon and West Africa. For the Siberia domain, with KF the basin averaged time series fit well to the observations of P but deficiencies exist for E a and T2. For hot and dry regions like the Sahara, the Betts–Miller–Janjić (BMJ) scheme outperforms KF with respect to the time series correlation and mean bias. Similar results are obtained for intermittent tropical conditions, e.g. for the basins of Lake Chad or Niger. For the Central Australian desert basin, the combination of KF+FDDA and INTERIM driving gives the best coherence with the observations. When NNRP driving is used the best results are obtained with when the BMJ scheme is activated.
The SST is important for the calculation of open water evaporation in the regional model. Two options can be selected for the representation of the SST. Either the values remain constant as initialized at model start or WRF ingests gridded SST data from observations or from global models. The results showed, that a variant SST is vital to the correct representation of the water budget in the regional model. However, for some study regions, modeled precipitation could be improved by using constant SST conditions. Nevertheless, a constant field usually results in large positive temperature bias values and in an unreasonable representation of other compartments of the hydrological cycle. Hence, with constant SST, substantiated results can only be obtained for the deserts where advection of moisture of oceanic origin is unimportant. The combination of INTERIM driving and constant SST leads to numerical problems within WRF. For regions where precipitation comes mainly from oceanic sources constant SST typically leads to wrong evaporation estimates and thus to an unrealistic simulation for the advection of moisture. Additional research on the coupling of SST and the water budget of regional atmospheric models is required.
Some model domains are located in zones that are largely affected by global circulation mechanisms and large scale patterns. Usually, the regional model connects to the global driving fields only through lateral boundaries. This information is not always sufficient for the development of reasonable structures in the regional domain. FDDA, also known as gridded nudging provides an opportunity to constrain the regional solution for selected three dimensional variables of the global driving fields. The FDDA option strongly affects the water budget for the Amazon domain. Remarkably, the most effective nudging variable is temperature and not wind or moisture. This suggest a strong coherence between overestimated convective precipitation with the Kain–Fritsch scheme and elevated air temperature (i.e. the 3-d temperature field as the 2 m-temperature is only a diagnostic variable in WRF). For the Siberia domain no remarkable impact on the results is found if the FDDA option is activated. Also for the North Africa domain no substantial difference is seen. However, especially the monsoonal conditions along the southern coast of West Africa do not improve by nudging. For Australia a slight improvement is experienced with FDDA and INTERIM driving but substantial errors remain for the northerly moisture advection during summer. Altogether, the analysis shows that the sensitivity of the FDDA option is only occasional. From the perspective of physical modeling, it is desired that the regional model resembles the conditions well with only being dependent on the global model for the lateral boundary conditions. With WRF this seem to be the case for all domains but the Amazon. The shortcoming with the spatial resemblance of temperature over the Amazon could also be caused by other reasons like erroneous water and energy exchange processes within the land surface and the surface exchange modules.
Performance of the regional atmospheric model The Weather Research and Forecasting modeling system WRF is a complex tool with many interchangeable modules and even more configuration options. The application for continental scale regions and for longer term periods was not the main intention of its developers. However, the chosen model resolution is not beyond the stated capabilities of WRF but the use of physical parametrization schemes is inevitable.
The validation analysis of regional simulations and global observational products leads to the conclusion that driving and physical configuration needs to be adapted and evaluated for every individual domain. If this approach is followed, the model results class among the uncertainties of the observations. The seasonal cycles are usually well resembled for the different compartments of the hydrological cycle and also for the near-surface temperature. However, it is experienced that the amplitudes differ for some regions or periods.
The SST has an important influence on the water budgets of the regional atmospheric simulation and no reasonable results can be achieved without a time-variant setup.
Precipitation is overestimated with many of the tested configurations and most sensitive to the cumulus parametrization. However, configurations leading to reasonable precipitation results can be identified for all of the regions tested in this study.
The seasonality of the regional simulations and the GLEAM evapotranspiration data are in good agreement. For the successfully validated model configurations, the amplitudes are met quite well. For the Amazon basin, a time lag is obtained between GLEAM and the global reanalysis and the regional model. Larger deviation between simulation and GLEAM is found for the Sahara basin. It cannot be stated which of the two approaches is more realistic in both cases. It is concluded that the GLEAM method depicts a reasonable and valuable assessment of the monthly land surface evapotranspiration, providing a sound data-set for the validation of global and regional atmospheric models.
Temperature is generally overestimated with the regional simulations. The effect may be caused by several factors, ranging from errors in the description of horizontal advection (sensitivity to cSST/vSST) or the vertical exchange in the planetary boundary layer to mismatching evapotranspiration guesses due to an inappropriate representation of land-surface states in the regional atmospheric model. Moreover, it is assumed that the Noah LSM contributes to the temperature bias of the WRF simulations. One reason for that could be the shallowness of the modeled soil layer, leading to a unrealistic small heat storage capacity. Also the storage capacity for water is limited and no groundwater storage exist. Water that percolates through the deepest soil layer leaves the model with no possibility of return by capillary rise. These hydrological shortcomings of the Noah LSM could intensely affect the exchange of energy and water at the surface layer of the regional model. Therefore, LSMs with extended physical detail for subsurface hydrological processes, like, e.g. the Community Land Model (CLM) or the Noah Multiple Physics (Noah MP) model available with the latest WRF version, should be tested with respect to the water budget in future studies.
For the regional model configurations that lead to reasonable results for P and E a the amount of generated runoff R is within reasonable bounds. The biases for R have usually the same sign and magnitude as seen for those of P or P − E.
Regional downscaling versus global data The quality of the global driving data is major issue for the dynamic downscaling approaches. Without accurate boundary information for wind, moisture, and temperature the regional atmospheric model will fail to produce physically reasonable conditions.
For the water budgets, in order to assess whether regional downscaling adds value to its global driving, it is important to analyze the spatial patterns instead of looking at basin averaged time series only. In this study the regional fields are validated against the prevalent global observation products for 2-m temperature and precipitation. For certain regions, the accuracy of these data sets is drastically reduced because of a lack of measuring stations (Lorenz and Kunstmann 2012), especially for the inland regions of North Africa and Australia.
With respect to the spatial patterns of precipitation and temperature, varying performance is seen for the selected study regions. Except for the summer period, for Australia, reasonable results are obtained with the regional model. The same applies for the Amazon domain if gridded nudging is used. With this configuration, WRF outperforms the global reanalysis of ECMWF ERA-INTERIM in terms of the temperature bias. However the resulting precipitation fields show a slight dry tendency. The downscaled results remain within the uncertainty bounds spanned by the observations. For the North Africa domain, the NNRP driven regional simulation with variable SST and BMJ cumulus scheme also adds value to the driving data but remains usually beyond the skill of the global ERA-INTERIM reanalysis. Except for the southern coastal region of Western Africa, the downscaled fields correct the bias tendencies of the global fields. As with Australia, the temperature is about 1–2 K warmer than found in the observations. But it must be taken into account that the global fields of INTERIM and NNRP are 1–2 K too cold. For Siberia the global reanalyses suggest wetter conditions than observed in reality. The regional simulations are able to correct the bias but produce dryer conditions than seen with GPCC. However, the resulting patterns are in agreement with CRUP and DELP and hence within the uncertainty bounds of the observations. While the global reanalyses contain a warm and cold bias for the eastern and western domain, respectively, a large warm bias is seen for the regional simulation. Thus it must be stated that the regional model contains structural problems for the 2-m temperature during the polar winter. Hence, for these periods, no additional skill could be added to the global fields.
6 Conclusion
The selection of physical parametrizations and driving data can largely affect water budgets derived by the regional atmospheric model WRF. We showed that the regional model is able to reduce the bias of precipitation and 2 m-temperature with respect to their global driving. For most of the study regions, ECMWF ERA-INTERIM outperformed NCEP/NCAR NNRP. Only for the dynamical downscaling for the dry regions NNRP is found to be sufficient. The strong deviation in terms of the water budget for the two convective parametrizations tested suggest additional research needs and a better integration of the steadily rising number of physical parametrizations in WRF. Moreover, the modest description of the subsurface hydrology in WRF poses additional constraints for a realistic representation of the water budget.
Accounting for the water budget in long term regional atmospheric simulations enables an enhanced classification of suitable model configurations. With the new GLEAM evapotranspiration data an additional verification option exists, allowing also for the checking of the atmospheric water balance \((\nabla \cdot {\bf Q})\). For a fully closed water balance evaluation for continental scale hydrological basins, the modeled terrestrial water storage variations could be additionally compared to observations from the Gravity Recovery And Climate Experiment (GRACE) (Fersch et al. 2012). In the future, the atmospheric water vapor distribution could be advantageously studied using remote sensing products like Interferometric Synthetic Aperture Radar (InSAR) or the Envisat Medium Resolution Imaging Spectrometer (MERIS) (Alshawaf et al. 2012).
References
Adler RF, Huffman GJ, Chang A, Ferraro R, Xie PP, Janowiak J, Rudolf B, Schneider U, Curtis S, Bolvin D, Gruber A, Susskind J, Arkin P, Nelkin E (2003) The Version-2 Global Precipitation Climatology Project (GPCP) Monthly Precipitation Analysis (1979–Present). Journal of Hydrometeorology 4(6):1147–1167. doi:10.1175/1525-7541(2003)004<1147:TVGPCP>2.0.CO;2
Alexandru A, de Elia R, Laprise R, Separovic L, Biner S (2009) Sensitivity study of regional climate model simulations to large-scale nudging parameters. Mon Weather Rev 137(5):1666–1686. doi:10.1175/2008MWR2620.1
Alshawaf F, Fersch B, Hinz S, Kunstmann H, Mayer M, Thiele A, Westerhaus M, Meyer F (2012) Analysis of atmospheric signals in spaceborne InSAR—toward water vapor mapping based on multiple sources. In: Geoscience and remote sensing symposium (IGARSS), 2012 IEEE international. pp 1960–1963. doi:10.1109/IGARSS.2012.6351118
Baldwin ME, Kain JS, Kay MP (2002) Properties of the convection scheme in NCEP’s eta model that affect forecast sounding interpretation. Weather Forecast 17(5):1063–1079. doi:10.1175/1520-0434(2002)017<1063:POTCSI>2.0.CO;2
Beck A, Ahrens B, Stadlbacher K (2004) Impact of nesting strategies in dynamical downscaling of reanalysis data. Geophys Res Lett 31(19):101. doi:10.1029/2004GL020115
Berg P, Wagner S, Kunstmann H, Schädler G (2013) High resolution regional climate model simulations for Germany: part I—validation. Clim Dyn 40(1–2):401–414. doi:10.1007/s00382-012-1508-8
Borge R, Alexandrov V, José del Vas J, Lumbreras J, Rodríguez E (2008) A comprehensive sensitivity analysis of the WRF model for air quality applications over the Iberian Peninsula. Atmos Environ 42(37):8560–8574. doi:10.1016/j.atmosenv.2008.08.032
Bowden JH, Otte TL, Nolte CG, Otte MJ (2012) Examining interior grid nudging techniques using two-Way nesting in the WRF model for regional climate modeling. J Clim 25(8):2805–2823. doi:10.1175/JCLI-D-11-00167.1
Brohan P, Kennedy JJ, Harris I, Tett SFB, Jones PD (2006) Uncertainty estimates in regional and global observed temperature changes: a new data set from 1850. J Geophys Res 111(D12):106. doi:10.1029/2005JD006548
Chen F, Dudhia J (2001) Coupling an advanced land surface-yydrology model with the Penn State–NCAR MM5 modeling system. Part I: model implementation and sensitivity. Mon Weather Rev 129(4):569–585. doi:10.1175/1520-0493(2001)129<0569:CAALSH>2.0.CO;2
Chotamonsak C, Salathé EP, Kreasuwan J, Chantara S, Siriwitayakorn K (2011) Projected climate change over Southeast Asia simulated using a WRF regional climate model. Atmos Sci Lett 12(2):213–219. doi:10.1002/asl.313
Chou MD, Suarez MJ (1994) Technical report series on global modeling and data assimilation, National Aeronautics and Space Administration, Goddard Space Flight Center, chap an efficient thermal infrared radiation parameterization for use in general circulation models. No. 104606 in NASA Tech. Memo., pp 85. http://purl.access.gpo.gov/GPO/LPS59306
Denis B, Laprise R, Caya D (2003) Sensitivity of a regional climate model to the resolution of the lateral boundary conditions. Clim Dyn 20(2–3):107–126. doi:10.1007/s00382-002-0264-6
Fersch B, Kunstmann H, Devaraju B, Sneeuw N (2012) Large scale water storage variations from regional atmospheric water budgets and comparison to the GRACE spaceborne gravimetry. J Hydrometeorol 13(5):1589–1603. doi:10.1175/JHM-D-11-0143.1
Flaounas E, Bastin S, Janicot S (2010) Regional climate modelling of the 2006 West African monsoon: sensitivity to convection and planetary boundary layer parameterisation using WRF. Clim Dyn 36(5):1083–1105. doi:10.1007/s00382-010-0785-3
Gochis D, Yu W, Yates D (2013) The WRF-Hydro model technical description and user’s guide, version 1.0. Ncar technical document. http://www.ral.ucar.edu/projects/wrf_hydro/
Heikkilä U, Sandvik A, Sorteberg A (2011) Dynamical downscaling of ERA-40 in complex terrain using the WRF regional climate model. Clim Dyn 37(7):1551–1564. doi:10.1007/s00382-010-0928-6
Hines KM, Bromwich DH, Bai LS, Barlage M, Slater AG (2010) Development and testing of Polar WRF. Part III. Arctic Land. J Clim. doi:10.1175/2010JCLI3460.1
Hong SY, Dudhia J, Chen SH (2004) A revised approach to ice microphysical processes for the bulk parameterization of clouds and precipitation. Mon Weather Rev 132:103–120. doi:10.1175/1520-0493(2004)132<0103:ARATIM>2.0.CO;2
Hong SY, Noh Y, Dudhia J (2006) A new vertical diffusion package with an explicit treatment of entrainment processes. Mon Weather Review 134(9):2318–2341. doi:10.1175/MWR3199.1
Janjić ZI (2000) Comments on “Development and Evaluation of a Convection Scheme for Use in Climate Models”. J Atmos Sci 57(21):3686–3686. doi:10.1175/1520-0469(2000)057<3686:CODAEO>2.0.CO;2
Jones P, Harris I (2008) CRU time series (TS) high resolution gridded data version 3.00. Internet, http://badc.nerc.ac.uk/view/badc.nerc.ac.uk__ATOM__dep_12562264599328294, visited 2010/01/13
Kain JS (2004) The Kain–Fritsch convective parameterization: an update. J Appl Meteorol 43:170–181. doi:10.1175/1520-0450(2004)043<0170:TKCPAU>2.0.CO;2
Kalnay E, Kanamitsu M, Kistler R, Collins W, Deaven D, Gandin L, Iredell M, Saha S, White G, Woollen J, Zhu Y, Leetmaa A, Reynolds R, Chelliah M, Ebisuzaki W, Higgins W, Janowiak J, Mo K, Ropelewski C, Wang J, Jenne R, Joseph D (1996) The NCEP/NCAR 40-year reanalysis project. Bull Am Meteorol Soc 77(3):437–471. doi:10.1175/1520-0477(1996)077<0437:TNYRP>2.0.CO;2
Kim EJ, Hong SY (2010) Impact of air–sea interaction on East Asian summer monsoon climate in WRF. J Geophys Res 115(D19):118. doi:10.1029/2009JD013253
Liu HB, Wang B (2011) Sensitivity of regional climate simulations of the summer 1998 extreme rainfall to convective parameterization schemes. Meteorol Atmos Phys 114(1–2):1–15. doi:10.1007/s00703-011-0143-y
Lorenz C, Kunstmann H (2012) The hydrological cycle in three state-of-the-art reanalyses: intercomparison and performance analysis. J Hydrometeorol 13(5):1397–1420. doi:10.1175/JHM-D-11-088.1
Matsuura K, Willmot CJ (2009a) Terrestrial air temperature: 1900–2008 gridded monthly time series (Version 2.01). http://climate.geog.udel.edu/~climate/, visited 2010/01/13
Matsuura K, Willmot CJ (2009b) Terrestrial precipitation: 1900–2008 gridded monthly time series (Version 2.01). http://climate.geog.udel.edu/~climate/, visited 2010/01/13
Miguez-Macho G, Stenchikov GL, Robock A (2004) Spectral nudging to eliminate the effects of domain position and geometry in regional climate model simulations. J Geophys Res 109(D13):104. doi:10.1029/2003JD004495
Miralles DG, Holmes TRH, De Jeu RAM, Gash JH, Meesters AGCA, Dolman AJ (2011) Global land-surface evaporation estimated from satellite-based observations. Hydrol Earth Syst Sci 15(2):453–469. doi:10.5194/hess-15-453-2011
Mlawer EJ, Taubman SJ, Brown PD, Iacono MJ, Clough SA (1997) Radiative transfer for inhomogeneous atmospheres: RRTM, a validated correlated-k model for the longwave. J Geophys Res 102:16663–16682. doi:10.1029/97JD00237
Peixoto JP, Oort AH (1992) Physics of climate (chap 12.2.2 Balance equations for water). American Institute of Physics, New York, pp 274–277
Peterson TC, Vose RS (1997) An overview of the global historical climatology network temperature database. Bull Am Meteorol Soc 78(12):2837–2849. doi:10.1175/1520-0477(1997)078<2837:AOOTGH>2.0.CO;2
Priestley CHB, Taylor RJ (1972) On the assessment of surface heat flux and evaporation using large-scale parameters. Mon Weather Rev 100(2):81–92. doi:10.1175/1520-0493(1972)100<0081:OTAOSH>2.3.CO;2
Rasmusson EM (1977) Hydrological application of atmospheric vapour-flux analyses, operational hydrology, vol. 11. World Meteorological Organization, iSBN 92-63-10476-X
Schneider U, Fuchs T, Meyer-Christoffer A, Rudolf B (2008) Global precipitation analysis products. http://gpcc.dwd.de, visited 2010/01/13
Skamarock WC, Klemp JB (2008) A time-split nonhydrostatic atmospheric model for weather research and forecasting applications. J Comput Phys 227(7):3465–3485. doi:10.1016/j.jcp.2007.01.037
Skamarock WC, Klemp JB, Dudhia J, Gill DO, Barker DM, Wang W, Powers JG (2008) A Description of the advance research WRF Version 3. NCAR technical note NCAR/TN-468+STR, National Center for Atmospheric Research, Boulder, Colorado, USA
Uppala S, Dee D, Kobayashi S, Berrisford P, Simmons A (2008) Towards a climate data assimilation system: status update of ERA-Interim. ECMWF Newsl 115:12–18
Wagner S, Berg P, Schädler G, Kunstmann H (2013) High resolution regional climate model simulations for Germany: part II—projected climate changes. Clim Dyn 40(1–2):415–427. doi:10.1007/s00382-012-1510-1
Wang W, Seaman NL (1997) A comparison study of convective parameterization schemes in a mesoscale model. Mon Weather Rev 125(2):252–278. doi:10.1175/1520-0493(1997)125<0252:ACSOCP>2.0.CO;2
Wang W, Bruyere C, Duda M, Dudhia J, Gill D, Lin HC, Michalakes J, Rizvi S, Zhang X (2009) WRF ARW version 3 modeling system user’s guide, April 2009. National Center for Atmospheric Research (NCAR), pp 310
Acknowledgments
This work was supported by the DFG (Deutsche Forschungsgemeinschaft KU 2090/1-2) and contributes to the Special Priority Program Mass Transport and Mass Distribution in the System Earth (http://www.massentransporte.de). The authors would like to thank ECMWF and NCAR/NCEP for providing the global atmospheric reanalysis products and we acknowledge Diego Miralles for providing the GLEAM evapotranspiration fields. We are grateful to the two anonymous reviewers who helped to improve the structure and clearness of the manuscript, considerably. Moreover, we thank Richard Foreman for helping to improve the language.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution License which permits any use, distribution, and reproduction in any medium, provided the original author(s) and the source are credited.
About this article
Cite this article
Fersch, B., Kunstmann, H. Atmospheric and terrestrial water budgets: sensitivity and performance of configurations and global driving data for long term continental scale WRF simulations. Clim Dyn 42, 2367–2396 (2014). https://doi.org/10.1007/s00382-013-1915-5
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00382-013-1915-5