Abstract
In most industrial products, granular materials are often required to flow under gravity in various kinds of silo shapes and usually through an outlet in the bottom. There are several interrelated parameters which affect the flow, such as internal friction, bulk and packing density, hopper geometry, and material type. Due to the low-spatial resolution of electrical capacitance tomography or scanning speed limitation of standard X-ray CT systems, it is extremely challenging to measure the flow velocity and possible centrifugal effects of granular materials flow effectively. However, ROFEX (ROssendorf Fast Electron beam X-ray tomography) opens new avenues of granular flow investigation due to its very high temporal resolution. This paper aims to track particle movements and evaluate the local grain velocity during silo discharging process in the case of mass flow. The study has considered the use of the Seramis material, which can also serve as a type of tracer particles after impregnation, due to its porous nature. The presented novel image processing and analysis approach allows satisfyingly measuring individual particle velocities but also tracking their lateral movement and three-dimensional rotations.
Similar content being viewed by others
1 Introduction
Granular materials play an important role in many industries, like in mining, agriculture, civil engineering, and pharmaceutical manufacturing. They are ubiquitous in our daily lives, displaying extremely complex behaviour (Jaeger and Nagel 1992; Duran and Behringer 2001). In most of the above-mentioned industries, silos are commonly used to store, protect and load for bulk materials into process machinery (Qiu et al. 2009; Chaniecki et al. 2014). It is generally agreed that there are two main types of silo discharging process. The first one is the so-called funnel flow, in which granulates are flowing only in the center of the silo, while in the rest is creating a stagnant zone of materials at the wall of the container (Schulze 2008). The second type of flow is called mass flow, which this paper focuses on and operates as the first material filled in will flow first out at the bottom as well with a uniform discharging velocity across the entire cross-section area (Drescher 1992; Schulze 2008).
The way the material is discharged through the outlet of the silo and the related dynamic effects of the flow are important questions, which are still not completely understood because they can have multiple causes. There are several interrelated parameters which can affect the discharging process of granulates, such as the internal friction, packing density, particle size distribution, hopper geometry, material type and inherent properties. These have direct influences on unwanted phenomena such as arching or ratholing, which are the most common problems for funnel flow (Michalowski 1984; Qiu et al. 2009; Wilde et al. 2010). Segregation is also an undesirable phenomenon when a homogeneous mixture is required, for example, in metallurgical and pharmaceutical industries (Ketterhagen et al. 2007). Mass flow is the desirable outcome when handling segregation-prone materials, as it highly reduces or eliminates the effects of sifting and dusting segregation mentioned above (Qiu et al. 2009).
Because granular materials are usually made of a very large number of individual cohesion-less elements, the prediction of their individual behaviour is also a very challenging task that can be difficult to support with experimental data. For instance, one can mention various numerical predictions, such as discrete element method (DEM) to predict global granular material flow behaviors, for instance discharging rate (Anand et al. 2008; Ketterhagen et al. 2007), flow mode prediction (Ketterhagen et al. 2009) or outflow or mean discharging velocity (Balevičius et al. 2011). However, the comparison between experiment and simulation for local measurements, such as local grain velocity prediction, has been rarely investigated (Ketterhagen et al. 2009). Hence, this study aims to provide trustful local non-invasive measurements of flow dynamics, with a focus on particles bed moving down through cylindrical silo model.
For the last decades, the silo discharging process has been studied using different imaging techniques, for instance, X-ray radiography or computed tomography (CT) (Babout et al. 2013; Chen et al. 2016; Grantham and Forsberg 2004), electrical capacitance tomography (ECT) (Garbaa et al. 2016; Grudzien et al. 2012a, b; Grudzien 2017; Grudzień et al. 2017) and high-speed cameras (Drescher and Ferjani 2004; Steingart and Evans 2005). However, due to the scanning speed limitation of CT and low resolution of ECT as compared to X-ray or lack of visualizing the interior flow part in the case of a high-speed camera, the local velocity and centrifugal effects of granular material flow were not measured effectively.
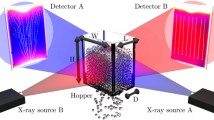
To overcome the above technological limitations, the ultrafast electron beam X-ray CT scanner from Helmholtz-Zentrum Dresden-Rossendorf is a possible solution. It offers a very high-temporal resolution and adequate spatial resolution to track specific translational and rotational motions of objects. It is originally developed to scan liquid–gas flow (Fischer et al. 2008; Fischer and Hampel 2010). This paper presents the first attempt for investigating granular material flow. Particularly, it focuses on the case of mass flow, with the main objective of validating the usage of ROFEX to obtain meaningful imaging information for extracting flow characteristics related to particle trajectory movement estimations. Additionally, as the CT scanner comes with two measurement planes, it gives information to determine the axial velocity of particles (Fischer et al. 2008; Fischer and Hampel 2010; Bieberle and Barthel 2016).
The paper is structured as follows: the part following this introduction presents the experimental set-up associated with silo design, granular material selection as well as ROFEX description. Then, data processing and analysis is presented with experimental results. Afterwards, the sensitivity analysis of applied methods and performance of the proposed algorithm have been discussed. Concluding remarks and work perspectives are enumerated at the end.
2 Experimental set-ups
2.1 Silo model and granular material
The experiments have been carried out using a cylindrical silo model having 100 mm inner diameter, a bin height of 1500 mm, as shown in Fig. 2a. The hopper used for this study has a cone shape with a vertical slant angle of 45° and an outlet diameter of 25 mm, which is adapted to generate silo discharging with the mass flow type. An especially designed shutter disk controls opening and closing of the silo outlet remotely. Before acquiring the images used for analysis, the shutter is opened and steady state flow evolves. Note, previous studies have proved that there is no much difference between the continuous and time-lapse study of discharge, as far as particle rearrangement and flow dynamics are concerned (Babout et al. 2013; Ketterhagen et al. 2007).
For the entire experiment, around 6.7 l of Seramis® is used as a granular material with an average grain size of 5 mm and estimated density of 1.6 mg/mm3 (dry clay). However, for tracking purpose and to fulfill the CT scanner requirement (4 to 5 times larger than spatial resolution), larger grain size tracer Seramis particles were selected and previously infiltrated with NaOH, which gave them a higher X-ray absorption and yet having similar size and density with overall particles. Seramis is a highly porous, processed, particulate clay composed of kaolinite, illite, and quartz, which has very high water retention qualities (Jaronski 2014). Seramis granulate particles have been considered as a suitable material to fulfill ROFEX requirements, due to their adapted size and low density that suit ROFEX spatial resolution and X-ray beam energy, respectively. The total height of the Seramis inside the silo model was around 1000 mm. Figure 2b shows 20 tracer particles set in a spiral pattern at height of 900 mm above the hopper level for tracking purpose (plus on the top covered with a 100 mm clean Seramis to involve the interrelated effects of particles movement such as packing density, pressure, and friction from the top side).
2.2 Ultrafast electron beam X-ray tomography system
The ultrafast electron beam X-ray CT scanner is a non-invasive imaging technique mainly dedicated to the fast measurement of multiphase flows (Fischer and Hampel 2010). The X-ray generator of ROFEX is based on a free electron beam, which is deflected by electron optics on a semi-circular target surrounding the investigated object and generating a very fast rotating X-ray source. The radiation is attenuated while penetrating the studied object and is acquired by a fast static multi-channel detector. The ROFEX system is typically operated with 150 kV high-voltage supply. By using the well-known filtered back projection algorithm, series of cross-sectional images of the object of interest are reconstructed.
During the experiment, the ROFEX scanner delivers cross-sectional images of flowing material with an in-plane spatial resolution of about 1 mm and, in the present experiment, a time-resolution of 500 µs. As shown in Fig. 1, the CT scanner comes with two measurement planes along a geometric distance of 11 mm to perform velocimetry.
2.3 Experimental protocol
Because of computational constraints, the ROFEX systems is limited to roughly a data acquisition of about 25–30 s, even though recent improvements have been published to increase the buffer capabilities of the data acquisition unit (Bieberle et al. 2017). Based on the acquisition frequency and usage of dual-plane, around 20,000 frames were recorded for each scan. Instead of positioning the ROFEX system at a fixed position along the silo, for instance near the hopper-bin transition, and acquire the entire discharging with a series or acquiring blocks of 20 s, the flow process has been investigated at three different positions, i.e., 800, 500 and 200 mm above the hopper level, as illustrated in Fig. 2a.
Preliminary studies have indicated that in the case of mass flow, the Seramis granular material moves with a downward speed of 10 mm/s. Consequently, it has been estimated that roughly 200 mm of packed material height can be scanned during one buffer acquisition. Therefore, during material filling, it has been checked that ROFEX acquisition planes are located 100 mm below the plane where tracer particles have been positioned. As mentioned above, the X-ray acquisition finishes when the free surface, which is above the tracer particle plane, has passed through the acquisition planes. Of course, it is assumed that the upper surface does not have its shape changed drastically during mass flow process and these conditions have held for the three chosen scanning positions.
Prior to filling the silo with the material, white (i.e., empty tube and X-ray ON) and black (i.e., X-ray OFF) references have been acquired to calibrate the reconstructed images of the granular material. After the scanning is performed at a specific silo height, the CT scan detector data is downloaded and finally reconstructed using the filtered back projection algorithm (Bieberle et al. 2017). Before starting any image analysis, all reconstructed raw images are re-centered at all scanning heights to make sure that the center of the tube matches with the center of the image.
3 Data processing and analysis
Efficient segmentation of the tracer particles is a crucial step before starting any particle tracking analysis. Up to now, there are many effective segmentation algorithms proposed by researchers. However, besides the noise on the original raw images, each tracer particle characterizes a different irregular size and slightly uneven infiltration of Sodium hydroxide, which gives different X-ray absorption and images brightness level. Additionally, the intensity ratio between tracer particles to the background particles (i.e., undoped) is tiny (in average 0.83), which causes the image binarization method a very challenging task. Algorithms like Otsu (Otsu 1979) will tend to be poor and even fail to segment tracer particles effectively.
Hence, to obtain segmented images with a clear and solid particle shape, a more sophisticated method is necessary than using general image threshold methods. The proposed approach is inspired and slightly adapted from deoxyribonucleic acid (DNA) microarray image processing techniques, which is commonly used to measure mass gene expressions (Hirata et al. 2001; Le Brese and Zou 2009).
The previous investigation of this study has shown that the flow analysis inside the silo model was characterized by a quasi-steady flow and particles did not change their position within few milliseconds (Waktola et al. 2016). As a result, each tracer particle can be segmented individually within its own bounding area, which also helps to apply different local threshold value depending on the brightness level of the particles.
The entire proposed algorithm, named IGLOS (Irregular Grid for Local Otsu Segmentation) consists of three major steps:
3.1 Manual threshold (image-A)
This step is for finding the projection area of each tracer particles and to make sure that all tracer particles are identified. Maximum intensity projection (MIP), average intensity projection (AIP) and minimum intensity projection (MinIP) are volume-rendering techniques used to define the region of interest on the two-dimensional CT image dataset. In the case of MIP, it produced high-contrast between tracer particles and surrounding undoped particles. As a result, all the 20 tracing particles were detected as shown in Fig. 3c. In comparison, the AIP technique was able to identify only 8 out of 20 tracing particles. As the original raw images contain air (outside the cylinder represented by zero intensity), MinIP displayed totally a blank image. Based on the MIP technique, first, all raw image frames (for i = 1, 2,…, N, where N is the total number of frames to be analysed) is rendered. Second, this rendered image is segmented by simply applying manually set threshold value so as to satisfyingly reveal all tracer particles. This first step is illustrated in Fig. 3.
3.2 Automatic global gridding (image-B)
This step intends to create a non-regular grid for image-A (Fig. 3c), with the aim of having in each grid cell one segmented particle with an optimal background space. To do so, the grid creation is divided into six sub-steps: we are looking for a regular grid of spots so we start by looking at the mean intensity for each column of the image. This will help to identify where the centers of the spots are and where the gaps between the spots can be found.
-
1.
Creating a mean horizontal profile This step is used to determine the center of each cell by plotting the mean intensity of each 256 columns of image-A (image-A is 256 by 256-pixel size, see Fig. 3c). As shown in Fig. 4, the original horizontal profile is irregular and it creates several peaks. If those peaks are used to estimate the gap between each cell, it will generate tiny cell space and a poor local segmentation result. Thus, there is need to enhance the profile by applying an auto-correlation method, which is detailed in the next step.
-
2.
Applying auto-correlation and estimate cell spacing To find the peaks and estimate a solid cell to cell gap, it is necessary to enhance the self-similarity of the mean profile by using auto-correlation, which estimates the auto-covariance sequence of the profile. A typical result applied on the mean intensity profile which is shown in the above figure (Fig. 4) is presented in Fig. 5, where the peaks are identified by red triangles based on the left and right slopes of the auto-correlated profile. In that case, the estimation of the cell spacing value can be found by calculating the mean difference of maxima.
Mean horizontal profile of segmented image (Fig. 3c) with identified peaks in a red triangle (ten black triangles at the bottom, shows positions where intensity value is zero)
-
3.
Applying top-hat filter To enhance the mean profile, a morphological top-hat filtering is applied to the profile with a linear structuring element of length equal to the obtained estimated cell spacing value (in the present case, the length is equal to 33 pixels). One can see in Fig. 6 the effect of such filtering on the original mean profile shown in Fig. 4. The number of triangles, which depicts the edges of zero-intensity value regions, but also intensity peaks, has increased.
-
4.
Applying automatic threshold and locating the centroid between adjacent-labeled peaks At this stage, a better separation of the peaks is obtained, hence it is possible to segment and label each peak region using Otsu’s method. Then, one can easily calculate its median position between each adjacent-labeled peak, where the intensity value is zero, as illustrated by the red circle in Fig. 7.
-
5.
Getting vertical lines of the grid between the adjacent-labeled peaks The midpoint between the adjacent center of each label peak provides locations of the vertical lines of the final grid, as illustrated in Fig. 8.
-
6.
Transposing image-A and repeating steps 1–5 This is the final step to retrieve the horizontal grid lines. The final result of the non-regular grid is shown in Fig. 9. Note that particles can be cut by grid lines and portions of more than one particle can occur in the same grid cell.
Final grid lines superimposed on the segmented MIP image shown on Fig. 3c
3.3 Segmentation using local threshold
First, the non-regular grid is used to set a 3D grid of size R × C × 1 cells, where R is the number of horizontal partition, C the number of vertical partition and one partition concerns the full height of tomographic frame compilation.
Finally, for individual segmentation of tracer particles, it is possible to use each grid cell to increase the contrast of the original raw image and determine its own local threshold level automatically using the Otsu method. In another word, the automatic local threshold level and the contrast value is set depending on the brightness of each tracer particles with the corresponding 3D grid cell. A final result is shown in Fig. 10b, c illustrates the poor segmented result after global Otsu segmentation (GOS) method was applied for a given cross-section. This naturally shows less segmented particles than in the case of the MIP (maximum intensity projection), since all tracer particles are not exactly located in the same plane. The performance of the proposed algorithm and sensitivity analysis of applied methods has been discussed in Sect. 4.5. The overall segmentation algorithm is summarized in the flowchart shown in Fig. 11.
4 Results
4.1 Tracking the lateral movement of tracer particles
After obtaining well-segmented tracer particles using the IGLOS method, each identified object is represented by a 5-pixel radius marker placed on its centroid to simplify its tracking analysis, as shown in Fig. 12.
The above steps are repeated for all frames in a time window until all tracer particles passed through each measuring plane. Figure 13 a and b presents the cross-sectional centroid positions of all identified particles by changing their marked color over discharging time as they pass through the two measurement planes.
Identified tracer particles positions at scanning height of 800 mm. a First measurement plane—color changes from green to blue over discharging time (9–10 s). b Second measurement plane—color changes from red to green over discharging time (10–11 s). c Average centroid positions of tracer particles between discharging time of 9–11 s
To detect if there was any lateral movement of tracer particles during silo discharging, the average centroid positions of all identified particles have been taken from the two measurement planes and the three different scanning heights (example: for scanning height 800 mm, see Fig. 13c). Then, all average positions of identified particles in the three different scanning heights are superimposed together with different RGB colours (red for 800 mm, green for 500 mm and blue for 200 mm). As Fig. 14a shows, positions where the RGB intersection yield white color indicate that the particles were flowing in a quite identical position throughout all the three scanned heights. This concerns most of the detected particles. Moreover, they keep a position which does match with the initial one prior to discharging (Fig. 14b).
It is fair to say that very few particles could not be found in the three scanning positions, which results in other superposition colors (e.g., yellow). As the particles are irregular in shape, the trajectory of their centroid in different scanning heights and the same projecting plane is not enough to detect if they possess any rotational movements. However, this does not alter the fact that no special lateral movement was observed during discharging, as it could have been guessed for such type of flow (i.e., mass flow). To investigate the rotational movements in x-, y-, and z-direction, the velocity of the particles should be calculated and their individual pixel size should also be evaluated to perform further angular momentum analysis, which is presented in the following sections.
4.2 Axial particle velocity during mass flow
The ROFEX scanner comes with two measurement planes, which gives an ability to determine the axial velocity of particles. The axial velocity of tracer particle was calculated based on the residence time of a particle in a CT plane, which is the statistical analysis of successive frames or discharging time of tracer particles while passing both measurement planes. The distance d between the two measurement planes is 11 mm, as already mentioned earlier. Hence, the axial velocity \({V_{{\text{axial}}}}\) can show the tracer particle movement rate in the axial direction, which is calculated as:
where \({t_{\text{u}}}\) and tl are the time detection of the same tracer particle in the upper and lower measurement planes respectively. In general, the velocity calculations considered when the particles enter the scanning planes.
The mean axial velocity of 12 different tracer particles had been analysed in different scanning heights in three different circular zones as shown in Fig. 15 (zone 1: center of the silo, zone 2: central ring, and zone 3: outer ring-close to the wall of the silo).
Table 1 summarizes the mean velocity and standard deviation of particles at three different zones and three distant scanning heights. The velocities of every particle are calculated independently inside each zone and their mean value was taken as shown in Table 1. The standard deviation was calculated to specify the uniformity and spread of the mean velocity: the smaller the number, the more uniform the velocity. One can notice that, in average, particle velocity tends to increase slightly as the particles flow down. Nevertheless, the overall axial mean velocity was quite uniform across the three selected zones, which was around 9.373 mm/s, based on the fact that the velocity variations along the three zones are within the range of uncertainties (i.e. around 0.1–0.5 mm/s). This, again, confirms the quasi-steady state nature of the mass flow, even though, measurements have been carried out relatively far from the outlet where a steep increase in velocity is normally observed. Besides the potential of accurately measure velocities, this knowledge is also an important parameter to reconstruct particle volume, as it is mentioned in the following section.
In addition, by placing tracer particles very close to the wall of the silo model, which was not done in this study, it would be useful to analyse if there is retardation in a boundary layer. Future work could consider conducting such experiments to verify if experimental results are in line with DES (detached eddy simulation) prediction of velocity deficit for spherical particles (Spalart et al. 1997; Liu et al. 2015).
4.3 Three-dimensional visualization of segmented tracer particles
To visualize and represent the real size of tracer particles in 3D, first, it needs to convert the time frames of segmented images into voxel size along the z-dimension (note that the z-dimension represents time in milliseconds). Since the mean axial velocity Vaxial of each tracer particle has been evaluated and the acquisition rate f and the spatial resolution SR of the X-ray system are known parameters, it is possible to estimate the average number of frames of an image Nv that corresponds to the same pixel size of the reconstructed cross-section as follows:
The segmented frames of tracer particles can now be separated into stacks of Nv frames at most that are averaged to allow the space conversion.
Figures 16a and 17 present, the isosurface of the rebuilt 3D tracer particles at the three different scanning heights along the silo. It is worth mentioning that all particles could not be reconstructed since, from the original 20 tracer particles, 15 of them were well segmented and shown in the 3D visualizations. Figure 16b presents the matching of rebuilt particles at position 800 mm with a photo taken at height 900 mm before discharging. Some discrepancy does occur but attributed to possible particle rearrangement during the filling of the last 100 mm layer of clean Seramis particles mentioned in Sect. 2. Moreover, the qualitative comparison of the positions of the tracer particles at the three different scanning heights confirms the previous results shown in Sect. 3.2. For a better visualization of identified tracer particles, the silo tube is also included in the below three-dimensional image views.
4.4 Investigation of three-dimensional rotation of the particles during mass flow
The previous sections have mainly considered the lateral positioning of the particles during discharging. The 3D reconstruction of the tracer particles enables the investigation of their possible three-dimensional rotation in any directions. Calculating the moment of inertia of a single tracer particle can determine its orbital motion during mass flow at different scanning height. Moment of inertia I is defined as the ratio of the angular momentum \(L\) of a system to its angular velocity ω around a principal axis (Winn 2010; Fullerton 2011):
In general for a three-dimensional rigid body, it is always possible to find three mutually orthogonal axes (x, y, z coordinate system) for which the products of inertia are zero, and the inertia matrix takes a diagonal form. These axes are special because when the body rotates about one of them, the angular momentum vector L becomes parallel to the angular velocity vector ω.
To find the principal axis of a rigid body, consider a sample tracer particle body shown in Fig. 18 which rotates about an unknown principal axis. The total angular momentum vector is I ω in the direction of the principal axis. For rotation about the principal axis, the angular momentum and the angular velocity are in the same direction.
Tracer particles are free to rotate in three dimensions, so their moments can be described by the following symmetric 3 by 3 matrix Ip.
With
where
In the previous equations, (x, y, z) i correspond to Cartesian coordinates of p i , which is a member of a set of voxels of size N that compose a given labeled particle. Afterwards, the three eigenvalues (the principal moments of inertia I1, I2, and I3) and the eigenvectors (principal axis of inertia) are calculated after diagonalization of matrix Ip.
The tracer particles are irregular in shape but can be represented by equivalent ellipsoids in a first approximation (that is an ellipsoid with the same volume as a given segmented particle, regardless its orientation). For the principal axes, the matrix of inertia of an ellipsoid is given by:
where a, b, and c are the semi-principal axes, with a < b < c and Vp is the volume of the corresponding segmented particle.
By comparing Ip after diagonalization and Iell, one can express the semi-principal axes as a function of the eigenvalues I1, I2, and I3 as follows:
In general, the semi-principal diameter values and volume of a specific tracing particle should remain invariant while the particle is flowing through different scanning heights. However, the translational and rotational movement could occur, which can be validated by comparing the obtained semi-principal diameter value for a specific particle at different scanning heights. It was verified earlier that the lateral movements are not encountered for the chosen tracer particles.
By taking the angles between the three principal axes of inertia, respectively, and the x-, y-, and z-axes, it is possible to compare if there was any angular shift of each identified tracer particles between two successive scanning heights (i.e., between 800 and 500, and 200 mm). From this insight investigation, the angular shift for all identified tracing particles, while flowing through the three scanning heights was 0°–5° in x-, y-, z-direction, which indicates that there was no significant amount of angular motion in every axis dimensions during the discharging process of the particles-mass flow. The work is ongoing to apply a similar approach to study the funnel flow, where the gradient of velocity and movements (rotational/translational) will occur, especially from the stagnant to the flowing zone transition.
Figure 19 presents a comparison between the volume and the aspect ratios c: a and b: a for 15 different tracer particles detected at scanning height 800 mm—represented by a red circle, 500 mm—green rectangle and 200 mm—blue diamond.
The previous analyses of this study have shown that the concentration of particles slightly decreases as the scanning position change from top to bottom position (around 3% changes between measurements at 800 and 500 mm) (Waktola et al. 2016). This is also in line with the fact that particle velocity tends to increase as the particles flow down (see Table 1). Accordingly, while the concentration decreases, the difference between the grey value baselines and the brightness level of tracer particles inside each grid cells are getting higher. In other words, there is a more distinct intensity difference between the tracer particle and the surrounding area. Thus, during segmentation, the voxel sizes of identified particles are decreased from top to bottom position as shown in Fig. 19. As a result, the volume and orthogonal diameter values of a single tracer particle was not 100% perfectly the same through those three different scanning heights. From 15 analysed tracer particles; 92.8% in volume and 98.7% in aspect ratio (c: a and b: a) were matched.
4.5 Sensitivity analysis of applied methods and performance of proposed algorithm
Sensitivity analyses of the applied methods enable to identify the effects of uncertainties in parameter values on the obtained results. In this study, three different image segmentation approaches were applied and compared based on the number of detected particles and their respective size.
The core part of the image processing algorithm is strongly related to the selected segmentation procedure, in which particle under-segmentation or over-segmentation can play a crucial role in the investigation of particle morphology and rotational movements based on moments of inertia calculation. In that matter, we investigated the effects of grid generation, automatic/manual and global/local segmentation.
The first approach generates the poorest result using global Otsu segmentation (GOS). It enabled to only identify 9 particles out of 20 and 61.8% of the particles volumes (in voxel) were matched between the three scanning heights. The next approach considers global manual threshold segmentation (GMTS) by setting the best manual threshold value (which is 0.62). In that case, the number of detected tracer particles was 12/20 with 78.9% matching. Both GOS and GMTS approaches are not using any gridding effect and they produce after segmentation particle objects with minimum volume of 9 voxels, whereas the minimum grain size of tracer particle was 3 mm in length, which is approximately equal to 77 pixel size.
The third approach used a regular grid local Otsu segmentation (RGLOS); it considers a fixed square cell size set manually (best value with 25 pixels cell size) and applies different local threshold values depending on the baseline grey value and the brightness level of the particles. Numbers of detected and matched particles were better than GOS and GMTS, which was 13/20 with 88.0% of matching, yet it fails to separate two particles while they are slightly connected to each other (this case happened at scanning height of 500 mm around the center of the silo). As a result, it generates a maximum volume of two connected particles as a single particle (5868 voxels).
The final approach is IGLOS, which was presented in details in Sect. 3; as a reminder, it applies a method which automatically sets a flexible interrogation window size containing at the best one single-tracer particle at a time. IGLOS helps to apply local segmentation for each tracer particle independently and detect 15/20 particles with 92.8% matching of identified particle volumes between three scanning heights. The sensitivity analysis of the applied segmentation approaches is summarized in Table 2.
5 Conclusions
The ROFEX is a valuable scanning technique to analyse various granular material flow behaviour. Seramis granulate has been considered as a good candidate to fulfill the scanner requirements, due to their size (4 to 5 times larger than spatial resolution) and low density. In this study, a novel unsupervised image-processing approach named IGLOS was applied to improve the segmentation accuracy of the tracer particles. It uses an irregular grid generated automatically, which serves as a region separator for local segmentation. After segmentation, the time residence of a particle on the two measurement planes of the CT scanner is used to calculate the axial velocity of tracer particles in different cross-sectional zones and three different scanning heights. The calculation shows the particles have a quite similar mean velocity along all cross-sectional area and at all scanning heights. Moreover, in order to detect the movement of tracer particles while flowing through those three scanning heights, their lateral movement has been tracked and their moment of inertia has been also analysed. The insight investigation demonstrates that there was no any special lateral movement and three-dimensional rotations in x-, y- and z- dimensions. Work is underway to process the image data in order to calculate the velocity and investigate the rotational and lateral movements of tracer particles during funnel flow.
References
Anand A, Curtis JS, Wassgren CR, Hancock BC, Ketterhagen WR (2008) Predicting discharge dynamics from a rectangular hopper using the discrete element method (DEM). Chem Eng Sci 63(24):5821–5830
Babout L, Grudzien K, Maire E, Withers PJ (2013) Influence of wall roughness and packing density on stagnant zone formation during funnel flow discharge from a silo: an X-ray imaging study. Chem Eng Sci 97:210–224
Balevičius R, Sielamowicz I, Mróz Z, Kačianauskas R (2011) Investigation of wall stress and outflow rate in a flat-bottomed bin: a comparison of the DEM model results with the experimental measurements. Powder Technol 214(3):322–336
Bieberle M, Barthel F (2016) Combined phase distribution and particle velocity measurement in spout fluidized beds by ultrafast X-ray computed tomography. Chem Eng J 285:218–227
Bieberle A, Frust T, Wagner M, Bieberle M, Hampel U (2017) Data processing performance analysis for ultrafast electron beam X-ray CT using parallel processing hardware architectures. Flow Meas Instrum 53:180–188
Chaniecki Z, Grudzień K, Romanowski A (2014) Tomographic visualization of dynamic industrial solid transporting and storage systems. In: Computer vision in robotics and industrial applications, pp 257–280
Chen C, Woźniak PW, Romanowski A, Obaid M, Jaworski T, Kucharski J, Grudzień K, Zhao S, Fjeld, M (2016) Using crowdsourcing for scientific analysis of industrial tomographic images. ACM Trans Intell Syst Technol 7(4):1–25
Drescher A (1992) On the criteria for mass flow in hoppers. Powder Technol 73(3):251–260
Drescher A, Ferjani M (2004) Revised model for plug/funnel flow in bins. Powder Technol 141:44–54
Duran J, Behringer RP (2001) Sands, powders, and grains: an introduction to the physics of granular materials. Phys Today 54:63–64
Fischer F, Hampel U (2010) Ultrafast electron beam X-ray computed tomography for two-phase flow measurement. Nucl Eng Design 240:2254–2259
Fischer F, Hoppe D, Schleicher E, Mattausch G, Flaske H, Bartel R, Hampel U (2008) An ultra fast electron beam X-ray tomography scanner. Meas Sci Technol 19(9):94002
Fullerton D (2011) Honors physics essentials: an aplusphysics guide, rotational motion. In: Honors physics essentials: an aplusphysics guide. Silly Beagle Productions, pp 139–146
Garbaa H, Jackowska-Strumiłło L, Grudzień K, Romanowski A (2016) Application of electrical capacitance tomography and artificial neural networks to rapid estimation of cylindrical shape parameters of industrial flow structure. Arch Electr Eng 65(4):657–669
Grantham SG, Forsberg F (2004) Measurement of granular flow in a silo using digital speckle radiography. Powder Technol 146:56–65
Grudzien K (2017) visualization system for large-scale silo flow monitoring based on ECT technique. IEEE Sens J 17(24):8242–8250
Grudzien K, Niedostatkiewicz M, Adrien J, Maire E, Babout L (2012a) Analysis of the bulk solid flow during gravitational silo emptying using X-ray and ECT tomography. Powder Technol 224:196–208
Grudzien K, Chaniecki Z, Romanowski A, Niedostatkiewicz M, Sankowski D (2012b) ECT image analysis methods for shear zone measurements during silo discharging process. Chin J Chem Eng 20(2):337–345
Grudzień K, Chaniecki Z, Babout L (2017) Study of granular flow in silo based on electrical capacitance tomography and optical imaging. Flow Meas Instrum, ISSN 0955–5986. https://doi.org/10.1016/j.flowmeasinst.2017.11.001
Hirata J, Barrera J, Hashimoto RF, Dantas DO (2001) Microarray gridding by mathematical morphology. In: Proceedings XIV Brazilian Symposium on Computer Graphics and Image Processing. IEEE Comput. Soc, pp 112–119
Jaeger HM, Nagel SR (1992) Physics of the Granular state. Science 255(5051):1523–1531
Jaronski ST (2014) Mass production of entomopathogenic fungi: state of the art. In: Morales-Ramos JA, Guadalupe Rojas M, Shapiro-Ilan DI (eds) Mass production of beneficial organisms. Academic Press, San Diego, pp 357–413, ISBN 9780123914538. https://doi.org/10.1016/B978-0-12-391453-8.00011-X
Ketterhagen WR, Curtis JS, Wassgren CR, Kong A, Narayan PJ, Hancock BC (2007) Granular segregation in discharging cylindrical hoppers: a discrete element and experimental study. Chem Eng Sci 62(22):6423–6439
Ketterhagen WR, Ende MT, Hancock BC (2009) Process modeling in the pharmaceutical industry using the discrete element method. J Pharm Sci 98(2):442–470
Le Brese C, Zou JJ (2009) Identification of spots in rotated and skewed microarray images. Opt Eng 48(12):127003 (International Society for Optics Photonics)
Liu C, Liu C, Ma W (2015) Rans, detached Eddy simulation and large Eddy simulation of internal Torque converters flows: a comparative study. Eng Appl Comput Fluid Mech 9(1):114–125
Michalowski RL (1984) Flow of granular material through a plane hopper. Powder Technol 39(1):29–40
Otsu N (1979) A threshold selection method from gray level histograms. IEEE Trans Syst Man Cybern 9(1):62–66
Qiu Y, Chen Y, Zhang GG, Yu L, Mantri RV (eds) (2009) Developing solid oral dosage forms. pharmaceutical theory and practice. Academic press, pp 469–499, ISBN 978-0-444-53242-8
Schulze D (2008) Silo design for flow. In: powders and bulk solids: behavior, characterization, Storage and Flow, pp 291–319
Spalart PR, Jou W-H, Stretlets M, Allmaras SR (1997) Comments on the feasibility of LES for wings and on the hybrid RANS/LES approach. In: Advances in DNS/LES, pp 137–147
Steingart DA, Evans JW (2005) Measurements of granular flows in two-dimensional hoppers by particle image velocimetry. Part I: experimental method and results. Chem Eng Sci 60:1043–1051
Waktola S, Bieberle A, Barthel F, Bieberle M, Hampel M, Grudzien K, Babout L (2016) Study of mass flow behavior of granular material inside cylindrical silo using ultrafast electron X-ray CT imaging technique. International Interdisciplinary Phd Workshop, pp 87–91
Wilde K, Tejchman J, Rucka M, Niedostatkiewicz M (2010) Experimental and theoretical investigations of silo music. Powder Technol 198(1):38–48
Winn W (2010) Centroids and moments of inertia. Introduction to understandable physics, rotational energy and angular momentum. Author House, Bloomington, pp 73–141
Acknowledgements
The experiment of this study has been conducted at HZDR during Erasmus exchange program. We would like to thank W. Zimmermann for technical help.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Waktola, S., Bieberle, A., Barthel, F. et al. A new data-processing approach to study particle motion using ultrafast X-ray tomography scanner: case study of gravitational mass flow. Exp Fluids 59, 69 (2018). https://doi.org/10.1007/s00348-018-2523-2
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1007/s00348-018-2523-2