Effect of humid-thermal environment on wave dispersion characteristics of single-layered graphene sheets

Abstract

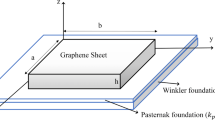
In the present article, the hygro-thermal wave propagation properties of single-layered graphene sheets (SLGSs) are investigated for the first time employing a nonlocal strain gradient theory. A refined higher-order two-variable plate theory is utilized to derive the kinematic relations of graphene sheets. Here, nonlocal strain gradient theory is used to achieve a more precise analysis of small-scale plates. In the framework of the Hamilton’s principle, the final governing equations are developed. Moreover, these obtained equations are deemed to be solved analytically and the wave frequency values are achieved. Some parametric studies are organized to investigate the influence of different variants such as nonlocal parameter, length scale parameter, wave number, temperature gradient and moisture concentration on the wave frequency of graphene sheets.

Appendix

In Eq. (32) ${k_{ij}}$ and ${m_{ij}}$, $\left( {i,j=1,2} \right)$ are defined as follows:

$$\left\{ {\begin{array}{*{20}{c}} \begin{aligned} {k_{11}} & = - \left( {1+{\eta ^2}\left( {{\beta _1}^{2}+{\beta _2}^{2}} \right)} \right)\left( {{D_{11}}{\beta _1}^{4}+2\left( {{D_{12}}+2{D_{66}}} \right){\beta _1}^{2}{\beta _2}^{2}+{D_{22}}{\beta _2}^{4}} \right) \\ & \quad +\left( {1+{\mu ^2}\left( {{\beta _1}^{2}+{\beta _2}^{2}} \right)} \right)\left( \begin{gathered} {N^T}\left( {{\beta _1}^{2}+{\beta _2}^{2}} \right) - {k_w} \\ - {k_{px}}\left( {{\beta _2}^{2}{{\sin }^2}(\theta )+{\beta _1}{\beta _2}\sin (2\theta )+{\beta _1}^{2}{{\cos }^2}(\theta )} \right) \\ - {k_{py}}\left( {{\beta _2}^{2}{{\sin }^2}(\theta ) - {\beta _1}{\beta _2}\sin (2\theta )+{\beta _1}^{2}{{\cos }^2}(\theta )} \right) \\ \end{gathered} \right) \\ \end{aligned} \\ \begin{aligned} {k_{12}} & = - \left( {1+{\eta ^2}\left( {{\beta _1}^{2}+{\beta _2}^{2}} \right)} \right)\left( {D_{{11}}^{s}{\beta _1}^{4}+2\left( {D_{{12}}^{s}+2D_{{66}}^{s}} \right){\beta _1}^{2}{\beta _2}^{2}+D_{{22}}^{s}{\beta _2}^{4}} \right) \\ & \quad +\left( {1+{\mu ^2}\left( {{\beta _1}^{2}+{\beta _2}^{2}} \right)} \right)\left( \begin{gathered} {N^T}\left( {{\beta _1}^{2}+{\beta _2}^{2}} \right) - {k_w} \\ - {k_{px}}\left( {{\beta _2}^{2}{{\sin }^2}(\theta )+{\beta _1}{\beta _2}\sin (2\theta )+{\beta _1}^{2}{{\cos }^2}(\theta )} \right) \\ - {k_{py}}\left( {{\beta _2}^{2}{{\sin }^2}(\theta ) - {\beta _1}{\beta _2}\sin (2\theta )+{\beta _1}^{2}{{\cos }^2}(\theta )} \right) \\ \end{gathered} \right) \\ \end{aligned} \\ \begin{aligned} {k_{21}} & = - \left( {1+{\eta ^2}\left( {{\beta _1}^{2}+{\beta _2}^{2}} \right)} \right)\left( {D_{{11}}^{s}{\beta _1}^{4}+2\left( {D_{{12}}^{s}+2D_{{66}}^{s}} \right){\beta _1}^{2}{\beta _2}^{2}+D_{{22}}^{s}{\beta _2}^{4}} \right) \\ & \quad +\left( {1+{\mu ^2}\left( {{\beta _1}^{2}+{\beta _2}^{2}} \right)} \right)\left( \begin{gathered} {N^T}\left( {{\beta _1}^{2}+{\beta _2}^{2}} \right) - {k_w} \\ - {k_{px}}\left( {{\beta _2}^{2}{{\sin }^2}(\theta )+{\beta _1}{\beta _2}\sin (2\theta )+{\beta _1}^{2}{{\cos }^2}(\theta )} \right) \\ - {k_{py}}\left( {{\beta _2}^{2}{{\sin }^2}(\theta ) - {\beta _1}{\beta _2}\sin (2\theta )+{\beta _1}^{2}{{\cos }^2}(\theta )} \right) \\ \end{gathered} \right) \\ \end{aligned} \\ \begin{aligned} {k_{22}} & = - \left( {1+{\eta ^2}\left( {{\beta _1}^{2}+{\beta _2}^{2}} \right)} \right)\left( \begin{gathered} H_{{11}}^{s}{\beta _1}^{4}+2\left( {H_{{12}}^{s}+2H_{{66}}^{s}} \right){\beta _1}^{2}{\beta _2}^{2}+H_{{22}}^{s}{\beta _2}^{4} \\ +A_{{55}}^{s}{\beta _1}^{2}+A_{{44}}^{s}{\beta _2}^{2} \\ \end{gathered} \right) \\ & \quad +\left( {1+{\mu ^2}\left( {{\beta _1}^{2}+{\beta _2}^{2}} \right)} \right)\left( \begin{gathered} {N^T}\left( {{\beta _1}^{2}+{\beta _2}^{2}} \right) - {k_w} \\ - {k_{px}}\left( {{\beta _2}^{2}{{\sin }^2}(\theta )+{\beta _1}{\beta _2}\sin (2\theta )+{\beta _1}^{2}{{\cos }^2}(\theta )} \right) \\ - {k_{py}}\left( {{\beta _2}^{2}{{\sin }^2}(\theta ) - {\beta _1}{\beta _2}\sin (2\theta )+{\beta _1}^{2}{{\cos }^2}(\theta )} \right) \\ \end{gathered} \right) \\ \end{aligned} \end{array}} \right.$$

(35)

$$\left\{ {\begin{array}{*{20}{c}} {{m_{11}}= - \left( {1+{\mu ^2}\left( {{\beta _1}^{2}+{\beta _2}^{2}} \right)} \right)\left( {{I_0}+{I_2}\left( {{\beta _1}^{2}+{\beta _2}^{2}} \right)} \right)} \\ {{m_{12}}= - \left( {1+{\mu ^2}\left( {{\beta _1}^{2}+{\beta _2}^{2}} \right)} \right)\left( {{I_0}+{J_2}\left( {{\beta _1}^{2}+{\beta _2}^{2}} \right)} \right)} \\ {{m_{21}}= - \left( {1+{\mu ^2}\left( {{\beta _1}^{2}+{\beta _2}^{2}} \right)} \right)\left( {{I_0}+{J_2}\left( {{\beta _1}^{2}+{\beta _2}^{2}} \right)} \right)} \\ {{m_{22}}= - \left( {1+{\mu ^2}\left( {{\beta _1}^{2}+{\beta _2}^{2}} \right)} \right)\left( {{I_0}+{K_2}\left( {{\beta _1}^{2}+{\beta _2}^{2}} \right)} \right)} \end{array}} \right.$$

(36)