Abstract
Exploiting Markoff’s theory for rational approximations of real numbers, we explicitly link how hard it is to approximate a given number to an idealized notion of growth capacity for plants which we express as a modular invariant function depending on this number. Assuming that our growth capacity is biologically relevant, this allows us to explain in a satisfying mathematical way why the golden ratio occurs in nature.










Similar content being viewed by others
Notes
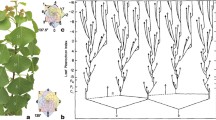
Photo: Richard Sniezko—US Forest Service.
This is the same Markov as in the well-known Markov chains theory; who used this surname spelling in his French publications.
Here, a number is considered to be equivalent to the golden ratio if its continued fraction expansion only contains 1 after a certain rank.
See for instance Serre (1970), Theorem 2 of chapter VII.
References
Adler I (1974) A model of contact pressure in phyllotaxis. J Theor Biol 45:1–79
Aigner M (2013) Markov’s theorem and 100 years of the uniqueness conjecture, a mathematical journey from irrational numbers to perfect matchings. Springer, Berlin
Atela P, Golé et C, Hotton S (2002) A dynamical system for plant pattern formation: a rigorous analysis. J Nonlinear Sci 12:641–676
Bacher R (2014) On geodesics of phyllotaxis. Confluentes Math 6(1):3–27
Couder Y, Douady S (1996a) Phyllotaxis as a dynamical self organizing process part I: the spiral modes resulting from time-periodic iterations. J Theor Biol 178:255–274
Couder Y, Douady S (1996b) Phyllotaxis as a dynamical self organizing process part II: the spontaneous formation of a periodicity and the coexistence of spiral and whorled patterns. J Theor Biol 178:275–294
Couder Y, Douady S (1996c) Phyllotaxis as a dynamical self organizing process part III: the simulation of the transient regimes of ontogeny. J Theor Biol 178:295–312
Coxeter HSM (1972) The role of intermediate convergents in Tait’s explanation for phyllotaxis. J Algebra 20:167–175
Douady S (1998) The selection of phyllotactic patterns. In: Jean RV, Barabe D (eds) Symmetry in plants. World Scientific, Singapore, pp 335–358
Hermite C (1916) Sur l’introduction des variables continues dans la théorie des nombres. J Reine Angew Math 41:191–216
Humbert G (1916) Sur la méthode d’approximation d’Hermite. J Math Pures App 7ème série 2:79–103
van Iterson G (1907) Mathematische und mikroskopisch-anatomische Studien über Blattstellungen, nebst Betrachtungen über den Schalenbau der Miliolinen, Verlag von Gustav Fischer in Jena
Jacobs B (2014) On Hermite’s algorithm. Bachelor’s thesis, Utrecht University
Jean RV, Barabé D (1998) Symmetry in plants. World Scientific, Singapore
Leigh EG Jr (1983) The golden section and spiral leaf-arrangement. Trans Conn Acad Arts Sci 44:163–176
Markoff AA (1879) Sur les formes quadratiques binaires indéfinies. Math Ann 15:381–496
Markoff AA (1880) Sur les formes quadratiques binaires indéfinies (second mémoire). Math Ann 17:379–399
Marzec C, Kappraff J (1983) Properties of maximal spacing on a circle related to phyllotaxis and to the golden mean. J Theor Biol 103:201–226
Okabe T (2012a) Systematic variations in divergence angle. J Theor Biol 313:20–41. arXiv:1212.3377
Okabe T (2012b) Geometric interpretation of phyllotaxis transition. arXiv:1212.3112
Refahi Y, Brunoud G, Farcot E, Jean-Marie A, Pulkkinen M, Vernoux T, Godin C (2016) A stochastic multicellular model identifies biological watermarks from disorders in self-organized patterns of phyllotaxis. eLIFE. https://doi.org/10.7554/eLife.14093
Reutenauer C (2018) From Christoffel words to Markoff numbers. Oxford University Press, Oxford
Ridley JN (1986) Ideal phyllotaxis on general surfaces of revolution. Math Biosci 79(1):1–24
Serre J-P (1970) Cours d’arithmétique. Presses universitaires de France, Paris
Acknowledgements
We would like to thank Stéphane Durand and Christiane Rousseau for drawing our attention to the notion that: “it is because it is hard to approximate by rational numbers that the golden ratio plays a key role in phyllotaxis”. Our objective in this work was to give a precise mathematical meaning to this statement. We also thank Nadia Lafrenière and Caroline Series for useful suggestions.
Author information
Authors and Affiliations
Corresponding author
Additional information
This work was supported by grants from NSERC.
Appendix
Appendix
We calculate here the limit of the averaging integral (7) in the case of the golden ratio \(x=\varphi \), whose Hermite’s convergents are the quotients \(F_{n+1}/F_{n}\). The required calculation is greatly simplified using the simplified expression
for the function \(f_\varphi ^{(n)}\), which follows from the fact that \((F_{n}-F_{n+1}\,\varphi )^2=\varphi ^{-2\,(n+1)}\). The corresponding minimum occurs at \(F_n\,\varphi ^{n+1}\), and takes the value
These assertions follows from the well known Binet formula
Exploiting that, \(0\le \left| {(-1/\varphi )^{n+1}}\right| \ll 1\), we also deduce from it the very good approximation \(F_n\approx {\varphi ^{n+1}}/{\sqrt{5}}\). Thus \( f_\varphi ^{(n)}(t)\) is very well approximated by \(\varphi ^{-2\,(n+1)}\,t+{\varphi ^{2\,(n+1)}}/{(5\,t)}\) when n is large enough. We may also calculate that
from which we get
as well as
Hence, applying formula (7), we find that
In the case of \(\psi :=1+\sqrt{2}\), one replaces Fibonacci numbers by Pell numbers, \(P_n\), and uses
to show that \(g_\psi ={1}/{2} +\log (\psi )/{\sqrt{8}}\) with a very similar calculation.
Rights and permissions
About this article
Cite this article
Bergeron, F., Reutenauer, C. Golden ratio and phyllotaxis, a clear mathematical link. J. Math. Biol. 78, 1–19 (2019). https://doi.org/10.1007/s00285-018-1265-3
Received:
Revised:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00285-018-1265-3