Development of model for studies on momentum transfer in electrochemical cells with entry region coil as turbulence promoter

Abstract

Entry region swirl promoters gain importance in industry because of its effectiveness in augmentation of mass and heat transfer augmentation. Design of equipment needs momentum transfer data along with mass or heat transfer data. Hence an experimental investigation was carried out with coaxially placed entry region spiral coil as turbulence promoters on momentum transfer in forced convection flow of electrolyte in circular conduits. Aqueous solution of sodium hydroxide and 0.01 M equimolal Ferri-ferro cyanide system was chosen for the study. The study covered parameters like effect of pitch of the coil, effect of length of the coil, diameter of the coil, diameter of the coil wire, diameter of the annular rod. The promoter is measured by limiting current technique using diffusion controlled electrochemical reactions. The study comprises of evaluation of momentum transfer rates at the outer wall of the electrochemical cell. Pressure drop measurements were also made to obtain the energy consumption pattern. Within the range of variables covered. The results are correlated by the momentum transfer similarity function. Momentum transfer coefficients were evaluated from measured limiting currents. Effect of each parameter was studied in terms of friction factor. A model was developed for momentum transfer. The experimental data on momentum transfer was modeled in terms of momentum transfer function and Reynolds number, geometric parameters.

1 Introduction

Augmentation of heat and mass transfer processes are never ending quest for an engineer or technologist. Augmentation of a transfer processes offer the following advantages. Increased throughputs for a particular size of an equipment or reduced size of equipment for a particular flow rate. The other advantages are less floor area, ease in handling of raw material and utilities. These factors leads to the reduction unit product cost. Hence the augmentation technique found attractive for researchers. To arrive at this above objective, several strategies have been followed. Efforts have been continued with the investigation being directed towards achieving energy- efficient mass transfer cells with assembly of the coils. The earliest augmentative technique is surface roughness [1] several works were reported in literature. Use of baffles [2] and surface alternations also come under this section. Works like spheres [3], fins [4], bluff bodies [5] and stream lined bodies [6] placed across the flow were also extensively found in literature. Flow through ducts and arched channels [7], jets [8] were also encountered. Investigations on insert promoters in heat and mass transfer operations were reported extensively. The work reported was on concentric rod placed in the circular conduit, since then heat and mass transfer studies with coaxially placed turbulence promoters were reported extensively. The investigation on co-axially placed promoters like twisted tapes [9], tapes wound on a rod [10], spiral coils [11], string of spheres [12] and cones [13], discs [14], orifices [15], circular rings places on a rod [16] were also studied. But works found in literature seemed to increase friction there by higher operating costs. This is particularly true for string of spheres, string of cone, string of discs [14], and flow past cylindrical rod [17], across stream lined bodies [18], and many devices like axially displaced promoters, and surface modifiers.

In the present study an effort is made in acquiring higher augmentation rate with lower frictional losses. It will lead to the construction of energy efficient transfer operation. Several researchers employed swirl flow for the augmentation of their process. Therefore an attempt is made to employ swirl motion in achieving this objective swirl flow devices were incorporated in circular conduits and found their effectiveness on heat and mass transfer processes. Among the swirl generating devices twisted tapes [19], tapes wound on a rod [10], spiral coils [11], spiral coils placed on central rod of an annular conduits [20] and tangential entry of fluid are prominent. Among the coaxially placed promoters, Entry region swirl generating promoters received the attention of several researchers. Nageswara Rao V [21] employed tape, tape-disc assembly as turbulence promoters in their study. Murali Mohan et al. [22] used entry region coil and coil-disc assembly as turbulence promoters in circular conduits generated useful data for the augmentation. Present investigation is directed towards achieving energy efficient transfer process. To that effect, it envisaged to obtain mass transfer data at the inner wall of annular conduits along the length of the column. Subsequently, local mass transfer data were obtained and the results were reported. These results could be adopted for enhancing mass transfer processes like electro dialysis [23], ultra filtration [24], reverse osmosis [25] and several other processes and reported increased transfer rates. The electrochemical processes like electro winning [26], electro refining [27], electro milling [28] and electro organic synthesis [29] could employ swirl generating promoters to obtain higher transfer rates. Swirl flows have wide range of applications in various engineering areas such as chemical processes like mechanical mixing and separation devices, combustion chambers, turbo machinery, rocketry, etc. It can be effectively used in heat and mass transfer enhancements. In view of these observations, the present research work is momentum transfer data are experimentally obtained in the presence of electrochemical cells with entry region coil as turbulence promoter. It deals with the presence of the momentum transfer rate at the wall through limiting current technique.

The study is carried out to obtain the following information.

• 1. To obtain limiting currents data on the outer wall of an annular conduits with entry region coil as turbulence promoters.

• 2. To study the effect of geometric parameters on mass transfer namely - pitch of the coil (P_c), length of the coil (L_c), diameter of the coil (D_c), diameter of the coil wire (D_w), and diameter of the annular rod (D_i) on the outer wall momentum transfer coefficients.

• 3. To generate pressure drop data with insert promoters and to identify the effect of geometric parameters such as pitch of the coil (P_c), length of the coil (L_c), diameter of the coil (D_c), diameter of the coil wire (D_w), and diameter of the annular rod (D_i).

• 4. To develop generalized correlations for momentum transfer in homogeneous flow.

The following information is derived out of the study.

• 1. Momentum transfer coefficient is increases with increasing in velocity.

• 2. Friction factor values are increasing with increase in pitch of the coil.

• 3. Momentum transfer is increasing monotonously with increase in length of the coil.

• 4. The effect of momentum transfer coefficient on the diameter of the coil has marginal effect on friction factor in the present study.

• 5. Correlations were developed based on semi theoretical considerations. Wall similarity concept is used in the development of correlations. The following Correlation developed for momentum transfer is presented as:

  • Homogeneous flow

  $$ R\left({h}^{+}\right)=18648\kern0.24em {\left[{\operatorname{Re}}_m^{+}\right]}^{-1}\kern0.24em {(Fr)}^{0.495}\kern0.24em {\left(\frac{D_W}{d_e}\right)}^{0.77}\kern0.24em {\left(\frac{D_i}{d_e}\right)}^{-0.175} $$

  (1)

This equation is useful for the design and development of energy efficient transfer processes.

2 Experimentation

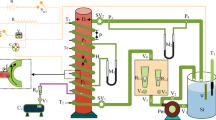
The Schematic diagram of experimental set up is shown in Fig. 1. It was essentially consisted of a recirculation tank, an entrance calming section (A), a test section (B), and an exit calming section (C), thermo wells (E₁, E₂), flanges (F₁, F₂), gland nuts (G₁ to G₄), coiled copper tube (H), pump (P), rotameter (R), recirculation tank (T), U-tube manometer (UM) and valves (V₁ to V₅).

Fig. 1

Schematic diagram of the experimental set up. A: Entrance calming section. B: Test section. C: Exit calming section. E₁, E_2: Thermo wells. G₁ to G₄: Gland nuts. F₁, F2_: Flanges. H: Coiled copper tube. P: Pump. R: Rota meter. T: Recirculation tank. UM: U tube manometer. V1 to V5: Valves

The recirculation tank was a cylindrical copper vessel of 100 l capacity with a drain pipe and a gate valve (V₁) for periodical cleaning of the tank. A copper coiled tube (H) provided with perforations. The perforations were meant for bubble of nitrogen through the electrolyte. The bubbling of nitrogen through the electrolyte expels the dissolved oxygen present if any. The tank was connected to the pump with a 0.025 m diameter copper pipe on the suction line of the centrifugal pump. The suction line was also provided with a gate valve (V₂). The discharge line from the pump divided into 2 lines. One line served as a bypass and a controlled by valve (V₃) is incorporated in it. The other line was connected to the entrance calming section (A). A control valve (V₄) and a rotameter were also incorporated in the line. The control valve was used to regulate the flow of electrolyte. The rotameter served as flow measuring device. The rotameter has a range of 0 to 347 × 10⁻⁶ m³/s. The entrance calming section was circular copper pipe of 0.046 m ID provided with a flange and closed at the bottom with a gland nut (G₁). To an extent of 0.1 m of entrance calming was filled with capillary tube to damp the flow fluctuations and to facilitate steady flow of the electrolyte through the test section.

The details of the test section are shown in Fig. 2. It was made of a graduated perspex tube of 0.68 m length with point electrodes fixed flush with the inner surface of an outer wall of the test section. The point electrodes were made out of a copper rod and machined to the size. The electrodes were fixed flush with the inner surface of the outer wall of the test section at an equal spacing of 0.0254 m. The diameter of the exit calming section was also of the same diameter. The entrance calming section made of copper tube of 1.8 m long, and it was provided with a flange on the upstream side for assembling with the test section. The exit calming is also made of copper tube of length 0.7 m and diameter of 0.046 m. The exit and entrance calming sections were provided with gland nuts (G₂, G₃) at the top and bottom ends. The column comprised of 3 sections namely the entrance calming section, the test section and the exit calming section. These sections were assembled by means of flanges F₁, F₂. Two thermo wells (E₁, E₂) were provided, one at upstream side of the entrance calming section and the other at the downstream side of exit calming section to measure the temperature of the electrolyte.

Fig. 2

Details of the test section

The coil is fixed at the entrance of the test section with the help of flanges. And the central rod is placed inside the column from top to bottom. The entry region coil was a spiral coil made from a copper wire of 0.006, 0.007, 0.008 m diameters. The copper wire was coiled to obtain coil diameters of 0.031, 0.034 and 0.038 m. The pitches of the coils were varied as 1.6, 2.6, 3.6, 4.6 cm. The spiral coil was welded to a flange. The flange has a matching perforation with that of test section. It is placed concentrically in the test section and fixed via flanged joints. The range of variables covered in a homogeneous flow of fluid is presented in Table 1.

Table 1 Range of variables covered in the present study

Multimeter of Motwane make with accuracy of 0.01 mA was used as an ammeter and another multimeter was acted as voltmeter and has an accuracy of 0.01 V. They were used for measuring the limiting currents and potentials respectively. The other equipment used in circuit was rheostat, key, commutator, selector switch and a lead acid battery. The battery served as the power source. The commutator facilitated to reverse the polarity. The measurement of limiting currents for reduction process was taken. The selector switch facilitated the measurements of limiting currents at any desired electrode. Details of the coil assembly promoter covered in a homogeneous flow of fluid are presented in Table 2.

Table 2 Details of the coil assembly promoter covered in the present study

The limiting current data were obtained for the case of reduction of ferricyanide ion in annular conduit in the presence of entry region coil as insert promoters in homogeneous flow. The cathodic reduction reaction of ferricyanide ion at the reacting electrode is given below

$$ {\left[\mathrm{Fe}{\left(\mathrm{CN}\right)}_6\right]}^{-3}+{\mathrm{e}}^{-}\to {\left[\mathrm{Fe}{\left(\mathrm{CN}\right)}_6\right]}^{-4} $$

(2)

Eighty liters of equimolal solution of 0.01 N Potassium ferricyanide and 0.01 N Potassium ferrocyanide with 0.5 N Sodium hydroxide as electrolyte was prepared used as the system. The electrolyte was analyzed for ferrocyanide ion concentration by volumetric titration method using standard potassium permanganate solution [1] and for ferricyanide ion using idometric method [2]. The viscosity of the solutions at different temperatures were measured with Ostwald Viscometer and densities were measured using specific gravity bottle. The point electrodes in the test section were polished using four zero emery to get a smooth surface followed by degreasing with trichloroethylene solution. The size of the electrode was measured with a traveling microscope. After fixing the promoter in position, blank runs i.e. were conducted with sodium hydroxide electrolyte alone to ensure that the limiting currents obtained were due to diffusion of reacting ions (Ferricyanide ion) only. Subsequently, known quantities of potassium ferricyanide and potassium ferrocyanide were added to get the concentration of electrolyte was maintained at equimolal 0.01 M Ferri-ferrocyanide couple was maintained.

The coils of known geometry were fitted at the entrance of the test section by means of flanged joint and the annular rods were fixed by means of gland nuts. The experiments were repeated by replacing the coil and /or annular rod. The electrolyte was pumped at a desired flow rate (through the test section) by operating the control and by-pass valves. After the steady state was attained, potential was applied across the test electrode and wall electrode in small increments of potential (100 mV) and the corresponding current values were measured for each increment. As the area of the wall electrode was relatively large in relation to the area of the test electrode, nearly constant potential was obtained at the test electrode. Since the potential values are not of criteria in the present study, the limiting currents only were obtained from the current and potential data.

The experiment was repeated by changing the flow rate of the electrolyte and the limiting currents measurements were taken for each flow rate. Measurement of limiting current: The plots of current versus potential data yields limiting currents. Increase in potential increases the current up to certain value and further increase in potential would be maintained nearly constant current values, which is taken as the limiting current. Mass transfer coefficients are computed from the measured limiting currents by the following expression:

$$ {k}_L=\frac{i_L}{n\;F\;A\;{C}_o} $$

(3)

Pressure drop measurements for each flow rate were made simultaneously by using a U – tube manometer with Carbon tetrachloride as manometer liquid.

3 Results and discussions

Experiments were conducted with entry region coil promoter assembly in a homogeneous flow of electrolyte. It deals with 7500 local limiting current data obtained at the outer wall of an annular conduit fitted with an entry region spiral coil as a turbulence promoter. Local limiting currents at the outer wall of an annulus were measured along the length of the column. Cathodic reduction of ferricyanide ion was chosen as the system for the present study.

3.1 Studies on homogeneous flow with entry region coil in annular conduits

The experimental measurements consists of the flow rate of an electrolyte (Q), limiting current (i_L). From the measured current potential data, limiting currents were identified. The concentration of reacting ion (C_o) was estimated by isometric. Physical properties of the solution namely density (ρ), viscosity (μ) were measured by suitable method. The values of Diffusivities (D_L) were estimated by the method mentioned in experimental procedure. Diameter of the test section (d) and dimensions of the promoter assembly viz., pitch of the coil (P_c), length of the coil (L_c), diameter of the coil (D_c)_, diameter of the wire of the coil (D_W)_, diameter of the annular rod (d_i) and temperature (T), were measured with suitable instruments.

The velocity of the fluid flow was computed from the following expression.

$$ V=\frac{Q}{\frac{\pi }{4}\left({d_e}^2\right)} $$

(4)

Where d_e = (d-D_i) is equivalent diameter.

3.2 Momentum transfer

Entry region coil induces swirl in the flowing fluid as the fluid passes through an annular conduits which is fitted with an entry region spiral coil. As the fluid moves along the coil, the fluid elements are guided by the coil and are transformed from the axial flow into swirl flow. The swirl approaches to a maximum value. The fluid elements leaves the coil with maximum swirl velocity followed a decaying zone due the absence of the coil. The swirl continues to some extent followed by a decaying zone. As we move along the length of the column the flow slowly transform from swirling flow to axial and finally the flow reaches smooth conduit flow without any promoter. Because of the induced swirl motion changes in pressure drops are anticipated higher. Sufficient study in this direction is not made so far. Therefore pressure drop measurements were also made along with mass transfer data. The effective friction factor values are computed from the measured pressure drops by the following equation for homogeneous flow.

$$ f=\frac{\Delta P\;{d}_e\;{g}_c}{2\;L\;{V}^2\rho } $$

(5)

Based on friction factor versus Reynolds number data one can analyze the energy losses. The information is highly useful in the design and development of energy efficient electrochemical cells. The frictional losses are directly related to the flow condition prevailed in the column. These friction factor data would be useful in the analysis of mass transfer data which is analyzed in terms of geometric parameters of the promoters.

3.3 Effect of pitch of the coil

To show the effect of coil pitch, the data of friction factor versus Reynolds number for 4 coils with different pitch are plotted and shown in Fig. 3. The figure reveals the friction factor values are increasing with increase in Reynolds number and converging at a higher velocity end. Further increase in velocity might lead to convergence and would result in the formation of fully turbulent region i.e. the friction values becomes constant.

Fig. 3

Variation of f – Effect of pitch of the coil

It is further observed that at any velocity within the range of variables covered in the present study, friction values are increasing with increase in pitch of the coil. The increase would continue up to certain pitch, on further increase in pitch would result in decrease in pitch because of the reduction in number of turns and thereby blockage or due to the reduction in cross flow element. Such pitch may be called a critical pitch. Similar observations were also made in mass transfer and by several other works [11, 20, 30, 31, and]. The early observation of this critical pitch is seen in mass transfer which may be an indication that the energy spent in the generation of turbulence is not fully utilized to augment mass transfer.

3.4 Effect of length of the coil

As length of the coil increases the generated swirl is more prominent. Increased coil length consumes more pressure force reducing the superficial velocity of the fluid therefore enhanced friction factors; this observation coincides with mass transfer. A graph is drawn for friction factor versus Reynolds number for the coils having the same pitch and different coil lengths and shown as Fig. 4. Friction factor values are found to decrease with Reynolds number. Friction factor values are increasing with the length of the coil but for the coil length 12 cm. It is an exception where the friction values are low within the range of variables studied. For better performance the coil with length 12 cm is recommended. But the reason for the decrease is not clearly understood.

Fig. 4

Effect of length of the coil on friction factor

3.5 Effect of coil diameter

A graph is drawn as f versus Re and shown in Fig. 5. Diameter of the coil has marginal effect on friction factor. Friction factor values are increasing marginally with diameter of the coil. The diameter of the oil could not be varied much because of narrow gap between annular rod and wall the of the test section.

Fig. 5

Effect of coil diameter on friction factor

3.6 Effect of the diameter of the coil wire diameter

Diameter of the coil wire has significant effect on friction factor. Its effect could be seen from Fig. 6. The values of f are decreasing with Reynolds number (Re). The slope is steep for the coil wire diameter of 0.008 m. On further increase in Re a sharp increase is followed at higher Re. At lower flow rates the coil wire diameter 0.06 is recommended.

Fig. 6

Effect of coil wire diameter on friction factor

3.7 Energy enhancements over the data of smooth pipe flow

The energy requirement for unit area of the cell is calculated by the following equation.

$$ E=\frac{Q\;\Delta P}{\left(\prod d\ L+\prod {d}_iL\right)} $$

The energy loss in the case of pipe without any insert in them is indicated by E₀. The energy factor is defined as E/E₀. A graph is drawn as energy factor versus Reynolds number and presented as Fig. 7. These figures reveal energy factors are decreasing with Reynolds number.

Fig. 7

Variation of augmentation factor with Reynolds number

3.8 Performance of the entry region coil promoter

Performance factor (η) is the ratio of augmentation factor to energy factor and defined by the following equation.

$$ \eta =\frac{k_L/{k}_{L0}}{E/{E}_0}=\frac{k_L/{k}_{L0}}{\Delta P/\Delta {P}_0} $$

A graph is drawn energy factor with Reynolds number for 2 different sets with coils of varying geometric configuration as shown in inset and shown as Fig. 7. The figure reveals the energy factor is decreasing with Reynolds number. Further increase in Reynolds number would remain constant which is could be seen when range flow rate increased further. The efficiency (η) is a measure for efficiency of the promoter. Efficiency of the promoters under study could be judged from graphs of Performance factor versus Reynolds number. A graph is drawn as performance factor versus Reynolds number and shown as Fig. 8. The Performance is increasing linearly with Re. The promoter producing maximum turbulence is augmenting better and the efficiencies are increasing steeply indicating higher augmentation at lower flow rates.

Fig. 8

Variation of effectiveness factor with Reynolds number

4 Development of generalized correlations

4.1 Momentum transfer

Flow of electrolyte through circular conduit with entry region spiral coil promoter generates a variety of flow fields. The development of momentum transfer correlations for the present situation could be carried out on the basis of semi empirical data. Conventional f – Re type correlations have been attempted to correlate the present data using the following format of equation.

$$ f=C{\operatorname{Re}}^m{\left({\Phi}_1\right)}^{n_1}{\left({\Phi}_2\right)}^{n_2}{\left({\Phi}_3\right)}^{n_3} $$

(6)

Where Φ₁, Φ₂, Φ₃ are the geometric parameters. Regression analysis of the data in accordance with the above format of equation yielded the following correlations for the data for flow through annular conduits with entry region coil as insert resulted high deviations.

$$ f=10.9{\operatorname{Re}}^{-0.203}{\left({P}_c/d\right)}^{-0.44}{\left({L}_c/d\right)}^{0.56}\;\left( Dc/ de\right)\left({D}_W/{d}_e\right) $$

(7)

In view of these large deviations, an alternative approach has been attempted by the use of the wall similarity concept proposed by Webb, R, L et al. [1], Dippery and Saborsky [32], Nikuradse, J [33] and Deissler R G [34]. The similar concept assumes velocity distribution is expected to experience the effect of viscosity at the surface. When an object is placed across the flow in a circular conduit, drag is generated and the drag enhances turbulence. Thus generated turbulence exerts tractive force at the wall and makes the boundary layers thinner. The flow is divided into 2 regions namely inner region and outer region. The inner region constituted with boundary layer whose thickness is δ at y⁺, where δ is small. The velocity distribution depends on y⁺, τ₀, μ.

For inner region the velocity profile in terms of dimensionless velocity is given by

$$ {u}^{+}={y}^{+} $$

(8)

Where u⁺ = u/u^∗, y⁺ = yu^∗/ν, For the outer wall region where the dependency of velocity distribution on molecular viscosity ceases to exist, the velocity distribution would follow the relationship

$$ {u}^{+}=\frac{1}{k}\ln {y}^{+}+{C}_1 $$

(9)

By the application of boundary conditions u = 0 at y = y_0, where y₀ is the thickness of laminar sub layer that depends on the turbulence generated, Eq. 9 reduces to

$$ {u}^{+}=\frac{1}{k}\ln \left(y/{y}_0\right) $$

(10)

The turbulence in the core and at the wall is significantly affected by the geometric parameters of the promoters employed in addition to the fluid velocity. In the present case, Pitch of the coil (P_c) and Length of the coil (L_c), diameter of the coil (D_c), diameter of the coil wire (D_W), and annular rod (D_i) are the major characteristic geometric parameters. As these are expected to be significantly affect the thickness of the laminar sub layer. In the present study the parameter (D_W), was chosen while computing u⁺ therefore,

$$ {y}_0\kern0.24em \alpha \kern0.24em {D}_W $$

(11)

Equation 10 could be modified as

$$ \frac{u_{\mathrm{max}}-u}{u^{\ast }}=\frac{1}{k}\ln \left(y/{D}_w\right) $$

(12)

Combination of Eqs. 11 and 12 gives the velocity distribution equation for the turbulent dominated part of the wall region

$$ {u}^{+}=2.5\;\ln \left[y/{D}_w\right]+\mathrm{R}\left({h}^{+}\right) $$

(13)

The above equation presents modified velocity profile for the case of out turbulent region in the presence of promoters. Assuming that Eq. 14 holds good for the entire cross section of the circular conduit, the friction factor for the turbulent flow with entry region coil inside the annular conduit can be given by integration of Eq. 13. The generated roughness function R(h⁺) is given by the following equation

$$ R\left({h}^{+}\right)=2.5\ln \left[2\left({D}_W\right)/{d}_e\right]+\sqrt{2/f}+3.75 $$

(14)

Where R(h⁺) is roughness momentum transfer function, This type of analysis is followed by the earlier workers (11, 23, 24) and successfully analyzed their data.

The resulting format of equation for correlating the momentum transfer data with entry region spiral coil as promoter in annular conduits can now be written as

$$ R\left({h}^{+}\right)={C}_1\;{\left[{{\operatorname{Re}}_m}^{+}\right]}^{b_1} $$

(15)

Here, C₁ is proportionality constant and b₁ is an exponent, Re_m⁺ is roughness Reynolds number defined by the following equations for entry region coil with annular conduits in homogeneous flow. The analysis could also be useful for fluidized beds with modification of particle Reynolds number defined in following text.

4.2 Homogeneous flow

Data on homogeneous flow is analyzed in terms of in terms of Rh⁺ v_s Re_m^+s

$$ R\left({h}^{+}\right)=2.5\ln \left[2\left({D}_W\right)/{d}_e\right]+\sqrt{2/f}+3.75 $$

(16)

$$ {{\operatorname{Re}}_m}^{+}=\left({D}_w/{d}_e\right).\operatorname{Re}.\sqrt{f/2}\kern1.8em $$

(17)

Where D_w is wire diameter, d_e is diameter of the conduit and f is friction factor. On regression analysis and by omitting geometric parameters of the promoter yielded the following equations.

$$ {\displaystyle \begin{array}{c}R\left({h}^{+}\right)=206.73\kern1.12em {\left[{{\operatorname{Re}}_m}^{+}\right]}^{-0.10\kern1em }\\ {}\mathbf{Average}\ \mathbf{deviation}=\mathbf{39.816}\kern0.5em \mathbf{Standard}\ \mathbf{deviation}=\mathbf{57.166}\end{array}} $$

(18)

Multiple regression analysis was conducted with relevant geometric groups also resulted very high deviations. An attempt is made to include Froude group,

$$ \mathrm{Where}\ \mathrm{For}\ \mathrm{homogeneous}\ \mathrm{flow}\ \mathrm{Fre}={\mathrm{V}}^2/\left({\mathrm{d}}_{\mathrm{e}}.\mathrm{g}\right), $$

(19)

The effect of Froude group is prominently appearing when ever vortex or swirl generating type of flow appears. The regression analysis was conducted with R (h⁺) and with 2 dimensionless numbers namely Reynolds number and Froude group.

The resultant equations are also associated with large deviations.

$$ {\displaystyle \begin{array}{c}R\left({h}^{+}\right)=3329.3\kern0.37em {\left[{{\operatorname{Re}}_m}^{+}\right]}^{-0.866}{\left[\mathrm{Fr}\right]}^{0.454\kern1em }\\ {}\mathbf{Average}\ \mathbf{deviation}=\mathbf{7.4194}\kern0.5em \mathbf{Standard}\ \mathbf{deviation}=\mathbf{8.7775}\end{array}} $$

(20)

Hence other geometric groups were also included in the correlation. The correlations resulted were of good accuracy and with very marginal deviation. These correlations were presented hereunder

$$ {\displaystyle \begin{array}{c}R\left({h}^{+}\right)=18648\kern0.24em {\left[{\operatorname{Re}}_m^{+}\right]}^{-1}{(Fr)}^{0.495}{\left(\frac{D_W}{d_e}\right)}^{0.77}{\left(\frac{D_i}{d_e}\right)}^{-0.175}\kern0.6em \\ {}\mathbf{Average}\ \mathbf{deviation}=\mathbf{2.1639}\kern0.5em \mathbf{Standard}\ \mathbf{deviation}=\mathbf{2.6012}\end{array}} $$

(21)

In Correlation graph for momentum transfer in homogeneous flow with entry region coil in annular conduits is presented along with the data of with that system in full length coils as turbulence promoters and can be seen in Fig. 9.

Fig. 9

Correlation graph for momentum transfer – homogeneous flow

5 Comparison of correlation

Present correlation is tested for its ability to predict with other works. Typical data (the coil which augments best of full length coil is recalculated in the lines of present study and embedded in the present correlation graph shown as Fig. 10. The figure reveals, that the present correlation could predict well. The data of entry region coil in circular conduit is deviating moderately.

Fig. 10

Comparison graph for momentum transfer correlation in homogeneous flow

5.1 Efficiency of the promoter

A graph is drawn as efficiency versus volumetric flow rate and the figure reveal that the present work is clearly efficient than the presented in the Fig. 11.

Fig. 11

Comparison graph for homogeneous flow in annular conduits

6 Conclusions

The following conclusions can be drawn from the present analysis:

• 1. Friction factor values are increasing with increase in pitch of the coil.

• 2. Larger the length of the coil greater the frictional values.

• 3. Diameter of the coil has marginal effect on friction factor in the present study.

• 4. Greater the coil wire diameter larger the friction factors.

• 5. The energy factor values are decreasing with Reynolds number.

• 6. The Performance of the coils are increasing linearly with Re. The promoter producing higher turbulence is also augmenting better and the efficiencies are increasing steeply indicating higher augmentation at lower flow rates.

• 7. A Model developed for momentum transfer in homogeneous flow is as follows:

  $$ R\left({h}^{+}\right)=18648\;{\left[{\operatorname{Re}}_m^{+}\right]}^{-1}{(Fr)}^{0.495}\;{\left(\frac{D_W}{d_e}\right)}^{0.77}{\left(\frac{D_i}{d_e}\right)}^{-0.175}\kern0.6em $$