Abstract
To a numerical semigroup S, Eliahou associated a number \({{\mathrm{E}}}(S)\) and proved that numerical semigroups for which the associated number is non negative satisfy Wilf’s conjecture. The search for counterexamples for the conjecture of Wilf is therefore reduced to semigroups which have an associated negative Eliahou number. Eliahou mentioned 5 numerical semigroups whose Eliahou number is \(-1\). The examples were discovered by Fromentin who observed that these are the only ones with negative Eliahou number among the over \(10^{13}\) numerical semigroups of genus up to 60. We prove here that for any integer n there are infinitely many numerical semigroups S such that \({{\mathrm{E}}}(S)=n\), by explicitly giving families of such semigroups. We prove that all the semigroups in these families satisfy Wilf’s conjecture, thus providing not previously known examples of semigroups for which the conjecture holds.












Similar content being viewed by others
References
Bras-Amorós, M.: Fibonacci-like behaviour of the number of numerical semigroups of a given genus. Semigroup Forum 76, 379–384 (2008)
Delgado, M.: “ intpic”, A GAP Package for Drawing Integers, Version 0.2.1 (2015). http://www.gap-system.org/
Delgado, M., García-Sánchez, P.A., Morais, J.: “ NumericalSgps”, A GAP Package for Numerical Semigroups, Version 1.0.1 (2015). http://www.gap-system.org/
Eliahou, S.: Wilf’s conjecture and Macaulay’s theorem. arXiv:1703.01761 [math.CO]
Fromentin, J., Hivert, F.: Exploring the tree of numerical semigroups. Math. Comput. 85, 2553–2568 (2016)
Rosales, J.C., García-Sánchez, P.A.: Numerical Semigroups. In: Developments in Mathematics, vol. 20. Springer (2010)
The GAP Group: GAP—groups, algorithms, and programming, Version 4.8.7 (2017). http://www.gap-system.org
Wilf, H.: A circle-of-lights algorithm for the money-changing problem. Am. Math. Monthly 85, 562–565 (1978)
Zhai, A.: Fibonacci-like growth of numerical semigroups of a given genus. Semigroup Forum 86, 634–662 (2013)
Acknowledgements
Besides the formal acknowledgement to the Centre for Mathematics of the University of Porto (CMUP) made somewhere in this paper, I would like to thank CMUP for providing me the computational tools necessary to this kind of works. I would like also to thank Shalom Eliahou for his suggestions and comments on preliminary versions. Special thanks to Shalom for encouraging me to publish this work. The anonimous referee, who carefully read the manuscript and gave me the appropriate remarks, deserves also my special ackowledgement.
Author information
Authors and Affiliations
Corresponding author
Additional information
Manuel Delgado was partially supported by CMUP (UID/MAT/00144/2013), which is funded by FCT (Portugal) with national (MCTES) and European structural funds (FEDER), under the partnership agreement PT2020, and also by the project MTM2014-55367-P.
Appendices
Appendix 1: A remark concerning the genus
Let n be an integer. Consider the set \(\mathcal S_n\) of numerical semigroups with Eliahou number n:
In Sect. 5 we proved that all the \(\mathcal S_n\)’s consist of infinitely many numerical semigroups. As a consequence, we have that, for all n, the set
of positive integers is, in particular, non empty and therefore has a minimum. Furthermore, since there are only finitely many numerical semigroups with a given genus, none of the \(GE_n\) is bounded (see below for an alternative proof).
We remark that Fromentin’s computations (see Sect. 2.4) show that the minimum of \(GE_{-1}\) is 43 and that if \(n<-1\), then \(\min GE_{n} > 60\).
A related and general question is:
Question 1
Le n be an integer. Find the minimum of \(GE_n\).
It seems to be difficult to get some hint on how to attack this question through (presently available) computational means. Finding some good bounds is probably challenging enough. To this end, we prove the following proposition:
Proposition 10
Let p be an even positive integer. Then
Proof
Using the fact that \({{\mathrm{c}}}(S(p))=p\mu \) (Corollary 3) and the formula for \(|{{\mathrm{L}}}(S(p))|\) given by Corollary 7, we get:
\(\square \)
One can state similar results for the others families considered, namely for \(S^{(0,j)}(p,\tau )\).
Proposition 11
Let p be an even positive integer and let \(\tau \) and j be non-negative integers. Then
Proof
By Proposition 7 and Proposition 9 (with \(i=0\)) we conclude that \({{\mathrm{c}}}(S^{(0,j)}(p,\tau ))= {{\mathrm{c}}}(S(p))+(\tau +j)\frac{p^2}{2}-\tau \). By Remark 11, all the semigroups under consideration have the same number of left elements: \(|{{\mathrm{L}}}(S(p)|\).
Since the Eliahou number of \(S^{(0,j)}(p,\tau )\) does not vary with j and, for any given n, there exist p and \(\tau \) such that \({{\mathrm{E}}}(S(p,\tau ))=n\), we have that \(\left\{ {{\mathrm{genus}}}(S^{(0,j)}(p,\tau ))\mid j\in \mathbb N\right\} \subseteq GE_n\). We can therefore conclude, as already observed, that the set \(GE_n\) is unbounded for any n.
Corollary 20
Let n be a negative integer and let \(p=\left\lceil 1 + \sqrt{1-8n}\right\rceil \). Then the numerical semigroup \(S=S\left( p,n-\frac{p}{4}(1-p/2)\right) \) is such that
In particular, we get the following bound:
Proof
Recall that, by Corollary 16, \({{\mathrm{E}}}(S)=n\). By Proposition 11, we have:
\(\square \)
The bound given by Corollary 20 is not tight in general, as the below discussion shows.
For \(n=-1\) we have \(p=4\) and \(n-\frac{p}{4}(1-p/2)=0\). As we know, \(S(4)=\langle 14, 22, 23\rangle _{56}\) is such that \({{\mathrm{E}}}(S(4))=-1\) and \({{\mathrm{genus}}}(S(4))=43\), which is a minimum, by Fromentin’s computations. Evaluating \(\frac{p^4}{16}+\frac{p^3}{12} +\frac{3p^2}{2} + \frac{14p}{12} + n\left( \frac{p^2}{2}-1\right) \) with \(p=4\) and \(n=-1\) one gets 43. Therefore, we can state the following remark.
Remark 13
The bound given by Corollary 20 is tight for \(n=-1\).
The tightness is no longer true for \(n=-2\). In this case \(p=6\) and \({n-\frac{p}{4}(1-p/2)=1}\). We have \(S(6,1)=\langle 26, 44, 45\rangle _{155}\), which is a semigroup of genus 126 (one can compute it directly or evaluate the right side of (13) at \(p=6\) and \(n=-2\)). But one can verify that \(\langle 30, 44, 48, 49\rangle _{118}\) has genus 99 and Eliahou number \(-2\), thus 126 is not tight. We do not know whether 99 is tight.
Question 2
Is 99 the minimum possible genus of all the numerical semigroups satisfying \({{\mathrm{E}}}(S)=-2\)?
The bound given by Corollary 20 for \(n=-3\) is smaller than the one given for \(n=-2\) and we do not know whether it is tight. For \(n=-3\), we get \(p=6\) and \(n-\frac{p}{4}(1-p/2)=0\). The semigroup \(S(6,0)=\langle 23, 39, 40\rangle _{138}\) has genus 109 and Eliahou number \(-3\).
Question 3
Is 109 a lower bound for the set of genus of all numerical semigroups satisfying \({{\mathrm{E}}}(S)=-3\)?
Let us now make some comments on a possible attempt to solve Questions 2 and 3 by exhaustive search.
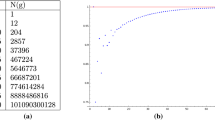
Denote by \(n_g\) the number of numerical semigroups of genus g and by \(N_g\) the number of numerical semigroups of genus not greater than g. The following was conjectured by Bras-Amoros [1] and proved by Zhai [9].
Proposition 12
The sequence of the number of numerical semigroups by genus behaves like the Fibonacci sequence, that is,
This implies that \(\lim _{g\rightarrow +\infty }\frac{n_{g}}{n_{g-1}}=\varphi \), where \(\varphi \) is the golden ratio. Since the golden ratio is greater than 1, 61, it is not surprising that one can experimentally observe \(n_g \ge n_{g-1}\cdot (1.6)\) even for small g. This can be observed in the various tables available in the literature containing the numbers \(n_g\). The one that, to the best of our knowledge, goes the farthest is the one given by Fromentin and Hivert [5] where, in particular, the number of numerical semigroups of genus 67 is given: \(n_{67}=377,866,907,506,273\). Summing up the number of numerical semigroups of genus not greater 67, one gets
One can guess that the number of numerical semigroups of genus \(67+i\) is approximately \(n_{67}\cdot (1.6)^{i}\) and consequently
By doing some computations (with several unfavourable rounding) one gets that the number of numerical semigroups up to genus 109 is well over \((3.2)\times 10^{23}\). It is out of reach using today’s computational means to do even the most trivial computation for such a number of semigroups.
Suppose that one could do some computation with \(10^6\) semigroups per second. The overall computation with the semigroups of genus up to 109 would require \((3.2)\times 10^{17}\) s. Taking into account that 1 year has less that \((1.6)\cdot 10^7\) s, the computation would take about \(2\times 10^{10}\) years, which is a little bit too much to wait for.
Although computing the Eliahou number of one numerical semigroup of small genus, up to 109, say, takes almost no time, the above discussion should make clear that exhaustive search is not satisfactory when one has to deal with huge numbers of numerical semigroups. Further theoretical results are needed.
To the best of our knowledge, exhaustive search has only been performed for semigroups up to genus 60. In particular, we are not able to guarantee that 61 is not the answer for one or both questions above.
Appendix 2: A variety of examples
In this section we give a number of examples of numerical semigroups whose Eliahou number is negative. We group these examples into various tables (Tables 6, 7 and 8). The choice of the examples, most of them obtained in the process that led to obtaining the families considered in the paper, deserves some comments. One of the aims is to furnish a source of (counter-) examples for some natural questions. Another one is to give some insight on possible answers to others. Others examples are probably mere curiosities, that, as frequently happens when doing experiments, may help to ask the appropriate questions.
How general are the families we considered in the paper? We believe that not much: its contribution to the characterization of \({\mathcal {E}}\) is probably very small. We present examples having more than 3 minimal left generators as well as examples where none of its pairs of minimal left generator consists of consecutive numbers. None of these examples is of the form \(S^{(i,j)}(p,\tau )\).
The tables presented in this appendix are similar to the ones that already appeared in the text, namely in Sect. 3.8 where an explanation for the meaning of the various columns is given. The only difference occurs in the first column: instead of the notation used for the semigroup, a number is used so that the examples in the table are numbered sequentially.
Several of our examples have more that 3 minimal left generators (see Tables 6 and 7). Thus we can state the following remark.
Remark 14
There exist numerical semigroups with more than 3 minimal left generators whose Eliahou number is negative.
Our examples just involve numerical semigroups with no more than 5 minimal left generators, but we would not be surprised if the following question has a negative answer.
Question 4
Is there an upper bound for the number of left primitives of the numerical semigroups in \({\mathcal {E}}\)?
Appendix 3: Wilf number of \(S^{(i,j)}(p\tau )\)
The aim of this section is to prove Theorem 4, which gives a formula in terms of i, j, p and \(\tau \) for the Wilf number of \(S^{(i,j)}(p,\tau )\).
Proof
By definition,
Using Lemma 9, Lemma 10 and Proposition 9, we get
Through small manipulations we get:
Now let us look separately to each of the numbered parcels. To deal with Parcel (14) we need to use Remark 6.
To deal with Parcel (15) we need to use Remark 4 (see also Corollary 7).
Next we rewrite Parcel (16):
Joining up, we get:
We proceed by slightly manipulating the right side of the above equality.
Simplifying a bit further:
Next we use Proposition 8 and Proposition 6 to obtain the requested expression.
\(\square \)
Rights and permissions
About this article
Cite this article
Delgado, M. On a question of Eliahou and a conjecture of Wilf. Math. Z. 288, 595–627 (2018). https://doi.org/10.1007/s00209-017-1902-3
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00209-017-1902-3