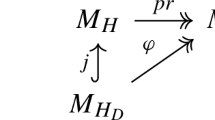Rationality results for the exterior and the symmetric square L-function (with an appendix by Nadir Matringe)

Abstract

Let $G=\mathrm{GL}_{2n}$ over a totally real number field F and $n\ge 2$. Let $\Pi$ be a cuspidal automorphic representation of $G(\mathbb {A})$, which is cohomological and a functorial lift from SO$(2n+1)$. The latter condition can be equivalently reformulated that the exterior square L-function of $\Pi$ has a pole at $s=1$. In this paper, we prove a rationality result for the residue of the exterior square L-function at $s=1$ and also for the holomorphic value of the symmetric square L-function at $s=1$ attached to $\Pi$. As an application of the latter, we also obtain a period-free relation between certain quotients of twisted symmetric square L-functions and a product of Gauß sums of Hecke characters.

1 Introduction

1.1 General background

Let F be an algebraic number field and let $\Pi$ be a cuspidal automorphic representation of $\mathrm{GL}_2(\mathbb {A}_F)$. Rationality results for special values of the associate automorphic L-function $L(s,\Pi )$ have been studied by several authors over the last decades. For the scope of this paper, we would like to mention Manin and Shimura, who were the first to study special values of $L(s,\Pi )$ in the particular case, when F is totally real, i.e., when $\Pi$ comes from a Hilbert modular form, cf. [27] and [33], and Kurchanov, who treated the case of a CM-field F in a series of papers, cf. [24, 25]. Shortly later, Harder published some articles, see [15, 16], in which he described a general approach to such rationality results. In [15], Harder considered the case of an arbitrary number field F, while in [16], he extended the methods of the above authors to some automorphic representations, which do not necessarily come from cusp forms (for F imaginary quadratic). The case of $\mathrm{GL}_2$ over a general number field F has also been considered independently by Hida, cf. [18] and later on also by Shimura, see [34].

It took some time until extensions of these results to general linear groups $\mathrm{GL}_n$ of higher rank n were available. Important achievements include Ash–Ginzburg, [1], Kazhdan–Mazur–Schmidt [22], and Mahnkopf [26].

Guided by the above methods, meanwhile, there is a growing number of results that have been proved about the rationality of special values of certain automorphic L-functions attached to $\mathrm{GL}_n$. As a selection of examples, relevant to the present paper, we refer to Raghuram [28, 29], Harder–Raghuram [17], Grobner–Harris [11]; Grobner–Raghuram [14], Grobner–Harris–Lapid [12] and Balasubramanyam–Raghuram [2].

In all of these references, the corresponding rationality result is obtained by writing the special L-value at hand as an algebraic multiple of a certain period invariant.¹ This period is defined by comparison of a rational structure on a cohomology space, attached to the given automorphic representation $\Pi$, with a rational structure on a model-space of (the finite part of) $\Pi$, such as a Whittaker model or a Shalika model. (The word “rational structure” here refers to a subspace of the vector space, carrying the action of $\Pi$, which is essentially defined over the field of rationality of $\Pi$ and at the same time stable under the group action.) While the first rational structure on the cohomology space is purely of geometric nature and has its origin in the cohomology of arithmetic groups (or better: the cohomology of arithmetically defined locally symmetric spaces), the latter rational structure is defined by reference to the uniqueness of the given model-space.

In this paper, we continue the above considerations. But while most of the aforementioned papers deal with special values of the Rankin–Selberg L-function (by some variation or the other), the principal L-function, or the Asai L-functions, here we would like to study the algebraicity of the exterior square L-function and the symmetric square L-function, attached to a cuspidal automorphic representation of the general linear group.

1.2 The main results of this paper

To put ourselves in medias res, let F be a totally real number field and let $G=\mathrm{GL}_{N}/F$, $N=2n$ with $n\ge 2$. The restrictions on F and the index of the general linear groups under consideration are owed to the inevitable, as it will become clear below. Indeed, let $\Pi$ be a cuspidal automorphic representation of $G(\mathbb {A})$ and let $\mathcal {W}^\psi (\Pi )$ be its $\psi$-Whittaker model. As we want to exploit the results of Bump–Friedberg [6], we shall assume that the partial exterior square L-function $L^S(s,\Pi ,\Lambda ^2)$ of $\Pi$ has a pole at $s=1$. (Here, S is a finite set of places of F, containing all archimedean ones, such that for a place $v\notin S$, the local components $\Pi _v$ and $\psi _v$ are unramified.) In particular, this forces $N=2n$ to be even, see [20, Theorem 2], and furthermore $\Pi$ to be self-dual, $\Pi \cong \Pi ^\vee$, and to have trivial central character.

Our first main result gives a rationality statement for the residue$\mathrm{Res}_{s=1}(L^S(s,\Pi ,\Lambda ^2))$ of the exterior square L-function. More precisely, we obtain the following result:

Theorem 1.1

Let F be a totally real number field and $G=\mathrm{GL}_{2n}/F$, $n\ge 2$. Let $\Pi$ be a unitary cuspidal automorphic representation of $G(\mathbb {A})$, which is cohomological with respect to an irreducible, self-contragredient, algebraic, finite-dimensional representation $E_\mu$ of $G_\infty$. Assume that $\Pi$ satisfies the equivalent conditions of Proposition 3.5, i.e., the partial exterior square L-function $L^S(s,\Pi ,\Lambda ^2)$ has a pole at $s=1$. Then, for every $\sigma \in \mathrm{Aut}(\mathbb {C})$, there is a non-trivial period $p^t({}^\sigma \Pi )$, defined by a comparison of a given rational structure on the Whittaker model of ${}^\sigma \Pi _f$ and a rational structure on a realization of ${}^\sigma \Pi _f$ in cohomology in top degree t, and a non-trivial archimedean period $p^t({}^\sigma \Pi _\infty )$, such that

$$\begin{aligned} \sigma \left( \frac{L(\tfrac{1}{2},\Pi _f)\cdot \mathrm{Res}_{s=1}(L^S(s,\Pi ,\Lambda ^2))}{p^t(\Pi ) \ p^t(\Pi _\infty )}\right) \ = \ \frac{L(\tfrac{1}{2},{}^\sigma \Pi _f)\cdot \mathrm{Res}_{s=1}(L^S(s,{}^\sigma \Pi ,\Lambda ^2))}{p^t({}^\sigma \Pi ) \ p^t({}^\sigma \Pi _\infty )}. \end{aligned}$$

In particular,

$$\begin{aligned} L(\tfrac{1}{2},\Pi _f)\cdot \mathrm{Res}_{s=1}(L^S(s,\Pi ,\Lambda ^2)) \ \sim _{\mathbb {Q}(\Pi _f)} \ p^t(\Pi ) \ p^t(\Pi _\infty ), \end{aligned}$$

where “$\sim _{\mathbb {Q}(\Pi _f)}$” means up to multiplication of the right hand side by an element in the number field $\mathbb {Q}(\Pi _f)$.

This is proved in details in Sect. 7.4, see Theorem 7.4. For a precise definition of the periods $p^t({}^\sigma \Pi )$ and $p^t({}^\sigma \Pi _\infty )$, as well as for a complete list of choices which enter their involved definitions, we refer to Proposition 4.3 and Remark 4.4, respectively (7.2) and Remark 7.3. The non-vanishing of the archimedean period $p^t({}^\sigma \Pi _\infty )$ is shown—building on a result of Sun—in our Theorem 7.1. The number field $\mathbb {Q}(\Pi _f)$ in the theorem is (by Strong Multiplicity One) the aforementioned field of rationality of the cuspidal automorphic representation $\Pi$. See Sects. 2.5 and 3.3.

The key result, which we use, in order to derive the above theorem, is a certain integral-representation, obtained by Bump–Friedberg [6], of the residue $\mathrm{Res}_{s=1}(L^S(s,\Pi ,\Lambda ^2))$ of the exterior square L-function in terms of integrating over a cycle $Z(\mathbb {A})H(F){\backslash }H(\mathbb {A})$. Here, Z is the centre of G and $H=\mathrm{GL}_n\times \mathrm{GL}_n$, suitably embedded into G, cf. 2.2.

More precisely, if one combines the three main results of [6], then, under the assumptions made in the theorem, one obtains the following equality, shown in our Theorem 6.1:

$$\begin{aligned}&c_n\cdot \hat{\Phi }(0) \int _{Z(\mathbb {A})H(F){\backslash } H(\mathbb {A})}\varphi (J(g,g')) \ dg \ dg'\nonumber \\&\quad = \frac{L^S(\tfrac{1}{2},\Pi )\cdot \mathrm{Res}_{s=1}(L^S(s,\Pi ,\Lambda ^2))}{L^S(n,{\mathbf {1}})^2}\cdot \prod _{v\in S}\frac{Z_v(\xi _v,f_{v,1})}{L(n,{\mathbf {1}}_v)}. \end{aligned}$$

(1.2)

Here, $\Phi$ is a certain global Schwartz–Bruhat function on $\mathbb {A}^n$, chosen with care in Sect. 6.1, and $c_n\cdot \hat{\Phi }(0)$ is the (non-zero) residue at $s=1$ of an Eisenstein series attached to a section $f_s=\otimes _v f_{v,s}$, which is defined by $\Phi$. See Sects. 6.1 and 6.4 for the precise definitions of the terms appearing in (1.2). What one should observe is that the value of the partial L-function $L^S(n,{\mathbf {1}})$ of the trivial character of $\mathbb {A}$ at n appears in the formula. In order for the pole of $L^S(s,\Pi ,\Lambda ^2)$ at $s=1$ not to cancel with the pole of $L^S(n,{\mathbf {1}})$ at $n=1$, we assumed $n\ge 2$, which explains the corresponding assumption in Theorem 1.1 (resp. Theorem 7.4). (As for the case of $n=1$, $L^S(s,\Pi ,\Lambda ^2)=L^S(s,{\mathbf {1}})$, the analogue of Theorem 1.1 would boil down to a rationality result for the central critical value of the L-function of unitary cusp forms of $\mathrm{GL}_2(\mathbb {A})$, which is known, e.g., by Harder [15]. Therefore, considering only $n\ge 2$ is not a serious restriction.)

Observe that the top degree t, mentioned in Theorem 1.1, where $\Pi$ has non-trivial cohomology, equals the dimension of the locally symmetric spaces, which are associated to the cycle $Z(\mathbb {A})H(F){\backslash } H(\mathbb {A})$, cf. Sect. 5.2. (Here, we necessarily have to use that F is totally real, which explains the last obstruction, set in the beginning.) As a consequence, we may use the de Rham isomorphism. Together with (1.2) and Matringe’s equivariance-result (Theorem A) in the Appendix, this finally gives Theorem 1.1.

We point out that, if $\Pi$ satisfies the assumptions made in the theorem, then $\Pi$ automatically satisfies the assumptions made in Grobner–Raghuram [14]. Hence, the non-zero periods $\omega ^{\epsilon _0}(\Pi _f)$ and $\omega (\Pi _\infty )$ constructed in loc. cit. are well-defined. See our Sect. 7.5 below for details. If we define the non-zero, top-degree Whittaker–Shalika periods,

$$\begin{aligned} P^t(\Pi ):=\frac{p^t(\Pi )}{\omega ^{\epsilon _0}(\Pi _f)}\quad \text {and}\quad P^t(\Pi _\infty ):=\frac{p^t(\Pi _\infty )}{\omega (\Pi _\infty )}, \end{aligned}$$

then we may get rid of the L-factor $L(\tfrac{1}{2},\Pi _f)$ in Theorem 1.1, as long as it does not vanish. The following result is Corollary 7.6.

Corollary 1.3

Let $\Pi$ be as in the statement of Theorem 1.1 (resp. Theorem 7.4). If $L(\tfrac{1}{2},\Pi _f)$ is non-zero, then

$$\begin{aligned} \mathrm{Res}_{s=1}(L^S(s,\Pi ,\Lambda ^2)) \ \sim _{\mathbb {Q}(\Pi _f)} \ P^t(\Pi ) \ P^t(\Pi _\infty ), \end{aligned}$$

where “$\sim _{\mathbb {Q}(\Pi _f)}$” means up to multiplication of the right hand side by an element in the number field $\mathbb {Q}(\Pi _f)$.

In order to obtain our second main theorem on the symmetric square L-function, we need a version of one of the main results of Grobner–Harris–Lapid [12] and Balasubramanyam–Raghuram [2], which is tailored to our present situation at hand. This is achieved in Sect. 8, applying [2] to our particular case. The aforementioned result reads as follows:

Theorem 1.3

Let $\Pi$ be a self-dual, unitary, cuspidal automorphic representation of $G(\mathbb {A})$ (with trivial central character), which is cohomological with respect to an irreducible, self-contragredient, algebraic, finite-dimensional representation $E_\mu$ of $G_\infty$. Then, for every $\sigma \in \mathrm{Aut}(\mathbb {C})$,

$$\begin{aligned} \sigma \left( \frac{\mathrm{Res}_{s=1}(L^S(s,\Pi \times \Pi ))}{p^t(\Pi ) \ p^b(\Pi ) \ p(\Pi _\infty )}\right) \ = \ \frac{\mathrm{Res}_{s=1}(L^S(s,{}^\sigma \Pi \times {}^\sigma \Pi ))}{p^t({}^\sigma \Pi ) \ p^b({}^\sigma \Pi ) \ p({}^\sigma \Pi _\infty )}. \end{aligned}$$

In particular,

$$\begin{aligned} \mathrm{Res}_{s=1}(L^S(s,\Pi \times \Pi )) \ \sim _{\mathbb {Q}(\Pi _f)^\times } \ p^t(\Pi ) \ p^b(\Pi ) \ p(\Pi _\infty ), \end{aligned}$$

where “$\sim _{\mathbb {Q}(\Pi _f)^\times }$” means up to multiplication by a non-trivial element in the number field $\mathbb {Q}(\Pi _f)$.

In the statement of the latter theorem, $p^t(\Pi )$ is the top-degree period defined above, while $p^b(\Pi )$ is defined analogously, but using the lowest degree b, where $\Pi$ has non-trivial cohomology. The non-vanishing archimedean period $p(\Pi _\infty )$ is defined in (7.1). We refer to Sects. 8.2 and 8.3 for precise assertions and definitions concerning these periods, in particular Remarks 8.1 and 8.4.

The second main theorem of this paper finally deals with the value of the symmetric square L-function at $s=1$. Recall that we have

$$\begin{aligned} L^S(s,\Pi \times \Pi )=L^S(s,\Pi ,\mathrm{Sym}^2)\cdot L^S(s,\Pi ,\Lambda ^2). \end{aligned}$$

As by assumption $L^S(s,\Pi ,\Lambda ^2)$ carries the (simple) pole of $L^S(s,\Pi \times \Pi )$ at $s=1$, the symmetric square L-function $L^S(s,\Pi ,\mathrm{Sym}^2)$ is holomorphic and non-vanishing at $s=1$. Our second main theorem hence follows by combining Theorem 1.1 (resp. Theorem 7.4) with Theorem 1.3 (resp. Theorem 8.5). We obtain, see Theorem 9.2,

Theorem 1.4

Let $\Pi$ be a unitary cuspidal automorphic representation of $G(\mathbb {A})$, as in the statement of Theorem 1.1. Then, for every $\sigma \in \mathrm{Aut}(\mathbb {C})$,

$$\begin{aligned} \sigma \left( \frac{L(\tfrac{1}{2},\Pi _f)\ p^b(\Pi ) \ p^b(\Pi _\infty )}{L^S(1,\Pi ,\mathrm{Sym}^2)}\right) \ = \ \frac{L(\tfrac{1}{2},{}^\sigma \Pi _f)\ p^b({}^\sigma \Pi ) \ p^b({}^\sigma \Pi _\infty )}{L^S(1,{}^\sigma \Pi ,\mathrm{Sym}^2)}. \end{aligned}$$

In particular,

$$\begin{aligned} L^S(1,\Pi ,\mathrm{Sym}^2) \sim _{\mathbb {Q}(\Pi _f)} L(\tfrac{1}{2},\Pi _f)\ p^b(\Pi ) \ p^b(\Pi _\infty ) \end{aligned}$$

where “$\sim _{\mathbb {Q}(\Pi _f)}$” means up to multiplication of $L^S(1,\Pi ,\mathrm{Sym}^2)$ by an element in the number field $\mathbb {Q}(\Pi _f)$.

Similar to before, we may define bottom-degree Whittaker–Shalika periods. Set

$$\begin{aligned} P^b(\Pi ):=p^b(\Pi )\cdot \omega ^{\epsilon _0}(\Pi _f)\quad \quad \text {and}\quad \quad P^b(\Pi _\infty ):=p^b(\Pi _\infty )\cdot \omega (\Pi _\infty ). \end{aligned}$$

Then, we have the following corollary, see Corollary 9.4, in which we may get once more rid of the L-factor $L(\tfrac{1}{2},\Pi _f)$, if it is non-zero.

Corollary 1.4

Let $\Pi$ be as in the statement of Theorem 1.4 (resp. Theorem 9.2). If $L(\tfrac{1}{2},\Pi _f)$ is non-zero, then

$$\begin{aligned} L^S(1,\Pi ,\mathrm{Sym}^2)\ \sim _{\mathbb {Q}(\Pi _f)^\times } \ P^b(\Pi ) \ P^b(\Pi _\infty ), \end{aligned}$$

where “$\sim _{\mathbb {Q}(\Pi _f)^\times }$” means up to multiplication of $L^S(1,\Pi ,\mathrm{Sym}^2)$ by a non-zero element in the number field $\mathbb {Q}(\Pi _f)$.

On a final note, we may also derive a theorem for quotients of symmetric square L-functions, which is independent of all periods appearing in this paper. We hope that this application of Theorem 1.4—our third main result—serves as an interesting example of the strength of the relation provided by Theorem 1.4 between the symmetric square L-function and our a priori only abstract Whittaker period $p^b(\Pi )$. More precisely, we obtain (cf. Theorem 10.1)

Theorem 1.5

Let $\Pi$ be a cuspidal automorphic representation of $G(\mathbb {A})$ and let $\chi _1$ and $\chi _2$ be two Hecke characters of finite order, such that $\Pi \otimes \chi _i$, $i=1,2$, both satisfy the conditions of Corollary 1.4. If $\chi _1$ and $\chi _2$ have moreover the same infinity-type, i.e., $\chi _{1,\infty }=\chi _{2,\infty }$, then,

$$\begin{aligned} \frac{L^S(1,\Pi \otimes \chi _1,\mathrm{Sym}^2)}{L^S(1,\Pi \otimes \chi _2,\mathrm{Sym}^2)}\ \sim _{\mathbb {Q}(\Pi _f,\chi _{1,f},\chi _{2,f})^\times } \mathscr {G}(\chi _{1,f})^{2n^2}\mathscr {G}(\chi _{2,f})^{-2n^2}, \end{aligned}$$

where “$\sim _{\mathbb {Q}(\Pi _f,\chi _{1,f},\chi _{2,f})^\times }$” means up to multiplication by a non-zero element in the composition of number fields $\mathbb {Q}(\Pi _f)$, $\mathbb {Q}(\chi _{1,f})$ and $\mathbb {Q}(\chi _{2,f})$.

It shall be noted that, whereas the quantities on the left hand side of the above equation all depend crucially on $\Pi$, the right hand side is not only independent of the all periods considered in this paper, but completely independent of $\Pi$.

2 Notation and conventions

2.1 Number fields

In this paper, F denotes a totally real number field of degree $d=[F:\mathbb {Q}]$ with ring of integers $\mathcal {O}$. For a place v, let $F_v$ be the topological completion of F at v. Let $S_\infty$ be the set of archimedean places of F. If $v \notin S_{\infty }$, we let $\mathcal {O}_v$ be the local ring of integers of $F_v$ with unique maximal ideal $\wp _v$. Moreover, $\mathbb {A}$ denotes the ring of adèles of F and $\mathbb {A}_f$ its finite part. We use the local and global normalized absolute values, the first being denoted by $|\cdot |_v$, the latter by $\Vert \cdot \Vert$. The fact that F has no complex place is crucial, see Sect. 5.2. Once and for all, we fix a non-trivial additive character $\psi : F{\backslash }\mathbb {A}\rightarrow \mathbb {C}^\times$ as in [14, §2.7].

2.2 Algebraic groups and real Lie groups

Throughout this paper G denotes $\mathrm{GL}_{2n}/F$, $n\ge 2$, the general linear group over F. Although much of the paper works also for $\mathrm{GL}_N$ with N arbitrary (e.g., the Diagram 5.2), it will be crucial for the main result that $N=2n$ is even (because only then, the exterior square L-function may have a pole, [20, Theorem 2, p. 224]) and that $n\ge 2$ (because the $\zeta$-function attached to F has a pole at n, if $n=1$). Let H be $\mathrm{GL}_n\times \mathrm{GL}_n$ over F. We identify H with a subgroup of G, defined as the image of the homomorphism $J:\mathrm{GL}_n\times \mathrm{GL}_n \rightarrow \mathrm{GL}_{2n}$, where

$$\begin{aligned} J(g,g')_{k,l}:=\left\{ \begin{array}{ll} g'_{i,j} &{}\quad \text {if k=2i-1 and l=2j-1}\\ g_{i,j} &{}\quad \text {if k=2i and l=2j}\\ 0 &{}\quad \text {else} \end{array} \right. \end{aligned}$$

The center of G / F is denoted Z / F. We write $G_\infty :=R_{F/\mathbb {Q}}(G)(\mathbb {R})$ (resp.,$H_\infty :=R_{F/\mathbb {Q}}(H)(\mathbb {R})$ or $Z_\infty :=R_{F/\mathbb {Q}}(Z)(\mathbb {R})$), where $R_{F/\mathbb {Q}}$ stands for Weil’s restriction of scalars. Lie algebras of real Lie groups are denoted by the same letter, but in lower case gothics.

At an archimedean place $v\in S_{\infty }$ we let $K_v$ be a maximal compact subgroup of the real Lie group $G(F_v)=\mathrm{GL}_{2n}(\mathbb {R})$. It is isomorphic to O(2n). We write $K_v^\circ$ for the connected component of the identity of $K_v$, which is isomorphic to SO(2n). We set $K_\infty :=\prod _{v\in S_\infty } K_v$ and $K^\circ _\infty :=\prod _{v\in S_\infty } K^\circ _v$. Moreover, we denote by $K_{H,v}$ the intersection $K_v\cap H(F_v)$, which is a maximal compact subgroup of $H(F_v)$, isomorphic to $O(n)\times O(n)$. As before, we write $K^\circ _{H,v}$ for the connected component of the identity and we let $K_{H,\infty }:=\prod _{v\in S_\infty } K_{H,v}$ and $K^\circ _{H,\infty }:=\prod _{v\in S_\infty } K^\circ _{H,v}$.

Let $A_G$ be the multiplicative group of positive real numbers $\mathbb {R}_+$, being diagonally embedded into the center $Z_{\infty }$ of $G_\infty$. It is a direct complement of the group$G(\mathbb {A})^{(1)}:=\{g\in G(\mathbb {A})| \Vert \det (g)\Vert =1\}$ in $G(\mathbb {A})$. According to our conventions, the Lie algebra of the real Lie group $A_G$ is denoted $\mathfrak {a}_G$. Furthermore, we let $\mathfrak {m}_G:=\mathfrak {g}_\infty /\mathfrak {a}_G$,$\mathfrak {m}_H:=\mathfrak {h}_\infty /\mathfrak {a}_G$ and $\mathfrak {s}:=\mathfrak {z}_\infty /\mathfrak {a}_G$. Observe that these spaces are Lie subalgebras of $\mathfrak {g}_\infty$.

2.3 Coefficient modules

In this paper, $E_\mu$ denotes an irreducible, algebraic representation of $G_{\infty }$ on a finite-dimensional complex vector space. It is determined by its highest weight $\mu =(\mu _v)_{v\in S_\infty }$, whose local components at an archimedean place v may be identified with $\mu _v=(\mu _{1,v},\ldots ,\mu _{2n,v})\in \mathbb {Z}^{2n}$, $\mu _{1,v}\ge \mu _{2,v}\ge \cdots \ge \mu _{2n,v}$. We assume that $E_\mu$ is self-dual, i.e., it is isomorphic to its contragredient, $E_\mu \cong E_\mu ^\vee$, or, in other words, that

$$\begin{aligned} \mu _{j,v}+\mu _{2n-j+1,v}=0, \quad 1\le j\le n \end{aligned}$$

at all places $v\in S_\infty$. Clearly, this condition implies that $\mu _{n,v}\ge 0\ge \mu _{n+1,v}$ for all $v\in S_\infty$. The self-duality hypothesis, hence incorporates that $\dim _\mathbb {C}\mathrm{Hom}_{H(\mathbb {C})}(E_{\mu _v},\mathbb {C})=1$ for all $v\in S_\infty$. (See [14, Proposition 6.3.1].)

2.4 Cohomology of locally symmetric spaces

Define the orbifolds

$$\begin{aligned} \mathcal {S}_G:=G(F){\backslash } G(\mathbb {A})/A_G K^\circ _\infty =G(F){\backslash } G(\mathbb {A})^{1}/K^\circ _\infty \end{aligned}$$

and

$$\begin{aligned} \tilde{\mathcal {S}}_H:=H(F){\backslash } H(\mathbb {A})/A_G K^\circ _{H,\infty }. \end{aligned}$$

A representation $E_\mu$ as in Sect. 2.3 defines a locally constant sheaf $\mathcal {E}_\mu$ on $\mathcal {S}_G$, whose espace étalé is $G(\mathbb {A})^1/K^\circ _\infty \times _{G(F)} E_\mu$ (with the discrete topology on $E_\mu$). Along the proper map $\mathcal J:\tilde{\mathcal {S}}_H\rightarrow \mathcal {S}_G$, which is induced by J, Sect. 2.2, we also obtain a sheaf on $\tilde{\mathcal {S}}_H$, which we will again denote by $\mathcal {E}_\mu$. Let $H^q_c(\mathcal {S}_G,\mathcal {E}_\mu )$ (resp. $H_c^q(\tilde{\mathcal {S}}_H,\mathcal {E}_\mu )$) be the corresponding space of sheaf cohomology with compact support. This is an admissible $G(\mathbb {A}_{f})$-module (resp. $H(\mathbb {A}_f)$-module), cf. [31, Corollary 2.13]. Observe that the proper map $\mathcal J$ from above gives rise to a non-trivial $H(\mathbb {A}_f)$-equivariant map

$$\begin{aligned} \mathcal J^q_\mu : H_c^q(\mathcal {S}_G,\mathcal {E}_\mu )\rightarrow H_c^q(\tilde{\mathcal {S}}_H,\mathcal {E}_\mu ). \end{aligned}$$

2.5 Complex automorphisms and rational structures

For $\sigma \in \text {Aut}(\mathbb {C})$, let us define the $\sigma$-twist ${}^\sigma \!\nu$ of an (abstract) representation $\nu$ of $G(\mathbb {A}_f)$ (resp., $G(F_v)$, $v\notin S_\infty$) on a complex vector space W, following Waldspurger [36], I.1: If $W'$ is a $\mathbb {C}$-vector space with a $\sigma$-linear isomorphism $\phi :W\rightarrow W'$ then we set

$$\begin{aligned} {}^\sigma \!\nu := \phi \circ \nu \circ \phi ^{-1}. \end{aligned}$$

This definition is independent of $\phi$ and $W'$ up to equivalence of representations, whence we may always take $W':=W\otimes _{\sigma }\mathbb {C}$, i.e., the abelian group W endowed with the scalar multiplication $\lambda \cdot _\sigma w:=\sigma ^{-1}(\lambda )w$.

Furthermore, if $\nu _\infty =\bigotimes _{v\in S_{\infty }}\nu _{v}$ is an (abstract) representation of the real Lie group $G_\infty$, we let

$$\begin{aligned}{}^{\sigma }\!\nu _\infty :=\bigotimes _{v\in S_{\infty }}\nu _{\sigma ^{-1} v},\end{aligned}$$

interpreting $v\in S_{\infty }$ as an embedding of fields $v:F\hookrightarrow \mathbb {R}$. Combining these two definitions, we may define the $\sigma$-twist on a global representation $\nu =\nu _\infty \otimes \nu _f$ of $G(\mathbb {A})$ as

$$\begin{aligned} {}^\sigma \!\nu :={}^{\sigma }\!\nu _\infty \otimes {}^\sigma \!\nu _f. \end{aligned}$$

We recall also the definition of the rationality field of a representation from [36], I.1. If $\nu$ is any of the representations considered above, then let $\mathfrak S(\nu )$ be the group of all automorphisms $\sigma \in \text {Aut}(\mathbb {C})$ such that ${}^\sigma \!\nu \cong \nu$. Then the rationality field $\mathbb {Q}(\nu )$ of $\nu$ is defined as the fixed-field of $\mathfrak S(\nu )$ within $\mathbb {C}$, i.e.,

$$\begin{aligned} \mathbb {Q}(\nu ):=\{z\in \mathbb {C}| \sigma (z)=z \text { for all } \sigma \in \mathfrak S(\nu )\}. \end{aligned}$$

We say that a representation $\nu$ on a $\mathbb {C}$-vector space W is defined over a subfield $\mathbb {F}\subset \mathbb {C}$, if there is a $\mathbb {F}$-vector subspace $W_\mathbb {F}\subset W$, stable under the given action, such that the canonical map $W_\mathbb {F}\otimes _\mathbb {F}\mathbb {C}\rightarrow W$ is an isomorphism. The following lemma is due to Clozel, [7, p. 122 and p. 128]. (See also [13, Lemma 7.1].)

Lemma 2.6

Let $E_\mu$ be an irreducible, algebraic representation as in Sect. 2.3. As a representation of the diagonally embedded group $G(F)\hookrightarrow G_\infty$, ${}^\sigma \!E_\mu$ is isomorphic to the abstract representation $E_\mu \otimes _\sigma \mathbb {C}$. Moreover, as a representation of G(F), $E_\mu$ is defined over $\mathbb {Q}(E_\mu )$.

We fix once and for all a $\mathbb {Q}(E_\mu )$-structure on $E_\mu$ as a representation of G(F). Clearly, this also fixes a $\mathbb {Q}(E_\mu )$-structure on $E_\mu$ as a representation of H(F). As a consequence, the $G(\mathbb {A}_f)$-module $H_c^q(\mathcal {S}_G,\mathcal {E}_\mu )$ and the $H(\mathbb {A}_f)$-module $H_c^q(\tilde{\mathcal {S}}_H,\mathcal {E}_\mu )$ carry a fixed, natural $\mathbb {Q}(E_\mu )$-structure, cf. [7, p. 123]. Moreover, this also pins down natural $\sigma$-linear, equivariant isomorphisms

$$\begin{aligned}&\mathcal H^{\sigma ,q}_\mu : H^q_c(\mathcal {S}_G,\mathcal {E}_\mu ){\mathop {\longrightarrow }\limits ^{\sim }}H^q_c(\mathcal {S}_G,{}^\sigma \!\mathcal {E}_\mu )\quad \text {and}\nonumber \\&\tilde{\mathcal H}^{\sigma ,q}_\mu : H^q_c(\tilde{\mathcal {S}}_H,\mathcal {E}_\mu ){\mathop {\longrightarrow }\limits ^{\sim }}H^q_c(\tilde{\mathcal {S}}_H,{}^\sigma \!\mathcal {E}_\mu ) \end{aligned}$$

(2.1)

for all $\sigma \in$ Aut$(\mathbb {C})$, cf. [7, p. 128]. The following lemma is obvious.

Lemma 2.7

For all $\sigma \in \mathrm{Aut}(\mathbb {C})$ the following diagram commutes,

3 Facts and conventions for cuspidal automorphic representations

3.1 Cohomological cusp forms

In this paper, we let $\Pi$ be an irreducible unitary cuspidal automorphic representation of $G(\mathbb {A})$ with trivial central character. Furthermore, we assume that $\Pi$ is self-dual, i.e., $\Pi \cong \Pi ^\vee$. This is no loss of generality, as the main result will only hold for such cuspidal representations. (Compare this to Proposition 3.5 below.) Recall that $\Pi$ has a (unique) Whittaker model (with respect to $\psi$). We write

$$\begin{aligned} W^{\psi }:\Pi \rightarrow \mathcal {W}^{\psi }(\Pi ) \end{aligned}$$

for the realization of $\Pi$ in its Whittaker model $\mathcal {W}^{\psi }(\Pi )$ by the $\psi$-Fourier coefficient. Recall that there is a canonical decomposition $\mathcal {W}^{\psi }(\Pi )=\otimes '_{v} \mathcal {W}^{\psi _v}(\Pi _v)$, in the sense that each space $\mathcal {W}^{\psi _v}(\Pi _v)$ is canonically determined by the uniqueness of local Whittaker models. We will furthermore assume that $\Pi$ is cohomological: By this we understand that there is an irreducible, algebraic representation $E_\mu$ of $G_\infty$, as in Sect. 2.3, such that the archimedean component $\Pi _\infty$ of $\Pi$ has non-vanishing $(\mathfrak {m}_G,K^\circ _\infty )$-cohomology with respect to $E_\mu$, i.e.,

$$\begin{aligned} H^q(\mathfrak {m}_G,K^\circ _\infty ,\Pi _\infty \otimes E_\mu )\ne 0, \end{aligned}$$

for some degree q.

Lemma 3.2

Let $\rho _\infty$ be an irreducible unitary $(\mathfrak {g}_\infty ,K_\infty ^\circ )$-module with trivial $A_G$-action. Then the following assertions are equivalent:

• 1. $H^*(\mathfrak {m}_G,K^\circ _\infty ,\rho _\infty \otimes E_\mu )\ne 0,$

• 2. $H^*(\mathfrak {g}_\infty ,K^\circ _\infty ,\rho _\infty \otimes E_\mu )\ne 0,$

• 3. $H^*(\mathfrak {g}_\infty ,(Z_\infty K_\infty )^\circ ,\rho _\infty \otimes E_\mu )\ne 0.$

Proof

This follows combining the following well-known results on relative Lie algebra cohomology :[5], I. 1.3 (the Künneth rule), I. 5.1, I. Theorem 5.3 (Wigner’s lemma) and II. Proposition 3.1 (all cochains are closed and harmonic). $\square$

As a consequence, the archimedean component $\Pi _\infty$ of a cuspidal automorphic representation $\Pi$, as above, is cohomological in our sense, if and only if $\Pi _\infty$ has non-vanishing $(\mathfrak {g}_\infty ,K^\circ _\infty )$-cohomology or equivalently, non-vanishing $(\mathfrak {g}_\infty ,(Z_\infty K_\infty )^\circ )$-cohomology with respect to the same algebraic, self-dual coefficient module $E_\mu$ (although the degrees and dimensions of non-trivial cohomology spaces may change).

The component group $\pi _0(G_\infty )\cong K_\infty /K^\circ _\infty$ acts on the cohomology groups $H^q(\mathfrak {m}_G,K^\circ _\infty ,\Pi _\infty \otimes E_\mu )$ in each degree. For a character $\epsilon \in \pi _0(G_\infty )^*$, which we identify with

$$\begin{aligned} \epsilon = (\epsilon _1,\ldots ,\epsilon _d) \in (\mathbb {Z}/2\mathbb {Z})^d \cong \pi _0(G_\infty )^*, \end{aligned}$$

one obtains a corresponding $\pi _0(G_\infty )$-isotypic component $H^q(\mathfrak {m}_G,K^\circ _\infty ,\Pi _\infty \otimes E_\mu )[\epsilon ]$. Put

$$\begin{aligned} t:=dn(n+1)-1. \end{aligned}$$

(3.1)

Then,

$$\begin{aligned} \dim _\mathbb {C}H^t(\mathfrak {m}_G,K^\circ _\infty ,\Pi _\infty \otimes E_\mu )[\epsilon ]=1 \end{aligned}$$

for all $\epsilon \in \pi _0(G_\infty )^*$. This is a direct consequence of the formula in Clozel [7, Lemma 3.14] (see also [26, 3.1.2] or [13, 5.5]), the Künneth rule ([5, I. 1.3]) and the fact that $\mathfrak {s}$ is a $d-1$-dimensional abelian real Lie algebra, whence $H^q(\mathfrak {s},\mathbb {C})\cong \Lambda ^q\mathbb {C}^{d-1}$.

Observe furthermore, that (for all degrees q and characters $\epsilon \in \pi _0(G_\infty )^*$) there is a natural $G(\mathbb {A}_f)$-equivariant inclusion

$$\begin{aligned} \Delta ^q_\Pi : H^{q}(\mathfrak {m}_G,K^\circ _\infty ,\Pi \otimes E_\mu )[\epsilon ]\hookrightarrow H_c^q(\mathcal {S}_G,\mathcal {E}_\mu ). \end{aligned}$$

(3.2)

This is well-known and follows from [4, §5].

3.2 Rational structures

We have the following result:

Proposition 3.3

Let $\Pi$ be a cuspidal automorphic representation of $G(\mathbb {A})$, which is cohomological with respect to $E_\mu$. Then, the $\sigma$-twisted representation ${}^\sigma \Pi$ is also cuspidal automorphic and it is cohomological with respect to ${}^\sigma \! E_\mu$. For every $\epsilon \in \pi _0(G_\infty )^*$, the irreducible unitary $G(\mathbb {A}_f)$-module $H^{t}(\mathfrak {m}_G,K^\circ _\infty ,\Pi \otimes E_\mu )[\epsilon ]$ is defined over the rationality field $\mathbb {Q}(\Pi _f)$. This field is a number field, containing $\mathbb {Q}(E_\mu )$.

Proof

This is essentially due to Clozel [7]. In order to derive the above result from [7], observe that $\Pi _\infty$ is “regular algebraic” in Clozel’s sense, if and only if it is cohomological in our sense: This follows using Lemma 3.2 and [13, Theorem 6.3]. Hence, ${}^\sigma \Pi _f$ is the non-archimedean part of a cuspidal automorphic representation, which is cohomological with respect to ${}^\sigma \! E_\mu$ by [7, Theorem 3.13]. By uniqueness, see e.g. [13, 5.5], the archimedean part of this cuspidal automorphic representation is isomorphic to ${}^\sigma \Pi _\infty$ as defined above. By [7, Proposition 3.1], $H^{t}(\mathfrak {m}_G,K^\circ _\infty ,\Pi \otimes E_\mu )[\epsilon ]$ is defined over $\mathbb {Q}(\Pi _f)$ (See also [13, Corollary 8.7].). Finally, it is an implicit consequence of [7, Theorem 3.13] and its proof that $\mathbb {Q}(\Pi _f)$ is a number field containing $\mathbb {Q}(E_\mu )$. For a detailed exposition of the latter assertion, we refer to [13, Theorem 8. 1] and the proof of [13, Corollary 8.7]. $\square$

Definition 3.4

The $\mathbb {Q}(\Pi _f)$-structure on $H^{t}(\mathfrak {m}_G,K^\circ _\infty ,\Pi \otimes E_\mu )[\epsilon ]$ is unique up to homotheties, i.e., up to multiplication by non-zero complex numbers, cf. [7, Proposition 3.1]. As $\mathbb {Q}(E_\mu )\subseteq \mathbb {Q}(\Pi _f)$, we may fix the $\mathbb {Q}(\Pi _f)$-structure on $H^{t}(\mathfrak {m}_G,K^\circ _\infty ,\Pi \otimes E_\mu )[\epsilon ]$ which is induced by $\Delta ^t_\Pi$, cf. (3.2), and our choice of a $\mathbb {Q}(E_\mu )$-structure on $H_c^t(\mathcal {S}_G,\mathcal {E}_\mu )$, cf Sect. 2.5.

3.3 Lifts from $\mathrm{SO}(2n+1)$

We resume the assumptions made on $\Pi$ from Sect. 3.1. As a last part of notation for $\Pi$, let us introduce $S=S(\Pi ,\psi )$, which is a (sufficiently large) finite set of places of F, containing $S_\infty$ and such that outside S, both $\Pi$ and $\psi$ are unramified.

Proposition 3.5

Let $\Pi$ be a cuspidal automorphic representation of $G(\mathbb {A})$ as in Sect. 3.1 above. Then the following assertions are equivalent:

• 1. The partial exterior square L-function, $L^S(s,\Pi ,\Lambda ^2)$, has a pole at $s=1$,

• 2. $\Pi$ is the lift of an irreducible unitary generic cuspidal automorphic representation of the split special orthogonal group $\mathrm{SO}(2n+1)$ in the sense of [8, §1].

Proof

With our assumptions on $\Pi$ this is [8, Theorem 7.1]. $\square$

This result is recalled for convenience, as it provides an alternative description of what it means that the exterior square L-function of $\Pi$ has a pole at $s=1$. We will have to make this assumption later, in order to obtain our main theorems. See, Theorems 6.1, 7.4, 9.2, and 10.1. It is not referred to until Sect. 6.4. In any case, the above result is accompanied by

Proposition 3.6

Let $\Pi$ be a cuspidal automorphic representation of $G(\mathbb {A})$ as in Sect. 3.1. Assume that $\Pi$ satisfies the equivalent conditions of Proposition 3.5, i.e., the partial exterior square L-function, $L^S(s,\Pi ,\Lambda ^2)$, has a pole at $s=1$. Then, for all $\sigma \in \mathrm{Aut}(\mathbb {C})$, ${}^\sigma \Pi$ is a cuspidal automorphic representation of $G(\mathbb {A})$ as in Sect. 3.1, which satisfies the equivalent conditions of Proposition 3.5, i.e., the partial exterior square L-function, $L^S(s,{}^\sigma \Pi ,\Lambda ^2)$, has a pole at $s=1$.

Proof

The first assertion has already been proved in Proposition 3.3. For the second assertion, observe that the set S does not change under the action of Aut$(\mathbb {C})$ and then combine [14, Theorem 3.6.2] and [20, Theorem 1, p. 213]. $\square$

4 Top-degree periods

4.1 The map $W^\sigma$

Recall the unique Whittaker model $\mathcal {W}^{\psi _f}(\Pi _f)=\otimes '_{v\notin S_\infty }\mathcal {W}^{\psi _v}(\Pi _v)$ of $\Pi _f$, its decomposition being canonical. Given a Whittaker function $\xi _v\in \mathcal {W}^{\psi _v}(\Pi _v)$ on $G(F_v)$, $v\notin S_\infty$, and $\sigma \in$ Aut$(\mathbb {C})$, we may define a Whittaker function ${}^{\sigma }\xi _v\in \mathcal {W}^{\psi _v}({}^\sigma \Pi _v)$ by

$$\begin{aligned} {}^{\sigma }\xi _v(g_v): = \sigma (\xi _v({\varvec{{t}}}_{\sigma ,v}\cdot g_v)), \end{aligned}$$

(4.1)

where ${\varvec{{t}}}_{\sigma ,v}$ is the (uniquely determined) diagonal matrix in $G(\mathcal {O}_v)$, having 1 as its last entry, which conjugates $\psi _v$ to $\sigma \circ \psi _v$. (Observe that ${\varvec{{t}}}_{\sigma ,v}$ does not depend on $\psi _v$). See [26, 3.3] and [30, 3.2]. This provides us a $\sigma$-linear intertwining operator

$$\begin{aligned} W^\sigma :\mathcal {W}^{\psi _v}(\Pi _v)\rightarrow & {} \mathcal {W}^{\psi _v}({}^\sigma \Pi _v)\\ \xi _v\mapsto & {} {}^\sigma \xi _v, \end{aligned}$$

for all $\sigma \in$ Aut$(\mathbb {C})$. In particular, we get a $\mathbb {Q}(\Pi _v)$ structure on $\mathcal {W}^{\psi _v}(\Pi _v)$ by taking the subspace of Aut$(\mathbb {C}/\mathbb {Q}(\Pi _v))$-invariant vectors. By the same procedure, we obtain a canonical $\mathbb {Q}(\Pi _f)$ structure on $\mathcal {W}^{\psi _f}(\Pi _f)$. (Cf. [15, p. 80], [26, 3.3] or [30, Lemma 3.2].)

4.2 The map $F^t_\Pi$

Let $\epsilon _0:=((-1)^{n-1},\ldots ,(-1)^{n-1})\in \pi _0(G_\infty )^*$. This choice of a character of the component group is forced upon us by the proof of Theorem 7.1 and so we restrict our attention from now on to it.

Recall the $\mathbb {Q}(\Pi _f)$-rational structure on $H^{t}(\mathfrak {m}_G,K^\circ _\infty ,\Pi \otimes E_\mu )[\epsilon _0]$, chosen in Definition 3.4 above and recall the canonical $\mathbb {Q}(\Pi _f)$-rational structure on the Whittaker model $\mathcal {W}^{\psi _f}(\Pi _f)$ of $\Pi _f$ just fixed in Sect. 4.1 above. As it has been mentioned briefly in the introduction, our top-degree Whittaker period—in abbreviated symbol $p^t(\Pi )$—will be determined by the comparison of these two rational structures. Hence, in order to actually compare them, we have to specify a concrete comparison isomorphism

$$\begin{aligned} F^t_\Pi :\mathcal {W}^{\psi _f}(\Pi _f){\mathop {\longrightarrow }\limits ^{\sim }}H^{t}(\mathfrak {m}_G,K^\circ _\infty ,\Pi \otimes E_\mu )[\epsilon _0]. \end{aligned}$$

It is the purpose of this section to explain this choice carefully, as it is all crucial for the definition of our periods. Our choices will be guided by the ideas in [15, p. 79], [26, 3.3 & 5.1.4], [29, 3.2.5], and [14, 4.1].

The first data we will fix once and for all consists of

Choice 4.2

• 1. A basis $\{X_j\}$ of $\mathfrak {m}_G/\mathfrak {k}_\infty$, which fixes the dual-basis $\{X_j^*\}$ of $\left( \mathfrak {m}_G/\mathfrak {k}_\infty \right) ^*$; given a multi-index $\underline{i}=(i_1,\ldots ,i_{t})$, we abbreviate $X^*_{\underline{i}}:=X^*_{i_1}\wedge \cdots \wedge X^*_{i_t}$.

• 2. Vectors $e_\alpha :=\otimes _{v\in S_\infty } e_{\alpha ,v}\in E_\mu =\otimes _{v\in S_\infty }E_{\mu _v}$, such that $\{e_{\alpha ,v}\}_{\alpha }$ defines a basis of $E_{\mu _v}$ for all $v\in S_\infty$.

• 3. For each $v\in S_\infty$, mulit-index $\underline{i}=(i_1,\ldots ,i_{t})$ and $\alpha$ as above a Whittaker function $\xi ^{\epsilon _0}_{v,\underline{i}, \alpha }\in \mathcal {W}^{\psi _v}(\Pi _v)$, such that (putting $\xi ^{\epsilon _0}_{\infty ,\underline{i}, \alpha }:=\otimes _{v\in S_\infty } \xi ^{\epsilon _0}_{v,\underline{i}, \alpha }\in \mathcal {W}^{\psi _\infty }(\Pi _\infty )$) the vector

  $$\begin{aligned}{}[\mathcal {W}^{\psi _\infty }(\Pi _\infty )]^t:=\sum _{\underline{i}=(i_1,\ldots ,i_{t})}\sum _{\alpha =1}^{\dim E_\mu } X^*_{\underline{i}}\otimes \xi ^{\epsilon _0}_{\infty ,\underline{i}, \alpha }\otimes e_\alpha , \end{aligned}$$

  is a generator of the one-dimensional space $\mathbb {C}$-vector space $H^{t}(\mathfrak {m}_G,K^\circ _\infty ,\mathcal {W}^{\psi _\infty }(\Pi _\infty )\otimes E_\mu )[\epsilon _0]$. (We may and will also assume that $\{X_j\}$ is the extension of a given ordered basis $\{Y_j\}$ of $\mathfrak {m}_H/\mathfrak {k}_{H,\infty }$ along our embedding $J:H\hookrightarrow G$. This assumption, however, will only be important later on. See, e.g., Sects. 5.2 and 7.1.)

By [5, II. Proposition 3.1] and the uniqueness of the archimedean Whittaker model and its canonical decomposition into local factors $\mathcal {W}^{\psi _\infty }(\Pi _\infty )=\otimes _{v\in S_\infty } \mathcal {W}^{\psi _v}(\Pi _v)$ this generator $[\mathcal {W}^{\psi _\infty }(\Pi _\infty )]^t$ is well-defined. For the sake of readability we suppress its various dependencies, listed in Choice 4.2 above, in its notation.

Next recall (e.g. from Sect. 2.5) that $\sigma \in \mathrm{Aut}(\mathbb {C})$ acts on objects at infinity, which are parameterized by $S_{\infty }$, by permuting the archimedean places. Having given a generator $[\mathcal {W}^{\psi _\infty }(\Pi _\infty )]^t$ of the one-dimensional space $H^{t}(\mathfrak {m}_G,K^\circ _\infty ,\mathcal {W}^{\psi _\infty }(\Pi _\infty )\otimes E_\mu )[\epsilon _0]$ hence provides us with a natural choice of a generator $[\mathcal {W}^{\psi _\infty }({}^\sigma \Pi _\infty )]^t$ of $H^{t}(\mathfrak {m}_G,K^\circ _\infty ,\mathcal {W}^{\psi _\infty }({}^\sigma \Pi _\infty )\otimes {}^\sigma \!E_\mu )[\epsilon _0]$:

$$\begin{aligned} \left[ \mathcal {W}^{\psi _\infty }({}^\sigma \Pi _\infty )\right] ^t:=\sum _{\underline{i}=(i_1,\ldots ,i_{t})}\sum _{\alpha =1}^{\dim E_\mu } X^*_{\underline{i}}\otimes {}^\sigma \xi ^{\epsilon _0}_{\infty ,\underline{i}, \alpha }\otimes {}^\sigma \! e_\alpha , \end{aligned}$$

where ${}^\sigma \xi ^{\epsilon _0}_{\infty ,\underline{i}, \alpha }=\otimes _{v\in S_\infty } \xi ^{\epsilon _0}_{\sigma ^{-1} v,\underline{i}, \alpha }$ (observe that $\epsilon _0$ does not change, when its local components are permuted) and ${}^\sigma \! e_\alpha =\otimes _{v\in S_\infty } e_{\alpha ,\sigma ^{-1} v}$.

Finally, this entails the description of the desired “comparison isomorphism” mentioned at the beginning of this subsection, i.e., of a fixed choice of isomorphism of $G(\mathbb {A}_f)$-modules defined by

$$\begin{aligned}&F^t_\Pi :\mathcal {W}^{\psi _f}(\Pi _f){\mathop {\longrightarrow }\limits ^{\sim }}H^{t}(\mathfrak {m}_G,K_{\infty }^\circ , \Pi \otimes \!E_{\mu })[\epsilon _0]\\&\xi _f\mapsto F^t_\Pi (\xi _f):=\sum _{\underline{i}=(i_1,\ldots ,i_{t})}\sum _{\alpha =1}^{\dim E_\mu } X^*_{\underline{i}}\otimes \varphi _{\underline{i}, \alpha }\otimes e_\alpha , \end{aligned}$$

where $\varphi _{\underline{i}, \alpha }:=(W^\psi )^{-1}(\xi ^{\epsilon _0}_{\infty ,\underline{i}, \alpha }\otimes \xi _f)\in \Pi$. It is important to observe that we did not have to decompose the global map $W^\psi$ computing the $\psi$-Fourier coefficient, hence there are no hidden ambiguities in this definition: A complete set of dependencies of our comparison isomorphism $F^t_\Pi$ is hence given by Choice 4.2. In light of Proposition 3.3 and our discussion above, we obtain isomorphisms $F^t_{{}^\sigma \Pi }$ for all $\sigma \in$ Aut$(\mathbb {C})$ with the same precise set of dependencies.

4.3 The map $H^{\sigma ,t}_\mu$

As a last ingredient in this section, we define a $\sigma$-linear, $G(\mathbb {A}_f)$-equivariant isomorphism

$$\begin{aligned} H^{\sigma ,t}_\mu :H^{t}(\mathfrak {m}_G,K_{\infty }^\circ , \Pi \otimes E_{\mu })[\epsilon _0]{\mathop {\longrightarrow }\limits ^{\sim }}H^{t}(\mathfrak {m}_G,K_{\infty }^\circ , {}^\sigma \Pi \otimes {}^\sigma \! E_\mu )[\epsilon _0]. \end{aligned}$$

To that end, recall the embedding $\Delta ^q_{\Pi }$ from (3.2) and the $\sigma$-linear isomorphism $\mathcal H^{\sigma ,q}_\mu$ from (2.1). Observe that Im$(\mathcal H^{\sigma ,t}_\mu \circ \Delta ^t_\Pi )=$Im$(\Delta ^t_{{}^\sigma \Pi })$. Indeed, by multiplicity one and strong multiplicity one for the discrete automorphic spectrum of $G(\mathbb {A})$, the ${}^\sigma \Pi _f$-isotypic component of the $G(\mathbb {A}_f)$-module $H^t_c(\mathcal {S}_G,{}^\sigma \!\mathcal {E}_\mu )$ is precisely the image of $H^t(\mathfrak {m}_G,K^\circ _\infty ,{}^\sigma \Pi \otimes {}^\sigma \!E_\mu )$. As the natural action of $\pi _0(G_\infty )$ and of $G(\mathbb {A}_f)$ on $H^t_c(\mathcal {S}_G,\mathcal {E}_\mu )$ commute, this shows that Im$(\mathcal H^{\sigma ,t}_\mu \circ \Delta ^t_\Pi )=$Im$(\Delta ^t_{{}^\sigma \Pi })$ as claimed. Since $\Delta ^t_{{}^\sigma \Pi }$ is injective, the map

$$\begin{aligned} H^{\sigma ,t}_\mu :=(\Delta ^t_{{}^\sigma \Pi })^{-1}\circ \mathcal H^{\sigma ,t}_\mu \circ \Delta ^t_\Pi \end{aligned}$$

is hence a well-defined $\sigma$-linear, $G(\mathbb {A}_f)$-equivariant isomorphism mapping$H^{t}(\mathfrak {m}_G,K_{\infty }^\circ , \Pi \otimes E_{\mu })[\epsilon _0]$ onto $H^{t}(\mathfrak {m}_G,K_{\infty }^\circ , {}^\sigma \Pi \otimes {}^\sigma \! E_\mu )[\epsilon _0]$ as desired. (Shortly speaking, this amounts to say that the restriction $H^{\sigma ,t}_\mu$ of $\mathcal H^{\sigma ,t}_\mu$ to the submodule $H^{t}(\mathfrak {m}_G,K_{\infty }^\circ , \Pi \otimes E_{\mu })[\epsilon _0]$ of $H^t_c(\mathcal {S}_G,\mathcal {E}_\mu )$ has image $H^{t}(\mathfrak {m}_G,K_{\infty }^\circ , {}^\sigma \Pi \otimes {}^\sigma \! E_\mu )[\epsilon _0]$.)

4.4 Top-degree Whittaker periods

Recall the maps $W^\sigma$ (Sect. 4.1), $F^t_\Pi$ (Sect. 4.2) and $H^{\sigma ,t}_\mu$ (Sect. 4.3). There is the following result:

Proposition 4.3

For every $\sigma \in {Aut }(\mathbb {C})$, there is a non-zero complex number $p^t({}^\sigma \Pi )$ (a “period”), uniquely determined up to multiplication by elements in $\mathbb {Q}({}^\sigma \Pi _f)^\times$, such that the normalized maps $\mathcal F^t_{{}^\sigma \Pi }:=p^t({}^\sigma \Pi )^{-1} F^t_{{}^\sigma \Pi }$ make the following diagram commutative:

Proof

This is essentially due to the uniqueness of essential vectors for $\Pi _v$, $v\notin S_\infty$: Otherwise put, the proof of Proposition/Definition 3.3 in Raghuram–Shahidi [30] goes through word for word in our (slightly different) situation at hand. $\square$

Remark 4.4

A lot of choices have been made in order to give the definition of our top-degree Whittaker periods, while (almost) none of them is reflected explicitly in our choice of notation “$p^t(\Pi )$”. So, for the sake of precision, we would like to summarize comprehensively at one place on which data, i.e., fixed chosen ingredients, $p^t(\Pi )$ actually depends:

• 1. $\Pi$, $\psi$ and the cohomological degree t.

• 2. The fixed concrete choices of a $\mathbb {Q}(\Pi _f)$-rational structure on the canonical Whittaker model $\mathcal {W}^{\psi _f}(\Pi _f)$ (Sect. 4.1) and on $H^{t}(\mathfrak {m}_G,K_{\infty }^\circ , \Pi \otimes E_{\mu })[\epsilon _0]$ (Definition 3.4).

• 3. The concrete choice of a comparison isomorphism $F^t_\Pi$ (Sect. 4.2), which depends itself precisely on the data fixed in Choice 4.2.

• 4. The $\sigma$-linear intertwining operator $W^\sigma :\mathcal {W}^{\psi _v}(\Pi _v)\rightarrow \mathcal {W}^{\psi _v}({}^\sigma \Pi _v)$ defined unambiguously in Sect. 4.1 and

• 5. The $\sigma$-linear intertwining operator $H^{\sigma ,t}_\mu$ defined unambiguously in Sect. 4.3.

The (Whittaker) periods $p^t(\Pi )$ defined by Proposition 4.3 are the analogues of the (Shalika) periods $\omega ^\epsilon (\Pi _f)$ defined in Grobner–Raghuram DefinitionProposition 4.2.1. The idea behind the construction of $p^t(\Pi )$ (as of $\omega ^\epsilon (\Pi _f)$), however, goes back to [15, 26, 30].

5 An Aut$(\mathbb {C})$-rational assignment for Whittaker functions

5.1 The map $T_\mu$

Let $E_\mu =\otimes _{v\in S_\infty }E_{\mu _v}$ be an irreducible, algebraic representation as in Sect. 2.3. We have $\dim _\mathbb {C}\mathrm{Hom}_{H(\mathbb {C})}(E_{\mu _v},\mathbb {C})=1$ for all $v\in S_\infty$. Let us fix $T_{\mu _v}\in \mathrm{Hom}_{H(\mathbb {C})}(E_{\mu _v},\mathbb {C})$ and set $T_\mu :=\otimes _{v\in S_\infty }T_{\mu _v}\in \mathrm{Hom}_{R_{F/\mathbb Q}(H)(\mathbb C)}(E_{\mu },\mathbb {C})$. For $\sigma \in$Aut$(\mathbb {C})$, we obtain $T_{{}^\sigma \! \mu }=\otimes _{v\in S_\infty }T_{\mu _{\sigma ^{-1}v}}\in \mathrm{Hom}_{R_{F/\mathbb {Q}(H)(\mathbb {C})}}({}^\sigma \!E_{\mu },\mathbb {C})$. The map induced on cohomology,

$$\begin{aligned} H^t_c(\tilde{\mathcal {S}}_H,{}^\sigma \!\mathcal {E}_\mu )\rightarrow H^t_c(\tilde{\mathcal {S}}_H,\mathbb {C}) \end{aligned}$$

will be denoted by the same letter $T_{{}^\sigma \! \mu }$.

5.2 The de-Rham-isomorphism $\mathcal R$

So far, we have not made any choice of a Haar measure on $H(\mathbb {A}_f)$. From this section on, we will restrict our possible choices on $\mathbb {Q}$-valued Haar measures on $H(\mathbb {A}_f)$. In Sect. 6.3 we will specify our concrete choice of a measure in details. (So far, this is not necessary.) Let $dh_f$ be any $\mathbb {Q}$-valued Haar measure of $H(\mathbb {A}_f)$. It is important to notice that we have $\dim _\mathbb {R}\tilde{\mathcal {S}}_H=dn(n+1)-1=t$, cf. Sect. 3.1, because we assumed that F is totally real. Knowing this, a short moment of thought shows that we obtain a surjective map $\mathcal R: H^t_c(\tilde{\mathcal {S}}_H,\mathbb {C})\rightarrow \mathbb {C}$, induced by the de Rham-isomorphism: Indeed, let $K_{f}$ be a compact open subgroup of $H(\mathbb {A}_f)$ and set

$$\begin{aligned} \tilde{\mathcal {S}}^{K_{f}}_H:=H(F){\backslash } H(\mathbb {A})/A_G K^\circ _{H,\infty } K_{f}. \end{aligned}$$

Then it is easy to see that $\tilde{\mathcal {S}}_H$ is homeomorphic to the projective limit

$$\begin{aligned} \tilde{\mathcal {S}}_H\cong \varprojlim _{K_{f}} \tilde{\mathcal {S}}^{K_{f}}_H \end{aligned}$$

running over the compact open subgroups $K_{f}$ of $H(\mathbb {A}_f)$, partially ordered by opposite inclusion, [31, Proposition 1.9]. As $\dim _\mathbb {R}\tilde{\mathcal {S}}^{K_{f}}_H=t$ for all $K_f$, we may use the de-Rham-isomorphism to define a surjective map $H^t_c(\tilde{\mathcal {S}}^{K_f}_H,\mathbb {C})\rightarrow \mathbb {C}$. More precisely, each of the (finitely many, cf. [3, Theorem 5.1]) connected components of $\tilde{\mathcal {S}}^{K_f}_H$ is homeomorphic to a quotient of $H^\circ _\infty /A_G K^\circ _{H,\infty }$ by a discrete subgroup of H(F). Recall the ordered basis $\{Y_j\}$ of $\mathfrak {m}_H/\mathfrak {k}_{H,\infty }$, from Sect. 4.2. It determines a choice of an orientation on $H^\circ _\infty /A_G K^\circ _{H,\infty }$, whence on each connected component of $\tilde{\mathcal {S}}^{K_f}_H$ and so finally also on $\tilde{\mathcal {S}}^{K_f}_H$. Hence, the de-Rham-isomorphism provides us a surjection

$$\begin{aligned} R^{K_f}: H^t_c(\tilde{\mathcal {S}}^{K_f}_H,\mathbb {C})\rightarrow \mathbb {C}. \end{aligned}$$

The normalized maps, $\mathcal R^{K_f}:=\mathrm{vol}_{dh_f}(K_f)\cdot R^{K_f}$ form a system of compatible maps with respect to the pull-backs, given by the coverings $\tilde{\mathcal {S}}^{K_{f}}_H\twoheadrightarrow \tilde{\mathcal {S}}^{K'_{f}}_H$, $K_f\subseteq K'_f$. Hence, taking the inductive limit, we obtain a surjection $\varinjlim _{K_f}\mathcal R^{K_f}:\varinjlim _{K_f} H^t_c(\tilde{\mathcal {S}}^{K_f}_H,\mathbb {C})\rightarrow \mathbb {C}.$ Since $H^t_c(\tilde{\mathcal {S}}_H,\mathbb {C})\cong \varinjlim _{K_f} H^t_c(\tilde{\mathcal {S}}^{K_f}_H,\mathbb {C})$, see [31, Corollary 2.12], this finally defines a surjection

$$\begin{aligned} \mathcal R:H^t_c(\tilde{\mathcal {S}}_H,\mathbb {C})\rightarrow \mathbb {C}, \end{aligned}$$

as mentioned above. (Compare this also to the considerations in [14, 6.4], [11, 3.8], [12, 5.1] and [29, 3.2.3] as well as to the corresponding references therein.)

5.3 In summary: a rational diagram

In the following proposition, we abbreviate $H^t(\mathfrak {m}_G,K^\circ _\infty ,\Pi \otimes E_\mu )[\epsilon _0]$ by $H^t(\Pi \otimes E_\mu )[\epsilon _0]$ (with analogous notation for the cohomology of the $\sigma$-twisted representations). Recollecting what we observed in Sects. 4.1–5.2, we find

Proposition 5.1

The following diagram is commutative:

(5.2)

Its horizontal arrows are linear, whereas its vertical arrows are $\sigma$-linear.

Proof

The first square from the left is commutative by Proposition 4.3, while the second square is commutative by the definition of $H^{\sigma ,t}_\mu$ in Sect. 4.3. Commutativity of the third square is the assertion of Lemma 2.7. The fourth square commutes by the very definition of $T_{{}^\sigma \!\mu }$ in Sect. 5.1, while commutativity of the last square is due to the $\mathbb {Q}$-rationality of the measure on $H(\mathbb {A}_f)$, Sect. 5.2. $\square$

6 An integral representation of the residue of the exterior square L-function

In this section, we will recapitulate some results from Jacquet–Shalika [21] and Bump–Friedberg [6].

6.1 Eisenstein series and a result of Jacquet–Shalika

We resume the notation and assumptions made in the previous sections. In addition, for any integer $m\ge 2$, we will now fix once and for all a Schwartz–Bruhat function $\Phi =\otimes _v\Phi _v\in \mathscr {S}(\mathbb {A}^m)$: We assume that $\Phi _v$ is the characteristic function of $\mathcal {O}^m_v$ at all $v\notin S_\infty$, while at the archimedean places $v\in S_\infty$, we assume to have chosen (O(m)-finite) local components $\Phi _v$, such the global Schwartz–Bruhat function $\Phi$ satisfies $\hat{\Phi }(0)\ne 0$. Here, we wrote

$$\begin{aligned} \hat{\Phi }(x):=\int _{\mathbb {A}^m}\Phi (y) \psi ({}^t y \cdot x)dy \end{aligned}$$

for the Fourier transform of $\Phi$ (at x) with respect to the self-dual Haar measure dy on $\mathbb {A}^m$, i.e., the unique Haar measure on $\mathbb {A}^m$ which satisfies $\hat{\hat{\Phi }}(x)=\Phi (-x)$ for all $x\in \mathbb {A}^m$. Let

$$\begin{aligned} f_{v,s}(g_v):=|\det (g_v)|^s_v\int _{F^\times _v}\Phi _v(t\cdot (0,\ldots ,0,1)g_v)|t|^{ms}_vd^\times t \end{aligned}$$

and

$$\begin{aligned} f_s(g):=\otimes _v f_{v,s}(g_v)=\Vert \det (g)\Vert ^s\int _{\mathbb {A}^\times }\Phi (t\cdot (0,\ldots ,0,1)g)\Vert t\Vert ^{ms}d^\times t \end{aligned}$$

for $\mathfrak {R}e(s)\gg 0$. Then $f_s\in \mathrm{Ind}^{\mathrm{GL}_m(\mathbb {A})}_{\mathrm{GL}_{m-1}(\mathbb {A})\times \mathrm{GL}_1(\mathbb {A})}[\delta ^s_P]$, (unnormalised parabolic induction) where

$$\begin{aligned} \delta _P\left( \!\!\left( \!\! \begin{array}{ccc} h &{} 0\\ 0 &{} a \end{array}\!\!\right) \!\!\right) =\Vert \det (h)\Vert \cdot \Vert a\Vert ^{-(m-1)} \end{aligned}$$

is the modulus character of the standard parabolic subgroup P of $\mathrm{GL}_m$, with Levi subgroup $L=\mathrm{GL}_{m-1}\times \mathrm{GL}_1$. Clearly, the analogous assertion holds for the local components $f_{v,s}$. There is the following result due to Jacquet–Shalika [21, Lemma 4.2].

Lemma 6.2

The Eisenstein series associated with $f_s$, formally defined as

$$\begin{aligned} E(f_s,\Phi )(g):=\sum _{\gamma \in P(F){\backslash } \mathrm{GL}_m(F)}f_s(\gamma g), \end{aligned}$$

extends to a meromorphic function on $\mathfrak {R}e(s) > 0$. It has a simple pole at $s=1$ with constant residue

$$\begin{aligned} \mathrm{Res}_{s=1}(E(f_s,\Phi ))(g)= c_m\cdot \hat{\Phi }(0). \end{aligned}$$

Here, $c_m$ is a certain non-zero complex number.

6.2 Measures

When dealing with rationality results of special values of L-functions, the choice of measures is all-important. In this section, we specify our choices of measures, which will be guided by the explicit choices made in Bump–Friedberg [6].

Let $m\ge 2$ be again any integer and consider the group $\mathrm{GL}_m/F$. A measure dg of $\mathrm{GL}_m(\mathbb {A})$ will be a product $dg=\prod _v dg_v$ of local Haar measures of $\mathrm{GL}_m(F_v)$. We write $dg^{BF}_v$ for the local Haar measure of $\mathrm{GL}_m(F_v)$ chosen in Bump–Friedberg [6]. See loc. cit. (3.2), p. 61. At $v\notin S_\infty$, these measures assign rational volumes to compact open subgroups of $\mathrm{GL}_m(F_v)$. Furthermore, the product measure $dg^{BF}_f:=\prod _{v\notin S_\infty }dg^{BF}_v$ gives rational volumes to compact open subgroups of $\mathrm{GL}_m(\mathbb {A}_f)$.

At $v\notin S_\infty$, we define our choice of a measure to be the one of Bump–Friedberg,

$$\begin{aligned} dg_v:=dg^{BF}_v \end{aligned}$$

whereas at an archimedean place $v\in S_\infty$, we let $dg_v$ be the local Haar measures of $\mathrm{GL}_m(\mathbb {R})$ such that SO(m) has volume 1. If we let $m=2n$ as in Sect. 2.2, we hence have chosen a measure dg on $G(\mathbb {A})=\mathrm{GL}_{2n}(\mathbb {A})$.

Recall the group $H=\mathrm{GL}_n\times \mathrm{GL}_n$, Sect. 2.2. We will use the notation $(g,g')$, to specify an element of $H(\mathbb {A})$ (and use analogous notation locally). A measure of $H(\mathbb {A})$ will be the product of a measures dg and $dg'$ as chosen above for $m=n$ of the two isomorphic copies of $\mathrm{GL}_n(\mathbb {A})$ inside $H(\mathbb {A})$. As $Z\subset H$, also the volume $\mathrm{vol}_{dg\times dg'}(Z(F){\backslash } Z(\mathbb {A})/A_G)$ is well-defined and finite.

6.3 A result of Bump–Friedberg

Let $U_n$ be the group of upper triangular matrices in $\mathrm{GL}_n$, having 1 on the diagonal and let $Z_n$ be the centre of $\mathrm{GL}_n$. Recall the finite set of places $S=S(\Pi ,\psi )$ from Sect. 3.4. By assumption, outside S, both $\Pi$ and $\psi$ are unramified (and $\psi$ normalised). Let $\xi =\otimes _v\xi _v\in \mathcal {W}^\psi (\Pi )\cong \otimes _v\mathcal {W}^{\psi _v}(\Pi _v)$ be a Whittaker function, such that for $v\notin S$, $\xi _v$ is invariant under $G(\mathcal {O}_v)$ and normalized such that $\xi _v(id_v)=1$. Recall the section $f_s=\otimes _v f_{v,s}$ from Sect. 6.1, defined by the choice of a Schwartz–Bruhat function $\Phi =\otimes _v\Phi _v$, where we now let $m=n$. Following Bump–Friedberg [6, p. 53], we define the integral

$$\begin{aligned} Z(\xi ,f_{s}):=\int _{U_n(\mathbb {A}){\backslash }\mathrm{GL}_n(\mathbb {A})}\int _{Z_n(\mathbb {A})U_n(\mathbb {A}){\backslash }\mathrm{GL}_n(\mathbb {A})}\xi (J(g,g'))\ f_{s}(g) \ dg \ dg'. \end{aligned}$$

It factors over all places of F as $Z(\xi ,f_s)=\prod _v Z_v(\xi _v,f_{v,s})$, where

$$\begin{aligned} Z_v(\xi _v,f_{v,s}):=\int _{U_n(F_v){\backslash }\mathrm{GL}_n(F_v)}\int _{Z_n(F_v)U_n(F_v){\backslash }\mathrm{GL}_n(F_v)}\xi _v(J(g_v,g'_v)) \ f_{v,s}(g_v) \ dg_v \ dg'_v. \end{aligned}$$

Recall the value $L^S(n,{\mathbf {1}})$ of the partial L-function of the trivial character ${\mathbf {1}}$ of $\mathbb {A}^\times$ at n. Since we assumed that $n\ge 2$, this number is well-defined and non-zero. The following result is crucial for us:

Theorem 6.1

Let $\Pi$ be a cuspidal automorphic representation of $G(\mathbb {A})$ as in Sect. 3.1. Let $\varphi :=(W^{\psi })^{-1}(\xi )\in \Pi$ be the inverse image of a Whittaker function $\xi$ as in Sect. 6.4 above and assume that $\Pi$ satisfies the equivalent conditions of Proposition 3.5, i.e., the partial exterior square L-function, $L^S(s,\Pi ,\Lambda ^2)$, has a pole at $s=1$. Then,

$$\begin{aligned}&c_n\cdot \hat{\Phi }(0) \int _{Z(\mathbb {A})H(F){\backslash } H(\mathbb {A})}\varphi (J(g,g')) \ dg \ dg'\\&\quad = \frac{L^S(\tfrac{1}{2},\Pi )\cdot \mathrm{Res}_{s=1}(L^S(s,\Pi ,\Lambda ^2))}{L^S(n,{\mathbf {1}})^2}\cdot \prod _{v\in S}\frac{Z_v(\xi _v,f_{v,1})}{L(n,{\mathbf {1}}_v)}. \end{aligned}$$

(Here, $L^S(\tfrac{1}{2},\Pi )$ is the partial principal L-function of $\Pi$ at $s'=\tfrac{1}{2}$.)

Proof

With our preparatory work, this is a direct consequence of our choice of measures in Sect. 6.3 and the three main results of Bump–Friedberg [6, Theorem 1, Theorem 2 and Theorem 3]. Indeed, our Lemma 6.2 together with [6, Theorem 1 and Theorem 2], identify the left hand side with

$$\begin{aligned} c_n\cdot \hat{\Phi }(0) \int _{Z(\mathbb {A})H(F){\backslash } H(\mathbb {A})}\varphi (J(g,g')) \ dg \ dg' = \mathrm{Res}_{s=1}\left( \frac{Z(\xi ,f_{s})}{L(n,{\mathbf {1}})}\right) , \end{aligned}$$

where $L(n,{\mathbf {1}})=\prod _v L(n,{\mathbf {1}}_v)$ is the global L-function of the trivial character ${\mathbf {1}}$ of $\mathbb {A}^\times$ at n. As by assumption $n\ge 2$, $L(n,{\mathbf {1}})$ is well-defined and non-zero. Factorizing $Z(\xi ,f_{s})$ as in Sect. 6.4, and using the description of $Z_v(\xi _v,f_{v,s})$, $v\notin S$, in [6, Theorem 3],

$$\begin{aligned} Z_v(\xi _v,f_{v,s})=\frac{L(\tfrac{1}{2},\Pi _v)\cdot L(s,\Pi _v,\Lambda ^2)}{L(n,{\mathbf {1}}_v)}, \end{aligned}$$

we obtain

$$\begin{aligned} \mathrm{Res}_{s=1}\left( \frac{Z(\xi ,f_{s})}{L(n,{\mathbf {1}})}\right) =\frac{L^S(\tfrac{1}{2},\Pi )\cdot \mathrm{Res}_{s=1}(L^S(s,\Pi ,\Lambda ^2))}{L^S(n,{\mathbf {1}})^2}\cdot \prod _{v\in S}\frac{Z_v(\xi _v,f_{v,1})}{L(n,{\mathbf {1}}_v)}, \end{aligned}$$

since by assumption $L^S(s,\Pi ,\Lambda ^2)$ carries the (simple) pole of the above expression. $\square$

6.4 Consequences for the $\sigma$-twisted case

Let $\Pi$ be a cuspidal automorphic representation of $G(\mathbb {A})$ as in Sect. 3.1 and assume that the partial exterior square L-function, $L^S(s,\Pi ,\Lambda ^2)$, has a pole at $s=1$. Then by Proposition 3.6, ${}^\sigma \Pi$ satisfies the same conditions. Hence, we see that once $\Pi$ satisfies the assumptions made in Theorem 6.1, then automatically also ${}^\sigma \Pi$ satisfies them, i.e., Theorem 6.1 holds for the whole Aut$(\mathbb {C})$-orbit of $\Pi$.

As we are going to use this in the proof of the main results, let us render this more precise. Let $\xi =\otimes _v\xi _v\in \mathcal {W}^\psi (\Pi )\cong \otimes _v\mathcal {W}^{\psi _v}(\Pi _v)$ be a Whittaker function, such that for $v\notin S$, $\xi _v$ is invariant under $G(\mathcal {O}_v)$ and normalized such that $\xi _v(id_v)=1$. Given $\sigma \in$Aut$(\mathbb {C})$, let ${}^\sigma \xi \in \mathcal {W}^\psi ({}^\sigma \Pi )$ be the $\sigma$-twisted Whittaker function, cf. Sect. 4.1 (the action of $\sigma$ on the archimedean part of $\xi$ being by permutations as in Sect. 4.2), and let ${}^\sigma \!\varphi :=(W^{\psi })^{-1}({}^\sigma \xi )\in {}^\sigma \Pi$ be the corresponding cuspidal automorphic form. Recall our Schwartz–Bruhat function $\Phi \in \mathscr {S}(\mathbb {A}^n)$ from Sect. 6.1, with $m=n$ now. We define the constant

$$\begin{aligned} c_n(\Phi ,\sigma ):=\sigma \left( \frac{\mathrm{vol}_{dg\times dg'}(Z(F){\backslash } Z(\mathbb {A})/A_G)}{c_n\hat{\Phi }(0)}\right) \cdot \frac{c_n\hat{\Phi }(0) }{\mathrm{vol}_{dg\times dg'}(Z(F){\backslash } Z(\mathbb {A})/A_G)}. \end{aligned}$$

This is done purely for cosmetic reasons, as it will become clear below (see the proof of Theorem 7.4). By Sect. 6.1, $c_n(\Phi ,\sigma )$ is non-zero. Let ${}^\sigma \Phi \in \mathscr {S}(\mathbb {A}^n)$ be the Schwartz–Bruhat function which is defined as follows: At $v\notin S_\infty$, $({}^\sigma \Phi )_v:=\Phi _v$, whereas $({}^\sigma \Phi )_\infty := c_n(\Phi ,\sigma )^{-1}\cdot \Phi _\infty$. As in Sect. 6.1, we obtain a function ${}^\sigma \! f_s=\otimes _v {}^\sigma \! f_{v,s}\in \mathrm{Ind}^{\mathrm{GL}_n(\mathbb {A})}_{\mathrm{GL}_{n-1}(\mathbb {A})\times \mathrm{GL}_1(\mathbb {A})}[\delta ^s_P]$ and an associated Eisenstein series $E({}^\sigma \! f_s,{}^\sigma \Phi )$. Clearly, $E({}^\sigma \! f_s,{}^\sigma \Phi )$ satisfies the assertions of Lemma 6.2, with $\Phi$ being replaced by ${}^\sigma \Phi$.

In summary, with this notation, saying that Theorem 6.1 holds for the whole Aut$(\mathbb {C})$-orbit of $\Pi$, amounts to the equation

$$\begin{aligned}&c_n^\sigma \hat{\Phi }(0) \int _{Z(\mathbb {A})H(F){\backslash } H(\mathbb {A})}{}^\sigma \!\varphi (J(g,g')) \ dg \ dg'\nonumber \\&\qquad = \frac{L^S(\tfrac{1}{2}, {}^\sigma \Pi )\cdot \mathrm{Res}_{s=1}(L^S(s,{}^\sigma \Pi ,\Lambda ^2))}{L^S(n,{\mathbf {1}})^2} \prod _{v\in S}\frac{Z_v({}^\sigma \xi _v,{}^\sigma \!f_{v,s})}{L(n,{\mathbf {1}}_v)}.\qquad \quad \end{aligned}$$

(6.2)

7 A rationality result for the exterior square L-function

7.1 Archimedean considerations

The integral representation of the exterior square L-function in Theorem 6.1 allows us to combine the results of Sects. 5 and 6. Before we derive out first main result, we need a non-vanishing theorem, which is an application of Sun’s main result in [35].

Recall the generator $[\mathcal {W}^{\psi _\infty }(\Pi _\infty )]^t=\sum _{\underline{i}=(i_1,\ldots ,i_{t})}\sum _{\alpha =1}^{\dim E_\mu } X^*_{\underline{i}}\otimes \xi ^{\epsilon _0}_{\infty ,\underline{i}, \alpha }\otimes e_\alpha$ of the cohomology space $H^{t}(\mathfrak {m}_G,K^\circ _\infty ,\mathcal {W}^{\psi _\infty }(\Pi _\infty )\otimes E_\mu )[\epsilon _0]$ from Sect. 4.2. Recall furthermore, that the basis $\{X^*_j\}$ of $\mathfrak {m}_G/\mathfrak {k}_\infty$ was the extension of a given ordered basis $\{Y^*_j\}^t_{j=1}$ of $\mathfrak {m}_H/\mathfrak {k}_{H,\infty }$, whence, for each multi-index $\underline{i}$ there is a well-defined complex number $s(\underline{i})$, such that the restriction of $X^*_{\underline{i}}$ to $\Lambda ^t(\mathfrak {m}_H/\mathfrak {k}_{H,\infty })^*$ along the injection $\Lambda ^t(\mathfrak {m}_H/\mathfrak {k}_{H,\infty })^*\hookrightarrow \Lambda ^t(\mathfrak {m}_G/\mathfrak {k}_\infty )^*$, induced by J, equals $s(\underline{i})\cdot Y_1\wedge ..\wedge Y_t$. As a last ingredient, before we can state the aforementioned non-vanishing theorem, we need the following lemma:

Lemma 7.2

For all $v\in S_\infty$, and $K^\circ _v$-finite $\xi _v\in \mathcal {W}^{\psi _v}(\Pi _v)$, the integrals

$$\begin{aligned} Z_v(s',\xi _{v},f_{v,1}):= & {} \int _{U_n(F_v){\backslash }\mathrm{GL}_n(F_v)}\int _{Z_n(F_v)U_n(F_v){\backslash }\mathrm{GL}_n(F_v)}\xi _v(J(g_v,g'_v))\\&\times f_{v,1}(g_v)\Bigg |\frac{\det (g'_v)}{\det (g_v)}\Bigg |_v^{s'-1/2} dg_v dg'_v \end{aligned}$$

are a holomorphic multiple (in $s'$) of the local archimedean L-function $L(s',\Pi _v)$.

Proof

This follows combining Theorem 6.1 with [9], Proposition 2.3 and Proposition 3.1 loc. cit. . $\square$

It follows that the factor $Z_\infty (\xi ^{\epsilon _0}_{\infty ,\underline{i}, \alpha },f_{\infty ,1}):=\prod _{v\in S_\infty }Z_v(\xi ^{\epsilon _0}_{v,\underline{i}, \alpha },f_{v,1})$ of the product $\prod _{v\in S}{Z_v(\xi _v,f_{v,1})}$ is well-defined. Indeed, using [23], Theorem 2 and Theorem 3 loc. cit., it is easy to see that

$$\begin{aligned} L(s',\Pi _v)=h(s')\cdot \prod _{k=1}^n\Gamma \left( s'+\mu _{v,k}+n-k+\tfrac{1}{2}\right) , \end{aligned}$$

where $h(s')$ is holomorphic and non-vanishing for all $s'\in \mathbb {C}$. Since $\mu _{v,k}\ge 0$ for all $1\le k\le n$, by the self-duality hypotheses, cf. Sect. 2.3, $L(s',\Pi _v)$ is holomorphic at $s'=\tfrac{1}{2}$, whence so is $Z_v(\xi ^{\epsilon _0}_{v,\underline{i}, \alpha },f_{v,1})=Z_v(\tfrac{1}{2},\xi ^{\epsilon _0}_{v,\underline{i}, \alpha },f_{v,1})$ by Lemma 7.2. Finally, we let

$$\begin{aligned} c^t(\Pi _\infty ):=(L^S(n,{\mathbf {1}})^2)^{-1} \cdot \sum _{\underline{i}=(i_1,\ldots ,i_{t})}\sum _{\alpha =1}^{\dim E_\mu } s(\underline{i})\cdot T_\mu (e_\alpha )\cdot \frac{Z_\infty \left( \xi ^{\epsilon _0}_{\infty ,\underline{i}, \alpha },f_{\infty ,1}\right) }{L(n,{\mathbf {1}}_\infty )}. \end{aligned}$$

Here, both numbers $L(n,{\mathbf {1}}_\infty )=\prod _{v\in S_\infty }L(n,{\mathbf {1}}_v)=\pi ^{-dn/2}\Gamma (\tfrac{n}{2})^d$ and $L^S(n,{\mathbf {1}})$ are non-zero. We claim that Sun’s aforementioned result now implies the following

Theorem 7.1

The number $c^t(\Pi _\infty )$ is non-zero.

Proof

As a first step and in order to be able to apply Sun’s result ([35], Theorem C), we reduce the problem of showing that $c^t(\Pi _\infty )$ is non-zero to showing that a similarly defined number, $d^t(\Pi _v)$ is non-zero. This latter number will only depend on one archimedean place $v\in S_\infty$, whence we find ourselves back in the setting of [35].

To this end, observe that there is a projection

$$\begin{aligned} L^t:\Lambda ^t(\mathfrak {m}_G/\mathfrak {k}_{\infty })^*{\mathop {\longrightarrow }\limits ^{\sim }}\bigoplus _{a+b=t}\Lambda ^a(\mathfrak {g}_\infty /\mathfrak {c}_\infty )^*\otimes \Lambda ^{b}\mathfrak {s}^*\twoheadrightarrow \Lambda ^r(\mathfrak {g}_\infty /\mathfrak {c}_\infty )^*\otimes \Lambda ^{d-1}\mathfrak {s}^*, \end{aligned}$$

where $\mathfrak {c}_\infty :=\mathfrak {z}_\infty \oplus \mathfrak {k}_\infty$ and $r=t-d+1$. By reasons of degree, $L^t$ induces an isomorphism of (one-dimensional) vector spaces

$$\begin{aligned}&\mathcal L^t: H^{t}(\mathfrak {m}_G,K^\circ _\infty ,\mathcal {W}^{\psi _\infty }(\Pi _\infty )\otimes E_\mu )[\epsilon _0]{\mathop {\longrightarrow }\limits ^{\sim }}\\&~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~H^{r}(\mathfrak {g}_\infty ,(Z_\infty K_\infty )^\circ ,\mathcal {W}^{\psi _\infty }(\Pi _\infty )\otimes E_\mu )[\epsilon _0]\otimes \Lambda ^{d-1}\mathfrak {s}^*_\mathbb {C}, \end{aligned}$$

whose effect on the generator $[\mathcal {W}^{\psi _\infty }(\Pi _\infty )]^t$ is by sending $X_{\underline{i}}^*$ to $L^t(X_{\underline{i}})\in \Lambda ^r(\mathfrak {g}_\infty /\mathfrak {c}_\infty )^*\otimes \Lambda ^{d-1}\mathfrak {s}^*$. Without loss of generality, we write $L^t(X_{\underline{i}})=L_r(X_{\underline{i}})\otimes L_{d-1}(X_{\underline{i}})$, where $L_r(X_{\underline{i}})\in \Lambda ^r(\mathfrak {g}_\infty /\mathfrak {c}_\infty )^*$ and $L_{d-1}(X_{\underline{i}})\in \Lambda ^{d-1}\mathfrak {s}^*$. Similarly, we factor $\mathcal L^t=\mathcal L_r\otimes \mathcal L_{d-1}$.

As $\mathfrak {z}_\infty \subset \mathfrak {h}_\infty$, and as moreover $r=\dim _\mathbb {R}\mathfrak {h}_\infty /\mathfrak {c}_{H,\infty }$, where $\mathfrak {c}_{H,\infty }:=\mathfrak {z}_\infty \oplus \mathfrak {k}_{H,\infty }$, we also have a canonical isomorphism

$$\begin{aligned} \Lambda ^t(\mathfrak {m}_H/\mathfrak {k}_{H,\infty })^*{\mathop {\longrightarrow }\limits ^{\sim }}\Lambda ^r(\mathfrak {h}_\infty /\mathfrak {c}_{H,\infty })^*\otimes \Lambda ^{d-1}\mathfrak {s}^*. \end{aligned}$$

Hence, $L^t$ and $\mathcal L^t$ factor over the injection $\Lambda ^t(\mathfrak {m}_H/\mathfrak {k}_{H,\infty })^*\hookrightarrow \Lambda ^t(\mathfrak {m}_G/\mathfrak {k}_\infty )^*$ induced by J. As a consequence, $c^t(\Pi _\infty )$ is a non-trivial multiple of

$$\begin{aligned} d^t(\Pi _\infty ):=\sum _{\underline{i}=(i_1,\ldots ,i_{t})}\sum _{\alpha =1}^{\dim E_\mu } u(\underline{i})\cdot T_\mu (e_\alpha )\cdot \frac{Z_\infty \left( \xi ^{\epsilon _0}_{\infty ,\underline{i}, \alpha },f_{\infty ,1}\right) }{L(n,{\mathbf {1}}_\infty )}, \end{aligned}$$

where $u(\underline{i})$ is the uniquely defined complex number, such that the restriction of $L_r(X^*_{\underline{i}})$ to $\Lambda ^r(\mathfrak {h}_\infty /\mathfrak {c}_{H,\infty })^*$ equals $u(\underline{i})\cdot L_r(Y_1\wedge ..\wedge Y_t)$. The number $d(^t\Pi _\infty )$ factors as $d^t(\Pi _\infty )=\prod _{v \in S_\infty } d^t(\Pi _v)$, where each local factor $d^t(\Pi _v)$ is defined analogously (using $\Lambda ^r(\mathfrak {h}_\infty /\mathfrak {c}_{H,\infty })^*\cong \bigoplus _{\sum r_v=r}\bigotimes _{v\in S_\infty }\Lambda ^{r_v}(\mathfrak {h}_v/\mathfrak {c}_{H,v})^*$). Therefore, we may finish the proof by showing that $d^t(\Pi _v)$ is non-zero for all $v\in S_\infty$ and we are in the situation considered by Sun [35].

Let $v\in S_\infty$ be an arbitrary archimedean place. For sake of simplicity, we drop the subscript “v” now everywhere, so, e.g., $\Pi =\Pi _v$, $H=GL_n(\mathbb {R})\times GL_n(\mathbb {R})$, $\mu =\mu _v$, $\mathfrak {g}=\mathfrak {gl}_{2n}(\mathbb {R})$ and analogously for all other local archimedean objects. The local integrals $Z(\xi ,f_{1})$ define a non-zero homomorphism

$$\begin{aligned} Z(.,f_1)\in \mathrm{Hom}_H(\mathcal {W}^{\psi }(\Pi ),\mathbb {C}). \end{aligned}$$

This follows from [6], Theorem 2 and Lemma 7.2. Hence, if we let $\chi :={\mathbf {1}}\times {\mathbf {1}}$ be the trivial character of H, then $Z(.,f_1)$ can be taken as the map $\varphi _\chi$ in Sun’s Theorem C [35]. Next, recall $T_\mu \in \mathrm{Hom}_{H(\mathbb {C})}(E_\mu \otimes \mathbb {C})$ from Sect. 5.1. If we set $w_1:=0=:w_2$, then we may take $T_\mu$ to be the non-zero homomorphism $\varphi _{w_1,w_2}$ from [35, Theorem C]. Hence, loc. cit. , Theorem C, asserts that the map

$$\begin{aligned}&D:\mathrm{Hom}(\Lambda ^{r}\mathfrak {g}/\mathfrak {c},\mathcal {W}^{\psi }(\Pi )\otimes E_\mu )\longrightarrow \mathrm{Hom}(\Lambda ^{r}\mathfrak {h}/\mathfrak {c}_H,\chi \otimes \mathbb {C})\\&h\mapsto D(h):=(Z(.,f_1)\otimes T_\mu )\circ h\circ \wedge ^{r}j_{2n} \end{aligned}$$

is non-zero on the one-dimensional sub-space $H^{r}(\mathfrak {g},(ZK)^\circ ,\mathcal {W}^{\psi }(\Pi )\otimes E_\mu )[\epsilon _0].$ (Here, $j_{2n}$ is Sun’s notation for the embedding $\mathfrak {h}/\mathfrak {c}_H\hookrightarrow \mathfrak {g}/\mathfrak {c}$.) By the one-dimensionality of the latter cohomology space, it is hence non-zero on $\mathcal L_r([\mathcal {W}^{\psi }(\Pi )]^t)$. But, then, D computes

$$\begin{aligned} D(\mathcal L_r([\mathcal {W}^{\psi }(\Pi )]^t))= & {} (Z(.,f_1)\otimes T_\mu )\circ \mathcal L_r([\mathcal {W}^{\psi }(\Pi )]^t)\circ \wedge ^{r}j_{2n}\\= & {} \sum _{\underline{i}=(i_1,\ldots ,i_{t})}\sum _{\alpha =1}^{\dim E_\mu } u(\underline{i})\,T_\mu (e_\alpha )\, Z(\xi ^{\epsilon _0}_{\underline{i}, \alpha },f_1)\\= & {} L(n,{\mathbf {1}})\cdot d^t(\Pi ). \end{aligned}$$

Hence, reintroducing the subscript “v”, and recalling that $L(n,{\mathbf {1}}_v)=\pi ^{-n/2}\Gamma (n/2)\ne 0$, the number $d^t(\Pi _v)$ is non-zero for all archimedean places, whence so is $c^t(\Pi _\infty )$.

$\square$

7.2 Definition of the archimedean top-degree period

As a consequence of Proposition 3.6, we may hence define the archimedean periods

$$\begin{aligned} p^t({}^\sigma \Pi _\infty ):=c^t({}^\sigma \Pi _\infty )^{-1} \end{aligned}$$

(7.2)

for all $\sigma \in$Aut$(\mathbb {C})$.

Remark 7.3

Analogously to the case of the top-degree Whittaker period $p^t(\Pi )$, which we dealt with in Remark 4.4, (almost) none of the various choices entering the definition of our archimedean top-degree period $p^t(\Pi _\infty )$ may be found in its notation. For the sake of precision, we would like to summarize at this place on which data, i.e., fixed chosen ingredients, $p^t(\Pi _\infty )$ actually depends:

• 1. $\Pi _\infty$, $\psi _\infty$, the cohomological degree t, as well as the archimedean measures $dg_v$ and $dg'_v$ chosen for all $v\in S_\infty$ in Sect. 6.3

• 2. The fixed generator $[\mathcal {W}^{\psi _\infty }(\Pi _\infty )]^t$ (cf. Sect. 4.2) of the one-dimensional cohomology space $H^{t}(\mathfrak {m}_G,K^\circ _\infty ,\mathcal {W}^{\psi _\infty }(\Pi _\infty )\otimes E_\mu )[\epsilon _0]$. We remark further that this generator depends itself precisely on the data fixed in Choice 4.2

• 3. The concrete choice of an intertwining operator $T_{\mu _v}\in \mathrm{Hom}_{H(\mathbb {C})}(E_{\mu _v},\mathbb {C})$ for all $v\in S_\infty$ (Sect. 5.1)

• 4. The sections $f_{v,1}\in \mathrm{Ind}^{\mathrm{GL}_{n}(F_v)}_{\mathrm{GL}_{n-1}(F_v)\times \mathrm{GL}_1(F_v)}[\delta _{P(F_v)}]$ chosen unambiguously in Sect. 6.1 for all $v\in S_\infty$.

It is hence clear that the archimedean top-degree period $p^t(\Pi _\infty )$ depends exclusively on data, which is associated with objects at archimedean places (which explains its name); and that its definition and existence is independent of the definition and proof of existence of our global Whittaker periods $p^t(\Pi )$ from Sect. 4.4.

7.3 Rationality of the residue of the exterior square L-function at $s=1$

This is our first main theorem. For the precise definitions of $p^t(\Pi )$ and $p^t(\Pi _\infty )$, a comprehensive list of their individual dependencies as well as for their mutual independence, we refer to Sects. 4.4, 7.3, Remarks 4.4 and 7.3

Theorem 7.4

Let F be a totally real number field and $G=\mathrm{GL}_{2n}/F$, $n\ge 2$. Let $\Pi$ be a unitary cuspidal automorphic representation of $G(\mathbb {A})$ (self-dual and with trivial central character), which is cohomological with respect to an irreducible, self-contragredient, algebraic, finite-dimensional representation $E_\mu$ of $G_\infty$. Assume that $\Pi$ satisfies the equivalent conditions of Proposition 3.5, i.e., the partial exterior square L-function $L^S(s,\Pi ,\Lambda ^2)$ has a pole at $s=1$. Then, for every $\sigma \in \mathrm{Aut}(\mathbb {C})$,

$$\begin{aligned} \sigma \left( \frac{L(\tfrac{1}{2},\Pi _f)\cdot \mathrm{Res}_{s=1}(L^S(s,\Pi ,\Lambda ^2))}{p^t(\Pi ) \ p^t(\Pi _\infty )}\right) \ = \ \frac{L(\tfrac{1}{2},{}^\sigma \Pi _f)\cdot \mathrm{Res}_{s=1}(L^S(s,{}^\sigma \Pi ,\Lambda ^2))}{p^t({}^\sigma \Pi ) \ p^t({}^\sigma \Pi _\infty )}. \end{aligned}$$

In particular,

$$\begin{aligned} L(\tfrac{1}{2},\Pi _f)\cdot \mathrm{Res}_{s=1}(L^S(s,\Pi ,\Lambda ^2)) \ \sim _{\mathbb {Q}(\Pi _f)} \ p^t(\Pi ) \ p^t(\Pi _\infty ), \end{aligned}$$

(7.3)

where “$\sim _{\mathbb {Q}(\Pi _f)}$” means up to multiplication of the right hand side by an element in the number field $\mathbb {Q}(\Pi _f)$.

Proof

Let $\Pi$ be as in the statement of the theorem. We consider the commutative diagram (5.2) in Proposition 5.1: Let

$$\begin{aligned} \Omega :=\mathcal R\circ T_\mu \circ \mathcal J^t_\mu \circ \Delta ^t_\Pi \circ \mathcal F^t_\Pi \end{aligned}$$

be the composition of the upper horizontal arrows, and analogously, let ${}^\sigma \Omega$ be the composition of the lower horizontal arrows. Let $\xi _f=\otimes _{v\notin S_\infty }\xi _v\in \mathcal {W}^{\psi _f}(\Pi _f)\cong \otimes _{v\notin S_\infty }\mathcal {W}^{\psi _v}(\Pi _v)$ be a Whittaker function, such that for $v\notin S$, $\xi _v$ is invariant under $G(\mathcal {O}_v)$ and normalized such that $\xi _v(id_v)=1$. Given $\sigma \in$Aut$(\mathbb {C})$, let $W^\sigma (\xi _f)={}^\sigma \xi _f\in \mathcal {W}^{\psi _f}({}^\sigma \Pi _f)$ be the $\sigma$-twisted Whittaker function, cf. Sect. 4.1. Then, Proposition 5.1 says that

$$\begin{aligned} \sigma (\Omega (\xi _f))={}^\sigma \Omega ({}^\sigma \xi _f). \end{aligned}$$

(7.6)

In order to prove the theorem, we make both sides of this equation explicit. To that end, let $[\mathcal {W}^{\psi _\infty }(\Pi _\infty )]^t$ (resp. $[\mathcal {W}^{\psi _\infty }({}^\sigma \Pi _\infty )]^t$) the generators of the respective cohomology spaces, Sect. 4.2. For each $\underline{i}$ and $\alpha$, let $\varphi _{\underline{i},\alpha }:=(W^{\psi })^{-1}(\xi ^{\epsilon _0}_{\infty ,\underline{i},\alpha }\otimes \xi _f)\in \Pi$ (resp. ${}^\sigma \!\varphi _{\underline{i},\alpha }:=(W^{\psi })^{-1}({}^\sigma \xi ^{\epsilon _0}_{\infty ,\underline{i},\alpha }\otimes {}^\sigma \xi _f)\in {}^\sigma \Pi$) be the corresponding cuspidal automorphic form. Recall our Schwartz-Bruhat function $\Phi \in \mathscr {S}(\mathbb {A}^n)$ (resp. ${}^\sigma \!\Phi \in \mathscr {S}(\mathbb {A}^n)$) from Sect. 6.1 (resp. Sect. 6.5), with $m=n$ now. Inserting these functions into Theorem 6.1 [likewise, also into (6.2)] and recalling the definition of our archimedean periods $p^t(\Pi _\infty )$ and $p^t({}^\sigma \Pi _\infty )$ from (7.2) shows that Eq. (7.6), induced by our Diagram (5.2), may be rewritten as

$$\begin{aligned}&\sigma \left( \frac{\mathrm{vol}_{dg\times dg'}(Z(F){\backslash } Z_(\mathbb {A})/A_G)}{c_n\cdot \hat{\Phi }(0)}\cdot \frac{L^S(\tfrac{1}{2},\Pi )\cdot \mathrm{Res}_{s=1}(L^S(s,\Pi ,\Lambda ^2))}{p^t(\Pi ) \ p^t(\Pi _\infty )} \prod _{v\in S{\backslash } S_\infty }\frac{Z_v(\xi _v,f_{v,s})}{L(n,{\mathbf {1}}_v)}\right) \\&\quad =\frac{\mathrm{vol}_{dg\times dg'}(Z(F){\backslash } Z_(\mathbb {A})/A_G)}{c_n\cdot {}^\sigma \hat{\Phi }(0)}\cdot \frac{L^S(\tfrac{1}{2},{}^\sigma \Pi )\cdot \mathrm{Res}_{s=1}(L^S(s,{}^\sigma \Pi ,\Lambda ^2))}{p^t({}^\sigma \Pi ) \ p^t({}^\sigma \Pi _\infty )}\\&\qquad \prod _{v\in S{\backslash } S_\infty }\frac{Z_v({}^\sigma \xi _v,{}^\sigma \!f_{v,s})}{L(n,{\mathbf {1}}_v)}. \end{aligned}$$

(Recall that $\Pi$ was assumed to have trivial central character.) Invoking our cosmetically tuned choice for ${}^\sigma \Phi \in {\mathscr {S}}({\mathbb {A}}^n)$ from Sect. 6.5, and observing that$L(n,{\mathbf {1}}_v)=(1-|\mathcal {O}_v/\wp _v|^{-n})^{-1}\in \mathbb {Q}^\times$ for $v\in S{\backslash } S_\infty$, this simplifies to

$$\begin{aligned}&\sigma \left( \frac{L^S(\tfrac{1}{2},\Pi )\cdot \mathrm{Res}_{s=1}(L^S(s,\Pi ,\Lambda ^2))}{p^t(\Pi ) \ p^t(\Pi _\infty )} \prod _{v\in S{\backslash } S_\infty }Z_v(\xi _v,f_{v,s})\right) \\&\quad =\frac{L^S(\tfrac{1}{2},{}^\sigma \Pi )\cdot \mathrm{Res}_{s=1}(L^S(s,{}^\sigma \Pi ,\Lambda ^2))}{p^t({}^\sigma \Pi ) \ p^t({}^\sigma \Pi _\infty )} \prod _{v\in S{\backslash } S_\infty }Z_v({}^\sigma \xi _v,{}^\sigma \!f_{v,s}). \end{aligned}$$

Since $\sigma (L(\tfrac{1}{2},\Pi _v))=L(\tfrac{1}{2},{}^\sigma \Pi _v)\ne 0$ for all $v\in S{\backslash } S_\infty$, cf. [29, Proposition 3.17], and recalling once more that $S=S(\Pi ,\psi )=S({}^\sigma \Pi ,\psi )$, we may rewrite this by

$$\begin{aligned}&\sigma \left( \frac{L(\tfrac{1}{2},\Pi _f)\cdot \mathrm{Res}_{s=1}(L^S(s,\Pi ,\Lambda ^2))}{p^t(\Pi ) \ p^t(\Pi _\infty )} \prod _{v\in S{\backslash } S_\infty }Z_v(\xi _v,f_{v,s})\right) \\&\quad =\frac{L(\tfrac{1}{2},{}^\sigma \Pi _f)\cdot \mathrm{Res}_{s=1}(L^S(s,{}^\sigma \Pi ,\Lambda ^2))}{p^t({}^\sigma \Pi ) \ p^t({}^\sigma \Pi _\infty )} \prod _{v\in S{\backslash } S_\infty }Z_v({}^\sigma \xi _v,{}^\sigma \!f_{v,s}). \end{aligned}$$

Observe that $\prod _{v\in S{\backslash } S_\infty }Z_v(\xi _v,f_{v,s})$ (and $\prod _{v\in S{\backslash } S_\infty }Z_v({}^\sigma \xi _v,{}^\sigma \!f_{v,s})$) are non-zero. Indeed, if the finite product $\prod _{v\in S{\backslash } S_\infty }Z_v(\xi _v,f_{v,s})$ were zero, then by the holomorphy of $L^S(s',\Pi )$ at $s'=\tfrac{1}{2}$ and the holomorphy of the integral $Z_\infty (s',\xi ^{\epsilon _0}_{\infty ,\underline{i}, \alpha },f_{\infty ,1})$ at $s'=\tfrac{1}{2}$ (Lemma 7.2 and the paragraph below),

$$\begin{aligned} \frac{L^S(\tfrac{1}{2},\Pi )\cdot L^S(s,\Pi ,\Lambda ^2)}{L^S(n,{\mathbf {1}})^2}\cdot \prod _{v\in S}\frac{Z_v(\xi _v,f_{v,1})}{L(n,{\mathbf {1}}_v)} \end{aligned}$$

would have no pole at $s=1$ (Here we let $\xi _v=\xi ^{\epsilon _0}_{v,\underline{i}, \alpha }$ at an archimedean place.). However, reading the proof of Theorem 6.1 backwards, respectively, by [6, Theorem 1 and Theorem 3], the latter expression equals

$$\begin{aligned} \frac{Z(\xi ,f_{s})}{L(n,{\mathbf {1}})} \end{aligned}$$

as meromorphic functions in s. By [6, Theorem 1] and our assumption that $\Pi$ is a functorial lift from SO$(2n+1)$, cf. Proposition 3.5, the integral $Z(\xi ,f_{s})$ has a pole at $s=1$, whereas $L(n,{\mathbf {1}})$ does not by the assumption that $n\ge 2$. Hence, we arrived at a contradiction.

We may therefore finish the proof of the first assertion of Theorem 7.4 by showing that

$$\begin{aligned} \sigma \left( \prod _{v\in S{\backslash } S_\infty }Z_v(\xi _v,f_{v,s})\right) =\prod _{v\in S{\backslash } S_\infty }Z_v({}^\sigma \xi _v,{}^\sigma \!f_{v,s}). \end{aligned}$$

Observing that by a simple change of variable and by our specific choice of $f_{v,s}={}^\sigma \! f_{v,s}$, $Z_v({}^\sigma \xi _v,{}^\sigma \!f_{v,s})=Z_v(\sigma \circ \xi _v,f_{v,s})$, this is achieved by Matringe in Theorem A of the Appendix.

The last assertion of the theorem follows by strong multiplicity one for cuspidal automorphic representations of $G(\mathbb {A})$. $\square$

7.4 Whittaker–Shalika periods and the exterior square L-function

Theorem 7.4 above is accompanied by the following corollary. Recall the non-zero Shalika periods $\omega ^\epsilon (\Pi _f)$ from Grobner–Raghuram [14]: These were defined by comparing a $\mathbb {Q}(\Pi _f)$-rational structure on a Shalika model of $\Pi _f$ and a $\mathbb {Q}(\Pi _f)$-rational structure on $H^{r}(\mathfrak {g}_\infty ,(Z_\infty K_\infty )^\circ ,\Pi \otimes E_\mu )[\epsilon ]$. For details, we refer to [14, Definition/Proposition 4.2.1]. Observe that $\omega ^{\epsilon _0}(\Pi _f)$ is well-defined, if we assume that $\Pi$ satisfies the assumptions made in the statement of Theorem 7.4: Indeed, as these assumptions include that the partial exterior square L-function $L^S(s,\Pi ,\Lambda ^2)$ has a pole at $s=1$, $\Pi$ has a $({\mathbf {1}},\psi )$-Shalika model by [14, Theorem 3.1.1]. (The extremely careful reader may also recall Lemma 3.2 at this place.) Moreover, by the same reasoning, also the archimedean Shalika period $\omega (\Pi _\infty )=\omega (\Pi _\infty ,0)$ from [14, Theorem 6.6.2] is well-defined (and non-zero). A complete list of all choices, which enter the definition of these Shalika periods $\omega ^{\epsilon _0}(\Pi _f)$ and $\omega (\Pi _\infty )$, can be extracted (similar to our considerations leading to Remarks 4.4 and 7.3 above) from [14, Definition/Proposition 4.2.1 and Theorem 6.6.2], where they have been constructed in details. We do not provide such a list here, for the reason that neither $\omega ^{\epsilon _0}(\Pi _f)$ nor $\omega (\Pi _\infty )$ appear in the statement of the main theorems (but only in some corollaries).

Define the Whittaker–Shalika periods

$$\begin{aligned} P^t(\Pi ):=\frac{p^t(\Pi )}{\omega ^{\epsilon _0}(\Pi _f)}\quad \text {and}\quad P^t(\Pi _\infty ):=\frac{p^t(\Pi _\infty )}{\omega (\Pi _\infty )}. \end{aligned}$$

Obviously the left hand side of (7.3) is uninteresting, if $L(\tfrac{1}{2},\Pi _f)=0$. Hence, we allow ourselves to make the strong assumption that $L(\tfrac{1}{2},\Pi _f)$ is non-zero in order to derive the following result:

Corollary 7.6

Let $\Pi$ be as in the statement of Theorem 7.4. If $L(\tfrac{1}{2},\Pi _f)$ is non-zero, then

$$\begin{aligned} \mathrm{Res}_{s=1}(L^S(s,\Pi ,\Lambda ^2)) \ \sim _{\mathbb {Q}(\Pi _f)} \ P^t(\Pi ) \ P^t(\Pi _\infty ), \end{aligned}$$

where “$\sim _{\mathbb {Q}(\Pi _f)}$” means up to multiplication of the right hand side by an element in the number field $\mathbb {Q}(\Pi _f)$.

Proof

This is obvious invoking Theorem 7.4 and [14, Theorem 7.1.2]. $\square$

8 A rationality result for the Rankin–Selberg L-function

8.1 The content of this section is very closely related to Grobner–Harris–Lapid [12, §4–§5] and a special case of Balasubramanyam–Raghuram [2, §2–§3]. Indeed, the main result, Theorem 8.5, of this section is Theorem 5.3 from [12] (but with the totally imaginary field E from [12] being replaced by the totally real field F as a ground-field), respectively Theorem 3.3.11 from [2] (but with the L-value $L(1,\mathrm{Ad}^0,\pi )$ from [2] being replaced by the residue of $L^S(s,\Pi \times \Pi ^\vee )$ at $s=1$). For the reason of these close analogies we allow ourselves to be rather brief, when it comes to details. Nevertheless, we think it is worthwhile writing down the following, already for reasons of notation, and in order to give precise statements of results in what follows.

8.1 Bottom-degree Whittaker periods

Let $\Pi$ be as in Sect. 3.1 and let $b:=dn^2$. Then,

$$\begin{aligned} \dim _\mathbb {C}H^b(\mathfrak {m}_G,K^\circ _\infty ,\Pi _\infty \otimes E_\mu )[\epsilon ]=1 \end{aligned}$$

for all $\epsilon \in \pi _0(G_\infty )^*$. As in Sect. 3.1, this is a direct consequence of the formula in Clozel [7], Lemma 3.14 and the Künneth rule. It is hence clear that the entire discussion of Sects. 3.3 and 4.1–4.4 carries over to $(\mathfrak {m}_G,K^\circ _\infty )$-cohomology in degree $q=b$. In particular, let $\epsilon _1:=((-1)^{n},\ldots ,(-1)^{n})\in \pi _0(G_\infty )^*$, i.e., the inverse of the character $\epsilon _0$. We obtain a $\mathbb {Q}(\Pi _f)$-structure on $H^b(\mathfrak {m}_G,K^\circ _\infty ,\Pi \otimes E_\mu )[\epsilon _1]$ imposed by the $\mathbb {Q}(E_\mu )$-structure on $H^b_c(\mathcal {S}_G,\mathcal {E}_\mu )$ (exactly as in Definition 3.4) and we may fix once and for all a generator $[\mathcal {W}^{\psi ^{-1}_\infty }(\Pi _\infty )]^b$ of the one-dimensional cohomology space $H^{b}(\mathfrak {m}_G,K^\circ _\infty ,\mathcal {W}^{\psi ^{-1}_\infty }(\Pi _\infty )\otimes E_\mu )[\epsilon _1]$,

$$\begin{aligned}{}[\mathcal {W}^{\psi ^{-1}_\infty }(\Pi _\infty )]^b:=\sum _{\underline{j}=(j_1,\ldots ,j_{b})}\sum _{\beta =1}^{\dim E_\mu } X^*_{\underline{j}}\otimes \xi ^{\epsilon _1}_{\infty ,\underline{j}, \beta }\otimes e_\beta , \end{aligned}$$

in complete analogy to Sect. 4.2, replacing the degree of cohomology t by b in Choice 4.2. Observe that here we exchanged the non-trivial additive character $\psi$ by its inverse $\psi ^{-1}$ and (for notational clearness only), also the index $\alpha$ by $\beta$.

Moreover, in light of Proposition 3.6, for all $\sigma \in$Aut$(\mathbb {C})$, we obtain non-trivial Whittaker periods $p^b({}^\sigma \Pi )$, unique up to multiplication by elements in $\mathbb {Q}({}^\sigma \Pi _f)^\times$, such that

commutes. This is the analogue of Proposition 4.3, whose proof goes through word for word in the current situation, i.e., for cohomology in degree b instead of t. See [30, Proposition/Definition 3.3]. In the above diagram, $H^{\sigma ,b}_\mu :=(\Delta ^{b}_{{}^\sigma \Pi })^{-1}\circ \mathcal H^{\sigma ,b}_\mu \circ \Delta ^b_\Pi$ is the restriction of $\mathcal H^{\sigma ,b}_\mu$ to $H^{b}(\mathfrak {m}_G,K_{\infty }^\circ , \Pi \otimes E_{\mu })[\epsilon _1]$, this map being well-defined following by the same argument as in Sect. 4.3. We leave it to the reader to fill in the remaining details.

Remark 8.1

A comprehensive list of all ingredients on which our bottom-degree period $p^b(\Pi )$ depends is now easily accomplished reading through Remark 4.4, mutatis mutandis, i.e., replacing t by b, $\psi$ by $\psi ^{-1}$ and $\epsilon _0$ by $\epsilon _1$.

8.2 Another archimedean period

Recall the Schwartz–Bruhat function $\Phi =\otimes _v\Phi _v\in \mathscr {S}(\mathbb {A}^{2n})$ from Sect. 6.1 with $m=2n$ in this case. Let $U_{2n}$ be the subgroup of upper triangular matrices in $G=\mathrm{GL}_{2n}$, whose diagonal entries are all equal to 1. For each $v\in S_\infty$ we let $\xi _v\in \mathcal {W}^{\psi _v}(\Pi _v)$ (resp. $\xi '_v\in \mathcal {W}^{\psi ^{-1}_v}(\Pi _v)$) be a local Whittaker function, which is SO(2n)-finite from the right. For such Whittaker functions, the local zeta-integrals

$$\begin{aligned} \Psi _v(s,\xi _v,\xi '_v,\Phi _v):= & {} \int _{U_{2n}(F_v){\backslash }\mathrm{GL}_{2n}(F_v)}\xi _v(g_v) \xi '_v(g_v)\\&\times \Phi _v((0,\ldots ,0,1) g_v) |\det (g_v)|_v^s\ dg_v \end{aligned}$$

converge for $\mathfrak {R}e(s)\ge 1$, cf. [21, Proposition (3.17)]. If $\xi _\infty =\otimes _{v\in S_\infty }\xi _v\in \mathcal {W}^{\psi _\infty }(\Pi _\infty )\cong \otimes _{v\in S_\infty } \mathcal {W}^{\psi _v}(\Pi _v)$ (resp. $\xi '_\infty =\otimes _{v\in S_\infty }\xi '_v\in \mathcal {W}^{\psi ^{-1}_\infty }(\Pi _\infty )\cong \otimes _{v\in S_\infty } \mathcal {W}^{\psi ^{-1}_v}(\Pi _v)$) is $K_\infty ^\circ$-finite, we abbreviate

$$\begin{aligned} \Psi _\infty (s,\xi _\infty ,\xi '_\infty ,\Phi _\infty ):=\prod _{v\in S_\infty }\Psi _v(s,\xi _v,\xi '_v,\Phi _v). \end{aligned}$$

Furthermore, by assumption $E_\mu \cong E_\mu ^\vee$. So, the canonical pairing $E_\mu \times E_\mu ^\vee \rightarrow \mathbb {C}$ induces a pairing $E_\mu \times E_\mu \rightarrow \mathbb {C}$, which we will denote by $\langle e_\alpha ,e_\beta \rangle :=e^{\vee }_\beta (e_\alpha )$. As a last ingredient, recall our generators $[\mathcal {W}^{\psi _\infty }(\Pi _\infty )]^t$ and $[\mathcal {W}^{\psi ^{-1}_\infty }(\Pi _\infty )]^b$ from Sects. 4.2 and 8.2. Similar to Sect. 7.1, we let $s(\underline{i},\underline{j})$ be the unique complex number, such that $X^*_{\underline{i}}\wedge X^*_{\underline{j}}=s(\underline{i},\underline{j})\cdot X_1\wedge \cdots \wedge X_{t+b}$. Putting things together, consider

$$\begin{aligned} c(\Pi _\infty ):= & {} \sum _{\underline{i}=(i_1,\ldots ,i_{t})}\sum _{\underline{j}=(j_1,\ldots ,j_{b})}\sum _{\alpha =1}^{\dim E_\mu } \sum _{\beta =1}^{\dim E_\mu } s(\underline{i},\underline{j})\ \langle e_\alpha ,e_\beta \rangle \\&\Psi _\infty (1,\xi ^{\epsilon _0}_{\infty ,\underline{i}, \alpha }, \xi ^{\epsilon _1}_{\infty ,\underline{j}, \beta },\Phi _\infty ). \end{aligned}$$

Then there is the following theorem, which follows from Proposition 5.0.3 in [2].

Theorem 8.2

The number $c(\Pi _\infty )$ is non-zero.

Proof

We may adapt the argument given at the beginning of the proof of Theorem 7.1, to see that the non-vanishing of $c(\Pi _\infty )$ may be reduced to showing the non-vanishing of a similarly defined number $d(\Pi _v)$, which only depends on one given archimedean place $v\in S_\infty$. Indeed, there is a projection

$$\begin{aligned} M_b:\Lambda ^b(\mathfrak {m}_G/\mathfrak {k}_{\infty })^*{\mathop {\longrightarrow }\limits ^{\sim }}\bigoplus _{u+v=b}\Lambda ^u(\mathfrak {g}_\infty /\mathfrak {c}_\infty )^*\otimes \Lambda ^{v}\mathfrak {s}^*\twoheadrightarrow \Lambda ^b(\mathfrak {g}_\infty /\mathfrak {c}_\infty )^*\otimes \Lambda ^{0}\mathfrak {s}^*, \end{aligned}$$

where we wrote again $\mathfrak {c}_\infty :=\mathfrak {z}_\infty \oplus \mathfrak {k}_\infty$. By reasons of degrees of cohomology, $M_b$ induces an isomorphism of (one-dimensional) vector spaces

$$\begin{aligned}&\mathcal M_b: H^{b}(\mathfrak {m}_G,K^\circ _\infty ,\mathcal {W}^{\psi ^{-1}_\infty }(\Pi _\infty )\otimes E_\mu )[\epsilon _1]{\mathop {\longrightarrow }\limits ^{\sim }}H^{b}(\mathfrak {g}_\infty ,(Z_\infty K_\infty )^\circ ,\\&\qquad \mathcal {W}^{\psi ^{-1}_\infty }(\Pi _\infty )\otimes E_\mu )[\epsilon _1]\otimes \Lambda ^{0}\mathfrak {s}^*_\mathbb {C}, \end{aligned}$$

whose effect on the generator $[\mathcal {W}^{\psi ^{-1}_\infty }(\Pi _\infty )]^b$ is by mapping $X_{\underline{j}}^*$ to $M_b(X_{\underline{j}})\in \Lambda ^b(\mathfrak {g}_\infty /\mathfrak {c}_\infty )^*\otimes \Lambda ^{0}\mathfrak {s}^*$. Whence, at the cost of re-scaling $M_b(X_{\underline{j}})$ by the non-trivial factor in $\Lambda ^{0}\mathfrak {s}^*=\mathbb {R}$, we may and will assume that $M_b(X_{\underline{j}})\in \Lambda ^b(\mathfrak {g}_\infty /\mathfrak {c}_\infty )^*$. Recall the projection $L^t=L_r\otimes L_{d-1}$ and the isomorphism $\mathcal L^t=\mathcal L_r\otimes \mathcal L_{d-1}$ from the proof of 7.1.² Moreover, observe that there is an isomorphism

$$\begin{aligned} N^{t+b}:\Lambda ^{t+b}(\mathfrak {m}_G/\mathfrak {k}_{\infty })^*{\mathop {\longrightarrow }\limits ^{\sim }}\Lambda ^{r+b}(\mathfrak {g}_\infty /\mathfrak {c}_\infty )^*\otimes \Lambda ^{d-1}\mathfrak {s}^*, \end{aligned}$$

which we factor similarly to $L^t$ as $N^{t+b}(X_1\wedge \cdots \wedge X_{t+b})=N_{r+b}(X_1\wedge \cdots \wedge X_{t+b})\otimes N_{d-1}(X_1\wedge \cdots \wedge X_{t+b})$, where $N_{r+b}(X_1\wedge \cdots \wedge X_{t+b})\in \Lambda ^{r+b}(\mathfrak {g}_\infty /\mathfrak {c}_\infty )^*$ and $N_{d-1}(X_1\wedge \cdots \wedge X_{t+b})\in \Lambda ^{d-1}\mathfrak {s}^*$. It hence follows that the number $c(\Pi _\infty )$ is a non-trivial multiple of

$$\begin{aligned} d(\Pi _\infty ):= & {} \sum _{\underline{i}=(i_1,\ldots ,i_{t})}\sum _{\underline{j}=(j_1,\ldots ,j_{b})}\sum _{\alpha =1}^{\dim E_\mu } \sum _{\beta =1}^{\dim E_\mu } u(\underline{i},\underline{j})\ \langle e_\alpha ,e_\beta \rangle \\&\Psi _\infty (1,\xi ^{\epsilon _0}_{\infty ,\underline{i}, \alpha }, \xi ^{\epsilon _1}_{\infty ,\underline{j}, \beta },\Phi _\infty ), \end{aligned}$$

where $u(\underline{i}, \underline{j})$ is the uniquely defined complex number, such that $L_r(X^*_{\underline{i}})\wedge M_b(X^*_{\underline{j}})=u(\underline{i},\underline{j})\cdot N_{r+b}(X_1\wedge \cdots \wedge X_{t+b})$. The number $d(\Pi _\infty )$ factors as $d(\Pi _\infty )=\prod _{v \in S_\infty } d(\Pi _v)$, where each local factor $d(\Pi _v)$ is defined analogously (using $\Lambda ^{r+b}(\mathfrak {g}_\infty /\mathfrak {c}_{\infty })^*\cong \bigotimes \Lambda ^{2n^2+n-1}(\mathfrak {g}_v/\mathfrak {c}_{v})^*$). Therefore, we may finish the proof by showing that $d(\Pi _v)$ is non-zero for all $v\in S_\infty$. This is the reduction to a single archimedean place $v\in S_\infty$, mentioned at the beginning of the proof. The result hence follows by [2, Proposition 5.0.3]. $\square$

In view of the latter non-vanishing result and Proposition 3.6, we may define

$$\begin{aligned} p({}^\sigma \Pi _\infty ):=c({}^\sigma \Pi _\infty )^{-1} \end{aligned}$$

(7.1)

for all $\sigma \in$ Aut$(\mathbb {C})$.

Remark 8.4

Analogously to Remark 7.3, let us recollect at one place the various choices which enter the definition of our archimedean period $p(\Pi _\infty )$, since (almost) none of them appear in its notation:

• 1. $\Pi _\infty$, $\psi _\infty$, the cohomological degrees b and t, as well as the archimedean measures $dg_v$ chosen for all $v\in S_\infty$ in Sect. 6.3.

• 2. The fixed generators $[\mathcal {W}^{\psi _\infty }(\Pi _\infty )]^t$ and $[\mathcal {W}^{\psi ^{-1}_\infty }(\Pi _\infty )]^b$ from Sects. 4.2 and 8.2. We remark further that these generators depend themselves on the data fixed in Choice 4.2.

• 3. The concrete choice of an archimedean Schwartz–Bruhat function $\Phi _\infty =\otimes _{v\in S_\infty }\Phi _v$ from Sect. 6.1 with $m=2n$.

It is hence clear that existence and definition of $p(\Pi _\infty )$ is independent of the other periods considered so far in this paper, $p^t(\Pi )$, $p^b(\Pi )$ and $p^t(\Pi _\infty )$.

8.3 Rationality of the residue of the Rankin–Selberg L-function at $s=1$

Having set up our additional notation above, we obtain the main result of this section.

Theorem 8.5

Let F be a totally real number field and $G=\mathrm{GL}_{2n}/F$, $n\ge 2$. Let $\Pi$ be a self-dual, unitary, cuspidal automorphic representation of $G(\mathbb {A})$ (with trivial central character), which is cohomological with respect to an irreducible, self-contragredient, algebraic, finite-dimensional representation $E_\mu$ of $G_\infty$. Then, for every $\sigma \in \mathrm{Aut}(\mathbb {C})$,

$$\begin{aligned} \sigma \left( \frac{\mathrm{Res}_{s=1}(L^S(s,\Pi \times \Pi ))}{p^t(\Pi ) \ p^b(\Pi ) \ p(\Pi _\infty )}\right) \ = \ \frac{\mathrm{Res}_{s=1}(L^S(s,{}^\sigma \Pi \times {}^\sigma \Pi ))}{p^t({}^\sigma \Pi ) \ p^b({}^\sigma \Pi ) \ p({}^\sigma \Pi _\infty )}. \end{aligned}$$

In particular,

$$\begin{aligned} \mathrm{Res}_{s=1}(L^S(s,\Pi \times \Pi )) \ \sim _{\mathbb {Q}(\Pi _f)^\times } \ p^t(\Pi ) \ p^b(\Pi ) \ p(\Pi _\infty ), \end{aligned}$$

where “$\sim _{\mathbb {Q}(\Pi _f)^\times }$” means up to multiplication by a non-trivial element in the number field $\mathbb {Q}(\Pi _f)$.

Proof

The first assertion follows from Theorem 3.3.11 of [2]. The second assertion of Theorem 8.5 follows from the first one, applying strong multiplicity one for the cuspidal automorphic spectrum of $G(\mathbb {A})$ and recalling that $\mathrm{Res}_{s=1}(L^S(s,\Pi \times \Pi ))$ is non-zero. In fact, $\mathrm{Res}_{s=1}(L^S(s,\Pi \times \Pi ))\ne 0$ is well-known and is a consequence of Theorem 8.2 together with [21] (5), p. 550 and Proposition (2.3) in loc. cit.. $\square$

9 A rationality result for the symmetric square L-function

9.1 Definition of the archimedean bottom-degree period

Let $\Pi$ be a cuspidal automorphic representation of $G(\mathbb {A})$ as in Sect. 3.1 and $\sigma \in$ Aut$(\mathbb {C})$. Recall the archimedean periods $p^t({}^\sigma \Pi _\infty )$ from (7.2) and $p({}^\sigma \Pi _\infty )$ from (7.1). We define our bottom-degree, archimedean period by

$$\begin{aligned} p^b({}^\sigma \Pi _\infty ):=\frac{p({}^\sigma \Pi _\infty )}{p^t({}^\sigma \Pi _\infty )}. \end{aligned}$$

Remark 8.1

Of course, by Theorems 7.1 and 8.2, $p^b({}^\sigma \Pi _\infty )$ is well-defined and non-zero. For the sake of the reader, we remark that a complete list of all concrete choices on which $p^b(\Pi _\infty )$ actually depends, is hence given by merging the precise lists provided by Remarks 7.3 and 8.4.

9.2 Rationality of the symmetric square L-function at $s=1$

Recall our bottom-degree periods $p^b(\Pi )$ and $p^b(\Pi _\infty )$, defined in Sects. 8.2 and 9.1, respectively. For a complete list of all data, entering the respective definition, we refer to Remarks 8.1 and 8.1 above. The following result is our second main theorem.

Theorem 9.2

Let F be a totally real number field and $G=\mathrm{GL}_{2n}/F$, $n\ge 2$. Let $\Pi$ be a unitary cuspidal automorphic representation of $G(\mathbb {A})$ (self-dual and with trivial central character), which is cohomological with respect to an irreducible, self-contragredient, algebraic, finite-dimensional representation $E_\mu$ of $G_\infty$. Assume that $\Pi$ satisfies the equivalent conditions of Proposition 3.5, i.e., the partial exterior square L-function $L^S(s,\Pi ,\Lambda ^2)$ has a pole at $s=1$. Then, for every $\sigma \in \mathrm{Aut}(\mathbb {C})$,

$$\begin{aligned} \sigma \left( \frac{L(\tfrac{1}{2},\Pi _f)\ p^b(\Pi ) \ p^b(\Pi _\infty )}{L^S(1,\Pi ,\mathrm{Sym}^2)}\right) \ = \ \frac{L(\tfrac{1}{2},{}^\sigma \Pi _f)\ p^b({}^\sigma \Pi ) \ p^b({}^\sigma \Pi _\infty )}{L^S(1,{}^\sigma \Pi ,\mathrm{Sym}^2)}. \end{aligned}$$

In particular,

$$\begin{aligned} L^S(1,\Pi ,\mathrm{Sym}^2) \sim _{\mathbb {Q}(\Pi _f)} L(\tfrac{1}{2},\Pi _f)\ p^b(\Pi ) \ p^b(\Pi _\infty ) \end{aligned}$$

(9.3)

where “$\sim _{\mathbb {Q}(\Pi _f)}$” means up to multiplication of $L^S(1,\Pi ,\mathrm{Sym}^2)$ by an element in the number field $\mathbb {Q}(\Pi _f)$.

Proof

Recall that $L^S(s,\Pi \times \Pi ) = L^S(s,\Pi ,\mathrm{Sym}^2) \cdot L^S(s,\Pi ,\Lambda ^2)$ as meromorphic functions in s, whence, by the assumptions on $\Pi$, we obtain

$$\begin{aligned} \mathrm{Res}_{s=1}(L^S(s,\Pi \times \Pi )) = L^S(1,\Pi ,\mathrm{Sym}^2) \cdot \mathrm{Res}_{s=1}(L^S(s,\Pi ,\Lambda ^2)). \end{aligned}$$

Since $L^S(1,\Pi ,\mathrm{Sym}^2)$ is non-zero (cf. [32, Theorem 5.1]), the first assertion of the theorem follows from Theorems 7.4 and 8.5. The second assertion is now again a consequence of strong multiplicity one for the cuspidal automorphic spectrum of $G(\mathbb {A})$. $\square$

9.3 Whittaker–Shalika periods and the symmetric square L-function

As in the case of the exterior square L-function, we obtain a corollary of our second main theorem, Theorem 9.2, using the main results of our paper [14]. Recall the non-zero Shalika periods $\omega ^\epsilon (\Pi _f)$ and $\omega (\Pi _\infty )=\omega (\Pi _\infty ,0)$ from Sect. 7.5 above, respectively from [14, Definition/Proposition 4.2.1 and Theorem 6.6.2], therein, their existence being guaranteed as in Sect. 7.5. Define the Whittaker–Shalika periods

$$\begin{aligned} P^b(\Pi ):=p^b(\Pi )\cdot \omega ^{\epsilon _0}(\Pi _f)\quad \text {and}\quad P^b(\Pi _\infty ):=p^b(\Pi _\infty )\cdot \omega (\Pi _\infty ). \end{aligned}$$

Analogously to the situation considered in Sect. 7.5 above, the right hand side of (9.3) is uninteresting if $L(\tfrac{1}{2},\Pi _f)=0$. Hence, we allow ourselves to make the strong assumption that $L(\tfrac{1}{2},\Pi _f)$ is non-zero in order to obtain the following result.

Corollary 9.4

Let $\Pi$ be as in the statement of Theorem 9.2. If $L(\tfrac{1}{2},\Pi _f)$ is non-zero, then

$$\begin{aligned} L^S(1,\Pi ,\mathrm{Sym}^2)\ \sim _{\mathbb {Q}(\Pi _f)^\times } \ P^b(\Pi ) \ P^b(\Pi _\infty ), \end{aligned}$$

where “$\sim _{\mathbb {Q}(\Pi _f)^\times }$” means up to multiplication of $L^S(1,\Pi ,\mathrm{Sym}^2)$ by a non-zero element in the number field $\mathbb {Q}(\Pi _f)$.

Proof

This follows directly from Theorem 9.2 and [14, Theorem 7.1.2]. $\square$

10 Applications for quotients of symmetric square L-functions

10.1 Gauß sums of algebraic Hecke characters

It is the purpose of this section to provide a result, independent of the all the periods mentioned above for certain quotients of symmetric square L-functions.

To that end, let $\chi$ be a Hecke character of finite order. We define the Gauß sum of its finite part $\chi _f$, following Weil [37, VII, Sect. 7]: Let $\mathfrak {c}_\chi$ stand for the conductor ideal of $\chi _f$ and let $y = (y_v)_{v \notin S_\infty } \in {\mathbb A}_f^{\times }$ be chosen such that $\mathrm{ord}_v(y_v) = -\mathrm{ord}_v(\mathfrak {c}_\chi ) -\mathrm{ord}_v(\mathfrak {D}_F)$. Here, $\mathfrak {D}_F$ stands for the absolute different of F, that is, $\mathfrak {D}_F^{-1} = \{x \in F : Tr_{F/\mathbb {Q}}(x \mathcal {O}) \subset \mathbb {Z}\}$.

Recall our fixed non-trivial additive character $\psi :F{\backslash } \mathbb {A}\rightarrow \mathbb {C}^\times$ from Sect. 2.1. The Gauß sum of $\chi _f$ with respect to y and $\psi$ is now defined as $\mathscr {G}(\chi _f,\psi _f,y) = \prod _{v \notin S_\infty } \mathscr {G}(\chi _v,\psi _v,y_v)$, where the local Gauß sum $\mathscr {G}(\chi _v,\psi _v,y_v)$ is defined as

$$\begin{aligned} \mathscr {G}(\chi _v,\psi _v,y_v) = \int _{\mathcal {O}_v^{\times }} \chi _v(u_v)^{-1}\psi _v(y_vu_v)\, du_v. \end{aligned}$$

For almost all v, we have $\mathscr {G}(\chi _v,\psi _v,y_v)=1$, and for all v we have $\mathscr {G}(\chi _v,\psi _v,y_v) \ne 0$. (See, for example, Godement [10, Eq. 1.22].) Note that, unlike in [37], we do not normalize the Gauß sum to make it have absolute value one. For the sake of easing notation and readability we suppress its dependence on $\psi$ and y, and denote $\mathscr {G}(\chi _f,\psi _f,y)$ simply by $\mathscr {G}(\chi _f)$.

10.2 An application of Theorem 9.2

Theorem 10.1

Let F be a totally real number field and $G=\mathrm{GL}_{2n}/F$, $n\ge 2$. Let $\Pi$ be any cuspidal automorphic representation of $G(\mathbb {A})$ and let $\chi _1$ and $\chi _2$ be two Hecke characters of finite order, such that $\Pi \otimes \chi _i$, $i=1,2$, both satisfy the conditions of Corollary 9.4. If $\chi _1$ and $\chi _2$ have moreover the same infinity-type, i.e., $\chi _{1,\infty }=\chi _{2,\infty }$, then,

$$\begin{aligned} \frac{L^S(1,\Pi \otimes \chi _1,\mathrm{Sym}^2)}{L^S(1,\Pi \otimes \chi _2,\mathrm{Sym}^2)}\ \sim _{\mathbb {Q}(\Pi _f,\chi _{1,f},\chi _{2,f})^\times } \mathscr {G}(\chi _{1,f})^{2n^2}\mathscr {G}(\chi _{2,f})^{-2n^2}, \end{aligned}$$

where “$\sim _{\mathbb {Q}(\Pi _f,\chi _{1,f},\chi _{2,f})^\times }$” means up to multiplication by a non-zero element in the composition of number fields $\mathbb {Q}(\Pi _f)$, $\mathbb {Q}(\chi _{1,f})$ and $\mathbb {Q}(\chi _{2,f})$.

It shall be noted that, whereas the quantities on the left hand side of the above equation all depend crucially on $\Pi$, the right hand side is not only independent of the all periods considered in this paper, but completely independent of $\Pi$.

Proof

Recall the Whittaker–Shalika periods $P^b(\Pi \otimes \chi _i)=p^b(\Pi \otimes \chi _{i})\cdot \omega ^{\epsilon _0}(\Pi _f\otimes \chi _{i,f})$ and $P^b(\Pi _\infty \otimes \chi _{i,\infty })=p^b(\Pi _\infty \otimes \chi _{i,\infty })\cdot \omega (\Pi _\infty \otimes \chi _{i,\infty })$, $i=1,2$, from Sect. 9.3. We remind the reader that since both $\Pi \otimes \chi _i$, $i=1,2$, satisfy the assumptions of Theorem 9.2, all periods appearing in their definition are well-defined and non-zero, cf. Sect. 7.5.

Since it follows directly from the definition of rationality fields that $\mathbb {Q}(\Pi _f\otimes \chi _{1,f})\mathbb {Q}(\Pi _f\otimes \chi _{2,f})=\mathbb {Q}(\Pi _f,\chi _{1,f},\chi _{2,f})$, our Corollary 9.4 (or, alternatively, Theorem 9.2 together with [14, Theorem 7.1.2]) implies that

$$\begin{aligned}&\frac{L^S(1,\Pi \otimes \chi _1,\mathrm{Sym}^2)}{L^S(1,\Pi \otimes \chi _2,\mathrm{Sym}^2)}\ \sim _{\mathbb {Q}(\Pi _f,\chi _{1,f},\chi _{2,f})^\times } \frac{P^b(\Pi \otimes \chi _1) \ P^b(\Pi _\infty \otimes \chi _{1,\infty })}{P^b(\Pi \otimes \chi _2) \ P^b(\Pi _\infty \otimes \chi _{2,\infty })}\\&\quad =\frac{p^b(\Pi \otimes \chi _{1})\cdot \omega ^{\epsilon _0}(\Pi _f\otimes \chi _{1,f})}{p^b(\Pi \otimes \chi _{2})\cdot \omega ^{\epsilon _0}(\Pi _f\otimes \chi _{2,f})} \frac{p^b(\Pi _\infty \otimes \chi _{1,\infty })\cdot \omega (\Pi _\infty \otimes \chi _{1,\infty })}{p^b(\Pi _\infty \otimes \chi _{2,\infty })\cdot \omega (\Pi _\infty \otimes \chi _{2,\infty })}. \end{aligned}$$

Moreover, the infinity-types of $\chi _1$ and $\chi _2$ are equal by assumption, which implies that $\Pi _\infty \otimes \chi _{1,\infty }$ and $\Pi _\infty \otimes \chi _{2,\infty }$ are not only isomorphic, but literally identical. As a consequence, the contribution of all archimedean periods above cancels out, and we are left with

$$\begin{aligned} \frac{L^S(1,\Pi \otimes \chi _1,\mathrm{Sym}^2)}{L^S(1,\Pi \otimes \chi _2,\mathrm{Sym}^2)}\ \sim _{\mathbb {Q}(\Pi _f,\chi _{1,f},\chi _{2,f})^\times } \frac{p^b(\Pi \otimes \chi _{1})\cdot \omega ^{\epsilon _0}(\Pi _f\otimes \chi _{1,f})}{p^b(\Pi \otimes \chi _{2})\cdot \omega ^{\epsilon _0}(\Pi _f\otimes \chi _{2,f})}.\quad \end{aligned}$$

(10.2)

(We remark aside that in order to see this cancellation it would also have been enough to know that the $\chi _i$ are of finite order, since then $\Pi _\infty \otimes \chi _{i,\infty }\cong \Pi _\infty$, for $i=1,2$, see [14, 5.3]. However, the equality $\Pi _\infty \otimes \chi _{1,\infty }=\Pi _\infty \otimes \chi _{2,\infty }$ makes the cancellation even more obvious.)

It is exactly the main result of [30, Theorem 4.1.], that—if $\chi _1$ and $\chi _2$ have the same infinity-type, which we assume—one has the relation

$$\begin{aligned} p^b(\Pi \otimes \chi _i)\sim _{\mathbb {Q}(\Pi _f,\chi _{i,f})^\times } p^b(\Pi )\cdot \mathscr {G}(\chi _{i,f})^{n(2n-1)}. \end{aligned}$$

(10.3)

Furthermore, it is the main result of section 5 of [14, Theorem 5.2.1], that we obtain

$$\begin{aligned} \omega ^{\epsilon _0}(\Pi _f\otimes \chi _{i,f})\sim _{\mathbb {Q}(\Pi _f,\chi _{i,f})^\times } \omega ^{\epsilon }(\Pi _f)\cdot \mathscr {G}(\chi _{i,f})^{n}. \end{aligned}$$

(10.4)

where $\epsilon \in K_\infty /K^\circ _\infty$ is the same for both $i=1,2$, because we assumed that $\chi _1$ and $\chi _2$ have the same infinity-type. Inserting the relations (10.3) and (10.4) into (10.2), we obtain

$$\begin{aligned} \!\frac{L^S(1,\Pi \otimes \chi _1,\mathrm{Sym}^2)}{L^S(1,\Pi \otimes \chi _2,\mathrm{Sym}^2)}\!\!&\sim _{\mathbb {Q}(\Pi _f,\chi _{1,f},\chi _{2,f})^\times }\!\!\frac{p^b(\Pi )\cdot \mathscr {G}(\chi _{1,f})^{n(2n-1)}\!\cdot \omega ^{\epsilon }(\Pi _f)\!\cdot \mathscr {G}(\chi _{1,f})^{n}}{p^b(\Pi )\cdot \mathscr {G}(\chi _{2,f})^{n(2n-1)}\!\cdot \omega ^{\epsilon }(\Pi _f)\cdot \mathscr {G}(\chi _{2,f})^{n}}\\&= \mathscr {G}(\chi _{1,f})^{2n^2}\mathscr {G}(\chi _{2,f})^{-2n^2}. \end{aligned}$$

This shows the claim. $\square$

Appendix

In this appendix,³ F denotes a non-archimedean local field with valuation v and absolute value |.| (normalised as usual). We will write |g| for $|\det (g)|$ when g is a square matrix, $\mathcal {O}$ for the ring of integers of F and let $\wp =\varpi \mathcal {O}$ be the maximal ideal of $\mathcal {O}$.

Proposition A

Let $\phi \in {\mathscr {C}}^{\infty }_c(F)$, $\chi$ a character of $F^\times$, and $m\ge 0$ and integer. Then,

$$\begin{aligned} T(q^{-s},\chi ,m,\phi ):=\int _{F^\times } \phi (x)\ \chi (x) \ v(x)^m|x|^s \ d^\times x \end{aligned}$$

(with $\mathrm{vol}_{d^\times x}(\mathcal {O}^\times )=1$) converges for $|q^{-s}|<|\chi (\varpi )|^{-1}$ and can be extended to an element of $L(s,\chi )^m\cdot \mathbb {C}[q^{\pm s}]$. Moreover, if $\sigma \in \mathrm{Aut}(\mathbb {C})$, then

$$\begin{aligned} \sigma (T(q^{-s},\chi ,m,\phi ))= T(\sigma (q^{-s}),\sigma (\chi ),m,\sigma (\phi )). \end{aligned}$$

Proof

For $k \in \mathbb {Z}$, we set

$$\begin{aligned}c_k(\chi ,\phi ):=\int _{\mathcal {O}^\times } \phi (\varpi ^k x)\ \chi (x) \ d^\times x,\end{aligned}$$

and

$$\begin{aligned} c(\chi ):=\int _{\mathcal {O}^\times } \chi (x)\ d^\times x, \end{aligned}$$

so that we have $c(\chi )=0$, if $\chi$ is ramified, and $c(\chi )=1$, if $\chi$ is unramified.

As $\mathcal {O}^\times$ is compact, take U an open compact subgroup of $\mathcal {O}^\times$ fixing $x\mapsto \phi (\varpi ^k x)$ and $\chi$, and let $\mathcal {O}^\times =\coprod _{i=1}^\ell x_i U$, then $c_k(\chi ,\phi )=\sum _{i=1}^\ell \frac{1}{\ell } \phi (\varpi ^k x_i)\chi (x_i)$, hence, as $\sigma (1/\ell )=1/\ell$, we have

$$\begin{aligned} \sigma (c_k(\chi ,\phi ))=c_k(\sigma (\chi ),\sigma (\phi )). \end{aligned}$$

Let a be a positive integer such that the support of $\phi$ is contained in $\wp ^{a-1}$. Let $b\ge a$ be such that $\phi$ is constant on $\wp ^b$. We have

$$\begin{aligned} T(q^{-s},\chi ,m,\phi )= \sum _{a\le k \le b} c_k(\chi ,\phi )k^m\chi (\varpi )^k q^{-ks} + \sum _{k \ge b} c(\chi ) k^m \chi (\varpi )^k q^{-ks}. \end{aligned}$$

We set

$$\begin{aligned} A(q^{-s},\chi ,m,\phi ):=\sum _{a\le k \le b} c_k(\chi ,\phi ) k^m \chi (\varpi )^kq^{-ks} \end{aligned}$$

and

$$\begin{aligned} B(q^{-s},\chi ,m,\phi ):=\sum _{k \ge b} c(\chi ) k^m \chi (\varpi )^k q^{-ks}. \end{aligned}$$

Suppose that $\chi$ is ramified, i.e., non trivial on $\mathcal {O}^\times$. Then

$$\begin{aligned} T(q^{-s},\chi ,m,\phi )=A(q^{-s},\chi ,m,\phi ). \end{aligned}$$

In this case, we have

$$\begin{aligned} \sigma (T(q^{-s},\chi ,m,\phi ))= & {} \sum _{a\le k \le b} \sigma (c_k(\chi ,\phi )) k^m \sigma (\chi (\varpi ))^k \sigma (q^{-ks})\\= & {} \sum _{a\le k \le b} c_k(\sigma (\chi ),\sigma (\phi )) k^m \sigma (\chi (\varpi ))^k\sigma (q^{-ks})\\= & {} A(\sigma (q^{-s}),\sigma (\chi ),m,\sigma (\phi ))\\= & {} T(\sigma (q^{-s}),\sigma (\chi ),m,\sigma (\phi )), \end{aligned}$$

which shows the claim in this case. Suppose now that $\chi$ is unramified. Then there is $P\in \mathbb {Q}[X,X^{-1}]$ (which can be determined explicitly, notice that the coefficients of P are in $\mathbb {Q}$, hence $\sigma$-invariant) such that

$$\begin{aligned} B(q^{-s},\chi ,m,\phi )= \sum _{k \ge b} k^m \chi (\varpi )^k q^{-ks}= P(\chi (\varpi )q^{-s})/ (1-\chi (\varpi )q^{-s})^m, \end{aligned}$$

which implies that

$$\begin{aligned} \sigma (B(q^{-s},\chi ,m,\phi ))= & {} P(\sigma (\chi (\varpi ))\sigma (q^{-s}))/(1-\sigma (\chi (\varpi ))\sigma (q^{-s}))^m\nonumber \\= & {} B(\sigma (q^{-s}),\sigma (\chi ),m,\sigma (\phi )). \end{aligned}$$

This implies again $\sigma (T(q^{-s},\chi ,\phi ))=T(\sigma (q^{-s}),\sigma (\chi ),\sigma (\phi ))$.

$\square$

We denote by $P_n$ the mirabolic subgroup of $G_n=GL(n,F)$, and by $A_n$ the diagonal torus of $G_n$, which is contained in the standard Borel $B_n$ with unipotent radical $N_n$. For $k\in \{1,\ldots ,n-1\}$, the group $G_k$ embeds naturally in $G_n$, so the center $Z_k$ of $G_k$ embeds in $A_n$, and $A_n=Z_1\cdots Z_n$ (direct product). The following result follows from Proposition 2.2 of [19]. We fix a non-trivial additive character $\psi$ of F. If $z_i$ belongs to $Z_i\subset A_n$, we set $t(z_i)$ to be the element of $F^*$ such that $z_i=diag(t(z_i),I_{n-i})$

Proposition B

Let $\pi$ be an irreducible generic representation of $G_n$, and $\xi \in \mathcal {W}^\psi (\pi )$. For each $k \in \{1,\ldots ,n-1\}$, there exists a finite set $I_k$, a string of characters $(c_{i_k})_{i_k\in I_k}$ of $F^*$, non-negative integers $(m_{i_k}^\xi )_{i_k\in I_k}$, and functions $(\phi _{i_k}^\xi )_{i_k\in I_k}$ such that

$$\begin{aligned} \xi (z_1\cdots z_{n-1})=\sum _{k=1}^{n-1}\sum _{i_k\in I_k} \prod _{k=1}^{n-1} c_{i_k}(t(z_k)) \ v(t(z_k))^{m_{i_k}^\xi } \ \phi _{i_k}^\xi (t(z_k)). \end{aligned}$$

(The characters $c_{ik}$, which we allow to be equal, depend only on $\pi$.)

We denote by $w_n$ the element of the symmetric group $\mathfrak {S}_n$ naturally embedded in $G_n$, defined by

$$\begin{aligned} \begin{pmatrix} 1 &{} 2 &{} \cdots &{} m-1 &{} m &{} m+1 &{} m+2 &{} \cdots &{} 2m-1 &{} 2m \\ 1 &{} 3 &{} \cdots &{} 2m-3 &{} 2m-1 &{} 2 &{} 4 &{} \cdots &{} 2m-2 &{} 2m \end{pmatrix} \end{aligned}$$

when $n=2m$ is even, and by

$$\begin{aligned} \begin{pmatrix} 1 &{} 2 &{} \cdots &{} m-1 &{} m &{} m+1 &{} m+2 &{}\cdots &{} 2m &{} 2m+1 \\ 1 &{} 3 &{} \cdots &{} 2m-3 &{} 2m-1 &{} 2m+1 &{} 2 &{} \cdots &{} 2m-2 &{} 2m \end{pmatrix} \end{aligned}$$

when $n=2m+1$ is odd. We denote by $L_n$ the standard Levi subgroup of $G_n$ which is $G_{\lfloor (n+1)/2 \rfloor }\times G_{\lfloor n/2 \rfloor }$ embedded by the map $(g_1,g_2)\mapsto diag(g_1,g_2)$. We denote by $H_n$ the group $L_n^{w_n}=w_n^{-1} L_n w_n$, by $J(g_1,g_2)$ the matrix $w_n^{-1} diag(g_1,g_2)w_n$ of $H_n$ (with $diag(g_1,g_2)\in L_n$). Let r be a positive integer. Thanks to the Iwasawa decomposition $G_r=N_r\cdot A_r \cdot G_r(\mathcal {O})$, if $\chi$ is an unramified character of $A_r$, then the map

$$\begin{aligned} \tilde{\chi }:n\cdot a\cdot k\mapsto \chi (a) \end{aligned}$$

is well defined on $G_r$. For example, if $\delta _r$ is the modulus character of the maximal parabolic subgroup of type $(r-1,1)$ restricted to $A_r$, we have a map $\tilde{\delta _r}$ on $G_r$. Similarly, if

$$\begin{aligned} \lambda :z_1\cdots z_r \in A_r \mapsto |t(z_1) \cdots t(z_{r-1})|, \end{aligned}$$

the map $\tilde{\lambda }$ is also defined on $G_r$, and left invariant under $Z_r$.

Theorem A

Let $\pi$ be an irreducible generic representation of $G_n$ with trivial central character and $\xi \in \mathcal {W}^\psi (\pi )$. Set $m'={\lfloor (n+1)/2\rfloor }$ and $m={\lfloor n/2\rfloor }$. The integral

$$\begin{aligned} Z(\xi ,q^{-s}):=\int _{N_{m}{\backslash } G_{m}}\int _{Z_{m'} N_{m'}{\backslash } G_{m'}} \xi (J(h,g))\ \tilde{\delta }_{m'}(g)\ |g|^s \ \tilde{\lambda }(h)^s \ dg \ dh \end{aligned}$$

(with the normalisations $dg=d^\times a \ dk$ with $d^\times a(A_m(\mathcal {O}))=1$ and $dk(G_{m}(\mathcal {O}))=1$, $dh=d^\times b \ dk$ with $d^\times b(Z_{m'}(\mathcal {O}){\backslash } A_{m'}(\mathcal {O}))=1$ and $dk(G_{m'}(\mathcal {O}))=1$) converges absolutely for $|q^{-s}|$ small enough. It extends to an element of $\mathbb {C}(q^{-s})$, which satisfies that for all $\sigma \in \mathrm{Aut}(\mathbb {C})$, one has

$$\begin{aligned} \sigma (Z(\xi ,q^{-s}))=Z(\sigma \circ \xi , \sigma (q^{-s})). \end{aligned}$$

Proof

Let $\delta '$ be the modulus character of $B_m$ and $\delta ''$ that of $B_{m'}$. Let $U'\times U$ be a compact open subgroup of $G_{m'}(\mathcal {O})\times G_m(\mathcal {O})$ such that $J(U'\times U)$ fixes $\xi$ on the right, and write $G_{m'}(\mathcal {O})\times G_n(\mathcal {O})=\coprod _{j=1}^\ell x_j U'\times y_j U$. We have

$$\begin{aligned} Z(\xi ,q^{-s})=\sum _{j=1}^\ell \frac{1}{\ell }\int _{A_m}\int _{A_{m'-1}} \xi _j(J(b,a)) \ \delta _{m'}(a)\ \delta '(a)^{-1} \ \delta ''(b)^{-1}|a|^s|b|^s \ d^\times a \ d^\times b, \end{aligned}$$

where $\xi _j(g)=\xi (g J(x_j,y_j))$. We identify $A_m\times A_{m'-1}$ with $A_{n-1}$ by$(a,b)\mapsto J(b,a)$, and set $\chi$ the character of $A_{n-1}$ defined by$J(b,a)\mapsto \delta _{m'}(a)\delta '(a)^{-1}\delta ''(b)^{-1}$. The previous integral becomes

$$\begin{aligned} Z(\xi ,q^{-s})=\sum _{j=1}^\ell \frac{1}{\ell }\int _{A_{n-1}} \xi _j(z)\ \chi (z)\ |z|^s \ d^\times z, \end{aligned}$$

We set $\chi _k$ to be the restriction of $\chi$ to $Z_k$. It takes values in $q^{\mathbb {Z}}\subset \mathbb {Q}$. If we now apply the second proposition of this appendix, we obtain that

$$\begin{aligned} Z(\xi ,q^{-s}) \end{aligned}$$

is the sum for k between 1 and $n-1$, $i\in I_k$, and $j\in \{1,\ldots ,\ell \}$ of

$$\begin{aligned} \frac{1}{\ell }\prod _{k=1}^{n-1}T\left( (q^{-s})^k,c_{i_k}\chi _k,m_{i_k}^{\xi _j},\phi _{i_k}^{\xi _j}\right) . \end{aligned}$$

This implies, according to the first proposition of this appendix, that

$$\begin{aligned} \sigma (Z(\xi ,q^{-s})) \end{aligned}$$

is the sum for k between 1 and $n-1$, $i\in I_k$, and $j\in \{1,\ldots ,\ell \}$ of

$$\begin{aligned} \frac{1}{\ell }\prod _{k=1}^{n-1}T\left( (\sigma (q^{-s}))^k,\sigma (c_{i_k})\chi _k,m_{i_k}^{\xi _j},\sigma \left( \phi _{i_k}^{\xi _j}\right) \right) . \end{aligned}$$

This means that $\sigma (Z(\xi ,q^{-s}))$ is equal to $Z(\sigma \circ \xi ,\sigma (q^{-s}))$. $\square$