Non-properly embedded H-planes in ${\mathbb H}^2\times {\mathbb R}$

Abstract

For any $H \in (0,\frac{1}{2})$, we construct complete, non-proper, stable, simply-connected surfaces embedded in ${\mathbb H}^2\times {\mathbb R}$ with constant mean curvature H.

1 Introduction

In their ground breaking work [2], Colding and Minicozzi proved that complete minimal surfaces embedded in $\mathbb {R}^3$ with finite topology are proper. Based on the techniques in [2], Meeks and Rosenberg [5] then proved that complete minimal surfaces with positive injectivity embedded in ${\mathbb {R}}^3$ are proper. More recently, Meeks and Tinaglia [7] proved that complete constant mean curvature surfaces embedded in $\mathbb {R}^3$ are proper if they have finite topology or have positive injectivity radius.

In contrast to the above results, in this paper we prove the following existence theorem for non-proper, complete, simply-connected surfaces embedded in ${\mathbb H}^2\times {\mathbb R}$ with constant mean curvature $H\in (0,1/2)$. The convention used here is that the mean curvature function of an oriented surface M in an oriented Riemannian three-manifold N is the pointwise average of its principal curvatures.

The catenoids in ${\mathbb H}^2\times {\mathbb R}$ mentioned in the next theorem are defined at the beginning of Sect. 2.1.

Theorem 1.1

For any $H\in (0,1/2)$ there exists a complete, stable, simply-connected surface $\Sigma _H$ embedded in ${\mathbb H}^2\times {\mathbb R}$ with constant mean curvature H satisfying the following properties:

• (1) The closure of $\Sigma _H$ is a lamination with three leaves, $\Sigma _H$, $C_1$ and $C_2$, where $C_1$ and $C_2$ are stable catenoids of constant mean curvature H in ${\mathbb {H}}^3$ with the same axis of revolution L. In particular, $\Sigma _{H}$ is not properly embedded in ${\mathbb H}^2\times {\mathbb R}$.

• (2) Let $K_L$ denote the Killing field generated by rotations around L. Every integral curve of $K_L$ that lies in the region between $C_1$ and $C_2$ intersects $\Sigma _H$ transversely in a single point. In particular, the closed region between $C_1$ and $C_2$ is foliated by surfaces of constant mean curvature H, where the leaves are $C_1$ and $C_2$ and the rotated images $\Sigma _H ({\theta })$ of $\Sigma$ around L by angle $\theta \in [0,2\pi )$.

When $H=0$, Rodríguez and Tinaglia [10] constructed non-proper, complete minimal planes embedded in ${\mathbb H}^2\times {\mathbb R}$. However, their construction does not generalize to produce complete, non-proper planes embedded in ${\mathbb H}^2\times {\mathbb R}$ with non-zero constant mean curvature. Instead, the construction presented in this paper is related to the techniques developed by the authors in [3] to obtain examples of non-proper, stable, complete planes embedded in ${\mathbb {H}}^3$ with constant mean curvature H, for any $H\in [0,1)$.

There is a general conjecture related to Theorem 1.1 and the previously stated positive properness results. Given X a Riemannian three-manifold, let ${\mathrm{Ch}}(X):= \inf _{S\in \mathcal {S}} \frac{\text {Area}(\partial S)}{\text {Volume}(S)},$ where $\mathcal {S}$ is the set of all smooth compact domains in X. Note that when the volume of X is infinite, $\hbox {Ch}(X)$ is the Cheeger constant.

Conjecture 1.2

Let X be a simply-connected, homogeneous three-manifold. Then for any $H\ge \frac{1}{2}\hbox {Ch}(X)$, every complete, connected H-surface embedded in X with positive injectivity radius or finite topology is proper. On the other hand, if $\hbox {Ch}(X)>0$, then there exist non-proper complete H-planes in X for every $H\in [0,\frac{1}{2} \hbox {Ch}(X))$.

By the work in [2], Conjecture 1.2 holds for $X=\mathbb {R}^3$ and it holds in ${\mathbb {H}}^3$ by work in progress in [6]. Since the Cheeger constant of ${\mathbb H}^2\times {\mathbb R}$ is 1, Conjecture 1.2 would imply that Theorem 1.1 (together with the existence of complete non-proper minimal planes embedded in ${\mathbb H}^2\times {\mathbb R}$ found in [10]) is a sharp result.

2 Preliminaries

In this section, we will review the basic properties of H-surfaces, a concept that we next define. We will call a smooth oriented surface $\Sigma _H$ in ${\mathbb H}^2\times {\mathbb R}$ an H-surface if it is embedded and its mean curvature is constant equal to H; we will assume that $\Sigma _H$ is appropriately oriented so that H is non-negative. We will use the cylinder model of ${\mathbb H}^2\times {\mathbb R}$ with coordinates $(\rho , \theta , t)$; here $\rho$ is the hyperbolic distance from the origin (a chosen base point) in $\mathbb H^2_0$, where $\mathbb H^2_t$ denotes $\mathbb H^2\times \{t\}$. We next describe the H-catenoids mentioned in the Introduction.

The following H-catenoids family will play a particularly important role in our construction.

2.1 Rotationally invariant vertical H-catenoids $\mathcal {C}^H_d$

We begin this section by recalling several results in [8, 9]. Given $H\in (0,\frac{1}{2})$ and $d\in [-2H,\infty )$, let

$$\begin{aligned} \eta _d=\cosh ^{-1}\left( \frac{2dH+\sqrt{1-4H^2+d^2}}{1-4H^2}\right) \end{aligned}$$

and let $\lambda _d:[\eta _d,\infty )\rightarrow [0,\infty )$ be the function defined as follows.

$$\begin{aligned} \lambda _d(\rho )= \int ^{\rho }_{\eta _d} \frac{d+2H\cosh r}{\sqrt{\sinh ^2 r - ( d+2H\cosh r)^2}}dr. \end{aligned}$$

(1)

Note that $\lambda _d(\rho )$ is a strictly increasing function with $\lim _{\rho \rightarrow \infty }\lambda _d(\rho )= \infty$ and derivative $\lambda '_d(\eta _d)=\infty$ when $d\in (-2H,\infty )$.

In [8] Nelli, Sa Earp, Santos and Toubiana proved that there exists a 1-parameter family of embedded H-catenoids $\{\mathcal {C}^H_d \ | \ d\in (-2H,\infty )\}$ obtained by rotating a generating curve $\lambda _d(\rho )$ about the t-axis. The generating curve $\widehat{\lambda }_d$ is obtained by doubling the curve $(\rho , 0, \lambda _d(\rho ))$, $\rho \in [\eta _d,\infty )$, with its reflection $(\rho , 0, -\lambda _d(\rho ))$, $\rho \in [\eta _d,\infty )$. Note that $\widehat{\lambda }_d$ is a smooth curve and that the necksize, $\eta _d$, is a strictly increasing function in d satisfying the properties that $\eta _{-2H}=0$ and $\lim _{d\rightarrow \infty }\eta _d=\infty$.

If $d=-2H$, then by rotating the curve $(\rho , 0, \lambda _d(\rho ))$ around the t-axis one obtains a simply-connected H-surface $E_H$ that is an entire graph over $\mathbb H^2_0$. We denote by $-E_H$ the reflection of $E_H$ across $\mathbb H^2_0$.

We next recall the definition of the mean curvature vector.

Definition 2.1

Let M be an oriented surface in an oriented Riemannian three-manifold and suppose that M has non-zero mean curvature H(p) at p. The mean curvature vector at p is $\mathbf {H}(p):=H(p)N(p)$, where N(p) is its unit normal vector at p. The mean curvature vector $\mathbf {H}(p)$ is independent of the orientation on M.

Note that the mean curvature vector $\mathbf {H}$ of $\mathcal {C}^H_d$ points into the connected component of ${\mathbb H}^2\times {\mathbb R}-\mathcal {C}^H_d$ that contains the t-axis. The mean curvature vector of $E_H$ points upward while the mean curvature vector of $-E_H$ points downward.

In order to construct the examples described in Theorem 1.1, we first obtain certain geometric properties satisfied by H-catenoids. For example, in the following lemma, we show that for certain values of $d_1$ and $d_2$, the catenoids $\mathcal {C}^H_{d_1}$ and $\mathcal {C}^H_{d_2}$ are disjoint.

Given $d\in (-2H,\infty )$, let $b_{d}(t):=\lambda _d^{-1}(t)$ for $t\ge 0$; note that $b_d(0)=\eta _{d}$. Abusing the notation let $b_d(t):=b_d(-t)$ for $t\le 0$.

Lemma 2.1

(Disjoint H-catenoids) Given $d_1>2$, there exist $d_0>d_1$ and $\delta _0>0$ such that for any $d_2\in [d_0,\infty )$, then

$$\begin{aligned} \inf _{t\in \mathbb R}( b_{d_2}(t)-b_{d_1}(t))\ge \delta _0. \end{aligned}$$

In particular, the corresponding H-catenoids are disjoint, i.e. $\mathcal {C}^H_{d_1}\cap \mathcal {C}^H_{d_2}=\emptyset$.

Moreover, $b_{d_2}(t)-b_{d_1}(t)$ is decreasing for $t>0$ and increasing for $t<0$. In particular,

$$\begin{aligned} \sup _{t\in \mathbb R}( b_{d_2}(t)-b_{d_1}(t))=b_{d_2}(0)-b_{d_1}(0)= \eta _{d_2}-\eta _{d_1}. \end{aligned}$$

The proof of the above lemma requires a rather lengthy computation that is given in the Appendix.

We next recall the well-known mean curvature comparison principle.

Proposition 2.2

(Mean curvature comparison principle) Let $M_1$ and $M_2$ be two complete, connected embedded surfaces in a three-dimensional Riemannian manifold. Suppose that $p\in M_1\cap M_2$ satisfies that a neighborhood of p in $M_1$ locally lies on the side of a neighborhood of p in $M_2$ into which $\mathbf {H}_2(p)$ is pointing. Then $|H_1|(p)\ge |H_2|(p)$. Furthermore, if $M_1$ and $M_2$ are constant mean curvature surfaces with $|H_1|=|H_2|$, then $M_1 =M_2$.

3 The examples

For a fixed $H\in (0,1/2)$, the outline of construction is as follows. First, we will take two disjoint H-catenoids $\mathcal {C}_1$ and $\mathcal {C}_2$ whose existence is given in Lemma 2.1. These catenoids $\mathcal {C}_1$, $\mathcal {C}_2$ bound a region $\Omega$ in ${\mathbb H}^2\times {\mathbb R}$ with fundamental group $\mathbb {Z}$. In the universal cover $\widetilde{\Omega }$ of $\Omega$, we define a piecewise smooth compact exhaustion $\Delta _1\subset \Delta _2\subset \cdots \subset \Delta _n\subset \cdots$ of $\widetilde{\Omega }$. Then, by solving the H-Plateau problem for special curves $\Gamma _n\subset \partial \Delta _n$, we obtain minimizing H-surfaces $\Sigma _n$ in $\Delta _n$ with $\partial \Sigma _n=\Gamma _n$. In the limit set of these surfaces, we find an H-plane $\mathcal {P}$ whose projection to $\Omega$ is the desired non-proper H-plane $\Sigma _H\subset {\mathbb {H}}^2\times \mathbb {R}$.

3.1 Construction of $\widetilde{\Omega }$

Fix $H\in (0,\frac{1}{2})$ and $d_1,d_2\in (2,\infty )$, $d_1<d_2$, such that by Lemma 2.1, the related H-catenoids $\mathcal {C}^H_{d_1}$ and $\mathcal {C}^H_{d_2}$ are disjoint; note that in this case, $\mathcal {C}_{d_1}^H$ lies in the interior of the simply-connected component of ${\mathbb H}^2\times {\mathbb R}-\mathcal {C}^H_{d_2}$. We will use the notation $\mathcal {C}_i:= \mathcal {C}^H_{d_i}$. Recall that both catenoids have the same rotational axis, namely the t-axis, and recall that the mean curvature vector $\mathbf {H}_i$ of $\mathcal {C}_i$ points into the connected component of ${\mathbb H}^2\times {\mathbb R}-\mathcal {C}_i$ that contains the t-axis. We emphasize here that H is fixed and so we will omit describing it in future notations.

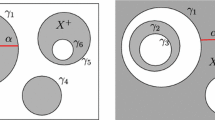
Let $\Omega$ be the closed region in ${\mathbb H}^2\times {\mathbb R}$ between $\mathcal {C}_1$ and $\mathcal {C}_2$, i.e., $\partial \Omega = \mathcal {C}_1\cup \mathcal {C}_2$ (Fig. 1-left). Notice that the set of boundary points at infinity $\partial _{\infty }\Omega$ is equal to $S^1_{\infty }\times \{-\infty \} \cup S^1_{\infty }\times \{\infty \}$, i.e., the corner circles in $\partial _\infty {\mathbb H}^2\times {\mathbb R}$ in the product compactification, where we view ${\mathbb {H}}^2$ to be the open unit disk $\{(x,y)\in \mathbb {R}^2 \mid x^2+y^2<1\}$ with base point the origin $\vec {0}$.

Fig. 1

The induced coordinates $(\rho , \widetilde{\theta }, t)$ in $\widetilde{\Omega }$

By construction, $\Omega$ is topologically a solid torus. Let $\widetilde{\Omega }$ be the universal cover of $\Omega$. Then, $\partial \widetilde{\Omega } = \widetilde{\mathcal {C}}_1\cup \widetilde{\mathcal {C}}_2$ (Fig. 1-right), where $\widetilde{\mathcal {C}}_1,\widetilde{\mathcal {C}}_2$ are the respective lifts to $\widetilde{\Omega }$ of ${\mathcal {C}}_1, {\mathcal {C}}_2$. Notice that $\widetilde{\mathcal {C}}_1$ and $\widetilde{\mathcal {C}}_2$ are both H-planes, and the mean curvature vector $\mathbf {H}$ points outside of $\widetilde{\Omega }$ along $\widetilde{\mathcal {C}}_1$ while $\mathbf {H}$ points inside of $\widetilde{\Omega }$ along $\widetilde{\mathcal {C}}_2$. We will use the induced coordinates $(\rho , \widetilde{\theta }, t)$ on $\widetilde{\Omega }$ where $\widetilde{\theta }\in (-\infty , \infty )$. In particular, if

$$\begin{aligned} \Pi :\widetilde{\Omega }\rightarrow \Omega \end{aligned}$$

(2)

is the covering map, then $\Pi (\rho _o, \widetilde{\theta }_o, t_o)= (\rho _o, \theta _o, t_o)$ where $\theta _o\equiv \widetilde{\theta _o} \mod 2\pi$.

Recalling the definition of $b_i(t)$, $i=1,2$, note that a point $(\rho , \theta , t)$ belongs to $\Omega$ if and only if $\rho \in [b_1(t), b_2(t)]$ and we can write

$$\begin{aligned} \widetilde{\Omega }= \{ (\rho , \widetilde{\theta }, t) \ | \ \rho \in [b_1(t), b_2(t)], \ \widetilde{\theta }\in \mathbb R,\ t\in \mathbb R\}. \end{aligned}$$

3.2 Infinite bumps in $\widetilde{\Omega }$

Let $\gamma$ be the geodesic through the origin in $\mathbb H^2_0$ obtained by intersecting $\mathbb H^2_0$ with the vertical plane $\{\theta =0\} \cup \{\theta =\pi \}$. For $s\in [0,\infty )$, let $\varphi _s$ be the orientation preserving hyperbolic isometry of $\mathbb H^2_0$ that is the hyperbolic translation along the geodesic $\gamma$ with $\varphi _s(0,0)=(s,0)$. Let

$$\begin{aligned} \widehat{\varphi }_s:{\mathbb H}^2\times {\mathbb R}\rightarrow {\mathbb H}^2\times {\mathbb R}, \quad \widehat{\varphi }_s(\rho ,\theta ,t)=(\varphi _s(\rho ,\theta ),t) \end{aligned}$$

(3)

be the related extended isometry of ${\mathbb H}^2\times {\mathbb R}$.

Let $\mathcal {C}_d$ be an embedded H-catenoid as defined in Sect. 2.1. Notice that the rotation axis of the H-catenoid $\widehat{\varphi }_{s_0}(\mathcal {C}_d)$ is the vertical line $\{ (s_0, 0, t) \mid t\in \mathbb R\}$.

Let $\delta :=\inf _{t\in \mathbb R}(b_2(t)-b_1(t))$, which gives an upper bound estimate for the asymptotic distance between the catenoids; recall that by our choices of $\mathcal {C}_1,\mathcal {C}_2$ given in Lemma 2.1, we have $\delta >0$. Let $\delta _1=\frac{1}{2}\min \{\delta , \eta _1\}$ and let $\delta _2=\delta -\frac{\delta _1}{2}$. Let $\widehat{\mathcal {C}}_{1}:=\widehat{\varphi }_{\delta _1}(\mathcal {C}_1)$ and $\widehat{\mathcal {C}}_{2}:=\widehat{\varphi }_{-\delta _2}(\mathcal {C}_2)$. Note that $\delta _1+\delta _2>\delta$.

Claim 3.1

The intersection $\Omega \cap \widehat{\mathcal {C}}_{i}$, $i=1,2$, is an infinite strip.

Proof

Given $t\in \mathbb R$, let $\mathbb H^2_t$ denote $\mathbb H^2\times \{t\}$. Let $\tau ^i_t:=\mathcal {C}_i\cap \mathbb H^2_t$ and $\widehat{\tau }^i_t:=\widehat{\mathcal {C}}_i\cap \mathbb H^2_t$. Note that for $i=1,2$, $\tau ^i_t$ is a circle in $\mathbb H^2_t$ of radius $b_i(t)$ centered at (0, 0, t) while $\widehat{\tau }^1_t$ is a circle in $\mathbb H^2_t$ of radius $b_1(t)$ centered at $p_{1,t}:=(\delta _1,0,t)$ and $\widehat{\tau }^2_t$ is a circle in $\mathbb H^2_t$ of radius $b_2(t)$ centered at $p_{2,t}:=(-\delta _2,0,t)$. We claim that for any $t\in \mathbb R$, the intersection $\widehat{\tau }^i_t\cap \Omega$ is an arc with end points in $\tau ^i_t$, $i=1,2$. This result would give that $\Omega \cap \widehat{\mathcal {C}}_{i}$ is an infinite strip. We next prove this claim.

Consider the case $i=1$ first. Since $\delta _1<\eta _1\le b_1(t)$, the center $p_{1,t}$ is inside the disk in $\mathbb H^2_t$ bounded by $\tau ^1_t$. Since the radii of $\tau ^1_t$ and $\widehat{\tau }^1_t$ are both equal to $b_1(t)$, then the intersection $\tau ^1_t\cap \widehat{\tau }^1_t$ is nonempty. It remains to show that $\widehat{\tau }^1_t\cap \tau ^2_t=\emptyset$, namely that $b_1(t)+\delta _1<b_2(t)$. This follows because

$$\begin{aligned} \delta _1<\delta =\inf _{t\in \mathbb R}(b_2(t)-b_1(t)). \end{aligned}$$

This argument shows that $\Omega \cap \widehat{\mathcal {C}}_{1}$ is an infinite strip.

Consider now the case $i=2$. Since $\delta _2<\delta < b_2(t)$, the center $p_{2,t}$ is inside the disk in $\mathbb H^2_t$ bounded by $\tau ^2_t$. Since the radii of $\tau ^2_t$ and $\widehat{\tau }^2_t$ are both equal to $b_2(t)$, then the intersection $\tau ^2_t\cap \widehat{\tau }^2_t$ is nonempty. It remains to show that $\tau ^1_t\cap \widehat{\tau }^2_t=\emptyset$, namely that $b_2(t)-\delta _2>b_1(t)$. This follows because

$$\begin{aligned} b_2(t)-b_1(t)\ge \inf _{t\in \mathbb R}(b_2(t)-b_1(t))=\delta >\delta _2 \end{aligned}$$

This completes the proof that $\Omega \cap \widehat{\mathcal {C}}_{2}$ is an infinite strip and finishes the proof of the claim. $\square$

Fig. 2

The position of the bumps $\mathcal {B}^\pm$ in $\widetilde{\Omega }$ is shown in the picture. The small arrows show the mean curvature vector direction. The H-surfaces $\Sigma _n$ are disjoint from the infinite strips $\mathcal {B}^\pm$ by construction

Now, let $Y^+:=\Omega \cap \widehat{\mathcal {C}}_2$ and let $Y^-:=\Omega \cap \widehat{\mathcal {C}}_1$. In light of Claim 3.1 and its proof, we know that $Y^+\cap \mathcal {C}_1=\emptyset$ and $Y^-\cap \mathcal {C}_2=\emptyset$.

Remark 3.2

Note that by construction, any rotational surface contained in $\Omega$ must intersect $\widehat{\mathcal {C}}_{1}\cup \widehat{\mathcal {C}}_{2}$. In particular, $Y^+\cup Y^-$ intersects all H-catenoids $\mathcal {C}_d$ for $d\in (d_1,d_2)$ as the circles $\mathcal {C}_d\cap \mathbb H^2_t$ intersect either the circle $\widehat{\tau }^2_t$ or the circle $\widehat{\tau }^1_t$ for some $t>0$ since $\delta _1+\delta _2>\delta$.

In $\widetilde{\Omega }$, let $\mathcal {B}^+$ be the lift of $Y^+$ in $\widetilde{\Omega }$ which intersects the slice $\{\widetilde{\theta }=-10\pi \}$. Similarly, let $\mathcal {B}^-$ be the lift of $Y^-$ in $\widetilde{\Omega }$ which intersects the slice $\{\widetilde{\theta }=10\pi \}$. Note that each lift of $Y^+$ or $Y^-$is contained in a region where the $\widetilde{\theta }$ values of their points lie in ranges of the form $(\theta _0-\pi ,\theta _0+ \pi )$ and so $\mathcal {B}^+\cap \mathcal {B}^-=\emptyset$. See Fig. 2.

The H-surfaces $\mathcal {B}^\pm$ near the top and bottom of $\widetilde{\Omega }$ will act as barriers (infinite bumps) in the next section, ensuring that the limit H-plane of a certain sequence of compact H-surfaces does not collapse to an H-lamination of $\widetilde{\Omega }$ all of whose leaves are invariant under translations in the $\widetilde{\theta }$-direction.

Next we modify $\widetilde{\Omega }$ as follows. Consider the component of $\widetilde{\Omega }-(\mathcal {B}^+\cup \mathcal {B}^-)$ containing the slice $\{\widetilde{\theta }=0\}$. From now on we will call the closure of this region $\widetilde{\Omega }^*$.

3.3 The compact exhaustion of $\widetilde{\Omega }^*$

Consider the rotationally invariant H-planes $E_H,-E_H$ described in Sect. 2. Recall that $E_H$ is a graph over the horizontal slice $\mathbb H^2_0$ and it is also tangent to $\mathbb H^2_0$ at the origin. Given $t\in \mathbb R$, let $E_H^t=-E_H+(0,0,t)$ and $-E_H^t=E_H-(0,0,t)$. Both families $\{E_H^t\}_{t\in \mathbb R}$ and $\{-E_H^t\}_{t\in \mathbb R}$ foliate ${\mathbb H}^2\times {\mathbb R}$. Moreover, there exists $n_0\in \mathbb N$ such that for any $n>n_0$, $n\in \mathbb N$, the following holds. The highest (lowest) component of the intersection $S_n^+:=E_H^n\cap \Omega$ ($S_n^-:=-E_H^n\cap \Omega$) is a rotationally invariant annulus with boundary components contained in $\mathcal {C}_1$ and $\mathcal {C}_2$. The annulus $S_n^+$ lies “above” $S_n^-$ and their intersection is empty. The region $\mathcal {U}_n$ in $\Omega$ between $S_n^+$ and $S_n^-$ is a solid torus, see Fig. 3-left, and the mean curvature vectors of $S_n^+$ and $S_n^-$ point into $\mathcal {U}_n$.

Fig. 3

$\mathcal {U}_n = \Omega \cap \widehat{\mathcal {U}}_n$ and $\widetilde{\mathcal {U}}_n$ denotes its universal cover. Note that $\partial \widetilde{\mathcal {U}}_n\subset \widetilde{\mathcal {C}}_1\cup \widetilde{\mathcal {C}}_2\cup \widetilde{S}^+_n\cup \widetilde{S}^-_n$

Let $\widetilde{\mathcal {U}}_n\subset \widetilde{\Omega }$ be the universal cover of $\mathcal {U}_n$, see Fig. 3-right. Then, $\partial \widetilde{\mathcal {U}}_n- \partial \widetilde{\Omega }= \widetilde{S}_n^+\cup \widetilde{S}_n^-$ where can view $\widetilde{S}_n^\pm$ as a lift to $\widetilde{\mathcal {U}}_n$ of the universal cover of the annulus $S_n^\pm$. Hence, $\widetilde{S}_n^\pm$ is an infinite H-strip in $\widetilde{\Omega }$, and the mean curvature vectors of the surfaces $\widetilde{S}_n^+, \widetilde{S}_n^-$ point into $\widetilde{\mathcal {U}}_n$ along $\widetilde{S}_n^\pm$. Note that each $\widetilde{\mathcal {U}}_n$ has bounded t-coordinate. Furthermore, we can view $\widetilde{\mathcal {U}}_n$ as $(\mathcal {U}_n\cap \mathcal {P}_0)\times \mathbb R$, where $\mathcal {P}_0$ is the half-plane $\{\theta =0\}$ and the second coordinate is $\widetilde{\theta }$. Abusing the notation, we redefine $\widetilde{\mathcal {U}}_n$ to be $\widetilde{\mathcal {U}}_n\cap \widetilde{\Omega }^*$, that is we have removed the infinite bumps $\mathcal {B}^\pm$ from $\widetilde{\mathcal {U}}_n$.

Now, we will perform a sequence of modifications of $\widetilde{\mathcal {U}}_n$ so that for each of these modifications, the $\widetilde{\theta }$-coordinate in $\widetilde{\mathcal {U}}_n$ is bounded and so that we obtain a compact exhaustion of $\widetilde{\Omega }^*$. In order to do this, we will use arguments that are similar to those in Claim 3.1. Recall that the necksize of $\mathcal {C}_2$ is $\eta _2=b_2(0)$. Let $\widehat{\mathcal {C}}_3= \widehat{\varphi }_{\eta _2}(\mathcal {C}_2)$, see equation (3) for the definition of $\widehat{\varphi }_{\eta _2}$. Then, $\widehat{\mathcal {C}}_3$ is a rotationally invariant catenoid whose rotational axis is the line $(\eta _2, 0)\times \mathbb R$ (Fig. 4-left).

Lemma 3.3

The intersection $\widehat{\mathcal {C}}_3\cap \Omega$ is a pair of infinite strips.

Proof

It suffices to show that $\widehat{\mathcal {C}}_3\cap \mathcal {C}_1$ and $\widehat{\mathcal {C}}_3\cap \mathcal {C}_2$ each consists of a pair of infinite lines. Now, consider the horizontal circles $\tau ^1_t, \tau ^2_t$, and $\widehat{\tau }^3_t$ in the intersection of $\mathbb H^2_t$ and $\mathcal {C}_1,\mathcal {C}_2$, and $\widehat{\mathcal {C}}_3$ respectively, where $\mathbb H^2_t= \mathbb H^2\times \{t\}$. For any $t\in \mathbb R$, $\tau ^i_t$ is a circle of radius $b_i(t)$ in $\mathbb H^2_t$ with center (0, 0, t). Similarly, $\widehat{\tau }^3_t$ is a circle of radius $b_2(t)$ in $\mathbb H^2_t$ with center $(\eta _2,0,t)$, see Fig. 4-right. Hence, it suffices to show that for any $t\in \mathbb R$ each of the intersection $\tau ^1_t\cap \widehat{\tau }^3_t$ and $\tau ^2_t\cap \widehat{\tau }^3_t$ consists of two points.

Fig. 4

$\tau ^i_t=\mathcal {C}_i\cap \mathbb H^2_t$ is a round circle of radius $b_i(t)$ with center O. $\widehat{\tau }^3_t=\widehat{\mathcal {C}}_3\cap \mathbb H^2_t$ is a round circle of radius $b_2(t)$ with center $C=(\eta _2,0,t)$

By construction, it is easy to see $\tau ^2_t\cap \widehat{\tau }^3_t$ consists of two points. This is because $\tau ^2_t$ and $\widehat{\tau }^3_t$ have the same radius, $b_2(t)$ and $\eta _2+b_2(t)>b_2(t)$ and $\eta _2-b_2(t)>-b_2(t)$. Therefore, it remains to show that $\tau ^1_t\cap \widehat{\tau }^3_t$ consists of two points. By construction, this would be the case if $\eta _2-b_2(t)<b_1(t)$ and $\eta _2-b_2(t)>-b_1(t)$. The first inequality follows because $\eta _2=\inf _{t\in \mathbb R}b_2(t)$. The second inequality follows from Lemma 2.1 because

$$\begin{aligned} \eta _2>\eta _2-\eta _1=\sup _{t\in \mathbb R}(b_2(t)-b_1(t)). \end{aligned}$$

$\square$

Now, let $\widehat{\mathcal {C}}_3\cap \Omega = T^+\cup T^-$, where $T^+$ is the infinite strip with $\theta \in (0,\pi )$, and $T^-$ is the infinite strip with $\theta \in (-\pi ,0)$. Note that $T^\pm$ is a $\theta$-graph over the infinite strip $\widehat{\mathcal {P}}_0=\Omega \cap \mathcal {P}_0$ where $\mathcal {P}_0$ is the half plane $\{\theta =0\}$. Let $\mathcal {V}$ be the component of $\Omega -\widehat{C}_3$ containing $\widehat{\mathcal {P}}_0$. Notice that the mean curvature vector $\mathbf {H}$ of $\partial \mathcal {V}$ points into $\mathcal {V}$ on both $T^+$ and $T^-$.

Consider the lifts of $T^+$ and $T^-$ in $\widetilde{\Omega }$. For $n\in \mathbb {Z}$, let $\widetilde{T}^+_n$ be the lift of $T^+$ which belongs to the region $\widetilde{\theta }\in (2n\pi , (2n+1)\pi )$. Similarly, let $\widetilde{T}^-_n$ be the lift of $T^-$ which belongs to the region $\widetilde{\theta }\in ((2n-1)\pi , 2n\pi )$. Let $\mathcal {V}_n$ be the closed region in $\widetilde{\Omega }$ between the infinite strips $\widetilde{T}^-_{-n}$ and $\widetilde{T}^+_n$. Notice that for n sufficiently large, $\mathcal {B}^\pm \subset \mathcal {V}_n$.

Next we define the compact exhaustion $\Delta _n$ of $\widetilde{\Omega }^*$ as follows: $\Delta _n:=\widetilde{\mathcal {U}}_n\cap \mathcal {V}_n$. Furthermore, the absolute value of the mean curvature of $\partial \Delta _n$ is equal to H and the mean curvature vector $\mathbf {H}$ of $\partial \Delta _n$ points into $\Delta _n$ on $\partial \Delta _n-[(\partial \Delta _n\cap \widetilde{\mathcal {C}}_1)\cup \mathcal {B}^-]$.

3.4 The sequence of H-surfaces

We next define a sequence of compact H-surfaces $\{\Sigma _n\}_{n\in \mathbb {N}}$ where $\Sigma _n\subset \Delta _n$. For each n sufficiently large, we define a simple closed curve $\Gamma _n$ in $\partial \Delta _n$, and then we solve the H-Plateau problem for $\Gamma _n$ in $\Delta _n$. This will provide an embedded H-surface $\Sigma _n$ in $\Delta _n$ with $\partial \Sigma _n=\Gamma _n$ for each n.

The Construction of $\Gamma _n$ in $\partial \Delta _n:$

First, consider the annulus $\mathcal {A}_n=\partial \Delta _n-(\widetilde{\mathcal {C}}_1\cup \widetilde{\mathcal {C}}_2\cup \mathcal {B}^+\cup \mathcal {B}^-)$ in $\partial \Delta _n$. Let $\widehat{l}_n^+= \widetilde{\mathcal {C}}_1\cap \widetilde{T}^+_n$, and $\widehat{l}_n^-= \widetilde{\mathcal {C}}_2\cap \widetilde{T}^-_{-n}$ be the pair of infinite lines in $\widetilde{\Omega }$. Let $l^\pm _n=\widehat{l}^\pm _n\cap \mathcal {A}_n$. Let $\mu _n^+$ be an arc in $\widetilde{S}^+_n\cap \mathcal {A}_n$, whose $\widetilde{\theta }$ and $\rho$ coordinates are strictly increasing as a function of the parameter and whose endpoints are $l^+_n\cap \widetilde{S}^+_n$ and $l^-_n\cap \widetilde{S}^+_n$ (Fig. 5-left). Similarly, define $\mu _n^-$ to be a monotone arc in $\widetilde{S}^-_n\cap \mathcal {A}_n$ whose endpoints are $l^+_n\cap \widetilde{S}^-_n$ and $l^-_n\cap \widetilde{S}^-_n$. Note that these arcs $\mu ^+_n$ and $\mu ^-_n$ are by construction disjoint from the infinite bumps $\mathcal {B}^\pm$. Then, $\Gamma _n=\mu ^+_n\cup l^+_n \cup \mu ^-_n\cup l^-_n$ is a simple closed curve in $\mathcal {A}_n\subset \partial \Delta _n$ (Fig. 5-right).

Fig. 5

In the left, $\mu ^n_+$ is pictured in $\widetilde{S}^+_n$. On the right, the curve $\Gamma _n$ is described in $\partial \Delta _n$

Next, consider the following variational problem (H-Plateau problem): Given the simple closed curve $\Gamma _n$ in $\mathcal {A}_n$, let M be a smooth compact embedded surface in $\Delta _n$ with $\partial M=\Gamma _n$. Since $\Delta _n$ is simply-connected, M separates $\Delta _n$ into two regions. Let Q be the region in $\Delta _n-\Sigma$ with $Q\cap \widetilde{\mathcal {C}}_2\ne \emptyset$, the “upper” region. Then define the functional $\mathcal {I}_H=\hbox {Area}(M)+2H\,\hbox {Volume}(Q)$.

By working with integral currents, it is known that there exists a smooth (except at the 4 corners of $\Gamma _n$), compact, embedded H-surface $\Sigma _n\subset \Delta _n$ with $\text {Int}(\Sigma _n)\subset \text {Int}(\Delta _n)$ and $\partial \Sigma _n=\Gamma _n$. Note that in our setting, $\Delta _n$ is not H-mean convex along $\Delta _n\cap \widetilde{\mathcal {C}}_1$. However, the mean curvature vector along $\Sigma _n$ points outside Q because of the construction of the variational problem. Therefore $\Delta _n\cap \widetilde{\mathcal {C}}_1$ is still a good barrier for solving the H-Plateau problem. In fact, $\Sigma _n$ can be chosen to be, and we will assume it is, a minimizer for this variational problem, i.e., $I(\Sigma _n)\le I(M)$ for any $M\subset \Delta _n$ with $\partial M =\Gamma _n$; see for instance [12, Theorem 2.1] and [1, Theorem 1]. In particular, the fact that $\text {Int}(\Sigma _n)\subset \text {Int}(\Delta _n)$ is proven in Lemma 3 of [4]. Moreover, $\Sigma _n$ separates $\Delta _n$ into two regions.

Similarly to Lemma 4.1 in [3], in the following lemma we show that for any such $\Gamma _n$, the minimizer surface $\Sigma _n$ is a $\widetilde{\theta }$-graph.

Lemma 3.4

Let $E_n:=\mathcal {A}_n\cap \widetilde{T}^+_n$. The minimizer surface $\Sigma _n$ is a $\widetilde{\theta }$-graph over the compact disk $E_n$. In particular, the related Jacobi function $J_n$ on $\Sigma _n$ induced by the inner product of the unit normal field to $\Sigma _n$ with the Killing field $\partial _{\widetilde{\theta }}$ is positive in the interior of $\Sigma _n$.

Proof

The proof is almost identical to the proof of Lemma 4.1 in [3], and for the sake of completeness, we give it here. Let $T_\alpha$ be the isometry of $\widetilde{\Omega }$ which is a translation by $\alpha$ in the $\widetilde{\theta }$ direction, i.e.,

$$\begin{aligned} T_{\alpha }(\rho , \widetilde{\theta }, t)=(\rho , \widetilde{\theta }+\alpha , t). \end{aligned}$$

(4)

Let $T_\alpha (\Sigma _n)=\Sigma ^\alpha _n$ and $T_\alpha (\Gamma _n)=\Gamma ^\alpha _n$. We claim that $\Sigma ^\alpha _n\cap \Sigma _n=\emptyset$ for any $\alpha \in {\mathbb {R}}\setminus \{0\}$ which implies that $\Sigma _n$ is a $\widetilde{\theta }$-graph; we will use that $\Gamma ^\alpha _n$ is disjoint from $\Sigma _n$ for any $\alpha \in {\mathbb {R}}\setminus \{0\}$.

Arguing by contradiction, suppose that $\Sigma ^\alpha _n\cap \Sigma _n\ne \emptyset$ for a certain $\alpha \ne 0$. By compactness of $\Sigma _n$, there exists a largest positive number $\alpha '$ such that $\Sigma ^{\alpha '}_n\cap \Sigma _n\ne \emptyset$. Let $p\in \Sigma ^{\alpha '}_n\cap \Sigma _n$. Since $\partial \Sigma ^{\alpha '}_n \cap \partial \Sigma _n =\emptyset$ and the interior of $\Sigma _n$, respectively $\Sigma ^{\alpha '}_n$, lie in the interior of $\Delta _n$, respectively $T_{\alpha '}(\Delta _n)$, then $p\in \mathrm{Int}(\Sigma ^{\alpha '}_n) \cap \mathrm{Int}(\Sigma _n)$. Since the surfaces $\mathrm{Int}(\Sigma ^{\alpha '}_n)$, $\mathrm{Int}(\Sigma _n)$ lie on one side of each other and intersect tangentially at the point p with the same mean curvature vector, then we obtain a contradiction to the mean curvature comparison principle for constant mean curvature surfaces, see Proposition 2.2. This proves that $\Sigma _n$ is graphical over its $\widetilde{\theta }$-projection to $E_n$.

Since by construction every integral curve, $(\overline{\rho },s,\overline{t})$ with $\overline{\rho }, \overline{t}$ fixed and $(\overline{\rho },s_0, \overline{t})\in E_n$ for a certain $s_0$, of the Killing field $\partial _{\widetilde{\theta }}$ has non-zero intersection number with any compact surface bounded by $\Gamma _n$, we conclude that every such integral curve intersects both the disk $E_n$ and $\Sigma _n$ in single points. This means that $\Sigma _n$ is a $\widetilde{\theta }$-graph over $E_n$ and thus the related Jacobi function $J_n$ on $\Sigma _n$ induced by the inner product of the unit normal field to $\Sigma _n$ with the Killing field $\partial _{\widetilde{\theta }}$ is non-negative in the interior of $\Sigma _n$. Since $J_n$ is a non-negative Jacobi function, then either $J_n\equiv 0$ or $J_n>0$. Since by construction $J_n$ is positive somewhere in the interior, then $J_n$ is positive everywhere in the interior. This finishes the proof of the lemma. $\square$

4 The proof of Theorem 1.1

With $\Gamma _n$ as previously described, we have so far constructed a sequence of compact stable H-disks $\Sigma _n$ with $\partial \Sigma _n = \Gamma _n \subset \partial \Delta _n$. Let $J_n$ be the related non-negative Jacobi function described in Lemma 3.4.

By the curvature estimates for stable H-surfaces given in [11], the norms of the second fundamental forms of the $\Sigma _n$ are uniformly bounded from above at points which are at intrinsic distance at least one from their boundaries. Since the boundaries of the $\Sigma _{n}$ leave every compact subset of $\widetilde{\Omega }^*$, for each compact set of $\widetilde{\Omega }^*$, the norms of the second fundamental forms of the $\Sigma _n$ are uniformly bounded for values n sufficiently large and such a bound does not depend on the chosen compact set. Standard compactness arguments give that, after passing to a subsequence, $\Sigma _n$ converges to a (weak) H-lamination $\widetilde{\mathcal {L}}$ of $\widetilde{\Omega }^*$ and the leaves of $\widetilde{\mathcal {L}}$ are complete and have uniformly bounded norm of their second fundamental forms, see for instance [5].

Let $\beta$ be a compact embedded arc contained in $\widetilde{\Omega }^*$ such that its end points $p_+$ and $p_-$ are contained respectively in $\mathcal {B}^+$ and $\mathcal {B}^-$, and such that these are the only points in the intersection $[\mathcal {B}^+\cup \mathcal {B}^-]\cap \beta$. Then, for n-sufficiently large, the linking number between $\Gamma _n$ and $\beta$ is one, which gives that, for n sufficiently large, $\Sigma _n$ intersects $\beta$ in an odd number of points. In particular $\Sigma _n\cap \beta \ne \emptyset$ which implies that the lamination $\widetilde{\mathcal {L}}$ is not empty.

Remark 4.1

By Remark 3.2, a leaf of $\widetilde{\mathcal {L}}$ that is invariant with respect to $\widetilde{\theta }$-translations cannot be contained in $\widetilde{\Omega }^*$. Therefore none of the leaves of $\widetilde{\mathcal {L}}$ are invariant with respect to $\widetilde{\theta }$-translations.

Let $\widetilde{L}$ be a leaf of $\widetilde{\mathcal {L}}$ and let $J_{\widetilde{L}}$ be the Jacobi function induced by taking the inner product of $\partial _{\widetilde{\theta }}$ with the unit normal of $\widetilde{L}$. Then, by the nature of the convergence, $J_{\widetilde{L}}\ge 0$ and therefore since it is a Jacobi field, it is either positive or identically zero. In the latter case, $\widetilde{\mathcal {L}}$ would be invariant with respect to $\widetilde{\theta }$-translations, contradicting Remark 4.1. Thus, by Remark 4.1, we have that $J_{\widetilde{L}}$ is positive and therefore $\widetilde{L}$ is a Killing graph with respect to $\partial _{\widetilde{\theta }}$.

Claim 4.2

Each leaf $\widetilde{L}$ of $\widetilde{\mathcal {L}}$ is properly embedded in $\widetilde{\Omega }^*$.

Proof

Arguing by contradiction, suppose there exists a leaf $\widetilde{L}$ of $\widetilde{\mathcal {L}}$ that is NOT proper in $\widetilde{\Omega }^*$. Then, since the leaf $\widetilde{L}$ has uniformly bounded norm of its second fundamental form, the closure of $\widetilde{L}$ in $\widetilde{\Omega }^*$ is a lamination of $\widetilde{\Omega }^*$ with a limit leaf $\Lambda$, namely $\Lambda \subset \overline{\widetilde{L}}-\widetilde{L}$. Let $J_{\Lambda }$ be the Jacobi function induced by taking the inner product of $\partial _{\widetilde{\theta }}$ with the unit normal of $\Lambda$.

Just like in the previous discussion, by the nature of the convergence, $J_{\Lambda }\ge 0$ and therefore, since it is a Jacobi field, it is either positive or identically zero. In the latter case, $\Lambda$ would be invariant with respect to $\widetilde{\theta }$-translations and thus, by Remark 4.1, $\Lambda$ cannot be contained in $\widetilde{\Omega }^*$. However, since $\Lambda$ is contained in the closure of $\widetilde{ L}$, this would imply that $\widetilde{L}$ is not contained in $\widetilde{\Omega }^*$, giving a contradiction. Thus, $J_{\Lambda }$ must be positive and therefore, $\Lambda$ is a Killing graph with respect to $\partial _{\widetilde{\theta }}$. However, this implies that $\widetilde{L}$ cannot be a Killing graph with respect to $\partial _{\widetilde{\theta }}$. This follows because if we fix a point p in $\Lambda$ and let $U_p\subset \Lambda$ be neighborhood of such point, then by the nature of the convergence, $U_p$ is the limit of a sequence of disjoint domains $U_{p_n}$ in $\widetilde{L}$ where $p_n\in \widetilde{L}$ is a sequence of points converging to p and $U_{p_n}\subset \widetilde{L}$ is a neighborhood of $p_n$. While each domain $U_{p_n}$ is a Killing graph with respect to $\partial _{\widetilde{\theta }}$, the convergence to $U_p$ implies that their union is not. This gives a contradiction and proves that $\Lambda$ cannot be a Killing graph with respect to $\partial _{\widetilde{\theta }}$. Since we have already shown that $\Lambda$ must be a Killing graph with respect to $\partial _{\widetilde{\theta }}$, this gives a contradiction. Thus $\Lambda$ cannot exist and each leaf $\widetilde{L}$ of $\widetilde{\mathcal {L}}$ is properly embedded in $\widetilde{\Omega }^*$. $\square$

Arguing similarly to the proof of the previous claim, it follows that a small perturbation of $\beta$, which we still denote by $\beta$ intersects $\Sigma _n$ and $\widetilde{\mathcal {L}}$ transversally in a finite number of points. Note that $\widetilde{\mathcal {L}}$ is obtained as the limit of $\Sigma _n$. Indeed, since $\Sigma _n$ separates $\mathcal {B}^+$ and $\mathcal {B}^-$ in $\widetilde{\Omega }^*$, the algebraic intersection number of $\beta$ and $\Sigma _n$ must be one, which implies that $\beta$ intersects $\Sigma _n$ in an odd number of points. Then $\beta$ intersects $\widetilde{\mathcal {L}}$ in an odd number of points and the claim below follows.

Claim 4.3

The curve $\beta$ intersects $\widetilde{\mathcal {L}}$ in an odd number of points.

In particular $\beta$ intersects only a finite collection of leaves in $\widetilde{\mathcal {L}}$ and we let $\mathcal {F}$ denote the non-empty finite collection of leaves that intersect $\beta$.

Definition 4.1

Let $(\rho _1, \widetilde{\theta }_0, t_0)$ be a fixed point in $\widetilde{\mathcal {C}}_1$ and let $\rho _2(\widetilde{\theta }_0, t_0)>\rho _1$ such that $(\rho _2(\widetilde{\theta }_0, t_0), \widetilde{\theta }_0, t_0)$ is in $\widetilde{\mathcal {C}}_2$. Then we call the arc in $\widetilde{\Omega }$ given by

$$\begin{aligned} (\rho _1+s(\rho _2-\rho _1), \widetilde{\theta }_0, t_0), \quad s\in [0,1]. \end{aligned}$$

(5)

the vertical line segment based at $(\rho _1, \widetilde{\theta }_0, t_0)$.

Claim 4.4

There exists at least one leaf $\widetilde{L}_{\beta }$ in $\mathcal {F}$ that intersects $\beta$ in an odd number of points and the leaf $\widetilde{L}_{\beta }$ must intersect each vertical line segment at least once.

Proof

The existence of $\widetilde{L}_{\beta }$ follows because otherwise, if all the leaves in $\mathcal {F}$ intersected $\beta$ in an even number of points, then the number of points in the intersection $\beta \cap \mathcal {F}$ would be even. Given $\widetilde{L}_{\beta }$ a leaf in $\mathcal {F}$ that intersects $\beta$ in an odd number of points, suppose there exists a vertical line segment which does not intersect $\widetilde{L}_{\beta }$. Then since by Claim 4.2 $\widetilde{L}_{\beta }$ is properly embedded, using elementary separation arguments would give that the number of points of intersection in $\beta \cap \widetilde{L}_{\beta }$ must be zero mod 2, that is even, contradicting the previous statement. $\square$

Let $\Pi$ be the covering map defined in equation (2) and let $\mathcal {P}_H:=\Pi (\widetilde{L}_{\beta })$. The previous discussion and the fact that $\Pi$ is a local diffeomorphism, implies that $\mathcal {P}_H$ is a stable complete H-surface embedded in $\Omega$. Indeed, $\mathcal {P}_H$ is a graph over its $\theta$-projection to $\mathrm{Int}(\Omega )\cap \{(\rho ,0,t)\mid \rho >0, \, t\in \mathbb {R}\}$, which we denote by $\theta (\mathcal {P}_H)$. Abusing the notation, let $J_{\mathcal {P}_H}$ be the Jacobi function induced by taking the inner product of $\partial _{\theta }$ with the unit normal of $\mathcal {P}_H$, then $J_{\mathcal {P}_H}$ is positive. Finally, since the norm of the second fundamental form of $\mathcal {P}_H$ is uniformly bounded, standard compactness arguments imply that its closure $\overline{\mathcal {P}}_H$ is an H-lamination $\mathcal {L}$ of $\Omega$, see for instance [5].

Claim 4.5

The closure of $\mathcal {P}_H$ is an H-lamination of $\Omega$ consisting of itself and two H-catenoids $L_1, L_2\subset \Omega$ that form the limit set of $\mathcal {P}_H$.

Remark 4.6

Note that these two H-catenoids are not necessarily the ones which determine $\partial \Omega$.

Proof

Given $(\rho _1, \widetilde{\theta }_0, t_0)\in {\widetilde{\mathcal {C}}}_1$, let $\widetilde{\gamma }$ be the fixed vertical line segment in $\widetilde{\Omega }$ based at $(\rho _1, \widetilde{\theta }_0, t_0)$, let $\widetilde{p}_0$ be a point in the intersection $\widetilde{L}_\beta \cap \widetilde{\gamma }$ (recall that by Claim 4.4 such intersection is not empty) and let $p_0=\Pi (\widetilde{p}_0)\in \Pi (\widetilde{\gamma })\cap \mathcal {P}_H$. Then, by Claim 4.4, for any $i\in \mathbb N$, the vertical line segment $T_{2\pi i}(\widetilde{\gamma })$ intersects $\widetilde{L}_\beta$ in at least a point $\widetilde{p}_i$, and $\widetilde{p}_{i+1}$ is above $\widetilde{p}_i$, where T is the translation defined in equation (4). Namely, $\widetilde{p}_0=(r_0, \widetilde{\theta }_0, t_0)$, $\widetilde{p}_i=(r_i, \widetilde{\theta }_0+2\pi i, t_0)$ and $r_i<r_{i+1}<\rho _2(\widetilde{\theta }_0, t_0)$. The point $\widetilde{p_i}\in \widetilde{L}_\beta$ corresponds to the point $p_i= \Pi (\widetilde{p}_i)=(r_i, \widetilde{\theta }_0\, \text {mod}\, 2\pi , t_0)\in \mathcal {P}_H$. Let $r(2):=\lim _{i\rightarrow \infty }r_i$ then $r(2)\le \rho _2(\widetilde{\theta }_0,t_0)$ and note that since $\lim _{i\rightarrow \infty }(r_{i+1}-r_i)=0$, then the value of the Jacobi function $J_{\mathcal {P}_H}$ at $p_i$ must be going to zero as i goes to infinity. Clearly, the point $Q:=(r(2), \widetilde{\theta }_0 \, \text {mod}\, 2\pi , t_0)\in \Omega$ is in the closure of $\mathcal {P}_H$, that is $\mathcal {L}$. Let $L_2$ be the leaf of $\mathcal {L}$ containing Q. By the previous discussion $J_{L_2}(Q)=0$. Since by the nature of the convergence, either $J_{L_2}$ is positive or $L_2$ is rotational, then $L_2$ is rotational, namely an H-catenoid.

Arguing similarly but considering the intersection of $\widetilde{L}_\beta$ with the vertical line segments $T_{-2\pi i}(\widetilde{\gamma })$, $i\in \mathbb N$, one obtains another H-catenoid $L_1$, different from $L_2$, in the lamination $\mathcal {L}$. This shows that the closure of $\mathcal {P}_H$ contains the two H-catenoids $L_1$ and $L_2$.

Let $\Omega _g$ be the rotationally invariant, connected region of $\Omega -[L_1\cup L_2]$ whose boundary contains $L_1\cup L_2$. Note that since $\mathcal {P}_H$ is connected and $L_1\cup L_2$ is contained in its closure, then $\mathcal {P}_H\subset \Omega _g$. It remains to show that $\mathcal {L}=\mathcal {P}_H\cup L_1\cup L_2$, i.e. $\overline{\mathcal {P}}_H-\mathcal {P}_H=L_1\cup L_2$. If $\overline{\mathcal {P}}_H-\mathcal {P}_H\ne L_1\cup L_2$ then there would be another leaf $L_3\in \mathcal {L}\cap \Omega _g$ and by previous argument, $L_3$ would be an H-catenoid. Thus $L_3$ would separate $\Omega _g$ into two regions, contradicting that fact that $\mathcal {P}_H$ is connected and $L_1\cup L_2$ are contained in its closure. This finishes the proof of the claim. $\square$

Note that by the previous claim, $\mathcal {P}_H$ is properly embedded in $\Omega _g$.

Claim 4.7

The H-surface $\mathcal {P}_H$ is simply-connected and every integral curve of $\partial _\theta$ that lies in $\Omega _g$ intersects $\mathcal {P}_H$ in exactly one point.

Proof

Let $D_g:=\mathrm{Int}(\Omega _g)\cap \{(\rho ,0,t)\mid \rho >0, \, t\in \mathbb {R}\}$, then $\mathcal {P}_H$ is a graph over its $\theta$-projection to $D_g$, that is $\theta (\mathcal {P}_H)$. Since $\theta :\Omega _g\rightarrow D_g$ is a proper submersion and $\mathcal {P}_H$ is properly embedded in $\Omega _g$, then $\theta (\mathcal {P}_H)=D_g$, which implies that every integral curve of $\partial _\theta$ that lies in $\Omega _g$ intersects $\mathcal {P}_H$ in exactly one point. Moreover, since $D_g$ is simply-connected, this gives that $\mathcal {P}_H$ is also simply-connected. This finishes the proof of the claim. $\square$

From this claim, it clearly follows that $\Omega _g$ is foliated by H-surfaces, where the leaves of this foliation are $L_1$, $L_2$ and the rotated images $\mathcal {P}_H ({\theta })$ of $\mathcal {P}_H$ around the t-axis by angles $\theta \in [0,2\pi )$. The existence of the examples $\Sigma _H$ in the statement of Theorem 1.1 can easily be proven by using $\mathcal {P}_H$. We set $\Sigma _H=\mathcal {P}_H$, and $C_i=L_i$ for $i=1,2$. This finishes the proof of Theorem 1.1.

5 Appendix: Disjoint H-catenoids

In this section, we will show the existence of disjoint H-catenoids in ${\mathbb H}^2\times {\mathbb R}$. In particular, we will prove Lemma 2.1. Given $H\in (0,\frac{1}{2})$ and $d\in [-2H,\infty )$, recall that $\eta _d=\cosh ^{-1}(\frac{2dH+\sqrt{1-4H^2+d^2}}{1-4H^2})$ and that $\lambda _d:[\eta _d,\infty )\rightarrow [0,\infty )$ is the function defined as follows.

$$\begin{aligned} \lambda _d(\rho )= \int ^{\rho }_{\eta _d} \frac{d+2H\cosh r}{\sqrt{\sinh ^2 r - ( d+2H\cosh r)^2}}dr. \end{aligned}$$

(6)

Recall that $\lambda _d(\rho )$ is a monotone increasing function with $\lim _{\rho \rightarrow \infty }\lambda _d(\rho )= \infty$ and that $\lambda '_d(\eta _d)=\infty$ when $d\in (-2H,\infty )$. The H-catenoid $\mathcal {C}^H_d$, $d\in (-2H,\infty )$, is obtained by rotating a generating curve $\widehat{\lambda }_d(\rho )$ about the t-axis. The generating curve $\widehat{\lambda }_d$ is obtained by doubling the curve $(\rho , 0, \lambda _d(\rho ))$, $\rho \in [\eta _d,\infty )$, with its reflection $(\rho , 0, -\lambda _d(\rho ))$, $\rho \in [\eta _d,\infty )$.

Finally, recall that $b_{d}(t):=\lambda _d^{-1}(t)$ for $t\ge 0$, hence $b_d(0)=\eta _{d}$, and that abusing the notation $b_d(t):=b_d(-t)$ for $t\le 0$.

Lemma 2.1 (Disjoint H-catenoids) Given $d_1>2$ there exist $d_0>d_1$ and $\delta _0>0$ such that for any $d_2\in [d_0,\infty )$ and $t>0$ then

$$\begin{aligned} \inf _{t\in {\mathbb {R}}}( b_{d_2}(t)-b_{d_1}(t))\ge \delta _0. \end{aligned}$$

In particular, the corresponding H-catenoids are disjoint, i.e., $\mathcal {C}^H_{d_1}\cap \mathcal {C}^H_{d_2}=\emptyset$.

Moreover, $b_{d_2}(t)-b_{d_1}(t)$ is decreasing for $t>0$ and increasing for $t<0$. In particular,

$$\begin{aligned} \sup _{t\in {\mathbb {R}}}( b_{d_2}(t)-b_{d_1}(t))=b_{d_2}(0)-b_{d_1}(0)= \eta _{d_2}-\eta _{d_1}. \end{aligned}$$

Proof

We begin by introducing the following notations that will be used for the computations in the proof of this lemma,

$$\begin{aligned} c:=\cosh r=\frac{e^r+e^{-r}}{2},\, s:=\sinh r=\frac{e^r-e^{-r}}{2}. \end{aligned}$$

Recall that $c^2-s^2=1$ and $c-s=e^{-r}$. Using these notations,

$$\begin{aligned} \lambda _d(\rho )= \int ^{\rho }_{\eta _d} \frac{d+2H\cosh r}{\sqrt{\sinh ^2 r - ( d+2H\cosh r)^2}}\ dr \end{aligned}$$

(7)

can be rewritten as

$$\begin{aligned} \lambda _d(\rho )= \int ^{\rho }_{\eta _d} \frac{d+2H(s+e^{-r})}{\sqrt{s^2 - ( d+2Hc)^2}}\ dr=f_d(\rho )+J_d(\rho ), \end{aligned}$$

(8)

where

$$\begin{aligned} f_d(\rho )=\int ^{\rho }_{\eta _d} \frac{2Hs}{\sqrt{s^2 - ( d+2Hc)^2}} \ dr \ \ \text{ and } \ \ J_d(\rho )= \int ^{\rho }_{\eta _d} \frac{d+2He^{-r}}{\sqrt{s^2 - ( d+2Hc)^2}} \ dr \end{aligned}$$

First, by using a series of substitutions, we will get an explicit description of $f_d(\rho )$. Then, we will show that for $d>2$, $J_d(\rho )$ is bounded independently of $\rho$ and d.

Claim 4.8

$$\begin{aligned} f_d(\rho )=\frac{2H }{\sqrt{1-4H^2}}\cosh ^{-1} \left( \frac{(1-4H^2)\cosh \rho - 2dH }{\sqrt{d^2+1-4H^2}} \right) . \end{aligned}$$

(9)

Remark 4.9

After finding $f_d(\rho )$, we used Wolfram Alpha to compute the derivative of $f_d(\rho )$ and verify our claim. For the sake of completeness, we give a proof.

Proof of Claim 4.8

The proof is a computation with requires several integrations by substitution. Consider

$$\begin{aligned} \int \frac{2Hs}{\sqrt{s^2 - ( d+2Hc)^2}} \ dr \end{aligned}$$

By using the fact that $s^2=c^2-1$ and applying the substitution $\{u=c,du=\frac{dc}{dr}dr=sdr\}$ we obtain that

$$\begin{aligned} \int \frac{2Hs}{\sqrt{s^2 - ( d+2Hc)^2}} \ dr=\int \frac{2H}{\sqrt{u^2-1 - ( d+2Hu)^2}}\ du. \end{aligned}$$

Note that

$$\begin{aligned} \begin{aligned}&u^2-1 - ( d+2Hu)^2=u^2-1-(d^2+4dHu+4H^2u^2)\\&=(1-4H^2)u^2-4dHu-d^2-1\\&=(1-4H^2)\left( u^2-\frac{4dH}{1-4H^2}u+\frac{4d^2H^2}{(1-4H^2)^2}\right) -\frac{4d^2H^2}{1-4H^2}-d^2-1\\&=(1-4H^2)\left[ \left( u-\frac{2dH}{(1-4H^2)}\right) ^2-\left( \frac{4d^2H^2}{(1-4H^2)^2}+\frac{d^2+1}{1-4H^2}\right) \right] \\&=(1-4H^2)\left[ \left( u-\frac{2dH}{(1-4H^2)}\right) ^2-\left( \frac{4d^2H^2+(1-4H^2)(d^2+1)}{(1-4H^2)^2}\right) \right] \\&=(1-4H^2)\left[ \left( u-\frac{2dH}{(1-4H^2)}\right) ^2-\left( \frac{d^2+1-4H^2}{(1-4H^2)^2}\right) \right] . \end{aligned} \end{aligned}$$

Therefore, by applying a second substitution, $\{w=u-\frac{2dH}{(1-4H^2)}, dw=du\}$, and letting $a^2=(\frac{d^2+1-4H^2}{(1-4H^2)^2})$ we get that

$$\begin{aligned} \int \frac{2H}{\sqrt{u^2-1 - ( d+2Hu)^2}}\ du=\int \frac{2H}{\sqrt{1-4H^2}\sqrt{w^2-a^2}}\ dw \end{aligned}$$

By using the fact that $\sec ^2x-1=\tan ^2x$ and applying a third substitution, $\{w=a\sec t, dw=a\sec t\tan t dt\}$, we obtain that

$$\begin{aligned} \begin{aligned} \int \frac{2Ha\sec t\tan t}{\sqrt{1-4H^2}\sqrt{a^2\sec ^2 t-a^2}} dt&=\int \frac{2H\sec t}{\sqrt{1-4H^2}}\ dt\\&=\frac{2H }{\sqrt{1-4H^2}}\ln |\sec t+\tan t| \end{aligned} \end{aligned}$$

Therefore

$$\begin{aligned} \begin{aligned} \int \frac{2H}{\sqrt{1-4H^2}\sqrt{w^2-a^2}}\ dw&=\frac{2H }{\sqrt{1-4H^2}}\ln |\frac{w}{a}+\sqrt{\frac{w^2}{a^2}-1}|\\&=\frac{2H }{\sqrt{1-4H^2}}\cosh ^{-1}\left( \frac{w}{a}\right) \end{aligned} \end{aligned}$$

Since $w=u-\frac{2dH}{(1-4H^2)}$ then

$$\begin{aligned} \begin{aligned} \int \frac{2H}{\sqrt{u^2-1 - ( d+2Hu)^2}}\ du&=\frac{2H }{\sqrt{1-4H^2}}\cosh ^{-1}\left( \frac{u-\frac{2dH}{(1-4H^2)}}{a}\right) \\&=\frac{2H }{\sqrt{1-4H^2}}\cosh ^{-1}\left( \frac{u-\frac{2dH}{(1-4H^2)}}{\frac{\sqrt{d^2+1-4H^2}}{(1-4H^2)}}\right) \\&=\frac{2H }{\sqrt{1-4H^2}}\cosh ^{-1}\left( \frac{(1-4H^2)u- 2dH }{\sqrt{d^2+1-4H^2}} \right) . \end{aligned} \end{aligned}$$

Finally, since $u=\cosh r$

$$\begin{aligned} \begin{aligned} \int ^{\rho }_{\eta _d} \frac{2Hs}{\sqrt{s^2 - ( d+2Hc)^2}}&=\frac{2H }{\sqrt{1-4H^2}}\cosh ^{-1}\left( \frac{(1-4H^2)\cosh r- 2dH }{\sqrt{d^2+1-4H^2}} \right) \bigg |_{\eta _d}^\rho \\&= \frac{2H }{\sqrt{1-4H^2}}\left( \cosh ^{-1}\left( \frac{(1-4H^2)\cosh \rho - 2dH }{\sqrt{d^2+1-4H^2}} \right) \right. \\&\left. -\,\cosh ^{-1}\left( \frac{(1-4H^2)\cosh \eta _d- 2dH }{\sqrt{d^2+1-4H^2}} \right) \right) \end{aligned} \end{aligned}$$

Recall that $\eta _d=\cosh ^{-1} (\frac{2dH+\sqrt{1-4H^2+d^2}}{1-4H^2})$ and thus

$$\begin{aligned} \frac{(1-4H^2)\cosh \eta _d- 2dH }{\sqrt{d^2+1-4H^2}}= \frac{(1-4H^2)(\frac{2dH+\sqrt{1-4H^2+d^2}}{1-4H^2})- 2dH }{\sqrt{d^2+1-4H^2}}=1. \end{aligned}$$

This implies that

$$\begin{aligned} f_d(\rho )=\frac{2H }{\sqrt{1-4H^2}}\cosh ^{-1} \left( \frac{(1-4H^2)\cosh \rho - 2dH }{\sqrt{d^2+1-4H^2}} \right) . \end{aligned}$$

$\square$

By Claim 4.8 we have that

$$\begin{aligned} \begin{aligned} f_d(\rho )&=\frac{2H }{\sqrt{1-4H^2}}\left( \cosh ^{-1} \frac{(1-4H^2)\cosh \rho - 2dH }{\sqrt{d^2+1-4H^2}} \right) \\&= \frac{2H }{\sqrt{1-4H^2}}\left( \rho +\ln \frac{1-4H^2 }{\sqrt{d^2+1-4H^2}}\right) +g_d(\rho ), \end{aligned} \end{aligned}$$

where $\lim _{\rho \rightarrow \infty }g_d(\rho )=0$.

Recall that $\lambda _d(\rho )= f_d(\rho )+J_d(\rho )$ where

$$\begin{aligned} J_d(\rho )= \int ^{\rho }_{\eta _d} \frac{d+2He^{-r}}{\sqrt{s^2 - ( d+2Hc)^2}}\ dr =\int ^{\rho }_{\eta _d} \frac{d+2He^{-r}}{\sqrt{c^2-1 - ( d+2Hc)^2}}\ dr. \end{aligned}$$

Claim 4.10

$$\begin{aligned} \sup _{d\in (2,\infty ),\rho \in (\eta _d,\infty )}J_d(\rho )\le \pi \sqrt{1-2H}. \end{aligned}$$

Proof of Claim 4.10

Let

$$\begin{aligned} \alpha =\dfrac{2dH+\sqrt{1-4H^2+d^2}}{1-4H^2}\,\text { and }\,\beta =\dfrac{2dH-\sqrt{1-4H^2+d^2}}{1-4H^2} \end{aligned}$$

be the roots of $c^2-1 - ( d+2Hc)^2$, i.e.

$$\begin{aligned} \begin{aligned} c^2-1 - ( d+2Hc)^2&= (1-4H^2)\left( c^2-\frac{4dH}{1-4H^2}c-\frac{1+d^2}{1-4H^2}\right) \\&=(1-4H^2)(c-\alpha )(c-\beta ). \end{aligned} \end{aligned}$$

Note that $\alpha =\cosh {\eta _d}$ and that as $H\in (0,\frac{1}{2})$, $\beta<0<\alpha$. Furthermore, $2He^{-r}<2H<1<d$. Thus we have,

$$\begin{aligned} \begin{aligned} J_d(\rho )&=\int ^{\rho }_{\eta _d} \frac{d+2He^{-r}}{\sqrt{1-4H^2}\sqrt{(c-\alpha )(c-\beta )}}dr \\&< \frac{2d}{\sqrt{1-4H^2}} \int _{\eta _d}^\infty \frac{dr}{\sqrt{(c-\alpha )(c-\beta )}}\\&< \frac{2d}{\sqrt{1-4H^2}\sqrt{\alpha -\beta }} \int _{\eta _d}^\infty \frac{dr}{\sqrt{c-\alpha }}, \end{aligned} \end{aligned}$$

where the last inequality holds because for $r>\eta _d$, $\cosh {r}>\alpha$ and thus $\sqrt{\alpha -\beta }< \sqrt{c-\alpha }$. Notice that $\alpha -\beta = \frac{2\sqrt{1-4H^2+d^2}}{1-4H^2}>\frac{2d}{1-4H^2}$. Therefore

$$\begin{aligned} \frac{2d}{\sqrt{1-4H^2}\sqrt{\alpha -\beta }}<\frac{2d}{\sqrt{1-4H^2}}\frac{\sqrt{1-4H^2}}{\sqrt{2d}}=\sqrt{2d} \end{aligned}$$

and

$$\begin{aligned} J_d(\rho )< \sqrt{2d} \int _{\eta _d}^\infty \frac{dr}{\sqrt{c-\alpha }}. \end{aligned}$$

Applying the substitution $\{ u=c-\alpha , du=sdr=\sqrt{(u+\alpha )^2-1}dr\}$, we obtain that

$$\begin{aligned} \int _{\eta _d}^\infty \frac{dr}{\sqrt{c-\alpha }}= \int _0^\infty \frac{du}{\sqrt{u}\sqrt{(u+\alpha )^2-1}} \end{aligned}$$

(10)

Let $\omega =\alpha -1$. Note that since $d\ge 1$ then $\alpha >1$ and we have that $(u+\alpha )^2-1> (u+\omega )^2$ as $u>0$. This gives that

$$\begin{aligned} \int _0^\infty \frac{du}{\sqrt{u}\sqrt{(u+\alpha )^2-1}}< \int _0^\infty \frac{du}{\sqrt{u}(u+\omega )} \end{aligned}$$

Applying the substitution $\{ v=\sqrt{u}, dv=\dfrac{du}{2\sqrt{u}}\}$ we get

$$\begin{aligned} \int _0^\infty \frac{du}{\sqrt{u}(u+\omega )}= \int _0^\infty \frac{2dv}{v^2+\omega }= \ \frac{2}{\sqrt{\omega }}\arctan {\frac{w}{\sqrt{\omega }}}\bigg |_0^\infty <\dfrac{\pi }{\sqrt{\omega }} \end{aligned}$$

and thus

$$\begin{aligned} J_d(\rho )< \sqrt{\frac{2d}{\omega }} \pi . \end{aligned}$$

Note that

$$\begin{aligned} \begin{aligned} \omega =\alpha -1&= \frac{2dH+\sqrt{1-4H^2+d^2}}{1-4H^2}-1\\&>\frac{(1+2H)d}{1-4H^2}-1=\frac{d}{1-2H}-1. \end{aligned} \end{aligned}$$

Since $d>2$, we have $2\omega >\dfrac{d}{1-2H}$ and $\dfrac{d}{\omega }<2(1-2H)$. Then $\sqrt{\dfrac{2d}{\omega }}<2\sqrt{1-2H}.$

Finally, this gives that

$$\begin{aligned} J_d(\rho )<2\pi \sqrt{1-2H} \end{aligned}$$

independently on $d>2$ and $\rho >\eta _d$. This finishes the proof of the claim. $\square$

Using Claims 4.8 and 4.10, we can now prove the next claim.

Claim 4.11

Given $d_2>d_1>2$ there exists $T\in \mathbb R$ such for any $t>T$, we have that

$$\begin{aligned} \begin{aligned} \frac{2H }{\sqrt{1-4H^2}}&(\lambda _{d_2}^{-1}(t)-\lambda _{d_1}^{-1}(t)) \\ >&\frac{1}{2} \ln \sqrt{\frac{d_2^2+1-4H^2 }{d_1^2+1-4H^2}}-2\pi \sqrt{1-2H}. \end{aligned} \end{aligned}$$

Proof of Claim 4.11

Recall that $\lambda _d(\rho )=f_d(\rho )+J_d(\rho )$ and that by Claims 4.8 and 4.10 we have that

$$\begin{aligned} f_d(\rho )= \frac{2H }{\sqrt{1-4H^2}}\left( \rho +\ln \frac{1-4H^2 }{\sqrt{d^2+1-4H^2}}\right) +g_d(\rho ), \end{aligned}$$

(11)

where $\lim _{\rho \rightarrow \infty }g_d(\rho )=0$, and that

$$\begin{aligned} \sup _{d\in (2,\infty ),\rho \in (\eta _d,\infty )}J_d(\rho )\le 2\pi \sqrt{1-2H} . \end{aligned}$$

(12)

Let $\rho _i(t):=\lambda _{d_i}^{-1}(t)$, $i=1,2$. Using this notation, since $t=\lambda _1(\rho _1(t))=\lambda _2(\rho _2(t))$ we obtain that

$$\begin{aligned} \begin{aligned} 0&=\lambda _2(\rho _2(t))-\lambda _1(\rho _1(t))\\&=f_{d_2}(\rho _2(t))+J_{d_2}(\rho _2(t)) -f_{d_1}(\rho _1(t))-J_{d_1}(\rho _1(t))\\&=\frac{2H }{\sqrt{1-4H^2}}\left( \rho _2(t) +\ln \frac{1-4H^2 }{\sqrt{d_2^2+1-4H^2}}\right) +g_{d_2}(\rho _2(t))+J_{d_2}(\rho _2(t))\\&\quad -\frac{2H }{\sqrt{1-4H^2}}\left( \rho _1(t) -\ln \frac{1-4H^2 }{\sqrt{d_1^2+1-4H^2}}\right) -g_{d_1}(\rho _1(t))-J_{d_1}(\rho _1(t)) \end{aligned} \end{aligned}$$

Recall that $\lim _{t\rightarrow \infty }\rho _i(t)=\infty$, $i=1,2$, therefore given $\varepsilon >0$ there exists $T_\varepsilon \in \mathbb R$ such that for any $t>T_\varepsilon$, $|g_{d_i}(\rho _i(t))|\le \varepsilon$. Taking

$$\begin{aligned} 4\varepsilon <\ln \sqrt{\frac{d_2^2+1-4H^2 }{d_1^2+1-4H^2}} \end{aligned}$$

for $t>T_\varepsilon$ we get that

$$\begin{aligned} \begin{aligned} \frac{2H }{\sqrt{1-4H^2}}&(\rho _2(t)-\rho _1(t)) \\&>\ln \sqrt{\frac{d_2^2+1-4H^2 }{d_1^2+1-4H^2}}+J_{d_1}(\rho _1(t))-J_{d_2}(\rho _2(t))-2\varepsilon \\&>\frac{1}{2} \ln \sqrt{\frac{d_2^2+1-4H^2 }{d_1^2+1-4H^2}}+J_{d_1}(\rho _1(t))-J_{d_2}(\rho _2(t)). \end{aligned} \end{aligned}$$

Notice that $J_{d_1}(\rho _1(t))>0$ and that Claim 4.10 gives that

$$\begin{aligned} \sup _{\rho \in (\eta _{d_2},\infty )}J_{d_2}(\rho )\le 2\pi \sqrt{1-2H}. \end{aligned}$$

Therefore

$$\begin{aligned} \begin{aligned} \frac{2H }{\sqrt{1-4H^2}}&(\rho _2(t)-\rho _1(t)) \\&> \frac{1}{2} \ln \sqrt{\frac{d_2^2+1-4H^2 }{d_1^2+1-4H^2}}-2\pi \sqrt{1-2H}. \end{aligned} \end{aligned}$$

This finishes the proof of the claim. $\square$

We can now use Claim 4.11 to finish the proof of the lemma. Given $d_1>2$ fix $d_0>d_1$ such that

$$\begin{aligned} \begin{aligned} \frac{\sqrt{1-4H^2}}{4H} \left( \ln \sqrt{\frac{d_0^2+1-4H^2 }{d_1^2+1-4H^2}}-4\pi \sqrt{1-2H}\right) =1. \end{aligned} \end{aligned}$$

Then, by Claim 4.11, given $d_2\ge d_0$ there exists $T>0$ such that $\lambda _{d_2}^{-1}(t)-\lambda _{d_1}^{-1}(t)>1$ for any $t>T$. Notice that since for any $\rho \in (\eta _2,\infty )$, $\lambda '_{d_2}(\rho )>\lambda '_{d_1}(\rho )$, then there exists at most one $t_0>0$ such that $\lambda _{d_2}^{-1}(t_0)-\lambda _{d_1}^{-1}(t_0)=0$. Therefore, since there exists $T>0$ such that $\lambda _{d_2}^{-1}(t)-\lambda _{d_1}^{-1}(t)>1$ for any $t>T$ and $\lambda _{d_2}^{-1}(0)-\lambda _{d_1}^{-1}(0)=\eta _{d_2}-\eta _{d_1}>0$, this implies that there exists a constant $\delta (d_2)>0$ such that for any $t>0$,

$$\begin{aligned} \lambda _{d_2}^{-1}(t)-\lambda _{d_1}^{-1}(t)>\delta (d_2). \end{aligned}$$

A priori it could happen that $\lim _{d_2\rightarrow \infty }\delta (d_2)=0$. The fact that $\lim _{d_2\rightarrow \infty }\delta (d_2)>0$ follows easy by noticing that by applying Claim 4.11 and using the same arguments as in the previous paragraph there exists $d_3> d_0$ such that for any $d\ge d_3$ and $t>0$,

$$\begin{aligned} \lambda _{d}^{-1}(t)-\lambda _{d_0}^{-1}(t)>0. \end{aligned}$$

Therefore, for any $d\ge d_3$ and $t>0$,

$$\begin{aligned} \lambda _{d}^{-1}(t)-\lambda _{d_1}^{-1}(t)> \lambda _{d_0}^{-1}(t)-\lambda _{d_1}^{-1}(t)>\delta (d_0) \end{aligned}$$

which implies that

$$\begin{aligned} \lim _{d_2\rightarrow \infty }\delta (d_2)\ge \delta (d_0)>0. \end{aligned}$$

Setting $\delta _0=\inf _{d\in [d_0,\infty )}\delta (d_2)>0$ gives that

$$\begin{aligned} \inf _{t\in \mathbb R_{\ge 0}}( \lambda _{d_2}^{-1}(t)-\lambda _{d_1}^{-1}(t))\ge \delta _0. \end{aligned}$$

By definition of $b_d(t)$ then

$$\begin{aligned} \inf _{t\in \mathbb R}( b_{d_2}(t)-b_{d_1}(t))= \inf _{t\in \mathbb R_{\ge 0}}( \lambda _{d_2}^{-1}(t)-\lambda _{d_1}^{-1}(t))\ge \delta _0. \end{aligned}$$

It remains to prove that $b_2(t)-b_1(t)$ is decreasing for $t>0$ and increasing for $t<0$. By definition of $b_d(t)$, it suffices to show that $b_2(t)-b_1(t)$ is decreasing for $t>0$. We are going to show $\frac{d}{dt}(b_2(t)-b_1(t))<0$ when $t>0$.

By definition of $b_i$, for $t>0$ we have that $\lambda _i(b_i(t))=t$ and thus $b_i'(t)=\frac{1}{\lambda _i'(b_i(t))}$. By definition of $\lambda _d(t)$ for $t>0$ the following holds,

$$\begin{aligned} b_1'(t)=\frac{1}{\lambda _1'(b_1(t))}>\frac{1}{\lambda _1'(b_2(t))}>\frac{1}{\lambda _2'(b_2(t))}=b_2'(t). \end{aligned}$$

The first inequality is due to the convexity of the function $\lambda _1(t)$ and the second inequality is due to the fact that $\lambda _1'(\rho )<\lambda _2'(\rho )$ for any $\rho >\eta _2$. This proves that $\frac{d}{dt}(b_2(t)-b_1(t))=b_2'(t)-b_1'(t)<0$ for $t>0$ and finishes the proof of the claim.

$\square$

Note that if d is sufficiently close to $-2H$ then $\mathcal {C}^H_d$ must be unstable. This follows because as d approaches $-2H$, the norm of the second fundamental form of $\mathcal {C}^H_d$ becomes arbitrarily large at points that approach the “origin” of ${\mathbb H}^2\times {\mathbb R}$ and a simple rescaling argument gives that a sequence of subdomains of $\mathcal {C}^H_d$ converge to a catenoid, which is an unstable minimal surface. This observation, together with our previous lemma suggests the following conjecture.

Conjecture: Given $H\in (0,\frac{1}{2})$ there exists $d_H>-2H$ such that the following holds. For any $d>d'>d_H$, $\mathcal {C}^H_{d}\cap \mathcal {C}^H_{d'}=\emptyset$, and the family $\{\mathcal {C}^H_d \mid d\in [d_H,\infty )\}$ gives a foliation of the closure of the non-simply-connected component of ${\mathbb H}^2\times {\mathbb R}-\mathcal {C}^H_{d_H}$. The H-catenoid $\mathcal {C}^H_d$ is unstable if $d\in (-2H, d_H)$ and stable if $d\in (d_H,\infty )$. The H-catenoid $\mathcal {C}^H_{d_H}$ is a stable-unstable catenoid.