Integrability of higher pentagram maps

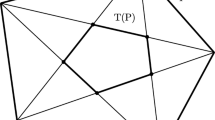
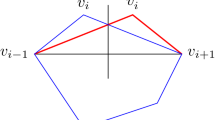
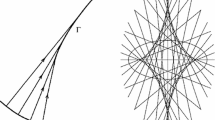
Abstract

We define higher pentagram maps on polygons in $\mathbb{P }^d$ for any dimension $d$, which extend R. Schwartz’s definition of the 2D pentagram map. We prove their integrability by presenting Lax representations with a spectral parameter for scale invariant maps. The corresponding continuous limit of the pentagram map in dimension $d$ is shown to be the $(2,d+1)$-equation of the KdV hierarchy, generalizing the Boussinesq equation in 2D. We also study in detail the 3D case, where we prove integrability for both closed and twisted polygons and describe the spectral curve, first integrals, the corresponding tori and the motion along them, as well as an invariant symplectic structure.

Appendices

Appendix A: Continuous limit in the 3D case

In this section we present explicit formulas manifesting Theorem A on the continuous limit of the 3D pentagram map. Consider a curve $G(x)$ in $\mathbb{R }^4$ given by the differential equation

$$\begin{aligned} G^{\prime \prime \prime \prime }+u(x)G^{\prime \prime }+v(x)G^{\prime }+w(x)G=0 \end{aligned}$$

with periodic coefficients $u(x),v(x),w(x)$. To find the continuous limit, we fix $\epsilon$ and consider a plane $P_\epsilon (x)$ passing through the three points $G(x-\epsilon ), G(x), G(x+\epsilon )$ on this curve. We are looking for an equation of the envelope curve $L_\epsilon (x)$ for these planes.

This envelope curve $L_\epsilon (x)$ satisfies the following system of equations:

$$\begin{aligned}&\det | G(x), G(x+\epsilon ), G(x-\epsilon ), L_\epsilon (x) |=0\\&\det | G(x), G(x+\epsilon ), G(x-\epsilon ), L^{\prime }_\epsilon (x) |=0\\&\det | G(x), G(x+\epsilon ), G(x-\epsilon ), L^{\prime \prime }_\epsilon (x) |=0. \end{aligned}$$

By considering the Taylor expansion and using the normalizations $\det | L_\epsilon , L^{\prime }_\epsilon , L^{\prime \prime }_\epsilon , L^{\prime \prime \prime }_\epsilon | =1$ and $\det | G, G^{\prime }, G^{\prime \prime }, G^{\prime \prime \prime } |=1$ we find that

$$\begin{aligned} L_\epsilon (x) = G(x)+ \frac{\epsilon ^2}{6} \left( G^{\prime \prime }(x)+\frac{u}{2} G(x) \right) +\mathcal{O }(\epsilon ^4) \end{aligned}$$

(11)

as $\epsilon \rightarrow 0$. Now, the equation $L^{\prime \prime \prime \prime }_\epsilon +u_\epsilon L^{\prime \prime }_\epsilon +v_\epsilon L^{\prime }_\epsilon +w_\epsilon L_\epsilon =0$ implies that:

$$\begin{aligned} u_\epsilon&= u + \frac{\epsilon ^2}{3}(v^{\prime }-u^{\prime \prime })+\mathcal{O }(\epsilon ^4),\\ v_\epsilon&= v + \frac{\epsilon ^2}{6}(2w^{\prime }+v^{\prime \prime }-uu^{\prime }-2u^{\prime \prime \prime })+\mathcal{O }(\epsilon ^4),\\ w_\epsilon&= w + \frac{\epsilon ^2}{12}(2w^{\prime \prime }-uu^{\prime \prime }-vu^{\prime }-u^{\prime \prime \prime \prime })+\mathcal{O }(\epsilon ^4). \end{aligned}$$

These equations describe the $(2,4)$-equation in the Gelfand-Dickey hierarchy:

$$\begin{aligned} \dot{L} = [Q_2,L] \Leftrightarrow \left\{ \begin{array}{ll} \dot{u} = 2v^{\prime }-2u^{\prime \prime },\\ \dot{v} = v^{\prime \prime }+2w^{\prime }-uu^{\prime }-2u^{\prime \prime \prime },\\ \dot{w} = w^{\prime \prime } - \frac{1}{2} vu^{\prime }-\frac{1}{2}uu^{\prime \prime } - \frac{1}{2} u^{\prime \prime \prime \prime }, \end{array} \right. \end{aligned}$$

where $L = \partial ^4 + u \partial ^2 + v \partial + w$ and $Q_2 = (L^{2/4})_+ = \partial ^2 + \frac{u}{2}$.

Remark 9.1

A different choice of the points defining the plane $P_\epsilon (x)$ on the original curve leads to the same continuous limit. For instance, the choice of $G(x-3\epsilon ),G(x+\epsilon ),G(x+2\epsilon )$ results in the same expression for $L_\epsilon (x)$, where in (11) instead of the coefficient $\epsilon ^2/6$ one has $7\epsilon ^2/6$. This leads to the same evolution of the curve $G$ with a different time parameterization, cf. Remark 4.4.

Appendix B: Higher terms of the continuous limit

Recall that in the continuous limit for the pentagram map in $\mathbb{RP }^d$ the envelope for osculating planes moves according to the $(2,d+1)$-KdV equation (Theorem 4.5). This evolution is defined by the $\epsilon ^2$-term of the expansion of the function $L_\epsilon (x)$.

The same proof works in the following more general setting. Let $L$ be a differential operator (5) of order $d+1$ and $G$ a non-degenerate curve defined by its solutions: $LG=0$.

Proposition 10.1

Assume that the curve $G$ evolves according to the law $\dot{G}= Q_m G$, where $Q_m:=(L^{m/(d+1)})_+$ is the differential part of the $m$th power of the operator $Q=L^{1/(d+1)}$. Then this evolution defines the equation $\dot{L}=[Q_m, L]$, which is the $(m,d+1)$-equation in the corresponding KdV hierarchy of $L$.

Furthermore, one can define the simultaneous evolution of all terms in the $\epsilon$-expansion of $L_\epsilon (x)$ using the following construction. For the pseudodifferential operator $Q:=L^{1/(d+1)}$ consider the formal series $\exp (\epsilon Q):=1+\epsilon Q +\frac{\epsilon ^2}{2} Q^2+\cdots$ and take its differential part:

$$\begin{aligned} \left( \exp (\epsilon Q)\right) _+\!=\!\left( 1+\epsilon Q +\frac{\epsilon ^2}{2} Q^2+\cdots \right) _+=1+\epsilon Q_1 +\frac{\epsilon ^2}{2} Q_2+\cdots \!=\!\sum _0^\infty \frac{\epsilon ^m}{m!}Q_m. \end{aligned}$$

For each power of $\epsilon$ this is a multiple of the differential operator $Q_m$, which is the differential part of the $m$th power $Q^m$ of the operator $Q=L^{1/(d+1)}$.

Corollary 10.2

The formal evolution equation $\dot{G}= \left( \exp (\epsilon Q)\right) _+ G$ corresponds to the full KdV hierarchy $\dot{L}=[\left( \exp (\epsilon Q)\right) _+ , L]$, where the operator $L$ is of order $d+1$ and the $(m,d+1)$-equation corresponds to the power $\epsilon ^m$. $\square$

A natural question is which equations of this hierarchy actually appear as the evolution of the envelope $L_\epsilon (x)$. Recall that only even powers of $\epsilon$ arise in the expansion of the function $L_\epsilon (x)$ for the continuous limit of the pentagram map. The $\epsilon ^2$-term gives the $(2,d+1)$-KdV equation. It turns out that the $\epsilon ^4$-term in the continuous limit of the 2D pentagram map results in the equation very similar to the $(4,3)$-equation in the KdV hierarchy (which is a higher-order Boussinesq equation). Although the numerical coefficients in these differential equations are different, one may hope to obtain the exact equations of the KdV hierarchy for different $m$ by using an appropriate rescaling. This allows one to formulate

Problem 10.3

Do higher $(m, d+1)$-KdV flows appear as the $\epsilon ^{m}$-terms in the expansion of the envelope $L_\epsilon (x)$ for the continuous limit of the pentagram map for any even $m>2$?

Appendix C: Bijection of the spectral map

In this appendix we sketch the proof of Proposition 6.17 and prove Proposition 6.18, which allows one to reconstruct the $L$-matrix from spectral data, and hence complete the proof of Theorem 6.15 on the spectral map.

Proposition 11.1

(= Proposition 6.18) For any $n$, given a generic spectral curve with marked points and a generic divisor $D$ of degree $g+3$ one can recover a sequence of matrices

$$\begin{aligned} \tilde{L}_{i,t}(\lambda ) = \begin{pmatrix} 0 &{}\quad 0 &{}\quad 0 &{}\quad -1\\ \lambda x_i y_i &{}\quad 0 &{}\quad 0 &{}\quad 1\\ 0 &{}\quad z_i &{}\quad 0 &{}\quad 1\\ 0 &{}\quad 0 &{}\quad \lambda x_i &{}\quad 1 \end{pmatrix}^{-1}, \end{aligned}$$

for $0 \le i \le n-1$ and any $t.$

Proof

Without loss of generality we describe the procedure to reconstruct the matrices $L_i(\lambda ):=\tilde{L}_{i,0}(\lambda ),$ for $0 \le i \le n-1$ and $t=0$.

• 1. First, we pick functions $\psi _{i,j}:=\psi _{i,0,j}$ for $\; 0 \le i \le n-1,\; 1 \le j \le 4,$ and $t=0$, satisfying Proposition 6.17. Note that according to the Riemann-Roch theorem, the functions $\psi _{i,1}$ and $\psi _{i,4}$ are defined up to a multiplication by constants, whereas the functions $\psi _{i,2}$ and $\psi _{i,3}$ belong to 2-dimensional subspaces. The functions $\psi _{i,1}$ and $\psi _{i,4}$ belong to the same subspaces. We pick the pairs of functions $\psi _{i,1},\; \psi _{i,3}$ and $\psi _{i,2},\; \psi _{i,4}$ to be linearly independent. Observe that any sets of functions $\psi _{i,1},\ldots ,\psi _{i,4}$ satisfying Proposition 6.17 are related by gauge transformations $\psi _i \rightarrow g_i^{-1} \psi _i$, where

  $$\begin{aligned} g_i = \begin{pmatrix} A_i &{}\quad 0 &{}\quad 0 &{}\quad 0\\ 0 &{}\quad B_i &{}\quad 0 &{}\quad E_i\\ F_i &{}\quad 0 &{}\quad C_i &{}\quad 0\\ 0 &{}\quad 0 &{}\quad 0 &{}\quad D_i \end{pmatrix},\quad g_i = g_{i+n}, \end{aligned}$$

  and $\psi _i$ stands for $\psi _i=(\psi _{i,1},\ldots ,\psi _{i,4})^T$. We also define $\psi _n$ to be $\psi _n=I_0k\psi _0$ for any $n$ in $(x,y,z)$-variables.

• 2. We find the unique matrix $L^{\prime }_i$ satisfying the equation $\psi _i = (L^{\prime }_i)^{-1} \psi _{i+1}$:

  $$\begin{aligned} L^{\prime }_i(\lambda ) = \begin{pmatrix} 0 &{}\quad 0 &{}\quad 0 &{}\quad t_{i,1}\\ \lambda t_{i,5} &{}\quad 0 &{}\quad \lambda t_{i,6} &{}\quad t_{i,2}\\ 0 &{}\quad t_{i,7} &{}\quad 0 &{}\quad t_{i,3}\\ \lambda t_{i,8} &{}\quad 0 &{}\quad \lambda t_{i,9} &{}\quad t_{i,4} \end{pmatrix}^{-1}. \end{aligned}$$

• 3. One can check that there exists the unique choice of the matrices $g_i, \; 0 \le i \le n-1,$ such that the equality $L_i(\lambda ) = g_{i+1} L^{\prime }_i(\lambda ) g_i^{-1}$ is possible. The latter is equivalent to the following system of equations ($0 \le i \le n-1$):

  $$\begin{aligned}&\frac{A_i t_{i,1}}{D_{i+1}}=-1; \quad \frac{B_i t_{i,2}+E_i t_{i,4}}{D_{i+1}}=1; \quad \frac{D_i t_{i,4}}{D_{i+1}}=1;\\&\frac{B_{i+1} F_i t_{i,1}+B_{i+1} C_i t_{i,3}-C_i E_{i+1} t_{i,7}}{B_{i+1} D_{i+1}}=1; \quad B_i t_{i,6} + E_i t_{i,9}=0;\\&\quad C_{i+1} t_{i,8} - F_{i+1} t_{i,9}=0. \end{aligned}$$

  These equations decouple and may be solved explicitly. One only needs to check the solvability of $n$ equations $\frac{D_i t_{i,4}}{D_{i+1}}=1, \; 0 \le i \le n-1,$ for $n$ variables $D_i, \; 0 \le i \le n-1$. A non-trivial solution exists provided that $\prod _{i=0}^{n-1} t_{i,4} = 1$. It depends on an arbitrary constant, which corresponds to multiplication of all matrices $g_i$ by the same number and does not affect the Lax matrices. One can check that

  $$\begin{aligned} t_{i,4} = \frac{\psi _{i+1,4}(O_1)}{\psi _{i,4}(O_1)} \quad \text{ and }\quad \prod _{i=0}^{n-1} t_{i,4} = \frac{\psi _{n,4}(O_1)}{\psi _{0,4}(O_1)}=I_0 k(O_1). \end{aligned}$$

  By using Lemma 6.8 we find the value $k(O_1) ={1}/{I_0}$ as required. Now the remaining variables $A_i,B_i,C_i,E_i,F_i,\; 0 \le i \le n-1,$ are uniquely determined.

$\square$

Corollary 11.2

For odd $n$, given a generic spectral curve with marked points and a generic divisor $D$ one can recover a sequence of matrices

$$\begin{aligned} L_{i,t}(\lambda ) = \begin{pmatrix} 0 &{}\quad 0 &{}\quad 0 &{}\quad -1\\ \lambda &{}\quad 0 &{}\quad 0 &{}\quad c_j\\ 0 &{}\quad 1 &{}\quad 0 &{}\quad b_j\\ 0 &{}\quad 0 &{}\quad \lambda &{}\quad a_j \end{pmatrix}^{-1} \end{aligned}$$

with $0 \le i \le n-1$ and any $t$.

Proof

The statement follows from Proposition 6.18 and the fact that $(a_j,b_j,c_j),\; 0 \le i \le n-1,$ are coordinates on the space $\mathcal P _n$ for odd $n$. $\square$

We complete the exposition with a sketch of the proof for Proposition 6.17 for even $n$ (the case of odd $n$ is similar).

Proposition 11.3

(= Proposition 6.17$^{\prime }$) For even $n$, the divisors of the coordinate functions $\psi _{i,t,1},\ldots , \psi _{i,t,4}$ for $0 \le i \le n-1$ and any integer $t$ satisfy the following inequalities, provided that their divisors remain non-special up to time $t$:

• $(\psi _{i,t,1}) \ge -D +O_2 + \lfloor \frac{i-t+2}{2} \rfloor W_{12}+ \lfloor \frac{i-t+1}{2} \rfloor W_{34}- \lfloor \frac{i+1}{2} \rfloor O_{24}-\lfloor \frac{i}{2} \rfloor O_{34}+tO_{14};$

• $(\psi _{i,t,2}) \ge -D + \lfloor \frac{i-t+1}{2} \rfloor W_{12}+ \lfloor \frac{i-t}{2} \rfloor W_{34}- \lfloor \frac{i-1}{2} \rfloor O_{24}-\lfloor \frac{i}{2} \rfloor O_{34}+tO_{14};$

• $(\psi _{i,t,3}) \ge -D + \lfloor \frac{i-t+2}{2} \rfloor W_{12}+ \lfloor \frac{i-t+1}{2} \rfloor W_{34}- \lfloor \frac{i+1}{2} \rfloor O_{34}- \lfloor \frac{i}{2} \rfloor O_{24}+tO_{14};$

• $(\psi _{i,t,4}) \ge -D +O_2 + \lfloor \frac{i-t+1}{2} \rfloor W_{12}+ \lfloor \frac{i-t}{2} \rfloor W_{34}- \lfloor \frac{i-1}{2} \rfloor O_{34}- \lfloor \frac{i}{2} \rfloor O_{24}+tO_{14};$

where $D$ is an effective divisor of degree $g+3$, and $\lfloor x \rfloor$ is the floor function of $x$.

Proof

First, we prove these inequalities for $t=0$ and $0 \le i \le n-1$. For illustration we find the multiplicities of the components of the vector $\psi _{i,0}$ at the point $O_2$, while other points can be treated in a similar fashion. We employ the matrices $\tilde{L}_{i,t}$ in the coordinates $x_i,y_i,z_i$.

Notice that a cyclic permutation of indices $(n-1,n-2,\ldots ,1,0)$ changes the monodromies $T_i \rightarrow T_{i+1}$ and the Floquet-Bloch solutions $\bar{\psi }_i \rightarrow \bar{\psi }_{i+1}$. For even $n$, it also permutes $\bar{\psi }_i(O_2) \leftrightarrow \bar{\psi }_i(O_3)$ and $W_{12} \leftrightarrow W_{34}$, i.e., the corresponding pairs of the vectors $\bar{\psi }_i$ at the points $(W_1,W_2)$ and $(W_3,W_4)$ are swapped.

Using the asymptotic expansion of $\tilde{T}_{0,t}(\lambda )$ at $\lambda =0$, the definition of the Floquet-Bloch solution, and the normalization condition, one can show that $\psi _{0,0}=(O(\lambda ),O(\lambda ),1+O(\lambda ),O(\lambda ))^T$ as $\lambda \rightarrow 0$ at the point $O_2$. Since

$$\begin{aligned} L_{1,0}(\lambda )L_{0,0}(\lambda ) = \begin{pmatrix} 1 &{}\quad 1 &{}\quad 0 &{}\quad 0\\ 0 &{}\quad 0 &{}\quad 0 &{}\quad 0\\ y_1 &{}\quad y_1 &{}\quad 0 &{}\quad 0\\ 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 \end{pmatrix} \frac{1}{x_0 x_1 y_0 y_1 \lambda ^2} + O\left( \frac{1}{\lambda } \right) \text{ as } \, \lambda \rightarrow 0, \end{aligned}$$

and $\psi _{2,0}=L_{1,0} L_{0,0} \psi _{0,0}$, generically one has $\psi _{2,0}=(O(1),O(1),O(1/\lambda ),O(1))^T$ at $O_2$.

By definition, the normalized vectors are $\bar{\psi }_{i,t} = f_{i,t} \psi _{i,t}$. Using a cyclic permutation, we find that $\bar{\psi }_{2k,0}=(O(\lambda ),O(\lambda ),1+O(\lambda ),O(\lambda ))^T$ and that $f_{2,0}(\lambda ) = O(\lambda )$ at $O_2$. Using the permutation argument again, we derive that $f_{i+2,0}(\lambda )/f_{i,0}(\lambda ) = O(\lambda )$ at $O_2$ for even $i$. Therefore, one has $f_{2k,0}(\lambda ) = O(\lambda ^k)$ at $O_2$. Now the required multiplicities for the vector $\psi _{2k,0}$ at $O_2$ follow. Furthermore, since $\psi _{2k+1,0} = L_{2k} \psi _{2k,0}$, one can check that generically $f_{2k+1,0}(\lambda )/f_{2k,0}(\lambda ) = O(1)$ and $\bar{\psi }_{2k+1,0}=(O(1),O(\lambda ),O(1),O(1))^T$ at the point $O_2$. This establishes also the multiplicities for the vector $\psi _{2k+1,0}$ at $O_2$.

Having proved the proposition for $t=0$, one can prove it for $t>0$ by using the formula $\psi _{i,t+1} = \tilde{P}_{i,t} \psi _{i,t}$. Note that it suffices to study the cases $t=0$ and $t=1$ only. Consider, for example, the multiplicity of the function $\psi _{i,1,1}$ at the point $O_2$. Since $\psi _{i,1,1}=(\psi _{i,0,2}-\psi _{i,0,4})/(x_i(1+y_i+z_{i+1}))$, one can check that the multiplicity of the right-hand side at $O_2$ is $1-k$ for $i=2k$ and it is equal to $-k$ for $i=2k+1$, i.e., $\psi _{i,1,1}$ and $\psi _{i,0,1}$ have the same multiplicities at $O_2$. Other cases are treated in a similar way. $\square$