Directional monotone comparative statics

Abstract

Many questions of interest in economics can be stated in terms of monotone comparative statics: If a parameter of a constrained optimization problem increases, when does its solution increase as well. We characterize monotone comparative statics in different directions in finite-dimensional Euclidean space by extending the monotonicity theorem of Milgrom and Shannon (Econometrica 62(1):157–180, 1994) to constraint sets ordered in Quah (Econometrica 75(2):401–431, 2007)’s set order. Our characterizations are ordinal and retain the same flavor as their counterparts in the standard theory, showing new connections to the standard theory and presenting new results. The results are highlighted with several applications (in consumer theory, producer theory, and game theory) which were previously outside the scope of the standard theory of monotone comparative statics.

Appendices

Appendix A: Relation to Quah (2007)

Quah (2007) uses different techniques based on new binary relations, denoted $\nabla _i^{\lambda }$ and $\Delta _i^{\lambda }$, and convex sets. Using these binary relations, he defines a new set order, termed $\mathcal {C}_i$-flexible set order, and a new notion of $\mathcal {C}_i$-quasisupermodular function. Some connections to these ideas are explored here.

Let X be a convex sublattice of $\mathbb {R}^N$ (that is, X is a sublattice that is also a convex set), and $i \in \{ 1,2,\ldots ,N \}$. For $a, b \in X$ and $\lambda \in [0, 1]$, let

$$\begin{aligned} a \Delta _i^{\lambda } b= & {} \left\{ \begin{array}{ll} a &{}\quad \text{ if } \ a_i \le b_i \\ \lambda b + (1-\lambda ) (a\wedge b) &{}\quad \text{ if } \ a_i> b_i, \end{array} \right. \ \text{ and } \\ a \nabla _i^{\lambda } b= & {} \left\{ \begin{array}{ll} b &{}\quad \text{ if } \ a_i \le b_i \\ \lambda a + (1-\lambda ) (a \vee b) &{}\quad \text{ if } \ a_i > b_i. \end{array} \right. \end{aligned}$$

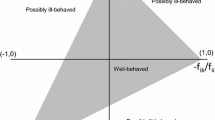
Figure 4 shows the graphical intuition.

Fig. 4

$\mathcal {C}_i$-Flexible set order

When $a_i > b_i$, the set $\left\{ a, a\Delta _i^{\lambda } b, a \nabla _i^{\lambda } b, b \right\}$ forms a “backward-bending” parallelogram, as compared to the standard lattice theory rectangle formed by the set $\left\{ a, a\wedge b, a \vee b, b \right\}$. The shape of this parallelogram varies with $\lambda$, ranging from the standard lattice theory rectangle when $\lambda = 0$ to the degenerate line segment formed by $\left\{ a, b \right\}$ when $\lambda = 1$.

The binary operations $\Delta _i^{\lambda }, \nabla _i^{\lambda }$ have some counter-intuitive properties when compared to the standard lattice operations $\wedge , \vee$. For example, the relations $\Delta _i^{\lambda }, \nabla _i^{\lambda }$ are non-commutative: suppose $N=2, i=1$, consider $a = (1,0)$, $b=(0,1)$, and $\lambda =\frac{1}{2}$. Then $a \Delta _i^{\lambda } b = \frac{1}{2}b \ne b = b \Delta _i^{\lambda } a$, and $a \nabla _i^{\lambda } b = (1, \frac{1}{2}) \ne a = b \nabla _i^{\lambda } a$. Moreover, $a \Delta _i^{\lambda } b$ and $a \nabla _i^{\lambda } b$ are not necessarily comparable in the underlying lattice order: suppose $N=2, i=1$, and consider $a = (1,1)$ and $b=(2,0)$. Then for every $\lambda \in [0, 1]$, $a \Delta _i^{\lambda } b = a \not \le b = a \nabla _i^{\lambda } b$. It is easy to see that additional classes of examples of these instances can be provided as well.

The binary relations $\Delta _i^{\lambda }, \nabla _i^{\lambda }$ are used to define the $\mathcal {C}_i$-flexible set order and the notion of a $\mathcal {C}_i$-quasisupermodular function, as follows.

Let X be a convex sublattice of $\mathbb {R}^N$ and $i \in \{ 1,2,\ldots ,N \}$. For subsets A, B of X, A is lower than B in the $\mathcal {C}_i$-flexible set order, denoted $A \sqsubseteq ^{\mathcal {C}}_i B$, if for every $a \in A, b \in B$, there is $\lambda \in [0, 1]$ such that $a \Delta _i^{\lambda } b \in A$ and $a \nabla _i^{\lambda } b \in B$. The $\mathcal {C}_i$-flexible set order is flexible in the sense that the choice of $\lambda$ may vary for each $a \in A$ and $b \in B$, and therefore, the “backward bendedness” of the parallelogram may vary for each $a \in A$ and $b \in B$. On convex sublattices, the $\mathcal {C}_i$-flexible set order is the same as the i-directional set order, as shown next.

Proposition 4

Let X be a convex sublattice of $\mathbb {R}^N$, $i \in \{ 1,2,\ldots ,N \}$, and A, B be subsets of X. The following are equivalent.

• (1) A is lower than B in the $\mathcal {C}_i$-flexible set order ($A \sqsubseteq ^{\mathcal {C}}_i B$).

• (2) A is lower than B in the i-directional set order ($A \sqsubseteq ^{dso}_i B$).

Proof

Suppose $A \sqsubseteq ^{\mathcal {C}}_i B$. Fix $a \in A, b \in B$, and suppose $a_i > b_i$. Let $\lambda \in [0, 1]$ be such that $a \Delta ^{\lambda }_i b \in A$ and $a \nabla ^{\lambda }_i b \in B$. Let $t = 1 - \lambda \in [0, 1]$. Then $b-v = b - t(b - a \wedge b) = (1-t)b + t(a \wedge b) = a \Delta ^{1-t}_i b \in A$, and $a+v = a + t(a \vee b - a) = (1-t)a + t(a \vee b) = a \nabla ^{1-t}_i b \in B$, as desired.

In the other direction, suppose $A \sqsubseteq ^{dso}_i B$. Fix $a \in A, b \in B$. Suppose $a_i \le b_i$. Then $a \Delta ^{1-t}_i b = a \in A$ and $a \nabla ^{1-t}_i b = b \in B$, as desired. Suppose $a_i > b_i$. Let $t \in [0, 1]$ be such that $v = t(b - a\wedge b) = t(a \vee b - a)$ satisfies $b-v \in A$ and $a+v \in B$. Then for $\lambda = 1-t$, $a \Delta ^{\lambda }_i b = (1-t)b + t(a \wedge b) = b - t(b - a \wedge b) = b-v \in A$, and $a \nabla ^{\lambda }_i b = (1-t)a + t(a \vee b) = a + t(a \vee b - a) = a+v \in B$, as desired. $\square$

The i-directional set order may be viewed as reformulating the $\mathcal {C}_i$-flexible set order to work more closely with monotone methods. In particular, i-directional set order does not invoke the binary relations $\Delta _i^{\lambda }, \nabla _i^{\lambda }$, it does not require convex sets, and it uses the standard properties of order and direction in $\mathbb {R}^N$.

Let X be a convex sublattice of $\mathbb {R}^N$, $f:X \rightarrow \mathbb {R}$, and $i \in \{ 1,2,\ldots ,N \}$. The function f is $\mathcal {C}_i$-quasisupermodular, if for every $a, b \in X$ and for every $\lambda \in [0, 1]$, $f(a) \ge (>) \ f(a \Delta _i^{\lambda } b) \Rightarrow f(a \nabla _i^{\lambda } b) \ge (>) \ f(b)$. One of the main results in Quah (2007) is the following: for every $i \in \left\{ 1,\ldots , N \right\}$, $\arg \max _A f$ is increasing in A in the $\mathcal {C}_i$-flexible set order, if, and only if, f is $\mathcal {C}_i$-quasisupermodular.

Notice that the property $\mathcal {C}_i$-quasisupermodular is symbolically similar to the notion of a quasisupermodular function. Its interpretation is more complex for two reasons: First, the use of the quantifier “for every $\lambda \in [0, 1]$” in the definition forces consideration of the whole line segment joining a and $a \vee b$ and the whole line segment joining $a \wedge b$ and b, and essentially forces consideration of convex sets, and second, the interpretive issues with using $\Delta _i^{\lambda }, \nabla _i^{\lambda }$ carry over to this definition.

The use of the quantifier “for every $\lambda \in [0, 1]$” in this definition is required by the $\mathcal {C}_i$-flexible set order. This can be seen as follows. Suppose we consider weakening the definition of f is $\mathcal {C}_i$-quasisupermodular by requiring it to hold for only some collection of $\lambda \in [0, 1]$, as follows. Let X be a convex sublattice of $\mathbb {R}^N$, $f:X \rightarrow \mathbb {R}$, $i \in \{ 1,2,\ldots ,N \}$, and $\Lambda$ be a non-empty subset of [0, 1]. The function f is $(i, \Lambda )$-quasisupermodular, if for every x, y in X, and every $\lambda \in \Lambda$, $f(x) \ge (>) \ f(x \Delta _i^{\lambda }y) \Rightarrow f(x \nabla _i^{\lambda }y) \ge (>) \ f(y)$. Notice that f is $\mathcal {C}_i$-quasisupermodular is a special case of this definition, when $\Lambda = [0, 1]$.

In order to characterize the type of monotone comparative statics possible with $(i, \Lambda )$-quasisupermodular functions, consider the following set order. Let X be a convex sublattice of $\mathbb {R}^N$, $i \in \{ 1,2,\ldots ,N \}$, and $\Lambda$ be a non-empty subset of [0, 1]. For subsets A, B of X, A is $(i, \Lambda )$-lower than B, denoted $A \sqsubseteq _i^{\Lambda } B$, if for every $a \in A$, for every $b \in B$, there is $\lambda \in \Lambda$ such that $a \Delta _i^{\lambda }b \in A$ and $a \nabla _i^{\lambda }b \in B$. Notice that A is lower than B in the $\mathcal {C}_i$-flexible set order is a special case of this definition, when $\Lambda = [0, 1]$. Say that a function $f:X \rightarrow \mathbb {R}$ has $(i, \Lambda )$-increasing property, if for every A, B subset of X, $A \sqsubseteq _i^{\Lambda } B \Longrightarrow \arg \max _A f \sqsubseteq _i^{\Lambda } \arg \max _B f$. We can prove the following result.

Proposition 5

Let X be a convex sublattice of $\mathbb {R}^N$, $f:X \rightarrow \mathbb {R}$, $i \in \{ 1,2,\ldots ,N \}$, and $\Lambda$ be a non-empty subset of [0, 1].

f is $(i, \Lambda )$-quasisupermodular, if, and only if, f has $(i, \Lambda )$-increasing property.

Proof

($\Rightarrow$) Suppose f is $(i, \Lambda )$-quasisupermodular. Fix $A \sqsubseteq _i^{\Lambda } B$. Let $a \in \arg \max _A f$ and $b \in \arg \max _B f$. Notice that $A \sqsubseteq _i^{\lambda } B$ implies that there is $\lambda \in \Lambda$ such that $a \Delta _i^{\lambda }b \in A$ and $a \nabla _i^{\lambda }b \in B$. Fix this $\lambda$. Thus $a \in \arg \max _A f \Longrightarrow f(a) \ge f(a \Delta _i^{\lambda }b) \Longrightarrow f(a \nabla _i^{\lambda }b) \ge f(b)$, where the last implication follows from $(i, \Lambda )$-quasisupermodularity of f. Moreover, as $b \in \arg \max _B f$, it follows that $f(a \nabla _i^{\lambda }b) = f(b)$, whence $a\nabla _i^{\lambda }b \in \arg \max _B f$. Furthermore, $f(a \nabla _i^{\lambda }b) = f(b) \Longrightarrow f(a \nabla _i^{\lambda }b) \not > f(b) \Longrightarrow f(a) \le f(a \Delta _i^{\lambda }b)$, where the last implication follows from $(i, \Lambda )$-quasisupermodularity of f. As $a \in \arg \max _A f$, it follows that $f(a) = f(a \Delta _i^{\lambda }b)$, whence $a\Delta _i^{\lambda }b \in \arg \max _A f$, as desired.

($\Leftarrow$) Considering the contrapositive, suppose f is not $(i, \Lambda )$-quasisupermodular. Then there exists $\lambda \in \Lambda$, and there exist a, b in X, such that either (1) $f(a) \ge f(a \Delta _i^{\lambda }b)$ and $f(a \nabla _i^{\lambda }b) < f(b)$, or (2) $f(a) > f(a \Delta _i^{\lambda }b)$ and $f(a \nabla _i^{\lambda }b) \le f(b)$. Notice that in either case, it must be that $a_i > b_i$. Therefore, $a \nabla _i^{\lambda }b \ne b$, $a \Delta _i^{\lambda }b \ne a$, and $a \Delta _i^{\lambda }b \ne a \nabla _i^{\lambda }b$. Let $C = \left\{ a, a \Delta _i^{\lambda }b \right\}$ and $C^{\prime } = \left\{ b, a \nabla _i^{\lambda }b \right\}$. Then $C \sqsubseteq _i^{\Lambda } C^{\prime }$. Suppose (1) is true. Then $a \in \arg \max _C f$ and $b = \arg \max _{C^{\prime }} f$, but for every $\lambda ^{\prime } \in \Lambda$, $a \nabla _i^{\lambda ^{\prime }} b \not \in \arg \max _{C^{\prime }} f$, because $a_i > b_i$ implies that for every $\lambda ^{\prime } \in [0, 1]$, $a \nabla _i^{\lambda ^{\prime }} b \ne b$. Therefore, f does not have $(i, \Lambda )$-increasing property (for $C \sqsubseteq _i^{\lambda } C^{\prime }$). Suppose (2) is true. Then $a = \arg \max _C f$ and $b \in \arg \max _{C^{\prime }} f$, but for every $\lambda ^{\prime } \in \Lambda$, $a \Delta _i^{\lambda ^{\prime }} b \not \in \arg \max _C f$, because $a_i > b_i$ implies that for every $\lambda ^{\prime } \in [0, 1]$, $a \Delta _i^{\lambda ^{\prime }} b \ne b$. Again, f does not have $(i, \Lambda )$-increasing property. $\square$

The result in Quah (2007) is a special case of this result, when $\Lambda = [0,1]$. The result here shows that if we want to weaken the notion of a $\mathcal {C}_i$-quasisupermodular function by requiring the condition to hold for fewer $\lambda$, then we must make the comparability of the set order more restrictive (that is, fewer sets can be ordered) by requiring less flexibility in the choice of $\lambda$ as well. To say this differently, if we want a monotone comparative statics result applicable to a larger collection of constraint sets, we can expand the collection of sets that can be ordered by allowing the greatest flexibility in choosing $\lambda$, by setting $\Lambda = [0,1]$. (This gives us the $\mathcal {C}_i$-flexible set order.) In this case, characterizing monotone comparative static requires imposing the strictest conditions on the objective function by requiring $\Lambda = [0,1]$. In particular, for every a and b, we are forced to consider the whole line segment joining a and $a \vee b$ and the whole line segment joining $a \wedge b$ and b, and we are essentially forced to consider convex sets.

As mentioned in the text, corollaries to theorem 1 and the equivalence of i-directional set order and $\mathcal {C}_i$-flexible set order shows that on convex sublattices, a $C_i$-quasisupermodular function is equivalent to a function that is i-quasisupermodular and satisfies i-single crossing property on X. The following proposition shows this directly. For convenience, a part of the proof is written as the lemmas below.

Lemma 1

For every $a, b \in \mathbb {R}^N$ with $a_i > b_i$, and for every $\lambda \in [0, 1]$, $a \wedge (a \Delta _i^{\lambda }b) = a \wedge b$.

Proof

Fix $a, b \in \mathbb {R}^N$ with $a_i > b_i$, and fix $\lambda \in [0, 1]$. Fix index $j = 1, \ldots , N$. As case 1, suppose $a_j \le b_j$. Then $(a \Delta _i^{\lambda }b)_j = \lambda b_j + (1 - \lambda )(a \wedge b)_j = \lambda b_j + (1- \lambda )a_j \ge a_j$, and therefore, $(a \wedge (a \Delta _i^{\lambda }b))_j = a_j = (a \wedge b)_j$. As case 2, suppose $a_j > b_j$. Then $(a \Delta _i^{\lambda }b)_j = \lambda b_j + (1-\lambda )(a\wedge b)_j = b_j = (a \wedge b)_j$, as desired. $\square$

Lemma 2

For every $a, b \in \mathbb {R}^N$ with $a_i > b_i$, and for every $\lambda \in (0, 1]$

• (1) $b = a \Delta _i^{\lambda }b + \frac{1-\lambda }{\lambda }(a \Delta _i^{\lambda }b - a\wedge b)$, and

• (2) $a \nabla _i^{\lambda }b = a + \frac{1 - \lambda }{\lambda }(a \Delta _i^{\lambda }b - a\wedge b)$.

Proof

Fix $a, b \in \mathbb {R}^N$ with $a_i > b_i$, and fix $\lambda \in (0, 1]$. In this case, $a \Delta _i^{\lambda }b - a\wedge b = \lambda b + (1-\lambda )(a \wedge b) - a\wedge b = \lambda (b - a \wedge b)$, and therefore, $b - a \Delta _i^{\lambda }b = b - \lambda b - (1 - \lambda ) (a\wedge b) = (1- \lambda )(b - a\wedge b) = \frac{1-\lambda }{\lambda } (a \Delta _i^{\lambda }b - a\wedge b)$, showing (1). Similarly, $a \vee b - a \nabla _i^{\lambda }b = a \vee b - \lambda a - (1-\lambda )(a \vee b) = \lambda (a \vee b - a) = \lambda (b - a \wedge b)$, and therefore, $a \nabla _i^{\lambda }b - a = \lambda a + (1-\lambda )(a \vee b) - a = (1- \lambda )(a \vee b - a) = (1- \lambda )(b- a \wedge b) = \frac{1-\lambda }{\lambda }(a \Delta _i^{\lambda }b - a \wedge b)$, showing (2). $\square$

Proposition 6

Let X be a convex sublattice of $\mathbb {R}^N$, $f:X \rightarrow \mathbb {R}$, and $i \in \{ 1, \ldots , N \}$. The following are equivalent.

• 1. f is $C_i$-quasisupermodular

• 2. f is i-quasisupermodular and satisfies i-single crossing property on X

Proof

For (1) implies (2), to show i-single crossing property, fix x, y in X with $y_i < x_i$, fix $t \ge 0$, and let $v = t(y - x \wedge y)$. Let $z = y+v$ and $u = z - x \wedge z$. It is easy to check that $z - x \wedge z = z - x \wedge y$, and therefore, $u = z - x \wedge y = y + t(y - x \wedge y) - x \wedge y = (1+t)(y - x \wedge y)$. Notice also that $u = x \vee z - x$. Consequently, $v = t(y - x \wedge y) = \frac{t}{1+t}(1+t)(y - x \wedge y) = \frac{t}{1+t}u$. Let $\lambda = \frac{1}{1+t} \in (0, 1]$. Then $v = (1-\lambda )u$, and this implies that $y - x \wedge y = \lambda u$, because $z = y + v = y + (1- \lambda )u = y + u - \lambda u = y + z - x \wedge z - \lambda u$. Moreover, notice that $x \Delta _i^{\lambda }z = \lambda z + (1-\lambda )(x \wedge z) = x \wedge z + \lambda (z - x \wedge z) = x \wedge z + \lambda u = y$, and that $x \nabla _i^{\lambda }z = \lambda x + (1-\lambda )(x \vee z) = x \vee z + \lambda (x \vee z - x) = x \vee z - \lambda u = x \vee z + v - u = x \vee z + v - (x \vee z - x) = x + v$. Now suppose $f(x) \ge f(y) = f(x \Delta _i^{\lambda }z)$. Then $f(x + v) = f(x \nabla _i^{\lambda }z) \ge f(z) = f(y + v)$, where the inequality follows from $C_i$-quasisupermodularity. The case for strict inequality follows similarly. Thus f satisfies i-single crossing property. i-quasisupermodularity of f follows from $C_i$-quasisupermodularity for $\lambda = 0$.

For (2) implies (1), fix i, fix $a, b \in \mathbb {R}^N$, and fix $\lambda \in [0, 1]$. As case 1, suppose $a_i \le b_i$. In this case, $a \Delta _i^{\lambda }b = a$, $a \nabla _i^{\lambda }b = b$, and therefore, $f(a) \ge f(a \Delta _i^{\lambda }b) \Rightarrow f(a \nabla _i^{\lambda }b) \ge f(b)$ holds trivially. Strict inequality holds vacuously. As case 2, suppose $a_i > b_i$. As subcase 1, suppose $\lambda \ne 0$. Let $x = a$, $y = a \Delta _i^{\lambda }b$, and $v = \frac{1-\lambda }{\lambda }\left( a \Delta _i^{\lambda }b - a \wedge (a \Delta _i^{\lambda }b) \right)$. Using lemma 1, $v = \frac{1-\lambda }{\lambda }(a \Delta _i^{\lambda }b - a \wedge b)$. Suppose $f(a) \ge f(a \Delta _i^{\lambda }b)$. That is, $f(x) \ge f(y)$. Then i-single crossing property implies $f(x + v) \ge f(y + v)$. By construction, $x + v = a + \frac{1-\lambda }{\lambda }(a \Delta _i^{\lambda }b - a \wedge b) = a \nabla _i^{\lambda }b$, where the last equality follows from lemma 2. Also, $y + v = a \Delta _i^{\lambda }b + \frac{1-\lambda }{\lambda }(a \Delta _i^{\lambda }b - a \wedge b) = b$, where the last equality follows from lemma 2. The case for strict inequality follows similarly. As subcase 2, suppose $\lambda = 0$. Then $a \Delta _i^{\lambda }b = a \wedge b$ and $a \nabla _i^{\lambda }b = a \vee b$, so the property follows from i-quasisupermodularity of f. $\square$

Appendix B: Some proofs

One set of conditions under which sets can be ordered in the i-directional set order is as follows. Let X be a sublattice of $\mathbb {R}^N$, $f:X \rightarrow \mathbb {R}$, and $i \in \{ 1,2,\ldots ,N \}$. The function f is i-quasisubmodular on X, if for every $a, b \in X$ with $a_i > b_i$, $f(a) \le (<) \ f(a \wedge b) \Longrightarrow f(a \vee b) \le (<) \ f(b)$. The function f satisfies dual i-single crossing property on X, if for every $a, b \in X$ with $a_i > b_i$, and for every $v \in \{ s(b - a \wedge b) \mid s \in \mathbb {R}, s \ge 0 \}$ such that $a+v, b+v \in X$, $f(a) \le (<) \ f(b) \Longrightarrow f(a + v) \le (<) \ f(b + v)$.

Proposition 7

Let X be a convex sublattice of $\mathbb {R}^N$, $f:X \rightarrow \mathbb {R}$, and $i \in \{ 1,2,\ldots ,N \}$.

If f is continuous, (weakly) increasing, i-quasisubmodular, and satisfies dual i-single crossing on X, then $\tau \le \tau ^{\prime } \Longrightarrow \{ x \mid f(x) \le \tau \} \sqsubseteq _i^{dso} \{ x \mid f(x) \le \tau ^{\prime } \}$.

Proof

Let $\tau \le \tau ^{\prime }$, $A = \{ x \mid f(x) \le \tau \}$, $B = \{ x \mid f(x) \le \tau ^{\prime } \}$, and suppose $a \in A$, $b \in B$ with $a_i > b_i$. As case 1, suppose $f(b) \le \tau$. In this case, let $v=0$. Then $b - v = b \in A$ and $f(a) \le \tau \le \tau ^{\prime }$ implies that $a + v = a \in B$. As case 2, suppose $f(b) > \tau$. Then f is (weakly) increasing implies that $f(a \wedge b) \le f(a) \le \tau$. For $s \in [0, 1]$, consider $v(s) = s(b - a \wedge b)$. Then $s=0$ implies $f(b - v(s)) > \tau$ and $s=1$ implies $f(b - v(s)) \le \tau$. By continuity, there is $\hat{s} \in (0, 1]$ such that $f(b - v(\hat{s})) = \tau$. Set $\hat{v} = \hat{s}(b - a\wedge b)$. Then $b - \hat{v} \in A$ and $f(b - \hat{v}) \ge f(a)$. As subcase 1, suppose $\hat{s}=1$. Then $f(a \wedge b) = f(b - \hat{v}) \ge f(a)$ and i-quasisubmodularity implies that $f(b) \ge f(a \vee b)$, whence $a + 1(a \vee b - a) \in B$. As subcase 2, suppose $\hat{s} \in (0, 1)$. Applying dual i-single crossing to vectors to a and $b-\hat{v}$, with the directional vector $w = \frac{\hat{s}}{1-\hat{s}}\left[ (b- \hat{v}) - a \wedge (b- \hat{v}) \right]$ implies $f(b - \hat{v} + w) \ge f(a+w)$. But notice that $\hat{v} = \hat{s}(b - a\wedge b) = \hat{s} \left[ (b- \hat{v}) - a \wedge b \right] + \hat{s} \hat{v} = \hat{s} \left[ (b- \hat{v}) - a \wedge (b- \hat{v}) \right] + \hat{s} \hat{v}$, and therefore, $\hat{v} = \frac{\hat{s}}{1-\hat{s}}\left[ (b-\hat{v}) - a \wedge (b-\hat{v}) \right] = w$. In other words, $f(b) \ge f(a + \hat{v})$, whence $a + \hat{v} \in B$. $\square$

It is easy to check that for given prices $p \gg 0$, the function $\phi : X \rightarrow \mathbb {R}$, $\phi (x) = p\cdot x$ satisfies these conditions. This provides another proof that with respect to wealth w, Walrasian budgets sets are ordered in the i-directional set order.

To show the equivalence of i-increasing differences (u) on X and i-increasing differences (*) on X, consider first the following slight modification of i-increasing differences (u) on X. Let X be a sublattice of $\mathbb {R}^N$, $f:X \rightarrow \mathbb {R}$, and $i \in \{ 1,2,\ldots ,N \}$. f satisfies i-increasing differences ($\sigma u$), if for every $b \in X, u \in \mathbb {R}^N$ with $u_i > 0$, for every $\sigma , s \ge 0$, such that $b+ \sigma u, b+s(-u)_+, b+ \sigma u + s(-u)_+ \in X$, $f(b+ \sigma u) - f(b) \le f(b+ \sigma u + s(-u)_+) - f(b + s(-u)_+)$. Consider the following equivalence.

Lemma 3

Let X be a sublattice of $\mathbb {R}^N$, $f:X \rightarrow \mathbb {R}$, and $i \in \{ 1,2,\ldots ,N \}$.

f satisfies i-increasing differences (u) on X, if, and only if, f satisfies i-increasing differences ($\sigma u$) on X.

Proof

For sufficiency, fix $b \in X$, $u \in \mathbb {R}^N$ with $u_i>0$, and fix $\sigma , s \ge 0$. If $\sigma = 0$, we are done, because left-hand side and right-hand side of the condition are both zero. Suppose $\sigma >0$. Let $\hat{u} = \sigma u$ and $\hat{s} = \frac{s}{\sigma } \ge 0$. Then $\hat{u}_i > 0$ and $\hat{s}(-\hat{u}_+) = s(-u)_+$, and therefore,

$$\begin{aligned} f(b + \sigma u) - f(b)&= f(b + \hat{u}) - f(b) \\&\le f(b + \hat{u} + \hat{s}(-\hat{u})_+) - f(b + \hat{s}(-\hat{u})_+) \\&= f(b + \sigma u + s(-u)_+) - f(b + s(-u)_+), \end{aligned}$$

as desired. For necessity, let $\sigma = 1$. $\square$

Now recall that f satisfies i-increasing differences (*) on X, if for every $b \in X, u \in \mathbb {R}^N$ with $u_i > 0$, for every $\sigma \ge 0$, $f(b + \sigma u + s(-u)_+) - f(b + s(-u)_+)$ is (weakly) increasing in s, (where we consider only points $b+ \sigma u+ s(-u)_+, b + s(-u)_+ \in X$). Consider the following equivalence.

Lemma 4

Let X be a sublattice of $\mathbb {R}^N$, $f:X \rightarrow \mathbb {R}$, and $i \in \{ 1,2,\ldots ,N \}$.

f satisfies i-increasing differences ($\sigma u$) on X, if, and only if, f satisfies i-increasing differences (*) on X.

Proof

Suppose f satisfies i-increasing differences ($\sigma u$) on X. To check for i-increasing differences (*) on X, fix $b \in X, u \in \mathbb {R}^N$ with $u_i > 0$, and $\sigma \ge 0$. Fix $s_1 \le s_2$. If $\sigma =0$, we are done, because the expression is 0 for all s. Suppose $\sigma > 0$. Let $\hat{b} = b + s_1(-u)_+$ and $\hat{s} = s_2 - s_1 \ge 0$. Then

$$\begin{aligned}&f(b + \sigma u + s_1(-u)_+) - f(b+ s_1(-u)_+) \\&\quad = f(\hat{b} + \sigma u) - f(\hat{b}) \\&\quad \le f(\hat{b} + \sigma u + \hat{s}(-u)_+) - f(\hat{b} + \hat{s}(-u)_+) \\&\quad = f(b + \sigma u + s_1(-u)_+ + (s_2 - s_1)(-u)_+) \\&\quad - f(b + s_1(-u)_+ + (s_2 - s_1)(-u)_+) \\&\quad = f(b + \sigma u + s_2(-u)_+) - f(b + s_2(-u)_+), \end{aligned}$$

as desired.

Suppose f satisfies i-increasing differences (*) on X. To check that f satisfies i-increasing differences ($\sigma u$) on X, fix $b \in X, u \in \mathbb {R}^N$ with $u_i > 0$, and fix $\sigma , s \ge 0$. Let $s_1 = 0$. Then $s_1 \le s$, and therefore, $f(b+ \sigma u) - f(b) = f(b + \sigma u +s_1(-u)_+) - f(b+ s_1(-u)_+) \le f(b + \sigma u + s(-u)_+) - f(b+ s(-u)_+)$, as desired. $\square$

These lemmas imply the equivalence of i-increasing differences (u) on X and i-increasing differences (*) on X, as desired.