Hybridized SLAU2–HLLI and hybridized AUSMPW$+$–HLLI Riemann solvers for accurate, robust, and efficient magnetohydrodynamics (MHD) simulations, part I: one-dimensional MHD

Abstract

SLAU2 and AUSMPW$+$, both categorized as AUSM-type Riemann solvers, have been extensively developed in gasdynamics. They are based on a splitting of the numerical flux into advected and pressure parts. In this paper, these two Riemann solvers have been extended to magnetohydrodynamics (MHD). The SLAU2 Riemann solver has the favorable attribute that its dissipation for low-speed flows scales as $O(M^{2})$, where M is the Mach number. This is the physical scaling required for low-speed flows, and the dissipation in SLAU2 for MHD is engineered to have this low Mach number scaling. The AUSMPW$+$, when its pressure flux is replaced with that of SLAU2, has the same low Mach number scaling. At higher Mach numbers, however, the pressure-split Riemann solvers were found not to function well for some MHD Riemann problems, despite the fact that they were engineered to have a dissipation that scales as $O(\vert M\vert )$ for high Mach number flows. The HLLI Riemann solver (Dumbser and Balsara in J Comput Phys 304:275–319, 2016) has a dissipation that scales as $O(\vert M\vert )$, which makes it unsuitable for low Mach number flows. However, it has very favorable performance for higher Mach number MHD flows. Since the two families of Riemann solvers perform very well over a range of intermediate Mach numbers, the best way to benefit from the mutually complementary strengths of both these Riemann solvers is to hybridize between them. The result is an all-speed Riemann solver for MHD. We, therefore, document hybridized SLAU2–HLLI and AUSMPW$+$–HLLI Riemann solvers. The hybrid Riemann solvers suppress the oscillations that appeared in single-solver solutions, and they also preserve contact discontinuities, as well as Alfvén waves, very well. Furthermore, their better resolution at low speeds has been demonstrated. We also present several stringent one-dimensional test problems.

Appendices

Appendices

1.1 Appendix 1: AUSMPW$+$, AUSMPW$+$–HLLI, AUSMPW$+$2, and AUSMPW$+$2–HLLI for MHD

The AUSMPW$+$ flux was already extended to MHD by Han et al. [53]. This form, however, turned out to be unstable in some numerical tests, as was the case with the original SLAU2. Thus, it is modified, as in SLAU2, in which the gasdynamic part and magnetic part are handled differently, as follows. The Euler part is

$$\begin{aligned} \mathbf{F}_{\mathrm{AUSMPW}+\left( {\mathrm{Euler}} \right) }= & {} \bar{M}_L^+ c_{1/2} {{\varvec{\Phi }} }_L +\bar{M}_R^- c_{1/2} {{\varvec{\Phi }} }_R+{\mathrm{P}}^{+}{} \mathbf{P}_L\nonumber \\&+\,\text {P}^{-}{\mathbf{P}_{R}}+\frac{1}{2}\left( {\mathbf{F}_{\mathrm{B},L} +\mathbf{F}_{\mathrm{B},R}} \right) , \end{aligned}$$

(13a)

$$\begin{aligned}&{{\varvec{\Phi }} }=\left( {\rho ,\rho u,\rho v,\rho w,\rho E+p_\mathrm{T}} \right) ^{\mathrm{T}}, \nonumber \\&\mathbf{F}_{\mathrm{B}} =\left( {0,-B_{1/2} B_x ,-B_{1/2} B_y ,-B_{1/2} B_z ,0} \right) ^{\mathrm{T}}, \end{aligned}$$

(13b)

$$\begin{aligned}&{} \mathbf{P}=\left( {0,p_\mathrm{T} ,0,0,-B_{1/2} \left( {\mathbf{u}\cdot \mathbf{B}} \right) } \right) ^{\mathrm{T}}, \end{aligned}$$

(13c)

where $B_{1/2} =\frac{B_{x,L} +B_{x,R} }{2}$ as in [53], and for $m_{1/2}=\overline{M}_L^+ +\overline{{M}}_R^- \ge 0$,

$$\begin{aligned} \overline{{M}}_L^+= & {} M_L^+ +M_R^- \cdot \left[ {\left( {1-w} \right) \cdot \left( {1+f_R } \right) -f_L } \right] ,\nonumber \\ \overline{{M}}_R^-= & {} M_R^- \cdot w\cdot \left( {1+f_R } \right) , \end{aligned}$$

(14a)

and for $m_{1/2}< 0$,

$$\begin{aligned}&\overline{{M}}_L^+ = M_L^+ \cdot w\cdot \left( {1+f_L } \right) , \nonumber \\&\overline{{M}}_R^- =M_R^- +M_L^+ \cdot \left[ {\left( {1-w} \right) \cdot \left( {1+f_L } \right) -f_R } \right] . \end{aligned}$$

(14b)

The pressure-based weighting functions are given by:

$$\begin{aligned}&w=1-\hbox {min}\left( {\frac{p_{\mathrm{T},L} }{p_{\mathrm{T},R} },\frac{p_{\mathrm{T},R} }{p_{\mathrm{T},L} }} \right) ^{3}, \end{aligned}$$

(14c)

$$\begin{aligned}&f_{L/R} =\left\{ {{\begin{array}{ll} \left( {\frac{p_{L/R} }{p_{\mathrm{T},s} }-1} \right) ,&{}\quad \hbox {if }\,\,p_{\mathrm{T},s} \ne 0, \\ \\ 0,&{}\quad \hbox {if}\,\,p_{\mathrm{T},s} =0, \\ \end{array} }} \right. \end{aligned}$$

(14d)

$$\begin{aligned}&p_{\mathrm{T},s} =\hbox {P}^{+}p_{\mathrm{T},L} +\hbox {P}^{-}p_{\mathrm{T},R}, \end{aligned}$$

(14e)

where the pressure flux, which was not given in [53] or [54], is assumed as the standard AUSM form as (3d) and (3e) (that drops off higher-order terms):

$$\begin{aligned} {{\text {P}}^ + } = \left\{ \begin{array}{ll} \frac{1}{2}\left( {1 + {\text {sign}}\left( {{M_L}} \right) } \right) ,&{}\quad {\text {if}}~\left| {{M_L}} \right| \ge 1 \\ \\ \frac{1}{4}{{\left( {{M_L} + 1} \right) }^2}\left( {2 - {M_L}} \right) ,&{}\quad {\text {otherwise}}, \end{array}\right. \end{aligned}$$

(3d)

$$\begin{aligned} {\text {P}}^{-} = \left\{ \begin{array}{ll} \frac{1}{2}\left( {1 - {\text {sign}}\left( {{M_R}} \right) } \right) ,&{}\quad {\text {if}}\,\left| {{M_R}} \right| \ge 1 \\ \\ \frac{1}{4}{{\left( {{M_R} - 1} \right) }^2}\left( {2 + {M_R}} \right) ,&{}\quad {\text {otherwise}}, \end{array}\right. \end{aligned}$$

(3e)

and the mass flux switch, again not given in [53] or [54], is assumed as follows (again dropping off higher-order terms):

$$\begin{aligned} M^{+}=\left\{ {{\begin{array}{ll} \frac{1}{2}\left( {M_L +\left| {M_L } \right| } \right) ,&{}\quad \hbox {if}\left| {M_L } \right| \ge 1 \\ \\ \frac{1}{4}\left( {M_L +1} \right) ^{2},&{}\quad \hbox {otherwise}, \\ \end{array} }} \right. \\ \end{aligned}$$

(9d)

$$\begin{aligned} M^{-}=\left\{ {{\begin{array}{ll} \frac{1}{2}\left( {M_R -\left| {M_R } \right| } \right) ,&{}\quad \hbox {if}\left| {M_R } \right| \ge 1 \\ \\ -\frac{1}{4}\left( {M_R -1} \right) ^{2},&{}\quad \hbox {otherwise}, \\ \end{array} }} \right. \end{aligned}$$

(9e)

Fig. 8

Problem 3 solutions, density; AUSMPW$+$ and AUSMPW$+$–HLLI

where

$$\begin{aligned}&M_L =\frac{u_L }{\bar{{c}}},\quad M_R =\frac{u_R }{\bar{{c}}}, \end{aligned}$$

(15a)

$$\begin{aligned}&\bar{{c}}=\min \left( {{\begin{array}{cc} {c_{f,L} ,}&{} {c_{f,R} } \\ \end{array} }} \right) , \end{aligned}$$

(15b)

that is, the minimum value of the left and the right c (fast magnetosonic speed) is taken.

The magnetic part is common to SLAU2 for MHD and hence omitted. Also, as in SLAU2, another version has also been developed which does not use HLL but a simple AUSM form in the magnetic part, and this works well as in the present AUSMPW$+$. The solutions are not shown. Furthermore, the same idea as in Sect. 3.2 will lead to “AUSMPW$+$–HLLI.”

The selected numerical results are shown in Fig. 8 for Problem 3 (Colliding Flow). In this problem, in contrast to SLAU2 and SLAU2–HLLI (Fig. 3), AUSMPW$+$ produces only small wiggles and very slight undershoot $(x \approx -\,0.0)$ that are similar in AUSMPW$+$–HLLI (Fig. 8). For this particular high-speed test, AUSMPW$+$ suppressed wiggles in SLAU2 which is designed for both high and low speeds. For the other problems, SLAU2 represents AUSMPW$+$, and SLAU2–HLLI does AUSMPW$+$–HLLI, respectively, except for Problem 2 (Ryu–Jones shock tube) in which SLAU2–HLLI, AUSMPW$+$, and AUSMPW$+$–HLLI removed small wiggles seen in SLAU2.

Furthermore, since AUSMPW$+$ does not have a low-speed scaling term, we replaced its pressure flux with that of the SLAU2, leading to “AUSMPW$+$2” and “AUSMPW$+$2–HLLI” as follows:

$$\begin{aligned} \mathbf{F}_{\mathrm{AUSMPW}+2\left( {\mathrm{Euler}} \right) }= & {} \overline{M}_L^+ c_{1/2} {\varvec{\Phi } }_L +\overline{M}_R^- c_{1/2} {{\varvec{\Phi }} }_R\nonumber \\&\quad +\,\mathbf{P}_{\mathrm{AUSMPW}+2} +\frac{1}{2}\left( {\mathbf{F}_{\mathrm{B},L} +\mathbf{F}_{\mathrm{B},R} } \right) ,\nonumber \\ \end{aligned}$$

(16a)

$$\begin{aligned}&\mathbf{P}_{\mathrm{AUSMPW}+2}\nonumber \\&\quad = \left( {{\begin{array}{c} 0 \\ {\tilde{p}} \\ 0 \\ 0 \\ \hbox {P}^{+}\cdot \left\{ {-u_L B_{x, L} -v_L B_{y,L} -w_L B_{z,\hbox {}L} } \right\} B_{1/2}\\ \quad +\hbox {P}^{-}\cdot \left\{ {-u_R B_{x,R} -v_R B_{y,R} -w_R B_{z,R} } \right\} B_{1/2} \\ \end{array} }} \right) ,\nonumber \\ \end{aligned}$$

(16b)

Fig. 9

Problem 7 solutions (including AUSMPW$+$2 and AUSMPW$+$2–HLLI)

where

$$\begin{aligned} \left( {\tilde{p}} \right) _{\mathrm{AUSMPW}+2}= & {} \left( {\tilde{p}} \right) _{\mathrm{SLAU}2} =\frac{p_{\mathrm{T},L} +p_{\mathrm{T},R} }{2}\nonumber \\&+\,\frac{\hbox {P}^{+}-\hbox {P}^{-}}{2}\left( {p_{\mathrm{T},L} -p_{\mathrm{T},R} } \right) \nonumber \\&+\,\sqrt{\frac{\mathbf{u}_L^2 +\mathbf{u}_R^2 }{2}} \cdot \left( {\hbox {P}^{+}+\hbox {P}^{-}-1} \right) \bar{\rho }\bar{c}\nonumber \\ \end{aligned}$$

(16c)

is borrowed from SLAU2. The rest of the parts are the same with AUSMPW$+$ or AUSMPW$+$–HLLI, resulting in AUSMPW$+$2 or AUSMPW$+$2–HLLI, respectively. We confirmed that in all the previous test cases this change did not affect the solutions. Let us mention that another all-speed version of AUSMPW$+$ is available in [87] for gasdynamics.

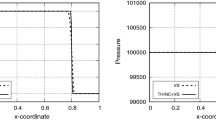
Figure 9 shows the pressure profiles in the first 20 cells at $t = 1$ of Problem 7. AUSMPW$+$2 preserved 13% of the initial amplitude, followed by AUSMPW$+$2–HLLI (13%). AUSMPW$+$ conserved slightly lower amplitude (12%), indicating the small but actual effect of the low Mach scaling introduced in AUSMPW$+$2 and AUSMPW$+$2–HLLI. In this problem, the SLAU2 showed the best performance (17%) and the Roe was the worst (11%).

1.2 Appendix 2: Analysis of SLAU2 for MHD

As conducted in [53], the SLAU2 for MHD behaviors at contact discontinuity and tangential discontinuity is compared with analytical solutions.

• 1. Contact discontinuity: $\rho _{L} \ne \rho _{R}, u_{L}=u_{R} = 0, v_{L}=v_{R}, w_{L}=w_{R}, B_{yL }=B_{yR}, B_{zL}=B_{zR}, p_{L}=p_{R}, B_{x} \ne 0$. Thus, referring to (1b),

  

  fluxes from left to right cells are: $F_{1,\mathrm{exact}}=\rho _{L}u_{L} = 0; F_{2,\mathrm{exact}}=p_{\mathrm{T}}-B_{x}^{2}; F_{3,\mathrm{exact}} = - B_{x} B_{y,L}; F_{4,\mathrm{exact}} = - B_{x} B_{z,L}; F_{5,\mathrm{exact}} = - B_{x} (v_{L}B_{y,L} + w_{L}B_{z,L}); (F_{6,\mathrm{exact}} = 0); F_{7,\mathrm{exact}} = - v_{L}B_{x}; F_{8,\mathrm{exact}} = - w_{L}B_{x}$.

• 2. Tangential discontinuity: $\rho _{L} \ne \rho _{R}, u_{L}=u_{R} = 0, v_{L} \ne v_{R}, w_{L} \ne w_{R}, B_{yL }\ne B_{yR}, B_{zL} \ne B_{zR}, p_{\mathrm{T},L}=p_{\mathrm{T},R}, B_{x} = 0$. The corresponding analytical fluxes are: $F_{1,\mathrm{exact}}=\rho _{L}u_{L} = 0; F_{2,\mathrm{exact}}=p_{\mathrm{T}}; F_{3,\mathrm{exact}} = 0; F_{4,\mathrm{exact}} = 0; F_{5,\mathrm{exact}} = 0; (F_{6,\mathrm{exact}} = 0); F_{7,\mathrm{exact}} = 0; F_{8,\mathrm{exact}} = 0$.

Fig. 10

Gresho vortex test solutions (Mach number contours, $0 \le M \le 0.01)$. a SLAU2 and b Roe

In the SLAU2,

$$\begin{aligned} {\left( \dot{m}\right) }_{\mathrm{SLAU}2}= & {} \frac{1}{2}\left\{ \rho _L \left( {u_L +\left| {\bar{V_n }} \right| ^{+}} \right) \right. \nonumber \\&\left. +\,\rho _R \left( {u_R -\left| {\bar{V_n }} \right| ^{-}} \right) \right. \nonumber \\&\left. -\frac{\chi }{\bar{c}}\left( {p_{\mathrm{T},R} -p_{\mathrm{T},L} } \right) \right\} =0 \end{aligned}$$

(17)

and

$$\begin{aligned} \left( {\tilde{p}} \right) _{\mathrm{SLAU}2}= & {} \frac{p_{\mathrm{T},L} +p_{\mathrm{T},R} }{2}+\frac{\hbox {P}^{+}-\hbox {P}^{-}}{2}\left( {p_{\mathrm{T},L} -p_{\mathrm{T},R} } \right) \nonumber \\&+\,\sqrt{\frac{\mathbf{u}_L^2 +\mathbf{u}_R^2 }{2}}\cdot \left( {\hbox {P}^{+}+\hbox {P}^{-}-1} \right) \bar{\rho }\bar{c}=p_{\mathrm{T}}\nonumber \\ \end{aligned}$$

(18)

at both discontinuities. Thus, the SLAU2 solutions are as follows:

• 1. Contact discontinuity

$$\begin{aligned} F_{1, \mathrm{SLAU2}}= & {} 0 = F_{1, \mathrm{exact}}, \end{aligned}$$

(19a)

$$\begin{aligned} F_{2,\mathrm{SLAU}2}= & {} p_\mathrm{T} -B_x^2 =F_{2,\mathrm{exact}}, \end{aligned}$$

(19b)

$$\begin{aligned} F_{3,\mathrm{SLAU}2}= & {} -B_x \frac{B_{y,L} +B_{y,R} }{2}=-B_x B_{y,L} =F_{3,\mathrm{exact}}, \nonumber \\ \end{aligned}$$

(19c)

$$\begin{aligned} F_{4,\mathrm{SLAU}2}= & {} -B_x \frac{B_{z,L} +B_{z,R} }{2}=-B_x B_{z,L} =F_{4,\mathrm{exact}}, \nonumber \\ \end{aligned}$$

(19d)

$$\begin{aligned} F_{5,\mathrm{SLAU}2}= & {} -B_x \frac{v_L B_{z,L} +w_L B_{z,L} +v_R B_{z,R} +w_R B_{z,R} }{2},\nonumber \\= & {} -B_x \left( {v_L B_{z,L} +w_L B_{z,L} } \right) =F_{5,\mathrm{exact}}, \end{aligned}$$

(19e)

since $\hbox {P}^{+} = \hbox {P}^{-} = 0.5$ at $u = 0$.

$$\begin{aligned} F_{7, \,\mathrm{SLAU2}}= & {} -v_{L}B_{\mathrm{x}}=F_{7, \,\mathrm{exact}}, \end{aligned}$$

(19f)

$$\begin{aligned} F_{8, \,\mathrm{SLAU2}}= & {} -w_{L}B_{\mathrm{x}}=F_{8, \,\mathrm{exact}}. \end{aligned}$$

(19g)

Thus, the contact discontinuity is preserved by SLAU2.

• 2. Tangential discontinuity

Similarly,

$$\begin{aligned} F_{1, \,\mathrm{SLAU2}}= & {} 0 = F_{1, \,\mathrm{exact}}, \end{aligned}$$

(20a)

$$\begin{aligned} F_{2, \,\mathrm{SLAU2}}= & {} p_{\mathrm{T}}=F_{2,\, \mathrm{exact}},\end{aligned}$$

(20b)

$$\begin{aligned} F_{3, \,\mathrm{SLAU2}}= & {} 0 = F_{3, \,\mathrm{exact}},\end{aligned}$$

(20c)

$$\begin{aligned} F_{4, \,\mathrm{SLAU2}}= & {} 0 = F_{4, \,\mathrm{exact}},\end{aligned}$$

(20d)

$$\begin{aligned} F_{5, \,\mathrm{SLAU2}}= & {} 0 = F_{5, \,\mathrm{exact}},\end{aligned}$$

(20e)

$$\begin{aligned} F_{7, \,\mathrm{SLAU2}}= & {} 0 = F_{7, \,\mathrm{exact}},\end{aligned}$$

(20f)

$$\begin{aligned} F_{8,\, \mathrm{SLAU2}}= & {} 0 = F_{8,\, \mathrm{exact}}. \end{aligned}$$

(20g)

Therefore, the tangential discontinuity is also proved to be conserved.

1.3 Appendix 3: Gresho Vortex

In order to confirm the efficacy of SLAU2 at a low Mach number, the Gresho vortex [91] is solved using SLAU2 (a three-wave solver with low Mach scaling) and Roe (a full-wave solver without low Mach scaling, as is the case also for the HLLI). The problem setup is as follows: A square domain of $[0, 1] \times [0, 1]$ is filled with $40 \times 40$ square cells, with the periodic boundary condition. The initial condition depends on the radius r from the vortex center, $(x_{\mathrm{c}}, y_{\mathrm{c}}) = (0.5, 0.5)$, i.e., $r=\sqrt{\left( {x-x_{\mathrm{c}} } \right) ^{2}+\left( {y-y_{\mathrm{c}} } \right) ^{2}}$.

$$\begin{aligned}&\rho =1.0, \end{aligned}$$

(21a)

$$\begin{aligned}&p_0 =\frac{\rho }{\gamma M^{2}}, \end{aligned}$$

(21b)

$$\begin{aligned}&u_\theta =\left\{ {{\begin{array}{ll} 5r,&{}\quad \hbox {if}\,\,0\le r\le 0.2, \\ \\ 2-5r,&{}\quad \hbox {if}\,\,0.2\le r\le 0.4, \\ \\ 0,&{}\quad \hbox {if}\,\,r\ge 0.4, \\ \end{array} }} \right. \end{aligned}$$

(21c)

$$\begin{aligned}&p=\left\{ {{\begin{array}{ll} p_0 +12.5r^{2},&{}\quad \hbox {if}\,\,0\le r\le 0.2, \\ \\ p_0 +12.5r^{2}+4\left( {1-5r-\hbox {ln}\left( {0.2} \right) +\hbox {ln}\left( r \right) } \right) ,&{}\quad \hbox {if}\,\,0.2\le r\le 0.4, \\ \\ p_0 -2+4\hbox {ln}\left( 2 \right) ,&{}\quad \hbox {if}\,\,r\ge 0.4, \\ \end{array} }} \right. \nonumber \\ \end{aligned}$$

(21d)

where M is Mach number, $M = 0.01$, $\gamma$ is the specific heat ratio, $\gamma = 1.4$, and $u_{{\theta }}$ is the angular velocity, converted to Cartesian velocity components as

$$\begin{aligned}&u=-u_\theta \hbox {sin}\theta =-u_\theta \frac{y-y_{\mathrm{c}} }{r}, \end{aligned}$$

(22a)

$$\begin{aligned}&v=-u_\theta \hbox {cos}\theta =u_\theta \frac{x-x_{\mathrm{c}} }{r}, \end{aligned}$$

(22b)

$$\begin{aligned}&\theta =\hbox {arctan}2\left( {y-y_{\mathrm{c}} ,x-x_{\mathrm{c}} } \right) . \end{aligned}$$

(22c)

The computations are run for 20,000 steps with $\varDelta t = 1 \times 10^{-4}\, (\hbox {CFL} \approx 0.4)$, i.e., until $t = 2$. The Mach number contours are compared in Fig. 10. The SLAU2 clearly maintains the vortex structure, while it is smeared by the Roe-type Riemann solver.

Note that this problem is 2D gasdynamic. The MHD version of such a problem is left for future work, since multi-dimensional MHD involves divergence-free treatment which is beyond the scope of the present paper.