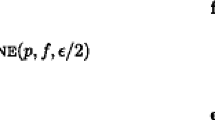Generalized average shadow prices and bottlenecks

Abstract

Usually some of the constraints of a 0-1-Mixed Integer Linear Programming problem correspond to resources and in this paper we suppose that they may be redefined. For the availability of the resources the average shadow price is the maximum price that the decision maker is willing to pay for an additional unit of the package (i.e. a combination) of resources defined by some direction. In this paper we present a generalization of the average shadow price and its relation with bottlenecks including the analysis relative to the coefficients matrix of resource constraints. The generalization presented does not have some limitations of the usual average shadow price. A mathematical programming approach to find the strategy for investment in resources is presented.

Appendix

Proof of Lemma 1:

(1) Let $Y(\theta ) = \lbrace \mathbf {y}\in {\lbrace 0,1 \rbrace }^k:\exists \mathbf {x} \, \text{ such } \text{ that } \,\mathbf {(x,y)} \in F(P(\theta )) \rbrace \forall \theta \in [0,1]$.

Because of $\varOmega$ is a compact set then there exists $\theta (\mathbf {y})$ such that $\theta (\mathbf {y}) = \hbox {min} \lbrace \theta : \mathbf {y} \in Y(\theta ),\;\;\theta \in [0,1] \rbrace$ $\forall \mathbf {y} \in Y(1)$.

If $Y(0) = Y(1)$ let $\delta _1 = 1$, otherwise let $\delta _1 =\hbox {min} \lbrace \theta (\mathbf {y}): \mathbf {y} \notin Y(0) \rbrace$ then $Y(0) = Y(\theta )\;\forall \theta \in [0,\delta _1)$.

(2) Let $\mathbf {y} \in Y(0)$. Let $P(\mathbf {y},\theta )$ be a problem in x defined as follows:

$$\begin{aligned} \begin{array}{lllll} (P(\mathbf {y},\theta ))\mathbf {d}^t\mathbf {y} +&\hbox {max}&\mathbf {c}^t\mathbf {x}&\hbox {s.t.}&\mathbf {(x,y)}\in F(P(\theta )) \end{array} \end{aligned}$$

$P(\mathbf {y},\theta )$ is a Linear Programming (LP) problem. Let $g_\mathbf {y}: [0,1] \longrightarrow \mathbb {R}$ be a function such that $g_\mathbf {y}(\theta ) = v(P(\mathbf {y},\theta ))$. Note that $v(P) = v(P(0)) = \hbox {max} \lbrace g_\mathbf {y}(0): \mathbf {y} \in Y(0) \rbrace$. It has been observed that $g_\mathbf {y}$ is locally rational and upper semicontinuous (Freund 1985; Gal 1984; Martin 1975; Zuidwijk 2005) . It follows that $g_\mathbf {y}$ is locally derivable at zero from the right.

Let $p(\mathbf {y}) = \frac{dg_\mathbf {y}(0)}{d\theta ^+}$. Let $\epsilon > 0$ then there exists $\delta (\mathbf {y})$ such that $\frac{g_\mathbf {y}(\theta ) - g_\mathbf {y}(0)}{\theta } \le p(\mathbf {y}) + \epsilon \;\forall \theta \in (0,\delta (\mathbf {y})) \forall \mathbf {y} \in Y(0)$.

(3) Let $\delta ^* = \hbox {min} \lbrace \delta _1, \hbox {min} \lbrace \delta (\mathbf {y}):\mathbf {y} \in Y(0) \rbrace \rbrace$. Let $p^* = \hbox {max} \lbrace p(\mathbf {y}): \mathbf {y} \in Y(0) \rbrace$ and let $\theta \in (0,\delta ^*)$. We have that:

$$\begin{aligned} \frac{f(\theta )}{\theta }= & {} \frac{v(P(\theta )) - v(P)}{\theta } = \hbox {max} \left\{ \frac{v(P(\mathbf {y},\theta )) - v(P)}{\theta }: \mathbf {y} \in Y(0)\right\} \\= & {} \hbox {max} \left\{ \frac{g_\mathbf {y}(\theta )) - v(P)}{\theta }: \mathbf {y} \in Y(0)\rbrace \right\} \le \hbox {max} \left\{ \frac{g_\mathbf {y}(\theta )) -g_\mathbf {y} (0)}{\theta }: \mathbf {y} \in Y(0)\rbrace \right\} \\\le & {} \hbox {max} \left\{ p(\mathbf {y}): \mathbf {y} \in Y(0) \right\} \ + \epsilon = p^* + \epsilon \end{aligned}$$

Therefore $\frac{f(\theta )}{\theta } \le p^* + \epsilon$ for all $\theta \in (0,\delta ^*)$. Let $p^{**} = \frac{f(1)}{\delta ^*}$ then $\frac{f(\theta )}{\theta } \le p^{**}$ for all $\theta \in [\delta ^*,1]$ and finally $\hbox {max} \lbrace \frac{f(\theta )}{\theta }:\theta \in (0,1] \rbrace \le \hbox {max} \lbrace p^{**},p^* + \epsilon \rbrace$ and Q is a bounded set. $\square$

Proof of Lemma 4:

Let $\theta ^*$ be an optimal solution for E(p) then $f(\theta ) - p\theta \le f(\theta ^*) - p\theta ^*$ for all $\theta \in [0,1]$. It follows that $f^+(\theta ) \le f(\theta ^*) + p(\theta - \theta ^*)$ for all $\theta \in [0,1]$, therefore:

$$\begin{aligned}&max\;\lbrace f^+(\theta )-p\theta : \theta \in [0,1] \rbrace \le max\;\lbrace f(\theta ^*)+p(\theta - \theta ^*) - p\theta : \theta \in [0,1] \rbrace \\&\quad =f(\theta ^*) - p\theta ^* = v(E(p)) = max\;\lbrace f(\theta )-p\theta : \theta \in [0,1] \rbrace \\&\quad \le max\;\lbrace f^+(\theta )-p\theta : \theta \in [0,1] \rbrace . \end{aligned}$$

$\square$

Proof of Lemma 5:

Let $f^+$ the concave envelope of f. Let $l \ge 1$ and let $C^+(f) = \lbrace (\overline{\theta }_i,q_i): i=1,\ldots ,l\rbrace$ with

• (i) $0=\overline{\theta _1}< \cdots< \overline{\theta _{l-1}} < \overline{\theta _l} =1$,

• (ii) $q=q_1> \cdots> q_{l-1} > q_l = 0$,

• (iii) $f^+ (\theta ) = q_1 \theta$ if $0 = \overline{\theta _1} \le \theta \le \overline{\theta _2}$ and

• (iv) $f^+ (\theta ) = f^+ (\overline{\theta _{i-1}}) + q_{i-1} (\theta - \overline{\theta _{i-1}})$ if $\overline{\theta _{i-1}} \le \theta \le \overline{\theta _i}\;\;(i=2,\ldots ,l)$

If $0 = q_l \le p_r < q_{l-1}$ then $v(E(p_r)) = f^+(\overline{\theta _l}) - p_r \overline{\theta _l}$ with $\overline{\theta _l} = 1$ the unique optimal solution for $E(p_r)$.

If $p_r = q_1 = q$ then $v(E(p_r)) = 0$ and the algorithm stops.

Let us suppose that $q_i< p_r < q_{i-1}$ for some $i \le l-1$ then $v(E(p_r)) = f^+(\overline{\theta _i}) - p_r \overline{\theta _i}$ with $\overline{\theta _i}$ the unique optimal solution for $E(p_r)$.

If $p_r=q_i$ for some $1< i < l$ then any $\theta$ in $[\overline{\theta _i},\overline{\theta _{i+1}}]$ is an optimal solution for $E(p_r)$ and $v(E(p_r)) > 0$. Let $\theta _{r+1} \in (\overline{\theta _i},\overline{\theta _{i+1}})$. In this case $\theta _{r+2} \le \overline{\theta _i}$.

It follows that each piece is visited at most two times. Because of the number of pieces is finite then the g.a.s.p algorithm is finite. $\square$

Proof of Lemma 6:

(1) We have that $0 \le v(E(p_{r+1})) < v(E(p_r))$ for all $r \ge 0$ and then there exists $s \ge 0$ such that $lim_{r \longrightarrow \infty } v(E(p_r)) = s$.

If $s > 0$ then $0 < s \le v(E(p_r)) = f(\theta _{r+1}) - p_r \theta _{r+1}$ for all $r \ge 0$ and then $p_{r+1} \ge p_r + \frac{s}{\theta _{r+1}} \ge p_r + s$ for all $r \ge 0$. Hence we have that $lim_{r \longrightarrow \infty } p_r = \infty$ and then $lim_{r \longrightarrow \infty } v(E(p_r)) = 0$ and we have a contradiction. Therefore $s=0$.

(2) We have that $0 \le p_{r+1} < p_r$ for all $r \ge 0$ and then there exists $\hat{p}$ such that $\hat{p} \le q$, $p_r \le \hat{p}$ for all $r \ge 0$ and $lim_{r \longrightarrow \infty } p_r = \hat{p}$. Let $\hat{\theta }$ an optimal solution for $E(\hat{p})$ then $v(E(\hat{p})) \le v(E(\hat{p})) + (\hat{p} - p_r) \hat{\theta }= f(\hat{\theta }) - p_r \hat{\theta }\le f(\theta _{r+1}) - p_r \theta _{r+1} = (p_{r+1} - p_r) \theta _{r+1} \le (p_{r+1}- p_r)$ for all $r \ge 0$ and then $v(E(\hat{p})) = 0$ because of $lim_{r \longrightarrow \infty } (p_{r+1}-p_r)=0$. Therefore $q = \hat{p}$. $\square$