Skip to main content
SpringerLink
Log in

The kinematic dynamo problem, part I: analytical treatment with the Bullard–Gellman formalism

  • Original Article
  • Published:
Continuum Mechanics and Thermodynamics Aims and scope Submit manuscript

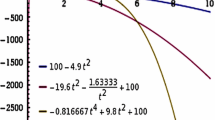
Abstract

This paper is dedicated to the description of kinematic dynamo action in a sphere and its analytical treatment with the Bullard–Gellman formalism. One goal of dynamo theory is to answer the question: Can magnetic fields of stellar objects be generated or sustained due to (fluid) motion in the interior? Bullard and Gellman were among the first to study this question, leading the way for many subsequent studies, cf. Bullard (Philos Trans R Soc A 247(928):213–278, 1954). In their publication the differential equations resulting from a toroidal–poloidal decomposition of the velocity and magnetic field are stated without an in-depth discussion of the employed methods and computation steps. This study derives the necessary formalism in a compact and concise manner by using an operator-based approach. The focus lies on the mathematical steps and necessary properties of the considered formalism. Prior to that a derivation of the induction equation is presented based on rational continuum electrodynamics. As an example of the formalism the decay of two magnetic fields is analyzed.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

Abbreviations

c :

Speed of light in vacuum

\(\mathcal {B}_R\) :

Spherical material body of radius R

\(\varvec{v}\) :

Velocity

\(\varvec{n}\) :

Surface unit normal vector

\(\varvec{e}\) :

Unit normal vector of a singular surface or material interface

\(w_\perp \) :

Normal component of the velocity of a singular surface or material interface

\(\,\mathrm {d}A\) :

Area element

\(\,\mathrm {d}\varOmega \) :

\(r^{-2}\,\mathrm {d}A\). Normalized area element

\(\,\mathrm {d}V\) :

Volume element

\(\mathcal {O}(\bullet )\) :

Order of magnitude of the considered field

\(\mathbf {A}\) :

Dimension matrix

\(\mathbf {k}_i\) :

Null space vectors of \(\mathbf {A}\)

\(\mathrm {\Pi }_i\) :

Dimensionless products

\( Re _\text {mag.}\) :

Magnetic Reynolds number

\(\lambda \) :

Eigenvalue of the induction equation

\(\varvec{B}\) :

Magnetic flux density

\(\varvec{E}\) :

Electric field

\(\varvec{H}\) :

Total current potential

\(\varvec{\mathfrak {H}}\) :

Free current potential

\(\varvec{M}\) :

Magnetization or bond current potential

\(\varvec{D}\) :

Total current potential

\(\varvec{\mathfrak {D}}\) :

Free current potential

\(\varvec{P}\) :

Magnetization or bond charge potential

q, \(q^{\text {f}}\), \(q^{\text {r}}\) :

Total, free and bond charge density

\(\varvec{J}\), \(\varvec{J}^{\text {f}}\), \(\varvec{J}^{\text {r}}\) :

Total, free and bond current density

\(V_\mathrm {m}\) :

Magnetic scalar potential

\(\sigma \) :

Electric conductivity

\(\varepsilon _0\), \(\mu _0\) :

Vacuum permittivity and permeability

\(Y^m_n\) :

Complex-valued spherical harmonics

\(C^m_n\) :

Real-valued cosine spherical harmonics

\(S^m_n\) :

Real-valued sine spherical harmonics

\(P^m_n\) :

Associated Legendre polynomials

\(J_n\) :

Bessel functions of 1\(\mathrm {st}\) kind

\(\nabla _S\) :

\((\varvec{1}-\varvec{n}\otimes \varvec{n})\cdot \nabla \) Surface del-operator

\(\nabla _{\theta ,\varphi }\) :

\(r\nabla _S=\varvec{e}_\theta \frac{\partial }{\partial \theta }+\varvec{e}_\varphi \frac{1}{\sin (\theta )}\frac{\partial }{\partial \varphi }\). Angular part of the spherical surface del-operator

\(\Delta _S\) :

\(\nabla _S\cdot \nabla _S\). Surface Laplace-operator

\(\Delta _{\theta ,\varphi }\) :

\(r^2\Delta _S=\frac{1}{\sin (\theta )}\frac{\partial }{\partial \theta }\big (\sin (\theta )\frac{\partial }{\partial \theta }\big )+\frac{1}{\sin ^2(\theta )}\frac{\partial ^2 }{\partial \varphi ^2}\). Angular part of the spherical surface Laplace-operator

\(\varvec{\mathcal {D}}_{\theta ,\varphi }\) :

\(\varvec{e}_\theta \frac{1}{\sin (\theta )}\frac{\partial }{\partial \varphi }-\varvec{e}_\varphi \frac{\partial }{\partial \theta }\). Differential operator related to toroidal vector fields

\( \mathcal {D}_{\theta ,\varphi }[f,g] \) :

\(\nabla _{\theta ,\varphi }f\cdot \varvec{\mathcal {D}}_{\theta ,\varphi }[g] \). Bilinear antisymmetric differential operator

\(D_{r}^{1}{[}{f}{]}\) :

\(\frac{1}{r}\frac{\mathrm{d}}{\mathrm{d}r}(r f(r))\)

\(\varvec{T}^{i}_{j}\) :

Complex-valued toroidal vector fields

\(\varvec{P}^{i}_{j}\) :

Complex-valued poloidal vector fields

\(t^i_j(r)\) :

Radial functions of \(\varvec{T}^{i}_{j}\)

\(p^i_j(r)\) :

Radial functions of \(\varvec{P}^{i}_{j}\)

\(\varvec{U}^{k}_{l}\) :

Complex-valued toroidal velocity fields

\(\varvec{Q}^{k}_{l}\) :

Complex-valued poloidal velocity fields

\(u^k_l(r)\) :

Radial functions of \(\varvec{U}^{k}_{l}\)

\(q^k_l(r)\) :

Radial functions of \(\varvec{Q}^{k}_{l}\)

\(\varvec{\mathcal {T}}^{m}_{n}\) :

Complex-valued toroidal projectors

\(\varvec{\mathcal {P}}^{m}_{n}\) :

Complex-valued poloidal projectors

\(\tilde{\varvec{T}}\phantom {\varvec{T}}^{i}_{j}\) :

Complex-valued toroidal vector fields

\(\tilde{\varvec{P}}\phantom {\varvec{P}}^{i}_{j}\) :

Complex-valued poloidal vector fields

\(\tilde{t}^i_j(r)\) :

Radial functions of \(\tilde{\varvec{T}}\phantom {\varvec{T}}^{i}_{j}\)

\(\tilde{p}^i_j(r)\) :

Radial functions of \(\tilde{\varvec{P}}\phantom {\varvec{P}}^{i}_{j}\)

\(\tilde{\varvec{U}}\phantom {\varvec{U}}^{k}_{l}\) :

Complex-valued toroidal velocity fields

\(\tilde{\varvec{Q}}\phantom {\varvec{Q}}^{k}_{l}\) :

Complex-valued poloidal velocity fields

\(\tilde{\varvec{\mathcal {T}}}\phantom {\varvec{\mathcal {T}}}^{m}_{n}\) :

Complex-valued toroidal projectors

\(\tilde{\varvec{\mathcal {P}}}\phantom {\varvec{\mathcal {P}}}^{m}_{n}\) :

Complex-valued poloidal projectors

\(K^{ikm}_{jln}\) :

Adams–Gaunt integral

\(L^{ikm}_{jln}\) :

Elsasser integral

w(i, j, k):

\(i(i+1)+j(j+1)-k(k+1)\)

ODE:

Ordinary differential equation

PDE:

Partial differential equation

ref.:

Reference scale

References

  1. Abramowitz, M., Stegun, I.A.: Handbook of Mathematical Functions. Applied Mathematics Series, vol. 55, 10th edn. National Bureau of Standards (1972). http://people.math.sfu.ca/~cbm/aands/

  2. Arfken, G.B., Weber, H.J.: Mathematical Methods for Physicists, 6th edn. Elsevier Academic Press, Amsterdam (2005)

    MATH  Google Scholar 

  3. Bronstein, I.N., Semendjajew, K.A., Musiol, G., Mühlig, H.: Handbook of Mathematics, 6th edn. Springer, Berlin (2015)

    MATH  Google Scholar 

  4. Bullard, E., Gellman, H.: Homogeneous dynamos and terrestrial magnetism. Philos. Trans. R. Soc. A 247(928), 213–278 (1954)

    Article  ADS  MathSciNet  MATH  Google Scholar 

  5. Collatz, L.: Eigenwertaufgaben mit technischen Anwendungen, 2nd edn. Akademische Verlagsgesellschaft, Leipzig (1963)

    MATH  Google Scholar 

  6. Dudley, M.L., James, R.W.: Time-dependent kinematic dynamos with stationary flows. Philos. Trans. R. Soc. Lond. Ser. A Math. Phys. Sci. 425, 407–429 (1989)

    Article  ADS  MathSciNet  Google Scholar 

  7. Dziubek, A.: Equations for two-phase flows: a primer. Meccanica 47(8), 1819–1836 (2012). https://doi.org/10.1007/s11012-012-9555-0

    Article  MathSciNet  MATH  Google Scholar 

  8. Elsasser, W.M.: On the origin of the earth’s magnetic field. Phys. Rev. 55, 489–498 (1939). https://doi.org/10.1103/PhysRev.55.489

    Article  ADS  MATH  Google Scholar 

  9. Elsasser, W.M.: Induction effects in terrestrial magnetism part I: theory. Phys. Rev. 69(3–4), 106 (1946a). https://doi.org/10.1103/PhysRev.69.106

    Article  ADS  MathSciNet  MATH  Google Scholar 

  10. Elsasser, W.M.: Induction effects in terrestrial magnetism part II: the secular variation. Phys. Rev. 70(3–4), 202 (1946b)

    Article  ADS  MathSciNet  MATH  Google Scholar 

  11. Elsasser, W.M.: Induction effects in terrestrial magnetism: part III. Electric modes. Phys. Rev. 72(9), 821 (1947)

    MATH  Google Scholar 

  12. Eringen, A.C., Maugin, G.A.: Electrodynamics of Continua I, 1st edn. Springer, Berlin (1990). https://doi.org/10.1007/978-1-4612-3226-1

    Book  Google Scholar 

  13. Gauß, C.F.: Allgemeine Theorie des Erdmagnetismus. In: Werke, Fünfter Band, Mathematische Physik, vol. 5. Dieterich, pp. 121–193 (1838)

  14. Glatzmaier, G.A., Roberts, P.H.: A three-dimensional self-consistent computer simulation of a geomagnetic field reversal. Nature 377, 203–208 (1995). https://doi.org/10.1038/377203a0

    Article  ADS  Google Scholar 

  15. Gubbins, D.: Numerical solutions of the kinematic dynamo problem. Philos. Trans. R. Soc. A 274(1241), 493–521 (1973). https://doi.org/10.1098/rsta.1973.0074

    Article  ADS  MATH  Google Scholar 

  16. Gubbins, D., Barber, C.N., Gibbons, S., Love, J.J.: Kinematic dynamo action in a sphere. I. Effects of differential rotation and meridional circulation on solutions with axial dipole symmetry. Proc. R. Soc. Lond. Ser. A Math. Phys. Eng. Sci. 456(1998), 1333–1353 (2000a)

    Article  ADS  MathSciNet  MATH  Google Scholar 

  17. Hansen, W.W.: A new type of expansion in radiation problems. Phys. Rev. 47, 139–143 (1935). https://doi.org/10.1103/PhysRev.47.139

    Article  ADS  MATH  Google Scholar 

  18. Hutter, K., Jöhnk, K.: Continuum Methods of Physical Modeling. Springer, Berlin (2004). https://doi.org/10.1007/978-3-662-06402-3

    Book  MATH  Google Scholar 

  19. Hutter, K., van de Ven, A.A.F., Ursescu, A.: Electromagnetic Field Matter Interactions in Thermoelastic Solids and Viscous Fluids. Lecture Notes in Physics, vol. 710. Springer, Berlin (2006)

  20. Itskov, M.: Tensor Algebra and Tensor Analysis for Engineers. Springer, Berlin (2009). https://doi.org/10.1007/978-3-540-93907-8

    Book  MATH  Google Scholar 

  21. Jackson, J.D.: Classical Electrodynamics, 3rd edn. Wiley, New York (1998)

    MATH  Google Scholar 

  22. Kovetz, A.: Electromagnetic Theory. Oxford University Press, Oxford (2000)

    MATH  Google Scholar 

  23. Kumar, S., Roberts, P.H.: A three-dimensional kinematic dynamo. Proc. R. Soc. Lond. A Math. Phys. Eng. Sci. 344(1637), 235–258 (1975). https://doi.org/10.1098/rspa.1975.0100

    Article  ADS  Google Scholar 

  24. Larmor, J.: How could a rotating body such as the sun become a magnet? Report of the British Association for the Advancement of Science 87th Meeting, pp. 159–160 (1919)

  25. Merrill, M.W., McElhinny, M.W., McFadden, P.L.: The Magnetic Field of the Earth: Paleomagnetism, the Core, and the Deep Mantle, vol. 63, 1st edn. Academic Press, Boca Raton (1998)

    Google Scholar 

  26. Müller, I.: Thermodynamics, 1st edn. Pitman Publishing, Boston (1985)

    MATH  Google Scholar 

  27. Müller, W.H.: An expedition to continuum theory. In: Gladwell, G.M.L. (ed.) Solid Mechanics and its Applications, vol. 210. Springer, Berlin (2014). https://doi.org/10.1007/978-94-007-7799-6

    Google Scholar 

  28. Roberts, P.H.: Kinematic dynamo models. Philos. Trans. R. Soc. A 272(1230), 663–698 (1972). https://doi.org/10.1098/rsta.1972.0074

    Article  ADS  Google Scholar 

  29. Roberts, P.H.: Theory of the geodynamo (chap. 3). In: Schubert, G., Olson, P. (eds.) Core Dynamics: Treatise on Geophysics, vol. 8, pp. 67–105. Elsevier, Amsterdam (2009)

    Google Scholar 

  30. Simpson, J., Weiner, E. (eds.): The Oxford English dictionary, 2nd edn. Oxford University Press, Oxford (1989)

    Google Scholar 

  31. Slattery, J.C., Sagis, L., Oh, E.S.: Interfacial Transport Phenomena, 2nd edn. Springer, Berlin (2007)

    MATH  Google Scholar 

  32. Stratton, J.A.: Electromagnetic Theory. The IEEE Press Series on Electromagnetic Wave Theory. McGraw-Hill, New York (1941)

    Google Scholar 

  33. Winch, D., James, R.: Computations with spherical harmonics and Fourier series in geomagnetism. In: Bolt, B.A. (ed.) Geophysics: Methods in Computational Physics: Advances in Research and Applications, vol. 13, pp. 93–132. Elsevier, Amsterdam (1973). https://doi.org/10.1016/B978-0-12-460813-9.50009-6

    Google Scholar 

  34. Wolfram Research, Inc.: Mathematica (Version 10.1). Champaign, Illinois (2015)

Download references

Author information

Authors and Affiliations

  1. Institut für Mechanik, Kontinuumsmechanik und Materialtheorie, Technische Universität Berlin, Sek. MS. 2, Einsteinufer 5, 10587, Berlin, Germany

    Sebastian Glane, Felix A. Reich & Wolfgang H. Müller

Authors
  1. Sebastian Glane
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Felix A. Reich
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Wolfgang H. Müller
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Sebastian Glane.

Additional information

Communicated by Andreas Öchsner.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Glane, S., Reich, F.A. & Müller, W.H. The kinematic dynamo problem, part I: analytical treatment with the Bullard–Gellman formalism. Continuum Mech. Thermodyn. 30, 731–774 (2018). https://doi.org/10.1007/s00161-018-0638-6

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00161-018-0638-6

Keywords

Search

Navigation