Skip to main content
SpringerLink
Log in

A combined parametric shape optimization and ersatz material approach

  • RESEARCH PAPER
  • Published:
Structural and Multidisciplinary Optimization Aims and scope Submit manuscript

Abstract

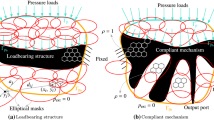
This article describes a parametric shape optimization approach using vertical or horizontal structures with a fine parametrization of their center lines and profiles. In this context horizontal means a lateral connection from left to right and vertical means a bottom-up connection. These structures are projected to a pseudo density field associated with a fixed mesh using a differentiable mapping. This enables the use of existing topology optimization tools with respect to the solution of the state problem based on the pseudo density field. The approach belongs to a class of geometry projection onto a fictitious domain methods. It therefore shares the property that sensitivity analysis is reduced to extend the well known gradient calculation from topology optimization by chain using the sensitivity of the mapping from shape variables to pseudo density. The contribution lies in the combination with our specific shape parametrization and the associated regularization. Optimization problems can be formulated concurrently in terms of shape variables and pseudo density. We discuss regularization, periodicity constraints, symmetry formulations and overhang constraints in terms of shape variables. Volume and perimeter constraints are easily formulated in terms of the pseudo density. We see our approach as being particularly beneficial for certain problem classes where it may be difficult to restrict the design space, e.g. restricting isolated structures or holes or where a strict control of solid to void transition is necessary. Consequently, we show examples for phononic band gap maximization, boundary driven heat optimization and perimeter maximization for a flow problem. We also present a formulation of overhang constraints for additive manufacturing in terms of shape variables.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12
Fig. 13
Fig. 14
Fig. 15
Fig. 16
Fig. 17
Fig. 18
Fig. 19
Fig. 20
Fig. 21
Fig. 22
Fig. 23
Fig. 24
Fig. 25

Similar content being viewed by others

Notes

  1. Solid Isotropic Material with Penalization.

  2. Local mesh refinement, as in Maute and Ramm (1995), does not appear to be widely applied.

  3. We note that the periodic design constraint is no replacement for periodic boundary conditions on the state problem.

  4. See Gill et al. (2002).

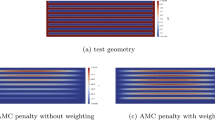
  5. Slope constraints, curvature constraints and possibly overhang constraints.

References

  • Allaire G, Jouve F, Michailidis G (2016) Thickness control in structural optimization via a level set method. Struct Multidiscip Optim 53(6):1349–1382

    Article  MathSciNet  Google Scholar 

  • Andreassen E, Clausen A, Schevenels M, Lazarov B, Sigmund O (2011) Efficient topology optimization in matlab using 88 lines of code. Struct Multidiscip Optim 43(1):1–16

    Article  MATH  Google Scholar 

  • Bendsøe MP (1989) Optimal shape design as a material distribution problem. Struct Multidiscip Optim 1:193–202

    Article  Google Scholar 

  • Bilal OR, Hussein MI (2012) Topologically evolved phononic material: breaking the world record in band gap size. In: SPIE OPTO, International society for optics and photonics, pp 826,911–826,911

  • Braibant V, Fleury C (1984) Shape optimal design using b-splines. Comput Methods Appl Mech Eng 44 (3):247–267

    Article  MATH  Google Scholar 

  • Bruggi M (2008) On an alternative approach to stress constraints relaxation in topology optimization. Struct Multidiscip Optim 36(2):125–141

    Article  MATH  MathSciNet  Google Scholar 

  • Bruns TE, Tortorelli DA (2001) Topology optimization of non-linear elastic structures and compliant mechanisms. Comput Methods Appl Mech Eng 190(26-27):3443–3459

    Article  MATH  Google Scholar 

  • Christiansen AN, Bærentzen JA, Nobel-Jørgensen M, Aage N, Sigmund O (2015) Combined shape and topology optimization of 3d structures. Comput Graph 46:25–35

    Article  Google Scholar 

  • Dunning PD (2017) Design parameterization for topology optimization by intersection of an implicit function. Comput Methods Appl Mech Eng 317:993–1011

    Article  MathSciNet  Google Scholar 

  • Gangl P, Langer U, Laurain A, Meftahi H, Sturm K (2015) Shape optimization of an electric motor subject to nonlinear magnetostatics. SIAM J Sci Comput 37(6):B1002–B1025

    Article  MATH  MathSciNet  Google Scholar 

  • Gaynor AT, Guest JK (2016) Topology optimization considering overhang constraints: Eliminating sacrificial support material in additive manufacturing through design. Struct Multidiscip Optim 5(54):1157–1172

    Article  MathSciNet  Google Scholar 

  • Gersborg AR, Andreasen CS (2011) An explicit parameterization for casting constraints in gradient driven topology optimization. Struct Multidiscip Optim 44(6):875–881

    Article  Google Scholar 

  • Gill PE, Murray W, Saunders MA (2002) SNOPT: An SQP algorithm for large-scale constrained optimization. SIAM J Optim 12(4):979–1006

    Article  MATH  MathSciNet  Google Scholar 

  • Guest JK (2009) Imposing maximum length scale in topology optimization. Struct Multidiscip Optim 37 (5):463–473

    Article  MATH  MathSciNet  Google Scholar 

  • Guest J, Prévost J, Belytschko T (2004) Achieving minimum length scale in topology optimization using nodal design variables and projection functions. Int J Numer Methods Eng 61(2):238–254

    Article  MATH  MathSciNet  Google Scholar 

  • Haftka RT, Grandhi RV (1986) Structural shape optimization: a survey. Comput Methods Appl. Mech Eng 57(1):91–106

    Article  MATH  MathSciNet  Google Scholar 

  • Haslinger J, Mäkinen R (2003) Introduction to Shape Optimization: Theory, vol 7. Siam

  • Hoang VN, Jang GW (2016) Topology optimization using moving morphable bars for versatile thickness control. Computer Methods in Applied Mechanics and Engineering

  • Imam MH (1982) Three-dimensional shape optimization. Int J Numer Methods Eng 18(5):661–673

    Article  MATH  Google Scholar 

  • Langelaar M (2017) An additive manufacturing filter for topology optimization of print-ready designs. Struct Multidisc Optim 55(3): 871–883

    Article  MathSciNet  Google Scholar 

  • Lazarov B, Wang F, Sigmund O (2016) Length scale and manufacturability in density-based topology optimization. Arch Appl Mech 86(1-2):189–218

    Article  Google Scholar 

  • Le C, Bruns T, Tortorelli D (2011) A gradient-based, parameter-free approach to shape optimization. Comput Meth Appl Mech Eng 200(9):985–996

    Article  MATH  MathSciNet  Google Scholar 

  • Maute K, Ramm E (1995) Adaptive topology optimization. Struct Optim 10(2):100–112

    Article  Google Scholar 

  • Norato J, Haber R, Tortorelli D, Bendsøe MP (2004) A geometry projection method for shape optimization. Int J Numer Methods Eng 60(14):2289–2312

    Article  MATH  MathSciNet  Google Scholar 

  • Norato J, Bell B, Tortorelli D (2015) A geometry projection method for continuum-based topology optimization with discrete elements. Comput Methods Appl Mech Eng 293:306–327

    Article  MathSciNet  Google Scholar 

  • Novotny AA, Sokołowski J (2012) Topological derivatives in shape optimization. Springer Science & Business Media, Berlin

    MATH  Google Scholar 

  • Petersson J, Sigmund O (1998) Slope constrained topology optimization. Int J Numer Methods Eng 41:1417–1434

    Article  MATH  MathSciNet  Google Scholar 

  • Petersson J, Beckers M, Duysinx P (1999) Almost isotropic perimeters in topology optimization: Theoretical and numerical aspects. In: Third world congress of structural and multidisciplinary optimization

  • Pingen G, Evgrafov A, Maute K (2007) Topology optimization of flow domains using the lattice Boltzmann method. Struct Multidiscip Optim 34(6):507–524

    Article  MATH  MathSciNet  Google Scholar 

  • Saxena A (2008) A material-mask overlay strategy for continuum topology optimization of compliant mechanisms using honeycomb discretization. J Mech Des 130(8):082,304

    Article  Google Scholar 

  • Saxena A (2011) Topology design with negative masks using gradient search. Struct Multidiscip Optim 44 (5):629–649

    Article  Google Scholar 

  • Semmler J, Pflug L, Stingl M, Leugering G (2015) Shape optimization in electromagnetic applications. In: New trends in shape optimization. Springer, pp 251–269

  • Sigmund O (2001) A 99 Line topology optimization code written in MATLAB. Struct Multidiscip Optim 21:120–127

    Article  Google Scholar 

  • Sigmund O (2007) Morphology-based black and white filters for topology optimization. Struct Multidiscip Optim 33(4):401–424

    Article  Google Scholar 

  • Sigmund O, Jensen JS (2003) Systematic design of phononic band-gap materials and structures by topology optimization. Philos Trans R Soc Math Phys Eng Sci 361(1806):1001–1019

    Article  MATH  MathSciNet  Google Scholar 

  • Sigmund O, Maute K (2013) Topology optimization approaches. Struct Multidiscip Optim 48(6):1031–1055

    Article  MathSciNet  Google Scholar 

  • Sigmund O, Petersson J (1998) Numerical instabilities in topology optimization: A survey on procedures dealing with checkerboards, mesh-dependencies and local minima. Struct Multidiscip Optim 16:68–75

    Article  Google Scholar 

  • Sokolowski J, Zolesio JP (1992) Introduction to shape optimization. In: Introduction to shape optimization. Springer, pp 5–12

  • Svanberg K (1987) The method of moving asymptotes-a new method for structural optimization. Int J Numer Methods Eng 24(2):359–373

    Article  MATH  MathSciNet  Google Scholar 

  • van Dijk NP, Maute K, Langelaar M, Van Keulen F (2013) Level-set methods for structural topology optimization: a review. Struct Multidiscip Optim 48(3):437–472

    Article  MathSciNet  Google Scholar 

  • Wang F, Lazarov B, Sigmund O (2011) On projection methods, convergence and robust formulations in topology optimization. Struct Multidiscip Optim 43(6):767–784

    Article  MATH  Google Scholar 

  • Warmuth F, Körner C (2015) Phononic band gaps in 2d quadratic and 3d cubic cellular structures. Materials 8(12):8327–8337

    Article  Google Scholar 

  • Yurkin MA, Hoekstra AG (2007) The discrete dipole approximation: an overview and recent developments. J Quant Spectrosc Radiat Transfer 106(1):558–589

    Article  Google Scholar 

  • Zhang W, Zhang J, Guo X (2016) Lagrangian description based topology optimization: A revival of shape optimization. J Appl Mech 83(4):041,010

    Article  Google Scholar 

  • Zhou M, Lazarov B, Wang F, Sigmund O (2015) Minimum length scale in topology optimization by geometric constraints. Comput Methods Appl Mech Eng 293:266–282

    Article  MathSciNet  Google Scholar 

Download references

Acknowledgements

The authors gratefully acknowledge the support of the Cluster of Excellence ‘Engineering of Advanced Materials’ at the University of Erlangen-Nuremberg, which is funded by the German Research Foundation (DFG) within the framework of its ‘Excellence Initiative’. The implementation of the heat and flow problems was done by Bich Ngoc Vu.

Author information

Authors and Affiliations

  1. Friedrich-Alexander-Universität Erlangen-Nürnberg, Zentralinstitut Scientific Computing, Martenstrasse 5a, 91080, Erlangen, Germany

    Fabian Wein & Michael Stingl

Authors
  1. Fabian Wein
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Michael Stingl
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Fabian Wein.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Wein, F., Stingl, M. A combined parametric shape optimization and ersatz material approach. Struct Multidisc Optim 57, 1297–1315 (2018). https://doi.org/10.1007/s00158-017-1812-3

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00158-017-1812-3

Keywords

Search

Navigation