Analytical sensitivity in topology optimization for elastoplastic composites

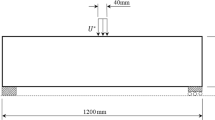
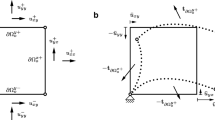
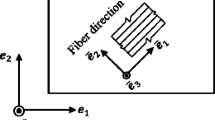
Abstract

The present study proposes a topology optimization of composites considering elastoplastic deformation to maximize the energy absorption capacity of a structure under a prescribed material volume. The concept of a so-called multiphase material optimization, which is originally defined for a continuous damage model, is extended to elastoplastic composites with appropriate regularization for material properties in order to regularize material parameters between two constituents. In this study, we formulate the analytical sensitivity for topology optimization considering elastoplastic deformationand its path-dependency. For optimization applying a gradient-based method, the accuracy of sensitivities iscritical to obtain a reliable optimization result. The proposed analytical sensitivity method takes the derivative of the total stress which satisfies equilibrium equation instead of that of the incremental stress and does not need implicit sensitivity terms. It is verified that the proposed method can provide highly accurate sensitivity enough to obtain reliable optimization results by comparing with that evaluated from the finite difference approach.

Appendices

Appendix A: Isotropic elastoplastic material model

The isotropic elastoplastic material, the return mapping algorithm and the consistent tangent modulus used in the present study are already well known and therefore detailed description of them is not necessary. However, since many of these relational equations are cited in the main text to analytically derive sensitivity in the approach formulated by the present study, we provide outlines of them in Appendix.

First, in elastoplastic deformation, the total strain tensor ε is expressed as the sum of the elastic strain tensor ε ^e and the plastic strain tensor ε ^p as follows:

$$ \boldsymbol{\varepsilon} = \boldsymbol{\varepsilon}^{\mathrm{e}} + \boldsymbol{\varepsilon}^{\mathrm{p}} . $$

(50)

Assuming that Hooke’s law is effective during plastic deformation, the equation below can be obtained,

$$ \dot{\boldsymbol{\sigma}} = \mathbb{C} : \left( \dot{\boldsymbol{\varepsilon}} - \dot{\boldsymbol{\varepsilon}}^{\mathrm{p}} \right) . $$

(51)

Here, σ and $\mathbb {C}$ represent the Cauchy stress tensor and the elastic stiffness tensor, respectively, which are expressed in the velocity form herein for the sake of convenience. Assuming, by employing the von Mises yield criterion, that the yield stress changes depending only on the equivalent plastic strain ${\bar {\varepsilon }^{\mathrm {p}}}$, the yield function Φ can be obtained as follows by using the hardening function ${k} \left (\bar {{\varepsilon }}^{\mathrm {p}} \right )$,

$$ {\Phi} \left( \boldsymbol{\sigma}^{\prime} , \bar{{\varepsilon}}^{\mathrm{p}} \right) = \frac{1}{2} \, \boldsymbol{\sigma}^{\prime} : \boldsymbol{\sigma}^{\prime} - \frac{1}{3} \, {k}^{2} \left( \bar{{\varepsilon}}^{\mathrm{p}} \right) . $$

(52)

Here, σ ^′ and $\bar {\varepsilon }^{\mathrm {p}}$ represent the deviatoric stress tensor and the equivalent plastic strain, respectively. To make it convenient to employ the return mapping algorithm described later, the yield function is presented here in squared form. Although the hardening law for a plastic material model can be set in various ways according to the actual material, the present study assumes a simple, rate-independent, isotropic hardening law, and provides the hardening law ${k} \left (\bar {{\varepsilon }}^{\mathrm {p}} \right )$ as follows:

$$ {k} \left( \bar{{\varepsilon}}^{\mathrm{p}} \right) = \sigma_{\mathrm{y}} + E^{\mathrm{h}} \bar{\varepsilon}^{\mathrm{p}} , $$

(53)

where, σ _y and E ^h represent the initial yield stress and the work-hardening modulus, respectively. Although a specific hardening law to be used for calculation is presented here, the sensitivity analysis in 4.3 describes the general hardening law in which the hardening law is represented by ${k} \left (\bar {{\varepsilon }}^{\mathrm {p}} \right )$. However, kinematic hardening is not considered. From (52), the equation below is derived,

$$ \frac{\partial {\Phi}}{\partial \boldsymbol{\sigma}} = \boldsymbol{\sigma}^{\prime} . $$

(54)

This demonstrates that the plastic flow direction coincides with the direction of deviatoric stress σ ^′. Therefore, the plastic strain rate $\dot {\boldsymbol {\varepsilon }}^{\mathrm {p}}$ is obtained with $\dot {\gamma }$ as the coefficient,

$$ \dot{\boldsymbol{\varepsilon}}^{\mathrm{p}} = \dot{\gamma} \boldsymbol{\sigma}^{\prime} . $$

(55)

This shows an associated flow rule in the flow theory, and γ shall hereafter be called the plastic multiplier. Regarding the plastic-strain work rate $\dot {W}^{\mathrm {p}}$, the relation below is assumed,

$$ \dot{W}^{\mathrm{p}} = \boldsymbol{\sigma} : \dot{\boldsymbol{\varepsilon}}^{\mathrm{p}} \equiv \bar{\sigma} \ \dot{\bar{\varepsilon}}^{\mathrm{p}} , $$

(56)

where, $\bar {\sigma }$ and $\dot {\bar {\varepsilon }}^{p}$ represent the equivalent stress and the equivalent plastic strain rate, respectively. After determining the inner product of the both sides of (55) and σ, and using the relation of (56), we can obtain the equation below,

$$ \dot{\gamma} = \frac{3}{2} \, \frac{ \dot{\bar{\varepsilon}}^{\mathrm{p}} }{ \bar{\sigma}} . $$

(57)

In the derivation of (57), the following equations are used,

$$ \bar{\sigma}^{2} = \frac{3}{2} \left( \boldsymbol{\sigma}^{\prime}: \boldsymbol{\sigma}^{\prime} \right) , $$

(58)

$$ \boldsymbol{\sigma}^{\prime} : \boldsymbol{\sigma}^{\prime} = \boldsymbol{\sigma} : \boldsymbol{\sigma}^{\prime}. $$

(59)

Appendix B: Return mapping algorithm

1.1 B1: The general three dimensional expression

Incremental analysis employing an elastoplastic model assumes incremental steps from time n to n+1. Subscript letters n and n+1 represent the values at respective times. (51), (55) and (57) are expressed with respect to increment as follows:

$$ \boldsymbol{\sigma}_{n+1} = \boldsymbol{\sigma}_{n} + \mathbb{C} : \left( {\Delta} \boldsymbol{\varepsilon} - {\Delta} \boldsymbol{\varepsilon}^{\mathrm{p}} \right) , $$

(60)

$$ {\Delta} \boldsymbol{\varepsilon}^{\mathrm{p}} = {\Delta} \gamma \, \boldsymbol{\sigma}^{\prime}{~}_{n+1} , $$

(61)

$$ {\Delta} \gamma = \frac{3}{2} \, \frac{ {\Delta} \bar{\varepsilon}^{\mathrm{p}} }{ \bar{\sigma}_{n+1} } . $$

(62)

Substituting (61) and (62) into (60) results in the equation below,

$$ \boldsymbol{\sigma}_{n+1} = \boldsymbol{\sigma}_{n} + \mathbb{C} : {\Delta} \boldsymbol{\varepsilon} - \frac{3}{2} \frac{ {\Delta} \bar{\varepsilon}^{\mathrm{p}}}{\bar{\sigma}_{n+1}} \, \mathbb{C} : \boldsymbol{\sigma}^{\prime}{~}_{n+1} . $$

(63)

Here, the known terms at time n are replaced with trial stress as follows:

$$ \boldsymbol{\sigma}^{(\mathrm{T})}_{n+1} = \boldsymbol{\sigma}_{n} + \mathbb{C} : {\Delta} \boldsymbol{\varepsilon} . $$

(64)

From this, the relation of trial stress and the final stress in return mapping can be obtained,

$$ \boldsymbol{\sigma}^{(\mathrm{F})}_{n+1} = \boldsymbol{\sigma}^{(\mathrm{T})}_{n+1} - \frac{3}{2} \frac{ {\Delta} \bar{\varepsilon}^{\mathrm{p}}}{ \bar{\sigma}^{(\mathrm{F})}_{n+1}} \, \mathbb{C} : \boldsymbol{\sigma}^{\prime}{~}^{(\mathrm{F})}_{n+1} , $$

(65)

where, superscript letters (T) and (F) represent trial stress and the final stress, respectively. (64) obtains the trial stress at time n+1 using the elastic stiffness tensor $\mathbb {C}$. Since the equation below is derived from (65),

$$ \text{tr} \left( \boldsymbol{\sigma}^{(\mathrm{F})}_{n+1}\right) = \text{tr} \left( \boldsymbol{\sigma}^{(\mathrm{T})}_{n+1} \right) $$

(66)

Equation (65) can be replaced with a equation of deviatoric stress below, using the shear elastic modulus G,

$$ \boldsymbol{\sigma}{~}^{\prime}{~}^{(\mathrm{F})}_{n+1} = \boldsymbol{\sigma}{~}^{\prime}{~}^{(\mathrm{T})}_{n+1} - \frac{3}{2} \frac{ {\Delta} \bar{\varepsilon}^{\mathrm{p}}}{ \bar{\sigma}{~}^{(\mathrm{F})}_{n+1}} \, 2G \, \boldsymbol{\sigma}^{\prime}{~}^{(\mathrm{F})}_{n+1} . $$

(67)

This can be rearranged into

$$ \boldsymbol{\sigma}^{\prime}{~}^{(\mathrm{F})}_{n+1} = \frac{ \bar{\sigma}^{(\mathrm{F})}_{n+1} }{ \bar{\sigma}^{(\mathrm{F})}_{n+1} + 3G {\Delta} \bar{\varepsilon}^{\mathrm{p}}} \boldsymbol{\sigma}^{\prime}{~}^{(\mathrm{T})}_{n+1} , $$

(68)

demonstrating that the final deviatoric stress $\boldsymbol {\sigma }^{\prime }{~}^{(\mathrm {F})}_{n+1}$ can be expressed with a scalar multiple of the trial deviatoric stress $\boldsymbol {\sigma }^{\prime }{~}^{(\mathrm {T})}_{n+1}$. Moreover, because the ratio of the norm of deviatoric stress is equal to the ratio of its equivalent stress,

$$ \boldsymbol{\sigma}^{\prime}{~}^{(\mathrm{F})}_{n+1} = \frac{ \bar{\sigma}^{(\mathrm{F})}_{n+1}}{ \bar{\sigma}^{(\mathrm{T})}_{n+1} } \boldsymbol{\sigma}^{\prime}{~}^{(\mathrm{T})}_{n+1} $$

(69)

can be obtained. In short, (69) obtains the final stress by correcting the trial stress in a radial direction in the deviatoric stress space. From (68) and (69), a conditional equation for the equivalent stress that makes $\boldsymbol {\sigma }^{\prime }{~}^{(\mathrm {T})}_{n+1}$ coincide with $\boldsymbol {\sigma }^{\prime }{~}^{(\mathrm {F})}_{n+1}$ is obtained,

$$ \bar{\sigma}^{(\mathrm{T})}_{n+1} = \bar{\sigma}^{(\mathrm{F})}_{n+1} + 3G {\Delta} \bar{\varepsilon}^{\mathrm{p}} . $$

(70)

Here, because the equivalent stress during plastic deformation coincides with the yield stress, or hardening law ${k} \left (\bar {{\varepsilon }}^{\mathrm {p}}_{n+1} \right )$,

$$ \bar{\sigma}^{(\mathrm{F})}_{n+1} = {k} \left( \bar{{\varepsilon}}^{\mathrm{p}}_{n+1} \right) $$

(71)

can be obtained. Moreover, the equivalent plastic strain at time $n+1\bar {{\varepsilon }}^{\mathrm {p}}_{n+1}$ can be explained as follows, using its increment ${\Delta } \bar {\varepsilon }^{p}$,

$$ \bar{{\varepsilon}}^{\mathrm{p}}_{n+1} = \bar{\varepsilon}^{\mathrm{p}}_{n} + {\Delta} \bar{\varepsilon}^{\mathrm{p}} . $$

(72)

Thus, substituting (71) and (72) into (70) and rearranging them results in

$$ {\Delta} \bar{\varepsilon}^{\mathrm{p}} = \frac{1}{3G} \left\{ \bar{\sigma}^{(\mathrm{T})}_{n+1} - {k} \left( \bar{\varepsilon}^{\mathrm{p}}_{n} + {\Delta} \bar{\varepsilon}^{\mathrm{p}} \right) \right\} , $$

(73)

where ${\Delta } \bar {\varepsilon }^{p}$ is the only unknown variable. ${\Delta } \bar {\varepsilon }^{\mathrm {p}}$ can be obtained by solving this equation, though when a nonlinear hardening law is employed for the material model, it should be obtained by conducting repetitive calculation according to the Newton-Raphson method, etc. Then, by substituting the obtained ${\Delta } \bar {\varepsilon }^{\mathrm {p}}$ into (70), $\bar {\sigma }^{(\mathrm {F})}_{n+1}$ can be obtained. Moreover, by substituting ${\Delta } \bar {\varepsilon }^{\mathrm {p}}$ and $\bar {\sigma }^{(\mathrm {F})}_{n+1}$ into (62) and (68) respectively, Δγ and $\boldsymbol {\sigma }^{\prime }{~}^{(\mathrm {F})}_{n+1}$ can be obtained.

B2: Plane stress expression

For a return mapping algorithm assuming a plane stress condition, specified constraints on stress components are considered unlike a general three dimensional problem. For this, we describe the return mapping formulation for a plane stress condition, assuming a plasticity model which has only in-plane components of stress and strain as state variables. Incidentally, the present paper refers to the expression for the plasticity model described in section 3.4 of Simo and Hueghes (1998). We apply the general isotropic linear hardening law without kinematic hardening for this study and describe it in the matrix formulation.

First of all, the relation between the final stress and the trial stress can be written as follows:

$$ \hat{{\sigma}}_{n+1}^{(\mathrm{F})} = \left[ {C} + {\Delta} \gamma {P} \right]^{-1} {C} \hat{{\sigma}}_{n+1}^{(\mathrm{T})} $$

(74)

where $\hat {(\bullet )}$ means a vector of which the components are occupied by in-plane components only, such as $\hat { {\sigma }} = \left \{ \sigma _{11} \ \sigma _{22} \ \sigma _{12} \right \}^{\mathrm {T}}$. C and P are the linear elastic constitutive matrix and the projection matrix, respectively, given by

$$ {C} = \frac{E}{1 - \nu^{2}} \left[ \begin{array}{ccc} 1 & \nu & 0 \\ \nu & 1 & 0 \\ 0 & 0 & \frac{1 - \nu}{2} \end{array} \right] , $$

(75)

$$ {P} = \frac{1}{3} \left[ \begin{array}{ccc} 2 & -1 & 0 \\ -1 & 2 & 0 \\ 0 & 0 & 6 \end{array} \right] . $$

(76)

Next, the yielding condition is expressed as

$$ \hat{\Phi} = \frac{1}{2} \left( \hat{{\sigma}}_{n+1}^{(\mathrm{F})} \right)^{\mathrm{T}} {P} \hat{{\sigma}}_{n+1}^{(\mathrm{F})} - \frac{1}{3} k^{2} \left( \bar{\varepsilon}_{n+1}^{\mathrm{p}} \right) = 0 , $$

(77)

and the evolution law of $\bar {\varepsilon }_{n+1}^{\mathrm {p}}$ can be written as follows:

$$ \bar{\varepsilon}_{n+1}^{\mathrm{p}} = \bar{\varepsilon}_{n}^{\mathrm{p}} + {\Delta} \gamma \sqrt{ \frac{2}{3} \left( \hat{{\sigma}}_{n+1}^{(\mathrm{F})} \right)^{\mathrm{T}} {P} \hat{{\sigma}}_{n+1}^{(\mathrm{F})} } . $$

(78)

Therefore, (74), (77), (78) can be gathered into one scaler nonlinear equation for an unknown Δγ as follows:

$$ \hat{\Phi} = \frac{1}{2} \xi \left( {\Delta} \gamma \right) - \frac{1}{3} k^{2} \left( \bar{\varepsilon}_{n}^{\mathrm{p}} + {\Delta} \gamma \sqrt{ \frac{2}{3} \xi \left( {\Delta} \gamma \right) } \right) = 0 , $$

(79)

where

$$ \xi \left( {\Delta} \gamma \right) = \left( \hat{{\sigma}}_{n+1}^{(\mathrm{\mathrm{T}})} \right)^{\mathrm{T}} {A}^{\mathrm{T}} \left( {\Delta} \gamma \right) {P} {A} \left( {\Delta} \gamma \right) \hat{{\sigma}}_{n+1}^{(\mathrm{T})} , $$

(80)

and

$$ {A} \left( {\Delta} \gamma \right) = \left[ {C} + {\Delta} \gamma {P} \right]^{-1} {C} . $$

(81)

Finally, determining Δγ by solving the nonlinear (79) and inserting it into (74) and (78) give the final stress sensitivity $\hat { {\sigma }}_{n+1}^{(\mathrm {F})}$ and the plastic equivalent strain $\bar {\varepsilon }_{n+1}^{\mathrm {p}}$.

Furthermore, considering the mathematical characteristics of an isotropic condition, matrices P, C and A can be diagonalized by the same orthogonal matrix Q as,

$$ {Q} = \left[ \begin{array}{ccc} \frac{1}{\sqrt{2}} & \frac{1}{\sqrt{2}} & 0 \\ -\frac{1}{\sqrt{2}} & \frac{1}{\sqrt{2}} & 0 \\ 0 & 0 & 1 \end{array} \right] . $$

(82)

Utilizing this diagonalization simplifies (80) and (81) as follows:

$$ \xi \left( {\Delta} \gamma \right) = \dfrac { \left( \sigma_{11}^{(\mathrm{T})} + \sigma_{22}^{(\mathrm{T})} \right)^{2} } { 6 \left\{ 1 + \frac{E {\Delta} \gamma}{3 (1 - \nu )} \right\}^{2} } + \dfrac { \frac{1}{2} \left( \sigma_{22}^{(\mathrm{T})} - \sigma_{11}^{(\mathrm{T})} \right)^{2} + 2 \left( \sigma_{12}^{(\mathrm{T})} \right)^{2} } { \left( 1 + 2 G {\Delta} \gamma \right)^{2} } \\ $$

(83)

$$ {A}\left( {\Delta} \gamma \right) = \left[ \begin{array}{ccc} \frac{1}{2}\left( A_{11}^{\ast} + A_{22}^{\ast} \right) & \frac{1}{2}\left( A_{11}^{\ast} - A_{22}^{\ast} \right) & 0 \\ \frac{1}{2}\left( A_{11}^{\ast} - A_{22}^{\ast} \right) & \frac{1}{2}\left( A_{11}^{\ast} + A_{22}^{\ast} \right) & 0 \\ 0 & 0 & A_{33}^{\ast} \end{array} \right] $$

(84)

$$ A_{11}^{\ast} = \frac{3(1 - \nu)}{3(1 - \nu) + E {\Delta} \gamma}, \ \ A_{22}^{\ast} = \frac{1}{1 + 2G {\Delta} \gamma}, \ \ A_{33}^{\ast} = A_{22}^{\ast} $$

(85)

Incidentally, the expression of A is referred to de Souza Neto et al. (2000).

Appendix C: Consistent elastoplastic tangent modulus

Here, the procedure to obtain a consistent tangent modulus $\mathbb {C}^{\mathrm {ep*}}$ for backward-Euler integration using the variables obtained by return mapping is described.

First, substitute a 4th-order tensor $\mathbb {P}$ that ensures $\boldsymbol {\sigma }^{\prime }_{n+1} = \mathbb {P} : \boldsymbol {\sigma }_{n+1}$ into (60) and (61), and rearrange them to obtain

$$\begin{array}{@{}rcl@{}} \boldsymbol{\sigma}_{n+1} &=& \boldsymbol{\sigma}_{n} + \mathbb{C} : \left( {\Delta} \boldsymbol{\varepsilon} - {\Delta} \gamma \, \mathbb{P} : \boldsymbol{\sigma}_{n+1} \right) \\ &=& \boldsymbol{\sigma}_{n} + \mathbb{C} : \left( \boldsymbol{\varepsilon}_{n+1} - \boldsymbol{\varepsilon}_{n} - {\Delta} \gamma \, \mathbb{P} : \boldsymbol{\sigma}_{n+1} \right) . \end{array} $$

(86)

Differentiate this equation with respect to time n+1 to obtain

$$\begin{array}{@{}rcl@{}} \mathrm{d} \, \boldsymbol{\sigma}_{n+1} = \mathbb{C} : \left\{ \mathrm{d} \, \boldsymbol{\varepsilon}_{n+1} - \mathrm{d} \, \left( {\Delta} \gamma \right) \mathbb{P} : \boldsymbol{\sigma}_{n+1} - {\Delta} \gamma \, \mathbb{P} : \mathrm{d} \, \boldsymbol{\sigma}_{n+1} \right\} \end{array} $$

(87)

$$\begin{array}{@{}rcl@{}} \iff \left( \mathbb{C}^{-1} + {\Delta} \gamma \, \mathbb{P} \right) : \mathrm{d} \, \boldsymbol{\sigma}_{n+1} = \mathrm{d} \, \boldsymbol{\varepsilon}_{n+1} - \mathrm{d} \, \left( {\Delta} \gamma \right) \mathbb{P} : \boldsymbol{\sigma}_{n+1} \end{array} $$

(88)

$$\begin{array}{@{}rcl@{}} \iff \mathrm{d} \, \boldsymbol{\sigma}_{n+1} = \mathbb{C}^{\ast} : \left\{ \mathrm{d} \, \boldsymbol{\varepsilon}_{n+1} - \mathrm{d} \, \left( {\Delta} \gamma \right) \boldsymbol{\sigma}^{\prime}_{n+1} \right\} . \end{array} $$

(89)

Here, $\mathbb {C}^{\ast } = \left (\mathbb {C}^{-1} + {\Delta } \gamma \, \mathbb {P} \right ) {~}^{-1}$ is assumed. Similarly, the equation below is obtained from (71),

$$\begin{array}{@{}rcl@{}} \mathrm{d} \, \bar{\sigma}_{n+1} &=& \left. \frac{ \partial {k} }{ \partial \, \bar{\varepsilon}^{\mathrm{p}} } \right|_{n+1} \, \mathrm{d} \, \bar{\varepsilon}^{\mathrm{p}}_{n+1} \\ &=& H^{\prime}_{n+1} \, \mathrm{d} \, \bar{\varepsilon}^{\mathrm{p}}_{n+1} , \end{array} $$

(90)

where, $\left . \frac { \partial {k} }{ \partial \, \bar {\varepsilon }^{\mathrm {p}} } \right |_{n+1} = H^{\prime }_{n+1}$ is assumed. When the linear hardening law is employed as in the present study, $H^{\prime }_{n+1} = E^{\mathrm {h}}$. Moreover, because $\bar {\varepsilon }^{\mathrm {p}}_{n+1}$ can be expressed as below using (62) and (72),

$$ \bar{\varepsilon}^{\mathrm{p}}_{n+1} = \bar{\varepsilon}^{\mathrm{p}}_{n} + \frac{2}{3} \, {\Delta} \gamma \, \bar{\sigma}_{n+1} , $$

(91)

the derivative at time n+1 is as follows:

$$ \mathrm{d} \, \bar{\varepsilon}^{\mathrm{p}}_{n+1} = \frac{2}{3} \, \mathrm{d} \left( {\Delta} \gamma \, \bar{\sigma}_{n+1} \right) + \frac{2}{3} \, {\Delta} \gamma \, \mathrm{d} \, \bar{\sigma}_{n+1} . $$

(92)

Substitute this into (90) to obtain

$$ \left(1 - \frac{2}{3} \, H^{\prime}_{n+1} {\Delta} \gamma \right) \mathrm{d} \, \bar{\sigma}_{n+1} = \frac{2}{3} \, H^{\prime}_{n+1} \, \mathrm{d} \left( {\Delta} \gamma \right) \bar{\sigma}_{n+1} , $$

(93)

$$ \mathrm{d} \, \bar{\sigma}_{n+1} = \frac{2}{3} \, \omega \, H^{\prime}_{n+1} \, \mathrm{d} \left( {\Delta} \gamma \right) \bar{\sigma}_{n+1} , $$

(94)

where, $\omega = \left (1 - \frac {2}{3} \, H^{\prime }_{n+1} {\Delta } \gamma \right )^{-1}$ is assumed.

From (58), the relational equation of deviatoric stress and equivalent stress at time n+1 can be obtained as follows:

$$ \bar{\sigma}^{2}_{n+1} = \frac{3}{2} \left( \boldsymbol{\sigma}^{\prime}_{n+1} : \boldsymbol{\sigma}^{\prime}_{n+1} \right) . $$

(95)

Differentiate both sides with respect to time n+1 and rearrange them to obtain

$$\bar{\sigma}_{n+1} \, \mathrm{d} \, \bar{\sigma}_{n+1} = \frac{3}{4} \, \mathrm{d} \left( \boldsymbol{\sigma}_{n+1} : \boldsymbol{\sigma}^{\prime}_{n+1} \right) $$

(96)

$$= \frac{3}{2} \, \mathrm{d} \, \boldsymbol{\sigma}_{n+1} : \boldsymbol{\sigma}^{\prime}_{n+1} .$$

(97)

Note here that one of the $\boldsymbol {\sigma }^{\prime }_{n+1}$ on the right-hand side is replaced with σ _n+1, using the relation of (59). Then, substitute (97) into (94) to obtain

$$ \mathrm{d} \, \boldsymbol{\sigma}_{n+1} : \boldsymbol{\sigma}^{\prime}_{n+1} = \frac{4}{9} \, \omega \, H^{\prime}_{n+1} \, \mathrm{d} \left( {\Delta} \gamma \right) \bar{\sigma}^{2}_{n+1} . $$

(98)

And substitute (89) here to obtain

$$\begin{array}{@{}rcl@{}} &&\frac{4}{9} \, \omega \, H^{\prime}_{n+1} \, \mathrm{d} \left( {\Delta} \gamma \right) \bar{\sigma}^{2}_{n+1} = \boldsymbol{\sigma}^{\prime}_{n+1} \\ &&\quad: \left[ \mathbb{C}^{\ast} : \left\{ \mathrm{d} \, \boldsymbol{\varepsilon}_{n+1} - \mathrm{d} \, \left( {\Delta} \gamma \right) \boldsymbol{\sigma}^{\prime}_{n+1} \right\} \right] , \end{array} $$

(99)

and rearrange this with respect to d(Δγ), to obtain

$$ \mathrm{d} \left( {\Delta} \gamma \right) = \frac{ \boldsymbol{\sigma}^{\prime}_{n+1} : \left( \mathbb{C}^{\ast} : \mathrm{d} \, \boldsymbol{\varepsilon}_{n+1} \right) }{ \boldsymbol{\sigma}^{\prime}_{n+1} : \left( \mathbb{C}^{\ast} : \boldsymbol{\sigma}^{\prime}_{n+1} \right) + \frac{4}{9} \, \omega \, H^{\prime}_{n+1} \, \bar{\sigma}^{2}_{n+1} } . $$

(100)

Then substituting this into (89) results in

$$\begin{array}{@{}rcl@{}} &{~}& \mathrm{d} \, \boldsymbol{\sigma}_{n+1} \\ &=& \mathbb{C}^{\ast} : \left\{ \mathrm{d} \, \boldsymbol{\varepsilon}_{n+1} - \frac{ \boldsymbol{\sigma}^{\prime}_{n+1} : \left( \mathbb{C}^{\ast} : \mathrm{d} \, \boldsymbol{\varepsilon}_{n+1} \right) }{ \boldsymbol{\sigma}^{\prime}_{n+1} : \left( \mathbb{C}^{\ast} : \boldsymbol{\sigma}^{\prime}_{n+1} \right) + \frac{4}{9} \, \omega \, H^{\prime}_{n+1} \, \bar{\sigma}^{2}_{n+1} } \boldsymbol{\sigma}^{\prime}_{n+1} \right\} \\ &=& \left\{ \mathbb{C}^{\ast} - \frac{ \left( \mathbb{C}^{\ast} : \boldsymbol{\sigma}^{\prime}_{n+1} \right) \otimes \left( \mathbb{C}^{\ast} : \boldsymbol{\sigma}^{\prime}_{n+1} \right) }{ \boldsymbol{\sigma}^{\prime}_{n+1} : \left( \mathbb{C}^{\ast} : \boldsymbol{\sigma}^{\prime}_{n+1} \right) + \frac{4}{9} \, \omega \, H^{\prime}_{n+1} \, \bar{\sigma}^{2}_{n+1} } \right\} : \mathrm{d} \, \boldsymbol{\varepsilon}_{n+1} \\ &\equiv& \mathbb{C}^{\mathrm{ep*}} : \mathrm{d} \, \boldsymbol{\varepsilon}_{n+1} , \end{array} $$

(101)

and the $\mathbb {C}^{\mathrm {ep*}}$ in this equation turns out to be the consistent elastoplastic tangent modulus.