Abstract
This study provides a growth-theoretic analysis of the effects of intellectual property rights on the take-off of an economy from an era of stagnation to a state of sustained economic growth. We incorporate patent protection into a Schumpeterian growth model in which take-off occurs when the population size crosses an endogenous threshold. We find that strengthening patent protection has contrasting effects on economic growth at different stages of development. Specifically, it leads to an earlier take-off but also reduces economic growth in the long run.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
“England [...] by 1700 [...] had developed an efficient set of property rights embedded in the common law [and...] begun to protect private property in knowledge with its patent law. The stage was now set for the industrial revolution.” North and Thomas (1973, p. 156)
1 Introduction
The differential timing of countries experiencing a transition from stagnation to growth has governed patterns of comparative economic development across the world and contributed significantly to the divergence in income across the world over the past two centuries.Footnote 1 Given the importance of intellectual property rights (IPR) to the pace of technological progress and therefore to the transition from stagnation to growth, this study explores the role that the patent system may have played in the pace of this transition and on economic growth in the long run.
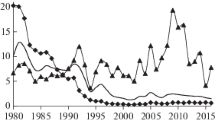
The UK experienced this transition during the late eighteenth/early nineteenth century. Figure 1 plots real GDP per capita in the UK.Footnote 2 Figure 2 plots the log level of real GDP per capita, in which the slope shows the growth rate of income. In the eighteenth century, income in the UK grew very slowly. Specifically, the average annual growth rate of income in the UK from 1701 to 1800 was 0.4%. Then, the average growth rate from 1801 to 1900 increased to 1.0%. From the twentieth century onwards, the average growth rate stabilized at about 1.7%.
We incorporate patent protection into the Schumpeterian growth model of endogenous take-off in Peretto (2015). In this model, the economy first experiences stagnation with zero growth in output per capita when the market size is small. Here, population size plays the crucial role of determining the market size, which in turn implies that population growth gives rise to an expansion of the market. As the market size becomes sufficiently large, innovation takes place and the economy gradually experiences growth. In the long run, the economy converges to a balanced growth path (BGP) with steady-state growth. Within this growth-theoretic framework that is consistent with the growth pattern in Figs. 1 and 2, we obtain the following results.
Strengthening patent protection leads to an earlier take-off. Incentives for innovation to take place depend on the market value of inventions, which in turn depends on the level of patent protection and the market size. Therefore, when stronger patent protection increases the market value of patents by reducing price competition and making firms more profitable, it also reduces the market size required for innovation to take place. As a result, the economy starts to experience innovation and growth at an earlier time (i.e., an earlier industrial revolution). Our finding that stronger IPR protection leads to an earlier (but not necessarily immediate) take-off is consistent with historical evidence on the effects of IPR on industrial revolution.Footnote 3 However, stronger patent protection eventually reduces innovation and growth as recent studies tend to find.Footnote 4 Intuitively, although stronger patent protection encourages entry and increases the number of products in the economy, this larger number of products reduces the market size of each product and redirects resources away from the quality-improving innovation of each product, which determines long-run growth.Footnote 5
This study relates to the literature on innovation and economic growth. Romer (1990) develops the seminal variety-expanding growth model in which innovation is driven by new products, whereas Aghion and Howitt (1992) develop the Schumpeterian quality-ladder growth model in which innovation is driven by higher-quality products. Peretto (1998, 1999) and Smulders and van de Klundert (1995) combine the two dimensions of innovation and develop a Schumpeterian growth model with an endogenous market structure. This study explores the effects of IPR in this vintage of the Schumpeterian growth model.
In the literature on IPR and innovation, other studies also explore the effects of IPR in the innovation-driven growth model.Footnote 6 These studies mostly focus on either variety expansion or quality improvement. Only a few studies, such as Chu et al. (2012) and Chu et al. (2016), explore the effects of IPR in the Schumpeterian growth model with both dimensions of innovation. However, these studies do not consider the case in which the effects of IPR can change at different stages of the economy. Iwaisako (2013), Chu et al. (2014) and Chu et al. (2019) show that the growth or welfare effects of IPR can depend on, respectively, the level of public services, the distance to the technology frontier, and the level of financial development in the economy. However, none of these studies consider how IPR affects the endogenous take-off of an economy. The novel contributions of this study are to explore the effects of IPR in a Schumpeterian growth model of endogenous take-off and to highlight the contrasting effects of IPR on economic growth at different stages of the economy with different dimensions of innovation.
This study also relates to the literature on endogenous take-off and economic growth. Galor and Weil (2000) provide the seminal study and develop unified growth theory,Footnote 7 which explores how the quality-quantity tradeoff in childrearing and human capital accumulation allow a country to escape from the Malthusian trap and lead to the endogenous take-off of the economy.Footnote 8Peretto (2015) develops a Schumpeterian growth model of endogenous take-off, which features exogenous population growth and does not capture the Malthusian trap; instead, it describes an economy in which take-off is driven by innovation, which also relates to the industrial revolution and is suitable for our analysis of patent policy. The Peretto model features both quality improvement and variety expansion, under which endogenous growth in the number of products provides a dilution effect that removes the scale effect of population size on long-run growth. Therefore, although the population size affects the timing of the take-off, it does not affect the steady-state growth rate. We incorporate patent protection into the Peretto model to explore its effects on endogenous take-off.
The rest of the paper is organized as follows. Section 2 presents the model. Section 3 explores the effects of patent policy at different stages of the economy. Section 4 concludes.
2 A Schumpeterian model of endogenous take-off
The theoretical framework is based on the Schumpeterian growth model with both variety-expanding innovation and quality-improving innovation in Peretto (2015). In this model, labor is used as a factor input for the production of final good. Final good is used for consumption and as a factor input for entry, in-house R&D, and the production and operation of intermediate goods. We incorporate a patent policy parameter into the model and analyze its effects on the take-off, transitional dynamics, and the BGP of the economy.
2.1 Household
The representative household has a utility function given by
where ct ≡ Ct/Lt denotes per capita consumption of final good (numeraire) at time t, and ρ > 0 is the subjective discount rate. Population grows at an exogenous rate λ ∈ (0,ρ) with initial population normalized to unity (i.e., Lt = eλt). The household maximizes (1) subject to
where at ≡ At/Lt is the real value of assets owned by each member of the household, and rt is the real interest rate. Each member supplies one unit of labor to earn wt. Standard dynamic optimization yields
2.2 Final good
Final output Yt is produced by competitive firms using the following production function:
where \(\left \{ \theta ,\alpha ,\sigma \right \} \in \left (0,1\right ) \). \( X_{t}\left (i\right ) \) is the quantity of non-durable intermediate goods \( i\in \left [ 0,N_{t}\right ] \). The productivity of \(X_{t}\left (i\right ) \) depends on its quality \(Z_{t}\left (i\right ) \) and the average quality of all intermediate goods Zt ≡ HCode \({\int \limits }_{0}^{N_{t}}Z_{t}\left (j\right ) dj/N_{t}\) capturing technology spillovers. The private return to quality is determined by α, and the degree of technology spillovers is determined by 1 − α. The parameter 1 − σ captures a congestion effect of variety, and hence, the social return to variety is measured by σ.
Profit maximization yields the following conditional demand functions for Lt and \(X_{t}\left (i\right ) \):
where \(p_{t}\left (i\right ) \) is the price of \(X_{t}\left (i\right ) \). Perfect competition implies that firms pay \(\theta Y_{t}={\int \limits }_{0}^{N_{t}}p_{t}\left (i\right ) X_{t}\left (i\right ) di\) for intermediate goods.
2.3 Intermediate goods and in-house R&D
Monopolistic firms produce differentiated intermediate goods with a linear technology that requires \(X_{t}\left (i\right ) \) units of final good to produce \(X_{t}\left (i\right ) \) units of intermediate good \(i\in \left [ 0,N_{t}\right ] \). Therefore, the marginal cost for the firm in industry i to produce \(X_{t}\left (i\right ) \) with quality \(Z_{t}\left (i\right ) \) is one. The firm also incurs \(\phi Z_{t}^{\alpha }\left (i\right ) Z_{t}^{1-\alpha }\) units of final good as a fixed operating cost. To improve the quality of its products, the firm devotes \(I_{t}\left (i\right ) \) units of final good to in-house R&D. The innovation process is
and the firm’s (before-R&D) profit flow at time t is
The value of the monopolistic firm in industry i is
The monopolistic firm maximizes (9) subject to Eqs. 7 and 8. We solve this dynamic optimization problem in the proof of Lemma 1 and find that the unconstrained profit-maximizing markup ratio is 1/𝜃. To analyze the effects of patent breadth, we introduce a policy parameter μ > 1, which determines the unit cost for imitative firms to produce \(X_{t}\left (i\right ) \) with the same quality \(Z_{t}\left (i\right ) \)Footnote 9 as the monopolistic firm in industry i.Footnote 10 Intuitively, a larger patent breadth μ increases the cost of imitation and allows the monopolistic producer of \(X_{t}\left (i\right ) \), who owns the patents, to charge a higher markup without losing her market share to potential imitators;Footnote 11 see also Li (2001), Goh and Olivier (2002) and Iwaisako and Futagami (2013). The equilibrium price becomes
We assume that μ < 1/𝜃. In this case, increasing patent breadth raises the markup.
We follow previous studies to consider a symmetric equilibrium in which \( Z_{t}\left (i\right ) =Z_{t}\) for \(i\in \left [ 0,N_{t}\right ] \) and the size of each intermediate-good firm is identical across all industries \( X_{t}\left (i\right ) =X_{t}\).Footnote 12 From Eq. 6 and \( p_{t}\left (i\right ) =\mu \), the quality-adjusted firm size is
We define the following transformed variable:
which is a state variable determined by the quality-adjusted firm size and not directly affected by μ (but indirectly via Nt). In Lemma 1, we derive the rate of return on quality-improving R&D, which is increasing in xt and μ.
Lemma 1
The rate of return on quality-improving in-house R&D is Footnote 13
Proof
See the Appendix. □
2.4 Entrants
Following previous studies, we assume that entrants have access to aggregate technology Zt to ensure symmetric equilibrium at any time t. A new firm pays βXt units of final good to enter the market with a new variety of intermediate goods and set up its operation. β > 0 is an entry-cost parameter. The asset-pricing equation implies that the return on assets is
When entry is positive, free entry implies
Substituting Eqs. 7, 8, 12, 15, and pt = μ into Eq. 14 yields the return on entry as
where \(z_{t}\equiv \dot {Z}_{t}/Z_{t}\) is the growth rate of aggregate quality.
2.5 Equilibrium
The equilibrium is a time path of allocations \(\left \{ A_{t},Y_{t},C_{t},X_{t},I_{t}\right \} \) and prices \(\left \{ r_{t},w_{t},p_{t},V_{t}\right \} \) such that
the household maximizes utility taking \(\left \{r_{t} ,w_{t}\right \}\) as given
competitive firms produce Yt and maximize profits taking \(\left \{ w_{t},p_{t}\right \} \) as given
incumbents for intermediate goods choose \(\left \{ p_{t},I_{t}\right \} \) to maximize Vt taking rt as given
entrants make entry decisions taking Vt as given
the value of all existing monopolistic firms adds up to the value of the household’s assets such that At = NtVt and
the following market-clearing condition of final good holds
$$ Y_{t}=C_{t}+N_{t}\left( X_{t}+\phi Z_{t}+I_{t}\right) +\dot{N}_{t}\beta X_{t} \text{.} $$(17)
2.6 Aggregation
Substituting Eq. 6 and pt = μ into Eq. 4 and imposing symmetry yield aggregate output as
The growth rate of output per capita is
where yt ≡ Yt/Lt denotes output per capita. Its growth rate gt is determined by both the variety growth rate \(n_{t}\equiv \dot {N}_{t}/N_{t}\) and the quality growth rate zt.
3 Dynamics of the economy
The dynamics of the economy is determined by the dynamics of \(x_{t}~=~\theta ^{1/\left (1-\theta \right ) }L_{t}/N_{t}^{1-\sigma }\). Its initial value is \( x_{0}=\theta ^{1/\left (1-\theta \right ) }/N_{0}^{1-\sigma }\). In the first stage of the economy, there is neither variety expansion nor quality improvement. At this stage, xt increases solely due to population growth. When xt becomes sufficiently large, innovation begins to happen. The following inequality ensures the realistic case in which the creation of products (i.e., variety-expanding innovation) happens before the improvement of products (i.e., quality-improving innovation).
Variety-expanding innovation happens when xt crosses the first threshold xN defined as
which is the value of xt that yields nt = 0 when zt = 0. Then, quality-improving innovation also happens when xt crosses the second threshold xZ defined as
which is the value of xt that yields zt = 0 when nt > 0. The inequality in Eq. 20 implies xN < xZ. In the long run, xt converges to its steady-state value x∗. The following inequalities ensure that when the economy is on the BGP, the variables {x∗,z∗,g∗} are positive:
The following proposition adapted from Peretto (2015) summarizes the dynamics of xt.
Proposition 1
When the initial condition of the economy satisfies Footnote 14
the dynamics of x t is given by Footnote 15
where
Proof
See the Appendix. □
3.1 Stage 1: Stagnation
When the market size is not large enough (i.e., xt ≤ xN), there are insufficient incentives for firms to develop new products or improve the quality of existing products. In this case, output per capita is
and the growth rate of yt is gt = 0. In this regime, strengthening patent protection μ decreases yt due to monopolistic distortion that reduces intermediate production Xt. However, stronger patent protection also leads to an earlier (but not necessarily immediate) take-off by decreasing xN in Eq. 21. Intuitively, stronger patent protection increases the profitability of firms and provides more incentives for firms to develop new products. As a result, the economy starts to experience innovation at an earlier time.
Proposition 2
Whenxt ≤ xN, stronger patent protection reduces the level of output per capita but leads to an earlier take-off.
Proof
Use Eqs. 21 and 26 to show that xN and yt are decreasing in μ. Given that xt increases at the exogenous rate λ when xt ≤ xN, a smaller xN implies an earlier take-off. □
3.2 Stage 2: Variety expansion
When the market size is sufficiently large (i.e., xt > xN), firms have incentives to develop new products. In this case, output per capita is
and the growth rate of yt is gt = σnt. In the Appendix, we show that whenever nt > 0, ct/yt always jumps to a steady state. Therefore, we can substitute \({r_{t}^{e}}\) in Eq. 16 into the Euler equation rt = ρ + gt = ρ + σnt in Eq. 3 and also use Eq. 12 to derive the variety growth rate asFootnote 16
For a given level of xt, a larger patent breadth μ raises the rate of return on variety-expanding innovation and increases the equilibrium growth rate gt = σnt as in previous studies, such as Li (2001) and O’Donoghue and Zweimuller (2004).
Proposition 3
For a givenxt ∈ (xN, xZ), stronger patent protection increases the equilibrium growth rate.
Proof
Use Eq. 28 to show that gt = σnt is increasing in μ for a given xt. □
3.3 Stage 3: Quality improvement and variety expansion
When the market size becomes even larger (i.e., xt > xZ), firms have incentives to improve the quality of products in addition to inventing new products. Then, output per capita is
and the growth rate of yt is gt = σnt + zt. We can then substitute \({r_{t}^{q}}\) in Eq. 13 into the Euler equation rt = ρ + gt = ρ + σnt + zt in Eq. 3 to derive the quality growth rate asFootnote 17
For a given level of xt, a larger patent breadth μ raises the rate of return on quality-improving innovation and continues to increase the equilibrium growth rate \(g_{t}=\sigma n_{t}+z_{t}={r_{t}^{q}}-\rho \), where \( {r_{t}^{q}}=\alpha \left [ \frac {\mu -1}{\mu ^{1/\left (1-\theta \right ) }} x_{t}-\phi \right ] \).
Proposition 4
For a givenxt ∈ (xZ, x∗), stronger patent protection increases the equilibrium growth rate.
Proof
Use Eq. 30 to show that gt = σnt + zt is increasing in μ for a given xt. □
3.4 Stage 4: Balanced growth path
In the long run, xt converges to x∗. Then, the steady-state quality growth rate is
where n∗ = λ/(1 − σ) > 0 and
which is decreasing in μ. Intuitively, stronger patent protection increases the number of products, which leads to a smaller market size for each product. This smaller firm size x∗ in turn reduces the incentives for quality-improving innovation and the steady-state equilibrium growth rate g∗ = σn∗ + z∗. This result generalizes the one in Chu et al. (2016), who assume zero social return to variety (i.e., σ = 0).
Proposition 5
On the BGP (i.e., xt = x∗), stronger patent protection decreases the steady-state equilibrium growth rate.
Proof
Use Eqs. 31 and 32 to show that g∗ = σn∗ + z∗ is decreasing in μ. □
3.5 Summary
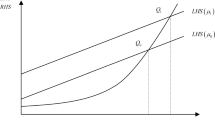
We summarize the dynamics of the economy in the following figures. Figure 3 plots the relationship between the quality-adjusted firm size xt and the equilibrium growth rate gt. It shows that when xt is below the first threshold xN, the economy does not grow due to the absence of variety-expanding innovation (and also quality-improving innovation). When xt crosses the first threshold xN, variety-expanding innovation begins to happen. When xt crosses the second threshold xZ, quality-improving innovation also happens. A larger patent breadth μ shifts the curve to the left giving rise to a higher growth rate for any given xt.
Figure 4 plots the transition path of the quality-adjusted firm size xt.Footnote 18 It shows how xt evolves from an initial state x0 to the steady state x∗, which is decreasing in the level of patent breadth μ. Finally, Fig. 5 summarizes the transition path of the equilibrium growth rate gt and shows that strengthening patent protection leads to an earlier take-off (by decreasing xN) but also lower long-run growth (by decreasing x∗).
4 Conclusion
In this study, we analyze the effects of IPR in a Schumpeterian growth model with endogenous take-off and find that strengthening patent protection causes an earlier take-off by increasing the profitability of firms and providing more incentives for firms to innovate. However, stronger patent protection eventually slows down economic growth by increasing the number of products that reduces the market size of each product and the incentives for quality-improving innovation. These contrasting effects of IPR at different stages of the economy are consistent with historical evidence on the industrial revolution and recent evidence on the effects of the patent system.
These results are also consistent with the fact that the UK implemented a patent system before the USA and experienced an earlier industrial revolution but eventually lower economic growth than the USA. Our analysis also addresses some critiques on the hypothesis that IPR contributed to the occurrence of the industrial revolution, see for example, Mokyr (2009). These critiques can be summarized as follows. First, the emergence of the patent system occurred much earlier than the industrial revolution. Second, many inventions at that time were not patented. Our analysis shows that strengthening IPR does not necessarily lead to an immediate take-off but only an earlier take-off. Furthermore, although our analysis does not feature unpatented inventions, the no-arbitrage condition in a model with both patented and unpatented inventions should imply that when the rate of return on patented inventions increases, the rate of return on unpatented inventions also increases.
Finally, this study considers a closed economy for simplicity. In an open economy, the strengthening of patent protection and the endogenous take-off of one country may have the following effects on other countries. On the one hand, it may lead to technology spillovers to other countries. On the other hand, it may cause the industrializing country to specialize in industrial production and other countries to specialize in agricultural production, resulting into a delay of their take-off.Footnote 19 We leave this interesting extension to future research.
Notes
For a discussion of the great divergence, see Pomeranz (2001).
Data source: Maddison Project Database.
See Peretto and Connolly (2007) for a theoretical explanation on quality-improving innovation being the only plausible engine of long-run growth.
Alternatively, one can assume that the imitative firms have the same unit cost of production as the incumbent monopolist but can only offer a lower-quality version of \(X_{t}\left (i\right ) \) due to the monopolist’s patents.
In other words, this setup implicitly assumes a knowledge diffusion of quality improvement, perhaps via the patents filed by the monopolistic firms.
Symmetry also implies \({\varPi }_{t}\left (i\right ) ={\varPi }_{t}\), \(I_{t}\left (i\right ) =I_{t}\) and \(V_{t}\left (i\right ) =V_{t}\).
Note that \((\mu -1)/\mu ^{1/\left (1-\theta \right ) }\) is increasing in μ for μ < 1/𝜃.
The inequality \(x_{0}>\mu ^{1/\left (1-\theta \right ) }\phi /\left (\mu -1\right ) \) implies that π0 > 0.
TN (TZ) is the time when variety-expanding (quality-improving) innovation is activated. In this example, we plot the case in which TZ increases and xZ decreases, but other cases are also possible.
See Galor and Mountford (2008).
References
Acemoglu D, Akcigit U (2012) Intellectual property rights policy, competition and innovation. J Eur Econ Assoc 10:1–42
Aghion P, Howitt P (1992) A model of growth through creative destruction. Econometrica 60:323–351
Ashraf Q, Galor O (2011) Dynamics and stagnation in the Malthusian epoch. Am Econ Rev 101:2003–41
Bessen J, Meurer M (2008) Patent failure: how judges, bureaucrats, and lawyers put innovators at risk. Princeton University Press, Princeton
Boldrin M, Levine D (2008) Against intellectual monopoly. Cambridge University Press, Cambridge
Chu A (2009) Effects of blocking patents on R&D: a quantitative DGE analysis. J Econ Growth 14:55–78
Chu A, Cozzi G, Fan H, Pan S, Zhang M (2019) Do stronger patents stimulate or stifle innovation? The crucial role of financial development. Journal of Money, Credit and Banking, forthcoming
Chu A, Cozzi G, Galli S (2012) Does intellectual monopoly stimulate or stifle innovation? Eur Econ Rev 56:727–746
Chu A, Cozzi G, Galli S (2014) Stage-dependent intellectual property rights. J Dev Econ 106:239–249
Chu A, Furukawa Y, Ji L (2016) Patents, R&D subsidies and endogenous market structure in a Schumpeterian Economy. South Econ J 82:809–825
Cozzi G (2001) Inventing or spying? Implications for growth. J Econ Growth 6:55–77
Cozzi G, Galli S (2014) Sequential R&D and blocking patents in the dynamics of growth. J Econ Growth 19:183–219
Desmet K, Parente S (2012) The evolution of markets and the revolution of industry: a unified theory of growth. J Econ Growth 17:205–234
Dutton H (1984) The patent system and inventive activity during the industrial revolution, 1750-1852. Manchester University Press, Manchester
Furukawa Y (2007) The protection of intellectual property rights and endogenous growth: is stronger always better? J Econ Dyn Control 31:3644–3670
Gallini N (1992) Patent policy and costly imitation. RAND J Econ 23:52–63
Galor O (2011) Unified growth theory. Princeton University Press, Princeton
Galor O, Moav O (2002) Natural selection and the origin of economic growth. Q J Econ 117:1133–1192
Galor O, Mountford A (2008) Trading population for productivity: theory and evidence. Rev Econ Stud 75:1143–1179
Galor O, Weil D (2000) Population, technology and growth: from the Malthusian regime to the demographic transition. Am Econ Rev 110:806–828
Gilbert R, Shapiro C (1990) Optimal patent length and breadth. RAND J Econ 21:106–112
Goh A-T, Olivier J (2002) Optimal patent protection in a two-sector economy. Int Econ Rev 43:1191–1214
Hansen G, Prescott E (2002) Malthus to Solow. Am Econ Rev 92:1205–1217
Huang C, Yang Y, Cheng C (2017) The growth and welfare analysis of patent and monetary policies in a Schumpeterian economy. Int Rev Econ Financ 52:409–426
Iwaisako T (2013) Welfare effects of patent protection and productive public services: why do developing countries prefer weaker patent protection?. Econ Lett 118:478–481
Iwaisako T, Futagami K (2013) Patent protection, capital accumulation, and economic growth. Econ Theory 52:631–668
Jaffe A, Lerner J (2004) Innovation and its discontents: how our broken system is endangering innovation and progress, and what to do about it. Princeton University Press, Princeton
Jones C (2001) Was an industrial revolution inevitable? Economic growth over the very long run. B. E J Macroeconomics (Advances) 1:1–45
Khan Z (2005) The democratization of invention: patents and copyrights in american economic development, 1790-1920. Cambridge University Press, Cambridge
Li C-W (2001) On the policy implications of endogenous technological progress. Econ J 111:C164–C179
Mokyr J (2009) Intellectual property rights, the industrial revolution, and the beginnings of modern economic growth. Am Econ Rev 99:349–355
North D (1981) Structure and change in economic history. W. W. Norton, New York and London
North D, Thomas R (1973) The rise of the western world: a new economic history. Cambridge University Press, Cambridge
O’Donoghue T, Zweimuller J (2004) Patents in a model of endogenous growth. J Econ Growth 9:81–123
Peretto P (1998) Technological change and population growth. J Econ Growth 3:283–311
Peretto P (1999) Cost reduction, entry, and the interdependence of market structure and economic growth. J Monet Econ 43:173–195
Peretto P (2015) From Smith to Schumpeter: a theory of take-off and convergence to sustained growth. Eur Econ Rev 78:1–26
Peretto P, Connolly M (2007) The Manhattan metaphor. J Econ Growth 12:329–50
Pomeranz K (2001) The great divergence: China, Europe, and the making of the modern world economy. Princeton University Press, Princeton
Romer P (1990) Endogenous technological change. J Polit Econ 98:S71–S102
Smulders S, van de Klundert T (1995) Imperfect competition, concentration and growth with firm-specific R&D. Eur Econ Rev 39:139–160
Weisdorf J (2004) From stagnation to growth: revisiting three historical regimes. J Popul Econ 17:455–472
Yang Y (2018) On the optimality of IPR protection with blocking patents. Rev Econ Dyn 27:205–230
Acknowledgments
The authors would like to thank Oded Galor, Madeline Zavodny, and three anonymous Referees for their helpful comments.
Funding
This work was supported by a financial support from the Ministry of Education of China for the Key Research Base Project (18JJD790003) in Humanities and Social Sciences and a financial support (grant no. 71773020) from the National Natural Science Foundation of China.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interests
The authors declare that they have no conflict of interest.
Additional information
Responsible editor: Oded Galor
Publisher’s note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
The previous version of this manuscript was circulated under the title “Effects of Patents on the Industrial Revolution.”
Please send all correspondence to Zonglai Kou.
Appendix
Appendix
Proof of Lemma 1
The current-value Hamiltonian for monopolistic firm i is
where \(\omega _{t}\left (i\right ) \) is the multiplier on \(p_{t}\left (i\right ) \leq \mu \). Substituting Eqs. 6–8 into Eq. A1, we can derive
If \(p_{t}\left (i\right ) <\mu \), then \(\omega _{t}\left (i\right ) =0\). In this case, \(\partial {\varPi }_{t}\left (i\right ) /\partial p_{t}\left (i\right ) =0\) yields \(p_{t}\left (i\right ) =1/\theta \). If the constraint on \( p_{t}\left (i\right ) \) is binding, then \(\omega _{t}\left (i\right ) >0\). In this case, we have \(p_{t}\left (i\right ) =\mu \). Therefore,
Given that we assume μ < 1/𝜃, the monopolistic firm sets its price at \(p_{t}\left (i\right ) =\mu \). Substituting Eqs. A3 and 12 and \(p_{t}\left (i\right ) =\mu \) into Eq. A4 and imposing symmetry yield
which is the rate of return on quality-improving in-house R&D. □
Before we prove Proposition 1, we first derive the dynamics of the consumption-output ratio Ct/Yt when nt > 0.
Lemma 2
Whennt > 0, the consumption-output ratio always jumps to
Proof
The total value of assets owned by the household is
When nt > 0, the no-arbitrage condition for entry in Eq. 15 holds. Then, substituting Eq. 15 and μXtNt = 𝜃Yt into Eq. A8 yields
which implies that the asset-output ratio At/Yt is constant. Substituting Eqs. A9, 3, and 5 into \(\overset {.}{A}_{t}=r_{t}A_{t}+w_{t}L_{t}-C_{t}\) yields
which can be rearranged as
Therefore, the dynamics of Ct/Yt is characterized by saddle-point stability, such that Ct/Yt jumps to its steady-state value in Eq. A7. □
Proof of Proposition 1
Using Eq. 12, we can derive the growth rate of xt as
When x0 ≤ xt ≤ xN, we have nt = 0 and zt = 0. In this case, the dynamics of xt is given by
When xN < xt ≤ xZ, we have nt > 0 and zt = 0. In this case, Lemma 2 implies that Ct/Yt is constant and \(\dot {c}_{t}/c_{t}=\dot {y}_{t}/y_{t}\). Therefore, we can substitute \({r_{t}^{e}}\) in Eq. 16 and A12 into rt = ρ + σnt in Eq. 3 to obtain Eq. 28. Substituting Eq. 28 into Eq. A12 yields the dynamics of xt as
Defining \(\overline {v}\equiv \frac {1-\sigma }{\beta }\left [ \mu -1-\beta \left (\rho +\frac {\sigma }{1-\sigma }\lambda \right ) \right ] \) and \( \overline {x}^{\ast }\equiv \frac {\phi \mu ^{1/\left (1-\theta \right ) }}{\mu -1-\beta \left (\rho +\frac {\sigma }{1-\sigma }\lambda \right ) }\), we can express (A14) as
When xt > xZ, we have nt > 0 and zt > 0. In this case, Lemma 2 implies that Ct/Yt is also constant, and \(\dot {c}_{t}/c_{t}=\dot {y}_{t}/y_{t}\). Then, we use Eqs. 3, 19, and \(\dot {c}_{t}/c_{t}=\dot {y}_{t}/y\) to obtain
Substituting \({r_{t}^{e}}\) in Eqs. 16 and A12 into Eq. A16 yields
We substitute Eq. 30 into Eq. A17 to derive
Substituting Eq. A18 into Eq. A12 yields the dynamics of xt as
Using \(v\equiv \frac {1-\sigma }{\beta -\sigma \mu ^{1/\left (1-\theta \right ) }/x_{t}}\left [ \left (1-\alpha \right ) \left (\mu -1\right ) -\beta \left (\rho +\frac {\lambda \sigma }{1-\sigma }\right ) \right ]\) and x∗ in Eq. 32, we express (A19) as
where we approximate \(\sigma \mu ^{1/\left (1-\theta \right ) }/x_{t}\cong 0\) for xt > xZ, so \(v\cong \frac {1-\sigma }{\beta }\left [ \left (1-\alpha \right ) \left (\mu -1\right ) -\beta \left (\rho +\frac {\lambda \sigma }{ 1-\sigma }\right ) \right ] \) becomes a constant. □
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Chu, A.C., Kou, Z. & Wang, X. Effects of patents on the transition from stagnation to growth. J Popul Econ 33, 395–411 (2020). https://doi.org/10.1007/s00148-019-00753-6
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00148-019-00753-6