Rising longevity, fertility dynamics, and R&D-based growth

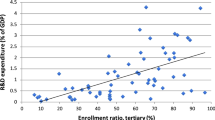
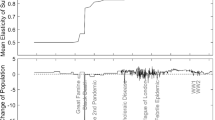
Abstract

This study constructs an overlapping-generations model with endogenous fertility, mortality, and R&D activities. We demonstrate that the model explains the observed fertility dynamics of developed countries. When the level of per capita wage income is either low or high, an increase in such income raises the fertility rate. When the level of per capita wage income is in the middle, an increase in such income decreases the fertility rate. The model also predicts the observed relationship between population growth and innovative activity. At first, both the rates of population growth and technological progress increase; that is, there is a positive relationship. Thereafter, the rate of population growth decreases but the rate of technological progress increases, showing a negative relationship.

Appendices

Appendix A: Proof of Proposition 1

To investigate the sign of $\frac {\partial n_{t}}{\partial w_{t}}$, we rearrange (20) as follows:

$$\begin{array}{@{}rcl@{}} \frac{\partial n_{t}}{\partial w_{t}} = \gamma \frac{{\Phi} (w_{t})}{\left[1 + \beta \lambda(w_{t}) + \gamma \right]^{2} (\rho w_{t} + \delta)^{2}}, \end{array} $$

where Φ(w_t) ≡ δ[1 + βλ(w_t) + γ] − βλ^′(w_t)w_t(ρw_t + δ). The sign of $\frac {\partial n_{t}}{\partial w_{t}}$ is determined by that of Φ(w_t), that is, ${\Phi }(w_{t}) \gtreqless 0$ implies $\frac {\partial n_{t}}{\partial w_{t}} \gtreqless 0$. Differentiating Φ(w_t) with respect to w_t and using Eqs. 19a and 19b yield

$$\begin{array}{@{}rcl@{}} {\Phi}^{\prime} (w_{t}) &=& - \beta w_{t} \left[ 2\rho \lambda^{\prime}(w_{t}) + \lambda^{\prime\prime}(w_{t}) (\rho w_{t} + \delta) \right],\\ &=& - \frac{\beta \nu \psi \chi w_{t} e^{-\psi w_{t}}}{\left( 1 + \chi e^{-\psi w_{t}}\right)^{3}} \left\{ 2\rho - \psi (\rho w_{t} + \delta) + \chi \left[2\rho + \psi(\rho w_{t} + \delta) \right] e^{-\psi w_{t}} \right\}, \\ &\equiv& - \frac{\beta \nu \psi \chi w_{t} e^{-\psi w_{t}}}{\left( 1 + \chi e^{-\psi w_{t}}\right)^{3}} {\Omega} (w_{t}). \end{array} $$

Here, Ω(w_t) satisfies

$$\begin{array}{@{}rcl@{}} {\Omega} (0) &=& 2\rho (1 + \chi ) + \psi \delta (\chi - 1), \\ {\Omega}^{\prime} (w_{t}) &=& - \psi \rho - \psi \chi \left[ \rho + \psi(\rho w_{t} + \delta) \right] e^{-\psi w_{t}} < 0. \end{array} $$

If Ω(0) < 0, we have Φ^′(w_t) > 0 for all w_t. On the other hand, if Ω(0) > 0, we have Φ^′(w_t) ⪌ 0 for any $w_{t} \lesseqgtr \tilde {w}$, where $\tilde {w}$ is defined as ${\Phi }^{\prime }(\tilde {w}) = 0$. Here, the condition of Ω(0) > 0 is as follows:

$$\begin{array}{@{}rcl@{}} \chi > \frac{\psi \delta - 2\rho}{\psi \delta + 2\rho}. \end{array} $$

These results imply that the relationship between Φ(w_t) and w_t has a U-shape and $\tilde {w}$ minimizes the value of Φ(w_t).

We then substitute Eqs. 18 and 19a into Φ(w_t) as follows:

$$\begin{array}{@{}rcl@{}} {\Phi}(w_{t}) = \delta(1+\gamma) + \frac{\delta \beta \nu}{1 + \chi e^{-\psi w_{t}}} - \frac{\beta \nu \psi w_{t} (\rho w_{t} + \delta) \chi e^{-\psi w_{t}}}{\left( 1 + \chi e^{-\psi w_{t}}\right)^{2}}. \end{array} $$

Using this, we obtain

$$\begin{array}{@{}rcl@{}} \lim\limits_{w_{t} \to 0} {\Phi}(w_{t}) &=& \delta(1+\gamma) + \frac{\delta \beta \nu}{1 + \chi} > 0, \\ \lim\limits_{w_{t} \to \infty} {\Phi}(w_{t}) &=& \delta(1+\gamma) + \delta \beta \nu > 0. \end{array} $$

In addition, if ${\Phi } (\tilde {w}) < 0$, we obtain the following relationship:

$$\begin{array}{@{}rcl@{}} {\Phi} (w_{t}) &>& 0 \hspace{10pt} when \hspace{10pt} 0<w_{t}<\bar{w}_{1} \hspace{7.5pt} or \hspace{7.5pt} w_{t} >\bar{w}_{2}, \\ {\Phi} (w_{t}) &<& 0 \hspace{10pt} when \hspace{10pt} \bar{w}_{1}<w_{t}<\bar{w}_{2}, \end{array} $$

where $\bar {w}_{1}$ and $\bar {w}_{2}$ are defined as ${\Phi }(\bar {w}_{1})= 0$ and ${\Phi }(\bar {w}_{2})= 0$ hold. In contrast, if ${\Phi } (\tilde {w}) > 0$, we have Φ(w_t) > 0 for all w_t.

Next, we examine the condition of ${\Phi } (\tilde {w}) < 0$. Because $\tilde {w}$ satisfies ${\Phi }^{\prime } (\tilde {w})= 0$, we obtain

$$\begin{array}{@{}rcl@{}} && 2\rho - \psi (\rho \tilde{w} + \delta) + \chi \left[2\rho + \psi(\rho \tilde{w} + \delta) \right] e^{-\psi \tilde{w}} = 0, \\ &\Leftrightarrow \ & 1 + \chi e^{-\psi \tilde{w}} = \frac{2\psi(\rho \tilde{w} + \delta)}{2\rho + \psi (\rho \tilde{w} + \delta)}. \end{array} $$

(25)

An investigation of Eq. 25 gives us the following properties:

$$\begin{array}{@{}rcl@{}} &&\frac{d \tilde{w}}{d \chi} = \frac{[2\rho + \psi(\rho\tilde{w} + \delta)] e^{-\psi \tilde{w}}}{\psi\rho + \psi\chi [\rho + \psi(\rho\tilde{w} + \delta)] e^{-\psi \tilde{w}}} > 0, \end{array} $$

(26)

$$\begin{array}{@{}rcl@{}} &&\tilde{w} \to \infty \hspace{15pt} when \hspace{15pt} \chi \to \infty. \end{array} $$

(27)

Using Eq. 25, we rearrange the condition of ${\Phi } (\tilde {w}) < 0$ as given below:

$$\begin{array}{@{}rcl@{}} &&{\Phi}(\tilde{w}) < 0, \\ &\Leftrightarrow \ & \delta(1\,+\,\gamma) \,+\, \frac{\delta \beta \nu}{1 \,+\, \chi e^{-\psi \tilde{w}}} - \frac{\beta \nu \psi \tilde{w} (\rho \tilde{w} \,+\, \delta) \chi e^{-\psi \tilde{w}}}{\left( 1 \,+\, \chi e^{-\psi \tilde{w}}\right)^{2}} < 0, \\ &\Leftrightarrow \ & \delta(1\,+\,\gamma) \,+\, \delta \beta \nu \frac{2\rho \,+\, \psi (\rho \tilde{w} \,+\, \delta)}{2\psi(\rho \tilde{w} + \delta)} \\ && \hspace{62pt} - \beta \nu \psi \tilde{w} (\rho \tilde{w} + \delta) \frac{\psi(\rho \tilde{w} + \delta) - 2\rho}{2\rho + \psi (\rho \tilde{w} + \delta)} \!\left[ \frac{2\rho + \psi (\rho \tilde{w} + \delta)}{2\psi(\rho \tilde{w} + \delta)} \right]^{2} \!< 0, \\ &\Leftrightarrow \ & 4\delta(1\,+\,\gamma) \psi(\rho \tilde{w} \,+\, \delta) \,+\, 2\delta \beta \nu [2\rho \,+\, \psi (\rho \tilde{w} + \delta)] < \beta \nu \tilde{w} \!\left\{ [\psi (\rho \tilde{w} + \delta)]^{2} - 4\rho^{2} \right\}, \\ &\Leftrightarrow \ & \psi\rho \!\left[ \!\frac{2(1\,+\,\gamma)}{\beta\nu} \,+\, 1 \!\right] \,+\, \left[\!\frac{2(1\,+\,\gamma)\psi\delta}{\beta\nu} \,+\, (2\rho\,+\,\psi\delta)\right] \!\frac{1}{\tilde{w}} \!<\! \frac{\psi^{2}(\rho\tilde{w} \,+\, \delta)^{2} \,-\, 4\rho^{2}}{2\delta}. \end{array} $$

(28)

Let us define the left- and right-hand sides of Eq. 28 as $\eta _{L}(\tilde {w})$ and $\eta _{R}(\tilde {w})$. $\eta _{L}(\tilde {w})$ is decreasing in $\tilde {w}$ and $\lim _{\tilde {w}\to 0} \eta _{L}(\tilde {w}) = \infty$ and $\lim _{\tilde {w}\to \infty } \eta _{L}(\tilde {w}) = \psi \rho \left [ \frac {2(1+\gamma )}{\beta \nu } + 1\right ]$ hold. On the other hand, $\eta _{R}(\tilde {w})$ is increasing in $\tilde {w}$ and $\lim _{\tilde {w}\to 0} \eta _{R}(\tilde {w}) = \frac {\psi ^{2}\delta ^{2} - 4\rho ^{2}}{2\delta }$ and $\lim _{\tilde {w}\to \infty } \eta _{R}(\tilde {w}) = \infty$ hold. From Eqs. 26 and 27, we find that there is a unique $\tilde {\chi }$ that satisfies $\eta _{L}(\tilde {w}) = \eta _{R}(\tilde {w})$. Hence, $\chi >\tilde {\chi }$ implies $\eta _{L}(\tilde {w}) < \eta _{R}(\tilde {w})$. In contrast, if $0<\chi <\tilde {\chi }$, $\eta _{L}(\tilde {w}) > \eta _{R}(\tilde {w})$ holds (that is, ${\Phi } (\tilde {w}) > 0$ holds).

Appendix B: Properties of Γ(A _t)

Using Eqs. 18, 19a, and 23, we obtain

$$\begin{array}{@{}rcl@{}} {\Gamma}^{\prime} (A_{t}) &=& \frac{A_{t}^{-\phi}}{\beta\nu} \left\{ (1\,-\,\phi)(1+\gamma+\beta\nu) + \left[ (1-\phi) - (1\,-\,\alpha)(1+\gamma)\psi w_{t} \right] \chi e^{-\psi w_{t}} \right\}, \\ &\equiv& \frac{A_{t}^{-\phi}}{\beta\nu} {\Theta}(w_{t}). \end{array} $$

Here, Θ(w_t) satisfies

$$\begin{array}{@{}rcl@{}} {\Theta}(0) &=& (1-\phi)(1+\gamma+\beta\nu) + (1-\phi) \chi > 0, \\ {\Theta}^{\prime}(w_{t}) &=& - \left[ (1-\alpha)(1+\gamma) + 1-\phi - (1-\alpha)(1+\gamma) \psi w_{t} \right] \psi \chi e^{-\psi w_{t}}. \end{array} $$

Hence, Θ^′(w_t) ⪌ 0 when w_t ⪌ w_Θ, where $w_{{\Theta }} \equiv \frac {(1-\alpha )(1+\gamma ) + 1-\phi }{(1-\alpha )(1+\gamma ) \psi }$. Using these results, we can define the following two cases: When Θ(w_Θ) > 0, we obtain

$$\begin{array}{@{}rcl@{}} {\Theta} (w_{t}) > 0 \hspace{15pt} for \hspace{5pt} all \hspace{5pt} w_{t}. \end{array} $$

On the other hand, when Θ(w_Θ) < 0, we obtain

$$\begin{array}{@{}rcl@{}} {\Theta} (w_{t}) &>& 0 \hspace{10pt} when \hspace{10pt} 0<w_{t}<w_{{\Gamma},1}, \hspace{2pt} w_{t} >w_{{\Gamma},2}, \\ {\Theta} (w_{t}) &<& 0 \hspace{10pt} when \hspace{10pt} w_{{\Gamma},1}<w_{t}<w_{{\Gamma},2}, \end{array} $$

where w_Γ,1 and w_Γ,2 are defined as Θ(w_Γ,1) = 0 and Θ(w_Γ,2) = 0. Because the sign of Γ^′(A_t) is the same as that of Θ(w_t) and w_t is determined by A_t, we can state the properties of Γ(A_t) as in Section 5.1.

We then investigate the condition Θ(w_Θ) < 0. Rearranging Θ(w_Θ) < 0 yields

$$\begin{array}{@{}rcl@{}} &&{\Theta}(w_{{\Theta}}) < 0, \\ &\Leftrightarrow \ & (1-\phi)(1+\gamma+\beta\nu) - (1-\alpha)(1+\gamma) \chi e^{-\psi w_{{\Theta}}} < 0. \end{array} $$

This implies that Θ(w_Θ) < 0 holds when $\chi >\hat {\chi }$, where $\hat {\chi }$ is defined as follows:

$$\begin{array}{@{}rcl@{}} \hat{\chi} \equiv \frac{(1-\phi)(1+\gamma+\beta\nu)}{(1-\alpha)(1+\gamma) e^{-\psi w_{{\Theta}}}}. \end{array} $$

In contrast, we obtain Θ(w_Θ) > 0 when $0<\chi <\hat {\chi }$.

Appendix C: Proof of Lemma 1

From Proposition 1, n_t has a local maximum (minimum) value at $w_{t} = \bar {w}_{1}$ ($w_{t} = \bar {w}_{2}$). Because $N_{t + 1} \gtreqless N_{t}$ is equivalent to $n_{t} \gtreqless 1$, we examine the following three cases. First, if n_t > 1 at $w_{t}=\bar {w}_{2}$, we obtain

$$\begin{array}{@{}rcl@{}} N_{t + 1} \gtreqless N_{t} \hspace{15pt} when \hspace{10pt} w_{t} \gtreqless \hat{w}_{1}, \end{array} $$

where $\hat {w}_{1}$ is defined as $n_{t} |_{w_{t}=\hat {w}_{1}} = 1$ and $\hat {w}_{1}<\bar {w}_{1}<\bar {w}_{2}$. This case corresponds to the panels on the left side of Fig. 4. Second, if n_t > 1 at $w_{t}=\bar {w}_{1}$ and n_t < 1 at $w_{t}=\bar {w}_{2}$, we obtain

$$\begin{array}{@{}rcl@{}} N_{t + 1} &>& N_{t} \hspace{10pt} when \hspace{10pt} \hat{w}_{1}<w_{t}<\hat{w}_{2} \hspace{7.5pt} or \hspace{7.5pt} w_{t} >\hat{w}_{3},\\ N_{t + 1} &<& N_{t} \hspace{10pt} when \hspace{10pt} 0<w_{t}<\hat{w}_{1} \hspace{7.5pt} or \hspace{7.5pt} \hat{w}_{2}<w_{t}<\hat{w}_{3}, \end{array} $$

where $\hat {w}_{2}$ and $\hat {w}_{3}$ are defined as $n_{t} |_{w_{t}=\hat {w}_{j}} = 1$ (j = 2, 3) and $\hat {w}_{1}<\bar {w}_{1}<\hat {w}_{2}<\bar {w}_{2}<\hat {w}_{3}$. This case corresponds to the panels on the right side of Fig.4. Finally, if n_t < 1 at $w_{t}=\bar {w}_{1}$, we obtain

$$\begin{array}{@{}rcl@{}} N_{t + 1} \gtreqless N_{t} \hspace{15pt} when \hspace{10pt} w_{t} \gtreqless \hat{w}_{1}. \end{array} $$

In this case, $\bar {w}_{1}<\bar {w}_{2}<\hat {w}_{1}$ holds. Therefore, the population size of young adults N_t decreases during economic development except for sufficiently high levels of w_t. Because this is contrary to the observed fact, we rule out this case.

Using Eq. 4b, we obtain the following relationship:

$$\begin{array}{@{}rcl@{}} n_{t} \gtreqless 1 \hspace{8pt} \Leftrightarrow \hspace{8pt} \gamma w_{t} \gtreqless \left[1 + \beta \lambda(w_{t}) + \gamma \right] (\rho w_{t} + \delta). \end{array} $$

Hence, the case where n_t > 1 at $w_{t}=\bar {w}_{2}$ corresponds to $\gamma \bar {w}_{2} > \left [1 + \beta \lambda (\bar {w}_{2}) + \gamma \right ] (\rho \bar {w}_{2} + \delta )$. On the other hand, the case where n_t > 1 at $w_{t}=\bar {w}_{1}$ and n_t < 1 at $w_{t}=\bar {w}_{2}$ corresponds to $\gamma \bar {w}_{1} > \left [1 + \beta \lambda (\bar {w}_{1}) + \gamma \right ] (\rho \bar {w}_{1} + \delta )$ and $\gamma \bar {w}_{2} < \left [1 + \beta \lambda (\bar {w}_{2}) + \gamma \right ] (\rho \bar {w}_{2} + \delta )$.

Appendix D: Calculation of Y _t

Substituting Eq. 16 into Eq. 15, we obtain

$$\begin{array}{@{}rcl@{}} Y_{t} = \left( \frac{\alpha^{2}}{1-\alpha} \right)^{\alpha} A_{t}^{1-\alpha} L_{Y,t}, \end{array} $$

(29)

We consider the labor market clearing condition to derive L_Y,t. By using Eqs. 9a and 16, the labor input into production of intermediate goods becomes

$$\begin{array}{@{}rcl@{}} A_{t} x_{t} = \frac{\alpha^{2}}{1-\alpha} L_{Y,t}. \end{array} $$

(30)

From Eqs. 13 and 30, we obtain

$$\begin{array}{@{}rcl@{}} L_{Y,t} = \frac{1-\alpha}{1-\alpha+\alpha^{2}} \left[ \left( 1 - \rho n_{t} \right) N_{t} - L_{A,t} \right] \hspace{10pt} if \hspace{10pt} L_{A,t} > 0. \end{array} $$

(31)

Furthermore, Eqs. 10, 11, and 17 yield

$$\begin{array}{@{}rcl@{}} L_{A,t} = \frac{\beta \lambda(w_{t}) N_{t}}{1 + \beta \lambda(w_{t}) + \gamma} - A_{t}^{1-\phi}. \end{array} $$

(32)

By using Eqs. 4b, 16, 29, 31, and 32, we can calculate the output of final goods Y_t.

Appendix E: Derivation of the growth rates along the BGP

1.1 E.1 Derivation of $g^{\ast }_{M}$

Because N_t+ 1 = n^∗N_t and $\lambda _{t} = \bar {\lambda }$ hold along the BGP, the growth rate of population along the BGP is given as follows:

$$\begin{array}{@{}rcl@{}} 1 + g^{\ast}_{M} = \frac{n^{\ast} N_{t + 1} + N_{t + 1} + \bar{\lambda} N_{t}}{n^{\ast} N_{t} + N_{t} + \bar{\lambda} N_{t-1}} = \frac{(n^{\ast})^{2} + n^{\ast} + \bar{\lambda}}{n^{\ast} + 1 + \frac{\bar{\lambda}}{n^{\ast}}} = n^{\ast}. \end{array} $$

1.2 E.2 Derivation of $g^{\ast }_{A}$

By using Eqs. 32 and 19d, we obtain the employment share of R&D along the BGP as follows:

$$\begin{array}{@{}rcl@{}} \frac{L_{A,t}}{N_{t}} = \frac{\beta \bar{\lambda}}{1 + \beta \bar{\lambda} + \gamma} - \frac{A_{t}^{1-\phi}}{N_{t}}. \end{array} $$

Because the employment share of R&D is constant, the term $A_{t}^{1-\phi }/N_{t}$ also becomes constant along the BGP. Thus, the growth rate of A_t along the BGP is as follows:

$$\begin{array}{@{}rcl@{}} \left( 1 + g_{A}^{\ast} \right)^{1-\phi} = \left( \frac{A_{t + 1}}{A_{t}} \right)^{1-\phi} = \frac{N_{t + 1}}{N_{t}} = n^{\ast}. \end{array} $$

1.3 E.3 Derivation of $g^{\ast }_{Y}$

From Eq. 29, the growth rate of Y_t is determined by those of A_t and L_Y,t. Equation 31 implies

$$\begin{array}{@{}rcl@{}} \frac{L_{Y,t}}{N_{t}} = \frac{1-\alpha}{1-\alpha+\alpha^{2}} \left( 1 - \rho n^{\ast} - \frac{L_{A,t}}{N_{t}} \right). \end{array} $$

Because the employment share of final goods production becomes a constant, the growth rate of L_Y,t along the BGP is equal to n^∗. Therefore, the growth rate of Y_t along the BGP is given by

$$\begin{array}{@{}rcl@{}} 1 + g_{Y}^{\ast} = \left( 1 + g_{A}^{\ast} \right)^{1-\alpha} n^{\ast} = \left( n^{\ast} \right)^{\frac{1-\alpha}{1-\phi}+ 1}. \end{array} $$

1.4 E.4 Derivation of $g^{\ast }_{Z}$ and $g^{\ast }_{Z}$

From the definition of Z_t, the growth rate of Z_t is as follows:

$$\begin{array}{@{}rcl@{}} 1 + g_{Z,t} &=& \frac{Z_{t + 1}}{Z_{t}} = \frac{Y_{t + 1} + w_{t + 1} L_{A,t + 1}}{Y_{t} + w_{t} L_{A,t}} = \frac{w_{t + 1}}{w_{t}} \frac{\frac{1}{1-\alpha} L_{Y,t + 1} + L_{A,t + 1}}{\frac{1}{1-\alpha} L_{Y,t} + L_{A,t}}, \\ &=& \frac{w_{t + 1}}{w_{t}} \frac{\frac{1}{1-\alpha} \frac{L_{Y,t + 1}}{N_{t + 1}} + \frac{L_{A,t + 1}}{N_{t + 1}}}{\frac{1}{1-\alpha} \frac{L_{Y,t}}{N_{t}} + \frac{L_{A,t}}{N_{t}}} \frac{N_{t + 1}}{N_{t}}. \end{array} $$

Along the BGP, $\frac {L_{Y,t}}{N_{t}}$ and $\frac {L_{A,t}}{N_{t}}$ become a constant. These results and (16) imply

$$\begin{array}{@{}rcl@{}} 1 + g_{Z}^{\ast} = \left( 1+g_{A}^{\ast} \right)^{1-\alpha} n^{\ast} = \left( n^{\ast} \right)^{\frac{1-\alpha}{1-\phi}+ 1}. \end{array} $$

Because $z_{t} = \frac {Z_{t}}{M_{t}}$, the growth rate of z_t along the BGP is given by

$$\begin{array}{@{}rcl@{}} 1 + g_{z}^{\ast} = \frac{z_{t + 1}}{z_{t}} = \frac{Z_{t + 1}}{Z_{t}} \frac{M_{t}}{M_{t + 1}} = \frac{1 + g_{Z}^{\ast}}{1 + g_{M}^{\ast}} = \left( n^{\ast} \right)^{\frac{1-\alpha}{1-\phi}}. \end{array} $$