Dispersion and Stability Condition of Seismic Wave Simulation in TTI Media

Abstract

For seismic waveform simulation in tilted transversely isotropic (TTI) media, we derive explicitly the numerical dispersion relation and the stability condition for the computation of a 2D pseudo-acoustic wave equation. The numerical dispersion relation indicates that the number of sampling points per wavelength has the greatest influence on the dispersion, while the anisotropic parameters of the TTI media and the mesh rotation angle have little influence on the dispersion. Given an appropriate spatial sampling, the stability condition is for the selection of the time step for the implementation of the TTI wave equation. We partition a numerical model using quadrangle grids in Cartesian coordinates, and map it to a computing model in which any non-rectangular meshes in Cartesian coordinates become rectangular meshes. Then we reformulate the pseudo-acoustic wave equation for the TTI media accordingly in the computational space. We implement seismic waveform simulation using the second-order finite-difference method straightforwardly, and show examples with a desirable accuracy using a model with non-rectangular meshes in Cartesian coordinates along a curved surface and fluctuating interfaces in the TTI media.

1 Introduction

Seismic anisotropy commonly exists in the Earth’s subsurface media (Tsvankin et al. 2010; Takanashi and Tsvankin 2012). Accurate waveform simulation in tilted transversely isotropic (TTI) media is of importance for seismic waveform inversion. The latter reconstructs the subsurface velocity model quantitatively based on seismic waveform data. Seismic waveform data routinely recorded by hydrocarbon explorations comprise of mainly P-wave reflection data. Therefore, we use an acoustic wave equation in this paper for waveform simulation through TTI media containing a curved surface and fluctuating interfaces. This waveform simulation scheme is a core engine employed by the iterative inversion of seismic P-wave reflection data (Wang 2003; Wang and Rao 2009).

Although the P-wave and S-wave are coupled in the elastic wave equation in TTI media, we can have a pseudo-acoustic wave equation if the S-wave velocity is fixed along the axis of symmetry (Alkhalifah 1998; Fletcher et al. 2009). This acoustic wave equation is defined by two anisotropic parameters $\varepsilon$ and δ measuring the difference between two axes of the elliptic wavefront and the deviation from a perfect elliptical shape, respectively (Thomsen 1986). In the context of seismic waveform inversion, Pratt and Shipp (1999) and Rao and Wang (2011) use an acoustic wave equation defined by a single anisotropic parameter $\varepsilon$. Rao et al. (2016) provide the derivation of this wave equation with a single anisotropic parameter. In this paper, we adopt the acoustic wave equation with two anisotropic parameters. That is the pseudo-acoustic wave equation.

We also consider the models with a curved surface and fluctuating interfaces in the subsurface. We use quadrangle grids to partition every individual layer, confined by two fluctuating interfaces, based on a body-fitting scheme. By solving Poisson’s equation, these grids also satisfy the pseudo-orthogonal condition (Rao and Wang 2013) in which grids should have the acute angles > 67° (90° for completely orthogonal grids). We transform non-rectangular meshes in Cartesian coordinates into rectangular ones through conformal mapping. These grids, as structured, keep the similar neighborhood relationships as they do in Cartesian coordinates. We reformulate the pseudo-acoustic wave equation accordingly in the computational space. For the reformulated TTI wave equation, we analytically derive the corresponding numerical dispersion relation and stability condition, which provide the basis of finite-difference parameter selection of the TTI media waveform simulation.

2 Wave Equation

The pseudo-acoustic wave equation in TTI media is (Fletcher et al. 2009)

$$\frac{{\partial^{2} }}{{\partial t^{2} }}\left( {\begin{array}{*{20}c} {p} \\ {q} \\ \end{array} } \right) = \left[ {\begin{array}{*{20}c} {v_{px}^{2} H_{x} + v_{sz}^{2} H_{z} } & {(v_{pz}^{2} - v_{sz}^{2} )H_{z} } \\ {(v_{pn}^{2} - v_{sz}^{2} )H_{x} } & {v_{sz}^{2} H_{x} + v_{pz}^{2} H_{z} } \\ \end{array} } \right]\left( {\begin{array}{*{20}c} {p} \\ {q} \\ \end{array} } \right) ,$$

(1)

where ${p}$ is the P wavefield, ${q}$ is an auxiliary wavefield, $v_{pz}$ is the P-wave velocity along the TTI symmetry axis, $v_{px}$ is the P-wave velocity perpendicular to the symmetry axis, $v_{pn}$ is the P-wave normal-moveout velocity, $v_{sz}$ is the SV-wave velocity along the TTI symmetry axis, and $H_{x}$ and $H_{z}$ are two 2D differential operators, $H_{x} \equiv \partial^{2} /\partial \hat{x}^{2}$ and $H_{z} \equiv \partial^{2} /\partial \hat{z}^{2}$, with respect to the rotated coordinate system ($\hat{x}$, $\hat{z}$). Denoting the anticlockwise rotation angle of the TTI symmetry axis $\hat{z}$ by $\phi$ (Fig. 1), we can present the two 2D differential operators as

$$\begin{aligned} H_{x} &= \frac{{\partial^{2} }}{{\partial x^{2} }} + \frac{{\partial^{2} }}{{\partial z^{2} }} - H_{z} , \\ H_{z} &= \sin^{2} \phi \frac{{\partial^{2} }}{{\partial x^{2} }} + \cos^{2} \phi \frac{{\partial^{2} }}{{\partial z^{2} }} + \sin 2\phi \frac{{\partial^{2} }}{\partial x\partial z}, \\ \end{aligned}$$

(2)

where (x, z) are Cartesian coordinates. Note that we use $H_{x}$ and $H_{z}$ here to present differentials with respect to $\hat{x}$ and $\hat{z}$, respectively. Fletcher et al. (2009) used $H_{1}$ and $H_{2}$ to present the two differentials with respect to $\hat{z}$ and $\hat{x}$, respectively. For the completeness, we summarize the derivation of this pseudo-acoustic wave equation in the appendix.

Fig. 1

In homogeneous TTI media, the anticlockwise rotation angle of the symmetry axis of the wavefront is $\phi .$ The ray vector points from the source to the receiver, and the corresponding wave (phase velocity) vector is normal to the wavefront. The wave angle with respect to the symmetry axis $\hat{z}$ is $\theta .$ The angle between the wave vector and the positive direction of the $\eta$ -axis in the computational space is $\gamma$. The rotation angle of a local mesh from the conventional finite-difference mesh, which is parallel and perpendicular to the Cartesian coordinates, is $\varphi$

In the pseudo-acoustic wave equation [Eq. (1)], the two anisotropic velocities ($v_{px}$, $v_{pn}$) are related to the TTI anisotropy parameters by $v_{px} = v_{pz} \sqrt {1 + 2\varepsilon }$ and $v_{pn} = v_{pz} \sqrt {1 + 2\delta }$, where $\varepsilon$ and $\delta$ are two anisotropy parameters (Thomsen, 1986). Note that the SV-wave velocity $v_{sz}$ in Eq. (1) does not have a significant effect on the P wavefront. It would have an effect on the SV-wave wavefront and in turn on the P–S converted wave imaging. However, from the P–P wave imaging/gradient calculation point of view, the SV-wave wavefront (traveling slowly) is simply an unwanted artefact and does not significantly affect the P-wave image.

We use body-fitted grids initially to partition the numerical model (Rao and Wang 2013). Because of the curved surface and fluctuating interfaces in the model, there must be non-rectangular meshes along the surface and the interfaces (Fig. 2a). Then, we map this initial Cartesian model into a computing model with a flat surface and flat interfaces (Fig. 2b). After this conformal mapping, the non-rectangular meshes in the Cartesian model become rectangular meshes in the computational space. Thus, we can adopt a simple finite-difference scheme straightforwardly for wave simulation.

Fig. 2

a Body-fitted grids in the physical space (x, z). b Non-rectangular meshes in the Cartesian coordinates are transformed into rectangular ones in the computational space ($\xi ,\eta$) through conformal mapping

Here, we transform the pseudo-acoustic wave equation from Cartesian coordinates (x, z) to the computational space ($\xi ,\eta$). In the computational space, the first-order spatial derivatives become

$$\begin{aligned} \frac{\partial }{\partial x} &= \frac{\partial }{\partial \xi }\dot{\xi }_{x} + \frac{\partial }{\partial \eta }\dot{\eta }_{x} \, , \hfill \\ \frac{\partial }{\partial z} &= \frac{\partial }{\partial \xi }\dot{\xi }_{z} + \frac{\partial }{\partial \eta }\dot{\eta }_{z} \, , \hfill \\ \end{aligned}$$

(3)

where $\dot{\xi }_{x} \equiv \partial \xi /\partial x$, $\dot{\eta }_{x} \equiv \partial \eta /\partial x$, and so on. These derivatives are known parameters, because of the relationship between the model coordinates and the computational coordinates. The second-order spatial derivatives are

$$\begin{aligned} \frac{{\partial^{2} }}{{\partial x^{2} }} = \frac{\partial }{\partial \xi }\left( {\dot{\xi }_{x}^{2} \frac{\partial }{\partial \xi }} \right) + \frac{\partial }{\partial \xi }\left( {\dot{\xi }_{x} \dot{\eta }_{x} \frac{\partial }{\partial \eta }} \right) + \frac{\partial }{\partial \eta }\left( {\dot{\xi }_{x} \dot{\eta }_{x} \frac{\partial }{\partial \xi }} \right) \\ + \frac{\partial }{\partial \eta }\left( {\dot{\eta }_{x}^{2} \frac{\partial }{\partial \eta }} \right) \, , \\ \frac{{\partial^{2} }}{{\partial z^{2} }} = \frac{\partial }{\partial \xi }\left( {\dot{\xi }_{z}^{2} \frac{\partial }{\partial \xi }} \right) + \frac{\partial }{\partial \xi }\left( {\dot{\xi }_{z} \dot{\eta }_{z} \frac{\partial }{\partial \eta }} \right) + \frac{\partial }{\partial \eta }\left( {\dot{\xi }_{z} \dot{\eta }_{z} \frac{\partial }{\partial \xi }} \right) \\ + \frac{\partial }{\partial \eta }\left( {\dot{\eta }_{z}^{2} \frac{\partial }{\partial \eta }} \right) \, , \\ \frac{{\partial^{2} }}{\partial x\partial z} = \frac{\partial }{\partial \xi }\left( {\dot{\xi }_{x} \dot{\xi }_{z} \frac{\partial }{\partial \xi }} \right) + \frac{\partial }{\partial \xi }\left( {\dot{\xi }_{x} \dot{\eta }_{z} \frac{\partial }{\partial \eta }} \right) + \frac{\partial }{\partial \eta }\left( {\dot{\xi }_{z} \dot{\eta }_{x} \frac{\partial }{\partial \xi }} \right) \\ + \frac{\partial }{\partial \eta }\left( {\dot{\eta }_{x} \dot{\eta }_{z} \frac{\partial }{\partial \eta }} \right) \, .\\ \end{aligned}$$

(4)

Substituting these spatial derivatives into the 2D differential operators $H_{x}$ and $H_{z}$, we rewrite wave equation [Eq. (1)] in the computational space ($\xi , \, \eta$). We numerically solve this time-space domain wave equation in the computational space using a second-order finite-difference method.

3 Numerical Dispersion

We analyze the numerical dispersion in this section, for the finite-difference implementation of the spatial derivatives in the pseudo-acoustic wave equation.

When $\varepsilon = \delta ,$ the P wavefield ${p}$ is approximately equal to the auxiliary wavefield ${q},$ and we can use any of the two expressions in Eq. (1) for the dispersion analysis. We rewrite the first expression as

$$\frac{{\partial^{2} {p}}}{{\partial t^{2} }} = v_{pz}^{2} [(1 + 2\varepsilon )H_{x} + H_{z} ]{p} ,$$

(5)

for which we exploit the relation of $v_{px}^{2} = (1 + 2\varepsilon )v_{pz}^{2}$. Assuming that the grids fully satisfy the orthogonality, and that the local mesh has a rotation of angle $\varphi$ from the conventional finite-difference mesh:

$$\dot{\xi }_{x} = \cos \varphi ,\quad \dot{\xi }_{z} = \sin \varphi ,\quad \dot{\eta }_{x} = - \sin \varphi ,\quad \dot{\eta }_{z} = \cos \varphi .$$

(6)

We can express the spatial derivatives in Eq. (4) as

$$\begin{aligned} \frac{{\partial^{2} }}{{\partial x^{2} }} = \cos^{2} \varphi \frac{{\partial^{2} }}{{\partial \xi^{2} }} - \sin 2\varphi \frac{{\partial^{2} }}{\partial \xi \partial \eta } + \sin^{2} \varphi \frac{{\partial^{2} }}{{\partial \eta^{2} }}, \\ \frac{{\partial^{2} }}{{\partial z^{2} }} = \sin^{2} \varphi \frac{{\partial^{2} }}{{\partial \xi^{2} }} + \sin 2\varphi \frac{{\partial^{2} }}{\partial \xi \partial \eta } + \cos^{2} \varphi \frac{{\partial^{2} }}{{\partial \eta^{2} }}, \\ \frac{{\partial^{2} }}{\partial x\partial z} = \frac{1}{2}\sin 2\varphi \left( {\frac{{\partial^{2} }}{{\partial \xi^{2} }} - \frac{{\partial^{2} }}{{\partial \eta^{2} }}} \right) + \cos 2\varphi \frac{{\partial^{2} }}{\partial \xi \partial \eta }. \\ \end{aligned}$$

(7)

Substituting these expressions into the differential operators $H_{x}$ and $H_{z}$ in Eq. (2), then we rewrite Eq. (5) as

$$\frac{{\partial^{2} {p}}}{{\partial t^{2} }} = v_{pz}^{2} \left( {A\frac{{\partial^{2} }}{{\partial \xi^{2} }} + B\frac{{\partial^{2} }}{\partial \xi \partial \eta } + C\frac{{\partial^{2} }}{{\partial \eta^{2} }}} \right){p} ,$$

(8)

where

$$\begin{aligned} A &= (1 + 2\varepsilon \cos^{2} \phi )\cos^{2} \varphi + (1 + 2\varepsilon \sin^{2} \phi )\sin^{2} \varphi \\ & \quad - \varepsilon \sin 2\phi \sin 2\varphi \, , \\ B & = - 2\varepsilon \sin (2\phi + 2\varphi ), \\ C &= (1 + 2\varepsilon \cos^{2} \phi )\sin^{2} \varphi + (1 + 2\varepsilon \sin^{2} \phi )\cos^{2} \varphi \\ & \quad + \varepsilon \sin 2\phi \sin 2\varphi \, . \\ \end{aligned}$$

(9)

We can approximate the temporal and spatial derivatives in Eq. (8) by finite differencing. Following the procedure of von Neumann stability analysis, we insert a plane wave $p(\xi ,\eta ,t) = p_{0} e^{{ - i(k_{\xi } \xi + k_{\eta } \eta )}} e^{i\omega t}$ into the finite-difference operators (Nilsson et al. 2007). For instance,

$$\frac{{\partial^{2} p}}{{\partial t^{2} }} \approx \frac{p(t + \Delta t) + p(t - \Delta t) - 2p(t)}{{\Delta t^{2} }} = \frac{{e^{i\omega \Delta t} + e^{ - i\omega \Delta t} - 2}}{{\Delta t^{2} }}p(t)$$

(10)

Then, we approximate the four derivatives in Eq. (8) as harmonic functions:

$$\begin{aligned} & \frac{{\partial^{2} }}{{\partial t^{2} }} \approx \frac{{e^{i\omega \Delta t} + e^{ - i\omega \Delta t} - 2}}{{\Delta t^{2} }} = \frac{ - 4}{{\Delta t^{2} }}\sin^{2} \frac{\omega \Delta t}{2}, \\ & \frac{{\partial^{2} }}{{\partial \xi^{2} }} \approx \frac{{e^{{ik_{\xi } \Delta \xi }} + e^{{ - ik_{\xi } \Delta \xi }} - 2}}{{\Delta \xi^{2} }} = \frac{ - 4}{{\Delta \xi^{2} }}\sin^{2} \frac{{k_{\xi } \Delta \xi }}{2}, \hfill \\ & \frac{{\partial^{2} }}{{\partial \eta^{2} }} \approx \frac{{e^{{ik_{\eta } \Delta \eta }} + e^{{ - ik_{\eta } \Delta \eta }} - 2}}{{\Delta \eta^{2} }} = \frac{ - 4}{{\Delta \eta^{2} }}\sin^{2} \frac{{k_{\eta } \Delta \eta }}{2}, \hfill \\& \frac{{\partial^{2} }}{\partial \xi \partial \eta } \approx \frac{{ - \sin (k_{\xi } \Delta \xi )\sin (k_{\eta } \Delta \eta )}}{\Delta \xi \Delta \eta }. \hfill \\ \end{aligned}$$

(11)

Now, assuming $\Delta \xi = \Delta \eta ,$ we express Eq. (8) as

$$\begin{aligned} & \frac{A}{{\Delta \xi^{2} }}\sin^{2} \left( {\frac{{k_{\xi } \Delta \xi }}{2}} \right) + \frac{B}{{4\Delta \xi^{2} }}\sin (k_{\xi } \Delta \xi )\sin (k_{\eta } \Delta \eta ) \\ & \quad \quad + \frac{C}{{\Delta \xi^{2} }}\sin^{2} \left( {\frac{{k_{\eta } \Delta \eta }}{2}} \right) = \frac{1}{{v_{pz}^{2} \Delta t^{2} }}\sin^{2} \left( {\frac{\omega \Delta t}{2}} \right) \, , \\ \end{aligned}$$

(12)

where $\omega = 2\pi v_{h} s/\Delta \xi$ is the angular frequency with velocity of wave propagation $v_{h} ,$ following De Basabe and Sen (2007), $s = \Delta \xi /\lambda$ represents the reciprocal number of sampling points per wavelength $\lambda ,$$k_{\xi } = 2\pi \sin \gamma /\lambda$ and $k_{\eta } = 2\pi \cos \gamma /\lambda$ are wavenumbers, and $\gamma$ is the angle between the wave vector and the positive direction of the $\eta$-axis in the computational space (Fig. 1).

Defining the Courant number as

$$Q = v_{pz} \frac{\Delta t}{\Delta \xi } ,$$

(13)

we rewrite Eq. (12) as

$$\frac{1}{{Q^{2} }}\sin^{2} \left( {\frac{{\pi sQv_{h} }}{{v_{pz} }}} \right) = \varLambda ,$$

(14)

where

$$\begin{aligned} \varLambda &= A\sin^{2} (\pi s\sin \gamma ) + \frac{B}{4}\sin (2\pi s\sin \gamma )\sin (2\pi s\cos \gamma ) \\ & \quad + C\sin^{2} (\pi s\cos \gamma ). \\ \end{aligned}$$

(15)

Therefore, we have

$$\frac{{v_{h} }}{{v_{pz} }} = \frac{{\sin^{ - 1} (Q\sqrt \varLambda )}}{\pi sQ} .$$

(16)

In the appendix, we have derived the P-wave phase velocity $v(\theta )$ as

$$\begin{aligned} \frac{{v^{2} (\theta )}}{{v_{pz}^{2} }} &= 1 - \frac{L}{2} + \varepsilon \sin^{2} \theta + \frac{L}{2}\left( {1 + \frac{{4\varepsilon^{2} \sin^{4} \theta }}{{L^{2} }}} \right. \\ & \quad \left. { + \frac{{4\sin^{2} \theta }}{L}(2\delta \cos^{2} \theta - \varepsilon \cos 2\theta )} \right)^{1/2}, \\ \end{aligned}$$

(17)

where $L = 1 - v_{sz}^{2} /v_{pz}^{2}$, and $\theta$ is the angle between the wave vector and the TTI symmetry axis (Fig. 1).

As we assume $\varepsilon = \delta$, and assuming $L = 1$, the maximum possible value of $L$, we can simplify Eq. (17) to be

$$v_{pz} = \frac{v(\theta )}{\sqrt D } ,$$

(18)

where

$$D = \frac{1}{2}\left( {1 + \sqrt {1 + 4\varepsilon \sin^{2} \theta + 4\varepsilon^{2} \sin^{4} \theta } } \right) + \varepsilon \sin^{2} \theta .$$

(19)

Therefore, we obtain the following dispersion relation:

$$\frac{{v_{h} }}{v(\theta )} = \frac{{\sin^{ - 1} (Q\sqrt \varLambda )}}{\pi sQ\sqrt D } .$$

(20)

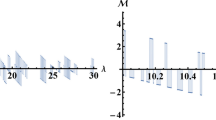
Figure 3 shows that the dispersion increases with the increase of the sampling rate s, which is the reciprocal number of sampling points per wavelength. In this test, the Courant number $Q = 0.1$, the anisotropy parameter $\varepsilon = 0.1$, the angle between the symmetry axis and the vertical direction of the TTI medium is $\phi = 30^{ \circ } ,$ and the meshing rotation angle $\varphi = 30^{ \circ } .$

Fig. 3

Numerical dispersion versus the reciprocal number of sampling points per wavelength. In the legend, $\theta$ is the angle between the wave vector and the symmetry axis of the TTI media

Numerical tests indicate that the dispersion is weakest when the propagation direction is perpendicular to the axis of TTI media ($\theta = 90^{ \circ }$). The dispersion is slightly increased when the propagation direction is close to the axis of symmetry ($\theta \to 0^{ \circ }$).

As it is well known, a general requirement for forward modeling in the isotropic media with the second-order finite-difference simulations is 10 grids per wavelength (Kreiss and Oliger 1972; Wu et al. 1996). Figure 3 indicates that satisfying the condition $s \le 0.1$, that is $\ge$ 10 grids per wavelength, means that the dispersion is less than 1% in wavefield simulation through anisotropic media. The smallest dispersion ratio is 0.99, for the anisotropic parameters $\varepsilon$ and $\delta$ between $-0.25$ and $0.25$ and for the mesh rotation angle $\varphi$ between 0 and 90^o. These numerical tests confirm that, as long as $s = 0.1$, the dispersion requirement of forward modeling is still satisfied.

Note that the points per wavelength quoted above is for wave propagation within one wavelength. Because of the error accumulation, the number of points required for a given tolerance depends on the number of wavelengths the wave is to propagate. According to Kreiss and Petersson (2012), a typical scaling is $(\lambda /\mu )^{1/n}$, where ($\lambda$, $\mu$) here are the Lame parameters, and $n$ is the order of accuracy of the method.

4 Numerical Stability

We derive the stability condition in this section, for the numerical implementation of the time derivatives in the wave equation, given appropriate sampling in the spatial domain. We investigate this numerical stability when the spatial grids are discretized in Cartesian coordinates.

Assuming $\varepsilon = \delta ,$ a similar procedure to that in the previous section, we approximate the auxiliary wavefield ${q}$ by the P wavefield ${p}$, and obtain the condition of numerical stability from the implementation of Eq. (5). Using the second-order finite-differencing operator to present the time-domain derivative, we express Eq. (5) as

$$p^{(n + 1)} = \{ \, 2 + \Delta t^{2} v_{pz}^{2} [(1 + 2\varepsilon )H_{x} + H_{z} ] \, \} p^{(n)} - p^{(n - 1)} ,$$

(21)

where $n$ is the time step. After Fourier transformation, it becomes

$$\tilde{p}^{(n + 1)} = \{ \, 2 - v_{pz}^{2} \Delta t^{2} [(1 + 2\varepsilon )\tilde{H}_{x} + \tilde{H}_{z} ] \, \} \tilde{p}^{(n)} - \tilde{p}^{(n - 1)} ,$$

(22)

where $\tilde{H}_{x}$ and $\tilde{H}_{z}$ are the wavenumber-domain 2D differential operators, and $\tilde{p}$ is the wavenumber-domain P wavefield. Now, we rewrite Eq. (22) in the form of a growth matrix as

$$\left[ {\begin{array}{*{20}c} {\tilde{p}^{(n + 1)} } \\ {\tilde{p}^{(n)} } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {2 - v_{pz}^{2} \Delta t^{2} [(1 + 2\varepsilon )\tilde{H}_{x} + \tilde{H}_{z} ]} & { - 1} \\ 1 & 0 \\ \end{array} } \right] \, \left[ {\begin{array}{*{20}c} {\tilde{p}^{(n)} } \\ {\tilde{p}^{(n - 1)} } \\ \end{array} } \right] \, .$$

(23)

Denoting the $2 \times 2$ growth matrix by ${\mathbf{A}}$, the stability condition of this differential equation is that the maximum absolute eigenvalue of matrix ${\mathbf{A}}$ is not greater than one. This maximum value defines the spectral radius of the matrix. Thus, the stability condition is

$$R({\mathbf{A}}) = \hbox{max} \{ |\lambda_{1} |, \, |\lambda_{2} |\} \le 1 .$$

(24)

The eigen-equation of matrix ${\mathbf{A}}$ is

$$\left| { \, \begin{array}{*{20}c} {2 - v_{pz}^{2} \Delta t^{2} [(1 + 2\varepsilon )\tilde{H}_{x} + \tilde{H}_{z} ] - \lambda } & { - 1} \\ 1 & { - \lambda } \\ \end{array} \, } \right| = 0 ,$$

(25)

which has two eigenvalues:

$$\lambda_{1,2} = \frac{1}{2}\left\{ { \, - \{ \, v_{pz}^{2} \Delta t^{2} [(1 + 2\varepsilon )\tilde{H}_{x} + \tilde{H}_{z} ] - 2 \, \} \pm \sqrt D } \right\}$$

(26)

with

$$D = \{ \, v_{pz}^{2} \Delta t^{2} [(1 + 2\varepsilon )\tilde{H}_{x} + \tilde{H}_{z} ] - 2 \, \}^{2} - 4 .$$

(27)

When $D > 0,$ both eigenvalues are real valued, and $R({\mathbf{A}})$ is larger than one. When $D \le 0$, both solutions $\lambda_{1,2}$ are complex valued. The moduli of both the complex eigenvalues $\lambda_{1,2}$ are identically equal to one. Therefore, to guarantee a stable iteration, the condition of $D \le 0$ must be satisfied. That is,

$$0 \le v_{pz}^{2} \Delta t^{2} [(1 + 2\varepsilon )\tilde{H}_{x} + \tilde{H}_{z} ] \le 4 .$$

(28)

According to Eq. (2), the wavenumber-domain 2D differential operators $\tilde{H}_{x}$ and $\tilde{H}_{z}$ may be expressed as

$$\begin{aligned} \tilde{H}_{x} = k_{x}^{2} \cos^{2} \phi + k_{z}^{2} \sin^{2} \phi - k_{x} k_{z} \sin 2 \phi , \hfill \\ \tilde{H}_{z} = k_{x}^{2} \sin^{2} \phi + k_{z}^{2} \cos^{2} \phi + k_{x} k_{z} \sin 2\phi . \hfill \\ \end{aligned}$$

(29)

The wavenumbers in Eq. (29) can be approximated as harmonic functions in the wavenumber domains, similarly to Eq. (11). Denoting the wavenumber-domain wavefield as

$$\begin{aligned} \tilde{p}(\ell ,m,t) & \to \tilde{p}_{0} (k_{x} ,k_{z} ,t), \hfill \\ \tilde{p}(\ell + 1,m,t) & \to \tilde{p}_{0} (k_{x} ,k_{z} ,t)e^{{ - ik_{x} \Delta x}} , \hfill \\ \tilde{p}(\ell ,m + 1,t) & \to \tilde{p}_{0} (k_{x} ,k_{z} ,t)e^{{ - ik_{z} \Delta z}} , \hfill \\ \end{aligned}$$

(30)

the wavenumber factors can be approximated by second-order finite-differencing as

$$\begin{aligned} k_{x}^{2} & = - \frac{{\partial^{2} }}{{\partial x^{2} }} = \frac{{2 - e^{{ - ik_{x} \Delta x}} - e^{{ik_{x} \Delta x}} }}{{\Delta x^{2} }} = \frac{4}{{\Delta x^{2} }}\sin^{2} \left( {\frac{{k_{x} \Delta x}}{2}} \right) \, , \\ k_{z}^{2} &= - \frac{{\partial^{2} }}{{\partial z^{2} }} = \frac{4}{{\Delta z^{2} }}\sin^{2} \left( {\frac{{k_{z} \Delta z}}{2}} \right) \, , \\ k_{x} k_{z} & = - \frac{\partial }{\partial x}\frac{\partial }{\partial z} = \frac{1}{\Delta x\Delta z}\sin (k_{x} \Delta x)\sin (k_{z} \Delta z) \, . \\ \end{aligned}$$

(31)

Then, the 2D differential operators $\tilde{H}_{x}$ and $\tilde{H}_{z}$ are rewritten as

$$\begin{aligned} \tilde{H}_{x} & = \frac{{4\cos^{2} \phi }}{{\Delta x^{2} }}\sin^{2} \left( {\frac{{k_{x} \Delta x}}{2}} \right) + \frac{{4\sin^{2} \phi }}{{\Delta z^{2} }}\sin^{2} \left( {\frac{{k_{z} \Delta z}}{2}} \right) \\ & \quad - \frac{\sin 2\phi }{\Delta x\Delta z}\sin (k_{x} \Delta x)\sin (k_{z} \Delta z) \, , \\ \tilde{H}_{z} & = \frac{{4\sin^{2} \phi }}{{\Delta x^{2} }}\sin^{2} \left( {\frac{{k_{x} \Delta x}}{2}} \right) + \frac{{4\cos^{2} \phi }}{{\Delta z^{2} }}\sin^{2} \left( {\frac{{k_{z} \Delta z}}{2}} \right) \\ & \quad + \frac{\sin 2\phi }{\Delta x\Delta z}\sin (k_{x} \Delta x)\sin (k_{z} \Delta z) \, . \\ \end{aligned}$$

(32)

Substituting Eq. (32) into Eq. (28) and setting $\Delta x = \Delta z = h$, the stability condition becomes

$$\Delta t^{2} \le \frac{{2h^{2} }}{{v_{pz}^{2} \left( {\left( {\frac{1 + \varepsilon }{\varepsilon \sin 2\phi } - \cos (k_{h} h)} \right)^{2} - \left( {\frac{1 + \varepsilon }{\varepsilon \sin 2\phi } - 1} \right)^{2} } \right)\varepsilon \sin 2 \phi }} ,$$

(33)

where $\sin 2\phi > 0$ is assumed, and $k_{h}$ is either $k_{x}$ or $k_{z}$, whichever $\Delta x$ or $\Delta z$ is the smallest $( = h)$. The denominator will be maximal only when $\cos (k_{h} h) = - 1.$ Hence, setting $k_{h} = \pm \pi /h,$ the Nyquist wave number, and replacing $v_{pz}$ with $v_{\hbox{max} }$, we express the stability condition finally as

$$\Delta t \le \frac{h}{{v_{\hbox{max} } \sqrt {2(1 + \varepsilon )} }} ,$$

(34)

where $v_{\hbox{max} }$ is the maximum value of the P-wave velocity along the symmetry axis. Note that the condition of $\varepsilon \ge \delta$ commonly exists and expression (34) is also applicable to parameter $\delta .$

Expression (34) is the stability condition for the $O(\Delta t^{2} , \, h^{2} )$ scheme, the second-order finite-differencing in both time and space. For selecting the time step using this expression, we set $h$ as the smallest cell size of non-rectangular grids generated by body fitting. It is worth mentioning that, setting $\varepsilon = 0$, the stability condition will reduce to the well-known formula of an $O(\Delta t^{2} , \, h^{2} )$ scheme in isotropic media (Lines et al. 1999).

5 Waveform Simulation in TTI Media

Figure 4 demonstrates the waveform simulation in TTI media. This is a homogeneous model (Fig. 4a) with a constant P-wave velocity and constant anisotropy parameters. The objective here is to show that the wave simulation method is able to generate an accurate wavefield, even for a model discretized with non-rectangular grids. The P-wave velocity is $v_{pz} = 2000$ m/s, the S-wave velocity is $v_{sz} = v_{pz} /\sqrt 3$ m/s, the dip angle of the symmetry axis is $\phi = 45^{ \circ } ,$ and the two anisotropy parameters are $\varepsilon = 0.24$ and $\delta = 0.1$.

Fig. 4

Wave simulation in TTI media. a A homogeneous model with constant velocity and anisotropy parameters. The body-fitted grid, plotted by each set of 10 grids, is a well-coincided irregular surface and a curved interface at the middle of model (red curves). b, c The snapshots of the wavefield at 200 ms and 450 ms, respectively, demonstrate that the numerical simulation method with non-rectangular grids is able to produce an accurate wavefield, without any artificial reflections, by strong variation in the cell sizes of body-fitted grids

Figure 4a shows that the body-fitted grids coincide well with the curved surface and a fluctuating interface at the middle of the model, and, meanwhile, there are non-rectangular meshes unavoidably existing on either side of the interface. As long as the media are discretized by body-fitted grids, there is no explicit enforcement of the normal stress and displacement continuity conditions at the interface. In order to avoid any instability caused by the low meshing precision, we adapt a summation-by-parts (SBP) finite-difference method (Kreiss and Scherer 1974; Nilsson et al. 2007) to the case here with the cell size variation of body-fitted grids. We use the finite-difference operators with the second-order accuracy in both temporal and spatial directions. According to Sjögreen and Petersson (2012), the SBP method is automatically stable for partial differential equations with the second-order spatial derivatives. The pseudo-acoustic wave equation is a system of partial differential equations with an initial condition which defines the source signature. For the absorbing boundary, we use the perfectly matched layer method, presented in the computational space, and discretized by finite differencing with a second-order accuracy (Rao and Wang 2013).

The snapshots (Fig. 4b, c) indicate that the non-rectangularity in the mesh does not have visible effect deteriorating wavefield simulation, once the numerical dispersion relation and the stability condition are satisfied. This example demonstrates that this numerical simulation method for a model with such irregular grids is able to produce an accurate wavefield, without any artificial reflections from the interface. In contrast, if using a standard finite-difference method, there must be some artificial reflections caused by strong variation in the cell sizes of body-fitted grids, and even the two-layer velocities are assumed to be constant.

We measure the amplitudes at a number of time samples, and compare them to the theoretical amplitudes as shown in Fig. 5. Measuring along the directions parallel and perpendicular to the TTI symmetry axis ($\phi = 45^{ \circ }$), the theoretical amplitude is $\sqrt {t_{0} /t}$, where $t_{0} = 100$ ms is used in this example. Normalized amplitudes measured at time steps $t =$ 100, 150, 200, 250, 300 ms show minor errors, which probably include picking errors.

Fig. 5

Normalized waveform amplitudes. The red dots are measured amplitudes along the directions parallel and perpendicular to the TTI symmetry axis ($\phi = 45^{ \circ }$). The blue curves are theoretical amplitudes

Figure 6 demonstrates wave simulation in a two-layer TTI media. The P-wave velocities of two layers are 2500 and 3000 m/s. The S-wave velocity is $v_{sz} = v_{pz} /\sqrt 3$ m/s. The rest of the parameters are the same as that used in Fig. 4. The two anisotropy parameters are constant for two layers, $\varepsilon = 0.24$ and $\delta = 0.1$. The dip angle of the symmetry axis is $\phi = 45^{ \circ }$. The body-fitted grid, plotted by each set of 10 grids, is a well-coincided irregular surface and a curved interface at the middle of the model. The snapshots of the wavefield at 350 and 480 ms clearly show reflections from the fluctuating interface.

Fig. 6

Wave simulation in TTI media. a A two-layer model with constant velocity and anisotropy parameters. The body-fitted grid, plotted by each set of 10 grids, is a well-coincided irregular surface and a curved interface at the middle of the model. b, c Snapshots of the wavefield at 350 and 480 ms, respectively. This example clearly shows reflections from fluctuating interface

Note that the geometrical configuration of Figs. 4a and 6a is the same. In waveform simulation, we always implement two steps. In the first step, we use a model with a constant velocity for all layers, such as Fig. 4a, to check the effectiveness of grids. In the second step, we use the proper model with layered velocities, such as Fig. 6a, to generate the desired waveform.

6 Conclusions

For seismic waveform simulation with the TTI wave equation, we have derived a numerical dispersion relation, and demonstrated that the number of sampling points per wavelength has the greatest influence on the dispersion, and both the anisotropic parameters and the mesh rotation angle have little influence on the dispersion. Further, we have derived the condition for the numerical stability for the selection of time step, given the spatial sampling is appropriately selected in Cartesian coordinates. In the derivation, we have used the second-order finite-differencing operators in both time and space and assumed an elliptical anisotropy.

Appendices

Appendix A: P-wave Phase Velocity

The wave equation for the homogeneous anisotropic media, following Newton’s second law, can be represented as (Tsvankin 2001)

$$\rho \frac{{\partial^{2} u_{i} }}{{\partial t^{2} }} = \frac{{\partial \tau_{ij} }}{{\partial x_{j} }} ,$$

(A1)

where $\tau_{ij}$ are the elements of the stress tensor, $x_{j}$ are Cartesian coordinates, $u_{i}$ are the components of the displacement vector, $t$ is time, and $\rho$ is density. According to the generalized Hooke’s law, the stress tensor is linearly related to the strain tensor by $\tau_{ij} = c_{ijm\ell } e_{m\ell }$, where $e_{m\ell }$ are the elements of the strain tensor, and $c_{ijm\ell }$ are the elastic constants in the stiffness tensor. The elements of the strain tensor are defined by $e_{m\ell } = \tfrac{1}{2}(\partial u_{m} /\partial x_{\ell } + \partial u_{\ell } /\partial x_{m} )$. Assuming the elastic constants $c_{ijm\ell }$ are constant in the space, equation (A1) can be written as

$$\rho \frac{{\partial^{2} u_{i} }}{{\partial t^{2} }} - c_{ijm\ell } \frac{{\partial^{2} u_{m} }}{{\partial x_{j} \partial x_{\ell } }} = 0 .$$

(A2)

In this wave equation, the media anisotropy property is accounted for by the stiffness tensor $c_{ijm\ell }$.

Let us present a harmonic plane wave as

$$u = U\exp^{{i\omega (n_{j} x_{j} /v - t)}} ,$$

(A3)

where $n_{j}$ is the direction vector of wave propagation and is normal to the wavefront, $v$ is phase velocity, $\omega$ is angular frequency, and $U$ is the amplitude component of the polarization vector ${\mathbf{U}} = [U_{1} ,U_{2} ,U_{3} ]^{T} .$ The relationship between the phase velocity $v$ and the polarization vector ${\mathbf{U}}$ can be obtained by inserting equation (A3) into equation (A2), as

$$\left[ {\begin{array}{*{20}c} {G_{11} - \rho v^{2} } & {G_{12} } & {G_{13} } \\ {G_{21} } & {G_{22} - \rho v^{2} } & {G_{23} } \\ {G_{31} } & {G_{32} } & {G_{33} - \rho v^{2} } \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {U_{1} } \\ {U_{2} } \\ {U_{3} } \\ \end{array} } \right] = 0 .$$

(A4)

This is the Christoffel equation (Musgrave, 1970), in which the elements in the Christoffel matrix are given by

$$G_{ij} = c_{ijm\ell } n_{i} n_{j} .$$

(A5)

The particular TTI media we study here are the coordinate-transformed VTI (transversely isotropy with a vertical symmetry) media. The elements in the Christoffel matrix of the standard VTI media are

$$\begin{aligned} G_{11} &= c_{11} n_{1}^{2} + c_{66} n_{2}^{2} + c_{55} n_{3}^{2} , \hfill \\ G_{12} &= C_{21} = (c_{11} - c_{66} )n_{1} n_{2} , \hfill \\ G_{13} &= C_{31} = (c_{13} + c_{55} )n_{1} n_{3} , \hfill \\ G_{22} &= c_{66} n_{1}^{2} + c_{11} n_{2}^{2} + c_{55} n_{3}^{2} , \hfill \\ G_{23} &= C_{32} = (c_{13} + c_{55} )n_{2} n_{3} , \hfill \\ G_{33} &= c_{55} (n_{1}^{2} + n_{2}^{2} ) + c_{33} n_{3}^{2} . \hfill \\ \end{aligned}$$

(A6)

As only a single axis of rotational symmetry exists in the isotropic medium, wave propagation can be represented in the $(x_{1} , \, x_{3} )$ plane. That is, $n_{2} = 0.$ Equation (A4), thus, is rewritten as

$$\left[ {\begin{array}{*{20}c} {c_{11} n_{1}^{2} + c_{55} n_{3}^{2} - \rho v^{2} } & {(c_{13} + c_{55} )n_{1} n_{3} } \\ {(c_{13} + c_{55} )n_{1} n_{3} } & {c_{55} n_{1}^{2} + c_{33} n_{3}^{2} - \rho v^{2} } \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {U_{1} } \\ {U_{3} } \\ \end{array} } \right] = 0 .$$

(A7)

This equation describes that $[U_{1} ,U_{3} ]^{T}$ are the eigenvectors corresponding to the two equal eigenvalues $\rho v^{2}$ of the $2 \times 2$ matrix. Solving the following eigenvalue problem,

$$\left| {\begin{array}{*{20}c} {c_{11} n_{1}^{2} + c_{55} n_{3}^{2} - \rho v^{2} } & {(c_{13} + c_{55} )n_{1} n_{3} } \\ {(c_{13} + c_{55} )n_{1} n_{3} } & {c_{55} n_{1}^{2} + c_{33} n_{3}^{2} - \rho v^{2} } \\ \end{array} } \right| = 0 ,$$

(A8)

it produces the P- and SV-wave phase velocities,

$$\begin{aligned} 2\rho v^{2} & = (c_{11} + c_{55} )n_{1}^{2} + (c_{33} + c_{55} )n_{3}^{2} \\ & \quad \pm \{ [(c_{11} - c_{55} )n_{1}^{2} - (c_{33} - c_{55} )n_{3}^{2} ]^{2} \\ & \quad + 4(c_{13} + c_{55} )^{2} n_{1}^{2} n_{3}^{2} \}^{1/2} . \\ \end{aligned}$$

(A9)

Sign “+” in front of the curved brackets represents the P-wave phase velocity, while sign “–” in front of the curved brackets represents the SV-wave phase velocity. When $n_{1} = 0$ and $n_{3} = 1$, the P-wave and SV-wave phase velocities along the z axis are $v_{pz} = \sqrt {c_{33} /\rho }$ and $v_{sz} = \sqrt {c_{55} /\rho }$, respectively.

Given $n_{1} = \sin \theta$ and $n_{3} = \cos \theta$, where $\theta$ is the phase angle, and using Thomsen’s anisotropy parameters,

$$\varepsilon = \frac{{c_{11} - c_{33} }}{{2c_{33} }},\quad \delta = \frac{{(c_{13} + c_{55} )^{2} - (c_{33} - c_{55} )^{2} }}{{2c_{33} (c_{33} - c_{55} )}},$$

(A10)

the P-wave phase velocity is presented as

$$\begin{aligned} \frac{{v^{2} (\theta )}}{{v_{pz}^{2} }} & = 1 - \frac{L}{2} + \varepsilon \sin^{2} \theta + \frac{L}{2}\left( {1 + \frac{{4\varepsilon^{2} \sin^{4} \theta }}{{L^{2} }}} \right. \\ &\quad \left. { + \frac{{4\sin^{2} \theta }}{L}(2\delta \cos^{2} \theta - \varepsilon \cos 2\theta )} \right)^{1/2} , \\ \end{aligned}$$

(A11)

where $L = 1 - {{v_{sz}^{2} } \mathord{\left/ {\vphantom {{v_{sz}^{2} } {v_{pz}^{2} }}} \right. \kern-0pt} {v_{pz}^{2} }}$. This equation is used as Eq. (17) in the main text.

Appendix B: The Pseudo-acoustic Wave Equation

Note that the phase angle $\theta$ is the wave vector with respect to the symmetry axis $\hat{z}.$ Therefore, the phase angle $\theta$ and phase velocity $v(\theta )$ are related to the wavenumber components by

$$\sin^{2} \theta = \frac{{\hat{k}_{x}^{2} }}{{\hat{k}_{x}^{2} + \hat{k}_{z}^{2} }},\,\quad \cos^{2} \theta = \frac{{\hat{k}_{z}^{2} }}{{\hat{k}_{x}^{2} + \hat{k}_{z}^{2} }},\,\quad v^{2} (\theta ) = \frac{{\omega^{2} }}{{\hat{k}_{x}^{2} + \hat{k}_{z}^{2} }},$$

(B1)

where $\hat{k}_{x}$ and $\hat{k}_{z}$ are the wavenumber components when the TTI symmetry axis is rotated (Fig. 1), and $\omega$ is the angular frequency. Equation (A11) then becomes

$$\begin{aligned} \omega^{4} &= v_{pz}^{2} [(2 - L)(\hat{k}_{x}^{2} + \hat{k}_{z}^{2} ) + 2\varepsilon \hat{k}_{x}^{2} ]\omega^{2} \\ & \quad + v_{pz}^{4} (1 + 2\varepsilon )(L - 1)\hat{k}_{x}^{4} + v_{pz}^{4} (L - 1)\hat{k}_{z}^{4} \\ & \quad + 2v_{pz}^{4} [(1 + \delta )L - (1 + \varepsilon )]\hat{k}_{x}^{2} \hat{k}_{z}^{2} \\ \end{aligned}$$

(B2)

Substituting $L$ into equation (B2), one obtains

$$\begin{aligned} \omega^{4} &= \{ [(1 + 2\varepsilon )v_{pz}^{2} + v_{sz}^{2} ]\hat{k}_{x}^{2} + (v_{pz}^{2} + v_{sz}^{2} )\hat{k}_{z}^{2} \} \omega^{2} \\& \quad - (1 + 2\varepsilon )v_{pz}^{2} v_{\text{sz}}^{2} \hat{k}_{x}^{4} - v_{pz}^{2} v_{sz}^{2} \hat{k}_{z}^{4} \\ & \quad + 2v_{pz}^{2} [(\delta - \varepsilon )v_{pz}^{2} - (1 + \delta )v_{sz}^{2} ]\hat{k}_{x}^{2} \hat{k}_{z}^{2} . \\ \end{aligned}$$

(B3)

Finally, denoting $v_{px}^{2} = (1 + 2\varepsilon )v_{pz}^{2}$ and $v_{pn}^{2} = (1 + 2\delta )v_{pz}^{2}$, we present the dispersion relation in TTI media as

$$\begin{aligned} \omega^{4} &= [(v_{px}^{2} + v_{sz}^{2} )\hat{k}_{x}^{2} + (v_{pz}^{2} + v_{sz}^{2} )\hat{k}_{z}^{2} ]\omega^{2} \\& \quad - v_{px}^{2} v_{sz}^{2} \hat{k}_{x}^{4} - v_{pz}^{2} v_{sz}^{2} \hat{k}_{z}^{4} \\ & \quad + [v_{pz}^{2} (v_{pn}^{2} - v_{px}^{2} ) - v_{sz}^{2} (v_{pn}^{2} + v_{pz}^{2} )]\hat{k}_{x}^{2} \hat{k}_{z}^{2} \, . \\ \end{aligned}$$

(B4)

Assuming the rotation angle of the symmetry axis to be $\phi ,$ the rotated wavenumber components are

$$\begin{aligned} \hat{k}_{x} = k_{x} \cos \phi - k_{z} \sin \phi , \hfill \\ \hat{k}_{z} = k_{x} \sin \phi + k_{z} \cos \phi , \hfill \\ \end{aligned}$$

(B5)

where $k_{x}$ and $k_{z}$ are the wavenumbers in Cartesian coordinates.

Denoting $f_{z} = \hat{k}_{z}^{2}$ and $f_{x} = \hat{k}_{x}^{2}$, we express equation (B4) as

$$\begin{aligned} \omega^{4}& =[(v_{px}^{2} + v_{sz}^{2} )f_{x} + (v_{pz}^{2} + v_{sz}^{2} )f_{z} ]\omega^{2} \\ & \quad - v_{px}^{2} v_{sz}^{2} f_{x}^{2} - v_{pz}^{2} v_{sz}^{2} f_{z}^{2} \\ & \quad + [v_{pz}^{2} (v_{pn}^{2} - v_{px}^{2} ) - v_{\text{sz}}^{2} (v_{pn}^{2} + v_{pz}^{2} )]f_{x} f_{z} \, , \\ \end{aligned}$$

(B6)

and the two f factors are

$$\begin{aligned} f_{x} &= k_{x}^{2} + k_{z}^{2} - f_{z} , \hfill \\ f_{z} &= k_{x}^{2} \sin^{2} \phi + k_{z}^{2} \cos^{2} \phi + k_{x} k_{z} \sin 2\phi \, . \hfill \\ \end{aligned}$$

(B7)

Setting an auxiliary wavefield as

$$q(\omega ,k_{x} ,k_{z} ) = \frac{{(v_{pn}^{2} - v_{sz}^{2} )f_{x} }}{{\omega^{2} - v_{sz}^{2} f_{x} - v_{pz}^{2} f_{z} }}p(\omega ,k_{x} ,k_{z} ) ,$$

(B8)

equation (B6) can be rewritten after multiplying both sides by the pressure wavefield

$$\begin{aligned} \omega^{2} p(\omega ,k_{x} ,k_{z} ) & = v_{px}^{2} f_{x} p(\omega ,k_{x} ,k_{z} ) \\ & \quad + v_{sz}^{2} f_{z} p(\omega ,k_{x} ,k_{z} ) \\ & \quad + (v_{pz}^{2} - v_{sz}^{2} )f_{z} q(\omega ,k_{x} ,k_{z} ). \\ \end{aligned}$$

(B9)

Applying an inverse Fourier transform to equations (B8) and (B9), we obtain the pseudo-acoustic wave equation in TTI media [Eq. (1) in the main text]:

$$\frac{{\partial^{2} }}{{\partial t^{2} }}\left( {\begin{array}{*{20}c} {p} \\ {q} \\ \end{array} } \right) = \left[ {\begin{array}{*{20}c} {v_{px}^{2} H_{x} + v_{sz}^{2} H_{z} } & {(v_{pz}^{2} - v_{sz}^{2} )H_{z} } \\ {(v_{pn}^{2} - v_{sz}^{2} )H_{x} } & {v_{sz}^{2} H_{x} + v_{pz}^{2} H_{z} } \\ \end{array} } \right]\left( {\begin{array}{*{20}c} {p} \\ {q} \\ \end{array} } \right) .$$

(B10)

Applying an inverse Fourier transform to Eq. (B7), we obtain the two differential operators $H_{x}$ and $H_{z}$ presented as Eq. (2) in the main text.