1 Introduction

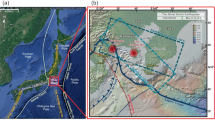
The northeast coast of South Island, New Zealand, was ruptured by a large earthquake (M w 7.8) on 13 November 2016 (UTC) which is widely known as the Kaikoura earthquake (Fig. 1). The United States Geological Survey (USGS) reported the epicenter of the earthquake at 173.054°E and 42.737°S, and its origin time at 11:02:56 UTC, at a depth of 15.1 km. The respective values from the GeoNet, which is the official source of geological hazard information in New Zealand, were 173.02°E and 42.69°S, 11:02:56 UTC and 15 km. The earthquake origin time was just after midnight (0:02:56) of 14 November in local time. Two deaths were reported due to the 2016 earthquake. The epicenters of the past three large earthquakes with moment magnitudes of 7.5 (in 1848), 7.0–7.3 (in 1888), and 7.0 (in 2010) are located ~100 km to the NE, ~50 km to the NW, and ~120 km SW of the 2016 Kaikoura epicenter, respectively (stars in Fig. 1). The other recent tsunamigenic earthquake in New Zealand occurred on 15 July 2009 in the southwest of the South Island (Fig. 1).

Fig. 1
figure 1

Epicentral area of the 13 November 2016 New Zealand tsunamigenic earthquake and location of sea-level stations used in this study (dark-blue rectangles). Dashed contours show tsunami travel times (TTT) in hours calculated using TTT program (Geoware 2011). Epicenters and information of the 1848 and 1888 earthquakes are from the New Zealand GeoNet catalogue and Cowan and McGlone (1991), respectively; other epicenters, mechanisms, as well as the 1-day aftershocks are from USGS

Full size image

The USGS W-phase moment-tensor solution resulted in an oblique thrust fault mechanism including a right-lateral strike-slip component for the 2016 event (strike 219°, dip 38°, rake 128°) (mechanism shown in Fig. 1), which is close to the mechanism reported by Global CMT (strike 226°, dip 33°, rake 141°). Hollinsworth et al. (2017) reported a focal mechanism similar to Global CMT. Detailed mechanism solution by Duputel and Rivera (2017) revealed that the initial part of the rupture was of strike-slip type followed by large ruptures both on strike-slip and thrust faults. The earthquake was associated with major surface deformation in the form of uplift and subsidence on several inland and onshore faults (at least 12 major faults, Hamling et al. 2017) and an extensive coastal area was exposed to air due to co-seismic uplift (e.g., Hamling et al. 2017). According to various media and expert reports, tens of thousands of landslides of various sizes were observed following the earthquake (e.g., Massey et al. 2017). In terms of surface deformation, obviously the Kaikoura earthquake was among the most complex earthquakes worldwide. Aftershocks were distributed toward the NE of the epicenter (Fig. 1). The earthquake was followed by a tsunami reaching a maximum runup height of around 7 m in the near field (Power et al. 2017; Bradley et al. 2017), although the maximum zero-to-crest tide gauge height observed at the near-field station of Kaikoura was ~2.6 m (Fig. 3). Other tide gauges recorded zero-to-crest heights of: 0.67 m (in Sumner), 0.4 m (in Wellington), 0.2 m (in Castlepoint), and 0.16 m (in Chatham Island) (see Fig. 1 for the locations and Fig. 3 for the wave records). GeoNet reported tsunami runup heights of 4.1 and 4.4 m in the near field which caused some small damage to property with no death (Lane et al. 2017).

In terms of regional tectonic setting, the 2016 Kaikoura earthquake occurred in one of the world’s complex tectonic settings comprising a transition zone between two subduction zones connecting the Australian and Pacific plates: Puysegur Trench in the south and Hikurangi and Kermadec Trenches in the north (Fig. 1). The area is home to many faults with dominating strike-slip mechanisms among which is the Hope fault (Fig. 1), located close to the 2016 epicenter. However, the Hope fault was not the only one responsible for the 2016 rupture; field observations revealed evidence for rupture on various faults (Hamling et al. 2017).

Here, we characterize the 2016 Kaikoura tsunami by analyzing the physical properties of the tsunami, namely amplitude and period, using available tsunami observations. We then perform numerical simulations to shed light on the type of the tsunami source and to study tsunami propagation in the region.

2 Data and Methods

Tsunami data used in this study include nine tide gauge records with sampling interval of 1 min (see Fig. 1 for locations). The data were provided by the Intergovernmental Oceanographic Commission of UNESO sea-level monitoring facility (http://www.ioc-sealevelmonitoring.org/). To obtain tsunami waveforms, tidal signals were calculated by applying the TidalFit package of Grinsted (2008) and then removed from the tsunami records. Spectral analysis of tsunami waveforms was performed using the Welch’s (1967) averaged modified-periodogram method. Wavelet, time–frequency, analysis was conducted applying the program provided by Torrence and Compo (1998) using the Morlet mother function having a wavenumber of 6 and a scale width of 0.10. We applied the numerical model of Satake (1995) for tsunami propagation with the initial seafloor deformation calculated by the analytical formula of Okada (1985). Time step for tsunami simulation was 1 s for a total simulation time of 8 h. Bathymetry data used for tsunami simulations is from General Bathymetric Charts of the Oceans (GEBCO, Weatherall et al. 2015) having a resolution of 30 arcsec.

Three different earthquake source models (slip models) are used in this study, called earthquake models, EMs, for simplicity hereafter (Fig. 2). EM1 is from USGS (the revised source model) including five fault planes, covering both crustal and plate–boundary (interface) slips: the northernmost shallow strike-slip fault (dip = 70°), shallow thrust fault (dip = 70°), deep oblique thrust fault (dip = 35°), and the southernmost strike-slip fault (dip = 70°) (Fig. 2a). The maximum slip value is 5.2 m (USGS 2017). Source models EM2 and EM3 are both from GNS Science (New Zealand) (Hamling et al. 2017); the former model considers only crustal slip, while the latter is based on slips on both crustal and plate-interface faults. The crustal model, EM2, takes into account slips on 19 faults located in the region with varying geometries and tectonic properties (strike, dip, and slip angles) whose maximum slip is 24.1 m (Fig. 2b). The combined crustal-interface model, EM3, adds a plate–boundary interface fault to EM2 with a maximum slip of 24.9 m (Fig. 2c). EM1 is based on seismic body-wave inversions, while EM2 and EM3 are based on geodetic and coastal uplift inversions. To obtain EM2 and EM3, two independent inversions were conducted for two different fault setups (i.e., with and without plate-interface fault). The plate-interface component of EM3 is mostly located inland (Fig. 2d); thus, it is not able to directly contribute to tsunami generation.

Fig. 2
figure 2

Various earthquake models. a EM1 including both crustal and plate-interface slips from USGS. b EM2 consisting of only crustal slips from GNS Science (Hamling et al. 2017). c EM3 adds a plate-interface slip on top of the EM2 from GNS Science (Hamling et al. 2017). d The plate-interface component of EM3

Full size image

3 Tsunami Waveforms and Physical Properties

3.1 Tsunami Waveforms

The tsunami signal was not detectable at two tide gauge stations of Puysegur and East Cape, located at southernmost and northeasternmost New Zealand, respectively (Fig. 1). This is an indication of the limitation of tsunami’s reach in the region and that the tsunami was not very strong. The maximum zero-to-crest amplitude was 257 cm recorded at the Kaikoura tide gauge station (Fig. 3), located within the co-seismic uplift zone (Fig. 6). The tide gauge station was uplifted ~1 m due to the earthquake based on the tidal levels before and after the earthquake (Fig. 3, left panel). It is worth noting that the maximum tsunami amplitude (point B in Fig. 3) was only ~20 cm larger than the normal high tidal level before the earthquake (point A in Fig. 3). At Sumner, the second closest tide gauge station to the earthquake source, the largest tsunami amplitude was recorded about 4 h after the earthquake origin time with zero-to-crest amplitude of 67 cm. At Wellington, with a similar distance, the tsunami amplitude was 40 cm, while Castlepoint, located further north, recorded wave amplitude of 20 cm. Arrivals of long tsunami waves are clear at Port Napier at around 15 h on 13 November, whereas tsunami signal cannot be easily distinguished from the background signal at Gisborne tide gauge station. In the southern station of Dunedin, the tsunami signal can be identified from the background signal, but the amplitudes are small (less than 3 cm). Chatham Island, located ~800 km to the east of the epicenter (Fig. 1), registered maximum tsunami amplitude of 13 cm. The tide gauge data reveal that the largest tsunami amplitudes were recorded to the north of the epicenter.

Fig. 3
figure 3

Tsunami data. Left original tsunami records on tide gauges (black) with tide predictions shown in pink. The area in blue rectangle is the part of the data shown in the middle panel. Middle de-tided signals. Right the 5-h part of the de-tided tsunami signals

Full size image

3.2 Tsunami Spectra

Figure 4 shows the tsunami spectra (Fig. 4a), spectral ratios (Fig. 4b), and averaged spectral ratio for the tsunami (Fig. 4c). To separate tsunami periods from the background, we apply the concept of spectral ratio (power of tsunami signals divided by that of background signals), first developed by Rabinovich (1997) and applied by Rabinovich et al. (2013), Heidarzadeh and Satake (2014), Vich and Monserrat (2009), and Heidarzadeh et al. (2016). Spectral ratios (Fig. 4b) indicate that tsunami energy is concentrated at periods <56 min; they also show two tsunami peak period bands. Such dual-peak tsunami spectrum, in which the second peak is located at the period band of 3.6–5.7 min, is unusual for purely tectonic tsunamis. Out of six spectral ratio plots shown in Fig. 4b, five revealed clear peaks at the band of 3.6–5.7 min (except for Wellington). We note that none of the major peaks in Fig. 4b can be attributed to the harbor resonant modes, because such modes are removed from spectral ratio plots as they exist in both tsunami and background signals. To better visualize the mentioned dual-peak tsunami spectrum, we averaged the spectral ratio plots (Fig. 4c). Two major peak periods are observed at 19 and 4.2 min with clear cutoff periods at 5.7 and 3.6 min. While the longer-period band of 5.7–56 min is attributed to the tectonic source of the tsunami, the shorter-period band of 3.6–5.7 min can be related to a more confined source which could be a co-seismic submarine landslide source. As thousands of landslides were observed following the 2016 Kaikoura earthquake, it is possible that some undersea slope failures also were involved although no marine geological investigation has been published yet (as of May 2017). Walters et al. (2006) reported substantial potential for underwater landslides offshore Kaikoura. The pattern of the dual-peak spectra obtained for this tsunami is similar to that previously reported for the famous 1998 Papua New Guinea earthquake–landslide tsunami (Heidarzadeh and Satake 2015a) and is opposed to that of tectonic tsunamis such as the 2009 Samoa and 2010 Maule (Chile) tsunamis as reported by Rabinovich et al. (2013).

Fig. 4
figure 4

a Fourier analysis of the tsunami signals. Solid and dashed lines represent the spectra for tsunami and background signals, respectively. Part of the waveform before the arrival of tsunami at each station was used as the background signal. b Spectral ratio (power of tsunami signals divided by that of background signals). The plots in various stations are normalized at their maximum values. c The averaged spectral ratio. The cyan and yellow painted areas represent the spectra of earthquake- and landslide-generated waves. EQ and LS stand for earthquake and landslide, respectively

Full size image

Using the water depth of 100–500 m for the offshore area and applying the tsunami phase velocity equation (Eq. 5 in Heidarzadeh and Satake 2015b), the dominant period of 19 min implies a source dimension of 18–40 km for the tectonic source of the tsunami. The landslide source dimension is estimated at 8–10 km by using the dominant period of 4.2 min and the water depth at offshore slopes (i.e., 400–600 m).

3.3 Wavelet Analysis

Wavelet analyses were performed for three near-field stations of Kaikoura, Sumner, and Wellington (Fig. 5). While the Fourier analysis performed in the previous section provides information about the spectral content of potential landslide-generated waves (i.e., 3.6–5.7 min), it does not identify the timing of these short-period waves because Fourier analysis is a time-independent analysis. Wavelet plots demonstrate the tsunami energy evolution at both frequency and time domains (Fig. 5). Patches of tsunami energy at the short-period band of 3.6–5.7 min are clear at two stations of Kaikoura (Fig. 5b) and Sumner (Fig. 5d), while they are not very strong at Wellington (Fig. 5f). Such patches occur around 20–40 and 120–150 min after the earthquake origin time at Kaikoura and Sumner, respectively (dashed circles in Fig. 5), which are indicative of the arrival times of landslide-generated waves at these stations. The potential landslide-generated waves may have been filtered out by bathymetric features before arriving at the Wellington station, and thus are of weak strength.

Fig. 5
figure 5

Wavelet analyses for three near-field tide gauge observations of 13 November 2016 Kaikoura tsunami (b, d, f) along with the respective tide gauge time series (a, c, e)

Full size image

4 Tsunami Simulations and Discussion

4.1 Tsunami Source

Figure 6 compares the seafloor deformations and simulated tsunami waveforms from three earthquake source models (EMs) with observed waveforms. Seafloor deformation from EM1 is significantly different from that of EM2 and EM3, both in terms of maximum uplift and spatial distribution of co-seismic deformation (Figs. 2, 6a). EM1 gives maximum uplift of 1.2 m at the onshore area and is extended ~20 km to the offshore region, whereas EM2 and EM3 produce a maximum uplift of 8 m at the inland area and their co-seismic uplift is mostly limited inland.

Fig. 6
figure 6

a Seafloor deformation from three different earthquake models (EMs) for the 13 November 2016 earthquake, namely EM1 from USGS, EM2 from GNS Science (only crustal slip), and EM3 from GNS Science (both crustal and plate-interface slips). b Results of tsunami simulations for various EMs (color) and comparison with observations (black)

Full size image

No single earthquake model provides a perfect match with the tsunami observations (Fig. 6b). However, the combination of these three simulations gives insights into the anatomy of the tsunami source. As the 2016 tsunami was not large enough, we look at three near-field tide gauge stations of Kaikoura, Sumner, and Wellington to compare the performance of the source models. In Kaikoura, the simulations from EM1 catch the first and second elevation waves in terms of amplitudes, but the period of the simulated tsunami is noticeably longer than that of observation. The simulated waves from EM2 and EM3 fail to reproduce the first peak, the largest amplitude of the observed tsunami. However, the later waves are reproduced well in terms of amplitude and period. In Sumner, all three models fairly reproduce the longer-period component (period >20 min) of the observations, but fail to reproduce the initial short-period waves (period <5 min). Only EM2 is capable of reproducing the largest amplitude, but it occurs ~50 min earlier than the observations. In Wellington, EM1 produces poor match with the observation in terms of both amplitude and period. The simulations from EM2 and EM3 match with the observation (Table 1).

Table 1 Source characterization and comparison of the observed and simulated waves from various earthquake models
Full size table

The EM2 and EM3 models produce similar tsunami waveforms because the plate-interface component of EM3 is located inland; hence, both models produce almost similar seafloor deformation. In other words, both EM2 and EM3 lack significant offshore uplift. The EM1 model can fairly reproduce the first peak (in terms of amplitude) because the seafloor uplift from this model is extended ~20 km to the offshore region, but it produces longer-period waves than observations. This result may indicate that an offshore forcing is necessary to be involved to reproduce the first peak in Kaikoura, but the offshore component needs to be smaller in size than the modeled offshore interplate fault. The most likely possibility for such a small-area offshore component is a submarine landslide as a potential secondary source. Tens of thousands of seismically triggered landslides have been recorded on land; hence submarine landslides may have been triggered as well. Landslide-generated waves are usually short-period waves with local and contained impacts whose signature cannot be easily found on seismic observations (Tappin et al. 2001; Synolakis et al. 2002; Fritz et al. 2004; Geist et al. 2009; Heidarzadeh et al. 2014; Heidarzadeh and Satake 2015a). The secondary landslide source hypothesis can be supported by the dual-peak tsunami spectrum shown in Fig. 4c. To confirm this, we also made Fourier analysis for the simulated waves from three EMs (Fig. 7). They revealed spectral energy deficits for the simulated waves in the period band of 3.6–5.7 min, indicating that simulations from fault models, either crustal or plate interface, lack dominant period band of 3.6–5.7 min.

Fig. 7
figure 7

Comparison of spectra of observed tsunami waveforms (black plots) with those of simulated ones (colored plots) at various tide gauge stations

Full size image

The contribution of plate-interface slip to the 2016 Kaikoura earthquake is not clear yet (as of May 2017). Since the occurrence of this event, there have been contradicting ideas about whether the earthquake ruptured the plate interface or not. Geodetic and coastal-uplift inversion by Hamling et al. (2017) showed that inclusion or exclusion of plate-interface slip does not change the results of inversion (i.e., the misfit between observation and simulations remains similar in both cases). Tsunami simulations conducted here indicates that an offshore plate-interface slip (as seen in EM1) is unlikely to be involved because it produces longer-period waves than tsunami observations. However, tsunami simulation is not capable of providing insights about the involvement of an inland plate-interface slip (as seen in EM3).

4.2 Regional Tsunami Propagation

Figure 8 shows snapshots of tsunami propagation (Fig. 8a) and maximum tsunami amplitudes (Fig. 8b). Most of the tsunami amplitude is confined between the east coast of New Zealand and the Chatham Island. The shallow sea in between, which is the result of the Chatham Rise and the shallow areas to the south (see Fig. 1 for location), prevents efficient propagation of the tsunami to the far field. The tsunami is funneled along the Chatham Rise to the Chatham Island (Fig. 8b). These bathymetric features confine the waves within the shallow areas near the coasts and are responsible for the creation of long-lasting edge waves. In addition to the relatively small size of the tsunami, this is possibly another reason that the tsunami was not detectable in the two southernmost and northeasternmost stations of Puysegur and East Cape (Fig. 1).

Fig. 8
figure 8

a Snapshots of tsunami simulations at different times for the 13 November 2016 tsunami. b Maximum tsunami amplitude. The tsunami simulation results from source EM3 is used for generating this figure

Full size image

5 Conclusions

We studied the 13 November 2016 Kaikoura, New Zealand tsunami through waveform analysis and numerical simulations. The main findings are:

  1. 1.

    Waveform analysis revealed that zero-to-crest tsunami amplitude was 257 cm at the Kaikoura tide gauge station, located within the co-seismic uplift zone; it was 67, 40, and 20 cm at the Sumner, Wellington and Castlepoint stations, respectively, located close to the rupture zone. Chatham Island tide gauge station, ~800 km to the east of epicenter, received tsunami amplitude of 13 cm. Most of the tsunami was confined within the shallow area between the east coast of New Zealand and Chatham Island which can be attributed to the presence of Chatham Rise in the region.

  2. 2.

    Fourier analysis revealed a dual-peak tsunami spectrum with two major peak periods of 4.2 and 19 min with a cutoff period of 5.7 min. The two major tsunami energy period bands are 3.6–5.7 and 5.7–56 min, which we attribute to potential landslide and earthquake sources of the tsunami, respectively. The timing of the potential landslide-generated waves was revealed by wavelet analysis. We estimate the dimension of the potential submarine landslide at 8–10 km.

  3. 3.

    Tsunami simulations reveal that a tsunami source with offshore plate-interface slip reproduces the near-field tsunami observation in terms of amplitude, but fails in terms of tsunami period by producing longer-period waves. On the other hand, a tsunami source without offshore plate-interface slip fails to reproduce the first (and the largest) peak of the tsunami observed in the near field, but matches fairly well both in terms of amplitude and period for the later waves. Tsunami simulation may indicate that an offshore forcing is necessary to be involved, but it needs to be smaller in size which most likely points to a confined submarine landslide source. This is consistent with the dual-peak tsunami spectrum of the observed tsunami waveforms. Furthermore, Fourier analysis for the simulated waves revealed spectral energy deficits for the simulated waves in the period band of 3.6–5.7 min, indicating that simulations lack a confined source with dominant period band of 3.6–5.7 min.