Abstract
Toeplitz matrices are typically non-Hermitian and hence they evade the well-elaborated machinery one can employ in the Hermitian case. In a pioneering paper of 1960, Palle Schmidt and Frank Spitzer showed that the eigenvalues of large banded Toeplitz matrices cluster along a certain limiting set which is the union of finitely many closed analytic arcs. Finding this limiting set nevertheless remains a challenge. We here present an algorithm in the spirit of Richard Beam and Robert Warming that reduces testing \(O(N^2)\) points in the plane for membership in the limiting set by testing only O(N) points along a one-dimensional curve. For tetradiagonal Toeplitz matrices, we describe all types of the limiting sets, we classify their exceptional points, and we establish asymptotic formulas for the analytic arcs near their endpoints.
Similar content being viewed by others
1 Introduction
It is well known that the properties of truncated \(n \times n\) Toeplitz matrices
as n goes to infinity are captured by the series \(a(z)=\sum _{j=-\infty }^\infty a_j z^j\) (\(z \in \mathbb {C}\)). We therefore denote the matrix (1.1) by \(T_n(a)\). The first Szegő limit theorem [12] describes the asymptotic eigenvalue distribution of \(T_n(a)\) in the case where the restriction of a to the complex unit circle \({\mathbb {T}}\) is (the Fourier series of) a real-valued \(L^\infty \) function. More recent studies extend this to real-valued \(L^1\) functions and even more general Hermitian situations; see, e.g., [6, 14,15,16]. The problem is of a completely different nature if the restriction \(a|{\mathbb {T}}\) is complex-valued. Here the path-breaking result is due to the 1960 paper [10] by Schmidt and Spitzer.
Thus, let us consider the banded Toeplitz matrix
Throughout what follows we always assume that \(a_j \in \mathbb {C}\), \(r \ge 1\), \(s \ge 1\), \(a_{-r} \ne 0\), and \(a_s \ne 0\). Schmidt and Spitzer [10] showed that the set \(\sigma (T_n(a))\) of the eigenvalues of \(T_n(a)\) converges in the Hausdorff metric to some limiting set \(\Lambda (a)\) which is the union of finitely many analytic arcs and their endpoints and which does not contain isolated points. Ullman [17] later proved that \(\Lambda (a)\) is connected.
It is tempting to say that once we know that the limiting set exists, we could simply compute the eigenvalues of \(T_n(a)\) for \(n=100\) and this should give a good approximation to \(\Lambda (a)\). Well, let
We thus have a pentadiagonal matrix. Figure 1a shows the curve \(a({\mathbb {T}})\) and the eigenvalues of \(T_{100}(a)\) delivered by Matlab. Clearly, part of the eigenvalues are erroneous. Even after zooming in it is impossible to guess what \(\Lambda (a)\) is.
Already Schmidt and Spitzer employed the key trick with banded Toeplitz matrices: namely, if \(D_\varrho =\mathrm{diag}(\varrho ^{j-1})_{j=1}^n\), then
and hence \(T_n(a)=(a_{j-k})_{j,k=1}^n\) and \((\varrho ^{j-k}a_{j-k})_{j,k=1}^n\) have the same eigenvalues. The last matrix may be written as \(T_n(a_\varrho )\) with \(a_\varrho (z)=\sum _{j=-r}^s \varrho ^j a_jz^j\). Figure 1b–d shows \(a_\varrho ({\mathbb {T}})\) and the (in part erroneous) eigenvalues of \(T_{100}(a_\varrho )\) computed with Matlab for three choices of the parameter \(\varrho \). Without knowing more on \(\Lambda (a)\) it is difficult to make a reliable guess.
Let us turn to the tetradiagonal case. A subset of \(\mathbb {C}\) consisting of two distinct points \(\mu ,\nu \in \mathbb {C}\) and an analytic arc (without self-intersection) joining these two points will be denoted by \([\mu \sim \nu ]\). Part of our main result is as follows.
Let \(\gamma \) be the piece of the curve \(\{b \in \mathbb {C}: |1+b|=2|b|^2\}\) that lies in the closed disk \(\{b \in \mathbb {C}: |1+b| \le 1\}\) (see Fig. 7) and let \(\Gamma \) be the curve
The ± indicates that we take both values of \((1+b+b^2)^{3/2}\). The curve \(\Gamma \) is the boundary of the blue domain \(\Omega \) shown in Fig. 2. The two red points are \(\pm 3\sqrt{3}\) and they correspond to \(b=-1/2 \in \gamma \).
As will be seen below, the key trick allows us to assume without loss of generality that \(a(z)=z^2+cz+cz^{-1}\) with \(c \in \mathbb {C}{\setminus } \{0\}\). Denote the roots of \(a'(z)=0\) by \(t_1,t_2,t_3\) and order them so that \(|t_3| \le |t_2| \le |t_1|\). Put \(\lambda _k=a(t_k)\). Then \(\Lambda (a)\) is a set of one of the following types. If c is in the interior of \(\Omega \), then the three points \(\lambda _1,\lambda _2,\lambda _3\) are distinct and
the three arcs intersect only in \(\lambda _0\). If c lies on the boundary of the set \(\Omega \), then \(\Lambda (a)=[\lambda _1 \sim \lambda _2] \cup [\lambda _1\sim \lambda _3]\); if \(c=\pm 3\sqrt{3}\), then \(\lambda _1 = \lambda _2 \ne \lambda _3\) and \(\Lambda (a)\) is actually the straight line segment \([\lambda _2,\lambda _3]\), while if \(c \ne \pm 3\sqrt{3}\), the three points \(\lambda _1,\lambda _2,\lambda _3\) are distinct and the two arcs intersect only in \(\lambda _1\), making there a cusp. Finally, if c is outside the closed set \(\Omega \), then \(\lambda _2 \ne \lambda _3\) and \(\Lambda (a)=[\lambda _2 \sim \lambda _3]\). Figure 3 shows some examples along with the eigenvalues of \(T_{60}(a)\).
Schmidt and Spitzer [10] gave two descriptions of the limiting set \(\Lambda (a)\). First, they showed that
where \(\sigma (T(a_\varrho ))\) is the spectrum of the Toeplitz operator generated by the infinite Toeplitz matrix \((\varrho ^{j-k}a_{j-k})_{j,k=1}^\infty \) on \(\ell ^2\). Note that \(\sigma (T(a_\varrho ))\) is just the union of the curve \(a_\varrho ({\mathbb {T}})\) and the points in the plane about which this curve has nonzero winding number. For the second description, pick \(\lambda \in \mathbb {C}\), consider the equation \(a(z)=\lambda \) (which after multiplication by \(z^r\) becomes an equation with an algebraic polynomial of degree \(r+s\)), and order the solutions \(z_j(\lambda )\) (\(j=1, \ldots , r+s\)) of this equation so that
Then \(\lambda \in \Lambda (a)\) if and only if \(|z_r(\lambda )|=|z_{r+1}(\lambda )|\).
The original reasoning of Schmidt and Spitzer was significantly simplified and accompanied with the density function for the eigenvalues along \(\Lambda (a)\) by Hirschman [7] and Widom [18, 19]; see also Chapter 11 of [2]. A new view at the matter is given by Duits and Kuijlaars in [5]. We should also note that in the tridiagonal case \(a(z)=a_1z+a_0+a_{-1}z^{-1}\) we have
If \(a(z)=\sum _{j=-r }^s a_jz^j\) takes only real values on \({\mathbb {T}}\), then
Recently, Shapiro and Štampach [11] very beautifully characterized the Laurent polynomials for which \(\Lambda (a)\) is a subset of the real line \({\mathbb {R}}\): this happens if and only if the pre-image \(a^{-1}({\mathbb {R}})\) contains a Jordan curve. We refer to the books [2, 3, 6, 8] for more on the eigenvalue cluster problem for Toeplitz matrices. An analogue of the Schmidt-Spitzer result for Wiener-Hopf integral operators is in [4]. We also want to mention the message of [9, 13] according to which in certain problems the eigenvalues of non-normal operators may drastically mislead us.
Finally, recall that \(T_n(a)\) and \(T_n(a_\varrho )\) have the same eigenvalues. It follows in particular that
If \(a_1=0\), this reads
and taking \(\varrho \) so that \(\varrho ^2a_2=\varrho ^{-1}a_{-1}\), we obtain that
which leads to a concrete single case. If \(a_1 \ne 0\), we choose \(\varrho \) so that \(\varrho a_1=\varrho ^{-1}a_{-1}\) and get
with \(c={\varrho a_1}/({\varrho ^2 a_2})={\varrho ^{-1}a_{-1}}/({\varrho ^2 a_2})\). The limiting set \(\Lambda (z^2+z^{-1})\) was already determined by Schmidt and Spitzer: it is the star-shaped set
Thus, we are left with the one-parameter family \(T_n(z^2+cz+cz^{-1})\), \(c \in \mathbb {C}{\setminus } \{0\}\).
2 An Algorithm for Calculating the Limiting Set
The algorithm presented here is based on looking at the algorithm designed by Beam and Warming in [1] from a different perspective.
A point \(\lambda \) is in \(\Lambda (a)\) if and only if \(\lambda =a(z_{r+1}(\lambda ))=a(z_r(\lambda ))\) holds with \(z_{r+1}(\lambda )/z_r(\lambda )=e^{i\varphi }\) for some \(\varphi \in (-\pi ,\pi ]\). Thus, the point \(z_r(\lambda )\) satisfies the two equations \(a(z)=\lambda \) and \(a(e^{i\varphi }z)=\lambda \) and consequently, it is a root of the equation
which is only of use for \(\varphi \ne 0\). Instead of considering \(a(z)=\lambda \) for \(\lambda \) in the two-dimensional plane \(\mathbb {C}\), we take \(\varphi \) from the one-dimensional set \((-\pi ,\pi ]{\setminus }\{0\}\) and solve Eq. (2.1). Let \(u_k(\varphi )\) (\(k=1, \ldots , r+s\)) be the solutions of this equation. For each k, we put \(\lambda _k(\varphi )=a(u_k(\varphi ))\) and label the roots \(z_{j,k}(\varphi )\) (\(j=1, \ldots , r+s\)) of the equation \(a(z)=\lambda _k(\varphi )\) so that
If \(|z_{r+1,k}(\varphi )|=|z_{r,k}(\varphi )|\), then \(\lambda _k(\varphi ) \in \Lambda (a)\), and otherwise \(\lambda _k(\varphi ) \notin \Lambda (a)\). To tackle the remaining case \(\varphi =0\), we replace Eq. (2.1) by
that is, by \(a'(z)=0\). Let \(t_k\) (\(k=1, \ldots ,r+s\)) be the solutions of this equation and put \(\lambda _k(0)=a(t_k)\) for each k. Then solve \(a(z)=\lambda _k(0)\) for each k and sort the roots \(z_{j,k}(0)\) so that
What results is that \(\lambda _k(0) \in \Lambda (a)\) if \(|z_{r+1,k}(0)|=|z_{r,k}(0)|\), while \(\lambda _k(0) \notin \Lambda (a)\) otherwise.
In summary, instead of finding the zeros of a polynomial of degree \(r+s\) parametrized by \(\lambda \) on a grid of order \(O(N^2)\) covering a bounded subset of \(\mathbb {C}\) (one may take the convex hull of the range \(a({\mathbb {T}})\) or even better some \(\sigma (T(a_\varrho ))\,\)), we have to find the zeros of \(r+s+1\) polynomials of degree \(r+s\) parametrized by \(\varphi \in (-\pi ,\pi ]\) and thus by points of a grid of order O(N).
If u satisfies \(a(u)-a(e^{i\varphi }u)=0\), then \(v=e^{i\varphi }u\) satisfies the equation \(a(v)-a(e^{-i\varphi }v)=0\). Thus, the solutions \(u_1(\varphi ), \ldots , u_{r+s}(\varphi )\) coincide with the solutions \(u_1(-\varphi ), \ldots , u_{r+s}(-\varphi )\), which implies that after appropriate sorting we get \(\lambda _k(\varphi )=\lambda _k(-\varphi )\) for all k. We therefore may restrict the algorithm to \(\varphi \in [0,\pi ]\).
Example 2.1
Figure 4 illustrates the algorithm for the septadiagonal matrix \(T_n(a)\) induced by
In a we see the range \(a({\mathbb {T}})\) (red), the result of the algorithm for \(\varphi =0.1:0.1:\pi \) (green), and the eigenvalues of \(T_{60}(a)\) (blue circles). b shows \(\lambda _1(\varphi ), \ldots , \lambda _6(\varphi )\) for \(\varphi =0.1:0.01:0.8\) (magenta). The black dots are the six values for \(\varphi =0.1\). c This is \(\lambda _1(\varphi ), \ldots , \lambda _6(\varphi )\) for \(\varphi =0.01:0.01:\pi \). In d we have \(\lambda _1(\varphi ), \ldots , \lambda _6(\varphi )\) for \(\varphi =0.01:0.01:2\) (magenta) and the parts of these curves that form a piece of \(\Lambda (a)\) (green). e is the same with \(\lambda _1(\varphi ), \ldots , \lambda _6(\varphi )\) for \(\varphi =2:0.01:2.7\), and f is the same with \(\lambda _1(\varphi ), \ldots , \lambda _6(\varphi )\) for \(\varphi =2.7:0.001:\pi \)
Example 2.2
We take the pentadiagonal matrix generated by the polynomial (1.2). Recall that the numerically obtained eigenvalues are in Fig. 1. The algorithm applied to \(a_\varrho \) with \(\varrho =0.4\) yields Fig. 5. In the left picture, the numerically computed eigenvalues of \(T_{100}(a_\varrho )\) are shown as blue circles and the limiting set computed with the algorithm is in green. The right picture is a zoom in of the left.
The true limiting set for the matrices of Fig. 1
3 The Different Points of the Limiting Set
A point \(\lambda \in \Lambda (a)\) is said to be a regular point if it has an open neighborhood \(V \subset \mathbb {C}\) such that \(\Lambda (a) \cap V\) is an analytic arc (without self-intersection) starting and ending at the boundary of V, and a point \(\lambda \in \Lambda (a)\) is called an exceptional point if it is not regular. This is a purely (differential-)topological classification of the points of \(\Lambda (a)\). As part of an analytic classification of the points of \(\Lambda (a)\) we call a point \(\lambda \in \Lambda (a)\) a simple point if
Example 3.1
(A simple point need not be regular.) Consider the pentadiagonal case given by (1.2) and studied in Example 2.2. Straightforward computation shows that we have the factorization
The origin \(\lambda =0\) belongs to \(\Lambda (a)\) if and only if \(|z_1(0)|=|z_2(0)|\). The solutions of \(a(z)=0\) are
Thus, the point \(\lambda =0\) is simple and \(z_2(0)/z_1(0)=e^{i\varphi _0}\) with \(\varphi _0=\pi /2\). If \(z=u(\varphi )\) is a solution of the equation
satisfying \(u(\pi /2)=1\), then \(\lambda (\varphi )=a(u(\varphi ))\) remains a simple point on \(\Lambda (a)\) for \(\varphi \) sufficiently close to \(\pi /2\). We have
From the representation (1.2) we get
Since \(\Phi _z(1,\pi /2)=0\) but \(\Phi _{zz}(1,\pi /2) \ne 0\), there is an open neighborhood \(U \subset \mathbb {C}\) of \(\lambda =0\) such that \(\Lambda (a) \cap U\) is formed by two analytic arcs perpendicularly intersecting in \(\lambda =0\). Thus, \(\lambda \) is not regular. The perpendicularly intersecting arcs are manifestly seen in Fig. 5b. \(\square \)
If a point \(\lambda \in \Lambda (a)\) is simple, that is, if it satisfies (3.1), then there is a unique number \(\varphi \in (-\pi ,\pi ] {\setminus } \{0\}\) such that \(z_{r+1}(\lambda )/z_r(\lambda )=e^{i\varphi }\). We say that the simple point \(\lambda \) is nondegenerate if
and otherwise we call it degenerate. The point \(\lambda =0\) in Example 3.1 was degenerate.
Theorem 3.2
A nondegenerate simple point is a regular point of \(\Lambda (a)\).
Proof
Let \(\lambda _0 \in \Lambda (a)\) be a simple point with
and \(z_r(\lambda _0) \ne z_{r+1}(\lambda _0)\). Then \(z_{r+1}(\lambda _0)/z_r(\lambda _0)=e^{i\varphi _0}\) with \(\varphi _0 \in (-\pi ,\pi ] {\setminus } \{0\}\). We consider the equation \(\Phi (u,\varphi ):=a(u)-a(e^{i\varphi }u)=0\) with the initial condition \(u(\varphi _0)=z_r(\lambda _0)=:u_0\). If \((\partial \Phi /\partial u)(u_0,\varphi _0) \ne 0\), the implicit function theorem ensures the existence of a unique analytic solution \(u=u(\varphi )\) in a sufficiently small open neighborhood V of \(\varphi _0\) satisfying \(u(\varphi _0)=u_0\). It follows that \(\lambda (\varphi )=a(u(\varphi ))\) describes an analytic arc in the plane. If V is sufficiently small, we infer from (3.1) that
which implies that the arc is part of \(\Lambda (a)\). Finally, the condition
is nothing but the condition
which in turn is just the nondegeneracy required. \(\square \)
Theorem 3.3
In the tetradiagonal case all simple points are nondegenerate and hence regular.
Proof
Let \(a(z)=a_2z^2+a_1z+a_0+a_{-1}z^{-1}\) and suppose \(\lambda _0\) is a simple point. This means that the zeros of \(a(z)-\lambda _0\) are \(z_0, e^{i\varphi _0}z_0,w_0\) with \(\varphi _0 \in (-\pi ,\pi ] {\setminus } \{0\}\) and \(|z_0| < |w_0|\). We have
and thus
Since \(e^{i\varphi _0}\ne 1\) and \(|z_0+e^{i\varphi _0}z_0| \le 2|z_0| < 2|w_0|\), the right-hand side of (3.3) cannot be zero. \(\square \)
The rest of the paper is devoted to tetradiagonal Toeplitz matrices. In that case we accompany the topological classification of the point in \(\Lambda (a)\) into regular end exceptional points by the following analytical classification. In accordance with the definition given above, we call \(\lambda \in \Lambda (a)\) a simple point if
We refer to a point \(\lambda \in \Lambda (a)\) as a branch point if two (or all three) of the points \(z_1(\lambda ),z_2(\lambda ),z_3(\lambda )\) coincide. In that case we may label the points so that
The remaining points \(\lambda \in \Lambda (a)\) are the points for which \(z_1(\lambda ), z_2(\lambda ), z_3(\lambda )\) are three distinct points satisfying
These points will be called multiple points.
4 Branch Points
Let for the moment \(a(z)=\sum _{j=-r}^s a_jz^j\) with \(r,s \ge 1\) and \(a_{-r}a_s \ne 0\) be a general Laurent polynomial. A point \(\lambda _0 \in \Lambda (a)\) is called a branch point if the equation \(\lambda _0=a(z)\) has a root of multiplicity at least 2. This is equivalent to saying that \(\lambda _0=a(z_0)\) and that \(z_0\) is a multiple zero of the polynomial \(z^r(a(z)-\lambda _0)\). The latter happens if and only if \(z_0\) is a root of
and since \(z_0 =0\) is impossible, we conclude that \(\lambda _0 \in \Lambda (a)\) is a branch point if and only if there is a \(z_0\) such that \(\lambda =a(z_0)\) and \(a'(z_0)=0\). As
the number of branch points is less than or equal to \(r+s\). (The argument employed in [2, Lemma 11.4] gave only the upper bound \(2(r+s)-1\).)
We now return to the tetradiagonal case \(a(z)=z^2+cz+cz^{-1}\) with \(c \ne 0\). Then
has three (possibly coinciding) zeros. We denote these zeros by \(t_1,t_2,t_3\) and label them so that \(|t_1| \ge |t_2| \ge |t_3|\).
Lemma 4.1
There is a complex number \(b \ne 0\) satisfying \({\mathrm{Re}\,}b \ge -1/2\) and \(|1+b| \le 1\) such that
and after fixing any value of \(w=(1+b+b^2)^{1/2}\) there is an \(\sigma \in \{-1,1\}\) such that
Proof
Vieta’s theorem for the equation \(2z^3+cz^2-c=0\) gives
Put \(b'=t_2/t_1\) and \(b=t_3/t_1\). Then \(0 < |b| \le |b'| \le 1\). The second equality of (4.3) implies that \(t_1^2(b'+b+b'b)=0\) with \(t_1 \ne 0\). It follows that \(b \ne -1\) and \(b'=-b/(1+b)\). From \(0 <|b| \le |b'| \le 1\) we therefore get \(0 <|b| \le |1+b| \le 1\). With \(b=\alpha +i \beta \), this is equivalent to the requirement \(0 < \alpha ^2+\beta ^2 \le (1+\alpha )^2+\beta ^2 \le 1\), which happens if and only if \(b \ne 0\), \(\alpha \ge -1/2\), \((1+\alpha )^2 +\beta ^2 \le 1\).
Inserting (4.1) in the first and third equalities of (4.3) we obtain
and hence \(t_1^2b^2=1+b+b^2\). Letting w be any square root of \(1+b+b^2\), we conclude that \(t_1=\sigma w/b\). Equalities (4.1) then give \(t_2=-\sigma w/(1+b)\), \(t_3=\sigma w\), and finally we have \(c=2t_1t_2t_3=-2\sigma w^3/(b(1+b))\). \(\square \)
Let \(\gamma \) be the piece of the curve \(\{b \in \mathbb {C}: |1+b|=2|b|^2\}\) that lies in the open disk \(\{b \in \mathbb {C}: |1+b| <1\}\). In polar coordinates,
The endpoints of \(\gamma \) on the circle \(|1+b|=1\) are \(G_\pm =-1/4\pm i\sqrt{7}/4\). The curve \(\gamma \) divides the domain \(\{b \in \mathbb {C}: {\mathrm{Re}\,}b > -1/2, |1+b| <1\}\) into three open sets \(D_0, D_+, D_-\) as seen in Fig. 7.
Lemma 4.2
For \(k=1,2,3\), let \(t_k\) and b be as in Lemma 4.1 and put \(\lambda _k=a(t_k)\). Then \(\lambda _2\) and \(\lambda _3\) are branch points belonging to \(\Lambda (a)\). The point \(\lambda _1\) is a branch point lying on \(\Lambda (a)\) if and only if b is in the closure of \(D_-\cup D_+\).
Proof
Let \(t_k, t_k, z_k\) be the roots of the equation
We have \(\lambda _k \in \Lambda (a)\) if and only if \(|t_k| \le |z_k|\). Vieta tells us that \(t_k^2z_k=-c\) and from (4.3) we know that \(c=2t_1t_2t_3\). Thus, \(|z_k|=2|t_1t_2t_3/t_k^2|\). It follows that \(|t_k| \le |z_k|\) if and only if \(|t_k|^3 \le 2|t_1t_2t_3|\).
If \(k=3\), Lemma 4.1 shows that \(|t_3|^3 \le 2|t_1t_2t_3|\) if and only if \(1 \le 2/(|b| |1+b|)\). But the latter inequality is certainly true because \(|b| \le 1\) and \(|1+b| \le 1\). For \(k=2\), the inequality \(|t_2|^3 \le 2|t_1t_2t_3|\) reads \(|b| \le 2|1+b|^2\) due to Lemma 4.1, and this is also always true since \(1/2 \le |1+b|\) and \(|b| \le |1+b|\), which gives \(2|1+b|^2 \ge |1+b| \ge |b|\). Finally, in the case \(k=1\), we obtain from Lemma 4.1 that \(|t_1|^3 \le 2|t_1t_2t_3|\) if and only if \(|1+b| \le 2|b|^2\), which is equivalent to the requirement that b is in the closure of \(D_- \cup D_+\). \(\square \)
The blue set \(\Omega \) in Fig. 2 is closed. Its left and right points are \(\pm 3\sqrt{3}\), and the upper and lower points are \(\pm i\). The set \(\Omega \) is symmetric about the real and the imaginary axes. Thus, it results from one of its quarters lying in one of the four quadrants by reflexions on the real and imaginary axes. Recall the connection between b and c given by Lemma 4.1. In dependence of the choice of \(\sigma w^3\), the closure of \(D_+\) is mapped by
onto either the quarter in the first quadrant or the quarter in the third quadrant. To be specific, suppose this quarter is the one in the first quadrant. Then the segment from \(b=-1/2\) to A is mapped to the segment from the (red) point \(3\sqrt{3}\) to the origin, the arc from A to \(G_+\) is mapped to the segment from 0 to i, and the arc of \(\gamma \) from \(G_+\) to \(b=-1/2\) is mapped to the boundary piece of \(\Omega \) from i to \(3\sqrt{3}\). The other choice \(-\sigma w^3\) maps the closure of \(D_+\) to the quarter of \(\Omega \) in the third quadrant. The closure of \(D_-\) is mapped into the union of the quarters in the second and fourth quadrants.
Combining the description of \(\Omega \) with Lemma 4.1 we arrive at the following result.
Theorem 4.3
Let \(a(z)=z^2+cz+cz^{-1}\) with \(c \ne 0\). Denote the roots of \(a'(z)=0\) by \(t_1,t_2,t_3\) and order them so that \(|t_3| \le |t_2| \le |t_1|\). Put \(\lambda _k=a(t_k)\). Then \(\lambda _2\) and \(\lambda _3\) are branch points of \(\Lambda (a)\), whereas \(\lambda _1\) is a branch point of \(\Lambda (a)\) if and only if \(c \in \Omega \).
Remark 4.4
The parameter c is immediately available but checking whether c is in \(\Omega \) or on \(\partial \,\Omega \) may be difficult if c is close to \(\partial \,\Omega \). However, one may proceed as follows. First solve the cubic equation \(a'(z)=0\), denote the roots by \(t_1,t_2,t_3\), label them so that \(|t_1| \ge |t_2| \ge |t_3|\), and put \(b=t_3/t_1\). Then
We now turn to the following question: how many analytic arcs do come out of the branch points and what is their asymptotic behavior near the branch points? Here is the result.
Theorem 4.5
Let \(a(z)=z^2+cz+cz^{-1}\) with \(c \ne 0\). Denote the roots of \(a'(z)=0\) by \(t_1,t_2,t_3\) and order them so that \(|t_3| \le |t_2| \le |t_1|\). Put \(\lambda _k=a(t_k)\).
-
(a)
If \(c \notin \Omega \), then there are two analytic arcs \(\ell _2\) and \(\ell _3\) belonging to \(\Lambda (a)\) and coming from the points \(\lambda _2=a(t_2)\) and \(\lambda _3=a(t_3)\), respectively, and these arcs have the following asymptotic representations in a neighborhood of the points \(\lambda _2,\lambda _3\):
$$\begin{aligned} \ell _j = \{\lambda \in \mathbb {C} : \lambda = \lambda _j + \frac{a''(t_j)}{2} d_{1,j}^2 \varphi ^2 + O(\varphi ^3),\ \varphi \in (0,\varepsilon )\}, \end{aligned}$$(4.4)where \(d_{1,j} = -i\dfrac{t_j}{2}\) \(\,(j=2,3)\).
-
(b)
If \(c \in \mathrm{int}\,\Omega \), then there are three analytic arcs \(\ell _1\), \(\ell _2\), and \(\ell _3\) belonging to \(\Lambda (a)\) and coming from the points \(\lambda _1 = a(t_1)\), \(\lambda _2=a(t_2)\) and \(\lambda _3=a(t_3)\), respectively, and these arcs have an asymptotic representation of the form (4.4) for \(j=1,2,3\).
-
(c)
If \(c \in \partial \Omega {\setminus } \{\pm 3\sqrt{3}\}\), then there are two analytic arcs that come from \(\lambda _2=a(t_2)\) and \(\lambda _3=~a(t_3)\) with asymptotic representations of the form (4.4) in a neighborhood of these points. The roots of the equation \(a(z)=\lambda _1\) are \(t_1,t_1,e^{i\varphi _0}t_1\) and there are two analytic arcs \(\ell _1^\pm \) that come from \(\lambda _1=a(t_1)\) and have the representations
$$\begin{aligned} \ell _1^\pm= & {} \left\{ \lambda \in \mathbb {C} : \lambda = a(t_1) + \frac{a''(t_1)}{2} d_1^2 (\varphi -\varphi _0)^2 \right. + \nonumber \\+ & {} \left. \left( a''(t_1)d_1d_2 + \frac{a'''(t_1)}{6} d_1^3\right) (\varphi -\varphi _0)^3 + O(|\varphi -\varphi _0|^4)\right\} , \end{aligned}$$(4.5)with
$$\begin{aligned} d_1 = -it_1, \quad d_2 = -\frac{1}{2} \left( 2+ i \cot \frac{\varphi _0}{2}\right) t_1, \end{aligned}$$(4.6)where \(\varphi \in (\varphi _0, \varphi _0 + \varepsilon )\) for \(\ell _1^+\) and \(\varphi \in (\varphi _0 - \varepsilon , \varphi _0)\) for \(\ell _1^-\). These two arcs make a cusp at the point \(\lambda _1\).
-
(d)
If \(c=\pm \mathbf{3}\sqrt{3}\), then \(\Lambda (a)\) is the line segment \([-9,\frac{45}{4}]=[-9,11.25]\).
Proof
Let \(\lambda _0 \in \Lambda (a)\) be a branch point and let \(t_0\in \{t_1,t_2,t_3\}\) be a point such that \(a(t_0)=\lambda _0\) and \(a'(t_0)=0\). The roots of the equation \(a(z)=\lambda _0\) are \(t_0,t_0,z_3\). From the proof of Lemma 4.2 we know that \(|t_0| < |z_3|\) if and only if \(|t_0|^3 < 2|t_1t_2t_3|\). The latter inequality is always true for \(t_0 \in \{t_2,t_3\}\) and it is satisfied for \(t_0=t_1\) if and only if \(|1+b| < 2|b|^2\), which happens if and only if \(c \in \mathrm{int}\,\Omega \). We know from Sect. 2 that if \(\lambda \in \Lambda (a)\) is sufficiently close to \(\lambda _0\), then \(\lambda =a(u(\varphi ))\) with a function \(u=u(\varphi )\) that is implicitly given by the equation \(a(u)-a(e^{i\varphi }u)=0\) and \(u(0)=t_0\). The solutions of the equation \(a(z)=\lambda \) are \(u(\varphi ), e^{i\varphi }u(\varphi ), v(\varphi )\) with \(u(\varphi )\) close to \(t_0\) and \(v(\varphi )\) close to \(z_3\). Thus, if \(|t_0| < |z_3|\), then any \(u(\varphi )\) satisfying \(a(u)-a(e^{i\varphi }u)=0\) and \(u(0)=t_0\) yields an arc starting at \(t_0\). We may suppose that \(\varphi \) ranges over \((0,\varepsilon )\) with sufficiently small \(\varepsilon >0\), because, as noted in Sect. 2, \(a(u(-\varphi ))=a(u(\varphi ))\).
We look for \(u(\varphi )\) in the form
Then
Taking into account that
we get \(a(u)-a(e^{i\varphi }u)= B_1\varphi ^2+B_2\varphi ^3 +O(\varphi ^4)\) with
The coefficients \(B_1\) and \(B_2\) must be zero. If \(a''(t_0) = 0\), then \(c=-t_0^3\), and as also \(a'(t_0)=0\), we conclude that \(t_0=\pm \sqrt{3}\) and hence \(c=\pm 3\sqrt{3}\). This case will be treated separately in part (d). Thus, let \(a''(t_0) \ne 0\). Then the equation \(B_1=0\) yields
It follows that \(B_2\) equals
and hence from the equation \(B_2=0\) we obtain
and thus
Replacing (4.7) by \(u(\varphi )=t_0+\sum _{k=1}^\infty d_k\varphi ^k\), taking the full power series for \(e^{i\varphi }\) and a(z), and proceeding as above, one will see that for \(k \ge 2\) the coefficient \(d_k\) enters \(B_{k}\) linearly and is completely determined by \(d_j\) for \(1 \le j \le k-1\). Consequently, there is a unique arc starting at \(\lambda _0\). Inserting (4.7), (4.9), (4.10) into the expansion
we get the expression on the right of (4.4) for the arc. At this point we have proved all assertions concerning \(\lambda _2\) and \(\lambda _3\) (because for them \(|t_0| < |z_3|\)) and we have also proved part (b), since, as said, for \(c \in \mathrm{int}\,\Omega \) we have \(|t_0| < |z_3|\), too.
We turn to part (c). In that case there is a positive number \(\varphi _0\) such that \(\{t_0,t_0, e^{i\varphi _0}t_0\}\) is the solution set of the equation \(a(z)=\lambda _0\). We have to look for solutions \(u=u(\varphi )\) of the equation \(a(u)-a(e^{i\varphi }u)=0\) satisfying \(u(0)=t_0\) or \(u(\varphi _0)=e^{i\varphi _0}t_0\). As noted above, for the initial condition \(u(0)=t_0\) we need only take \(\varphi \) from \([0,\varepsilon )\), but the initial condition \(u(\varphi _0)=e^{i\varphi _0}t_0\) requires taking \(\varphi \) from \((\varphi _0-\varepsilon , \varphi _0+\varepsilon )\).
We first consider the initial condition \(u(0)=t_0\). As above, we get a unique solution \(u(\varphi )=t_0+\sum _{k=1}^\infty d_k \varphi ^k\) with \(d_1,d_2\) given by (4.9), (4.10). Vieta for the equation
gives \(2t_0+e^{i\varphi _0}t_0=-c\) and \(e^{i\varphi _0}t_0^3=-c\). This implies
and results in
Consequently,
It follows that \(|u(\varphi )| >|t_0|\). The zeros of \(z(a(z)-\lambda )=z^3+cz^2-\lambda z +c\) are \(u(\varphi ),e^{i\varphi }u(\varphi ),v(\varphi )\), and Vieta tells us that \(e^{i\varphi }u^2(\varphi )v(\varphi )=-c\). Thus,
and because \(\lambda \in \Lambda (a)\) would require that \(|u(\varphi )|=|e^{i\varphi }u(\varphi )| \le |v(\varphi )|\) we conclude that (4.7) does not give an arc of \(\Lambda (a)\).
We are left with the equation \(a(u)-a(e^{i\varphi }u)=0\) in neighborhood of the point \(\varphi =\varphi _0\). Using power series one can show that the solution is unique. We may write
and calculations as before give
It follows that
This time \(|u(\varphi )| < |t_0|\) and hence
which shows that the two arcs induced by \(\varphi \in (\varphi _0-\varepsilon ,\varphi _0)\) and \(\varphi \in (\varphi _0,\varphi _0+ \varepsilon )\) are part of \(\Lambda (a)\). Inserting the expressions obtained for \(u(\varphi )\) in (4.11) with \(t_0\) replaced by \(t_1\) we get (4.5) and (4.6). It is clear that \(\ell _1^\pm \) make a cusp at \(\lambda _1\).
We finally prove (d). Equality (1.3) with \(\varrho =-1\) shows that always
Thus, the limiting sets for \(c=\pm 3\sqrt{3}\) are the same. Let \(a(z)=z^2-cz-cz^{-1}\) with \(c=3\sqrt{3}\). Using (1.3) with \(\varrho =\sqrt{3}\), we get
Consequently, with \(f(z):=z^2-3z-z^{-1}\), we have \(\Lambda (a)=3\Lambda (f)\) and we are left with proving that \(\Lambda (f)=[-3,15/4]\).
We first show that \(\Lambda (f)\) is a subset of \({\mathbb {R}}\). So let \(\lambda \in \Lambda (f)\). From Sect. 2 we know that \(\lambda =f(z)\) where z satisfies \(f(z)-f(e^{i\varphi }z)=0\) for some \(\varphi \ne 0\) or where \(z=t_k\) is a root of the equation \(f'(z)=0\). The zeros of \(f'(z)\) are \(t_1=1, t_2=1, t_3=-1/2\) and \(\lambda _2=f(t_2)=-3\) as well as \(\lambda _3=f(t_3)=15/4\) are real. So suppose \(f(z)-f(e^{i\varphi }z)=0\) with \(\varphi \ne 0\). Adding 3 to both sides of the equation \(f(z)=f(e^{i\varphi }z)\) we obtain the equation
and writing \(v:=e^{i\varphi /3}\), this equation becomes
Consequently, \((v^2z-v^{-1})/(z-1)=\varepsilon \) where \(\varepsilon ^3=1\). It follows at once that \(z=(v^{-1}-\varepsilon )/(v^2-\varepsilon )\) and thus
This gives
and therefore implies that \(\lambda \in {\mathbb {R}}\), as asserted.
In summary, \(\Lambda (f)\) is a closed and connected subset of \({\mathbb {R}}\) and thus some closed line segment in \({\mathbb {R}}\). To conclude that \(\Lambda (f)=[-3,15/4]\), we may have recourse to part (a), according to which \(\Lambda (f)\) is an analytic arc starting at \(\lambda _2=f(t_2)=-3\) and terminating at \(\lambda _3=f(t_3)=15/4\). An argument avoiding part (a) is as follows. We know that \(\Lambda (f)\) is the intersection of the spectra of the Toeplitz operators \(T(f_\varrho )\) for \(\varrho \in (0,\infty )\). So consider the curve \(f_\varrho ({\mathbb {T}})\). If \(\varrho =1\), this curve and thus also the spectrum of \(T(f_\varrho )\) are located in the half-plane \({\mathrm{Re}\,}\lambda \ge -3\), and if \(\varrho =-1/2\), the curve and hence the spectrum of \(T(f_\varrho )\) are contained in the half-plane \({\mathrm{Re}\,}\lambda \le 15/4\). Consequently, \(\Lambda (f)\) is a subset of \([-3,15/4]\), and since \(-3=\lambda _2\) and \(15/4=\lambda _3\) belong to \(\Lambda (f)\), it follows that \(\Lambda (f)=[-3, 15/4]\). \(\square \)
Remark 4.6
The referee kindly pointed out that part of assertion (d), namely that \(\Lambda (f) \subset {\mathbb {R}}\), may also be derived from the main result of [11], according to which \(\Lambda (f)\) is contained in \({\mathbb {R}}\) if and only if the pre-image \(f^{-1}({\mathbb {R}})\) contains a Jordan curve. To see this, let \(q(t)=\sin (3t)/\sin (2t)\) and consider the set \(K=\{\kappa (t):=1-q e^{it}: t \in [-\pi /3,\pi /3]\}\). This is a Jordan curve and we have
Consequently, the imaginary part of \(f(\kappa (t))\) is
which shows that \(f(K) \subset {\mathbb {R}}\) and thus, by [11], \(\Lambda (f) \subset {\mathbb {R}}\). \(\square \)
We recall that \(t_1,t_2,t_3\) are the zeros of \(a'(z)\). We therefore have
The first of these equalities gives \(c/t_k^3=2+c/t_k\), and inserting this in the second equality we get \(a''(t_k)=6+2c/t_k\). Thus the repeatedly occurring \(a''(t_k)\) in the theorem may simply be replaced by \(6+2c/t_k\).
5 Multiple Points
Let again \(a(z)=z^2+cz+cz^{-1}\) with \(c \ne 0\). Recall that a point \(\lambda _0 \in \Lambda (a)\) is said to be a multiple point if the roots \(z_1(\lambda _0), z_2(\lambda _0), z_3(\lambda _0)\) of the equation \(a(z)=\lambda _0\) are pairwise distinct but have the same absolute value.
Lemma 5.1
Let \(r=|c|^{1/3}\) and write \(c=-r^3e^{i\theta }\) with \(\theta \in (-\pi ,\pi ]\). Put \(d =r^2 e^{2i\theta /3}\). Then the following are equivalent:
-
(i)
there is a point \(\lambda _0 \in \Lambda (a)\) such that the equation \(a(z)=\lambda _0\) has three solutions of the same absolute value,
-
(ii)
the equation
$$\begin{aligned} h_p(\psi ):=p e^{-i\psi }+e^{2i\psi }=d \end{aligned}$$(5.1)has a solution \((\psi ,p) \in {\mathbb {R}}\times [-2,2]\).
If (i), (ii) hold, then \(\lambda _0\) necessarily equals \(-r^4 \,(\,=-|c|^{4/3}\,)\).
Proof
(i) \(\Rightarrow \) (ii). Suppose the equation \(a(z)=\lambda _0\) has three solutions of the same modulus. They are \(z_k(\lambda _0)=re^{i\varphi _k}\) with \(r >0\) and \(\varphi _k \in {\mathbb {R}}\). Vieta’s theorem applied to the equation
gives
It follows that \(r=|c|^{1/3}\) and \(\varphi _1+\varphi _2+\varphi _3=\theta +\xi \) with \(\xi \in 2\pi {\mathbb {Z}}\). From (5.3) we now infer that
or equivalently,
Putting
we get \(e^{i(\theta /3-\psi )}p+e^{i\theta }e^{-2i(\theta /3-\psi )}=-{c}/{r}\), that is,
and finally
(ii) \(\Rightarrow \) (i). Let \((\psi ,p) \in {\mathbb {R}}\times [-2,2]\) be a solution of (5.1). Then (5.6) holds, and with arbitrary \(\varphi _1,\varphi _2\) satisfying (5.5), we obtain (5.4) with \(\xi =0\). After putting \(\varphi _3=\theta -\varphi _1-\varphi _2\) we arrive at (5.3). Equation (5.2) is then satisfied by \(z_k=re^{i\varphi _k}\) when taking
Now suppose (i) is true. Then the solutions of the equation \(a(z)=\lambda _0\) are \(re^{i\varphi _k}\) as above and Vieta implies (5.3) and (5.7). Since \(\varphi _1+\varphi _2+\varphi _3-\theta \in 2\pi {\mathbb {Z}}\), we obtain from (5.7) that
and hence
\(\square \)
We emphasize that in the previous lemma we admit \(\varphi _1 \le \varphi _2 \le \varphi _3\). The cases \(\varphi _1=\varphi _2\) and \(\varphi _2=\varphi _3\) occur for branch points. For multiple points we have strict inequalities.
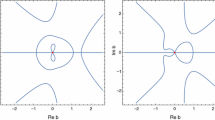
Let \(D_2\) be the set of all \(d \in \mathbb {C}\) for which Eq. (5.1) has a solution \(p \in [-2,2]\) and \(\psi \in {\mathbb {R}}\). Note that the function \(h_p: {\mathbb {R}}\rightarrow \mathbb {C}\) is \(2\pi \)-periodic and that \(h_{-p}({\mathbb {R}})=h_p({\mathbb {R}})\). Figure 8a shows the ranges \(h_p({\mathbb {R}})\) for several values of p and suggests that \(D_2\) is the set bounded by \(h_2({\mathbb {R}})\). This can indeed be proved, but we do not need this for our purposes. Moreover, writing \(-c=r^3e^{i\theta }\) and \(d=r^2e^{2\pi i/3}\) as in Lemma 5.1, we get
The map \(c \mapsto (-c)^{2/3}\) maps \(\Omega \) to the set shown in Fig. 8b. The blue set is the image of the part of \(\Omega \) that lies on the right of the imaginary axis for some \(k\in \{0,1,2\}\), the red and green sets are the images for the other two values of k. The left piece of \(\Omega \) is mapped onto the same set. Thus, the set in Fig. 8b is covered twice. Comparison of Fig. 8a, b indicates that \(D_2=(-\Omega )^{2/3}\), and since \(\Omega =-\Omega \), that actually \(D_2=\Omega ^{2/3}\). This can again be rigorously verified, but we will not embark on this issue here. The conclusion is that \(\Lambda (a)\) has a point \(\lambda _0\) for which the equation \(a(z)=\lambda _0\) has three solutions of the same modulus if and only if \((-c)^{2/3} \in D_2\) and that this happens if and only if \(c \in \Omega \). The result of genuine interest to us is that \(\Lambda (a)\) has a multiple point, that is, a point \(\lambda _0\) such that \(a(z)=\lambda _0\) is satisfied by three pairwise distinct numbers of the same modulus, if and only if \(c \in \mathrm{int}\,\Omega \). This will be a consequence of Theorem 6.1 below.
Theorem 5.2
Let \(\lambda _0\) be a multiple point of \(\Lambda (a)\) and let \(re^{i\varphi _1}, re^{i\varphi _2}, re^{i\varphi _3}\) with
be the solutions of the equation \(a(z)=\lambda _0\). Then there are exactly three analytic arcs of \(\Lambda (a)\) coming from \(\lambda _0\). Their local representations are
for \(j=1,2,3\) with
and
In (5.8) one has to take \(\varphi > \varphi _0\) or \(\varphi < \varphi _0\) to enforce that
Proof
We proceed as in the case of branch points. Now the equation \(a(z)-\lambda _0=0\) has the solutions \(re^{i\varphi _1},re^{i\varphi _2},re^{i\varphi _3}\), where \(r>0\), \(\varphi _j\in (-\pi ,\pi ]\), and \(\varphi _1<\varphi _2<\varphi _3\). In order to find the analytic arcs that pass through \(\lambda _0\) in a neighborhood around it, we consider again the equation \(a(u)-a(e^{i\varphi }u)=0\). We have \(a(u_0)-a(e^{i\varphi _0}u_0)=0\) in the following three cases:
Pick one of these cases. In a neighborhood of \((u_0,\varphi _0)\) we look for \(u(\varphi )\) in the form
Of course, q depends on j and will eventually become \(q_j\). We obtain
and thus
implying that \(a'(u_0)q-e^{i\varphi _0}a'(e^{i\varphi _0}u_0)(q+iu_0)=0\). This gives
Let us calculate \(a'(u_0)\) at \(u_0=re^{i\varphi _1}\). We have
Using the Vieta equalities (5.3) we get
Analogously,
Inserting the two expressions obtained into (5.10) we arrive at
We have \({\mathrm{Re}\,}(q/u_0) \ne 0\). Indeed, if \({\mathrm{Re}\,}(q/u_0)=0\), then, by (5.10), \(s(u_0,\varphi _0)\) must be a real number, which implies that \({\mathrm{Im}\,}\big ( e^{{i(\varphi _2-\varphi _1)}/{2}}\big )=0\), whence \(\varphi _2=\varphi _1\), contradicting our requirement \(\varphi _2 > \varphi _1\). From (5.9) we now get
It follows that \(a(u(\varphi ))\) belongs to \(\Lambda (a)\) if and only if
since if we have (5.11), then the roots of the equation \(a(z)=\lambda (\varphi )\) with \(\lambda (\varphi )=a(u(\varphi ))\) have absolute value smaller than r, which means that the third root \(v(\varphi )\) of this equation has absolute value \( |v(\varphi )|=\frac{|c|}{|u(\varphi )|^2}=\frac{r^3}{|u(\varphi )|^2}>r, \) while if (5.11) does not hold, then \(|v(\varphi )| < |u(\varphi )|\). The reasoning is analogous for \(j=2\) and \(j=3\). Thus, we have shown that three analytic arcs with the asserted local representation start at \(\lambda _0\). Inserting the full power series for \(u(\varphi )\) in the equation \(a(u)-a(e^{i\varphi }u)=0\) one can check that all its coefficients are uniquely determined, which implies that no more than three analytic arcs come from \(\lambda _0\). \(\square \)
6 The Types of the Limiting Set
We say that \(\Lambda (a)\) is of type \(L_j\) (\(j=1,2,3\)) if \(\Lambda (a)\) is the closure of the union of exactly j analytic arcs and \(\Lambda (a)\) has exactly \(j+1\) exceptional points.
Theorem 6.1
Let \(a(z)=z^2+cz+cz^{-1}\) with \(c \ne 0\). Denote the roots of \(a'(z)=0\) by \(t_1,t_2,t_3\) and order them so that \(|t_3| \le |t_2| \le |t_1|\). Put \(\lambda _k=a(t_k)\).
-
(a)
The set \(\Lambda (a)\) is of type \(L_1\) if and only if \(c \notin \Omega \) or \(c=\pm 3\sqrt{3}\). In that case \(\Lambda (a)=[\lambda _2 \sim \lambda _3]\).
-
(b)
The set \(\Lambda (a)\) is of type \(L_2\) if and only if \(c \in \partial \,\Omega {\setminus } \{\pm 3\sqrt{3}\}\). In that case the set \(\Lambda (a)\) is \(\Lambda (a)=[\lambda _1 \sim \lambda _2] \cup [\lambda _1 \sim \lambda _3]\) with a cusp at \(\lambda _1\).
-
(c)
The set \(\Lambda (a)\) is of type \(L_3\) if and only if \(c \in \mathrm{int}\,\Omega \). In that case we have \(\Lambda (a)=[\lambda _0 \sim \lambda _1] \cup [\lambda _0 \sim \lambda _2] \cup [\lambda _0 \sim \lambda _3]\) with \(\lambda _0=-|c|^{4/3}\).
Proof
If \(c=\pm 3 \sqrt{3}\), then \(\Lambda (a)\) is a line segment by Theorem 4.5(d). Let \(c \notin \Omega \). Then, by Theorems 4.3 and 4.5, \(\Lambda (a)\) has exactly \(\lambda _2\) and \(\lambda _3\) as branch points and in each of them there is one outgoing arc. If \(\Lambda (a)\) had a multiple point \(\lambda _0\), then due to Theorem 5.2 there would be three arcs starting at \(\lambda _0\). Note that, by Lemma 5.1, \(\Lambda (a)\) can have at most one multiple point. It is impossible to weld these five arcs together without creating additional exceptional points and without increasing the number of outgoing arcs in \(\lambda _2\) and \(\lambda _3\). Thus, \(\Lambda (a)\) cannot posses a multiple point and we must have \(\Lambda (a)=[\lambda _2 \sim \lambda _3]\).
Now suppose \(c \in \mathrm{int}\,\Omega \). Then, again by Theorems 4.3 and 4.5, \(\lambda _1,\lambda _2,\lambda _3\) are branch points with a single arc starting in each of them. One cannot glue together these three arcs without creating additional exceptional points or increasing the number of outgoing arcs in the branch points. Consequently, \(\Lambda (a)\) must have a multiple point \(\lambda _0\) with three outgoing arcs. The only possibility to join these arcs in order to get a connected set with no more exceptional points and without increasing the number of outgoing arcs in the branch points is \(\Lambda (a)=[\lambda _0 \sim \lambda _1] \cup [\lambda _0 \sim \lambda _2] \cup [\lambda _0 \sim \lambda _3]\). By Lemma 5.1, \(\lambda _0=-|c|^{4/3}\).
Finally, let \(c \ne \pm 3\sqrt{3}\) belong to \(\partial \,\Omega \). Theorems 4.3 and 4.5 tell us that \(\lambda _1,\lambda _2,\lambda _3\) are branch points and that \(\lambda _1\) has two outgoing arcs and \(\lambda _2,\lambda _3\) have one outgoing arc. If \(\Lambda (a)\) had a multiple point, it would be impossible to join the seven arcs without getting new exceptional points or increasing the number of outgoing arcs. It follows that \(\Lambda (a)\) has no multiple point and that \(\Lambda (a)=[\lambda _1 \sim \lambda _2] \cup [\lambda _1 \sim \lambda _3]\). \(\square \)
The two arcs (4.5) emerging for \(c \in \partial \Omega {\setminus } \{\pm 3\sqrt{3}\}\) make a cusp at the point \(\lambda _1\). If c moves along \(\partial \Omega \) to \(\pm 3\sqrt{3}\), one of these arcs becomes smaller and smaller, and at \(c=\pm 3\sqrt{3}\) it disappears while the other arc becomes the line segment \([-9,11.25]\). This line segment changes to an analytic arc outside \(\Omega \) whereas inside \(\Omega \) it transforms into a star with three analytic legs by giving birth to two legs at one of its ends. At \(c=\pm i\), the set \(\Lambda (a)\) is formed by two arcs making a cusp. As c moves from \(\pm i\) into the exterior of \(\Omega \), the cusp is bulging out to an analytic curve, and as c moves from \(\pm i\) into the interior of \(\Omega \), the cusp mutates into a star with three legs by creating a new arc at the cusp point and opening the zero angle of the two arcs of the cusp to a positive angle.
We excluded the parameter \(c=0\). Trivially, in that case \(\Lambda (z^2)=\{0\}\). If \(c \ne 0\) approaches the origin, then the star \(\Lambda (z^2+cz+cz^{-1})\) with the three legs becomes smaller and smaller and eventually it collapses to the point \(\{0\}\).
Theorem 6.2
Let \(a(z)=z^2+cz+cz^{-1}\) with \(c \notin \Omega \). Denote the roots of \(a'(z)=0\) by \(t_1,t_2,t_3\) and order them so that \(|t_3| \le |t_2| \le |t_1|\). Put \(\lambda _k=a(t_k)\). The limiting set \(\Lambda (a)=[\lambda _2 \sim \lambda _3]\) is a line segment if and only if \(c \in (-\infty , -3\sqrt{3})\cup (3\sqrt{3},\infty )\). In that case \(\lambda _2\) and \(\lambda _3\) are real.
Proof
Suppose first that \(\pm c \in (3\sqrt{3},\infty )\). Such c may be represented in the form (4.2) with \(-1/2< b <0\). It follows that \(w=(1+b+b^2)^{1/2}\) may be taken as a positive real number and (4.2) then tells us that all \(t_k\) are also real numbers. Consequently,
The set \(\Lambda (a)\) is the intersection of the spectra of the operators \(T(a_\varrho )\) for \(\varrho \in (0,\infty )\). Since \(\overline{a_\varrho (\overline{z})}=a_\varrho (z)\), the curves \(a_\varrho ({\mathbb {T}})\) are symmetric about the real line. Hence so also are the spectra of all \(T(a_\varrho )\) and thus also \(\Lambda (a)\). But an arc starting and ending on \({\mathbb {R}}\) and being symmetric about \({\mathbb {R}}\) must be a line segment in \({\mathbb {R}}\).
Conversely, assume now that \(\Lambda (a)=[\lambda _2 \sim \lambda _3] \subset \mathbb {C}\) is a line segment. Then the tangents to the arc at \(\lambda _2\) and \(\lambda _3\) point into opposite directions. By representation (4.4), this means that there is a real number \(\mu >0\) such that \({a''(t_2)t_2^2}/({a''(t_3)t_3^2})=-\mu \). By the remark at the end of Sect. 4, we have \(a''(t_k)=6+2c/t_k\). We may write the numbers \(t_2,t_3,c\) in the form (4.2) with \(-1/2< {\mathrm{Re}\,}b <0\). It follows that
Put \(\mu =1/\nu \). The equation \((2b+1)/(1-b^2)=1/\nu \) is a quadratic equation with the two solutions \(b=-\nu \pm \sqrt{\nu ^2-\nu +1}\). Since \(\nu ^2-\nu +1 >0\) for all \(\nu \), we conclude that b is a real number. As also \(-1/2< {\mathrm{Re}\,}b <0\), it is only \(b \in (-1/2,0)\) which can give oppositely directed tangents. But these b correspond just to \(\pm c \in (3\sqrt{3},\infty )\). \(\square \)
Remark 6.3
The referee again kindly turned attention to the fact that the “if portion” of Theorem 6.2 can also be deduced from the more general result of [11]. Indeed, let \(c \in [3\sqrt{3},\infty )\). For \(x \ge 0\), the function \(x^3-x\) decreases from 0 to \(-2/(3\sqrt{3}) \le -2/c\) and then increases to infinity. Consequently, there are numbers \(0< x_2< x_1 < x_0\) such that
It follows that the set \(\{r >0: -2/c \le 1/r^3-1/r \le 2/c\}\) is of the form \([r_0,r_1] \cup [r_2, \infty )\) with \(r_j=1/x_j\). Consider the curve
with
Note that \(\tau (r) >0\) for \(r \in (r_0,r_1)\) and that \(\tau (r_0)=\tau (r_1)=0\). This reveals that K is a Jordan curve. We have \(\sigma ^2+\tau ^2=r^2\), and hence \(\kappa =\kappa (r)\) satisfies the quadratic equation
Dividing by \(\kappa r^2\) we get
The last two equations imply
showing that \(f(K) \subset {\mathbb {R}}\) and hence, by [11], proving that \(\Lambda (f)\) is a real line segment. \(\square \)
References
Beam, R.M., Warming, R.F.: The asymptotic spectra of banded Toeplitz and quasi-Toeplitz matrices. SIAM J. Sci. Comput. 14, 971–1006 (1993)
Böttcher, A., Grudsky, S.M.: Spectral Properties of Banded Toeplitz Matrices. SIAM, Philadelphia, PA (2005)
Böttcher, A., Silbermann, B.: Introduction to Large Truncated Toeplitz Matrices. Universitext. Springer, New York (1999)
Böttcher, A., Widom, H.: Two remarks on spectral approximations for Wiener-Hopf operators. J. Integral Equations Appl. 6, 31–36 (1994)
Duits, M., Kuijlaars, A.B.J.: An equilibrium problem for the limiting eigenvalue distribution of banded Toeplitz matrices. SIAM J. Matrix Anal. Appl. 30, 173–196 (2008)
Garoni, C., Serra-Capizzano, S.: Generalized Locally Toeplitz Sequences: Theory and Applications, vol. I. Springer, Cham (2017)
Hirschmann Jr., I.I.: The spectra of certain Toeplitz matrices. Illinois J. Math. 11, 145–159 (1967)
Nikolski, N.: Toeplitz Matrices and Operators. Cambridge University Presss, Cambridge (2020)
Reichel, L., Trefethen, L.N.: Eigenvalues and pseudo-eigenvalues of Toeplitz matrices. Linear Algebra Appl. 162/164, 153–185 (1992)
Schmidt, P., Spitzer, F.: The Toeplitz matrices of an arbitrary Laurent polynomial. Math. Scand. 8, 15–38 (1960)
Shapiro, B., Štampach, F.: Non-self-adjoint Toeplitz matrices whose principal submatrices have real spectrum. Constr. Approx. 49, 191–226 (2019)
Szegő, G.: Ein Grenzwertsatz über die Toeplitzschen Determinanten einer reellen positiven Funktion. Math. Ann. 76, 490–503 (1915)
Trefethen, L.N., Embree, M.: Spectra and Pseudospectra. The Behavior of Nonnormal Matrices and Operators. Princeton University Press, Princeton, NJ (2005)
Tyrtyshnikov, E.E.: A unifying approach to some old and new theorems on distribution and clustering. Linear Algebra Appl. 232, 1–43 (1996)
Tyrtyshnikov, E.E., Zamarashkin, N.L.: Distribution of the eigenvalues and singular numbers of Toeplitz matrices under weakened requirements on the generating function. Sb. Math. 188, 1191–1201 (1997)
Tyrtyshnikov, E.E., Zamarashkin, N.L.: Toeplitz eigenvalues for Radon measures. Linear Algebra Appl. 343/344, 345–354 (2002)
Ullman, J.L.: A problem of Schmidt and Spitzer. Bull. Am. Math. Soc. 73, 883–885 (1967)
Widom, H.: Eigenvalue distribution of nonselfadjoint Toeplitz matrices and the asymptotics of Toeplitz determinants in the case of nonvanishing index. Oper. Theory Adv. Appl. 48, 387–421 (1990)
Widom, H.: Eigenvalue distribution for nonselfadjoint Toeplitz matrices. Oper. Theory Adv. Appl. 71, 1–8 (1994)
Funding
Open Access funding enabled and organized by Projekt DEAL.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Böttcher, A., Gasca, J., Grudsky, S.M. et al. Eigenvalue Clusters of Large Tetradiagonal Toeplitz Matrices. Integr. Equ. Oper. Theory 93, 8 (2021). https://doi.org/10.1007/s00020-020-02619-z
Received:
Revised:
Published:
DOI: https://doi.org/10.1007/s00020-020-02619-z