Zloković’s Understandings of Reciprocal Concatenation

Abstract

In this paper, we present Milan Zloković’s theorisation of reciprocal concatenation and its application in his architectural design. For two decades architect Milan Zloković (1898–1965), one of the founders of Modern Movement in Yugoslavia, studied what he called “the science of proportions”. His findings have not received the attention they deserve. Here we analyse his research on proportional method of reciprocal concatenation through the ancient concept of analogy, the correlation among proportional systems, an ideal set of preferential numbers and the use of proportional dividers. Based on his theoretical views, we examined proportions in two of his buildings: the Elementary School in Jagodina (1937–1940) and the Teacher Training School in Prizren (1960). Finally, we show that Zloković combined reciprocal concatenation with various proportional systems, proving it to be a valuable tool for contemporary architectural design.

Introduction

Milan Zloković (1898 Trieste–1965 Belgrade) was an architect, theoretician of proportions and professor in the Faculty of Architecture of the University of Belgrade. As one of the founders of the Group of Architects of the Modern Movement (1928–1934), Zloković promoted modern architecture in Serbia and actively discussed the urban growth of Belgrade. Although his biographers (Manević 1989; Đurđević 1991) often referred to his practical (pre-war) and theoretical (post-war) work separately, Zloković strongly believed that a true architect should simultaneously develop his theoretical and practical standings.¹ In the post-WWII period, he published approximately 30 theoretical papers and in parallel incorporated those findings into his practice. Geometry, harmony and proportions were inseparable from his architectural design (Blagojević 2003).

Zloković’s work was partly researched: biographical overview (Manević 1976, 1989; Đurđević 1991), modern period (Blagojević 2000, 2003; Perović 2003) or public buildings (Panić 2009, 2013). Zloković’s students left valuable but sparse testimonies on his theoretical research (Brkić 1992; Petrović 1974; Zloković 2011). Several comprehensive studies emphasized a need for clarification of Zloković’s mathematical analysis and the contribution of his condensed work on architectural proportions (Purić-Zafiroski 2001; Marjanović 2010, 2012).

Besides the intention to reconstruct Zloković’s understanding of reciprocal concatenation, our goal here is also to emphasise its roots in the legacy of antiquity and its application in practice, as a valuable insight for contemporary architects. The paper has five sections. We have traced Zloković’s research of the principle of analogy in the theory of proportions all the way back to Antiquity and showed his explanation of correlation among various proportional systems. Two key issues for reciprocal concatenation are the analysis of an ideal set of preferential numbers and the question of application of ancient dividers. In order to illustrate how Zloković applied his discoveries, we analyse façade proportions in two of his buildings. In the case of the Elementary School in Jagodina (1937–1940), one of Zloković’s early masterworks, we reconstructed the missing proportional diagram. In the Teacher Training School in Prizren (1960), an example of practical application of his last great theoretical achievement on ancient dividers, proportions were analysed based on author’s original diagrams. Both cases demonstrate application of reciprocal concatenation.

Reciprocal Concatenation

Principle of Analogy in the Theory of Proportions

Due to his education—he attended German elementary school, Realschule in Trieste and High Technical School in Graz—Milan Zloković was influenced by German books, the German approach in technical education, rationalism and simplifying analysis by identifying logical subcomponents (Manević 1976: 288).² He even found a certain philosophical comfort in resolving mathematical problems, especially during the terror of WWI (Đurđević 1991: 146). Although he was an Orthodox Christian, in his scientific research he put aside mysticism and religious beliefs.³ Looking for the ‘distilled truth’ and striving to define a reliable tool for designers, Zloković adopted a strictly mathematical approach. While studying the Byzantine art and architecture,⁴ he analysed various vernacular and sacred buildings, realising that all proportional methods, secretly passed down through masonry lodges from the Middle Ages onward, have their bases in the ancient methods of architectural composition (Zloković 1955a: 210). Therefore, he followed the theory of architectural proportions all the way to Antiquity.

Even pre-Socratic philosophers used analogies to reveal the harmony of the cosmos and reach knowledge beyond our experience. Pythagoreans reduced every process or phenomenon to numbers and their ratios—All things are number—so mathematics became a fundamental science that supported the macro–micro analogy of the world. This analogy refers to the idea that characteristics, parts or relations inside one larger entity can also be found in the smaller units of the same entity. In other words, analogy embodies the notion that the ‘portions of the world that vary in size exhibit similarities in structures and processes, indicating that one portion imitates another or others on a different scale’ (Conger 1922: xiii). In Antiquity, this macrocosm-microcosm analogy was embedded in architecture through geometry. It was considered inherent in nature rather than the framework which we use to describe the world (Capra 1975). This analogy was recognized in the golden section. Zloković was impressed with its presence in natural forms, believing it perfectly demonstrates the well-balanced relationship between natural creations and works of art. Therefore, he quoted Gottfried Semper, who compared the repetition of just a few motives in nature, since its very beginning until today, to the repetition of a few basic shapes in the history of arts (Zloković 1955b: 12).

In 1885, August Thiersch wrote about the ‘law of analogy’ (Thiersch 1926), which he explained as a ‘repetition of the fundamental form of the plan throughout its subdivisions’ (Scholfield 2011: 102).⁵ Basing himself mainly on the law of analogy, in the 1920s Le Corbusier drew the wider public attention to the ‘method of diagonals’.⁶ Zloković also realised the rooting of Thiersch’s idea in ancient knowledge, so he pointed out ‘the far-reaching importance of constant proportions’ and the principle of analogy (Zloković 1954b: 833). Following the thought of Thiersch—harmony occurs only with the repetition of main figure in its subdivisions, Zloković tended to explain the origin and importance of the principle of analogy in architectural composition. He wrote:

Ancient mathematics had a significant contribution in solving foundational problems in the science of harmony and proportions within practical metrology… mostly due to the excellent knowing of geometry and skilfully developed system of selected numbers (Zloković 1955a: 191).

Zloković often referred to the theory of proportions as the ‘science of proportions’, believing it might progress due to new findings, just like any other science.

In Zloković’s terminology ‘analogy’ indicates the ‘method of reciprocal concatenation’: a sequence of the same geometric images at different scales by the principle of reciprocal diagonals (diagonals at right angles). Consequently, this method is also referred to as the ‘method of diagonals’.

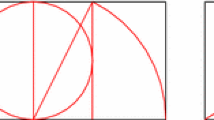
As the starting point, Zloković used the construction of the ‘mean geometric proportional’, that is, the right triangle inscribed in the semicircle. It allows construction of the first four members of geometrical progression (b = $\sqrt {ac}$). It also means that the sides of two rectangles, ab and bc, stand in the proportion a:b = b:c (Fig. 1). Zloković highlighted that this geometric progression is embodied in the method of reciprocal concatenation. The construction from Fig. 1 is further developed in Fig. 2 but now the diameter of semicircle is AC = RS. The extension of triangle RPS’s shorter cathetus (RP) forms right triangle PST. Right triangles RPS and PST are similar, thus analogous. This represents the beginning of both the reciprocal concatenation and the geometrical progression, as demonstrated in Fig. 2: 1, $\frac{m}{n}$, $\left( {\frac{m}{n}} \right)^{2}$, $\left( {\frac{m}{n}} \right)^{3} .$ The main principle of reciprocal diagonals is shown in Fig. 3: two neighbouring rectangles in the sequence have diagonals positioned at right angles.

Fig. 1

The construction method of mean geometric proportional. A circle diameter AD is divided with a random line at right angle, intersecting circle at the point E. Shaded figures have equal surfaces: the square is equal to the rectangle, b² = ac. This is the main construction that Zloković further used for reciprocal concatenation

Fig. 2

Zloković’s original drawing that explains the method of reciprocal concatenation, using the construction of mean geometrical proportional (Zloković 1954b: 1001). This method provides geometrical progression 1, m/n, (m/n)², (m/n)³ (Marjanović 2012: 311)

Fig. 3

Reciprocal concatenation—the sequence of the rectangles in different scales by the principle of reciprocal diagonals (diagonals at right angles)

While researching ancient knowledge on proportions Zloković realized the significance of the mean geometric proportional construction. In his copy of Euclid’s Elements, at Book II Zloković sketched over the explanatory illustration of proposition 11: ‘To cut a given straight line so that the rectangle contained by the whole and one of the segments equals the square on the remaining segment’ (Euclid 1956: II, 402). On his drawing (Fig. 4), Zloković pointed out the construction method of the mean geometric proportional in the illustration of Euclid’s text. Zloković also highlighted that the mean geometric proportional was very important throughout ancient works, especially in Plato’s Timaeus (Zloković 1954b: 833). As we show further on, Zloković revealed its presence in the ancient method of using dividers. He then combined it with a musical analogy in order to make these ancient methods useful for contemporary architects. His method was based on arithmetic and geometric analyses.

Fig. 4

The explanatory illustration of proposition 11, from Zloković’s personal copy of Euclid’s Elements (book 2). Zloković draw additional lines in pencil, thus pointing out the mean geometrical proportional inbuilt in Euclid’s original diagram

Correlation Among Proportional Systems

One of the problems Zloković dealt with was the correlation among proportional systems. He relied on two geometric diagrams as proof of this correlation.

Firstly, he referred to Adolf Zeising’s diagram⁷ of the sides of regular polygons derived from the rectangle 1:Ф (Zloković 1949: 56). He found a method to construct side lengths of 3, 4, 5, 6 and 10-sided inscribed polygons that share a circumcicle radius (Fig. 5, left). Each polygon is also a key figure for a different proportional system, as it embodies a proportional ratio (Fig. 5, right). Thus, regular polygons are key figures for geometrical construction of proportional systems: (1) triangulation (system √3), embodied in the triangle and regular hexagon; (2) quadrature (system √2), embodied in the square and regular octagon; (3) golden section, embodied in the pentagon and decagon.

Fig. 5

The division of the Golden rectangle 1:Φ (Zeising 1968) provide side lengths of regular polygons (Zloković 1965: 145; highlights in colour by Authors). Zeising has found a method how to construct side lenghts of 3, 4, 5, 6 and 10-sided inscribed polygons that share circumcicle radius. Each polygon is also a key figure for a different proportional system as it embodies a proportional ratio (image on the right: Authors)

Secondly, Zloković referred to another summary diagram derived from a square as the starting shape (Fig. 6). Due to the interrelation of irrational proportions √5, √3 and √2 with Ф, showed inside the rectangle √5:1, he emphasized that it is possible to combine various proportional systems. Accordingly, while all above-mentioned proportional systems could be expressed by the means of golden section, the inverse is rarely true. This fact strengthened Zloković’s belief in the superiority of the golden section over other proportional systems (Zloković 1965: 164). In short, geometrical construction of all proportional systems derives from two basic geometric shapes: circle and square.

Fig. 6

Zloković’s summary diagram of irrational proportional systems (√Φ, √2, Φ, √3 and √5) and ratios 1:1 and 1:2 (Zloković 1965: 164; Marjanović 2012: 263)

Probably obtaining the idea of simultaneous representation of different proportional systems from Benoit’s diagrams of the façade of Notre Dame in Paris (Benoit 1934: 303), Zloković considered all above-mentioned methods as supplementing each other, so he used them in a single diagram. In an example of skeletal system façade, he showed the application of harmonic ratio 4:3 by means of the square method, reciprocal concatenation and the translation of heights into the golden section system (Fig. 7).

Fig. 7

On the left: Proportional diagrams of Notre Dame in Paris front façade (Benoit 1934: 303) based on square method (I), harmony of similar figures (II and III) and rhythm based on Golden section (IV). On the right: Zloković’s proportional diagram of a contemporary façade represented simultaneously by square method, reciprocal concatenation and heights translating into Golden section system (Zloković 1954b: 1005)

Both the geometric and the arithmetic approaches of ancient mathematics had their implications in the science of proportions. For example, David Fowler defined ‘anthyphairetic computations’ as a ‘process of repeated, reciprocal subtractions which is then used to generate a definition of ratio as a sequence of repetition numbers’ (Fowler 1987: 31). In his pictorial example, Lionel March (1999: 450) showed how anthyphairetic calculations are used in the geometric process of obtaining a unit remainder, the greatest unit module which measures any chosen rectangle (with rational sides). Zloković did not use the geometrical method as defined by March; instead, he used the arithmetic process of obtaining a unit remainder for a certain rectangle. He positioned a modular grid over either the main or reciprocal rectangle (Fig. 8, left). The grid module is obtained from the ratio. For example, in Fig. 8, on the right, the ratio is 3/2. The square of the denominator equals 4 (2² = 4), which means the rectangle’s shorter side is to be divided into four parts to obtain the module (Zloković 1954b: 834).

Fig. 8

Reciprocal concatenation of ratio 2:3 (Zloković 1954b: 834) and its application on a contemporary façade based on window ratio 2:3 (Zloković 1954b: 837) (highlights in red by authors)

Zloković opposed the mainstream belief that ‘proportional application depends only on artist’s intuition, as it is innate and thus unreachable by reason’ (Zloković 1955b: 82). His view was that an experienced architect who relies on pure intuition actually applies the system of the golden section, even though he might not be familiar with geometrical mechanism of continuous division (Zloković 1954b: 209). However, he maintained that an architect should be familiar with the science of proportions, the same way a musician studies musical harmony. Zloković believed that intuition would never lead an architect to apply systems √2 and √3 in his design. These two systems can only be obtained by strictly geometrical means (by use of dividers or triangles) as they are essentially ‘monotonous, not elastic enough and sometimes too rigid’ (Zloković 1955b: 176). Zloković supported this conviction with the analysis of Vignola’s classical orders (Zloković 1956).⁸ Vignola’s modular numbers were empirically obtained by artist’s intuition. The almost four centuries long application of Vignola’s modular numbers in architecture was a positive proof that the shapes based on these numbers ‘please the eye’ (Zloković 1955b: 82). Based on this, Zloković analysed Vignola’s classical orders and proved that all of them could be derived from geometrical constructions of continuous division (Zloković 1956, 1957a).

Whenever he wanted to apply certain proportional systems in his design, Zloković started from geometrical outlines, and only after obtaining a satisfying diagram, he passed to arithmetical control and modular dimensioning (Zloković 1949: 45–46).⁹ Based on his practical experience in contemporary architecture, he claimed this was the most appropriate way to apply chosen proportional system in design. Always concerned with practical application, Zloković was aware that there were two possible ways to show an applied proportional system on a technical drawing: by writing rational modular numbers on dimension lines or by drawing geometrical construction lines. Uniting both approaches, Zloković emphasized their correlation. When applying chosen proportional system in design, Zloković claimed that, based on his experience, the geometrical method should be given priority. Then, derived ratios would be translated into rational modular numbers by means of arithmetical calculations (Zloković 1949: 45, 54).

When it came to translating irrational numbers into rational ones, Zloković considered the knowledge on perception. He referred to Milutin Borisavljević’s explanations of the physiology of optics and visual comma,¹⁰ in order to show that translating irrational numbers into rational values implies visually imperceptible corrections. In other words, we achieve the same architectural result by using the rational values of the set F rather than the irrational values of the Φ system (Zloković 1955b: 83).

Preferential Numbers

In order to apply reciprocal concatenation in contemporary architectural design, Zloković was looking for the set of preferential coefficients—the set of numbers that enables as many as possible applicable measures in building and also provides composing characteristics (addition and multiplication), but stays aesthetically neutral (Milenković 1977: 23). He was searching for the ideal combination which would offer an architect the sufficient, but not excessive, number of elements (multiples of the main module, e.g. M = 60 cm). He believed that the solution lies within the smallest ‘Pythagorean triple’,¹¹ Plato’s double lambda, harmonic consonants, geometric and recurrent sequences. These sets of prime numbers have many common members. However, probably the best combination would be the one whose members provide ratios that are integrated in as many proportional systems as possible.

Zloković’s common method of evaluating sets of numbers was their comparison to anthropomorphic systems of measures. He examined various sets of prime numbers distinguishing the smallest ‘Pythagorean triple’: 3, 4, 5. Quadruple values of 3, 4 and 5 represent typical unit divisions in 12, 16 and 20 equal parts integrated in anthropomorphic systems of measures (Zloković 1958: 9). That proof encouraged him that his research was heading in the right direction. He wrote:

Geometric sequences with a coefficient 2 and 3, based on Plato’s double Tetraktys (lambda) 1, 2, 4, 8 and 1, 3, 9, 27, integrated, without distinction, in all the [preferential coefficients proposals], only partially solve the problem itself (Zloković 1958: 8).

Zloković examined the system of Plato’s lambda, crossing two or more geometric sequences with factors 2, 3 and 4, then 2, 3, 4 and 5 (Fig. 9), as well as 2, 3, 5 and 6. He compared these geometrical sequences with recurrent sequences based on the golden section: 1, n, 1 + n, 1 + 2n, 2 + 3n, 3 + 5n, 5 + 8n, 8 + 13n…. Finally, he concluded that recurrent sequences ‘adapt more easily to common proportional systems applied in architectural composition in order to harmonize certain parts with the entire composition’ (Zloković 1958: 9).

Fig. 9

Zloković’s examination of geometric sequences with factors 2 and 4 (vertical direction) and factors 3 and 5 (in oblique directions) based on Plato’s lambda (Zloković 1965: 165); text translated from Serbian by authors

Ancient Proportional Dividers with Unequal Legs

In Zloković’s time, dividers seemed redundant. Architects mainly used 45° and 30°–60° triangles, well known in the history of building, derived by diagonal division of a square and vertical division of an equilateral triangle. These triangles were symbols of triangulation and quadrature (Zloković 1955a: 199). Zloković proved that both triangles could be easily replaced by the application of adequate dividers with asymmetrical legs (Fig. 10).

Fig. 10

Zloković’s explanatory diagram showing that right angle triangles can be easily replaced by adequate proportional dividers (Zloković 1960: 45)

In 1957 Zloković had published an interpretation of the possible manner of using ancient proportional dividers with four points, showing how they enabled the application of geometrical sequences, and thus the reciprocal concatenation of a ratio defined by the divider’s legs (Fig. 11). The inspiration for this significant study was the published drawing of a bronze divider with asymmetrical legs found in 1892 in a Roman archaeological site in Gradac (Bosnia and Hercegovina).¹² Measuring on his own, Zloković was intrigued to find that the ratio of the divider’s legs was 9:5. He was eager to discover its origin and its role in compositional methods of the past. Finally, he offered a convincing explanation of the method used in practice, which he demonstrated on a few ancient monuments.¹³

Fig. 11

Zloković’s explanatory drawing shows how ancient proportional dividers enable the application of geometrical sequences. Divider’s legs define a ratio further applied by means of the reciprocal concatenation (Zloković 1960: 44)

There are three different ratios defined by the length of the dividers’ asymmetrical legs: 2:1, 8:5 and 9:5. Those three, found in museums, were the only asymmetrical dividers known to Zloković.¹⁴ The ratio 2:1 is a double square, an octave in musical harmony and a sequence of the Pythagorean lambda. Due to its Fibonacci sequence numbers, the minor sixth ratio 8:5 is directly related to the golden section, that is, the recurrent series that starts with 1 and 2: 1, 2, 3, 5, 8, 13… Zloković assumed that ratio 9:5 may have derived from the 3 × 3 magic square,¹⁵ in which numbers 5 and 9 play an important role: the number of cells is 9 and the number 5 has a central position as the arithmetic mean of two neighbour cells integers in column, row and diagonal. Zloković emphasized three such magic squares: Neo-Pythagorean (100 AD), Chinese (1000 BC) and a cross with equal arms filled with the numbers of Jehovah (Fig. 12). Numbers 5 and 9 also appear in the recurrent series that starts with 1 and 4: 1, 4, 5, 9, 14, 23, 37, 60. Zloković underlined the significance of all the recurrent series because of their relation to golden section. Using limit function, ratio of two consecutive numbers of any given recurrent series will result in irrational ratio corresponding to golden section ratio.

Fig. 12

Zloković’s drawing of three types of magic squares: a neopythagorean, b, c Chinese, d cross with arms of equal length and numbers of Jehovah (1, 3, 5, 7, 9) also contained in Chinese magic square (Zloković 1960: 47)

Zloković predicted that proportional dividers with ratios 3:1, 3:2 and 5:3 are yet to be discovered, because the 3:2 and 5:3 dividers were mainly based on the relation with the Fibonacci sequence and the 3:1 divider Zloković considered inseparable from already found 2:1 divider. These dividers together enable twofold and threefold divisions and reciprocal concatenation—two geometrical sequences from Plato’s double tetractys (Zloković 1960: 48). Numbers derived from the double tetractys were incorporated in anthropomorphic measure units in ancient architecture (Zloković 1955a: 189). Another proof in favour of their possible existence is a drawing of two proportional dividers—3:1 and 2:1—in Juan Caramuel’s study Architectura civis recta y obliqua of 1678 (Zloković 1960: 49).¹⁶

The dividers were used to construct a larger or a smaller image of one figure. This common explanation is not entirely satisfying, leaving divider’s use mysterious (Zloković 1960: 46). Zloković’s analyses proved quite the opposite: the divider was used with a tightened joint, so the distance between divider’s legs was not enlarged nor decreased once the joint was fixed. Its practical use was actually a geometric method that consisted only of subtraction and addition of two dimensions defined by divider’s legs distances (Table 1). The practical application of such a divider is based on a diagram of mean geometrical proportional, where k is the ratio of the shorter and longer leg or smaller and larger opening of the divider (a:b = p:q): a geometrical progression.

Table 1 Zloković’s façade system for a modern skeleton building based on the usage of divider 9:5 (Zloković 1958, XIX; Marjanović 2012: 291)

Zloković claimed that ancient dividers facilitate the construction of a special case of geometrical proportion, which he called ‘square proportion’ (Zloković 1960: 53). The ordinary geometric proportion expressed in formula a:b = b:c, does not always allow the use of rational numbers. However, its special case derives only rational numbers: a²: (a × b) = (a × b): b². Zloković graphically showed how square proportion is integrated in ancient 2:1, 3:1 and 3:2 dividers (Fig. 13).

Fig. 13

Zloković’s graphical explanation of square proportion, integrated in dividers 2:1, 3:1 and 3:2 (Zloković 1960: 53)

Zloković considered ancient preferential numbers important for contemporary architectural design, because the number sequences are best suited for the coefficients of the basic building module compared to any others known up to date. Zloković developed the numerical combinations based on ratios 8:5 and 9:5 (Fig. 14). Preferential numbers appearing in both numerical combinations were highlighted as ‘ultra-preferential’. By means of ultra-preferential numbers, irrational proportional systems can be transposed into rational numbers fractions. Thus, Φ:1, √3:2, √5:2 or √Φ:1 are approximated by 24:15, 24:18, 20:18 and 23:18, respectively. In order to show an application of this, he provided a geometric scheme of the Parthenon’s main façade constructed with the 9:5 divider. For a building module he chose 3 Greek palms and for the divider’s openings 15 and 27 palms. The axial distance was a modular measure for the proportional diagram (Fig. 15). He did not consider this group of numbers to be an original discovery, but rather a reconstruction of a method widely used in the Greek and Roman periods. Due to the findings of continuous division in ancient art and architecture, Zloković wanted to mathematically prove the significance of the golden section for architectural composition.¹⁷ However, the method of its practical application remained unknown. Even Euclid’s definition was merely a geometrical construction, with no evidence of its application in practice. Zloković’s explanation was very simple, yet thorough and convincing. He concluded that ratio 9:5 was forgotten in time, but well-known in Antiquity. Consequently, he thought of the 9:5 proportional divider as the most prestigious one among three existing divider types, because the wide range of preferential numbers derives from it. Zloković demonstrated that 9:5 dividers enable quick and easy construction in any proportional system.

Fig. 14

Zloković developed numerical combinations (ultra-preferential numbers) based on ratios 9:5 and 8:5 (Zloković 1960: 78)

Fig. 15

Zloković’s geometric scheme of Parthenon’s main façade constructed with divider 9:5. He used 3 Greek palms for building module, 15 and 27 palms for divider’s openings and axial distance as a modular measure for the proportional diagram (Zloković 1960: 81)

Application of Reciprocal Concatenation in the Architectural Practice of Zloković

Although Thiersch and Le Corbusier drew public attention to reciprocal concatenation, Zloković realised the need for further research in order to make these ancient methods useful for contemporary architects and the building problems of the time. He suggested that musical analogy¹⁸ could be used for reciprocal concatenation. Consequently, he examined the systems of fifths (Fig. 8) and fourths, using a diagram of mean geometric proportional, where $\frac{m}{n}$ is a harmonic relation—4:3 for the system of fourths and 3:2 for the system of fifths. For the system of the fourths, he wrote:

The similar manner of concatenation I found in secular stone architecture of our south sea coast, between the sixteenth and twentieth centuries. I believe that the occurrence of reciprocal measures on many buildings is nevertheless only the consequence of inherited and mechanically transmitted recipes whose origins should be looked for in medieval guilds and even further in the past—in the composing methods of Antiquity (Zloković 1954b: 1002).

In order to demonstrate the application of this method in practice, Zloković analysed two one-story skeletal building system façades. He used axial distance a and storey height h, as key measures for modular coordination and the proportions of the façade.¹⁹ Firstly, he adopted harmonic relation 4:3 and 3:2 as the ratio of window sides and the basis for the reciprocal concatenation of façade system. Secondly, in order to continue the process of application he underlined the necessity of checking whether the adapted dimensions correspond to the building’s function.

Zloković compares the façade based on the system of fifths 3:2 with ‘typical examples of Balkan wooden skeletal buildings’ (Zloković 1954a: 179). He also traced it in contemporary public buildings for administration, education and health care. Since the ratio 3:2 belongs to Fibonacci sequence, Zloković underlined its kinship with the irrational Ф system. He applied the golden section in his villa and house designs: Villa Zloković, 1927–1928; Villa Prendić, Belgrade, 1922–1933; Nevena Zaborski house, Belgrade, 1928 (Blagojević 2003: 198–221).

In order to show his application of reciprocal concatenation, we analysed proportions in two schools designed and built in two distinctive periods (middle and late) of Zloković’s architectural practice.

The Elementary School, Jagodina

The Elementary School in Jagodina (1937–1940) provides a good example of his idea of combining reciprocal concatenation with other proportional systems. The school (Figs. 16, 17) is considered to be one of his masterpieces. It is thought that this design was influenced by Italian Rationalism and Giuseppe Terragni’s Casa del Fascio (Blagojević 2003: 215), although with a different proportional diagram.²⁰ Since neither the plan nor the original proportional diagrams were published, we analysed the main facade, relying on Zloković’s theoretical standings.

Fig. 16

Elementary School in Jagodina—South façade contour, fenestrated part on the main façade and a window contain the same proportion 9:4. Reciprocal concatenation of proportion 9:4 incorporates ratios 5:8 and 8:13, i.e. 1:√5 and 1:Ф (image: authors)

Fig. 17

Elementary School in Jagodina. Photograph of the main façade under construction (top, Milan Zloković Foundation). South elevation with positions of constructional elements—beams and columns (middle, by Authors). Proportional analysis of the South elevation shows the possible application of reciprocal concatenation and ratios 4:9 and 8:4 (bottom, by authors)

The proportional analysis of the facade unit showed the existence of reciprocal concatenation. In order to provide the required illumination of classrooms, window design was highly important. Minimum distance between windows determined the axial distances between the columns and beams of the building’s skeletal system. The ratio of the sides of the windows is 4:9, which is approximately 1:√5 (Fig. 16). This ratio defined the fenestrated part of main façade’s surface as well as the façade’s contour. The height of building’s base equals the height of the window. Basic ratio has symmetrical subdivisions: a central square and two lateral rectangles. Rectangles’ sides stand in ratio 5:8, numbers from Fibonacci sequence. The √5 system is derived from the golden sequence: √5 = (2Ф − 1). Reciprocal concatenation repeated form provided 4:9, 5:8 and 8:13, the first of which approximates 1:√5 and the second and third of which approximate 1:Ф (Figs. 16, 17). Proportional analyses (Fig. 17) shows that Zloković carefully chose the dimensions and positions of all main compositional components: the fenestrated part of main façade, its position relative to façade’s contour, window dimensions and the body of the foyer.

The Teacher Training School, Prizren

The Teacher Training School in Prizren (1960), Zloković’s penultimate project and the first prefabricated concrete building in Yugoslavia (Fig. 18), was designed together with his son and daughter, architects Djordje Zloković and Milica Mojović (Zloković et al. 1961).²¹ This building is an example of the practical application of his last great theoretical achievement: the geometric method based on the 9:5 divider. The technical drawings were simplified by expressing all dimensions in modules. The basic module was 1 M = 1 dm = 10 cm.²² School building site was divided by modular grid 90 M × 90 M = 9 m × 9 m (Fig. 19). This site module equals 5 unit façade modules (5 × 1.8 m = 9 m) (Fig. 20). As highlighted on the façade diagram, all dimensions were controlled by the geometrical method based on the 9:5 divider. The method consists only of subtraction and addition of two dimensions defined by the distances between the divider’s legs, which is shown as black curved surfaces on the side of the diagram (Fig. 21). The larger opening equals 9 M and the smaller 5 M. Thus, the façade unit, enlarged in a separate proportional diagram, is 2 × 9 M = 18 M wide and 3 × 9 M + 2 × 5 M = 37 M high. The unit is inscribed in a double square with a slight extension of 1 M to form the storey height (37 M = 370 cm) (Fig. 20). All main modular dimensions marked on the façade and plan diagrams belong to recurrent series: 1, 4, 5, 9, 14, 23, 37, 60… (Figs. 21, 23, Table 2). This series also defined the three-dimensional geometry of hood moulds and parapets, forming a geometric play and creating shadows on the prefabricated façade wall (Fig. 21).

Fig. 18

Teacher Training School in Prizren built in 1960 (Milan Zloković Foundation)

Fig. 19

Teacher Training School in Prizren—Zloković’s drawing of the building site divided by modular grid 90 M × 90 M = 9 m × 9 m (Zloković et al. 1961: 49)

Fig. 20

Teacher Training School in Prizren. Zloković’s proportional diagram of façade unit, 18 M wide (Zloković 1965: 185). Proportions are verified with proportional 9:5 and 8:5 dividers. The proportioning method consists only of the subtraction and addition of the two dimensions defined by the distances between the divider’s legs (black curved surfaces on the side of the diagram). The façade unit is inscribed in a double square with a slight extension of 1 M to form the storey height

Fig. 21

Teacher Training School in Prizren—Zloković’s proportional diagram of main façade (left); Axonometric aspect of facade elements’ joints and montage (right) (Zloković 1965: 183)

Table 2 Teacher Training School in Prizren—Table with modular measures of School’s prefabricated elements

The other proportional diagram showed that Zloković combined dividers 9:5 and 8:5, possibly to prove their compatibility and the possibility of simultaneous application of more than one proportional system in the same architectural design (Fig. 20). He used both reciprocal concatenation and modular measures. Reciprocal concatenation of ratio 1:2 is traceable in the designs of both the plan and the façade (Figs. 22, 23, 24), demonstrating the deep inner relatedness of the horizontal and vertical dimensions.

Fig. 22

Teacher Training School in Prizren. Proportional analysis of Zloković’s original layout (Zloković 1965: 183). It shows the possible application of reciprocal concatenation of ratio 1:2 (Authors)

Fig. 23

Teacher Training School in Prizren. East façade (Zloković 1965: 183) and its proportional analysis (image: authors). Analysis shows the repetition of a basic façade unit (presented in Table 2). Square diagonals (dashed lines in green) and half-square diagonals (in red) regulate the entire façade composition

Fig. 24

Teacher Training School in Prizren—South façade (top) and its proportional analysis (bottom, image: authors). Analysis shows the main proportion 1:2 (double square 6 × 12 units, dashed lines in green) and the building base 1 M high

The standardization of the façade openings was inherited from vernacular architecture (Blagojević 2015: 65). Here, the prefabricated façade unit defined the rhythm of the façade. On the east façade, units with high restroom windows broke the repetition of the basic façade unit. The three-storey restroom block unit represents a rectangle inscribed in the double square, whose main proportion 1:2. The south façade is also inscribed in a double square (6 × 12 units wide) positioned on a base 1 unit high. Like the School in Jagodina, the height of the building’s base corresponds to the modular unit that is 1.8 m. However, the base height is used to overcome the terrain’s slope. The prefabricated concrete elements on the south façade are faced with a local traditional stone gable wall, proportionally incorporated. The proportional analysis (Figs. 22, 23, 24) shows that the repetition of the prefabricated façade unit was skilfully interrupted when needed (stone gable walls, restroom block’s unit) while still respecting the chosen proportional system.

A period of about 20 years separates these two analysed buildings. The first building is considered to be one of his early Modernist masterpieces. The second belongs to the period of modular coordination and prefabrication. However, we can discern similarities in the designs: they both demonstrate the possibility of application of reciprocal concatenation. The analysis shows that Zloković applied his theoretical findings in practice, changing the practical approach over time based upon his theoretical research on proportions.

In Jagodina we demonstrated the possible combination of more than one proportional system and in Prizren the use of preferential numbers needed in modular coordination. The dimensions and position of all main compositional components have been carefully chosen even in the prefabricated building where unit repetition might endanger the dynamic effect of the façade. The main difference is that in his last constructed building, Zloković applied his most innovative theoretical achievement based on a forgotten ancient method. Using the same preferential numbers that defined the Parthenon façade, Zloković achieved completely different result on a modern building. As Zoran Manević (1980: 50) noted, ‘modular design when built loses its repetitiveness and uncovers author’s inner visions’. Zloković showed that modern architects can use this ancient mathematical tool without fear of over-control.

Conclusion

Milan Zloković researched proportions in several ways: investigating the heritage of the the Balkans and Europe, analysing ancient recommendations on proportions and creating modular coordination as a solution for building problems of post-war Europe. Researching ancient proportional dividers and examining their possible applications in building, Zloković mathematically analysed the proportional solutions of ancient builders and hypothesised that the method of reciprocal concatenation is rooted in the ancient philosophical concept of analogy. He also pointed out that, due to its compatibility with various proportional systems, the method of reciprocal concatenation is a very useful tool for contemporary architects. Besides its aesthetical and functional justification, ‘geometrical proportion narrows the number of combinations to some extent, but on the other hand, their range remains wide enough, so it most certainly does not convert architect’s choices into mechanical actions and definitely does not threaten freedom of design’ (Zloković and 1954b: 1006). Our proportional analysis of the Elementary School in Jagodina (1937) and the Teacher Training School in Prizren (1960) suggests that in his architectural practice Zloković applied reciprocal concatenation, combining it with other proportional systems.