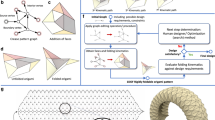
Abstract
The objective of this research is to explore the ability of folded origami tessellations to adapt to free-form surface configurations and to evaluate the structural behavior of these folded tessellations for architectural and engineering applications. A mathematical exploration of the kinematics of folding provides the basis for understanding the relationship between the geometric parameters of the Miura-Ori origami fold pattern and the flexibility of the three-dimensional folded form. The structural behavior of folded plate structures derived from the Miura pattern on an architectural scale is studied in an effort to answer the question: does function follow fold? A parametric workflow provides the platform for evaluating the effect of fold pattern variations on the structural performance of the folded geometry, and computational methods are used to optimize the performance of the structure.
Similar content being viewed by others
Introduction
The geometric flexibility of folded origami tessellations, combined with the structural efficiency of folded plate structures, gives origami strong potential for architectural and engineering applications. The flexibility of the folded Miura pattern can be attributed to the auxetic nature of the fold pattern. This auxetic nature implies that the folded form has a negative Poisson ratio, so that when the folded tessellation is pulled along one axis, it will expand along the orthogonal axis. This enables the folded tessellation to be globally distorted into shapes with both single and double curvature, unlike the flat sheet that the tessellation was folded from. Compared to the unfolded flat sheet, the folded Miura tessellation not only demonstrates increased deformability, but also increased structural stiffness, as a result of the increased second moment of area due to the folds in the sheet. Researchers, including Tomohiro Tachi and Mark Schenk, have explored this dichotomy of the geometric flexibility and structural stiffness of folded origami tessellations in their studies of the mechanical properties of origami and the kinematics of folding. In his work, Tachi has established mathematical rules in order to simulate folding and to design free-form shapes from origami (Tachi 2009), while Schenk has examined the process of folding in order to better understand how the increased stiffness of folded sheets can be used for engineering applications. The research summarized in this paper aims to build upon the work of Tachi and Schenk by exploring how folded plate structures derived from the Miura tessellation can be used to design free-form architectural surface structures.
The research examines the relationship between the geometric parameters of the Miura fold pattern and the structural performance of the associated folded plate structure in order to establish the strengths and weaknesses of the pattern and the viability of using the folded tessellation as a structural system to support free-form surface geometries on an architectural scale. The research was a collaborative effort between architects at La Sapienza University in Italy and computational designers and structural engineers at Leslie E. Robertson Associates in New York, and was performed in two phases. The first part of the research explored the geometric and mathematical rules of folding. Visual scripting using Grasshopper, a parametric modelling plug-in for the 3D modelling software Rhino, was used to generate origami-based architectural folded plate structures. Parametric modelling techniques were used to deform the digital representations of the folded Miura tessellation to match the curvature of various mathematical surfaces, including the doubly curved paraboloid and hyperbolic paraboloid.
In the second part of the research, the structural behavior of these origami-based folded plate structures was evaluated in order to gain an understanding of how variations in the fold pattern, as well as global shape parameters and structural support conditions, affect the strength and stability of the overall folded form. An integrated workflow was established to digitally generate the 3D geometric representation of an origami-inspired folded plate structure, to analyze the structure under anticipated loading conditions, and to optimize the performance of the structure by adjusting the distribution of material over the plate structure.
Research Part 1: Geometry and Kinematics of the Origami Unit Module
Origami tessellations are built up from a unit module which is arrayed across a surface. The geometry of this unit module and the kinematics of folding the module dictate the range of distortions that can be achieved by the folded origami tessellation. The unit module is composed of rigid panels that are connected along their edges by hinges, which enable movement of the panels relative to one another. With an understanding of the kinematics of the unit module, the movement of one module can be digitally simulated and, subsequently, digital models of the entire surface pattern can be controlled. Two methods for controlling the folding simulation of the unit module, and consequently the deformation of the surface pattern, were developed: (1) The first method uses an algorithm based on geometric rules to generate a folded form from a flat crease pattern, and (2) the second method employs a physics engine to simulate folding.
Folding by Geometric Rules
A folded origami tessellation is created by repeating the basic folded unit module in an array over a surface to create a network of mountain and valley edges which act as hinges to allow the model to move and achieve various geometric configurations (Fig. 1). Mountain edges (shown in green in the accompanying figures) are assumed to move in a positive direction in space, while valley edges (shown in red) are assumed to move in a negative direction in space relative to the start position. The relative movement of these edges as the flat pattern is folded is based on the geometric relationship between the mountain and valley lines of the flat fold pattern.
The fold pattern shown in Fig. 1 represents the unit module of the Miura tessellation. The designation of mountain and valley lines will result in a standard ‘reverse fold.’ The following geometric relationships and movement rules were used to develop an algorithm that simulates the folding of a digital model of the reverse fold:
-
Panel S1 will move in direction V1 and panel S2 will synchronously move in direction V2
-
Edges EF and HG move closer together, causing edge IL to move upward (since it is designated as a mountain fold line) as panels S3 and S4 rotate about edges EF and HG. Edges EF, HG, and IL remain parallel to one another during this transformation.
-
Point P is shared by panel S3 and S4, and K1 and K2 are the projections of P onto edges EF and HG, respectively. Point P moves simultaneously along circular paths c and d, which are centered on points K1 and K2, respectively. There are two solutions to the intersection of Paths c and d. The solution that is selected to describe the location of point P is based on the designation of hinge line IL as either mountain or valley fold line.
A digital model was built in the 3D modelling software Rhino and the Grasshopper plug-in for Rhino was used to implement the algorithm and simulate folding. Folding of the model is initiated by imposing a translation of point E along vector V1. This translation then drives changes in the orientation of panels S1, S2, S3, S4, and S5. Figure 1b illustrates the movement trajectories of the panels. Panel S1 moves as a result of translation of point E along vector V1. The movement of panel S3 is the result of translation of point E along vector V1 and rotation about hinge EF. The movement of panel S5 is the result of translation along vector V1, rotation about hinge EF, and rotation about hinge EI.
Folding by Physics Simulation
In the second approach to folding simulation, the digital model of the unit module in Rhino is converted into a network of spring elements using Kangaroo, a physics engine that runs within the Grasshopper environment. Kangaroo is also used to apply virtual forces, as well as translational and rotational restraints to the spring model in order to simulate folding and control the overall configuration of the folded pattern. With the use of visual programming in Grasshopper, an algorithm is developed to parametrically generate the flat fold pattern of the tessellation and subsequently impose bending forces on the surface model in order to generate a 3D folded shape. The subsequent sections discuss in more detail how the simulation process was used to fold and deform digital models of the folded Miura tessellation.
Digital Folding of the Miura Unit Module
The first step is to build the unit module in the 3D modelling software Rhino, using Grasshopper (Fig. 2a). The unit module consists of four quadrilateral panels, defined by mountain and valley edges. The designation of the fold lines as mountains and valleys is based on the reverse fold mechanism, in which folding occurs simultaneously about two orthogonal axes (Fig. 2b).
The unit module was modelled in a partially folded state in order to facilitate application of the algorithm, which applies forces to generate movement. This unit module is then repeated over a surface area to build the tessellation. Any duplicate edges in the resulting array are eliminated to ensure that each panel in the surface pattern shares a single edge with adjacent panels. The mountain and valley edges of the partially folded tessellation are polylines v and w (heretofore referred to as ‘zig-zags’ and ‘strips’, respectively) (Fig. 2b). In order to simulate movement of the surface pattern in digital space, the edges of the geometric model must be converted to spring elements, with an assigned stiffness value. This is achieved using Kangaroo, a physics engine that operates within Grasshopper. The entire folded surface can then be activated by applying a bending force to the hinges between adjacent faces of the folded mesh. Varying the fold angles generates movement throughout the entire model. Controlling the degree of this angle is one method that can be used to control the shape of the folded surface. By applying “attraction” forces between the lowest or highest vertices of the folded surface pattern and a target surface, these vertices of the fold pattern will be pulled and guided to match the curvature of the target surface (Fig. 3).
In order to fold the origami pattern, Kangaroo must balance the effect of several forces acting on the system of springs defined by the fold pattern, including the stiffness of the springs, bending force about hinges, planarization of mesh faces, and the ‘PowerLaw’ force that pulls the folded origami to the target surface. During the development of the folding simulation script, the strengths with which each of these different forces was applied to the mesh model were varied in order to find the combination that yielded a correctly folded mesh. Based on the results of testing combinations of force strength values, it can be concluded that there must be one governing force. For example, if the strength given to the mesh stiffness is high, the strength given to the PLaw force should be relatively low. It should also be noted that this difficulty in balancing the effect of forces on the spring system occurs because the quad-based Miura pattern is over constrained. When the quadrilateral faces of the pattern mesh are triangulated, the system is no longer over-constrained, and the mesh folds correctly, regardless of the strengths of the applied forces.
If the tessellation is assumed to be rigidly foldable, all of the quadrilateral panels would be able to fold continuously from a flat to a fully folded state without deformation of the panels, and only hinging about the fold lines (Schenk 2011). A rigidly foldable tessellation will exhibit only one degree of freedom in its movement range when forces are applied to distort the tessellation. However, if the quadrangular mesh faces are triangulated by introducing an additional neutral fold-line along the shorter diagonal of each quadrilateral face (Casale and Valenti 2013), small deformations in the panels will enable the tessellation to adapt its overall shape to a doubly curved surface under the influence of applied twisting or bending forces. In order to accurately simulate the physical behavior of the folded Miura surface pattern under distortion forces, additional forces must be applied to the system to prevent stretching of the mesh faces and to control planarity of the panels. Mesh stretching is controlled by limiting all edges of the triangulated mesh to a constant length. Planarity of the mesh faces is achieved by controlling the degree of bending about the neutral fold line on each mesh face. If rigid foldability is to be preserved, bending about this neutral fold should not occur, and the fold angle should be 180°. When the folded surface pattern is adapted to a continuous, doubly curved target surface, the bend angle about the neutral fold line can be reduced to enable further flexibility of the surface pattern.
It was observed that the folding simulation of the quad-based mesh worked much more smoothly when the target surface was a hyperbolic paraboloid or an arch (bent about the longitudinal—“strip”—axis). This may be because the natural physical response of the Miura pattern is to assume a hyperbolic paraboloid shape when twisted and a saddle shape when bent (Fig. 4). It is expected that pulling the Miura pattern to an arch target shape (as well as a paraboloid) will cause some distortion in the panels because physical models show that the folded Miura is more easily twisted into a saddle shape (negative Gaussian curvature) than it is bent into an arch shape (zero Gaussian curvature).
Research Part 2: Structural Evaluation of Architectural Origami
Once the method of generating folded tessellations that match target surfaces was established, these digital representations of origami-based surface structures were analyzed as architectural structures to understand their inherent strengths and weaknesses. Pattern densities of mountain and valley fold-lines, as well as global shape parameters, such as Gaussian curvature, were varied and the structural behavior of the folded tessellation was assessed.
The structural analysis aimed to determine the effect of both global geometric parameters, including span, curvature, and support condition, as well as origami pattern parameters, including ‘zig-zag’ and ‘strip’ density, on the structural behavior of the folded origami when pulled to match a target surface. Three target surfaces were studied: paraboloid (positive double curvature), hyperbolic paraboloid (negative double curvature), and parabolic arch (single curvature). The support conditions were also varied in order to study variations in the force flow through the origami structure and to potentially identify a strong and weak direction of the folded origami structure. Table 1 summarizes the models that were studied.
A parametric workflow provided the platform for evaluating the effect of fold pattern variations on the structural performance of the folded geometry, and computational methods were used to optimize the performance of the structure by varying pattern geometry. The following software and Plug-ins have been included in the workflow followed for this study:
-
Rhinoceros 3D;
-
Grasshopper (parametric definition of fold pattern and target surface);
-
Kangaroo (for digital simulation of fold folding);
-
Karamba (for finite element analysis of folded form);
-
CSI SAP2000 (for verification of FE analysis results);
-
Microsoft Excel (for optimization loop).
Parameters for Structural Evaluation
The origami pattern was first defined parametrically in Grasshopper and then folded digitally using the Kangaroo physics engine. Rigid foldability, flat-foldability and developability properties of origami have been respected for this study. The folded mesh was then converted to shell elements and analyzed as a concrete folded plate structure (concrete strength = 16.7 MPa) using Karamba. The supports are all assumed to pins, restraining translation only. All loads are defined as mesh loads, applied to mesh vertices. The self-weight is calculated as a function of the mesh area, the thickness of the shell elements, and the unit weight of the concrete material specified. The self-weight (SW), live load (LL), and wind load (Wx and Wy) are applied according to the global axes, while the superimposed dead load (SDL) is applied locally to the mesh. As an approximation of windward and leeward wind load, half of the wind load value is applied to all of the mesh vertices. Table 2 summarizes the loads and load combinations that were used in the analysis.
Optimization
In order to compare the various origami models in terms of utilization, the maximum utilization (calculated as Von Mises stress/material yield strength) for all models should be approximately 1. For each model, an iterative loop evaluates the maximum utilization of all shell elements at a given thickness. For each new thickness, it applies an updated self-weight, and calculates the Von Mises stress in each shell element and compares it to the material strength. If this utilization is greater than 1 or less than 0.6, then a new thickness must be tested. If the utilization is greater than 1, the thickness is increased by a percentage of the current input thickness. If the utilization is less than 1, the thickness is decreased by a percentage of the current input thickness. This iterative process continues until the following criteria (Table 3) are met.
To avoid creating a circular reference within the Grasshopper script, the optimization loop sends the adjusted thicknesses, which are calculated within Grasshopper, to Excel and then reads them back into the Grasshopper script for the next iteration. A python script, which is run in Rhino, was written to automate and control the loop. The criteria for stopping the loop are defined in this Python script. Figure 5 illustrates how the loop works using Grasshopper, Excel, and Python.
Initial analyses of the folded origami structures revealed that the structure was sensitive to buckling for various combinations of loading and shell thickness distributions. Therefore, the optimization process is based on second order analysis, which takes into account the effect of the in-plane forces in the shell elements on their stiffness during loading.
When the optimization routine yields a large range of different thicknesses for a folded structure, an additional step in the routine can group the optimized thicknesses into ranges to reduce the amount of variability. For construction, it is preferable to have only a few different shell thicknesses in order to reduce the number of unique elements that need to be fabricated. However, for the purpose of comparing structural behavior, this large variety of thicknesses is acceptable.
The optimization loop was limited to 30 iterations, however, many models with opposite edges supported did not achieve a maximum utilization of 1.0 within these 30 iterations. This was because there were often a few elements along the unsupported edges that were overstressed, and the optimization loop continued to add material to these elements. For future analysis, an edge beam along unsupported edges or a diaphragm between the folds along unsupported edges will be added to the structural model to stiffen the free edges.
Analysis Results
In the assessment of the analysis results, a model was considered to be “more efficient” if more elements achieved a utilization closer to 1, if less material volume was required per unit area, and if the vertical displacement was less. A total of 37 models were analyzed for the Miura pattern to test the effect of span length, Gaussian curvature, boundary conditions, and pattern density on the behavior of the folded structures. Although the folded plate structures were analyzed under combinations of vertical loading (DL, SDL, LL) and lateral wind loading, only the analysis results for the worst-case combination of vertical loading (DL, SDL, LL) were considered in the evaluation of structural performance. For each analysis performed, the numerical results of element utilization, vertical displacement, and volume per unit surface area were collected and plotted as shown in the representative set of results for the Miura pattern in Fig. 6. Graphical results displayed in the analysis model, including thickness distribution, utilization, vertical displacement, force isolines, and planarity (Fig. 7) were generated and used to qualitatively verify expected behavior under the assigned loading.
Discussion
The analysis aimed to answer the following questions: how do curvature and boundary condition affect the “efficiency” of the folded structure, compared to a shell surface of similar shape? How does pattern density and pattern direction affect the efficiency of the folded structure?
Several conclusions can be drawn from the structural analysis of the folded Miura tessellation with respect to the type of surface (described by its Gaussian curvature), the degree of curvature of the target surface, the support conditions, and the density of the pattern, as described by the number of ‘strips’ or ‘zig-zags’ in the pattern. Shell element utilization in all cases was generally low due to sensitivity to buckling, since buckling will occur before the element stress reaches the material capacity.
Effect of Curvature on Structural Efficiency
In all three surface geometry models (paraboloid, hyperbolic paraboloid, and arch), a lower degree of curvature in the surface shape yielded better utilization of the panels of the folded plate structure, with more panels performing closer to their capacity. Shallower curvature also resulted in increased deflection, as expected. However, greater curvature resulted in the need for more material, which is not the case for basic thin shell structures of similar shape, which utilize the increased curvature to help resist bending forces due to loading. The need for thicker plates in certain regions of the folded plate structure at higher degrees of surface curvature may suggest that the plates weaken locally as they distort in order to match the target curvature.
Effect of Support Condition on Structural Efficiency and Stability
The models were analyzed under three different support conditions: supports along all edges, supports along zig-zag edges, and supports along strip edges. For all of these support conditions, the paraboloid-shaped Miura tessellation consistently required more volume per unit area to resist the applied vertical load. This suggests that forcing the tessellation to match a surface with positive Gaussian curvature, by bending it with positive curvature simultaneously about two orthogonal axes, introduced distortion in the panels of the folded plate structure, making them inherently weaker. For all support conditions, the arch-shaped and paraboloid-shaped origami models showed similar results in terms of utilization distribution, while the hyperbolic paraboloid model was consistently most efficient in terms of material use (low volume/unit area). The folded plate structure showed the best utilization distribution when forced to match the negative Gaussian curvature of the hyperbolic paraboloid target surface. This may be attributed to the auxetic nature of the origami tessellation.
When the strip edges were supported as opposed to the zig-zag edges, the models for all of the surface geometries demonstrated a more even utilization distribution (all panels were working at a similar capacity to resist the loading), but required more volume per unit area and deflected more under the applied loading. This suggests that the ‘zig-zag’ axis is the stronger axis (Fig. 8).
Deflection primarily occurred along the unsupported edges. In future analyses, a stiffening element or additional restraints will be added to the unsupported edges in order to obtain a better distribution of deflection over the entire structure.
Effect of Origami Pattern Geometry on Structural Efficiency
Reducing the number of zig-zag polylines in a given Miura surface pattern increases the overall depth of the folded section and, as a result, reduces deflections. Increasing the number of strip polylines increases the number of folds and reduces the panel size, making the folded plate structure more efficient in terms of utilization distribution.
Planarity of Panels
Planarity of the rigid panels in the folded origami structures is measured as the perpendicular distance between the two diagonals of a quadrilateral surface (Fig. 9) and provides an indication of the degree of distortion due to form-matching. A future study on the relationship between element planarity and utilization could provide valuable insight into construction strategies for architectural origami.
Conclusions
The ability to distort origami tessellations, such as the Miura Ori tessellation, to match a given surface shape, paired with the inherent stiffness exhibited by folded plate structures, gives origami tessellations great potential to be used in architectural applications. Scaling up origami for architectural applications requires structural evaluation of the folded form under anticipated loading conditions and boundary constraints, and consideration of material properties. By isolating the unit module that makes up an origami tessellation and gaining an understanding of the geometric relationships that define the fold pattern and of the kinematics of folding the pattern, mathematical algorithms can be developed to generate digital representations of the folded tessellations. This rule-based approach to generating geometric configurations of folded origami embeds flexibility into the design of origami-based folded plate structures.
In this research, a digital workflow integrated the generation of geometric models of the folded Miura tessellation in various configurations and provided a platform for evaluating the structural capacity of these architectural models. The results of the structural analysis suggest that the geometry of the tessellation’s fold pattern directly influences the structural performance of the folded plate structure. As demonstrated by the analysis results, the functional capacity of a folded plate structure based on a standard Miura fold pattern to resist bending is dependent on the orientation of the pattern with respect to the support conditions of the structure. Furthermore, the frequency of repetition of the unit module in the tessellation directly influences the strength and stability of the structure. The efficiency of a Miura-inspired folded plate structure is dictated by the fold pattern and therefore, modifications to the fold pattern can be made to improve the structural performance of the structure. It can thus be concluded that function therefore follows fold. This research provides a framework for designing folded plate structures derived from origami tessellations on an architectural scale and sets the stage for future work regarding the fabrication of these structures.
References
Casale, A. and G.M. Valenti. 2013. Architettura delle superfici piegate. Le geometrie che muovono gli origami. Rome: Edizioni Kappa.
Schenk, Mark. 2011. Folded Shell Structures. Ph.D. Thesis, University of Cambridge.
Tachi, Tomohiro. 2009. Generalization of Rigid Foldable Quadrilateral Mesh Origami. Proceedings of the IASS Symposium 2009, 2287–2294.
Author information
Authors and Affiliations
Corresponding author
About this article
Cite this article
Tsiamis, M., Oliva, A. & Calvano, M. Algorithmic Design and Analysis of Architectural Origami. Nexus Netw J 20, 59–73 (2018). https://doi.org/10.1007/s00004-017-0361-9
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00004-017-0361-9