Abstract
The human spine is the flexible support structure of our body. Its geometric shape is a result of the human evolutionary history, where especially the lumbar spine area (L1–L5) is most at risk of causing discomfort resulting from mechanical stresses. Herein, the intervertebral discs (IVD) between the vertebral bodies are the most susceptible elements, as these avascular structures have to provide the flexibility. It is widely accepted that the IVD are often the trigger for back pain. In the context of biomechanical research, it is therefore important to develop a model for the human lumbar spine with particular focus on the IVD.
The objective of the presented work is to subject the IVD of the lumbar spine to continuum-biomechanical research. Herein, a three-dimensional (3-d) finite-element model is developed that allows to estimate the influence of lumbar spine motion, i.e., bending, torsion and compression, on the resulting stress-field inside the IVD. Following this, the model can be utilised to detect inappropriate or excessive loading of the spine. The theoretical description of the IVD is based on a multi-phase continuum approach in the framework of the well-known “Theory of Porous Media” (TPM). This is a natural choice resulting from the avascular composition of the IVD. In general, IVD tissue is categorised as charged hydrated material with mechanical and electro-chemical internal coupling mechanisms. In order to capture these couplings, the underlying model incorporates an extracellular matrix (ECM) with fixed negative charges, which is saturated by a mixture of a liquid solvent and ions. Following the basic concept of the TPM, a volumetric averaging process is prescribed leading to volume fractions for the pore space and the solid skeleton as well as molar concentrations for the ion species in the pore fluid.
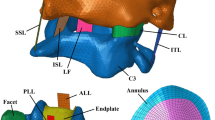
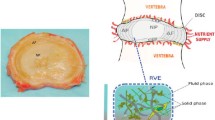
In detail, the IVD exhibits a gelatinous core known as the nucleus pulposus (NP), and an onion-like surrounding structure consisting of anisotropic crosswise fibre-reinforced lamellae, the annulus fibrosus (AF). Both regions are seamlessly merging into each other and consist of mostly collagen fibres of varying strength and direction as well as proteoglycans with adhering negative charges. As a result of these fixed negative charges and the fact that the interstitial fluid carries positively and negatively charged ions, a model is created that describes the mutually coupled behaviour of solid deformation and fluid flow. To illustrate the resulting coupled swelling and shrinkage process, it is sufficient to recall that the size of the human body is reduced by roughly 2 centimetres during the waking phase of the day. This change in height is triggered by mechanical loads stemming from the body weight, which squeezes the interstitial fluid out of the IVD, thereby losing altitude. Simultaneously, an electro-chemical imbalance is generated, which is compensated during the nocturnal resting phase, where the interstitial fluid is driven back into the IVD due to osmotic effects.
In summary, the presented paper provides a review on IVD mechanics and can be understood as a compilation of relevant information giving valuable guidance to researchers starting to work in this challenging field. In this regard, the paper opens with anatomical and chemical fundamentals of IVD tissue with a particular focus on the inherent inhomogeneities. This is followed by an introduction to the continuum-mechanical fundamentals including an overview of the TPM as well as the inelastic non-linear kinematics and the balance equations of the resulting porous continua. Thereafter, the constitutive modelling process is illustrated with a particular focus on the thermo-dynamically consistent modelling process of the intrinsic viscoelasticity of the ECM as well as the inhomogeneous characteristics of the embedded collagen fibres and the viscous pore fluid. The resulting system of coupled partial differential equations is then numerically discretised using the finite-element method which finally allows the simulation of deformation processes of the IVD using either single- or multi-processor machines. Moreover, an automated computation scheme is presented to systematically capture the inhomogeneities of the IVD. The paper is closed with several sample applications, which embrace the capabilities of the presented computational model on the one hand and give advice for further validation in terms of the applied material parameters.
































Similar content being viewed by others
Notes
In vivo means “in the living organism” and is contrary to ex vivo standing for “out of the body”.
Clayey silt has a hydraulic conductivity of about 10−8 m/s, while IVD tissue reaches down to a value of about 10−11 m/s.
Porous media Adaptive Nonlinear finite element solver based on Differential Algebraic Systems (http://www.get-pandas.com).
Mesh, Multigrid and More of C. Wieners (http://www.mathematik.uni-karlsruhe.de/~wieners).
Calculations were executed on the Beowulf Linux cluster of the Institute of Applied Mechanics (Chair of Continuum Mechanics) at the Universität Stuttgart. It consists of 98 Opteron CPU (2.2 GHz, 47 dual boards and one quad board), 104 GB RAM (at least 1 GB/CPU) and two Gigabit networks, which share the load stemming from the system administration and the data transfer of the parallel computations.
References
Acartürk A (2009) Simulation of charged hydrated porous media. Dissertation, Bericht Nr. II-18 aus dem Institut für Mechanik (Bauwesen), Universität Stuttgart
Ammann M (2005) Parallel finite element simulations of localization phenomena in porous media. Dissertation, Bericht Nr II-11 aus dem Institut für Mechanik (Bauwesen), Universität Stuttgart
Antoniou J, Steffen T, Nelson F, Winterbottom N, Hollander AP, Poole RA, Aebi M (1996) The human lumbar intervertebral disc: evidence for changes in the biosynthesis and denaturation of the extracellular matrix with growth. J Clin Invest 98:996–1003
Apel N (2004) Approaches to the description of anisotropic material behaviour at finite elastic and plastic deformations—Theory and numerics. Dissertation, Bericht Nr I-12 aus dem Institut für Mechanik (Bauwesen), Universität Stuttgart
Argoubi M, Shirazi-Adl A (1996) Poroelastic creep response analysis of a lumbar motion segment in compression. J Biomech 29:1331–1339
Arnold DN, Brezzi F, Fortin M (1984) A stable finite element for the Stokes equations. Calcolo 21:337–344
Ayad S, Weiss JB (1987) Biochemistry of the intervertebral disc. In: Jayson MIV (ed) The lumbar spine and back pain, 3rd edn. Churchill Livingstone, New York, pp 100–137
Ball JM (1977) Convexity conditions and existence theorems in nonlinear elasticity. Arch Ration Mech Anal 63:337–403
Balzani D (2006) Polyconvex anisotropic energies and modeling of damage applied to arterial walls. Dissertation Bericht Nr 2, Fachbereich Bauwissenschaften
Balzani D, Neff P, Schröder J, Holzapfel G (2006) A polyconvex framework for soft biological tissues. Adjustment to experimental data. Int J Solids Struct 43:6052–6070
Bathe KJ (1990) Finite-Elemente-Methoden. Springer, Berlin
Benzi M, Golub GH, Liesen J (2005) Numerical solution of saddle point problems. Acta Numer 14:1–137
Biot MA (1941) General theory of three dimensional consolidation. J Appl Phys 12:155–164
Bishop AW (1959) The effective stress principle. Tekn Ukebl 39:859–863
Boehler JP (1977) On irreducible representations for isotropic scalar functions. Z Angew Math Mech 57:323–327
Boehler JP (1979) A simple derivation of representations for non-polynominal constitutive equations in some case of anisotropy. Z Angew Math Mech 59:157–167
Boehler JP (1987) Introduction of the invariant formulation of anisotropic constitutive equations. In: Boehler JP (ed) Applications of tensor functions in solid mechanics. CISM courses and lectures, vol 292. Springer, Wien, pp 13–30
Bowen RM (1976) Theory of mixtures. In: Eringen AC (ed) Continuum physics, vol III. Academic Press, New York, pp 1–127
Bowen RM (1980) Incompressible porous media models by use of the theory of mixtures. Int J Eng Sci 18:1129–1148
Brezzi F, Fortin M (1991) Mixed and hybrid finite element methods. Springer, New York
Broberg KB (1993) Slow deformation of intervertebral discs. J Biomech 26:501–512
Chen Y, Chen X, Hisada T (2006) Non-linear finite element analysis of mechanical electrochemical phenomena in hydrated soft tissues based on triphasic theory. Int J Numer Methods Eng 65:147–173
Ciarlet PG (1988) Mathematical elasticity, vol 1: three dimensional elasticity. North-Holland, Amsterdam
Coleman BD, Noll W (1963) The thermodynamics of elastic materials with heat conduction and viscosity. Arch Ration Mech Anal 13:167–178
de Boer R (1982) Vektor und Tensorrechnung für Ingenieure. Springer, Berlin
de Boer R (2000) Theory of porous media. Springer, Berlin
Diebels S (2000) Mikropolare zweiphasenmodelle: formulierung auf basis der theorie poröser medien. Habilitation, Bericht Nr II-4 aus dem Institut für Mechanik (Bauwesen), Universität Stuttgart
Diebels S, Ellsiepen P, Ehlers W (1999) Error-controlled Runge-Kutta time integration of a viscoplastic hybrid two-phase model. Tech Mech 19:19–27
Donnan FG (1911) Theorie der Membrangleichgewichte und Membranpotentiale bei Vorhandensein von nicht dialysierenden Elektrolyten. Ein Beitrag zur physikalisch-chemischen Physiologie. Z Elektrochem Angew Phys Chem 17:572–581
Ebara S, Iatridis JC, Setton LA, Foster RJ, Mow C, Weidenbaum M (1996) Tensile properties of nondegenerate human lumbar anulus fibrosus. Spine 21:452–461
Eberlein R, Holzapfel GA, Schulze-Bauer CAJ (2001) An anisotropic model for annulus tissue and enhanced finite element analysis of intact lumbar disc bodies. Comput Methods Biomech Biomed Eng 4:209–229
Eberlein R, Holzapfel GA, Fröhlich M (2004) Multi-segment FEA of the human lumbar spine including the heterogeneity of the anulus fibrosus. Comput Mech 34:147–165
Effelsberg J (2007) Untersuchung der Diffusions- und Strömungsprozesse in der menschlichen Bandscheibe mittels Magnetresonanztomographie. Diploma Thesis, Bericht Nr 07-II-2 aus dem Institut für Mechanik (Bauwesen), Universität Stuttgart
Ehlers W (1989) Poröse Medien—ein kontinuumsmechanisches Modell auf der Basis der Mischungstheorie. Habilitation, Forschungsberichte aus dem Fachbereich Bauwesen, Heft 47, Universität-GH-Essen
Ehlers W (1991) Toward finite theories of liquid-saturated elasto-plastic porous media. Int J Plast 7:433–475
Ehlers W (1993) Constitutive equations for granular materials in geomechanical context. In: Hutter K (ed) Continuum mechanics in environmental sciences and geophysics. CISM courses and lectures, vol 337. Springer, Wien, pp 313–402
Ehlers W (1995–2009) Vector and tensor calculus: An introduction. Lecture notes, Institute of Applied Mechanics (Chair of Continuum Mechanics), Universität Stuttgart, http://www.mechbau.uni-stuttgart.de/ls2
Ehlers W (2002) Foundations of multiphasic and porous materials. In: Ehlers W, Bluhm J (eds) Porous media: theory, experiments and numerical applications. Springer, Berlin, pp 3–86
Ehlers W, Acartürk A (2009) The role of weakly imposed Dirichlet boundary conditions for numerically stable computations of swelling phenomena. Comput Mech 43:545–557
Ehlers W, Ellsiepen P (1998) PANDAS: Ein FE-System zur Simulation von Sonderproblemen der Bodenmechanik. In: Wriggers P, Meißner U, Stein E, Wunderlich W (eds) Finite Elemente in der Baupraxis—FEM ’98. Ernst & Sohn, Berlin, pp 391–400
Ehlers W, Ellsiepen P (2001) Theoretical and numerical methods in environmental continuum mechanics based on the Theory of Porous Media. In: Schrefler BA (ed) Environmental geomechanics. CISM courses and lectures, vol 417. Springer, Wien, pp 1–81
Ehlers W, Markert B (2001) A linear viscoelastic biphasic model for soft tissues based on the Theory of Porous Media. J Biomech Eng 123:418–424
Ehlers W, Ellsiepen P, Blome P, Mahnkopf D, Markert B (1999) Theoretische und numerische Studien zur Lösung von Rand- und Anfangswertproblemen in der Theorie Poröser Medien, AbschlußBericht zum DFG-Forschungsvorhaben eh 107/6-2. Bericht Nr 99-II-1 aus dem Institut für Mechanik (Bauwesen), Universität Stuttgart
Ehlers W, Markert B, Acartürk A (2005) Swelling phenomena of hydrated porous materials. In: Abousleiman YN, Cheng AHD, Ulm FJ (eds) Poromechanics III, proceedings of the 3rd Biot conference on poromechanics. Balkema at Taylor & Francis, Leiden, pp 781–786
Ehlers W, Karajan N, Markert B (2006) A porous media model describing the inhomogeneous behaviour of the human intervertebral disc. Mater Sci Eng Technol 37:546–551
Ehlers W, Markert B, Karajan N (2006) A coupled FE analysis of the intervertebral disc based on a multiphasic TPM formulation. In: Holzapfel GA, Ogden RW (eds) Mechanics of biological tissue. Springer, Berlin, pp 373–386
Ehlers W, Karajan N, Wieners C (2007) Parallel 3-d simulation of a biphasic porous media model in spine mechanics. In: Ehlers W, Karajan N (eds) Proceedings of the 2nd GAMM seminar on continuum biomechanics, Bericht Nr II-16 aus dem Institut für Mechanik (Bauwesen). Universität Stuttgart, Stuttgart, pp 11–20
Ehlers W, Karajan N, Markert B (2009) An extended biphasic model for charged hydrated tissues with application to the intervertebral disc. Biomech Model Mechanobiol 8:233–251
Ehlers W, Acartürk A, Karajan N (2010) Advances in modelling saturated biological soft tissues and chemically active gels. Arch Appl Mech 80:467–478
Eipper G (1998) Theorie und Numerik finiter elastischer Deformationen in fluidgesättigten Porösen Medien. Dissertation, Bericht Nr II-1 aus dem Institut für Mechanik (Bauwesen), Universität Stuttgart
Elliott DA, Setton LA (2000) A linear material model for fiber-induced anisotropy of the anulus fibrosus. J Biomech Eng 122:173–179
Ellsiepen P (1999) Zeit- und ortsadaptive Verfahren angewandt auf Mehrphasenprobleme pröser Medien. Dissertation Bericht Nr II-3 aus dem Institut für Mechanik (Bauwesen), Universität Stuttgart
Ellsiepen P, Hartmann S (2001) Remarks on the interpretation of current non-linear finite element analyses as differential-algebraic equations. Int J Numer Methods Eng 51:679–707
Managing musculoskeletal disorders European Foundation for the Improvement of Living and Working Conditions (2007). Dublin, http://www.eurofound.europa.eu/ewco/studies/tn0611018s
Eyre DR (1979) Biochemistry of the intervertebral disc. Connect Tissue Res 8:227–291
Eyre DR, Muir H (1977) Quantitative analysis of types I and II collagens in human intervertebral discs at various ages. Biochim Biophys Acta 492:29–42
Frijns AJH, Huyghe JM, Janssen JD (1997) A validation of the quadriphasic mixture theory for intervertebral disc tissue. Int J Eng Sci 35:1419–1429
Frijns AJH, Huyghe JM, Kaasschieter EF, Wijlaars MW (2003) Numerical simulation of deformations and electrical potentials in a cartilage substitute. Biorheology 40:123–131
Fung YC (1981) Biomechanics: mechanical properties of living tissues. Springer, New York
Godfrey MD, Hendry DF (1993) The computer as von Neumann planned it. IEEE Ann Hist Comput 15:11–21
Grace H, Young A (1903) The algebra of invariants. Cambridge University Press, Cambridge
Gu WY, Mao XG, Foster RJ, Weidenbaum M, Mow VC, Rawlins B (1999) The anisotropic hydraulic permeability of human lumbar anulus fibrosus. Spine 24:2449–2455
Gurtin ME, Williams WO (1966) On the inclusion of the complete symmetry group in the unimodular group. Arch Ration Mech Anal 23:163–172
Hairer E, Wanner G (1991) Solving ordinary differential equations II—stiff and differential-algebraic problems. Springer, Berlin
Hassanizadeh SM, Gray WG (1979) General conservation equations for multi-phase systems: 1. Averaging procedure. Adv Water Resour 2:131–144
Hassanizadeh SM, Gray WG (1987) High velocity flow in porous media. Transp Porous Media 2:521–531
Haupt P (1993) Foundations of continuum mechanics. In: Hutter K (ed) Continuum mechanics in environmental sciences and geophysics. CISM courses and lectures, vol 337. Springer, Wien, pp 1–77
Hayes WC, Bodine AJ (1978) Flow-independent viscoelastic properties of articular cartilage matrix. J Biomech 11:407–419
Holm S, Nachemson A (1983) Variations in the nutrition of the canine intervertebral disc induced by motion. Spine 8:866–974
Holzapfel G, Gasser TC, Ogden RW (2000) A new constitutive framework for arterial wall mechanics and a comparative study of material models. J Elast 61:1–48
Holzapfel GA, Schulze-Bauer CAJ, Feigl G, Regitnig P (2005) Mono-lamellar mechanics of the human lumbar anulus fibrosus. Biomech Model Mechanobiol 3:125–140
Hsieh AH, Wagner DR, Cheng LY, Lotz JC (2005) Dependence of mechanical behavior of the murine tail disc on regional material properties: a parametric finite element study. J Biomech Eng 127:1158–1167
Hukins DWL (1987) Properties of spinal materials. In: Jayson MIV (ed) The lumbar spine and back pain, 3rd edn. Churchill Livingstone, New York, pp 138–160
Huyghe JM, Houben GB, Drost MR (2003) An ionised/non-ionised dual porosity model of intervertebral disc tissue. Biomech Model Mechanobiol 2:3–19
Iatridis C, Weidenbaum M, Setton LA, Mow VC (1996) Is the nucleus pulposus a solid or a fluid? Mechanical behaviors of the human intervertebral disc. Spine 21:1174–1184
Iatridis JC, Setton A, Weidenbaum M, Mow VC (1997) The viscoelastic behavior of the non-degenerate human lumbar nucleus pulposus in shear. J Biomech 30:1005–1013
Iatridis JC, Setton LA, Foster RJ, Rawlins A, Weidenbaum M, Mow VC (1998) Degeneration affects the anisotropic and nonlinear behaviors of human anulus fibrosus in compression. J Biomech 31:535–544
Iatridis JC, Laible JP, Krag MH (2003) Influence of fixed charge density magnitude and distribution on the intervertebral disc: Applications of a Poroelastic and Chemical Electric (PEACE) model. J Biomech Eng 125:12–24
Itskov M, Aksel N (2004) A class of orthotropic and transversely isotropic hyperelastic constitutive models based on a polyconvex strain energy function. Int J Solids Struct 41:3833–3848
Kaasschieter EF, Frijns AJH, Huyghe JM (2003) Mixed finite element modelling of cartilaginous tissues. Math Comput Simul 61:549–560
Karajan N, Ehlers W, Röhrle O, Schmitt S (2011) Homogenisation method to capture the non-linear behaviour of intervertebral discs in multi-body systems. Proc. Appl. Math. Mech. 11:95–96
Klawonn A, Pavarino LF (1998) Overlapping Schwarz methods for mixed linear elasticity and Stokes problems. Comput Methods Appl Mech Eng 165:233–245
Klawonn A, Pavarino LF (2000) A comparison of overlapping Schwarz methods and block preconditioners for saddle point problems. Numer Linear Algebra Appl 7:1–25
Kleiber M (1975) Kinematics of deformation processes in materials subjected to finite elastic-plastic strains. Int J Eng Sci 13:513–525
Klisch SM, Lotz JC (1999) Application of a fiber-reinforced continuum theory to multiple deformations of the annulus fibrosus. J Biomech 32:1027–1036
Klisch SM, Lotz JC (2000) A special theory of biphasic mixtures and experimental results for human annulus fibrosus tested in confined compression. J Biomech Eng 122:180–188
Lai WM, Hou JS, Mow VC (1991) A triphasic theory for the swelling and deformation behaviours of articular cartilage. J Biomech Eng 113:245–258
Laible JP, Pflaster DS, Krag MH, Simon BR, Haugh LD (1993) A poroelastic-swelling finite element model with application to the intervertebral disc. Spine 18:659–670
Lambrecht M (2002) Theorie und Numerik von Materialinstabilitäten elastoplastischer Festkörper auf der Grundlage inkrementeller Variationsformulierungen. Dissertation, Bericht Nr I-8 aus dem Institut für Mechanik (Bauwesen), Universität Stuttgart
Lanir Y (1987) Biorheology and fluid flux in swelling tissues I. Bicomponent theory for small deformations, including concentration effects. Biorheology 24:173–187
Lee CK, Kim YE, Lee CS, Hong YM, Jung JM, Goel VK (2000) Impact response of the intervertebral disc in a finite-element model. Spine 25:2431–2439
Lee EH (1969) Elastic-plastic deformation at finite strains. J Appl Mech 36:1–6
Li LP, Shirazi-Adl A, Buschmann MD (2003) Investigation of mechanical behavior of articular cartilage by fibril reinforced poroelastic models. Biorheology 40:227–233
Lide DR (2003) CRC handbook of chemistry and physics. CRC Press, Boca Raton
Lis AM, Black M, Korn H, Nordin M (2007) Association between sitting and occupational LBP. Eur Spine J 16:283–298
Liu IS (1972) Method of Lagrange multipliers for exploitation of the entropy principle. Arch Ration Mech Anal 46:131–148
Liu IS, I M (1984) Thermodynamics of mixtures of fluids. In: Truesdell C (ed) Rational thermodynamics, 2nd edn. Springer, New York, pp 264–285
Ludescher B, Effelsberger J, Martirosian P, Steidle G, Markert B, Claussen C, Schick F (2008) T2- and diffusion-maps reveal diurnal changes of intervertebral disc composition: An in vivo MRI study at 1.5 Tesla. J Magn Reson Imaging 28:252–257
Marchand F, Ahmed AM (1990) Investigation of the laminate structure of the lumbar disc anulus. Spine 15:402–410
Markert B (2005) Porous media viscoelasticity with application to polymeric foams. Dissertation, Bericht Nr II-12 aus dem Institut für Mechanik (Bauwesen), Universität Stuttgart
Markert B (2008) A biphasic continuum approach for viscoelastic high-porosity foams: comprehensive theory, numerics, and application. Arch Comput Methods Eng 15:371–446
Markert B, Ehlers W, Karajan N (2005) A general polyconvex strain-energy function for fiber-reinforced materials. Proc Appl Math Mech 5:245–246
Marsden JE, Hughes TJR (1994) Mathematical foundations of elasticity. Dover, New York. Reprint of Prentice-Hall 1983
Mayer J (2007) A multilevel crout ILU preconditioner with pivoting and row permutation. Numer Linear Algebra Appl, 14, 771–789
Mayer J (2008) Symmetric permutations for I-matrices to delay and avoid small pivots during factorization. SIAM J Sci Comput 30:982–996
Mills N (1966) Incompressible mixture of Newtonian fluids. Int J Eng Sci 4:97–112
Mohr PJ, Taylor BN, Newell DB (eds) (2007) CODATA recommended values of the fundamental physical constants: 2006. National Institute of Standards and Technology, Gaithersburg
Mooney M (1940) A theory of large elastic deformation. J Appl Phys 11:582–592
Morrey CB (1952) Quasi-convexity and the lower semicontinuity of multiple integrals. Pac J Math 2:25–53
Mow VC, Hayes WC (1997) Basic orthopaedic biomechanics. Lippincott-Raven, New York
Mow VC, Ratcliffe A (1997) Structure and function of articular cartilage and meniscus. In: Mow VC, Hayes WC (eds) Basic orthopaedic biomechanics. Lippincott-Raven, New York, pp 113–177
Mow VC, Kuei C, Lai WM, Armstrong CG (1980) Biphasic creep and stress relaxation of articular cartilage in compression: theory and experiments. J Biomech Eng 102:73–84
Mow VC, Gibbs MC, Lai WM, Zhu WB, Athanasiou KA (1989) Biphasic indentation of articular cartilage—II. A numerical algorithm and an experimental study. J Biomech 22:853–861
Mow VC, Ateshian GA, Lai WM, Gu WY (1998) Effects of fixed charges on the stress-relaxation behavior of hydrated soft tissues in a confined compression problem. Int J Solids Struct 35:4945–4962
Nachemson AL (1987) Lumbar intradiscal pressure. In: Jayson MIV (ed) The lumbar spine and back pain, 3rd edn. Churchill Livingstone, New York, pp 191–203
Naylor A (1962) The biophysical and biochemical aspects of intervertebral disc herniation and degeneration. Ann R Coll Surg Engl 31:91–114
Noll W (1955) On the continuity of the fluid and solid states. J Ration Mech Anal 4:3–81
Noll W (1958) A mathematical theory of the mechanical behavior of continuous media. Arch Ration Mech Anal 2:197–226
Ochia RS, Ching RP (2002) Hydraulic resistance and permeability in human lumbar vertebral bodies. J Biomech Eng 124:533–537
Ogden RW (1972) Large deformation isotropic elasticity—on the correlation of theory and experiment for incompressible rubberlike solids. Proc R Soc Lond Ser A, Math Phys Sci 326:565–584
Parent-Thirion A, Macías EF, Hurley J, Vermeylen G (2007) Fourth European working conditions survey. Report of the European Foundation for the Improvement of Living and Working Conditions. Dublin, http://www.eurofound.europa.eu/publications/htmlfiles/ef0698.htm
Powell MJD (1994) A direct search optimization method that models the objective and constraint functions by linear interpolation. In: Gomez S, Hennart JP (eds) Advances in optimization and numerical analysis. Kluwer Academic, Dordrecht, pp 51–67
Press WH, Teukolsky SA, Vetterling WT, Flannery BP (2007) Numerical recipes: the art of scientific computing, 3rd edn. Cambridge University Press, Cambridge
Reese S, Govindjee S (1998) A theory of finite viscoelasticity and numerical aspects. Int J Solids Struct 35:3455–3482
Riches PE, Dhillon N, Lotz J, Woods AW, McNally DS (2002) The internal mechanics of the intervertebral disc under cyclic loading. J Biomech 35:1263–1271
Rivlin RS (1948) Large elastic deformations of isotropic materials. Proc R Soc Lond Ser A, Math Phys Sci 241:379–397
Rivlin RS, Ericksen JL (1955) Stress-deformation relations for isotropic materials. J Ration Mech Anal 4:323–425
Rohlmann A, Zander T, Schmidt H, Wilke HJ, Bergmann G (2006) Analysis of the influence of disc degeneration on the mechanical behaviour of a lumbar motion segment using the finite element method. J Biomech 39:2484–2490
Saad Y, Schultz MH (1986) GMRES: A generalized minimal residual algorithm for solving nonsymmetric linear systems. SIAM J Sci Stat Comput 7:856–869
Sandhu RS, Wilson EL (1969) Finite-element analysis of seepage in elastic media. J Eng Mech Div 95:641–652
Schenke M (2008) Development of an interface between ABAQUS and PANDAS. Master thesis, Bericht Nr 08-II-12 aus dem Institut für Mechanik (Bauwesen), Universität Stuttgart
Schmidt CO, Raspe H, Pfingsten M, Hasenbring M, Basler HD, Eich W, Kohlmann T (2007) Back pain in the German adult population. Prevalence, severity, and sociodemographic correlations in a multiregional survey. Spine 32:2005–2011
Schmidt H, Heuer F, Simon U, Kettler A, Rohlmann A, Claes L, Wilke HJ (2006) Application of a new calibration method for a three-dimensional finite element model of a human lumbar annulus fibrosus. Clin Biomech 21:337–344
Schmidt H, Heuer F, Drumm J, Klezl Z, Claes L, Wilke HJ (2007) Application of a calibration method provides more realistic results for a finite element model of a lumbar spinal segment. Clin Biomech 22:377–384
Schröder J (1996) Theoretische und algorithmische Konzepte zur phänomenologischen Beschreibung anisotropen Materialverhaltens. Dissertation, Bericht Nr I-1 aus dem Institut für Mechanik (Bauwesen), Universität Stuttgart
Schröder J (2000) Homogenisierungsmethoden der nichtlinearen Kontinuumsmechanik unter Beachtung von Stabilitätsproblemen. Habilitation, Bericht Nr I-7 aus dem Institut für Mechanik (Bauwesen), Universität Stuttgart
Schröder J, Neff P (2003) Invariant formulation of hyperelastic transverse isotropy based on polyconvex free energy functions. Int J Solids Struct 40:401–445
Schröder Y, Sivan S, Wilson W, Merkher Y, Huyghe JM, Maroudas A, Baaijens FPT (2007) Are disc pressure, stress and osmolarity affected by intra- and extrafibrillar fluid exchange? J Orthop Res 25:1317–1324
Schwarz HR (1991) Methode der finiten Elemente. Teubner, Stuttgart
Shirazi-Adl A (1994) Nonlinear stress analysis of the whole lumbar spine in torsion-mechanics of facet articulation. J Biomech 27:289–299
Shirazi-Adl A (2006) Analysis of large compression loads on lumbar spine in flexion and torsion using a novel wrapping element. J Biomech 39:267–275
Shirazi-Adl A, Ahmed AM, Shrivastava SC (1986) A finite element study of a lumbar motion segment subjected to pure sagittal plane moments. J Biomech 19:331–350
Shirazi-Adl A, Ahmed AM, Shrivastava SC (1986) Mechanical response of a lumbar motion segment in axial torque alone and combined with compression. Spine 11:914–927
Šilhavý M (1997) The mechanics and thermodynamics of continuous media. Springer, Berlin
Simo JC, Taylor RL (1985) Consistent tangent operators for rate-independent elastoplasticity. Comput Methods Appl Mech Eng 48:101–118
Skaggs L, Weidenbaum M, Iatridis C, Ratcliffe A, Mow VC (1994) Regional variation in tensile properties and biochemical composition of the human lumbar anulus fibrosus. Spine 19:1310–1319
Skempton AW (1960) Significance of Terzaghi’s concept of effective stress (Terzaghi’s discovery of effective stress). In: Bjerrum L, Casagrande A, Peck RB, Skempton AW (eds) From theory to practice in soil mechanics. Wiley, New York, pp 42–53
Smith GF (1971) On isotropic functions of symmetric tensors, skew-symmetric tensors and vectors. Int J Eng Sci 9:899–916
Snijders H, Huyghe JM, Janssen JD (1995) Triphasic finite element model for swelling porous media. Int J Numer Methods Fluids 20:1039–1046
Spencer AJM (1971) Theory of invariants. In: Eringen AC (ed) Continuum physics, vol 1. Academic Press, New York, pp 239–353
Spencer AJM (1982) The formulation of constitutive equations for anisotropic solids. In: Boehler JP (ed) Mechanical behavior of anisotropic solids. Proceedings of the Euromech colloquium, vol 115. Martinus Nijhoff, The Haque, pp 2–26
Spencer AJM (1984) Constitutive theory for strongly anisotropic solids. In: Spencer AJM (ed) Continuum theory of the mechanics of fibre reinforced composites. CISM courses and lectures, vol 282. Springer, Wien, pp 1–32
Spencer AJM (1987) Isotropic polynominal invariants and tensor functions. In: Boehler JP (ed) Applications of tensor functions in solid mechanics. CISM courses and lectures, vol 292. Springer, Wien, pp 141–169
Spencer AJM, Rivlin RS (1962) Isotropic integrity bases for vectors and second-order tensors. Arch Ration Mech Anal 9:45–63
Sten-Knudsen O (2002) Biological membranes: theory of transport, potentials and electric impulses. Cambridge University Press, Cambridge
Svendson B, Hutter K (1995) On the thermodynamics of a mixture of isotropic materials with constraints. Int J Eng Sci 33:2021–2054
Szirmai JA (1970) Structure of the intervertebral disc. In: Balazs EA (ed) Chemistry and molecular biology of the intercellular matrix, vol 3. Academic Press, London, pp 1279–1308
Taylor C, Hood P (1973) A numerical solution of the Navier-Stokes equations using the finite element technique. Comput Fluids 1:73–100
Treloar LRG (1975) The physics of rubber elasticity, 3rd edn. Clarendon Press, Oxford
Truesdell C (1949) A new definition of a fluid, II. The Maxwellian fluid. Tech Rep P-3553, §19, US Naval Research Laboratory
Truesdell C (1984) Thermodynamics of diffusion. In: Truesdell C (ed) Rational thermodynamics, 2nd edn. Springer, New York, pp 219–236
Truesdell C, Noll W (1965) The nonlinear field theories of mechanics. In: Flügge S (ed) Handbuch der physik, vol III/3. Springer, Berlin
Truesdell C, Toupin RA (1960) The classical field theories. In: Flügge S (ed) Handbuch der physik, vol III/1. Springer, Berlin
Tsuji H, Hirano N, Ohshima H, Ishihara H, Terahata N, Motoe T (1993) Structural variation of the anterior and posterior anulus fibrosus in the development of human lumbar intervertebral disc. A risk factor for intervertebral disc rupture. Spine 18:204–210
Tyrrell AR, Reilly T, Troup JDG (1985) Circadian variation in stature and the effects of spinal loading. Spine 10:161–164
Urban JPG, Holm S (1986) Intervertebral disc nutrition as related to spinal movements and fusion. In: Hargens AR (ed) Tissue nutrition and viability. Springer, Berlin, pp 101–119
Urban G, Maroudas A (1979) The measurement of fixed charged density in the intervertebral disc. Biochim Biophys Acta 586:166–178
Urban JPG, Roberts S (1996) Intervertebral disc. In: Comper WD (ed) Extracellular matrix, vol 1: tissue function. Harwood Academic, Amsterdam, pp 203–233
Urban JPG, Holm S, Maroudas A, Nachemson A (1982) Nutrition of the intervertebral disc: effect of fluid flow on solute transport. Clin Orthop 170:296–302
Vanharanta H, Guyer RD, Ohnmeiss DD, Stith WJ, Sachs BL, Aprill C, Spivey M, Rashbaum RF, Hochschuler SH, Videman T, Selby DK, Terry A, Mooney V (1988) Disc deterioration in low-back syndromes. A prospective, multi-center CT/discography study. Spine 13:1349–1351
van Loon R, Huyghe FM, Wijlaars MW, Baaijens FPT (2003) 3D FE implementation of an incompressible quadriphasic mixture model. Int J Numer Methods Eng 57:1243–1258
Varga OH (1966) Stress-strain behavior of elastic materials. Interscience, New York
Walker DW, Dongarra JJ (1996) MPI: a standard message passing interface. Supercomputer 12:56–68
Wall WA (1999) Fluid-Struktur-Interaktion mit stabilisierten finiten elementen. Dissertation, Bericht Nr 31 aus dem Institut für Baustatik, Universität Stuttgart
Wang CC (1969) On representations for isotropic functions, part I and II. Arch Ration Mech Anal 33:249–287
Wang CC (1970) A new representation theorem for isotropic functions: an answer to Professor G.F. Smith’s criticism of my papers on representations for isotropic functions, part I and II. Arch Ration Mech Anal 36:166–223
Wang C, Truesdell C (1973) Introduction to rational elasticity. Noordhoff International, Leyden
Weyl H (1946) The classical groups, their invariants and representation. Princeton University Press, Princeton
White AA, Panjabi MM (1990) Clinical biomechanics of the spine, 2nd edn. Lippincott Williams, Philadelphia
Wieners C (2003) Taylor-Hood elements in 3D. In: Wendland WL, Efendiev M (eds) Analysis and simulation of multifield problems. Springer, Berlin, pp 189–196
Wieners C (2004) Distributed Point Objects. A new concept for parallel finite elements. In: Kornhuber R, Hoppe R, Périaux J, Pironneau O, Widlund O, Xu J (eds) Domain decomposition methods in science and engineering. Lecture notes in computational science and engineering, vol 40. Springer, Berlin, pp 175–183
Wieners C, Ammann M, Ehlers W, Graf T (2005) Parallel Krylov methods and the application to 3-d simulations of a tri-phasic porous media model in soil mechanics. Comput Mech 36:409–420
Wieners C, Ehlers W, Ammann M, Karajan N, Markert B (2005) Parallel solution methods for porous media models in biomechanics. Proc Appl Math Mech 5:35–38
Wieners C, Ammann M, Ehlers W (2006) Distributed Point Objects: a new concept for parallel finite elements applied to a geomechanical problem. Future Gener Comput Syst 22, 532–545
Wilke HJ, Claes LE (eds) (1999) Die traumatische und degenerative Bandscheibe. Hefte zur Zeitschrift, Der Unfallchirurg, vol 271. Springer, Berlin
Wilke HJ, Neef P, Caimi M, Hoogland T, Claes LE (1999) New in vivo measurements of pressures in the intervertebral disc in daily life. Spine 24:755–762
Wilson W, van Donkelar CC, Huyghe JM (2005) A comparison between mechano-electrochemical and biphasic swelling theories for soft hydrated tissues. J Biomech Eng 127:158–165
Wriggers P (1988) Konsistente Linearisierung in der Kontinuumsmechanik und ihre Anwendung auf die Finite-Elemente-Methode. Habilitation, Technischer Bericht F88/4, Forschungs und Seminarberichte aus dem Bereich der Mechanik der Universität Hannover
Wu JSS, Chen JH (1996) Clarification of the mechanical behavior of spinal motion segments through a three-dimensional poroelastic mixed finite element model. Med Eng Phys 18:215–224
Zheng QS (1994) Theory of representations for tensor functions—a unified invariant approach to constitutive equations. Appl Mech Rev 47:545–587
Zheng QS, Boehler JP (1994) The description, classification, and reality of material and physical symmetries. Acta Mech 102:73–89
Zheng QS, Spencer AJM (1993) Tensors which characterize anisotropies. Int J Eng Sci 31:679–693
Zienkiewicz OC, Taylor RL (2005) The finite element method for solid and structural mechanics, vol 2, 6th edn. Butterworth–Heinemann, Oxford
Zienkiewicz OC, Taylor RL (2005) The finite element method. The basis, vol 1, 6th edn. Butterworth–Heinemann, Oxford
Zienkiewicz OC, Taylor RL, Sherwin SJ, Peiró J (2003) On discontinuous Galerkin methods. Int J Numer Methods Eng 58:1119–1148
Acknowledgements
I thank the German Research Foundation (DFG) for funding the research project “Diffusions- und Strömungsprozesse in der anisotropen menschlichen Bandscheibe” under grant number ‘Eh 107/16’.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Karajan, N. Multiphasic Intervertebral Disc Mechanics: Theory and Application. Arch Computat Methods Eng 19, 261–339 (2012). https://doi.org/10.1007/s11831-012-9073-1
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11831-012-9073-1