Abstract
We use an overlapping generations model of a small open economy with perfect capital mobility to evaluate the long-term effects of pension reforms on output and net foreign assets. We compare reforms that achieve similar fiscal targets and show the existence of a tradeoff. Reforms that increase the retirement age have an expansionary effect on output, but a small (and oftentimes) negative effect on the net foreign asset position. In contrast, reforms that cut pension benefits improve the net foreign asset position but reduce output. Only mixed reforms that increase the retirement age and cut pension benefits sufficiently can boost both output and net foreign assets.






Similar content being viewed by others
Notes
As the economy is stationary, we suppress the subscript that indicates a generation’s birth time when denoting household-specific variables. The instantaneous utility function is assumed to be strictly increasing and concave, i.e. u'(c) > 0 , and u''(c) < 0.
These two dimensions have been traditionally emphasized in the pension reform literature; see Lindbeck and Persson (2003) and the papers cited therein.
The no-Ponzi game condition prevents the household from dying indebted: a(L) ≥ 0. In addition, utility maximization and the non-satiation property of the utility function (always increasing in consumption) imply that a household will never choose to die with strictly positive asset holdings: a(L) ≤ 0. Hence, a(L) = 0.
The household’s optimal profile of asset holdings by age is obtained by solving the first order differential equation \( \overset{\bullet }{a}(s)=r\cdot a(s)+H(s)-c \) (where c is the optimal consumption) and imposing the initial and terminal conditions a(0) = a(L) = 0. The solution is given by: \( a(s)=\left(\frac{w-\tau -c}{r}\right)\cdot \left({e}^{rs}-1\right) \) for 0 ≤ s ≤ R and \( a(s)=\left(\frac{c-b}{r}\right)\cdot \left(1-{e}^{-r\left(L-s\right)}\right) \) for R < s ≤ L.
When the economy is in a stationary equilibrium, there is no accumulation of net foreign assets; hence, the current account balance is zero. The aggregate flow constraint is given by \( {\dot{A}}^{*}=0=Y-C+r\cdot {A}^{*} \), where the first two terms in the right-hand side equal the trade balance, and the last term is the net factor income from abroad.
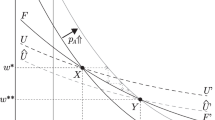
As shown in Figure 1 (bottom quadrant), the pension benefit increases at an increasing rate as the retirement age increases. Intuitively, the collection of taxes grows linearly in R and the pension benefit would also grow linearly if the retired population remained constant. However, the retired population (L − R) declines as R increases; hence, the pension benefit per retiree can increase more than linearly without violating the government budget constraint.
Note that A h(R, b) and A h(R, τ) are different functions, and only the latter is shown in Figure 1. For a precise relation between these functions, see the proof of lemma 2.
Reforms achieve similar reductions in the tax paid by individual households at each time instant. However, the lifetime taxes paid by individual households, and the total tax collection by the government (τ ⋅ R) can vary across reforms, depending on whether or not the retirement age is changed.
The effect would be even smaller under a less elastic labor supply. In this paper, a single parameter (γ) determines the preference for leisure and is calibrated to match the fraction of time worked by a household. This is standard in the literature—see, for example, Miles (1999)—but it implies a labor supply elasticity that is unrealistically high. To see why, ignore the second term in the right-hand side of the household’s consumption-leisure decision (Table 3 in the appendix)—which increases the elasticity—and hold consumption constant: the wage elasticity of leisure at age s is unitary and the elasticity of work effort is given by \( \frac{1-{n}^s}{n^s}. \) The aggregate effective labor supply elasticity is \( \frac{\partial {N}^h}{N^h}\cdot \frac{\tilde{W}}{\partial \tilde{W}}={\displaystyle \sum_{s=1}^T{e}^s\cdot \left(1-{n}^s\right)\cdot \frac{P^s}{P}} \) and is greater than 2 given our parameterization, where \( \tilde{W}=W\cdot \left(1-\tau -{\tau}^I\right)/\left(1+{\tau}^c\right) \) is the tax-adjusted wage rate. Alternatively, a Frisch-type utility function would provide more flexibility to simultaneously match a lower elasticity and the hours worked; however, it would not affect the main (qualitative) result of this paper: the existence of a tradeoff between the output and current account effects of pension reform.
In standard inter-temporal models of household optimization, households increase work effort in anticipation of future (exogenous) income losses. In contrast, in this model the reform reduces the return on labor effort through the pension benefit formula: a smaller replacement parameter implies that higher wage earnings in the working life result in smaller increases in the pension benefit received during retirement. The labor disincentive effect is captured by the term \( {W}_{t+s-1}\cdot {e}^s\cdot \frac{\psi }{T_t}\cdot {\beta}^{T_t+1-s}\cdot {V}_b\left({A}_{t+{T}_t}^{T_t+1},{b}_{t+{T}_t}^{T_t+1}\right) \) in the household’s consumption-leisure decision (Table 3 in the appendix).
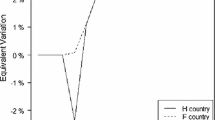
In the context of our model, the welfare gains of pension reforms relative to the baseline can be measured using (stationary-transformed) household utility levels. Normalizing household lifetime utility to 1 in the baseline, the reforms along the A-D curve yield the following gains: reform A: 1.0035 (a 0.35% gain relative to the baseline); reform B: 1.0046; reform C: 1.0058; and reform D: 1.0069.
In this case, the current account improves because aggregate saving (as a share of output) increases. When the pension system is large, pension benefits are generous relative to wage earnings prior to retirement. Hence, an increase in the retirement age results in a smaller increase in disposable income at the end of the working life. In response, a smaller number of household cohorts reduce saving during their working lives.
An issue that deserves further attention but exceeds the scope of this paper is whether such tradeoff could also be present in the short- and medium terms, and if so, under what conditions. At such horizons, the presence of the tradeoff could be sensitive to grandfathering arrangements and the sequencing of fiscal targets.
All aggregate variables except labor are adjusted for labor-augmenting technological progress (ξ) and population size (P). For example, denote \( \widehat{Y} \) the aggregate output before transformation; the transformed output Y is given by: \( {Y}_t=\frac{{\widehat{Y}}_t}{{\left(1+\xi \right)}^t\cdot {P}_t}. \) Aggregate labor (N) is adjusted for population size: \( {N}_t=\frac{{\widehat{N}}_t}{P_t}. \) Household’s age-specific consumption and asset holdings (c s and A s), and the wage rate (W), are adjusted for technological progress: \( {W}_t=\frac{{\widehat{W}}_t}{{\left(1+\xi \right)}^t};{c}_t^s=\frac{{\widehat{c}}_t^s}{{\left(1+\xi \right)}^t};{A}_t^s=\frac{{\widehat{A}}_t^s}{{\left(1+\xi \right)}^t}. \) The interest rate (r) and household’s age-specific labor effort (n s) are not adjusted.
For simplicity, the income taxes levied on labor income and asset earnings are assumed to be the same. Pension benefits are assumed to be below the minimum taxable income level.
In an economy with balanced growth, non-stationary transformed wages grow at the rate of labor-augmenting technological progress (see footnote 15).
The economy’s aggregate flow constraint is obtained from the aggregate constraint of the household sector, the first-order conditions of firms, the market equilibrium conditions, and the government budget constraint. The aggregate constraint of the household sector at time t is given by \( {A}_{t+1}^h\cdot \left(1+\xi \right)\cdot \frac{P_{t+1}}{P_t}=\left[1+{r}_t\cdot \left(1-{\tau}_t^I\right)\right]\cdot {A}_t^h+\left(1-{\tau}_t^I-{\tau}_t\right)\cdot {W}_t\cdot {N}_t^h+{\displaystyle \sum_{s={T}_t+1}^{T_t+{T}_t^R}{b}_{t+{T}_t+1-s}^{T_t+1}\cdot \frac{P_t^s}{P_t}}-\left(1+{\tau}_t^c\right)\cdot {C}_t^h. \)
Assuming that an individual sleeps/rests 9 hours per day, the leisure-work decision is made for the remaining 15 hours (105 weekly hours). Assume that the individual works 40 hours per week (38.1% of non-sleep time). Adjusting the fraction of time worked by a labor force participation rate of 77% yields 0.293.
See Catalán et al. (2010b).
Specifically, following Catalán et al. (2010b), the income tax rate (τ I) is set to match Spain’s direct tax revenues and other current revenues as percentage of GDP (average 1994–2004). The value of the payroll tax rate (τ) and the replacement parameter (ψ) are set to obtain social security revenue equal to 9.5% of GDP and pension spending equal to 8% of GDP. The government debt corresponds roughly to the value projected for Spain at mid-2012 (IMF).
Skills are low at the beginning of the working life, peak at 50 years of age at twice the initial level, and then gradually decline to reach an end-of-working-life level that is 5% lower than at the peak.
Note that the value function V(.) depends also on future interest rates and income tax rates.
References
Attanasio O, Kitao S, Violante GL (2007) Global demographic trends and social security reform. J Monet Econ 54:144–198
Beetsma R, Bettendorf L, Broer P (2003) The budgeting and economic consequences of ageing in the Netherlands. Econ Model 20:987–1013
Borsch-Supan A, Ludwig A, Winter J (2006) Aging, pension reform, and capital flows: a multicountry simulation model. Economica 73:625–658
Catalán M, Hoffmaister A, Guajardo J (2010a) Dealing with global aging and declining world interest rates: fiscal costs and pension reform in small open economies. Pensions: An International Journal 15:191–203
Catalán M, Hoffmaister A, Guajardo J (2010b) Coping with Spain’s aging: retirement rules and incentives. J Pension Econ Financ 9(4):549–581
Domeij D, Floden M (2006) Population aging and international capital flows. Int Econ Rev 47(3):1013–1032
Edwards S (2005) Is the US current account deficit sustainable? If not, how costly is adjustment likely to be? Brook Pap Econ Act 1(2005):211–288
Fehr H, Jokisch S, Kotlikoff L (2008) Fertility, mortality and the developed world’s demographic transition. J Policy Model 30:455–473
Guest R (2006) Population ageing, capital mobility and optimal saving. J Policy Model 28:89–102
Hansen G (1993) The cyclical and secular behavior of the labor input: comparing efficiency units and hours worked. J Appl Econ 8(1):71–80
Huang H, Imrohoroglu S, Sargent TJ (1997) Two computations to fund social security. Macroecon Dyn 1:7–44
International Monetary Fund (2014) Are global imbalances at a turning point? World Economic Outlook, Chapter 4, October
Krueger D, Ludwig A (2007) On the consequences of demographic change for rates of return to capital, and the distribution of wealth and welfare. J Monet Econ 54:49–87
Lindbeck A, Persson M (2003) The gains from pension reform. J Econ Lit 41:74–112
Miles D (1999) Modeling the impact of demographic change upon the economy. Econ J 109:1–36
Obstfeld M (2012) Does the current account still matter? Am Econ Rev Pap Proc 102(3):1–23
Obstfeld M, Rogoff K (2005) Global current account imbalances and exchange rate adjustments. Brook Pap Econ Act 1(2005):67–146
Acknowledgments
We thank Robert Flood, Jorge Roldós, Bertrand Gruss, Luis Brandao Marques, Dora Iakova, Kamil Dybczak, Sebastian Sosa, and Pablo Lopez Murphy for valuable comments.
Author information
Authors and Affiliations
Corresponding author
Appendices
Appendix 1 Proofs
1.1 Proof of Lemma 1
-
a)
In the function A h(R, τ), the first factor \( w-\tau \cdot \left(\frac{L}{L-R}\right)>0 \) for all \( R\in \left(0,\overline{R}\right) \); this follows directly from assumption 1 (which is satisfied if and only if \( R<L\cdot \left(1-\frac{\tau }{w}\right) \)). The second factor \( L\cdot \left(\frac{1-{e}^{-rR}}{1-{e}^{-rL}}\right)-R>0 \) for all \( R<\overline{R}<L \). Hence A h(R, τ) > 0 for all \( R\in \left(0,\overline{R}\right) \).
-
b)
The first derivative of A h(R, τ) with respect to R is given by: \( \frac{\partial {A}^h}{\partial R}=-\frac{\tau \cdot L}{r\cdot {\left(L-R\right)}^2}\cdot \left[\frac{L\cdot \left(1-{e}^{-rR}\right)}{\left(1-{e}^{-rL}\right)}-R\right]+\left(\frac{1}{r}\right)\cdot \left(w-\frac{\tau \cdot L}{L-R}\right)\cdot \left[\frac{r\cdot L\cdot {e}^{-rR}}{\left(1-{e}^{-rL}\right)}-1\right]. \) Since \( \underset{R\to 0}{ \lim}\left(\frac{\partial {A}^h}{\partial R}\right)=\frac{\left(w-\tau \right)}{r}\cdot \left[\frac{r\cdot L}{1-{e}^{-rL}}-1\right]>0 \) (note that \( \frac{r\cdot x}{1-{e}^{-rx}}-1>0 \) for x > 0), the function A h is increasing in R when R approaches 0. In addition, \( \underset{R\to \overline{R}}{ \lim}\left(\frac{\partial {A}^h}{\partial R}\right)=-\frac{\tau \cdot L}{r\cdot {\left(L-\overline{R}\right)}^2}\cdot \left[\frac{L}{1-{e}^{-rL}}-\frac{\overline{R}}{1-{e}^{-r\overline{R}}}\right]\cdot \left(1-{e}^{-r\overline{R}}\right)<0 \); thus, the function A h is decreasing in R when R approaches \( \overline{R} \). Note that in the expression for \( \frac{\partial {A}^h}{\partial R} \), the first term in the right hand side is always negative, and the second term can be either positive or negative depending on the value of R (the function \( \frac{r\cdot L\cdot {e}^{-rR}}{1-{e}^{-rL}}-1 \) is decreasing in R and becomes negative for values sufficiently close to L).
-
c)
The second derivative of A h(R, τ) with respect to R is given by:
$$ \frac{\partial^2{A}^h}{{\left(\partial R\right)}^2}=-\frac{2\cdot \tau \cdot L}{r\cdot {\left(L-R\right)}^3}\cdot \left[\frac{L\cdot \left(1-{e}^{-rR}\right)}{\left(1-{e}^{-rL}\right)}-R\right]-\frac{2\cdot \tau \cdot L}{r\cdot {\left(L-R\right)}^2}\cdot \left[\frac{r\cdot L\cdot {e}^{-rR}}{\left(1-{e}^{-rL}\right)}-1\right]-\left(w-\frac{\tau \cdot L}{L-R}\right)\cdot \frac{r\cdot L\cdot {e}^{-rR}}{\left(1-{e}^{-rL}\right)}. $$
The first and third terms in the right hand side are non-positive; the second term is negative for all R < R m , but it becomes positive as the value of R approaches L. Cases in which the second term is positive and more than offsets the sum of the first and third terms (in absolute value) cannot be ruled out. For example, the function A h becomes convex when R approaches \( \overline{R} \), and \( \overline{R} \) approaches L. In this case, \( \underset{R\to \overline{R}}{ \lim}\left(w-\frac{\tau \cdot L}{L-R}\right)=0 \); the first and third terms in the expression for \( \frac{\partial^2{A}^h}{{\left(\partial R\right)}^2} \) equal 0, and the second term is positive. Thus, \( \frac{\partial^2{A}^h}{{\left(\partial R\right)}^2}>0 \).
1.2 Proof of Lemma 2
The function A h(b, R) and its first and second derivatives with respect to R are given by:
The first derivative could be positive or negative: the first term is always positive, but the second term becomes negative for R values that are sufficiently high. As the second derivative is always negative, the function is strictly concave.
The first derivative can also be expressed as follows:
In the limit, when R approaches L, \( \underset{R\to L}{ \lim}\left(w-\frac{b\cdot L}{R}\right)\cdot \left[\frac{r\cdot L\cdot {e}^{-rR}}{1-{e}^{-rL}}-1\right]<0 \) and \( \underset{R\to L}{ \lim}\left[\frac{L\cdot \left(1-{e}^{-rR}\right)}{R\cdot \left(1-{e}^{-rL}\right)}-1\right]=0 \). Hence, \( \underset{R\to L}{ \lim}\frac{\partial {A}^h\left(b,R\right)}{\partial R}<0 \).
The following “envelope” condition can be used to establish a relation between the derivatives of the functions A h(R, b) and A h(R, τ) = A h[R, τ(b, R)]:
At the point \( R={R}_m^{*} \), \( \frac{\partial {A}^h\left({R}_m^{*},b\right)}{\partial R}>\frac{\partial {A}^h\left({R}_m^{*},\tau \right)}{\partial R}=\alpha \cdot {\left(\frac{\alpha }{r}\right)}^{\frac{1}{1-\alpha }} \) (slope of K line in Fig. 1). The convexity of the function A h(R, b) implies that if R * is the value of R such that \( \frac{\partial {A}^h\left({R}^{*},b\right)}{\partial R}=\alpha \cdot {\left(\frac{\alpha }{r}\right)}^{\frac{1}{1-\alpha }} \), then \( {R}^{*}>{R}_m^{*} \).
Appendix 2. Model for Numerical Simulations
Households
In the model, which is presented in stationary form,Footnote 15 the utility of a household born at time t is determined by consumption (c) and leisure (l), and is given by
where the working life lasts T t years and retirement lasts \( {T}_t^R \) years. The household is endowed with a fixed number of hours per year, normalized to one, and distributed between work (n) and leisure (l): \( {l}_{t+s-1}^s=1-{n}_{t+s-1}^s,\mathrm{where}\ {n}_{t+s-1}^s=0 \) during retirement.
A household accumulates assets (A) according to the following budget constraint:
where \( {H}_{t+s-1}^s=\left(1-{\tau}_{t+s-1}-{\tau}_{t+s-1}^I\right)\cdot {W}_{t+s-1}\cdot {e}^s\cdot {n}_{t+s-1}^s \) represents net (of taxes) wage income during the working phase, and \( {H}_{t+s-1}^s={b}_{t+s-1}^s \) is the pension benefit during retirement. ξ denotes the annual rate of labor-augmenting technological progress.
The household takes as given the payroll (τ), income (τ I ), and consumption (τ c) tax rates, and the interest (r) and wage (W) rates.Footnote 16 During the household’s working life, next year’s assets are determined by adding savings to this year’s assets; savings, in turn, are computed as the sum of the net return on assets plus net wage income, minus gross consumption. The household’s labor productivity per hour varies with age, according to an exogenous skill premium (e s) defined as the relative productivity of an s-year old household to that of a one-year old (unskilled) household.
At retirement, the first pension benefit is calculated based on average past wage earnings, indexed by the economy-wide wage growth; in stationary form, it is given by: \( {b}_{t+{T}_t}^{T_t+1}=\psi \cdot \frac{1}{T_t}\cdot {\displaystyle \sum_{j=1}^{T_t}{W}_{t+j-1}\cdot {e}^j\cdot {n}_{t+j-1}^j} \), where (ψ) stands for the replacement parameter. Subsequent pension benefits are indexed annually with wage growth: \( {b}_{t+s-1}^s={b}_{t+{T}_t}^{T_t+1},s={T}_t+2,\ldots {T}_t+{T}_t^R. \) Footnote 17 The household’s optimization problem is to choose the sequence of consumption, leisure, and asset holdings \( {\left\{{c}_{t+s-1}^s,{l}_{t+s-1}^s,{A}_{t+s-1}^s\right\}}_{s=1}^{T_t+{T}_t^R} \) to maximize its utility (1) subject to the budget constraint (2), the pension benefit formula, and the no intergenerational bequest or inheritance condition \( {A}_t^1={A}_t^{T_t+{T}_t^R+1}=0 \) (for details, see below). Given a total population (P t ) and a population of age s (\( {P}_t^s \)) in year t, aggregate household effective labor supply (\( {N}_t^h \)), assets (\( {A}_t^h \)), and consumption (\( {C}_t^h \)), are respectively given by:
Firms
Firms maximize profits net of capital depreciation, \( {\Pi}_t^f \), using a constant-returns-to-scale production function with labor-augmenting technological progress \( {\Pi}_t^f=\mathrm{Z}\cdot {\left({K}_t^f\right)}^{\alpha}\cdot {\left({N}_t^f\right)}^{1-\alpha }-\left({r}_t+\delta \right)\cdot {K}_t^f-{W}_t\cdot {N}_t^f \). In this expression, Z denotes the level of total factor productivity, α is the share of capital in domestic output, \( {K}_t^f \) denotes the capital stock, and δ is the rate of capital depreciation. Both output and factor markets are perfectly competitive and firms face given wages (W t ) and rental rates (r t ). The first order conditions require that W t and r t + δ equal, respectively, the marginal product of labor and of capital:
Government
The government collects payroll, income, and consumption taxes from households. Tax revenues are used to finance (exogenous) public consumption (G) and pension benefits, and to redeem government debt (D), implying the following budget constraint:
where the non-pension primary balance (in square brackets), and the pension system’s balance (last two terms) are shown separately.
Equilibrium
Given initial conditions and an exogenous path of international interest rates, an equilibrium is defined as a set of allocations for households and firms, prices, and government variables, that simultaneously place all households and firms on their maximizing paths, ensure the intertemporal solvency of the government, and clear all markets. The market-clearing conditions and the economy’s aggregate flow constraint are respectively given by: \( {N}_t={N}_t^f={\displaystyle \sum_{s=1}^{T_t}\left({e}^s\cdot {n}^s\cdot \frac{P_t^s}{P_t}\right)}, \) \( {K}_t^f+{D}_t+{A}_t^{*}={A}_t^h={\displaystyle \sum_{s=1}^{T_t+{T}_t^R}\left({A}_t^s\cdot \frac{P_t^s}{P_t}\right)}, \) and \( {A}_{t+1}^{*}\cdot \left(1+\xi \right)\cdot \frac{P_{t+1}}{P_t}-{A}_t^{*}={r}_t\cdot {A}_t^{*}+{Y}_t-{C}_t-{G}_t-\left[{K}_{t+1}\cdot \left(1+\xi \right)\cdot \frac{P_{t+1}}{P_t}-\left(1-\delta \right)\cdot {K}_t\right] \).Footnote 18 In the last expression, the left-hand side is the current account balance, where A * denotes the economy’s net foreign assets. The right-hand side is the economy’s balance of saving (\( {r}_t\cdot {A}_t^{*}+{Y}_t-{C}_t-{G}_t \)) minus gross investment (\( {K}_{t+1}\cdot \left(1+\xi \right)\cdot \frac{P_{t+1}}{P_t}-\left(1-\delta \right)\cdot {K}_t \)), where \( {Y}_t={Y}_t^f \) and \( {C}_t={C}_t^h \) are the equilibrium aggregate output and consumption, respectively. Note that due to the absence of current transfers, non-debt foreign assets, and factor income other than interest in the model, the primary current account balance (CAP) is always equal to net exports (NX): \( {CAP}_t={NX}_t={Y}_t-{C}_t-{G}_t-\left[{K}_{t+1}\cdot \left(1+\xi \right)\cdot \frac{P_{t+1}}{P_t}-\left(1-\delta \right)\cdot {K}_t\right] \).
Balanced Growth Equilibrium
It is defined assuming constant population growth rate (p), labor augmenting technological progress (ξ), working life (T t = T), retirement period (\( {T}_t^R={T}^R \)), and a fiscal policy characterized by constant tax rates and unchanged public expenditure and debt-to-output ratios. This equilibrium is expressed as a steady state solution in terms of detrended variables in the stationary-transformed model.
It is important to stress that along a balanced growth equilibrium path, the (detrended) current account balance is constant but not necessarily zero. The current account balance CA is fully consistent with a stable path of net foreign assets A *, and satisfies the following condition: CA = A * ⋅ [(1 + ξ) ⋅ (1 + p) − 1]. The optimal net foreign assets A * are determined endogenously by household’s decisions, government policies, and the conditions in the international capital markets.
Note that the primary current account balance is consistent with the intertemporal sustainability of the net external debt (−A *): CAP = NX = − A * ⋅ [(1 + r) − (1 + ξ) ⋅ (1 + p)]. Thus, if the interest rate is greater than the rate of output growth (1 + r) > (1 + ξ) ⋅ (1 + p) and the economy is externally indebted, it must run a trade surplus in the steady state.
Parameter Values
The Table below shows our choice of parameter values. Parameter values corresponding to the utility and production functions (α and β), and the rate of depreciation (δ) are standard in the literature. The leisure parameter (γ) is set so that the fraction of time worked by a representative household is 0.293.Footnote 19 The values for the rate of labor-augmenting technological progress (ξ) and population growth (p) match those observed historically in Spain.Footnote 20 The international interest rate (r) and the discount factor (β) jointly determine the economy’s current account and net foreign investment position; we set them to obtain a current account deficit of 3% of GDP in the baseline (Table 1). The choice of parameter values related to fiscal and pension systems is guided by historical observations from Spain.Footnote 21 Also based on Spanish data, the working life (T t = T) and retirement period (\( {T}_t^R={T}^R \)) are set so that households enter the labor force when they are 23 years old, retire at age 63, and die at 81 years old. The labor skill profile (e s) is hump-shaped, as reported by Hansen (1993).Footnote 22 Unless otherwise indicated, the qualitative results presented below are robust to plausible changes in parameter values.
Household’s Optimization Problem
It can be expressed as a sequence of two dynamic optimization problems, as follows:
subject to (2); \( {b}_{t+{T}_t}^{T_t+1}=\psi \cdot \frac{1}{T_t}\cdot {\displaystyle \sum_{j=1}^{T_t}{W}_{t+j-1}\cdot {e}^j\cdot {n}_{t+j-1}^j} \); \( {b}_{t+s-1}^s={b}_{t+{T}_t}^{T_t+1},s={T}_t+2,\dots {T}_t+{T}_t^R \); and \( {A}_t^1={A}_t^{T_t+{T}_t^R+1}=0. \) \( V\left({A}_{t+{T}_t}^{T_t+1},{b}_{t+{T}_t}^{T_t+1}\right) \) is the household’s value function or discounted indirect utility when it retires at time t + T t having reached the age of T t + 1 years. Upon retirement, the household’s optimization problem can be expressed recursively, and a closed-form solution for the value function (V) follows from the log utility assumption.Footnote 23 We first show the derivation of the value function; then we show the first order conditions of the household’s optimization problem.
Value Function at Retirement
The value function is the solution of the following problem: \( V\left({A}_{t+{T}_t}^{T_t+1},{b}_{t+{T}_t}^{T_t+1}\right)=\underset{{\left\{{c}_{t+s-1}^s,{A}_{t+s}^{s+1}\right\}}_{s={T}_t+1}^{T_t+{T}_t^R}}{Max}{\displaystyle \sum_{s={T}_t+1}^{T_t+{T}_t^R}{\beta}^{s-1}\cdot \log \left({c}_{t+s-1}^s\right)} \) subject to (2); \( {b}_{t+{T}_t}^{T_t+1}=\psi \cdot \frac{1}{T_t}\cdot {\displaystyle \sum_{j=1}^{T_t}{W}_{t+j-1}\cdot {e}^j\cdot {n}_{t+j-1}^j} \); \( {b}_{t+s-1}^s={b}_{t+{T}_t}^{T_t+1},s={T}_t+2,\dots {T}_t+{T}_t^R \); \( {A}_t^{T_t+{T}_t^R+1}=0 \); and given \( {A}_{t+{T}_t}^{T_t+1} \) and \( {b}_{t+{T}_t}^{T_t+1} \). The household’s asset holdings at retirement (\( {A}_{t+{T}_t}^{T_t+1} \)), and the annual pension benefit (\( {b}_{t+{T}_t}^{T_t+1} \)) are given, as they are determined by household’s past decisions. We obtain the value function by backward induction, starting with the household’s problem in its last year of life.
-
1.
The household’s problem at date \( t+{T}_t+{T}_t^R-1 \) (household’s age is \( s={T}_t+{T}_t^R \)) is given by
$$ V\left({A}_{t+{T}_t+{T}_t^R-1}^{T_t+{T}_t^R},{b}_{t+{T}_t}^{T_t+1}\right)=\underset{A_{t+{T}_t+{T}_t^R}^{T_t+{T}_t^R+1}}{Max} \log \left\{\left(1+{\tilde{r}}_{t+{T}_t+{T}_t^R-1}\right)\cdot {A}_{t+{T}_t+{T}_t^R-1}^{T_t+{T}_t^R}+{b}_{t+{T}_t}^{T_t+1}-\left(1+\xi \right)\cdot {A}_{t+{T}_t+{T}_t^R}^{T_t+{T}_t^R+1}\right\}. $$
The household consumes all its remaining assets in its last period of life, as it leaves no bequests and the no-Ponzi condition (\( {A}_{t+{T}_t+{T}_t^R}^{T_t+{T}_t^R+1}=0 \)) is satisfied. Thus, the solution is given by
-
2.
The household’s problem at date \( t+{T}_t+{T}_t^R-2 \) (household’s age is \( {T}_t+{T}_t^R-1 \)) is given by
$$ \begin{array}{l}V\left({A}_{t+{T}_t+{T}_t^R-2}^{T_t+{T}_t^R-1},{b}_{t+{T}_t}^{T_t+1}\right)=\underset{A_{t+{T}_t+{T}_t^R-1}^{T_t+{T}_t^R}}{Max} \log \left\{\left(1+{\tilde{r}}_{t+{T}_t+{T}_t^R-2}\right)\cdot {A}_{t+{T}_t+{T}_t^R-2}^{T_t+{T}_t^R-1}+{b}_{t+{T}_t}^{T_t+1}-\left(1+\xi \right)\cdot {A}_{t+{T}_t+{T}_t^R-1}^{T_t+{T}_t^R}\right\}\\ {}\begin{array}{lll}\hfill \begin{array}{ccc}\hfill \begin{array}{cc}\hfill \hfill & \hfill \hfill \end{array}\hfill & \hfill \hfill & \hfill \hfill \end{array}\hfill & \hfill \hfill & \hfill \hfill \end{array}\begin{array}{ccc}\hfill \hfill & \hfill \hfill & \hfill \hfill \end{array}+\beta \cdot V\left({A}_{t+{T}_t+{T}_t^R-1}^{T_t+{T}_t^R},{b}_{t+{T}_t}^{T_t+1}\right).\end{array} $$
Plug the solution of \( V\left({A}_{t+{T}_t+{T}_t^R-1}^{T_t+{T}_t^R},{b}_{t+{T}_t}^{T_t+1}\right) \) found in 1 to obtain the following expression:
Find the first order condition of this optimization problem and solve for \( {A}_{t+{T}_t+{T}_t^R-1}^{T_t+{T}_t^R} \),
plug this expression into the value function \( V\left({A}_{t+{T}_t+{T}_t^R-2}^{T_t+{T}_t^R-1},{b}_{t+{T}_t}^{T_t+1}\right) \) and solve, as follows:
where Ω1 is a constant: \( {\Omega}_1= \log \left(1+{\tilde{r}}_{t+{T}_t+{T}_t^R-1}\right)+\left(1+\beta \right)\cdot \log \left(1+\beta \right)+\beta \cdot \log \left(1+\xi \right)-\beta \cdot \log \left(\beta \right). \)
-
3.
The household’s problem at date \( t+{T}_t+{T}_t^R-3 \) (household’s age is \( s={T}_t+{T}_t^R-2 \)):
$$ \begin{array}{l}V\left({A}_{t+{T}_t+{T}_t^R-3}^{T_t+{T}_t^R-2},{b}_{t+{T}_t}^{T_t+1}\right)=\underset{A_{t+{T}_t+{T}_t^R-2}^{T_t+{T}_t^R-1}}{Max} \log \left\{\left(1+{\tilde{r}}_{t+{T}_t+{T}_t^R-3}\right)\cdot {A}_{t+{T}_t+{T}_t^R-3}^{T_t+{T}_t^R-2}+{b}_{t+{T}_t}^{T_t+1}-\left(1+\xi \right){A}_{t+{T}_t+{T}_t^R-2}^{T_t+{T}_t^R-1}\right\}\\ {}\begin{array}{ccc}\hfill \begin{array}{ccc}\hfill \begin{array}{cc}\hfill \hfill & \hfill \hfill \end{array}\hfill & \hfill \hfill & \hfill \hfill \end{array}\hfill & \hfill \hfill & \hfill \hfill \end{array}\begin{array}{ccc}\hfill \hfill & \hfill \hfill & \hfill \hfill \end{array}+\beta \cdot V\left({A}_{t+{T}_t+{T}_t^R-2}^{T_t+{T}_t^R-1},{b}_{t+{T}_t}^{T_t+1}\right).\end{array} $$
Replacing \( V\left({A}_{t+{T}_t+{T}_t^R-2}^{T_t+{T}_t^R-1},{b}_{t+{T}_t}^{T_t+1}\right) \) from 2, we can write the previous expression as follows:
Find the first order condition and solve for \( {A}_{t+{T}_t+{T}_t^R-2}^{T_t+{T}_t^R-1} \),
Plug this previous expression into the value function \( V\left({A}_{t+{T}_t+{T}_t^R-3}^{T_t+{T}_t^R-2},{b}_{t+{T}_t}^{T_t+1}\right) \) and solve,
where Ω2 is a constant: \( {\Omega}_2= \log \left(1+{\tilde{r}}_{t+{T}_t+{T}_t^R-1}\right)+ \log \left(1+{\tilde{r}}_{t+{T}_t+{T}_t^R-2}\right)+\left(1+\beta +{\beta}^2\right)\cdot \log \left(1+\beta +{\beta}^2\right) \) +β ⋅ (1 + β) ⋅ log (1 + ξ) − β ⋅ (1 + β) ⋅ log [β ⋅ (1 + β)] + β ⋅ Ω1.
-
4.
Repeating the procedure backwards, the value function at date t + T t (household’s age is T t + 1) is given by
$$ V\left({A}_{t+{T}_t}^{T_t+1},{b}_{t+{T}_t}^{T_t+1}\right)=\left({\displaystyle \sum_{j=1}^{T_t^R}{\beta}^{j-1}}\right)\cdot \log \left\{{A}_{t+{T}_t}^{T_t+1}\cdot {\displaystyle \prod_{i=1}^{T_t^R}\left(1+{\tilde{r}}_{t+{T}_t+{T}_t^R-i}\right)}+{b}_{t+{T}_t}^{T_t+1}\cdot \right.\left\{{\displaystyle \prod_{i=1}^{T_t^R-1}\left(1+{\tilde{r}}_{t+{T}_t+{T}_t^R-i}\right)}\left.+\left(1+\xi \right)\cdot \left[1+\xi +{\displaystyle \sum_{j=1}^{T_t^R-2}{\displaystyle \prod_{i=1}^j\left(1+{\tilde{r}}_{t+{T}_t+{T}_t^R-i}\right)}}\right]\right\}\right\}-\Omega, $$where Ω is a constant. The derivatives of the value function with respect to changes in asset holdings (V A ) and pension benefits (V b ) are given by
$$ \begin{array}{l}{V}_A(.)=\frac{\left({\displaystyle \sum_{j=1}^{T_t^R}{\beta}^{j-1}}\right)\cdot {\displaystyle \prod_{i=1}^{T_t^R}\left(1+{\tilde{r}}_{t+{T}_t+{T}_t^R-i}\right)}}{A_{t+{T}_t}^{T_t+1}\cdot {\displaystyle \prod_{i=1}^{T_t^R}\left(1+{r}_{t+{T}_t+{T}_t^R-i}\right)}+{b}_{t+{T}_t}^{T_t+1}\cdot \left\{{\displaystyle \prod_{i=1}^{T_t^R-1}\left(1+{r}_{t+{T}_t+{T}_t^R-i}\right)}+\left(1+\xi \right)\cdot \left[1+\xi +{\displaystyle \sum_{j=1}^{T_t^R-2}{\displaystyle \prod_{i=1}^j\left(1+{\tilde{r}}_{t+{T}_t+{T}_t^R-i}\right)}}\right]\right\}},\\ {}{V}_b(.)=\frac{\left({\displaystyle \sum_{j=1}^{T_t^R}{\beta}^{j-1}}\right)\cdot \left\{{\displaystyle \prod_{i=1}^{T_t^R-1}\left(1+{r}_{t+{T}_t+{T}_t^R-i}\right)}+\left(1+\xi \right)\cdot \left[1+\xi +{\displaystyle \sum_{j=1}^{T_t^R-2}{\displaystyle \prod_{i=1}^j\left(1+{\tilde{r}}_{t+{T}_t+{T}_t^R-i}\right)}}\right]\right\}}{A_{t+{T}_t}^{T_t+1}\cdot {\displaystyle \prod_{i=1}^{T_t^R}\left(1+{r}_{t+{T}_t+{T}_t^R-i}\right)}+{b}_{t+{T}_t}^{T_t+1}\cdot \left\{{\displaystyle \prod_{i=1}^{T_t^R-1}\left(1+{r}_{t+{T}_t+{T}_t^R-i}\right)}+\left(1+\xi \right)\cdot \left[1+\xi +{\displaystyle \sum_{j=1}^{T_t^R-2}{\displaystyle \prod_{i=1}^j\left(1+{\tilde{r}}_{t+{T}_t+{T}_t^R-i}\right)}}\right]\right\}}.\end{array} $$
Rights and permissions
About this article
Cite this article
Catalán, M., Magud, N.E. A Tradeoff between the Output and Net Foreign Asset Effects of Pension Reform. Open Econ Rev 28, 685–709 (2017). https://doi.org/10.1007/s11079-016-9429-5
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11079-016-9429-5