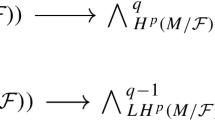Abstract
In an earlier paper, we studied manifolds M endowed with a generalized F structure \(\Phi \in \mathrm{End}(TM\oplus T^*M)\), skew-symmetric with respect to the pairing metric, such that \(\Phi ^3+\Phi =0\). Furthermore, if \(\Phi \) is integrable (in some well-defined sense), \(\Phi \) is a generalized CRF structure. In the present paper, we study quasi-classical generalized F and CRF structures, which may be seen as a generalization of the holomorphic Poisson structures (it is well known that the latter may also be defined via generalized geometry). The structures that we study are equivalent to a pair of tensor fields \((A\in \mathrm{End}(TM),\pi \in \wedge ^2TM)\), where \(A^3+A=0\) and some relations between A and \(\pi \) hold. We establish the integrability conditions in terms of \((A,\pi )\). They include the facts that A is a classical CRF structure, \(\pi \) is a Poisson bivector field and \(\mathrm{im}\,A\) is a (non)holonomic Poisson submanifold of \((M,\pi )\). We discuss the case where either \(\mathrm{ker}\,A\) or \(\mathrm{im}\,A\) is tangent to a foliation and, in particular, the case of almost contact manifolds. Finally, we show that the dual bundle of \(\mathrm{im}\,A\) inherits a Lie algebroid structure and we briefly discuss the Poisson cohomology of \(\pi \), including an associated spectral sequence and a Dolbeault type grading.
Similar content being viewed by others
Notes
The upper index c denotes complexification and the bar denotes complex conjugation.
It was pointed out to me by M. Aldi that Proposition 3.4 also follows from [1], Corollary 7.7.
References
Aldi, M., Grandini, D.: An abstract Morimoto theorem for generalized F-structures. Q. J. Math. 67, 161–182 (2016). doi:10.1093/qmath/haw004
Blair, D.E.: Riemannian Geometry of Contact and Symplectic Manifolds, (second edition 2010), Progress in Math., vol. 203. Birkhäuser, Boston (2002)
Cattaneo, A.S., Zambon, M.: Coisotropic embeddings in Poisson manifolds. Trans. Am. Math. Soc. 361(7), 3721–3746 (2009)
Crainic, M.: Generalized complex structures and Lie brackets. Bull. Braz. Math. Soc. 42, 559–578 (2011)
Dragomir, S., Tomassini, G.: Differential Geometry and Analysis on CR Manifolds, Progress in Math, vol. 246. Birkhäuser Verlag, Basel (2006)
Duchamp, T., Kalka, M.: Deformation theory for holomorphic foliations. J. Differ. Geom. 14, 317–337 (1979)
Gelfand, I.M., Dorfman, I.Y.: The Schouten bracket and Hamiltonian operators. Funkt. Anal. Prilozhen. 14(3), 71–74 (1980)
Gualtieri, M.: Generalized complex geometry, Ph.D. thesis, Univ. Oxford (2003). arXiv:math.DG/0401221
Hitchin, N.: Generalized Calabi-Yau manifolds. Q. J. Math. 54, 281–308 (2003)
Laurent-Gengoux, C., Stiénon, M., Xu, P.: Holomorphic poisson manifolds and holomorphic lie algebroids. Int. Math. Res. Not. IMRN, Art. ID rnn 088, pp 46 (2008)
Morimoto, A.: On normal almost contact structures. J. Math. Soc. Jpn. 15, 420–436 (1963)
Vaisman, I.: The Poisson-Nijenhuis manifolds revisited. Rend. Sem. Mat. Torino 52, 377–394 (1994)
Vaisman, I.: Lectures on the Geometry of Poisson Manifolds, Progress in Math, vol. 118. Birkhäuser, Boston (1994)
Vaisman, I.: Foliation-coupling Dirac structures. J. Geom. Phys. 56, 917–938 (2006)
Vaisman, I.: Reduction and submanifolds of generalized complex manifolds. Differ. Geom. Appl. 25, 147–166 (2007)
Vaisman, I.: Dirac structures and generalized complex structures on \(TM\times {R}^h\). Adv. Geom. 7, 453–474 (2007)
Vaisman, I.: Generalized CRF-structures. Geom. Dedicata 133, 129–154 (2008). doi:10.1007/s10711-008-9239-z
Yano, K.: On a structure defined by a tensor field \(f\) of type \((1,1)\) satisfying \(f^3+f=0\). Tensor 14, 99–109 (1963)
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Vaisman, I. Quasi-classical generalized CRF structures. Ann Glob Anal Geom 51, 53–71 (2017). https://doi.org/10.1007/s10455-016-9523-3
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10455-016-9523-3