Abstract
In recent decades, the need of future climate information at local scales have pushed the climate modelling community to perform increasingly higher resolution simulations and to develop alternative approaches to obtain fine-scale climatic information. In this article, various nested regional climate model (RCM) simulations have been used to try to identify regions across North America where high-resolution downscaling generates fine-scale details in the climate projection derived using the “delta method”. Two necessary conditions were identified for an RCM to produce added value (AV) over lower resolution atmosphere-ocean general circulation models in the fine-scale component of the climate change (CC) signal. First, the RCM-derived CC signal must contain some non-negligible fine-scale information—independently of the RCM ability to produce AV in the present climate. Second, the uncertainty related with the estimation of this fine-scale information should be relatively small compared with the information itself in order to suggest that RCMs are able to simulate robust fine-scale features in the CC signal. Clearly, considering necessary (but not sufficient) conditions means that we are studying the “potential” of RCMs to add value instead of the AV, which preempts and avoids any discussion of the actual skill and hence the need for hindcast comparisons. The analysis concentrates on the CC signal obtained from the seasonal-averaged temperature and precipitation fields and shows that the fine-scale variability of the CC signal is generally small compared to its large-scale component, suggesting that little AV can be expected for the time-averaged fields. For the temperature variable, the largest potential for fine-scale added value appears in coastal regions mainly related with differential warming in land and oceanic surfaces. Fine-scale features can account for nearly 60 % of the total CC signal in some coastal regions although for most regions the fine scale contributions to the total CC signal are of around ∼5 %. For the precipitation variable, fine scales contribute to a change of generally less than 15 % of the seasonal-averaged precipitation in present climate with a continental North American average of ∼5 % in both summer and winter seasons. In the case of precipitation, uncertainty due to sampling issues may further dilute the information present in the downscaled fine scales. These results suggest that users of RCM simulations for climate change studies in a delta method framework have little high-resolution information to gain from RCMs at least if they limit themselves to the study of first-order statistical moments. Other possible benefits arising from the use of RCMs—such as in the large scale of the downscaled fields– were not explored in this research.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
In the context of a changing climate due to anthropogenic factors, it is generally argued that the planning for adaptation requires climate information accounting for specificities on scales at which human activities occur, for example about climatic characteristics within countries, provinces and even cities (Oreskes et al. 2010). This need of very fine-scale climatic information has important consequences for climate research and it has pushed climate modeling research centres to perform increasingly higher resolution climate simulations and to look for alternative techniques to produce fine-scale climatic information.
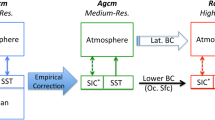
One such approach has been the development of nested, limited-area, regional climate models (RCMs). Basically, the RCM technique allows for an increase in resolution by concentrating the degrees of freedom, and hence the computational resources, over a limited region of the globe where the main interest of a user lies (Laprise et al. 2008). Technically, it consists of using time-dependent large-scale atmospheric fields and ocean surface boundary conditions to drive a high-resolution atmospheric model integrated over a limited-area domain (Giorgi et al. 2001). The atmospheric driving data are either derived from simulations of lower resolution coupled Atmosphere-Ocean General Circulation Models (AOGCMs) or analyses of observations.
From the beginning of RCMs development, nearly 20 years ago, a large effort has ensued to assess their capability as climate downscaling tools by comparing RCM-simulated climate to observed data sets. Moreover, particularly in the last decade, important efforts were also devoted to assess the ability of RCMs to improve the simulated climate compared to their driving data in order to identify the value added by RCMs. The various added value (AV) studies (for a review of these studies the reader is referred to Prömmel et al. (2010) and Feser et al. (2011) and references therein) have clearly shown that RCMs do not generate AV in an unequivocal way but it seems to depend upon a variety of factors such as the season and time scale, the variable and the climate statistics of interest, the region of analysis, etc.
The AV is generally defined as the ability of RCM simulations to improve some particular aspect of the driving fields compared to observations. The necessary use of observed data in order to identify this AV restricts its study to only recent past RCM climate simulations (i.e., hindcast simulations) either driven by reanalyses or AOGCM outputs. Moreover, the scarceness of fine-scale observations and the limited number of variables available for validation limits even more those cases where the AV can be evaluated. In order to circumvent the limitations imposed by the necessity of observations, Di Luca et al. (2012a) have developed a framework, denoted as potential added value (PAV), that uses the presence of fine-scale variability in RCM-derived climate statistics as a prerequisite condition for an RCM to generate some real fine-scale AV.
Due to its independence from observational data, the PAV framework is particularly interesting when considering the problem of ascertain whether increasing model resolution can improve climate projections. As it will be shown later, when downscaling climate projections from AOGCMs, our interest is not necessarily directed towards the RCM climate simulation itself but sometimes towards the climate change (CC) signal computed from the difference between climate statistics derived from present and future RCM simulations. For example, in order to account for systematic biases in RCM projections, a popular approach used to estimate future climate is through the “delta method” (e.g., see Rummukainen 2010). The delta method consists of adding to the observed climate data the RCM-simulated climate change signal. This suggests that the RCM’s added value in climate projections may not come directly from the simulation of future scenario periods but rather from the climate-change signal itself.
Implicit in the last argument is the idea that some changes in climate will occur in spatial scales smaller than those resolved by current AOGCMs. Several sources of fine-scale climate change can be conceived. For example, fine-scale climate forcings (e.g., land cover) can change in the future due to the influence of human activities (e.g., in agricultural activities). The non-linear interaction between a large-scale variable and fine-scale surface forcings can induce small-scale changes if the large-scale variable changes in the future. Feedback processes can also induce small-scale changes in meteorological variables due to the fine scale heterogeneity of surface physical properties.
It should be emphasised, however, that the arguments from which fine-scale features would appear in the climate change signal are not the same as those asserted for the climate itself. One example can help to understand the difference. A simple mechanism that can generate AV in mountainous regions in present climate simulations is related with the general relation between temperature and terrain elevation. The more detailed representation of terrain elevation gradients will create stationary temperature gradients even when no fine-scale atmospheric processes occur. But this mechanism may not generate AV in the CC signal because their effects may be cancelled out when computing the difference between future and climate statistics.
The objective of this article is twofold. First, to quantify the fine-scale part of the RCM-derived CC signal and to evaluate its relative importance compared to either the large-scale CC part or to present climate statistics. Second, to characterise the robustness of the fine-scale quantitative results in terms of the sampling uncertainty that results from interannual variability. The analysis concentrates on time-averaged seasonal temperature and precipitation climate change signals as reproduced by several RCM-AOGCM pairs in a domain that covers most of North America, thus encompassing a wide range of climate regimes. That is, following the classification proposed by Castro et al. (2005) in which the RCM technique is separated according to the boundary conditions used to drive the RCM, in this article we will focus on the PAV of Type 4 RCM simulations.
The paper is organized as follows. The next section discusses in some detail the added value issue with special emphasis on two particular aspects: the difference between AV and PAV and; the difference between looking for AV in present climate statistics and in future changes in climate statistics. Section 3 presents a brief description of the data used. Section 4 describes the methodology used to analyze the importance of fine scale features and the metrics used to quantify the PAV and its related sampling uncertainty. Temperature and precipitation results are presented in Sects. 5.1 and 5.2 respectively. Some discussion of the results and conclusions is given in Sect. 6.
2 Added value issue
2.1 Present climate statistics
In order to illustrate the AV issue, let us consider a hypothetical AV study. Let us suppose that we are trying to decide whether an RCM adds value over a lower resolution climate model (hereafter denoted by GCM) in the representation of some climate statistics X (e.g., seasonal-averaged precipitation). Assuming that the metric chosen to assess model’s performance is given by the squared error (SE), then the AV can be defined by
Defined in this way, the RCM generates some AV if its SE is smaller than the GCM’s one, i.e., if AV is positive.
In order to gain more insight on the sources of AV, let us separate the field according to different spatial scales and express the value of X OBS as follows:
where the superscripts ls and ss designate, respectively, the large scales and small scales that are permitted or not by the GCM grid. Hence by definition X ss GCM = 0 and
Similarly the RCM-derived climate statistics (X RCM ) may be decomposed as
Replacing Eqs. (2), (3) and (4) in Eq. (1), rearranging and neglecting covariance terms (see below and in "Appendix" for details), we obtain:
where
and
That is, the AV can be approximately decomposed into a small-scale term (AV ss) and a large-scale term (AV ls). We recall that these equations were arrived at neglecting two covariance terms: one corresponds to assuming that large-scale errors of GCM are uncorrelated with small-scale variance of observations, and the other that large-scale and small-scale errors of RCM are uncorrelated.
From Eq. (6) it is clear that three conditions must be satisfied for the RCM to generate small-scales added value (AV ss > 0):
-
1.
the observed climate statistics X OBS must contain non-negligible fine-scale information, i.e., (X ss OBS )2 > 0,
-
2.
the RCM-derived climate statistics X RCM must contain non-negligible fine-scale information, i.e., (X ss RCM )2 > 0, and
-
3.
the error associated with the fine-scale RCM-derived information must be smaller than the information itself, i.e., (X ss RCM − X ss OBS )2 < (X ss OBS )2.
This analysis suggests that a measure of the potential of RCMs to add value can be obtained by quantifying the maximum or available AV derived using observations:
The quantity MAV ss is called maximum added value of the small scales and gives an estimation of the maximum value that an RCM or any other downscaling technique can add. In those cases where observations are not available, an estimation of the maximum added value can be done in terms of fine-scale RCM features:
with PAV ss denoting the potential for small-scale added value suggested by a given RCM simulation. It is important to note that if (X ss OBS )2 ≠ (X ss RCM )2 then the PAV quantity (X ss RCM )2 will under- or over- estimate MAV ss by simulating too little or too much fine-scale variability. An under/over estimation of MAV ss can be related with either positive or negative AV ss, depending on the values of SE ss RCM and (X ss OBS )2. That is, even if PAV ss can give an erroneous estimation of MAV ss, it is still an interesting and useful quantity because allows to estimate the small-scale part of PAV in those cases where we do not have any knowledge about the observed climate statistics.
Figure 1 shows the dependence of AV ss as a function of X ss RCM for three different values of X ss OBS . In the case where X ss OBS = 0 everywhere, an increase in fine-scale variance of X RCM can only subtract value by making AV ss negative. Where X ss OBS ≠ 0, the fine-scale feature of X RCM can add value over the GCM estimation wherever Eq. (6) is positive. The maximum AV ss is found when X ss OBS = X ss RCM and is given by \(\overline{({X_{RCM}^{ss}})^2}\). Furthermore, Fig. 1 shows that the term AV ss can potentially increase as X ss OBS increase, justifying the idea of using the increase in the observed fine-scale variance as a proxy of an increase in AV ss.
The term AV ls in Eq. (5) represents the AV that can be generated by an RCM due to an improvement in the large-scale part of the climate statistics X. It is still a subject of discussion and debate in the RCM community whether or not we should hope to find that RCMs are able to generate AV at large scales, with some authors (e.g., Mesinger et al. 2002 and Veljovic et al. 2010) arguing for a positive answer and others (e.g., Castro et al. 2005; Laprise et al. 2008) promoting the use of large-scale nudging thus reducing the chances of RCMs to produce AV ls. In any case, it is generally accepted (e.g., Feser 2006; Prömmel et al. 2010) that the raison d’être of RCMs is related with the existence of AV of fine scales (i.e., AV ss > 0), justifying the fact that most AV and PAV studies, including this article, have concentrated in the AV ss and PAV ss terms.
The PAV ss concept as described above was used to study the potential benefits of using high-resolution RCMs to simulate present climate precipitation (Di Luca et al. 2012a) and temperature (Di Luca et al. 2012b), and the PAV ss dependence on several factors such as the season, the region and the climate statistics of analysis. In what follows, the application of the PAV framework to climate change studies will be considered.
2.2 Future changes in climate statistics
A variety of approaches may be used to show how a given climate statistics X can change between present and future climate simulations. A popular approach, generally designated as the “delta method” (e.g., see Rummukainen 2010), consists on computing the future climate statistics (X future) by adding the climate change as estimated from climate model simulations (CC simulated ) to the past observed climate (X present OBS ). That is, the delta method approximation can be expressed as:
where CC simulated is computed in the usual form as the difference between X in future and present climate (X future simulated − X present simulated ) using either RCM (CC RCM ) or GCM (CC GCM ) simulations.
Another popular approach used to show changes in climate statistics X is through the use of the climate change signal (CC simulated ) itself, with no explicit consideration of present and future climate statistics. That is, in this case, we are not interested in the future value of the climate statistics but only on how much X may change between present and future periods.
Following the development in Sect. 2.1, the CC signal added value (AV CC ) generated by an RCM simulation over a GCM can be defined using the delta method by:
where the subscript “true” denotes the still unknown climate statistics that will arise in future climate conditions. That is, the RCM generates some AV if its error in the CC signal estimation is smaller that the GCM one, i.e., if AV CC is positive. It is important to note that, when using the delta method, the AV of RCM simulations in future climate statistics does not depend directly on the future climate statistics (X future simulated ) but on the CC signal (CC simulated ).
Replacing the total CC signal in Eq. (11) according to the contribution of large (CC ls) and small (CC ss) scales and neglecting the two covariance terms as in Sect. 2.1 (see also "Appendix") we have,
with
and
As with the present climate case, three necessary conditions for the RCM to add value in the fine-scale CC signal can be identified:
-
1.
the true CC signal (CC true ) must contain non-negligible fine-scale information, i.e., (CC ss true )2 > 0,
-
2.
the RCM-derived CC signal (CC RCM ) must contain non-negligible fine-scale information, i.e., (CC ss RCM )2 > 0, and
-
3.
the error of the fine-scale RCM-derived CC information must be smaller than the information itself, i.e., (CC ss true )2 > (CC ss RCM − CC ss true )2.
Given that we do not have any knowledge about the true CC signal, the available or maximum small-scale AV cannot be measured for future climate projections (see Eq. (8) for comparison) and the first condition cannot be explicitly addressed. However, in a similar way as done in the last section, a quantity measuring the importance of fine scales in the CC signal can be used to characterise the PAV:
Defined in this way, a near zero value of \( PAV_{CC_{1}}^{ss}\) suggests that no fine-scale variability is created by the RCM simulation and hence no AV ss CC should be expected.
Moreover, in those cases where \( PAV_{CC_{1}}^{ss}\) > 0, the third condition can be used to define a second PAV quantity:
where \(\Updelta_{RCM}^{ss}\) constitutes a measure of the uncertainty in the estimation of CC ss RCM and is used as a proxy of the error SE ss CC,RCM . The quantity \( PAV_{CC_{2}}^{ss}\) measures the magnitude of the fine-scale CC signal (CC ss RCM ) compared to its uncertainty (\(\Updelta_{RCM}^{ss}\)) and can be used to quantify the robustness of the CC ss RCM estimation and the associated chances to produce some AV ss CC . \( PAV_{CC_{2}}^{ss}\) values close to or less than zero suggest a large uncertainty associated with CC ss RCM and a high chance to get the wrong value of CC ss true . Relatively large values of both \( PAV_{CC_{1}}^{ss}\) and \( PAV_{CC_{2}}^{ss}\) would be related with a large and robust estimation of the fine-scale component of the CC signal and with a large potential for added value.
Finally, for the large-scale part, the PAV in the CC signal could be simply defined as:
That is, there exists some PAV CC in large scales if and only if the climate projections derived using the RCM and the driving GCM simulations are different. Several arguments can be presented to expect a large-scale component of the PAV CC quantity. For example, Gao et al. (2011) argue that because AOGCMs do not adequately simulate higher elevations where temperature changes have less effect on snow cover (where temperatures are still cold enough to retain snow), the large-scale temperature change can be differently simulated in an RCM compared to a GCM. As argued in Sect. 2.1, we suppose that the primary AV of RCM simulations would come from the direct influence of the small-scale part and so, in this article, we will concentrate in the study of PAV ss CC with no explicit consideration of the large-scale counterpart PAV ls CC or the covariance terms (see "Appendix" for details).
3 NARCCAP data
The RCM simulations used in this study were provided by the North American Regional Climate Change Assessment Program (NARCCAP; http://www.narccap.ucar.edu/; Mearns et al. 2009). In NARCCAP, RCMs were run with a horizontal grid spacing of about 50 km over similar North American domains covering Canada, United States and most of Mexico. Acronyms, full names and a reference, and the modelling group of the RCMs used in this study are presented, respectively, in the first three columns in Table 1.
Five RCM-AOGCM pairs are used in this study to analyze the climate change signal, with two RCMs (CRCM and RCM3) driven by two AOGCMs and one RCMs (HRM3) driven by only one AOGCM. Four AOGCMs are used to drive the RCMs: the Canadian Global Climate Model version 3 (CGCM3, Flato and Boer (2001) and Flato (2005)), the NCAR Community Climate Model version 3 (CCSM3, Collins et al. 2006), the Geophysical Fluid Dynamics Laboratory Climate Model version 2.1 (GFDL, GFDL Global Atmospheric Model Development Team 2004) and the United Kingdom Hadley Centre Coupled Climate Model version 3 (HadCM3, Gordon et al. 2000). The fourth column in Table 1 provides the LBCs used to drive each RCM. A total of ten RCM simulations are considered, five of them simulating a present period (1971–1995) and the other five simulating the future climate (2041–2065) using the A2 scenario (Mearns et al. 2009).
For each RCM simulation, several 3-hourly variables are available in their original map projection; but in this article we will concentrate only on the instantaneous 2-m temperature and on the 3-hourly average total precipitation. Sea surface temperatures (SST) and sea ice (SI) surface boundary conditions comes from AOGCM data and are updated every 6 h by using a linear interpolation between consecutive monthly-mean values. Similarly, boundary conditions are interpolated from the low resolution to the ∼50-km grid meshes by using a linear interpolation in the horizontal.
All NARCCAP RCMs include some more or less sophisticated representation of land surface and the upper soil levels. The representation of lakes depends on each RCM and on the LBCs used to drive the RCM. RCMs do not share the fraction of water in every grid point (i.e., the land-water mask is model dependent) although most RCMs, with the only exception of the RCM3, represents the Great Lakes, Winnipeg Lake and other relatively large lakes in the west northern part of Canada. In all cases, as with oceanic regions, surface temperatures in lakes are prescribed using the driving AOGCM data.
4 Methodology
The methodology used to study the importance of fine scales in the determination of the climate change signal is based on a perfect model approach designated as the potential added value framework. A main advantage of this framework is that it allows to estimate PAV ss CC quantities independently of the relative performance between the RCM and the driving AOGCM without necessity of having high-resolution observations. A brief description of the framework is given here but a more detailed discussion can be found in Di Luca et al. (2012a, b).
4.1 PAV measures
Let us consider a two-dimensional field representing the projected change of a given climate statistics X computed using ∼50 km grid-spacing RCM simulations that we denote by CC RCM . A domain of analysis, common to all RCMs, is selected and divided in non-overlapping boxes of 300 km by 300 km leading to a low-resolution grid mesh containing a total of 288 grid boxes (see Fig. 2). Using this grid mesh, we can define a lower resolution version of CC RCM , that we denote by the virtual GCM version of the climate change signal (CC VGCM ), by aggregating the CC RCM over each 300-km side grid boxes. For any RCM-AOGCM simulation, the upscaling is simply performed by computing the arithmetic average of the statistics X over all the RCM grid points inside the region of interest.
As discussed in Sect. 2.2, a question that arises naturally in the context of the PAV framework is whether the high-resolution CC RCM contains fine-scale information that is absent in the low-resolution part (CC VGCM ). Given that some of the most important factors of anthropogenic climate change are large scale in nature (e.g., greenhouse gases concentration changes), it is unclear whether the CC signal would contain a significant high-resolution component. A simple way to quantify the importance of fine scales in the high-resolution CC signal can be done by defining:
where σ2 (CC RCM ) denotes the spatial variance of the high-resolution CC signal field over a given 300-km side region. Similarly, we can define a relative PAV quantity that evaluates the proportion of the CC signal that is accounted only by the fine-scale part by writing
where CC 2 VGCM is the square of the spatial-mean climate change signal in each region. Defined in this way, \( rPAV_{CC_{1}}^{ss}\) varies between 0 and +\(\infty\); \( rPAV_{CC_{1}}^{ss}\) ∼0 would indicate that the high-resolution estimation does not add extra information over the coarse-resolution one. For a given region, \( rPAV_{CC_{1}}^{ss}\) ∼1 indicates that the change in the fine-scale temperature is as large as the large-scale part change.
For the seasonal-averaged temperature, CC VGCM is always greater than zero in continental North America and Eq. (19) is well defined. When considering seasonal-averaged precipitation, CC VGCM can be near zero and so an alternative rPAV quantity should be considered to avoid that rPAV be indefinite. This can be done, for example, by normalising the \( PAV_{CC_{1}}^{ss}\) with the square of the mean precipitation of the region:
where pr present VGCM represents the spatial-mean precipitation over each 300-km side region in present climate. Again, with this definition, \( rPAV_{CC_{1}}^{ss}\) varies between 0 and +\(\infty\); \( rPAV_{CC_{1}}^{ss}\) ∼0 indicating that the high-resolution estimation does not add extra information over the coarse-resolution one. For a given region, \( rPAV_{CC_{1}}^{ss}\) ∼1 indicates that the change in the fine-scale precipitation is as large as the spatial-mean precipitation itself.
It should be emphasised that the quantities \( PAV_{CC_{1}}^{ss}\) and \( rPAV_{CC_{1}}^{ss}\) defined in Eq. (18), (20) and (19) only account for the potential added value of the small scales (PAV ss CC ), that is, the PAV arising from the simulation of fine-scale features in the statistics X that are absent in GCM fields. The two quantities are mute about the potential of RCMs to add value in the large scale or in the covariance terms (see Sect. 2 and "Appendix").
4.2 Sampling uncertainty in PAV measures
Inherent to the process of computing climate statistics from a finite length time series (i.e., 25 years periods in our case) there is an uncertainty related to sampling. The existence of sampling uncertainty implies that two adjacent grid points can show somewhat different present and future statistics (e.g., time-averaged values), leading to differences in the CC signal and its derived spatial variance, even if physical mechanisms that determine the climate in both grid points are essentially the same. Ideally, in any grid point and for any given RCM-AOGCM simulation, the sampling uncertainty can be quantified using several RCM simulations performed employing different boundary conditions arising from running the AOGCM with slightly different initial conditions (i.e., using several members of the driving AOGCM). In NARCCAP, modelling efforts has been put on the number of RCM-AOGCM pairs and there is only one realisation of each pair available for analysis thus preventing the internal variability sampling study.
In order to circumvent this practical limitation, the sampling uncertainty will be quantified by estimating the fine-scale CC signal in each 300-km side region using a Monte Carlo approach. First, for each RCM-AOGCM simulation, the high-resolution climate change signal CC RCM is computed 100 times by sampling randomly with replacement over the 25-year seasonal averages of present (X present RCM ) and future (X future RCM ) simulations, thus obtaining a distribution for CC RCM that we denote by CC i RCM .
Second, for each sample of CC i RCM , we compute the spatial variance obtaining a 100 sample distribution of variances in each region, denoted by σ 2 i (CC RCM ), that can be used to estimate the mean spatial variance and some measure of the spread around the mean. Defined in this way, the sampling uncertainty gives a measure of the interannual variability in each region.
A similar method to estimate sampling uncertainty was used by Déqué et al. (2011). Using a Monte Carlo procedure and a 10 members sampling they found a very good agreement between the sampling uncertainty computed using various runs only differing on initial conditions and the Monte Carlo approximation for time-averaged precipitation. For time-averaged temperature, they found a good agreement in summer season but they found that the Monte Carlo approximation underestimates by nearly 30 % the “true” spread in winter. Although these results are encouraging, a more detailed study should be undertaken to confirm that the Monte Carlo estimation constitutes a good approximation.
The existence of sampling uncertainty has implications when attempting to evaluate the necessary conditions for AV that were discussed in Sect. 2.2 (see Eqs. 15 and 16). First, when trying to identify regions containing non-negligible fine-scale variance (i.e., \( PAV_{CC_{1}}^{ss}\) = σ2 (CC RCM ) > 0), the sampling uncertainty implies that we cannot use a zero threshold but some non-zero threshold that measures the level of noise inside each region. That is, a “variance noise” threshold must be used in order to determine whether the fine-scale variance is induced by physical mechanisms or only arising from sampling uncertainty. We will refer to the use of such threshold as “physically significant” condition.
The physically significant condition is defined here in a simple way by arbitrarily choosing a minimum value, the same for all regions, for \( PAV_{CC_{1}}^{ss}\) to be statistically different from zero. In order to take into account the sampling uncertainty in the variance computations and the possibility of getting a value below the threshold by chance, the criterion imposes that 95 % of the Monte Carlo-generated variances must be larger than the threshold:
For the absolute quantity (PAV ss CC ), relatively small values are chosen for both temperature ((0.1 K)2 threshold) and precipitation ((0.04mm/day)2 threshold). Assuming that CC RCM values are normally distributed inside each region, this implies that 95 % (99 %) of the CC RCM differences between two grid points are smaller than 0.2 K (0.3 K) for temperature and smaller than 0.08 mm/day (0.12 mm/day) for precipitation. Similarly, for relative PAV quantities (rPAV ss CC ), regions will be considered as physically significant when rPAV ss CC values are larger than 0.052 and 0.02 2 for temperature and precipitation respectively.
Another implication introduced by the existence of sampling uncertainty is related with the second PAV quantity defined in Eq. (16). As discussed in Sect. 2.2, a measure of the uncertainty of CC ss RCM can be used to estimate the condition (CC ss true )2 > SE ss CC,RCM that suggests that a large error in the estimation of CC ss true can prevent the RCM from adding value. In particular, the sampling uncertainty can be used as a lower limit of the unknownable error SE ss CC,RCM to quantify the “potential skill” of the fine-scale spatial variance estimation. That is, although we can never decide on the actual skill of the RCM-derived CC signal, we can be confident that the CC ss RCM skill will be poor if the associated uncertainty is large. In this sense, the potential skill can be partially quantified through the use of the sampling uncertainty and will tend to diminish as the uncertainty increases.
In order to define the potential skill condition, let us suppose that the mean value of σ 2 i (CC RCM ) is a good estimation of the spatial variance of the true climate-change signal (i.e., \(\overline{{ \sigma^2 (CC_{RCM}) }} \sim \sigma^2 (CC_{true})\)). In this case, for any sample σ 2 i (CC RCM ), there will be some AV in the fine-scale climate-change signal if and only if \(\sigma^2_i (CC_{RCM}) < 2\cdot \overline{{ \sigma^2 (CC_{RCM})}}\) (see Eq. 13). That is, in order to guarantee some form of skill in the estimation of a \( PAV_{CC_{1}}^{ss}\) we will consider as potentially skillful those regions in which at least 95 % of the σ 2 i (CC RCM ) samples verify:
with q 95 the 95th percentile of the σ 2 i (CC RCM ) distribution.
Several uncertainty sources can influence PAV quantities; see Foley (2010) for a detailed discussion. The uncertainty related with the use of different RCM and AOGCMs will not be directly addressed here, although PAV quantities derived from individual pairs of RCM-AOGCM simulations will be shown. Also, NARCCAP future climate simulations are available only based on the A2 scenario (see IPCC 2007), thus preventing any scenario uncertainty analysis. While this can be a main source of uncertainty when looking at the end of the twentyfirst century climate, it is probably less important when looking at the first half of the century.
It should be noted that quantitative results related to the “physically significant” and the “potential skill” conditions depend on the arbitrary choice of the threshold and the sampling uncertainty measure, respectively. The use of other thresholds and sampling uncertainty measures would lead to different quantitative results. However, we expect results to be qualitatively similar.
5 Results
5.1 Temperature
Figures 3 and 4 show the seasonal-averaged projected temperature change (2041–2065 to 1971–1995) for individual RCM simulations in winter and summer seasons respectively. In both seasons, results show warmer conditions in the future with generally a stronger warming in continental compared to oceanic regions. In winter season, the spatial pattern of CC RCM shows a general increase to the north and to the interior of the continent that reaches almost 7 K in the centre of the Hudson Bay for all RCM simulations with the only exception of the RCM3-GFDL simulation. This pattern of warming is related with the positive feedback induced by the reduction of the period of snow sea-ice cover and the associated increase in absorbed solar radiation (see for example IPCC 2007).
Same as Fig. 3 but for summer season results
Warming is smaller in summer than in winter in northern regions and generally larger in central and southern regions. The spatial pattern of CC RCM shows maximum values in continental-middle latitudes with changes as large as 4 K in central United States in most RCM simulations. This pattern of warming is mainly explained by the positive feedback induced by the decrease of latent heat fluxes and the increase in sensible fluxes due to negative anomalies in surface soil moisture in most central-western regions (Seneviratne et al. 2010).
Figures 5 and 6 show the square root of the \( PAV_{CC_{1}}^{ss}\) measure (see Eq. 18) for the RCM-AOGCM simulations and for the ensemble-mean results in winter and summer seasons, respectively. As stressed in Sect. 3, oceanic boundary conditions in NARCCAP simulations are obtained by interpolating SST and SI fields coming from the driving AOGCM simulations. This means that stationary fine-scale patterns in the ocean fields, if they exist, are artificial and do not reflect any physical processes. For this reason, we decided to mask oceanic regions in the PAV analysis. Oceanic regions are defined as those containing 100 % water-fraction and the total number depends on the RCM considered, varying between 50 in the CRCM to 58 in the HRM3 model.
Square root of the temperature potential added value (see Eq. 18) in winter season for individual RCM-AOGCM simulations and for the ensemble mean. White regions designate those regions that do not satisfy the “physically significant” condition. Large crosses (x) designate those regions that do not satisfy the “skill” criteria. Oceanic regions are in black
Same as Fig. 5 but for summer season results
In winter season (Fig. 5), the largest \(\sqrt{PAV_{CC_{1}}^{ss}}\) values (∼1.2 K) appear in northern-coastal regions mainly along the Hudson Bay and the Canadian Archipelago coasts with relatively large values also along the Pacific Coast (∼0.5 K) and in central western United States. Different mechanisms appear to produce the relatively large values in coastline regions depending on whether or not sea ice is present during the winter. For example, most RCM-AOGCM simulations show large values of \( PAV_{CC_{1}}^{ss}\) over the northern part of the Pacific Coast, associated with larger warming over land compared to water (see Fig. 3), probably explained by the snow-albedo feedback that is present in land but absent in water surfaces. On the contrary, large values of \( PAV_{CC_{1}}^{ss}\) in the Hudson Bay and the Canadian Archipelago coasts are generally related with a more pronounced warming over oceanic regions, maybe due to a stronger albedo feedback in sea ice compared to land surfaces. A mechanism that can be important in regions along the Rocky Mountains is related with the snow-albedo feedback resulting from the differential snow cover change in varying altitude regions.
A large number of regions show that at least 5 % of winter \(\sqrt{PAV_{CC}^{ss}}\) sample values are smaller than the 0.1 K threshold established for physical significance (white mask in Figs. 5 and 6). The number of these regions depends on the simulation and varies between 74 in the HRM3-HADCM3 and 170 in the RCM3-GFDL simulations, with all simulations showing “zero” values in the south-eastern part of the continent.
Figure 5f shows the square root of the average of \( PAV_{CC_{1}}^{ss}\) across the five individual simulations (\(\sqrt{\langle PAV_{CC_{1}}^{ss} \rangle}\)) in winter season. A total of 154 out of 230 non-oceanic regions appear to be physically significant and these regions are mostly located along a coast (Canadian Archipelago, Hudson Bay, Pacific and Atlantic Oceans) and in the central-western part of the continent.
In summer season (Fig. 6), the largest \(\sqrt{PAV_{CC_{1}}^{ss}}\) values (∼0.6 K) appear also in coastal regions along the Hudson Bay, but in this case relatively large values extend to the south, along the Pacific and the Atlantic coasts and over the Great Lakes and other smaller lakes in Canada, at least in those simulations containing lakes (CRCM and HRM3). In this season, the relatively large \( PAV_{CC_{1}}^{ss}\) values in coastal regions seem to be forced mainly by a larger warming over land compared to oceanic regions (see Fig. 4) probably due to the slower response of the ocean because of its larger heat capacity. The number of regions that verify the “physically significant” criterion (see Eq. 21) varies between 105 in the HRM3-HADCM3 and 158 in the RCM3-GFDL simulations, thus showing similar values although less variability than the winter case.
Figure 7 shows the square root of the ensemble-mean temperature relative PAV measure (computed using Eq. (19)) in winter and summer seasons, respectively. \(\sqrt{\langle rPAV_{CC_{1}}^{ss} \rangle}\) values are always smaller than 0.6, suggesting that fine-scale mean-temperature changes are generally smaller than the large scale ones. The domain-averaged \(\sqrt{\langle rPAV_{CC_{1}}^{ss} \rangle}\) in winter (summer) is 0.086 (0.093) with a maximum value of 0.31 (0.58). That is, averaged over continental North America, the contribution of the fine scales to the total climate change signal is of the order of 10 % although it can attain 60 % in specific regions.
Same as Fig. 5 but for the ensemble-mean rPAV ss CC quantity
In both seasons, as with the absolute \( PAV_{CC_{1}}^{ss}\) measure, the largest ensemble-mean rPAV ss CC values appear along coastal regions due to the differential heating observed in land and ocean surfaces. In winter (summer), there is a total of 101 (93) out of 230 non-oceanic regions where at least 5 % of \(\sqrt{\langle rPAV_{CC_{1}}^{ss} \rangle}\) sample values are smaller than the threshold imposed for physical significance. Other than in coastal regions, relatively large winter \(\langle rPAV_{CC_{1}}^{ss} \rangle\) values appear over west-central United States (probably associated with fine-scale topography) and over the Great Lakes. The general spatial pattern of \(\sqrt{\langle rPAV_{CC_{1}}^{ss} \rangle}\) closely resembles the \(\sqrt{\langle PAV_{CC_{1}}^{ss} \rangle}\) field suggesting that fine-scale variances of the CC signal tend to follow the mean CC.
Interestingly, according to the potential skill condition (see Eq. 22), the estimation of \(\langle PAV_{CC_{1}}^{ss} \rangle\) and \(\langle rPAV_{CC_{1}}^{ss} \rangle\) quantities appear to be robust in all regions for both summer and winter seasons.
5.2 Precipitation
A similar analysis to the one presented above is also performed for the precipitation variable. Figures 8 and 9 show the seasonal-averaged precipitation change (2041–2065 to 1971–1995) for individual RCM-AOGCM simulations (CC RCM ) in winter and summer seasons, respectively. The high-resolution CC signal is normalised by the present climate mean precipitation in order to account for the important mean-precipitation gradients across the North American continent.
Same as Fig. 8 but for summer season results
In winter, most simulations tend to produce an increase in precipitation over most of the continent mainly as a result of the increase of atmospheric moisture due to the temperature dependence of the water vapour saturation pressure together with a displacement of the westerlies to the north (see IPCC 2007). Increments are generally smaller than 30–40 %, with maximum values generally located over the Hudson Bay. In absolute terms (not shown), the maximum increase in precipitation amounts appear along the northern part of the Pacific Coast, with values of the order of 3 mm/day. Most RCM-AOGCM simulations tend to show a decrease of precipitation in the south-western part of the domain, a feature that seems to be related with an enhanced subsidence in this region due to an intensification of the subtropical anticyclone in this season (IPCC 2007).
In summer, in agreement with results found in IPCC (2007), the precipitation CC signal is strongly dependent on the RCM-AOGCM simulation and, in some simulations, the increase in precipitation is only limited to the northern part of the domain. Some simulations suggest a decrease of about 30 % in mean-precipitation in the northern part of the Pacific Coast.
Figures 10 and 11 show the square root of the precipitation \( PAV_{CC_{1}}^{ss}\) measure for individual RCM-AOGCM simulations and for the ensemble-mean results in winter and summer seasons, respectively. In winter season (Fig. 10), the largest \(\sqrt{PAV_{CC_{1}}^{ss}}\) values are found along the Pacific coast, mainly in the northern part, with values attaining 1.15 mm/day. In some individual simulations, the \(\sqrt{PAV_{CC_{1}}^{ss}}\) winter season field shows a secondary maximum in the south-eastern part of the domain, with values of about 0.4 mm/day. In regions located in central United States and most of Canada, the 5th percentile of the \(\sqrt{PAV_{CC_{1}}^{ss}}\) distribution is generally smaller than the 0.04 mm/day threshold, suggesting that most of these regions are physically non-significant.
Square root of the precipitation potential added value in winter season for individual RCM-AOGCM simulations and for the ensemble-mean. White regions designate those regions that do not satisfy the “physically significant” condition. Crosses (x) designate those regions that do not satisfy the “potential skill” criteria. Oceanic regions are in black
Same as Fig. 10 but for summer season results
In summer, no clear pattern of \( PAV_{CC_{1}}^{ss}\) can be identified and, in most regions, mean \(\sqrt{PAV_{CC_{1}}^{ss}}\) values are generally smaller than 0.3 mm/day. In this season, the PAV precipitation analysis in individual RCM-AOGCM simulations shows that a minimum of 107 and a maximum of 213 appear as physically non significant according to the criterion defined in Eq. (21).
Figure 12 shows the square root of the relative PAV precipitation measure (see Eq. 20) for the ensemble-mean results in winter and summer seasons, respectively. In both seasons, it is clear that the fine-scale component of the CC signal is much smaller than the present seasonal-averaged precipitation. Domain-average \(\sqrt{\langle rPAV_{CC_{1}}^{ss} \rangle}\) values are about 0.045 and 0.048 in winter and summer seasons respectively, suggesting that fine scales induce a precipitation change of about 5 % compared to the present time-averaged precipitation.
Same as Fig. 10 but for the ensemble-mean rPAV ss CC quantity
In winter season (Fig. 12a), the largest changes in mean precipitation (∼10 %) seem to arise related with the presence of fine-scale topographic features along the Rocky Mountains and with a small-scale process taking place in the northern part of the domain.
In summer season (Fig. 12b), the largest \(\sqrt{\langle rPAV_{CC_{1}}^{ss} \rangle}\) values appear in the south-western part of the continent with values attaining 0.3 in some regions. Interestingly, most of these regions seem to be non-robust to the sampling uncertainty criterion indicating that in these regions negative added value could be the net result due the generation of too much or too little fine-scale features.
According to the potential skill condition, the estimations of \( PAV_{CC_{1}}^{ss}\) and \( rPAV_{CC_{1}}^{ss}\) for precipitation are much more uncertain than for the temperature case. For the \( PAV_{CC_{1}}^{ss}\) quantity, a total of 9 (11) regions appear to show that the 95th percentile of their sampling distribution (σ 2 i (CC RCM )) is larger than two times their mean value in summer (winter) season. Table 2 shows that the number of regions increases to 41 (24) in the same seasons for the \( rPAV_{CC_{1}}^{ss}\). The last two results suggest that, for precipitation, the sampling uncertainty induced by interannual variability can be relatively large not only to determine fine-scale variances σ2 (CC RCM ) but also the seasonal-average precipitation CC 2 VGCM .
6 Discussion
The need of future climate information at local and regional scales together with objective evidence supporting the improvement of climate simulations arising from the use of higher resolution models have pushed the climate modelling community to perform increasingly higher resolution simulations and to develop alternative approaches to obtain the fine-scale climatic information.
In this article, various nested RCM simulations have been used to try to identify regions across North America for which the higher resolution afforded by RCMs will effectively generate non-negligible fine-scale information in the climate change signal. It is first noted that the issue of looking for AV in future climate is equivalent to searching for AV in the climate change signal instead of in the climate itself, at least when considering the “delta method” to approximate future climate statistics. Further, the absence of knowledge about the “true” climate change implies that only necessary (but not sufficient) conditions for AV can be studied leading to the concept of potential added value. This concept has already been discussed for present climate applications in Di Luca et al. (2012a, b).
It is shown that an RCM simulation must satisfy two conditions in order to have chances to produce added value over lower resolution AOGCMs in the fine-scale component of the climate change signal. First, the RCM-derived climate change signal must contain some non-negligible fine-scale information. Second, the uncertainty related with the estimation of this fine-scale information should be small enough to suggest some potential skill in future climate projections. That is, since non-negligible fine-scale information can either add value to or deteriorate the representation of the climate change signal compared to its large-scale part, large spread in the potential added value indicates a high chance to deteriorate the large-scale CC signal.
The importance of fine scales in the climate change signal is studied using the potential added value framework as presented in Di Luca et al. (2012a). For each NARCCAP RCM simulation, large-scale CC values are computed by aggregating the high-resolution CC signal over a lower resolution 300-km grid spacing mesh (denoted as virtual GCM grid) that tries to emulate the grid of a real low resolution GCM. Using a common North American domain for all NARCCAP RCM simulations, a total of 288 non-overlapping virtual GCM grid boxes are defined. An absolute potential added value measure is then defined by estimating the fine-scale variability of the CC signal inside each 300 km side region and a relative quantity is similarly derived by calculating the fraction of the total CC signal accounted for by the small-scale component.
For the temperature variable, the largest potential for added value appears in coastal regions mainly related with differential warming in land and oceanic surfaces. In northern regions along the Hudson Bay and the Canadian Archipelago this seems to be related with a differential snow-sea-ice albedo feedback. Along the Pacific and Atlantic coasts, the relatively large PAV seems to be more related with the differential warming due to the dissimilar thermodynamical properties (e.g., heat capacity) of water and land surfaces. Fine-scale features can account for nearly 60 % of the total CC signal in some coastal regions although for most regions the fine scale contributions to the total CC signal are of only ∼5 %.
For the precipitation variable, fine scales contribute to a change of generally less than 15% of the seasonal-averaged precipitation in present climate with a continental North American average of ∼5% in both summer and winter seasons. In winter, the largest PAV appears in mountainous regions and in the north part of the continent. In the first case, fine-scale features may be related with the interaction between large-scale precipitation changes in mid-latitudes (see IPCC 2007) and the fine-scale topography of the Rocky Mountains.
An important aspect to take into account when estimating the future change of a given climate statistics is related with its uncertainties. As expected, and in agreement with Giorgi (2002), we found that the sampling uncertainty due to interannual variability tends to increase as the spatial scale of the data used to compute climate statistics decreases (not shown).
The analysis also shows that the uncertainty due to interannual variability associated with fine-scale features in the CC signal seems to be much larger in precipitation than in temperature. This has as a consequence that while the RCMs may add fine-scale features to precipitation fields at all time scales, some of this gain may be lost due to the lack of robustness associated with the relatively short time periods usually analyzed (i.e., 25 years periods in our case). This result may be of importance for impact and adaptation studies and for this reason deserves further exploration.
Probably the most important limitation of this study is related with the choice of seasonal-averaged quantities in the PAV analysis without explicit consideration of, for example, higher order statistics. The dissimilar sensitivity to changes in spatial resolution exhibited by different climate statistics and their associated climate change signal can have important implications for CC signal PAV studies and it could be very interesting to repeat the analysis using a variety of climate change statistics (e.g., variances and percentiles).
A second important caveat is that the analysis of the uncertainty of the fine-scale part of the CC signal and its implications on PAV quantities was performed only in terms of the sampling uncertainty, with no consideration of others sources of uncertainties such as structural model uncertainties. As a consequence, the number of potential skilful regions obtained in this study probably corresponds to an upper limit compared to a more complete analysis including other uncertainty sources.
References
Castro CL, Pielke RA, Leoncini G (2005) Dynamical downscaling: an assessment of value added using a regional climate model. J Geophys Res 110:D05,108. doi:10.1029/2004JD004721
Caya D, Laprise R (1999) A semi-implicit semi-lagrangian regional climate model: the Canadian RCM. Mon Wea Rev 127(3):341–362
Collins WD, Bitz CM, Blackmon ML, Bonan GB, Bretherton CS, Carton JA, Chang P, Doney SC, Hack JJ, Henderson TB, Kiehl JT, Large WG, McKenna DS, Santer BD, Smith RD (2006) The community climate system model version 3 (ccsm3). J Clim 19:2122–2143. doi:10.1175/JCLI3761.1
Déqué M, Somot S, Sanchez-Gomez E, Goodess CM, Jacob D, Lenderink G, Christensen OB (2011) The spread amongst ensembles regional scenarios: regional climate models, driving general circulation models and interannual variability. Clim Dyn. doi:10.1007/s00382-011-1053-x
Di Luca A, de Elía R, Laprise R (2012a) Potential for added value in precipitation simulated by high-resolution nested regional climate models and observations. Clim Dyn 38:1229–1247. doi:10.1007/s00382-011-1068-3
Di Luca A, de Elía R, Laprise R (2012b) Potential for added value in RCM-simulated surface temperature. Clim Dyn. doi:10.1007/s00382-012-1384-2
Feser F (2006) Enhanced detectability of added value in limited-area model results separated into different spatial scales. Mon Wea Rev 134:2180–2190
Feser F, Rockel B, von Storch H, Winterfeldt J, Zahn M (2011) Regional climate models add value to global model data: a review and selected examples. Bull Am Meteorol Soc. doi:10.1175/2011BAMS3061.1
Flato G (2005) The third generation coupled global climate model (CGCM3). Available from http://wwwecgcca/ccmac-cccma/
Flato G, Boer G (2001) Warming asymmetry in climate change simulations. Geophys Res Lett 28:195–198
Foley A (2010) Uncertainty in regional climate modelling: a review. Prog Phys Geogr 34(5):647–670
Gao Y, Vano JA, Zhu C, Lettenmaier DP (2011) Evaluating climate change over the colorado river basin using regional climate models. J Geophys Res (in press). doi:10.1029/2010JD015278
GFDL Global Atmospheric Model Development Team (2004) The new GFDL global atmosphere and land model am2–lm2: Evaluation with prescribed sst simulations. J Clim 17(24):4641–4673. doi:10.1175/JCLI-3223.1. http://journals.ametsoc.org/doi/abs/10.1175/JCLI-3223.1
Giorgi F (2002) Dependence of the surface climate interannual variability on spatial scale. Geophys Res Lett 29(23):16.1–16.4
Giorgi F, Marinucci M, Bates G (1993) Development of a second generation regional climate model (regcm2) i: boundary layer and radiative transfer processes. Mon Wea Rev 121:2794–2813
Giorgi F, Christensen J, Hulme M, von Storch H, Whetton P, Jones R, Mearns L, Fu C, Arritt R, Bates B, Benestad R, Boer G, Buishand A, Castro M, Chen D, Cramer W, Crane R, Crossly J, Dehn M, Dethloff K, Dippner J, Emori S, Francisco R, Fyfe J, Gerstengarbe F, Gutowski W, Gyalistras D, Hanssen-Bauer I, Hantel M, Hassell D, Heimann D, Jack C, Jacobeit J, Kato H, Katz R, Kauker F, Knutson T, Lal M, Landsea C, Laprise R, Leung L, Lynch A, May W, McGregor J, Miller N, Murphy J, Ribalaygua J, Rinke A, Rummukainen M, Semazzi F, Walsh K, Werner P, Widmann M, Wilby R, Wild M, Xue Y (2001) Regional climate information- evaluation and projections. In: Houghton JT (ed) Climate change 2001: the scientific basis. Contribution of working group I to the third assessment report of the intergovernmental panel on climate change. Cambridge University Press, Cambridge, pp 583–638
Gordon C, Cooper C, Senior C, Banks H, Gregory J, Johns T, Mitchell J, Wood R (2000) The simulation of sst, sea ice extents and ocean heat transports in a version of the Hadley Centre coupled model without flux adjustments. Clim Dyn 16:147–168. doi:10.1007/s003820050010
IPCC (2007) Contribution of working group I to the fourth assessment report of the intergovernmental panel on climate change. Cambridge University Press, Cambridge
Jones RG, Noguer M, Hassel DC, Hudson D, Wilson SS, Jenkins GJ, Mitchell JFB (2004) Generating high resolution climate change scenarios using precis. Tech. rep., Met Office Hadley Centre
Laprise R, de Elía R, Caya D, Biner S, Lucas-Picher P, Diaconescu E, Leduc M, Alexandru A, Separovic L (2008) Challenging some tenets of regional climate modelling. Meteor Atmos Phys 100 Special Issue on Regional Climate Studies(20):3–22
Mearns L, Gutowski W, Jones R, Leung R, McGinnis S, Nuñes A, Qian Y (2009) A regional climate change assessment program for north america. Eos Trans AGU 90(36):311
Mesinger F, Brill K, Chuang HY, DiMego G, Rogers E (2002) Limited area predictability: can “upscaling” also take place? Tech. Rep. 32, 5.30–5.31, Research Activities in Atmospheric and Oceanic Modelling, WMO, CAS/JSC WGNE, Geneva
Oreskes N, Stainforth D, Smith L (2010) Adaptation to global warming: do climate models tell us what we need to know?. Philos Sci 77(5):1012–1028
Prömmel K, Geyer B, Jones J, Widmann M (2010) Evaluation of the skill and added value of a reanalysis-driven regional simulation for alpine temperature. Int J Climatol 30:760–773
Rummukainen M (2010) State-of-the-art with regional climate models. WIRE Adv Rev 1(1):82–96
Seneviratne S, Corti T, Davin E, Hirschi M, Jaeger E, Lehner I, Orlowsky B, Teuling A (2010) Investigating soil moisture-climate interactions in a changing climate: a review. Earth Sci Rev 99(3-4):125–161. doi:10.1016/j.earscirev.2010.02.004
Veljovic K, Rajkovic B, Fennessy MJ, Altshuler EL, Mesinger F (2010) Regional climate modeling: should one attempt improving on the large scales? Lateral boundary condition scheme: any impact? Meteorol Z 19(3):237–246
Acknowledgments
This research was done as part of the PhD project of the first author and as a project within the Canadian Regional Climate Modelling and Diagnostics (CRCMD) Network, funded by the Canadian Foundation for Climate and Atmospheric Sciences (CFCAS) and Ouranos. The authors would like to thank Mourad Labassi, Abderrahim Khaled and Georges Huard for maintaining a user-friendly local computing facility, the helpful comments of two anonymous reviewers and to the North American Regional Climate Change Assessment Program (NARCCAP) for providing the data used in this paper. NARCCAP is funded by the National Science Foundation (NSF), the US Department of Energy (DOE), the National Oceanic and Atmospheric Administration (NOAA) and the US Environmental Protection Agency Office of Research and Development (EPA). Finally, thanks are extended to the Global Environmental and Climate Change Centre (GEC3), funded by the Fonds québécois de la recherche sur la nature et les technologies (FQRNT), for extra financial support.
Open Access
This article is distributed under the terms of the Creative Commons Attribution License which permits any use, distribution, and reproduction in any medium, provided the original author(s) and the source are credited.
Author information
Authors and Affiliations
Corresponding author
Appendix: Added value as a spatial scale issue
Appendix: Added value as a spatial scale issue
This section contains the development of a more detailed expression for the AV as a function of spatial scales (see Eq. 1) as the one presented in Sect. 2.
Let us assume that we can compute a two-dimensional high-resolution climate statistics X based on observations and let us also assume that a perfect spatial decomposition method is available that allows to separate the field according to different spatial scales as follows:
Super-index ls designates the large scales that can be resolved by the GCM and ss denotes the small scales that can be resolved by the RCM and are absent in the GCM.
Before applying the spatial decomposition method to the RCM- and GCM-simulated X, both X RCM and X GCM fields are projected into some high-resolution grid mesh on which an analysis of observations is available. For simplicity, the projection consists of assigning the value of the RCM and GCM fields on each grid points of the observed high-resolution mesh that fall inside the corresponding RCM and GCM grid box. For this particular projection we have X ss GCM and
and
The added value can be simply defined as the difference between the GCM and the RCM errors
with \(\overline{{ (\delta)^2 }} = \frac{1}{N} \sum\nolimits_{i=0}^{N-1} \delta_i^2\) denoting the average of the square differences between observed and simulated climate statistics X over all grid points i. Defined in this way, an RCM generates some added value if AV is larger than 0, i.e., if the RCM constitutes a better approximation of the observed field compared to the GCM. Using Eqs. (23), (24) and (25) the RCM and GCM mean square errors can be expressed as:
and
By replacing Eqs. (27) and (28) in Eq. (26) we obtain:
where
and
Hence the total AV can be decomposed in a small-scale (AV ss), a large-scale (AV ls) and a covariance (AV cov) part. Terms AV ss and AV ls were already described in Sect. 2.1. The term AV cov includes the contribution of covariances between the error in the GCM-simulated climate statistics and the fine scale observed statistics and between the errors in the small and large scale RCM-simulated statistics. As with AV ls, the term AV cov was not explicitly considered in our analysis although ultimately its magnitude as a source of AV should be quantified and compared with the other two terms.
An analogous development can be performed to obtain expressions for the PAV in the CC signal by replacing observed and simulated climate statistics X by their respective climate projections CC.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Di Luca, A., de Elía, R. & Laprise, R. Potential for small scale added value of RCM’s downscaled climate change signal. Clim Dyn 40, 601–618 (2013). https://doi.org/10.1007/s00382-012-1415-z
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00382-012-1415-z