Keywords

Introduction

Background

The seasonal hydrological flow regime is of utmost importance in understanding potential water allocation schemes and subsequent environmental standards flow regulation. Streamflow is a fundamental component of the water cycle and a major source of freshwater availability for humans, animals, plants, and natural ecosystems. It is severely being impacted upon by human activities and climate change variability (Makkeasorn et al. 2008; Null et al. 2010).

Climate change variability has a profound impact on water resources, biophysical, and socioeconomic systems as they are highly interconnected in complex ways (Graham et al. 2011; Null and Prudencio 2016). A change in any one of these induces a change in another. The effects of climate indices on streamflow predictability are seasonal and region dependent (Katz et al. 2002). Although, there are different approaches to assess a basin response to climate variables change. Hydrologists have devised different approaches to investigate how water, the environment, and human activities are mutually dependent and interactive under various climatic conditions (Bayazit 2015). Most of the morphoclimatic challenge studies in any region are usually customized and basin specific. Though many studies have investigated the effects of changing temperature, precipitation, and evaporation as climate variables on water resources management (Katz 2013; Kundzewicz et al. 2008; Null and Prudencio 2016; Taylor et al. 2013), only few have examined seasonal fluctuations of water allocations in nonstationary climates and captured the hydrologic variability trend characterization based on different temporal scales on the whole catchment (Egüen et al. 2016; Gober 2018; Katz 2013; Poff 2018).

Topographic effects on rainfall vary seasonally due to the particular hydrologic process in the region which makes seasonal water allocation and varying environmental flow projection to be based on available meteorological past data for various design purposes (Jakob 2013). Seasonal fluctuations are commonly observed in quarterly or monthly hydrologic flow regime studies. As seasonality is a dominant feature in time series (Sultan and Janicot 2000), hydrologists have developed methodologies to routinely deseasonalized data for modelling and forecasting different annual conditions (Benkachcha et al. 2013). The common variation of inflow from one season to another mainly reflects the climatic variability which includes seasonality of rainfall and amount of evapotranspiration which is dependent on air temperature as well as precipitation in the basin (Ufoegbune et al. 2011). The understanding of these hydrological dynamics in a basin is crucial for sustainable water allocation planning and management. Different literature work reviews across the globe have found a nonlinear or linear relationship between station elevation and rainfall pattern, e.g., the Kruger National Park, South Africa and Mount Kenya, East Africa (Hawinkel et al. 2016; MacFadyen et al. 2018). Likewise, a linear pattern was found in a Spatio-temporal Island study in a European City (Arnds et al. 2017; Sohrabi et al. 2017) while a nonlinear relation exists in a central Asia Basin study (Dixon and Wilby 2019).

Rainfall heterogeneity obviously needs to be considered in a number of hydrological process studies in larger catchments area since it influences: infiltration dynamics, hydrograph regime, runoff volume, and peak flow (Bonaccorso et al. 2017; Fanelli et al. 2017; Gao et al. 2019; Tarasova et al. 2018). However, some hydrology studies still rely on small numbers of synoptic-scale rainfall measurements, and the problem of limited rainfall gauges is common in many watershed investigations, especially in developing countries (Birhanu et al. 2019; Liu et al. 2017; Moges et al. 2018). Therefore, prior to investigating the watershed functions and their contributions to the Mkomazi River flow, we examined the spatial attributes of rainfall in the area based on existing data. The past works conducted on the Basin includes Flügel et al.’s (2003) that had used a geographical information system (GIS) to regressed the local rainfall to the elevation, while Oyebode et al. (2014) has used genetic algorithm and ANN for the streamflow modelling at the upstream. Taylor et al. (2003) and Wotling et al. (2000) used rainfall intensity distribution and principal component analysis (PCA) to assess the complexity of the terrain in addition to the elevation. In general, differences in rainfall patterns may have involved a combination of two statistical outcomes: a shift in the mean and a change in the scale of the distribution functions. The gamma distribution is a popular choice for fitting probability distributions to rainfall totals because its shape is similar to that of the histogram of rainfall data (Kim et al. 2019; Svensson et al. 2017).

Similarly, Najafi and Kermani (2017) observed that in recent years, many researchers have used various empirical rainfall-runoff models to study the impacts of climatic change on basin hydrology. However, a good understanding of the future rainfall distribution across these zones is of vital importance if any meaningful development is to take place in the water resource management and agricultural sector which has been of utmost priority in recent times (Arnds et al. 2017). However, in order to address the foregoing issues, there is a need for the study of this nature. It will help in developing long-term strategic plans for climate change adaptation and mitigation measures and implementing effective policies for sustainable water resources and management of irrigation projects and reservoir operations for the overall sustenance of human well-being in the region (Al-Kalbani et al. 2014). This chapter utilizes regression analysis to investigate the upstream–downstream linkages under seasonal climate variability. Hydrological trend characterization was based on available morphoclimatic past data. Sen’s slope (Pettitt’s) abrupt change detection and the Mann-Kendall parametric trend analysis were used in detecting long-term variability in precipitation while ANN was used for seasonal classifiers and potential future streamflow quantification. Quintile regression was used to establish the relationship between climate indicators (historical rainfall and streamflow) and past catchment conditions to forecast future hydrological dynamics in the MRB. The main novelty in this study is that such a time-series representation is useful for considering the influence of projected shifts in environmental factors on the hydrologic budget, and subsequent coping strategies can be provided.

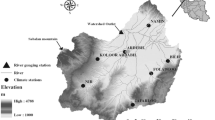
The Mkomazi catchment is located in the U Basin within the semiarid province of KwaZulu- Natal in South Africa as shown in Fig. 1. It is the third largest catchment in the province, draining an area of about 4400 km2 with several large tributaries like Loteni, Nzinga, Mkomanzi, and Elands Rivers. The climatic condition of the study area varies with the seasonality of dry winters and wet summers (Flügel et al. 2003). Rainfall distribution is inconsistent along the catchment, ranging from nearly 1200 mm per annum at the headwaters to 1000 mm p.a. in the middle and 700 mm p.a. in the lower reaches of the catchment with highly intra- and interseasonal streamflows (Flügel and Märker 2003; Oyebode et al. 2014; Taylor et al. 2003). Prior water allocations were entirely based on “who got there first,” which have become unstable and irrational with climate change. Thus, examining how climate-driven spatial and temporal changes to streamflows may reallocate water among the riparian users considering its seasonal variability is of immense importance. The Mkomazi River can be subdivided into five physiographic zones as shown in Fig. 2, namely:

  1. (I)

    The coastal lowlands up to 620 m (mean annual sea level – m a.s.l.)

  2. (II)

    The interior lowland area (“middle berg area”) from 620 to 1079 m (m.a.s.l.)

  3. (III)

    Lowland area up to 1494 m (m.a.s.l.)

  4. (IV)

    The mountain area up to 2011 m (m.a.s.l.)

  5. (V)

    The highlands, with elevations up to 3342 m (m.a.s.l.)

Fig. 1
figure 1

The study area: Mkomazi River basin

Full size image
Fig. 2
figure 2

Mkomazi Physiographic description with elevation zones

Full size image

Like other catchments in Southern Africa, the study area is characterized by high varying seasonality of dry winters and wet summer (Schulze and Pike 2004a). Many authors have suggested longer record lengths, approximately 20-year oscillations interval, in measuring the seasonal hydrological fluctuation (Abhishek et al. 2012; Schulze 1995; Tyson 1986). This variability was adjudged to be as a result of the influence of the currents in the Atlantic and the Indian Ocean that surround the country. The cold Benguela Current in the Atlantic Ocean (South West) brings not only cold air but also influences the pressure system (Haigh et al. 2010; King et al. 2000), while the warmer currents of the Indian Ocean influence the milder warmer sea temperatures and the humid air on the Northeastern Coastline in the country. These seasons are opposite to the seasons in the northern hemisphere (King et al. 2000). There are no clear-cut seasonal calendar based on phenology for the country; however, conventional seasonal variability run through summer (Dec–Feb), autumn (March–May), winter (June–August), and spring usually between September and November, to which the average temperature ranges from 20 to 30; 10 to 15, 7 to 10, and 15 to 20 °C respectively (De Coning 2006; Schulze and Pike 2004a, b).

Procedural Summary

The various stations source data from South Africa Weather Information System (SAWs), the Agricultural Research Council (ARC), and the Department of Water Affairs (DWA), South Africa, were processed and subjected to a rigorous scientific method to test their accuracy, reliability, homogeneity, consistency, and localization gaps. The detection of trends in a series of extreme values needs highly reliable data. Thus, only five stations met the above requirements and, as a result, corrected data sets were available for the hydrological years from 2008 to 2015 (for U10L 30530, U10J 30587, U10L 30813, U10 at Shelburn, and U10 at Giant Castle locations). Table 1 gives the statistical summary of the selected stations variables for (1985-2015) years. 

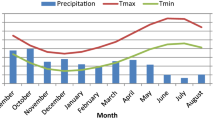
Table 1 Statistical summary of the selected stations year (1985–2015) variables
Full size table

Since the studied variables have different variances and units of measurements as shown in Table 1, the data set was standardized. This step was done by subtracting off the mean and dividing by the standard deviation (Ikudayisi and Adeyemo 2016). At the end of the standardization process, each variable in the dataset is converted into a new variable with zero mean and unit standard deviation. The original and standardized variables are displayed in Figs. 3 and 4, respectively. The standardized results are needed for minimization of bias and accumulation of predicted error from the observed data. These data were further subjected to various test/processing regarding homogeneity, consistency, and gaps closure before adaptation for model inputs. This helps to improve their predictive abilities and reduce uncertainty in data usage.

Fig. 3
figure 3

Original data distribution of the climatic variables

Full size image
Fig. 4
figure 4

Data standardization (normalization) of the climatic variables data

Full size image

Thus, the normalized data were used as input to the ANN classifier for seasonal forecasting and classification. Microsoft Statistical software XLSTAT by Addinsoft was used for Factor Analysis (FA) to explain the contribution of the unobserved common features in a target event from observed ones. FA as a choice of principal component analysis (PCA) was employed to reduce the variety of hydroclimatic data matrix to form a few selected derived component variables, which form a true representative of the original sets. The FA relates the trend, pattern, and fluctuations into wet or dry season in order to identify hydroclimatic variables responsible for streamflow characteristics as a basis for determining available water. This explains seasonal variation in water availability in the downstream environments. FA shows their level of influence and degree of different percentage contribution to the total streamflow volume (latent class). The regression relationships between the collected hydroclimatic data were developed as scatter plots and correlated to know their significance parameter sensitivity. Thereafter, the seasonal variability and trend detection were evaluated using Sen’s method abrupt change detection and Mann-Kendall trend analysis in forecasting the hydrologic flow regime.

Key Findings

Seasonal Trend and Variability Changes among the Climatic Variables

A cursory run of the nonparametric and parametric approaches of Mann–Kendall and Sen’s methods across the months (Dec–Nov) for the study duration (1985–2015) shows the discernible trend and variability changes among the climatic variables. The value of Sen’s slope is given in Table 2 column 7. The closer it is to 0, the lesser the trend, while the sign of the slope indicates if the trend is increasing or decreasing. A Mann–Kendall test with a very high positive value of S (column 4) is an indication of an increasing trend while a very low negative value indicates a decreasing trend.

Table 2 The results of the Sen’s slope and Mann–Kendall test. Seasonal Mann–Kendall Test/period = 12/serial independence /two-tailed test
Full size table

As shown in Table 2, decreasing trends are found generally among the variables across the months except for maximum temperature and solar radiation. This is understandable, as increased solar radiation brings about an increase in temperature. Increases in temperature and radiation forcing variables also alter the hydrological cycle. The resultant effect determines the amount of precipitation, its frequency, intensity duration, and the type of rainfall. In all, the hydro-meteorological variable shows a decreasing trend except for maximum temperature and evapotranspiration in the seasonal distribution pattern. The results show how changes in temperature and evapotranspiration could affect both the timing and total amounts of runoff, though the patterns of possible changes are both spatially and temporally complex. Future changes to allocation of water during seasonal water shortages is an important decision, which not only needs to be better coordinated within any given legal jurisdiction but needs to be better coordinated across any upstream and downstream uses and users.

Factor Analysis (FA) Findings

FA explores the dimensionality of a measurement instrument by finding the smallest number of interpretable factors needed to explain the correlations among the set of variables. This was particularly useful in the analysis of the meteorological parameters input for the ANN model. It places no structure on the linear relationships between the observed variables and the factors but only specifies the number of latent factors, determines the quality of the measurement instrument, identifies variables that are poor factor indicators, and are also poorly measured (Hu et al. 2014). The FA loading is shown in Table 3 to reduce the data into a smaller number of components which indicates what constructs underlies the data latent class. The bold squared cosine values depict the most significant variables that affect discharge flow.

Table 3 Factor loadings of the variables
Full size table

The diagrammatical representation of the Factor Analysis as shown in Fig. 5 indicates each variable’s level of significance on how they contribute to the total streamflow volume latent class. The table shows their proportionate percentage significance towards streamflow. All the meteorological data influence the streamflow except the wind speed presented in the statistical factor analysis biplot which stands alone thus depicting the least effect. This may suggest that air temperature is a more important climatic factor for water mass balance than precipitation.

Fig. 5
figure 5

The factor analysis based on their contributing factor of importance

Full size image

ANN Pattern Classifier and Flow Regime Variation

Insights into the ANN configuration for the four seasons’ classification are given in Fig. 6. The ANN internal algorithm using the gradient descent method for the hidden layer was able to classify them into the four prominent seasons based on collected data which were sorted on monthly basis and labeled inclusively with 1 - Summer, 2- Autumn, 3-Winter, and 4- Spring, respectively. The developed ANN model in the present study consisted of eight input layers that represent the input vectors of the hydro-meteorological parameters considered and four output layers representing the four seasons. The different monthly hydro-meteorological data of each of the six-catchment location serves as the raw data which was preprocessed to obtain the input vectors that was fed into the ANN. The MATLAB interface indicating the size of the input vector, a number of hidden layers, and neurons applied at the layers (which were experimentally determined) as well as the output layer is presented in Fig. 6, while Fig. 7 shows the confusion matrix obtained for the seasonal classification.

Fig. 6
figure 6

MATLAB interphase for seasonal classification using hydro-meteorological data

Full size image
Fig. 7
figure 7

Seasonal classification by ANN model

Full size image

The confusion matrix indicating a 93.7% classification accuracy was achieved by the ANN classifier in cataloging the labeled data into the appropriate season. Given any unknown data set for the test, the developed model was able to distinguish it and classify it into the appropriate season. The corresponding number in the diagonal elements of the matrix indicates the number of instances that could be correctly classified for each of the seasons and how best the ANN classifier can recognize and distinguish data mined for each seasonal (summer, autumn, winter, and spring) classification respectively. The result of the optimal seasonal discharge forecast model is as presented in Fig. 8.

Fig. 8
figure 8

Training output values for the optimal seasonal discharge model

Full size image

The ANN forecasted results provide the likelihood of high, near medium or low streamflow. The changes in the discharge regime were identified with the 5th, 10th, and 90th tercile streamflow magnitude curve as depicted in Fig. 9.

Fig. 9
figure 9

Seasonal variability flow dynamic across the river

Full size image

The streamflows in winter (wetter months) have increased slightly over the time period, whereas streamflows in summer (drier months) have decreased slightly. Figure 9 represents the estimated seasonal catchment yield of higher surface flow in winter with decreasing lower base flow across the seasons. Streamflow is observed to be at its lowest in the autumn period as the results further assert that climate change is real and have significance effects on the river flow regime (Archer et al. 2010; Schulze and Pike 2004a; Taylor et al. 2003; Viviroli et al. 2010). The coping strategy suggests sustainable use of any resource relies on the action of a number of regulatory mechanisms that prevent the user from reducing the ability of the system to provide services. “Polluter pays” principle was conceived as a way to proportionally allocate the effects of such alterations to those users that are responsible for them, thus producing a regulatory effect on the use of the resource. Also, the water allocation criteria include economic criteria with the aim of optimizing the economic value of the water resource.

Model Performance and Evaluation Measures

For improved accuracy, the root means square error (RMSE) and coefficient of correlation (CC) was used for performance evaluation measures during ANN training, testing, and validation procedures (Paswan and Begum 2014). They are defined as shown in Eqs. (1) and (2), respectively.

$$ RMSE=\sqrt{\frac{1}{n}\sum \limits_{i=1}^n{\left({Q}_i-{P}_i\right)}^2} $$
(1)
$$ CC=\frac{\sum \limits_{i=1}^n\left[\left({Q}_i-{\hat{Q}}_i\right).\left({P}_i-{\hat{P}}_i\right)\right]}{\sqrt{\sum \limits_{i=1}^n{\left({Q}_i-{\hat{Q}}_i\right)}^2.\sum \limits_{i=1}^n{\left({P}_i-{\hat{P}}_i\right)}^2}} $$
(2)

where Qi is the observed value at time i, Pi is the simulated value at time i and \( \overline{P} \) is the mean for the observed values. Observed runoff is used for model calibration and validation. Correlations are useful because they can indicate a predictive relationship that can be exploited in practice. The performance measures of RMSE and CC values obtained are 29% and 61% respectively during the calibration period. During the verification period, the RMSE and CC values are slightly improved as 18% and 75% were achieved respectively. Figure 10 shows the result of the training test as well as the optimum prediction performance of the network architecture.

Fig. 10
figure 10

Performance evaluation measures

Full size image

Using FA as part of PCA has helped in screening the data and identifying the level of importance based on their contributing factor. The observed MRB runoff at (Mkomazi drift UIH009) station was used to compare with the ANN-model-simulated output in Shrestha (2016) Calibration Helper v1.0 Microsoft Excel Worksheet. The model performance was evaluated using statistical parameters and the result is represented in Fig. 11. Comparing ANN simulated value and observed runoff variables show a satisfactory ANN forecasting model for the seasons run.

Fig. 11
figure 11

Comparison of ANN simulated value and observed runoff

Full size image

The resulting data from the four seasons were detrended and deseasonalized (Wang et al. 2011) before forecasting the time series using neural networks. The results show that the neural networks with the right configurations give almost the same accuracy with or without decomposition of the time series. The streamflows in wetter months have increased slightly over the time period from 1985 to 2015, whereas streamflows in drier months have decreased slightly. These trends are also evident for the minimum and maximum temperature and relative humidity multiday events. The relationship between runoff and Mkomazi rainfall has been high and stable over the recording period. Other data analysis not presented shows a decreasing trend of precipitations. The summer rainfall variations are related more closely to maximum than minimum temperatures, with higher temperatures associated with lower rainfall. Lower rainfall in winter tends to be linked with higher maximum and lower minimum temperatures. These relationships were relatively stable over time. For this reason, there is a need to consider a range of possible future climate conditions in a region of increasing population, coupled with increasing demand for water resources for domestic, agricultural, and industrial activities and how these will affect water availability.

Limitations of the Study

Like all modeling studies, this research has assumptions and uncertainties which limit the findings. Many of the previous studies indicate that stationary climatic and streamflow data were used while we applied the historical probability that each water year type is based on the 2008 water year. This method assumes stationary climatic water year types. Future water year type frequencies varied somewhat with climate change (nonstationarity in data), although those changes are statistically insignificant. Also, decadal to multidecadal variability which includes the probability of extreme floods and droughts (Herrfahrdt-Pähle 2010) were not considered. Our findings likely underestimate water allocation impacts from extreme floods and droughts anticipated with climate change. In addition, for environmental flow allocations and streamflow, there is still substantial room for model misspecification through overfitting, thus the selection of optimal internal neural algorithms choice again raises the issue of robust neural network modeling.

Seasonal Coping and Adaption Strategies to Climate Variability

Practical field investigation of views of stakeholders and their involvement should be simulated with model computer software in evolving solutions to water availability. Government political will and strategical alignment of various duplicating agencies in providing data for Sub-seasonal to Seasonal (S2S) Prediction should be harmonized toward a unified goal. Historically disadvantaged communities must be strongly supported and be encouraged to apply for water use licenses and the region must be in readiness to fast-track the processing of these water use license applications. Other available strategies to cope with climate variability include integrated water resources management by improving public water supply, regulating final users by facilitating the emergence of mediating agencies, the use of energy pricing and supply to manage agricultural water use overdraft, and better sensitization campaigns on rain water capture and recharge. The formalization of the water sector through the transfer of water rights and the more efficient use of water resources are among evolving strategies to achieve a sustainable water supply for the Mkomazi River Basin. Turning all these adaption strategies into opportunity requires a need for both water technology innovation and water behavioral change to manage the scarcity of water resources in a sustainable manner. This chapter offers intuitive suggestions on how human being policies and cautious approaches can be used to manage and sustain the already depleted environment. Such intuitive agendum should be catalyzed through the institutionalization of proactive and capacity developmental platforms where climate change experts transfer knowledge, skills and expertise to upcoming researchers.

Conclusion

Understanding of climate change is continually improving, but the future climate remains uncertain (Yuan et al. 2016). For this purpose, a regression nonparametric approach consisting of the Mann–Kendall test and Sen’s method and a parametric approach (ANN) based on factor analysis of extremes statistical theory have been applied. Owing to the seasonal character of the upstream–downstream variables linkages, the result concludes that all the variables considered the temperature as the most important factor in the estimation of streamflow. The results suggest a significant impact of input vector length, a few hidden nodes neurons, and the choice of activation function as ANN potentiality in characterizing the individual season and project maximum likelihood trend for the surface water patterns. Thus, careful assessment of the available water resources and reasonable needs of the basin/region in foreseeable future for various purposes must be based on reliable information concerning the meteorological variable trend which in turn impacts the peak flow to be expected after a rainstorm of a given probability of occurrence. The methods applied further confirms our assertion that these patterns are indeed unique across each month in the season. The water resources manager and agricultural water management sector would find optimal use in the developed ANN classifier model that links hydrologic variability on different temporal trend scales based on available past data and rainfall anomaly.