Key words

1 Introduction

We are in the population genomics era where data sets from the 1000 human genomes project [1], the great apes project [2], and the 1001 arabidopsis genomes project [3] are available. The underlying data sets contain genotypic information for thousands of individuals in one or several species, in the form of de novo sequenced genomes or variation compared to an available “reference” genome (a.k.a. resequencing). By comparing genomes from several individuals of the same species or closely related species, we can obtain information about split times, population sizes, recombination events, and selection in contemporary and ancestral species (see Fig. 1). In this chapter we discuss various models for obtaining this information.

Fig. 1
figure 1

Left: Isolation model of two species. Right: The coalescent process along the genomes of the two species. By comparing the two genomes we obtain information about the split time of the species and the ancestral population size. Furthermore the breakpoints along the genomes correspond to recombination events, so we also have information about the recombination process

Full size image

Comparing homologous sequences available for a given locus to infer their degree of relatedness enables the discovery of the parental relationships of the sequences, depicted as a tree thereby named genealogy. When one sequence sampled from one individual of one species is compared with sequences from other species, the resulting genealogy contains information about the history of species, the so-called phylogeny. The phylogeny summarizes the relationship and the divergence times between the species.

Conversely, when sequences from several individuals within a species are sampled, we have access to the genetic variation in contemporary populations. The evolutionary forces that shape genetic variation within a species are genetic drift, mutation, recombination, and selection and are the subject of population genetics. The key modeling tool in population genetics is coalescent theory. Classical coalescent theory describes the genetic ancestry of a sample of homologous DNA sequences from the same species. This genealogical description includes times to common ancestry, which is measured back into the past.

Molecular phylogenetics and population genetics have accumulated 50 years of methodological developments. The convergence of these two fields and their key mathematical and statistical tools is needed in order to fully understand genomic sequence alignments, because comparing genealogies and phylogenies is at the heart of the study of the speciation process [4].

We describe the interplay between population genetics and phylogenetics by reviewing the methods and models that have been developed to understand evolutionary history from genomic data (see Table 1 for a comparative summary of all methods).

Table 1 Methods comparison
Full size table

2 Coalescent Theory and Speciation

We start by describing the standard coalescent model within one population. The coalescent model describes the shape of the genealogy of several sequences sampled from a single population. For more information on the coalescent, we refer to [21, 22] and [23]. This section describes the coalescent process as a chronological process. In the next section, we will see how it can be modeled as a spatial process along the genome. In subsequent sections we extend the standard model to include two or more populations. In the cases where multiple populations are present we describe both the isolation model and the isolation-with-migration model.

2.1 The Standard Coalescent Model

The standard coalescent model is a continuous-time approximation of the neutral Wright–Fisher model. In the Wright–Fisher model the number of chromosomes 2N (we consider diploid organisms) is fixed in each non-overlapping generation. Each chromosome in a new generation chooses its ancestor uniformly at random from the previous generation.

Consider two chromosomes. The probability of the two chromosomes choosing the same ancestor is 1∕(2N) and the probability of the two chromosomes not finding a common ancestor is 1 − 1∕(2N). Let R 2 denote the number of generations back in time when the two individuals find a most recent common ancestor (MRCA). By repeating the argument above, the probability of the two chromosomes not finding a common ancestor r generations back in time is

$$ P\left({R}_2>r\right)={\left(1-\frac{1}{2N}\right)}^r.\kern1.00em $$

If we scale time t in units of 2N, i.e., set r = 2Nt, we get

$$ P\left({R}_2>r\right)={\left(1-\frac{1}{2N}\right)}^r={\left(1-\frac{1}{2N}\right)}^{2 Nt}\approx {e}^{-t},\kern1.00em $$

where the approximation is valid for large N. In coalescent time units the waiting time T 2 = R 2∕(2N) before coalescence of two individuals is therefore exponentially distributed with mean one.

These considerations can be extended to multiple individuals. In general the time T n before two of n individuals coalesce is exponentially distributed with rate \( \left(\genfrac{}{}{0ex}{}{n}{2}\right) \).

The waiting time W n for a sample of n individuals to find the most recent common ancestor (MRCA) is given by

$$ {W}_n={T}_n+{T}_{n-1}+\cdots +{T}_2,\kern1.00em $$

where T k are independent exponential random variables with parameter \( \left(\genfrac{}{}{0ex}{}{k}{2}\right) \); see Fig. 2 for an illustration. It follows that the mean of W n is

$$ {\displaystyle \begin{array}{rll}E\left[{W}_n\right]=\sum \limits_{k=2}^nE\left[{T}_k\right]=\sum \limits_{k=2}^n\frac{2}{k\left(k-1\right)}=2\sum \limits_{k=2}^n\left(\frac{1}{k-1}-\frac{1}{k}\right)& & \\ {}=2\left(1-\frac{1}{n}\right).& & \end{array}} $$

Note that limn→∞ E[W n] = 2.

Fig. 2
figure 2

Illustration of the coalescent process. The waiting time before two out of n individuals coalesce is T n and the time before a sample of n individuals find common ancestry is W n

Full size image

The variance of W n is

$$ {\displaystyle \begin{array}{rll}\mathrm{Var}\left[{W}_n\right]=\sum \limits_{k=2}^n\mathrm{Var}\left[{T}_k\right]=\sum \limits_{k=2}^n{\left(\genfrac{}{}{0ex}{}{k}{2}\right)}^{-2}& & \\ {}=8\sum \limits_{k=1}^{n-1}\frac{1}{k^2}-4\left(1-\frac{1}{n}\right)\left(3+\frac{1}{n}\right).& & \end{array}} $$

Note that \( {\lim}_{n\to \infty}\mathrm{Var}\left[{W}_n\right]=\left(\frac{8{\pi}^2}{6}-12\right)=1.16 \).

The consequences of these calculations are that when we only sample within a population we are limited to relatively recent events. The expected time for a large sample to find their MRCA is approximately 2 × (2N) = 4N generations with standard deviation \( \sqrt{1.16}\times (2N)=2.15N \) generations. As a consequence, a neutral sample within a population contains little information beyond 6N generations.

Humans have a generation time of approximately 20 years and an effective population size of approximately N = 10, 000 (see [21, p. 251]), and therefore 6N generations correspond to approximately 1.2 million years (My) for humans. Therefore human diversity at neutral loci contains little demographic information beyond 1.2 My.

2.2 Adding Mutations to the Standard Coalescent Model

Now suppose mutations occur at a rate u per locus per generation. In a lineage of r generations, we then expect ru mutations or in the coalescent time units with r = 2Nt we expect 2Ntu mutations. We let θ = 4Nu be the mutation rate parameter. Since u is small we can make a Poisson approximation of the binomial number of mutations in a lineage of r generations

$$ \mathrm{Bin}\left(r,u\right)=\mathrm{Bin}\left(2 Nt,\theta / \left(2\cdot 2N\right)\right)\approx \mathrm{Pois}\left( t\theta / 2\right).\kern1.00em $$

We have thus arrived at the following two-step process for simulating samples under the coalescent: (a) simulate the genealogy by merging lineages uniformly at random and with waiting times exponentially distributed with rate \( \left(\genfrac{}{}{0ex}{}{n}{2}\right) \) when n lineages are present; (b) on each lineage in the tree add mutations according to a Poisson process with rate θ∕2.

Another possibility is to scale the coalescent process such that one mutation is expected in one time unit. In this case the exponentially distributed waiting times in (a) have rate \( \left(\genfrac{}{}{0ex}{}{n}{2}\right)\left(2/ \theta \right) \), and in (b) the mutations are added with unit rate. We use the latter version of the coalescent-with-mutations process below.

2.3 Taking Recombination into Account

For species where recombination occurs, different parts of the genome come from distinct ancestors, and therefore have a distinct history. Figure 3 exemplifies this phenomenon for two species. It displays the genealogical relationships for two sequences which underwent a single recombination event. In the presence of recombination, each position of a genome alignment therefore has a specific genealogy, and close positions are more likely to share the same one (recall Fig. 1). The genome alignment can therefore be described as an ordered series of genealogies, spanning a variable amount of sites, and then changing because of a recombination event [4]. The genealogy is therefore depicted as a complex graph with nodes representing both coalescence and recombination events, the ancestral recombination graph (ARG, Fig. 3c). A single genome thus contains different samples from the distribution of the age of the MRCA, and the distribution contains information about the ancestral population size and speciation time. The coalescent with recombination serves as a basis for modeling genome-wide genealogy, a point that we will further develop in Subheading 4.

Fig. 3
figure 3

Ancestral recombination graph for two species. (a) Genealogy of four sampled sequences from two species. The bold line shows the divergence of two sequences of interest. (b) A single recombination event happened between the lineages of sequences 3 and 4 (horizontal line), so that in a part of the sequences, the genealogy is as depicted by the bold line and therefore displays an older divergence. (c) The corresponding ancestral recombination graph (in black) with the trees of each side of the recombination break point superimposed (red: left tree; blue: right tree). When going backward in time, a split corresponds to a recombination event and a merger to a coalescence event

Full size image

3 Adding Genetic Barriers and Gene Flow to the Picture: The Structured Coalescent

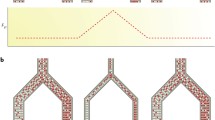
In this section we extend the standard coalescent model. We consider coalescent models with multiple species and introduce population splits or speciation events. The models that we describe are shown in Fig. 4 (see also Table 1) and include: (a) The two species isolation model; (b) The two species isolation-with-migration models; (c) The three species isolation model (and incomplete lineage sorting); and (d) The three species isolation-with-migration model. We also discuss the general multiple species isolation-with-migration model. The two species isolation model was introduced in [24] and the isolation-with-migration model was introduced in [25].

Fig. 4
figure 4

Speciation models and associated parameters. In all exemplified models effective population size is constant between speciation events, represented by dash lines. The timing of the speciation events, noted T are parameters of the models, together with ancestral effective population sizes, noted N A. In some cases, contemporary population sizes can also be estimated, and are noted N i, where i is the index of the population. Models with post-divergence genetic exchanges have additional migration parameters labeled m from→to. The number of putative migration rates increases with the number of contemporary populations under study, and some models might consider some of them to be equal or eventually null to reduce complexity. (a) Isolation model with two species. (b) Isolation-migration model with two species. (c) Isolation model with three species. (d) Isolation-Migration model with three species

Full size image

3.1 Isolation Model with Two Species

If the sequences are sampled from two distinct species that have diverged a time T ago (see Fig. 4a), then the distribution of the age of the MRCA is shifted to the right with the amount T, resulting in the distribution

$$ {f}_{T_2}(t)=\left\{\begin{array}{ll}0& \mathrm{if}\kern0.3em t<T\\ {}\frac{2}{\theta_A}{e}^{-2\left(t-T\right)/ {\theta}_A}& \mathrm{if}\kern0.3em t>T\end{array}\right.,\kern1.00em $$

where θ A = 4N A ⋅ u is the ancestral mutation rate. The mean time to coalescent is E[T 2] = T + θ A∕2 and the average divergence time between two sequences is twice this quantity, that is, 2T + θ A. Since θ A = 4N A u it follows that the larger the size of the ancestral population, the bigger the difference between the speciation time and the divergence time.

The variance of the divergence time is \( \mathrm{Var}\left[{T}_2\right]={\theta}_A^2/ 4 \). With access to the distribution of divergence times, we could estimate the speciation time and population size from the mean and variance of the distribution. Unfortunately we do not know the complete distribution of divergence times and it is not immediately available to us, because long regions are needed for precise divergence estimation but have experienced one or more recombination events.

3.2 Isolation Model with Three or More Species and Incomplete Lineage Sorting

Now consider the isolation model with three species depicted in Fig. 4c. Such a model is often used for the human–chimpanzee–gorilla (HCG) triplet (e.g., [10,11,12]).

The density function for the time to coalescence between sample 1 and sample 2 is given by

$$ {f}_{T_2}(t)=\left\{\begin{array}{ll}0& \mathrm{if}\kern0.3em t<{T}_1\\ {}\frac{2}{\theta_{A1}}{e}^{-2\left(t-{T}_1\right)/ {\theta}_{A1}}& \mathrm{if}\kern0.3em {T}_1<t<{T}_{12}\\ {}{P}_{12}\frac{2}{\theta_{A2}}{e}^{-2\left(t-{T}_{12}\right)/ {\theta}_{A2}}& \mathrm{if}\kern0.3em t>{T}_{12},\\ {}\end{array}\right.\kern1.00em $$
(1)

where

$$ {T}_{12}={T}_1+{T}_2\kern1em \mathrm{and}\kern1em {P}_{12}={e}^{-2\left({T}_{12}-{T}_1\right)/ {\theta}_{A1}}\kern1.00em $$

is the probability of the two samples not coalescing in the ancestral population of sample 1 and sample 2. In the upper right corner of Fig. 5 we plot the density (Eq. 1) with parameters that resemble the HCG triplet.

Fig. 5
figure 5

Illustration of the density for coalescent in various models and data layout. The curves are the probability density functions. In the most simple case with two species, a constant ancestral population size and a punctual speciation (top left panel), more genomic regions find a common ancestor close to the species split (the vertical line), while a few regions have a more ancient common ancestor, distributed in an exponential manner (see Eq. 1). If speciation is not punctual and migration occurred after isolation of the species, then some sequences have a common ancestor which is more recent than the species split and the distribution in the ancestor becomes more complex (bottom left panel, see Eqs. 4 and 6). When a third species is added (right panel), then another discontinuity appears and all distributions depend on additional parameters, particularly when migration is allowed. We use θ A1 = 0.0062, θ A2 = 0.0033 and τ 1 = 0.0038 (the first vertical line), τ 2 = 0.0062 (the second vertical line) corresponding to the HCG triplet. Ancestral population sizes are taken from the simulation study in Table 6 in Wang and Hey [8]: θ 1 = 0.005 and θ 2 = 0.003. Migration parameters are all set to 50

Full size image

If sample 1 and sample 2 do not coalesce in the ancestral population of sample 1 and sample 2, then the three trees ((1,2),3), ((1,3),2), and ((2,3),1) are equally likely. The probability of the gene tree being different from the species tree is thus

$$ \Pr \left(\mathrm{incongruence}\right)=\frac{2}{3}{P}_{12}=\frac{2}{3}{e}^{-2\left({T}_{12}-{T}_1\right)/ {\theta}_{A1}}.\kern1.00em $$
(2)

The event that the gene tree is different from the species tree is called incomplete lineage sorting (ILS). ILS is important because species tree incongruence often manifests itself as a relatively clear signal in a sequence alignment and thereby allows for accurate estimation of population parameters. In Fig. 6 we show the (in)congruence probability Eq. 2. We also refer to Exercise 1 (see Subheading 8.1) and Exercise 2 (see Subheading 8.2) for more discussion of ILS.

Fig. 6
figure 6

Probability (Eq. 2) of gene tree and species tree being incongruent. In case of the HCG triplet we obtain (T 12 − T 1)∕θ A1 = (0.0062 − 0.0038)∕0.0062 = 0.39 which corresponds to an incongruence probability of 30%

Full size image

In the three species isolation model the mean coalescent time for a sample from population 1 and a sample from population 2 is given by

$$ E\left[{T}_2\right]={T}_1+\left(1-{P}_{12}\right)\frac{\theta_{A1}}{2}+{P}_{12}\frac{\theta_{A2}}{2}.\kern1.00em $$
(3)

Burgess and Yang [9] describe the speciation process for human, chimpanzee, gorilla, orangutan (O), and macaques (M) using an isolation model with five species. The HCGOM model contains four ancestral parameters θ HC, θ HCG, θ HCGO, and θ HCGOM. In this case (Eq. 3) extends to

$$ {\displaystyle \begin{array}{rll}E\left[{T}_2\right]={T}_{\mathrm{HC}}+\left(1-{P}_{\mathrm{HC}}\right)\frac{\theta_{\mathrm{HC}}}{2}{P}_{\mathrm{HC}}\left(1-{P}_{\mathrm{HC}\mathrm{G}}\right)\frac{\theta_{\mathrm{HC}\mathrm{G}}}{2}& & \\ {}+{P}_{\mathrm{HC}}{P}_{\mathrm{HC}\mathrm{G}}\left(1-{P}_{\mathrm{HC}\mathrm{G}\mathrm{O}}\right)\frac{\theta_{\mathrm{HC}\mathrm{G}\mathrm{O}}}{2}& & \\ {}+{P}_{\mathrm{HC}}{P}_{\mathrm{HC}\mathrm{G}}{P}_{\mathrm{HC}\mathrm{G}\mathrm{O}}\left(1-{P}_{\mathrm{HC}\mathrm{G}\mathrm{O}\mathrm{M}}\right)\frac{\theta_{\mathrm{HC}\mathrm{G}\mathrm{O}\mathrm{M}}}{2}.& & \end{array}} $$

3.3 Isolation-with-Migration Model with Two Species and Two Samples

The isolation-with-migration (IM) model with two species is shown in Fig. 4b. The IM-model has six parameters: The mutation rates θ 1, θ 2, and θ A, the migration rates m 1 and m 2, and the speciation time T. We let Θ = (θ 1, θ 2, θ A, m 1, m 2, T) be the vector of parameters.

Wang and Hey [8] consider a situation with two genes. Before time T the system is in one of the following five states:

S 11 : :

Both genes are in population 1.

S 22 : :

Both genes are in population 2.

S 12 : :

One gene is in population 1 and the other is in population 2.

S 1 ::

The genes have coalesced and the single gene is in population 1.

S 2 : :

The genes have coalesced and the single gene is in population 2.

The instantaneous rate matrix Q is given by

Starting in state a, the density for coalescent in population 1 at time t < T is given by [26]

$$ {f}_1(t)={\left({e}^{Qt}\right)}_{a{S}_{11}}\left(2/ {\theta}_1\right),\kern1.00em $$
(4)

the density for coalescent in population 2 at time t < T is

$$ {f}_2(t)={\left({e}^{Qt}\right)}_{a{S}_{22}}\left(2/ {\theta}_2\right),\kern1.00em $$
(5)

and the total density for a coalescent at time t < T is

$$ f(t)={f}_1(t)+{f}_2(t).\kern1.00em $$
(6)

Here \( {e}^A={\sum}_{i=0}^{\infty }{A}^i/ \left(i!\right) \) is the matrix exponential of the matrix A and (e A)ij is entry (i, j) in the matrix exponential.

After time T the system only has two states: S AA corresponding to two genes in the ancestral population and S A corresponding to one single gene in the ancestral population. The rate of going from state S AA to state S A is 2∕θ A. The density for coalescent in the ancestral population at time t > T is therefore

$$ f(t)=\left[{\left({e}^{QT}\right)}_{a{S}_{11}}+{\left({e}^{QT}\right)}_{a{S}_{12}}+{\left({e}^{QT}\right)}_{a{S}_{22}}\right]\frac{2}{\theta_A}{e}^{-\left(2/ {\theta}_A\right)\left(t-T\right)}.\kern1.00em $$
(7)

In Fig. 5 we illustrate the coalescent density in the two species isolation-with-migration model.

The likelihood for a pair of homologous sequences X is given by

$$ P\left(X|\varTheta \right)=L\left(\varTheta |X\right)={\int}_0^{\infty }P\left(X|t\right)f\left(t|\varTheta \right) dt\kern1.00em $$
(8)

where f(t) = f(t|Θ) given by Eqs. 6 and 7 is the density of the two sequences finding a MRCA at time t and P(X|t) is the probability of the two sequences given that they find a MRCA at time t. The latter term is calculated using a distance-based method. One possibility is to use the infinite sites model where it is assumed that substitutions happen at unique sites, i.e., there are no recurrent substitutions. In this case the number of differences between the two sequences follows a Poisson distribution with rate 1.

For an application of the isolation-with-migration model with two sequences, we refer to [8]; a discussion of their approach can be found in [27].

3.4 Isolation-with-Migration Model with Three or More Species and Three or More Samples

Hey [28] considered the multipopulation isolation-with-migration (IM) model. Recall from Fig. 4b that the two-population IM model has six parameters: two present population sizes, one ancestral population size, one speciation time, and two migration rates. The three-population IM model in Fig. 4d has fifteen parameters: three present population sizes, two ancestral population sizes, two speciation times, and eight migration rates. In general a k-population IM model has 3k − 2 + 2(k − 1)2 parameters:

  • k present population sizes,

  • (k − 1) ancestral population sizes,

  • (k − 1) speciation times, and

  • 2(k − 1)2 migration rates.

See Fig. 5 for an example of divergence distribution with three species and migration and Exercise 3 (see Subheading 8.3) for a derivation of the number of migration rates in the general k-population model. For k = 5, 6, and 7 we obtain 45, 66, and 91 parameters. Because the number of parameters becomes very large even for small k, Hey [28] suggests adding constraints to the migration rates, e.g., setting some rates to zero or introducing symmetry conditions where rates between populations are the same.

4 Approximating the Coalescent with Recombination Along Genomes

Before the genomic era, multilocus population genetics models were addressing a small fraction of the complete ancestral recombination graph (ARG) by considering independent loci. As sequencing technologies evolved and allowed access to larger samples of genomic diversity, this independence assumption had to be relaxed and more explicit modeling of the ARG was required. Yet the complexity of the coalescent with recombination process makes its application to genome-scale data sets very challenging. Two directions of analysis methods have emerged: simulation-based or spatial approximations along the genome. In this chapter we focus on the latter and refer to Kelleher et al. [29] and Staab et al. [30] for the former. Simonsen and Churchill [31] described the first model of the joint distribution of genealogies at two loci for two genomes. Wiuf and Hein [32] extended this approach and described the coalescent as a spatial process along the genome. McVean and Cardin [33] further approximated the description with a Markov process. In this section we describe and discuss these types of approximations.

4.1 The Independent Loci Approach: Free Recombination Between, No Recombination Within

The simplest way to handle issues relating to the ancestral recombination graph is to divide the data into presumably independent loci. Such analyses are therefore restricted to candidate regions that are not too large (to avoid including a recombination point) and not too close (to ensure several recombination events happened between loci). Each region can then be described by a single underlying tree, reducing the analytical and computational load.

Using 15,000 loci distant from 10 kb totaling 7.4 Mb and the isolation model introduced above, Burgess and Yang [9] (Table 2, model (b) sequencing errors) find the following ancestral population sizes and speciation times estimates for human (H), chimpanzee (C), gorilla (G), orangutan (O), and macaque (M) ancestors: θ HC = 0.0062, θ HCG = 0.0033, θ HCGO = 0.0061, θ HCGOM = 0.0118 and T HC = 0.0038, T HCG = 0.0062, T HCGO = 0.0137, T HCGOM = 0.0260. Converting these estimates into time units requires an estimate of the substitution rate, either absolute or deduced from a scaling point. Using u = 10−9 as an estimate for substitutions per year, this leads to an estimate of 3.8 My for the human–chimpanzee speciation, a very recent estimate. Using the same data, Yang [10] showed that the isolation-with-migration model was preferred. Yang finds a more ancient speciation time T HC = 0.0053 (5.3 My with u = 10−9) when migration is accounted for.

4.2 State-Space Model: Simonsen–Churchill Framework

The coalescent with recombination for two loci and two sequences is originally described in Simonsen and Churchill [31] as a continuous-time Markov chain backward in time with eight states as shown in Fig. 7. This Markov chain is given a careful treatment in the textbooks by Durrett [34, Section 3.1.1] and Wakeley [21, Section 7.2.4], and we therefore only briefly explain the basic properties of the model here.

Fig. 7
figure 7

State transition diagram for two loci and two sequences described as a continuous-time Markov chain backward in time. The figure is adapted from Figure 7.7 in Wakeley [21]. A line with a bullet or a cross at both ends is a linked sequence (ancestral material to the sample at both loci), whereas a line with a bullet or a cross at one end only is a sequence with ancestral material at one locus only. A cross denotes common ancestry. s and t denote the heights of the left and right trees, respectively

Full size image

A single sequence is either linked (, , , or meaning that it contains material ancestral to the sample at both loci, or it is unlinked (, , , or ) when it contains material ancestral to the sample at only one locus. The coalescent rate is one for any two sequences, and the recombination rate is ρ∕2 for any linked sequence. The chain begins at time zero in state 1 with two linked sequences. After an exponential waiting time with rate 1 + ρ the chain enters state 8 with probability 1∕(1 + ρ) or state 2 with probability ρ∕(1 + ρ). The transition from state 1 to state 8 is a coalescent event, and the left and right tree heights are identical. The transition from state 1 to state 2 is a recombination event that breaks apart one of the two sequences. All other transitions have similar interpretations. Common ancestry for a locus is marked with a ×, so the transition from, e.g., state 1 to state 8 is a transition to the state .

The height S of the left tree is the first time at which the process enters one of the states 5, 7, or 8 (states with a left ×), and the height T of the right tree is the first time at which one of the states 4, 6, or 8 is entered (states with a right ×). When state 8 is entered from state 1 the two tree heights are identical. State 8 is absorbing because only the tree heights are of interest.

The two key ingredients for the state-space model are the conditional probability for staying in a state P(T = s|S = s) and the conditional density q(t|s) of a new tree height t conditional on a change and a previous tree height s. Hobolth and Jensen [35] show that the conditional probability of no change from the left to the right tree is

$$ P\left(T=s|S=s\right)={e}^s{\left[{e}^{\varLambda s}\right]}_{11},\kern1.50em $$
(9)

and the conditional density q(t|s) of T given S = s and given T ≠ S is

$$ q\left(t|s\right)=\left\{\begin{array}{ll}{e}^{-\left(s-t\right)}\frac{{\left[{e}^{\varLambda t}\right]}_{12}+{\left[{e}^{\varLambda t}\right]}_{13}}{e^{-s}-{\left[{e}^{\varLambda s}\right]}_{11}}\kern1em & t<s,\\ {}\kern1em & \\ {}{e}^{-\left(t-s\right)}\frac{{\left[{e}^{\varLambda s}\right]}_{12}+{\left[{e}^{\varLambda s}\right]}_{13}}{e^{-s}-{\left[{e}^{\varLambda s}\right]}_{11}}\kern1em & t>s,\end{array}\right.\kern1.00em $$
(10)

where Λ denotes the 8 × 8 rate matrix from Fig. 7.

Wakeley [21, Section 7.2.4] noted that the transitions between state 4 and 6 and the transitions between state 5 and 7 can be removed from the chain if we are only interested in the tree heights. Actually, even more transitions can be removed from the chain. Note from Eqs. 9 and 10 that we only need the entries (1, 1), (1, 2), and (1, 3) in e Λt for calculating the probability of the same tree height in the next position and the transition density conditional on a change. These entries can be found from a reduced rate matrix where states 4, 5, 6, and 7 are removed and the rate from states 2 and 3 to a new absorbing state equals 2. In other words, define the reduced rate matrix

$$ \overset{\sim }{\varLambda }=\left(\begin{array}{cccc}-\left(1+\rho \right)& \rho & 0& 1\\ {}1& -\left(3+\rho / 2\right)& \rho / 2& 2\\ {}0& 4& -6& 2\\ {}0& 0& 0& 0\end{array}\right),\kern1.50em $$

where states are numbered 1, 2, 3, and 4. The holding time and transition density for the model are now given by Eqs. 9 and 10 with Λ substituted by \( \overset{\sim }{\varLambda } \).

In the left plot in Fig. 8 we illustrate the probability (Eq. 9) of the same tree height in the left and right loci conditional on the tree height in the left locus and different recombination rates. As expected the probability for identical tree heights decreases with the height of the left tree and with the recombination rate.

Fig. 8
figure 8

(a) Probability of same tree height. (b) Density for right tree height conditional on the left tree height being equal to s and a recombination rate equal to ρ

Full size image

In the right plot in Fig. 8 we illustrate the density (Eq. 10) of the right tree height conditional on the left tree height and a change in tree height. When the recombination rate increases, the density for the right tree height moves toward smaller tree heights. The reason is that at least one recombination is needed for having a change in tree height. We also observe that the density is continuous but not differentiable in the position of the left tree height.

4.3 Time Discretization: Setting Up the Finite State HMM

Li and Durbin [14] and Mailund et al. [13] analyze pairs of sequences using a hidden Markov model (HMM). The hidden states are tree heights (times to the most recent common ancestor), and the tree height is discretized to obtain a finite hidden state space. The observed states of the HMM are alignment columns, with probabilities corresponding to a substitution process on the tree (see Fig. 9). In the Li and Durbin model, an infinite site model is assumed and observed states are converted to binary data, telling whether the site is heterozygous (one mutation) or homozygous (no mutation).

Fig. 9
figure 9

(a) Graphical structure of the hidden Markov Model. (b) Simulation from the hidden Markov model

Full size image

We now describe how we discretize time for the case of two sequences considered in the previous section. The discrete version of the Markov process is used to build a finite Markov chain along the two sequences. When the finite Markov chain is combined with a substitution process, we obtain an HMM as in Li and Durbin [14].

Let the discrete time points (backward in time) of the Markov chain be d 0 = 0 < d 1 < d 2 < ⋯ < d M−1 < d M = ∞ and denote the corresponding states by 1, 2, …, M. State m (m ∈{1, …, M}) then corresponds to a tree height in the interval between d m−1 and d m. The continuous stationary distribution is \( \pi (t)=\exp \left(-t\right) \), and therefore the discrete times are chosen such that \( 1-\exp \left(-{d}_m\right)=m/ M \), or \( {d}_m=-\log \left(1-m/ M\right) \), where we define \( \log (0)=-\infty \).

We now get for 1 ≤ ℓ, r ≤ M the joint density

$$ {\displaystyle \begin{array}{r}P\left(L=\ell, R=r\right)\\ {}\kern1em =\left\{\begin{array}{l}{\sum}_{k\in \left\{5,7\right\}}{\sum}_{j\in \left\{5,7\right\}}{\sum}_{i\in \left\{1,2,3\right\}}{\left[{e}^{\varLambda {d}_{\ell -1}}\right]}_{1i}\kern1em \\ {}{\left[{e}^{\varLambda \left({d}_{\ell }-{d}_{\ell -1}\right)}\right]}_{ij}{\left[{e}^{\varLambda \left({d}_{r-1}-{d}_{\ell}\right)}\right]}_{jk}{\left[{e}^{\varLambda \left({d}_r-{d}_{r-1}\right)}\right]}_{k8} \mathrm{if}\kern0.3em \ell <r\\ {}{\sum}_{i\in \left\{1,2,3\right\}}{\left[{e}^{\varLambda {d}_{\ell -1}}\right]}_{0i}{\left[{e}^{\varLambda \left({d}_{\ell }-{d}_{\ell -1}\right)}\right]}_{i8} \mathrm{if}\kern0.3em \ell =r\\ {}P\left(L=r,R=\ell \right) \mathrm{if}\kern0.3em \ell >r.\\ {}\kern1em \end{array}\right. \end{array}} $$
(11)

The reason for the first case is that in order for the left tree height to be in state ℓ < r, it must be in state 1, 2, or 3 at time d ℓ−1 and in state 5 or 7 at time d ℓ (i.e., there have been no coalescent events before time d ℓ−1 and a left coalescent event between time d ℓ−1 and d ℓ), and similarly it must still be in state 5 or 7 at time d r−1 and in state 8 at time d r (i.e., there have been no coalescent events between time d ℓ and time d r−1 and a right coalescent event between time d r−1 and time d r). The next case corresponds to no coalescent events before time d ℓ−1 and both a left and a right coalescent event between time d ℓ−1 and d ℓ. The last case is due to symmetry of the chain.

From the joint tree states (ℓ, r) we easily get the conditional tree states

$$ {P}_{\left(\ell, r\right)}=P\left(r|\ell \right)=P\left(R=r|L=\ell \right)=\frac{P\left(L=\ell, R=r\right)}{P\left(L=\ell \right)},\kern1.50em $$

where P(L = ℓ) =∑r P(R = r, L = ℓ). These probabilities are used in the HMM.

4.4 Careful Treatment of Mutation Process

A careful treatment of the mutation process allows for a more coarse binning procedure and is needed to avoid biasing the results. In continuous time the probability for a mutation given a tree height t is given by \( \mu (t)=1-\exp \left(-\theta t\right) \), and the stationary tree height distribution is \( \pi (t)=\exp \left(-t\right) \). The probability of a mutation conditionally on the hidden state m becomes

$$ {\displaystyle \begin{array}{r}{\mu}_m=p\left({y}_i=1|{x}_i=m\right)\\ {}=p\left({y}_i=1|t\in \left({d}_{m-1},{d}_m\right)\right)=\frac{p\left({y}_i=1|t\in \left({d}_{m-1},{d}_m\right)\right)}{p\left(t\in \left({d}_{m-1},{d}_m\right)\right)}\\ {}=\frac{\int_{d_{m-1}}^{d_m}p\left({y}_i=1|t\right)\pi (t) dt}{\int_{d_{m-1}}^{d_m}\pi (t) dt}=\frac{\int_{d_{m-1}}^{d_m}\left(1-{e}^{-\theta t}\right){e}^{-t} dt}{\int_{d_{m-1}}^{d_m}{e}^{-t} dt}\\ {}=1-{e}^{-\theta {d}_{m-1}}\frac{\left(1-{e}^{-\left(1+\theta \right)\left({d}_m-{d}_{m-1}\right)}\right)}{\left(1+\theta \right)\left(1-{e}^{-\left({d}_m-{d}_{m-1}\right)}\right)}.\end{array}} $$
(12)

Note that with a fine discretization we have that the interval d m − d m−1 is small and the first-order Taylor expansion \( \exp \left(- az\right)\approx 1- az \) for z small gives

$$ p\left({y}_i=1|{x}_i=m\right)\approx 1-{e}^{-\theta {d}_{m-1}},\kern1.50em $$

as perhaps expected. We are, however, discretizing the interval [0, ∞[, so it is not possible to avoid one or more large bins. Generally we have found that a careful treatment of the mutation process is crucial for accurate inference [36].

4.5 Statistical Inference of Population Parameters from Sequences

Here we choose to focus on three inference methods for estimating the recombination rate. The first method is based on the full likelihood obtained from the classical forward (or backward) algorithm for HMMs. The second is based on the distribution of the distance between segregating sites. This summary statistics was used in Harris and Nielsen [37] for demographic inference. It is sometimes also described as the distribution of the distance between heterozygote sites, runs of homozygosity, or the nearest-neighbor distribution. The third summary statistics is the probability that two sites at certain distance apart are both heterozygote sites. This probability is closely related to the pair correlation function from spatial statistics [36] and to the zygosity correlation introduced in [38].

4.5.1 Summary Statistics: Runs of Homozygosity and Pair Correlation

Recall that in continuous time the probability for a mutation given a tree height t is given by \( \mu (t)=1-\exp \left(-\theta t\right) \), and the stationary tree height distribution is \( \pi (t)=\exp \left(-t\right) \). The marginal probability for a mutation is therefore given by

$$ {\int}_0^{\infty}\mu (t)\pi (t) dt=\theta / \left(1+\theta \right).\kern1.50em $$
(13)

We also get the stationary distribution

$$ \phi (t)=\frac{\mu (t)\pi (t)}{\int_0^{\infty}\mu (t)\pi (t) dt}=\frac{1+\theta }{\theta }{e}^{-t}\left(1-{e}^{-\theta t}\right)\kern1.50em $$

for a tree height t conditional on a mutation. Figure 10a shows ϕ(t) for different values of θ. Note that small mutation rates imply a higher tree height when we condition on a mutation. In discrete time the probability for a mutation given a tree height m was given by Eq. 12. Let μ = (μ 1, …, μ M) be the vector of mutation probabilities. The stationary distribution ϕ = (ϕ 1, …, ϕ M) for a state m conditional on a mutation is given by

$$ {\phi}_{\ell }=\frac{\mu_{\ell }{\pi}_{\ell }}{\sum \limits_{m=1}^M{\mu}_m{\pi}_m},\kern1.50em $$

where π m = 1∕M because this is how the time discretization was chosen.

Fig. 10
figure 10

(a) Stationary distribution of tree height conditional on a mutation. (b) Probability of a mutation at various distances away from a mutation. (c) Probability of the first mutation at various distances away from a mutation

Full size image

The probability for a mutation at a distance r from a typical mutation is then given by

$$ \kappa (r)={\boldsymbol{\phi}}^{\prime }{P}^r\mu, \kern1.50em $$

where ′ denotes vector transpose. In Fig. 10b we show κ(r) as a function of ρ and θ. Note that the curves converge to θ∕(1 + θ) and that the behavior for small r is determined by the recombination rate.

The distribution of runs of homozygosity is given by

$$ \nu (r)={\boldsymbol{\phi}}^{\prime }{\left[P\operatorname{diag}\left(e-\mu \right)\right]}^{r-1}P\boldsymbol{\mu} .\kern1.50em $$

Here e = (1, …, 1) is the vector of length M with 1 in every entry and diag(e − μ) is the diagonal matrix with e − μ on the diagonal. In Fig. 10c we show ν(r) as a function of ρ and θ.

4.5.2 Parameter Estimation

We estimate the mutation rate using an estimating equation based on the marginal probability for a mutation (Eq. 13). If the observed frequency of a mutation is \( \widehat{p} \), then the mutation rate is \( \widehat{\theta}=\widehat{p}/ \left(1-\widehat{p}\right) \) (see left plot in Fig. 11). The recombination rate is estimated using maximum likelihood for the HMM and goodness of fit for the pair correlation (see middle plot in Fig. 11) and runs of homozygosity (see right plot in Fig. 11).

Fig. 11
figure 11

Parameter estimation for summary statistics. (a) The mutation rate θ is estimated from the observed number of mutations and length of the region. (b) The recombination rate ρ is estimated using the empirical distribution of a mutation at various distances from a mutation. (c) The recombination rate is estimated using the empirical distribution of the first mutation from a mutation

Full size image

We simulated 50 sequences of length 20,000 base pairs and with mutation rate θ = 0.1 and recombination rate ρ = 0.1. We estimated the mutation rate using the estimating equation and the recombination rate using maximum likelihood and the HMM, and goodness of fit for the pair correlation and nearest neighbor (Fig. 12) [35]. As expected the HMM procedure shows the best results because here we are using all the available information. It seems, however, that we are not losing too much power when applying the pair correlation function. This is in contrast to the nearest-neighbor summary statistics that perform much worse than the other two methods.

Fig. 12
figure 12

Results of parameter estimation for simulation study. The pair correlation summary performs rather well compared to the full HMM data analysis. Nearest neighbor is a poor summary statistics

Full size image

We have provided a detailed treatment of the main components involved in an analysis of pair of DNA sequences based on an HMM derived from coalescent theory. Pairwise sequentially Markov coalescent (PSMC) models have been extensively applied to various organisms, see, for instance [39,40,41,42,43].

5 Extending the Pairwise Sequentially Markov Coalescent

Extending the SMC to more than two genomes has proved to be challenging. The number of hidden states becomes prohibitive, as several divergence times have to be modeled and combined with distinct possible topologies. Further simplifications are therefore needed to account for an increasing number of genomes.

5.1 From 2 to n Genomes

5.1.1 The Multiple Sequentially Markov Coalescent (MSMC)

Schiffels and Durbin [15] proposed to extend the PSMC model [14] to more than two haploid genomes by modeling the most recent coalescence event in the sample. In this framework, the hidden states of the model are a combination of divergence times, taken from a discretized distribution, and identity of the corresponding haplotypes involved. The rationale for such simplification was that the PSMC showed poor resolution in the recent past [14], and considering more genomes would bring additional signal. The drawback of this implementation is that the more genomes are considered, the more “shifted” toward the present is the timeframe where population parameters can be inferred. As a result, the authors reported that with more than 8 diploid individuals (16 haploid genomes), parameters can virtually not be estimated (see also [44] for an illustration of this effect with simulations). Another consequence of this approach is that the recombination rate parameter cannot be reliably estimated [15]. The MSMC was used to infer the recent history of human population. In particular, the authors introduced the possibility to label individuals and look at cross-coalescence rate between groups, a way to get a fine-tuned view of population divergence [15, 45].

5.1.2 The Demographic Inference with Composite Approximate Likelihood (diCal)

An alternative approach was introduced by Song and colleagues [16,17,18]. The demographic inference with composite approximate likelihood (diCal) approach is based on the conditional sampling distribution, which computes the likelihood of one genome conditioned on the observation of others. Using the so-called composite likelihood formula, it is therefore possible to compute the likelihood of the data for n genomes as the product of the likelihood of one genome given the n − 1 other ones and the likelihood the remaining n − 1 genomes:

$$ P\left({D}_{1\dots n}|\varTheta \right)=\Pr \left({D}_1|{D}_{2\dots n},\varTheta \right)\times P\left({D}_{2\dots n\mid \varTheta}\right),\kern1.00em $$

where Θ is the set of model parameters and D 1…n denotes the data set with n genomes. By further noting that

$$ P\left({D}_{2\dots n}|\varTheta \right)=P\left({D}_2|{D}_{3\dots n},\varTheta \right)\times P\left({D}_{3\dots n-1}|\varTheta \right)\kern1.00em $$

the likelihood of the full data set can be computed by recursion. The terms P(D i|D i+1…n) form the conditional sampling distribution (CSD). Paul et al. [16] proposed a way to compute the CSD at the cost of introducing several additional hypotheses: (a) the haplotypes upon which the sample is conditioned are considered independent, that is, no coalescence events involving these haplotypes are allowed and (b) mutations can only occur once in any lineage (infinite site hypothesis). The likelihood resulting from this approximated CSD is therefore not exact. This approach was introduced by Li and Stephens [46] and is referred to as the product of approximate conditionals (PAC) model. Under the PAC model, the likelihood depends on the order by which the data is conditioned, which can be circumvented with permutation procedures. While the CSD-based SMC does not have the same drawbacks as the MSMC of Schiffels and Durbin [15], its computational efficiency decreases as the number of haplotypes considered increases and becomes impractical for more than 10 genomes [19]. An elegant feature of the diCal approach is that it can be extended to more complex demographic models, including population structure and gene flow [18, 45]. Such extension is of interest as the SMC approximation has been shown to be sensitive to strong population structure [47].

5.1.3 Extending the SMC with Conditional Site Frequency Spectra (CSFS)

In order to use the large amount of data available in “1000 genomes” projects, Terhorst et al. [19] extended the PSMC in a different direction. Instead of modeling the genealogy of the complete sample, the authors proposed to model the divergence of two haplotypes (the PSMC model) as hidden states, yet considering the full set of genomes as observed states. In this approach, the transition probabilities of the coalescent HMM are similar to the PSMC (or to be more precise, similar to the MSMC with two haplotypes, as the original PSMC uses the SMC of McVean and Cardin [33] and not the SMC’ of Marjoram and Wall [48]), but the emission probabilities are extended to account for the full site frequency spectrum of hundreds of genomes. This conditional site frequency spectrum (CSFS) is computed using coalescence theory, offering a generalization of the Poisson random field (PRF) model introduced by Sawyer and Hartl [49]. Just like the original PRF, however, the CSFS ignores linkage of observed states, only linkage between the two conditioned haplotypes is modeled via the SMC. Additional data reduction steps are therefore required to ensure that the independence condition of sampled sites is met.

5.1.4 Explicit Reconstruction of the Ancestral Recombination Graph

While the ARG contains all historical information about a sample of genomes, genomes themselves contain very little information regarding the underlying ARG. As a result, in most statistical inference methods is the ARG treated as a variable accounted for, but not directly inferred. In the SMC models presented above, this is taken care of by the hidden Markov methodology, which computes a likelihood for a given sample by summing over all possible ARG (via the so-called forward algorithm). The Viterbi algorithm and the posterior decoding procedure are HMM algorithms that allow to reconstruct a posteriori the most likely ARG for a sample, such procedures are notably used for the inference of patterns of incomplete lineage sorting along genomes [11, 12, 50, 51]. Yet the variance in such estimation is typically very large [12].

Rasmussen et al. [20] proposed a different approach: they developed a Bayesian sampler of ARGs conditioned on a set of genome sequences. Similar in principle to the PAC and CSD approaches, the authors proposed to generate the ARG of n genomes conditioned on the ARG of n − 1 genomes, a procedure they refer to as threading. The generated ARGs can then be used to infer evolutionary processes of interest. Palacios et al. [52] developed a non-parametric method that allows to estimate the variation in time of the effective population size based on such reconstructed ARG. Rasmussen et al. further showed that while the model used for inference is purely neutral, the a posteriori inferred ARG contains signature of selection, visible for instance as a decrease of the time of the most common ancestor of two samples in the data close to coding sequences. Such approaches offer promising avenues for the development of new statistical methods to detect genomic regions with unusual history.

5.2 The Case of Multiple Species

Hobolth et al. [11] developed a hidden Markov model (HMM) to infer the ancestral recombination graph between three closely related species. Because this model only contains one haploid genome per species, it only allows to infer population parameters in the ancestral species. Dutheil et al. [12] reparametrized this model in the context of the sequentially Markov coalescent. In contrast to the previous approaches, only four hidden states were considered, corresponding to four alternative scenarios of lineage segregation (Fig. 13). In states 1 and 2, the genealogy is consistent with the phylogeny and lineages segregate in the same order as the species. In states 2, 3, and 4, allele divergence predates the first speciation event and ancestral polymorphism persists between the two speciation events, leading to incomplete lineage sorting. The scenarios depicted by states 2, 3 and 4 are equally likely, and in the case of states 3 and 4, the resulting topology is inconsistent with the phylogenetic tree. This model therefore does not rely directly on divergence variation along the genome alignment but uses patterns of topology variation instead to compute the speciation times and ancestral population sizes.

Fig. 13
figure 13

The coalescent process along genomes of three closely related species. (a) Four archetypes of coalescence scenarios with three species, exemplified with human, chimpanzee, and gorilla. In the first scenario, human and chimpanzee coalesce within the human–chimpanzee common ancestor. In the three other scenarios, all sequences coalesce within the common ancestor of all species, with probability 1∕3 depending on which two sequences coalesce first. (b) Example of genealogical changes along a piece of an alignment. The alignment was simulated using the true coalescent process and parameters corresponding to the human–chimpanzee–orangutan history. The blue line depicts the variation along the genome of the human–chimpanzee divergence. The background colors depict the change in topology, red and yellow corresponding to incomplete lineage sorting. Each change in color or break of the blue line is the result of a recombination event

Full size image

Using this approach, Hobolth et al. estimated a speciation time between human and chimpanzee around 4.1 My and a large ancestral effective population size of 60,000 for the human–chimpanzee ancestor. Dutheil et al. [12] found similar estimates with the same data set while accounting for substitution rate variation across sites and estimated an average recombination rate of 1.7 cM/Mb. With sequencing of more great ape genomes, this approach allowed to estimate population size in several ape ancestors ( [27, 50, 53], reviewed in [54]). As ILS is a proxy for ancestral effective population size, a major result of these studies is that the distribution of ILS is not uniform along the genome. For instance, it is reduced in proximity of genes, a pattern that can be explained by background selection [27, 50]. Large regions of the X chromosome were also found to be devoid of ILS, a pattern resulting from recurrent selective sweeps along the chromosomes [55].

6 Specific Issues Faced When Dealing with Genomic Data

In previous sections we discussed population genetic models and methods for parameter estimation. We now describe several challenges encountered when analyzing whole-genome data sets, at the intra- and interspecific levels.

6.1 Sequencing Errors and Rate Variation

Sequencing errors are a well-described source of bias in population genetics analyses, resulting in an excess of singletons [56]. At both the intra- and interspecific/populational level, such error therefore leads to incorrect estimates of local divergence, in particular for recent times. When more divergent sequences are compared, for instance, from distinct species, the issue becomes more complex as the error rate differs between and within sequences due to coverage variation, but also properties of the genome (base composition, repeated elements, etc.). Such errors result in a departure from the molecular clock hypothesis, thus potentially leading to biases in parameter estimates, such as asymmetries in genealogy frequencies [57, 58]. In this respect, data preprocessing becomes a crucial step in any genomic analysis. Methods would also benefit in many cases of inclusion of a proper modeling of such errors. Burgess and Yang noticed that sequencing errors can be seen as a contemporary acceleration in external branches, resulting in an extra branch length [9]. Such an extra length can be easily accommodated in many models. It has to be noted that only a differential in error rates between lineages results in a departure from molecular clock, and in such approaches, one still has to consider that at least one sequence is error-free. In addition, as noted by the authors, assuming a constant error rate over all genomic positions may also turn out to be inappropriate, and better models should allow this rate to vary across the sequence. Such approaches still have to be explored. Moreover, sequencing errors are not distinguishable from lineage-specific acceleration (or deceleration in another species). In that respect, sequence quality scores can be a valuable source of information. They are currently used to preprocess the data by removing doubtful regions, but can ultimately be used in the modeling framework.

The substitution rate also varies along the genome, which potentially affects the reconstruction of sequence genealogy, a phenomenon well known by phylogeneticists. In such case the tools developed for phylogenetic analysis can be applied with a reasonable cost. This generally consists in assuming a prior distribution of the site-specific rate and integrating the likelihood over all possible rates [8, 9, 12]. Alternatively, one can also use one or more outgroup sequences to calibrate the rate, as in [6, 7].

6.2 Diploid Data and Phasing

While sequencing of diploid individuals allows to infer the two alleles present at heterozygous positions, establishing how these alleles are combined on each homologous chromosome requires an additional, error-prone step calling phasing. Analyses based on the comparison of individuals from distinct species do not require such information, as the coalescence time of two alleles from the same species is expected to have happened much after the speciation time of the compared species. In such case alleles at each heterozygous position can be sampled randomly [13] in order to build a composite haploid genome. The same rationale applies with respect to the use of the human reference genome, a composite genome obtained from multiple individuals. Conversely, inferences at the population level typically rely on the modeling of haploid genomes and therefore require phased data. A notable exception is the PSMC [14], as well as its extension SMC++ [19], which, when applied to one diploid individual, only requires the knowledge of the position of heterozygous positions.

6.3 Structural Variation and Genome Alignment

Genome data are intrinsically fragmented, firstly because of chromosomal organization, but also because of rearrangements that prevent molecule-to-molecule alignment from one species to another. A genome data set is therefore a set of distinct alignments, one per synteny block. Synteny information can only be extracted when individual genomes are available, which is typically not the case for most “re-sequencing” data sets. At the population level, however, such large-scale variation is considered negligible (but see, for instance, [59] for an exception), while it becomes more prominent when genomes from distinct species are compared. In such cases, a genome alignment is constructed with potential errors ultimately leading to the comparison of nonhomologous regions. So far, the only way to deal with such errors is to restrict the analysis on regions where orthology can be unambiguous resolved, mostly by removing short synteny blocks and regions that contain a high proportion of repeated elements, gaps, and duplications.

7 Discussion

Studying the speciation process with genome data implies new modeling challenges, as the basic configuration of a population genetics data set is drastically changed: instead of having a few loci sequenced in several individuals, we have an (almost) exhaustive set of loci sequenced in several individuals for multiple closely related species. The change involves the spatial dimension, but also time, as the process under study occurred much further back in time than the ones that are commonly studied with a “standard” population genetics data set. The use of the spatial signal has a major consequence, namely, that recombination has to be taken into account, even if it is not directly modeled.

Apart from these considerations, ancestral population genomics, as population genetics, heavily relies on the study of sequence genealogy, its shape, but also its variation. The underlying models build on existing intraspecies population modeling, as they only need to add the species divergence process, that is, a moment in time where two populations stop exchanging genetic material and evolve fully independently. The simplest isolation model assumes that the speciation is instantaneous, while the isolation-with-migration model assumes that the two neo-species can still exchange some material, at least for a certain time after the split. Such a model is not different from a pure isolation model where the ancestral population is structured into two subpopulations: in the first case the speciation time is defined as the time of the split, while in the second case it is the time of the last genetic exchange. Recent work on primates [10] suggests that the speciation of human and chimpanzee was not instantaneous. If the average divergence of the human and chimpanzee is a bit more than 6 My (using widely accepted mutation rate), then the split of the two species initiated around 5.5 My ago, and the last genetic exchange can be dated around 4 My.

The fact that we sample a large number of positions in the genome thus appears to have the power to counterbalance the reduced sampling of individuals within population, allowing the estimation of demographic parameters in the ancestor. Nonetheless, complexity limits are rapidly reached, when considering, for example, three closely related species that can exchange migrants. More complex demographic scenarios, incorporating, for instance, variation in population sizes, will also add additional parameters that might not all be identifiable.

If the ancient speciation processes have left signatures in the contemporary genomes, we do not know yet how far back in time this is true. Intuitively, the signal is maximal when the variation in divergence due to polymorphism is large enough compared to the total divergence. The divergence due to polymorphism is proportional to the ancestral population size, while the divergence of species is only dependent on the time when it happened. So the further back in time we are looking at, the bigger the population sizes need to be so that the ancient polymorphism leaves a signature in the total divergence time. In addition to this, one has to take into consideration sequence saturation due to the too large number of substitutions that accumulated since ancient splits, and the fact that demographic scenarios complexity increases with time. For instance, when considering the evolution of a species over several millions of generations, the probability that a bottleneck, resetting the signal from past events, occurred once is not negligible.

We are in the population genomics era. Data sets are available that allow us to understand the evolutionary processes that are associated with the formation and evolution of species. Analyzing such data sets with the current methodologies however offers major challenges: (1) developing the appropriate computational tools able to handle such data sets with current machines (both in terms of processor speed and memory usage) and (2) design realistic models with enough complexity to capture the most important historical events while remaining computationally tractable.

8 Exercises

8.1 ILS in Primates

Assuming that there are 5 My between the speciation times of human with the gorilla and the orangutan, that the HG ancestral effective population size was 50,000, what is the expected amount of ILS between human, gorilla, and orangutan? Assuming that another 2.5 My separates the speciations of human with chimpanzee and gorilla, with an HC effective ancestral population size of 50,000, what is the expected amount of ILS between human, chimpanzee, and orangutan? We assume a generation time of 20 years for all extent and ancestral primates.

8.2 Estimating Ancestral Population Size from the Observed Amount of ILS

Given that 30% of incomplete lineage sorting is observed between human, chimpanzee, and gorilla and assuming a generation time of 20 years and a that 2.5 My separate the splits between human/chimpanzee and human—chimpanzee/gorilla, what is the effective ancestral population size compatible with this observed amount? Using Burgess and Yang’s method [9], a researcher finds a higher estimate of Ne than expected. What could explain this discrepancy?

8.3 Number of Migration Rates in the General k-Population IM Model

In this exercise we show that a k-population IM model has 2(k − 1)2 migration rates.

  1. 1.

    Starting at the bottom of the k-population IM model argue that the number of migration rates at the level of k populations is k(k − 1).

  2. 2.

    Moving up to the next level where (k − 1) populations are present (one of them being an ancestral population, we assume that there two speciation events are never simultaneous) argue that the new ancestral population introduces 2(k − 1) new migration rates.

  3. 3.

    Moving up yet another level where (k − 2) populations are present argue that the new ancestral population introduces 2(k − 2) new migration rates.

  4. 4.

    Show that the total number of migration rates is 2(k − 1)2.