Linear Modes for Channels of Constant Cross-Section and Approximate Dirichlet–Neumann Operators

Abstract

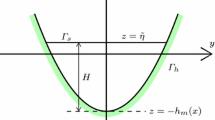
We study normal modes for the linear water wave problem in infinite straight channels of bounded constant cross-section. Our goal is to compare semi-analytic normal mode solutions known in the literature for special triangular cross-sections, namely isosceles triangles of equal angle of $45^{\circ }$ and $60^{\circ }$, see Lamb (Hydrodynamics. Cambridge University Press, Cambridge, 1932) , Macdonald (Proc Lond Math Soc 1:101–113, 1893), Greenhill (Am J Math 97–112, 1887), Packham (Q J Mech Appl Math 33:179–187, 1980), and Groves (Q J Mech Appl Math 47:367–404, 1994), to numerical solutions obtained using approximations of the non-local Dirichlet–Neumann operator for linear waves, specifically an ad-hoc approximation proposed in Vargas-Magaña and Panayotaros (Wave Motion 65:156–174, 2016), and a first-order truncation of the systematic depth expansion by Craig et al. (Proc R Soc Lond A: Math, Phys Eng Sci 46:839–873, 2005). We consider cases of transverse (i.e. 2-D) modes and longitudinal modes, i.e. 3-D modes with sinusoidal dependence in the longitudinal direction. The triangular geometries considered have slopping beach boundaries that should in principle limit the applicability of the approximate Dirichlet–Neumann operators. We nevertheless see that the approximate operators give remarkably close results for transverse even modes, while for odd transverse modes we have some discrepancies near the boundary. In the case of longitudinal modes, where the theory only yields even modes, the different approximate operators show more discrepancies for the first two longitudinal modes and better agreement for higher modes. The ad-hoc approximation is generally closer to exact modes away from the boundary.

Appendix A

We present some computations related to symmetrization, parity, and the operator $D \tanh (h(\cdot ) D)$.

The notion of adjoint ${\mathscr {A}}^*$ applies to operators ${\mathscr {A}}:D({\mathscr {A}}) \subset L^2 \rightarrow L^2$, with $D({\mathscr {A}})$ dense in $L^2 = L^2(\mathbb {R};\mathbb {R})$. Operators that map real-valued functions to real-valued (resp. imaginary-valued) functions will be denoted as real (resp. imaginary) operators. Imaginary operators map $D({\mathscr {A}}) \subset L^2$ to $i L^2$. The adjoint and symmetrization of a real operator is real. We extend the definition of the adjoint to imaginary operators by linearity: if ${\mathscr {A}}$ is imaginary, then ${\mathscr {B}} = i {\mathscr {A}}$ is real and ${\mathscr {A}} = -i {\mathscr {B}}$ and we let ${\mathscr {A}}^* = -i {\mathscr {B}}^*$. We note that D and $\tanh (h(x) D) f$ are imaginary, and, therefore, $D\tanh (h(x) D) f$ is real. Similarly, we check that operators ${\mathscr {A}}_1$, ${\mathscr {A}}_2$, ${\mathscr {A}}_{1,\kappa }(\beta )$, ${\mathscr {A}}_{G_{0,\kappa }}(\beta )$ are also real.

Also, for $\beta$, h even we check that ${\mathscr {A}}_1$, ${\mathscr {A}}_2$, $D\tanh (h(x) D)$, ${\mathscr {A}}_{1,\kappa }(\beta )$, and ${\mathscr {A}}_{G_{0,\kappa }}(\beta )$ preserve parity, i.e. map even (resp. odd) real-valued functions to even (resp. odd) real-valued functions. This follows by examining the various operators appearing in the, respective. definitions and their compositions.

For instance, the operator D maps even (resp. odd) real-valued functions to odd (resp. even) imaginary-valued functions. Also, by the definition of $\tanh (h(x)D)$ on the line,

$$\begin{aligned} g_1(x)= & {} \tanh (h(x)D) \cos k x = \frac{1}{2} [\tanh (h(x)k) e^{i k x} + \tanh (h(x) (- k) e^{- ik x}] \\= & {} i \tanh (h(x)k) \sin k x, \\ g_2(x)= & {} \tanh (h(x)D) \sin k x = \frac{1}{2 i} [\tanh (h(x) k ) e^{i k x} - \tanh (h(x) (- k)) e^{-i k x}] \\= & {} - i \tanh (h(x) k) \cos k x. \end{aligned}$$

Then h even implies $g_1(-x) = - g_1(x)$, and $g_2(-x) = g_2(x)$, for all x. Therefore, $\tanh (h(x)D)$ maps even (resp. odd) real-valued functions to odd (resp. even) imaginary-valued functions, and $D \tanh (h(x)D)$ is real and preserves parity Similar calculations apply to $b-$periodic functions, e.g. with k integer if $b = 2 \pi$. Operators ${\mathscr {A}}_{1,\kappa }(\beta )$ of (35) and ${\mathscr {A}}_{G_{0,\kappa }}(\beta )$ of (36) are compositions of real operators that preserve parity.

We use the above observations to discretize and symmetrize the operator $D \tanh (h(\cdot ) D)$. We assume h$2\pi -$periodic, and we apply these operators to real $2\pi -$periodic functions. Let $\mathcal{T}$ be either D or $\tanh (h(\cdot ) D)$. We consider the decomposition of real $2\pi -$periodic $L^2$ functions f of vanishing average into even and odd components $f_E$, $f_O$, respectively. Truncations to K Fourier modes of $\mathcal{T}$ are obtained applying $\mathcal{T}$ to finite cosine and sine series

$$\begin{aligned} f_E^K = \frac{1}{\pi } \sum _{k = 1}^K x_k \cos k x, \quad f_O^K = \frac{1}{\pi } \sum _{k = 1}^K y_k \sin k x, \end{aligned}$$

(59)

respectively. Since D and $\tanh (h(\cdot ) D)$ map real even functions to imaginary odd functions we have

$$\begin{aligned} \mathcal{T} f_E^K = \frac{i}{\pi } \sum _{\lambda =1}^K x_{\lambda } (\mathcal{T} \cos \lambda x) = \frac{i}{\pi } \sum _{k=1}^K {{\tilde{y}}}_k \sin k x; \end{aligned}$$

(60)

therefore,

$$\begin{aligned} {{\tilde{y}}}_k = -\frac{i}{\pi } \sum _{\lambda =1}^K \left( \int _{0}^{2\pi } \sin k x (\mathcal{T} \cos \lambda x) {\text{ d }} \right) x_{\lambda }. \end{aligned}$$

(61)

Also, D and $\tanh (h(\cdot ) D)$ map real odd functions to imaginary even functions and we similarly obtain

$$\begin{aligned} \mathcal{T} f_O^K = \frac{i}{\pi } \sum _{\lambda =1}^K y_{\lambda } (\mathcal{T} \sin \lambda x) = \frac{i}{\pi } \sum _{k=1}^K {{\tilde{x}}}_k \cos k x; \end{aligned}$$

(62)

therefore,

$$\begin{aligned} {{\tilde{x}}}_k = -\frac{i}{\pi } \left( \sum _{\lambda =1}^K \int _{0}^{2\pi } \cos k x (\mathcal{T} \sin \lambda x) {\text{ d }} \right) y_{\lambda }. \end{aligned}$$

(63)

We can, therefore, represent $\mathcal{T}$ on the truncated functions by the matrix

$$\begin{aligned} \left[ \begin{array}{cc} 0 &{} -i R \\ -i L &{} 0 \end{array}\right] , \quad R_{k,\lambda }&= \int _{0}^{2\pi } \cos k x (\mathcal{T} \sin \lambda x) \frac{{\text{ d }}}{\pi }, \quad L_{k,\lambda }\nonumber \\&= \int _{0}^{2\pi } \sin k x (\mathcal{T} \cos \lambda x) \frac{{\text{ d }}}{\pi }, \end{aligned}$$

(64)

k, $\lambda = 1,\ldots K$. Representing D, $\tanh (h(\cdot ) D)$ by matrices $M_1$, $M_2$, respectively, obtained as above, we symmetrize numerically by considering $1/2(M_1 M_2 + M^T_2 M^T_1)$, $M^T$ the transpose of M. $M_1 M_2$ and its symmetrization are block diagonal in the odd and even subspaces. We, therefore, compute even and odd numerical eigenfunctions. By the discussion above, the discretization of the operators ${\mathscr {A}}_1$, ${\mathscr {A}}_2$, ${\mathscr {A}}_{1,\kappa }(\beta )$, and ${\mathscr {A}}_{G_{0,\kappa }}(\beta )$ follows the same scheme and leads to symmetric matrices that are block diagonal in the odd and even subspaces.

Computations of eigenvalues and eigenvectors used the Matlab implementation of the QR algorithm, see [26] also used in LAPACK. We used discretizations with $K = 2^4$ to $2^9$, results in figures use $K = 2^6$. Computations by the MacBook Pro 3.1 Ghz Intel Core i5 take up to two seconds.

We now consider the operator ${\mathscr {A}}_{G_0}$ up to order one in $\beta$. We have

$$\begin{aligned}{}[D\tanh (h(x) D)f](x)= & {} -i\partial _x (2 \pi )^{-1} \int _{\mathbb {R}} \tanh (h(x) k){\hat{f}}(k) e^{ik x} {\text{ d }} \nonumber \\= & {} (2 \pi )^{-1} [-i \int _{\mathbb {R}}[(\partial _x\tanh (h(x)k)){\hat{f}}(k) e^{i k x} {\text{ d }} k \nonumber \\&\quad + \int _{\mathbb {R}} (\tanh (h(x) k)){\hat{f}}(k)k e^{i k x} {\text{ d }}] \nonumber \\= & {} (2 \pi )^{-1} [i\beta '(x) \int _{\mathbb {R}} \text {sech}^2(h(x) k) k {\hat{f}} (k ) e^{i k x} {\text{ d }} \nonumber \\&\quad + \int _{\mathbb {R}} (\tanh (h(x) k)){\hat{f}}( k) k e^{i k x} {\text{ d }}] \nonumber \\= & {} i\beta '(x) [\text {sech}^2(h(x)D)Df](x) + [\tanh (h(x)D)Df](x),\nonumber \\ \end{aligned}$$

(65)

using

$$\begin{aligned} \partial _x(\tanh (h(x) k))= & {} -\text {sech}^2(h(x) k)\beta '(x) k, \end{aligned}$$

and $\partial _xh(x)=\partial _x(h_0-\beta (x))=-\beta '(x)$. Furthermore,

$$\begin{aligned}{}[i\beta '(x)\text {sech}^2(h(x)D)Df](x)= & {} i\beta '(x) (2 \pi )^{-1} \int _{\mathbb {R}} [\text {sech}^2(h_0 k)+ O(\beta ^2)] k {\hat{f}}(k) e^{i k x} {\text{ d }} \\= & {} i\beta '(x)[\text {sech}^2(h_0D)D^2f](x) + O(\beta ^2), \end{aligned}$$

and

$$\begin{aligned}{}[\tanh (h(x)D)Df](x)= & {} \int _{\mathbb {R}}\left( \tanh (h_0 k)-\text {sech}^2(h_0 k)\beta (x) k+ O(\beta ^2)\right) {\hat{f}}(k) k e^{i k x} \frac{{\text{ d }}}{2 \pi } \\= & {} [\tanh (h_0D)Df](x) - \beta (x)[\text {sech}^2(h_0 D)D^2 f](x) + O(\beta ^2). \end{aligned}$$

Therefore, (65) leads to

$$\begin{aligned} D \tanh (h(x)D)= & {} \tanh (h_0 D)D + i\beta '\text {sech}^2(h_0 D)D - \beta \text {sech}^2(h_0 D)D^2 + O(\beta ^2). \end{aligned}$$

We also have $(\tanh (h_0 D))^* = - \tanh (h_0 D)$, $D^*= - D$, $(\text {sech}^2(h_0 D))^* = \text {sech}^2(h_0 D)$, $(i\beta \cdot )^* = i\beta \cdot$, $(\beta \cdot )^* = \beta \cdot$, so that

$$\begin{aligned} \textit{Sym}(D\tanh (h(x)D))= & {} D\tanh (h_0 D) + \frac{1}{2}[ i\beta '\text {sech}^2(h_0 D)D - \beta \text {sech}^2(h_0 D)D^2 \nonumber \\&- i D \text {sech}^2(h_0 D) \beta ' + D^2 \text {sech}^2(h_0 D) \beta ] + O(\beta ^2). \end{aligned}$$

(66)

Operators $\text {sech}^2 (h_0 D)$, $\beta \cdot$ (with $\beta$ even) are real and preserve parity, while $i \beta ' \cdot$, and D are imaginary and reverse parity. It follows that the operator ${\mathscr {A}}_2$ of (16) obtained by truncating (66) to $O(\beta ^2)$ is real and preserves parity.