Surrogate modeling and risk-based analysis for solute transport simulations

Abstract

This study is driven by the question of how quickly a solute will be flushed from an aquatic system after input of the solute into the system ceases. Simulating the fate and transport of a solute in an aquatic system can be performed at high spatial and temporal resolution using a computationally demanding state-of-the-art hydrodynamics simulator. However, uncertainties in the system often require stochastic treatment and risk-based analysis requires a large number of simulations rendering the use of a physical model impractical. A surrogate model that represents a second-level physical abstraction of the system is developed and coupled with a Monte Carlo based method to generate volumetric inflow scenarios. The surrogate model provides an approximate 8 orders of magnitude speed-up over the full physical model enabling uncertainty quantification through Monte Carlo simulation. The approach developed here consists of an stochastic inflow generator, a solute concentration prediction mechanism based on the surrogate model, and a system response risk assessment method. The probabilistic outcome provided relates the uncertain quantities to the relevant response in terms of the system’s ability to remove the solute. We develop a general approach that can be applied in a generality of system configurations and types of solute. As a test case, we present a study specific to salinization of a lake.

Appendix

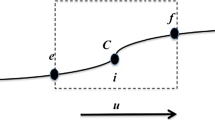
1.1 First CSTR

From Eq. (1) and the assumptions above, the mass balance for CSTR 1 is Accumulation = – Output, and is given by

$$\begin{aligned} V_1 \frac{dC_1}{dt} = -Q_1C_1, \end{aligned}$$

(9)

where $V_1$, $C_1$, and $Q_1$ are, respectively, the volume, the tracer concentration, and the inflow rate for the first CSTR, and t is time. Eq. (9) is rearranged and integrated as follows,

$$\begin{aligned} \int _{C_0}^{C_1}\frac{dC_1}{C_1}= -\frac{Q_1}{V_1}\int _0^tdt, \end{aligned}$$

(10)

$$\begin{aligned} \ln \frac{C_1}{C_0}= -\frac{Q_1}{V_1}. \end{aligned}$$

(11)

Finally, rearranging and defining $\tau _1 = V_1/Q_1$ as the residence time for CSTR 1, the resulting expression for the concentration as a function of time is

$$\begin{aligned} C_1 = C_0 e^{-t/\tau _1}. \end{aligned}$$

(12)

1.2 Second CSTR

The mass balance for the second CSTR is $\text {Accumulation} = \text {Input} - \text {Output}$, or respectively,

$$\begin{aligned} V_2 \frac{dC_2}{dt} = (Q_1 + Q_2)C_1 - (Q_1 + Q_2)C_2, \end{aligned}$$

(13)

where $V_2$, $Q_2$, and $C_2$ are, respectively, the volume, the inlet inflow, and the tracer concentration for the second CSTR.

By defining $\tau _2 = V_2/(Q_1 + Q_2)$ as the residence time of CSTR 2, replacing (12) in (13), and rearranging, the expression below is obtained,

$$\begin{aligned} \frac{dC_2}{dt} + \frac{1}{\tau _2}C_2 = \frac{C_0}{\tau _2}e^{-t/t_1}, \end{aligned}$$

(14)

which is a first-order linear differential equation with integrating factor $\mu (t) = \exp ({\int \frac{1}{\tau _2}dt}) = \exp (t/\tau _2)$. Eq. (14) is multiplied by $\mu (t)$, and rearranged to obtain

$$\begin{aligned} e^{t/\tau _2}\frac{dC_2}{dt} + \frac{e^{t/\tau _2}}{\tau _2}C_2 = \frac{C_0}{\tau _2}e^{\left( \frac{1}{\tau _2} - \frac{1}{\tau _1} \right) t}, \end{aligned}$$

(15)

where the left-hand side is the derivative of $e^{t/\tau _2} C_2$. Integrating Eq. (15) results in

$$\begin{aligned} e^{t/\tau _2} C_2 = -\frac{C_0 \tau _1}{\tau _1-\tau _2}e^{\left( \frac{1}{\tau _2} - \frac{1}{\tau _1} \right) t} + K_1, \end{aligned}$$

(16)

where the integration constant $K_1$ is determined by applying the initial condition $C_2(t=0) = C_0$,

$$\begin{aligned} K_1 = -\frac{C_0\tau _2}{\tau _1-\tau _2}. \end{aligned}$$

(17)

The expression for the tracer concentration in CSTR 2 is obtained by replacing $K_1$ back in Eq. (16) and manipulating,

$$\begin{aligned} C_2 = \frac{C_0}{\tau _1-\tau _2} \left( \tau _1e^{-t/\tau _1} - \tau _2e^{-t/\tau _2} \right) . \end{aligned}$$

(18)

1.3 Third CSTR

As in the previous case, the conceptual mass balance for CSTR 3 is Accumulation = Input – Output, resulting in

$$\begin{aligned} V_3 \frac{dC_3}{dt} = (Q_1 + Q_2 + Q_3)C_2 - (Q_1 + Q_2 + Q_3)C_3, \end{aligned}$$

(19)

where $V_3$, $Q_3$, and $C_3$ are volume, inflow and tracer concentration for the third CSTR, respectively. Similarly to the previous case, defining the residence time of the reactor as $\tau _3 = V_3/(Q_1 + Q_2 + Q_3)$, replacing Eq. (18) in (19) and rearranging yields the differential equation

$$\begin{aligned} \frac{dC_3}{dt} + \frac{1}{\tau _3}C_3 = \frac{C_0}{\tau _3(\tau _1-\tau _2)} \left( \tau _1e^{-t/\tau _1} - \tau _2e^{-t/\tau _2} \right) . \end{aligned}$$

(20)

The equation is multiplied by the integration factor $e^{t/\tau _3}$ resulting in

$$\begin{aligned} e^{t/\tau _3}\frac{dC_3}{dt} + \frac{e^{t/\tau _3}}{\tau _3}C_3 = \frac{C_0}{\tau _3(\tau _1-\tau _2)} \left[ \tau _1e^{\left( \frac{1}{\tau _3} - \frac{1}{\tau _1}\right) t} - \tau _2e^{\left( \frac{1}{\tau _3} - \frac{1}{\tau _2} \right) t} \right] . \end{aligned}$$

(21)

Eq. (21) is integrated yielding

$$\begin{aligned} e^{t/\tau _3}C_3 = \frac{C_0}{\tau _1-\tau _2} \left[ \frac{\tau _1^2}{\tau _1-\tau _3} e^{-t/\tau _1} - \frac{\tau _2^2}{\tau _2-\tau _3}e^{-t/\tau _2} \right] + K_2 e^{-t/\tau _3}, \end{aligned}$$

(22)

where the constant $K_2$ is found using the initial condition $C_3(t=0) = C_0$, giving

$$\begin{aligned} K_2 = \frac{C_0\tau _3^2 (\tau _1-\tau _2)}{(\tau _1-\tau _2)(\tau _1-\tau _3)(\tau _2-\tau _3)}. \end{aligned}$$

(23)

Finally, Eq. (23) is replaced back in (22) and the necessary operations result in

$$\begin{aligned} C_3 = \frac{C_0 \left[ \tau _1^2(\tau _2-\tau _3)e^{-t/\tau _1} - \tau _2^2(\tau _1-\tau _3)e^{-t/\tau _2} + \tau _3^2(\tau _1-\tau _2)e^{-t/\tau _3} \right] }{(\tau _1-\tau _2)(\tau _1-\tau _3)(\tau _2-\tau _3)}. \end{aligned}$$

(24)