Ultrafast heat transfer on nanoscale in thin gold films

Abstract

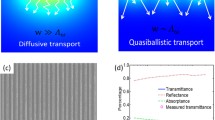
Heat transfer processes, induced by ultrashort laser pulses in thin gold films, were studied with a time resolution of 50 fs. It is demonstrated that in thin gold films heat is transmitted by means of electron–phonon and phonon–phonon interactions, and dissipated on nanoscale within 800 fs. Measurements show that the electron–phonon relaxation time varies versus the probe wavelength from 1.6 to 0.8 ps for λ=560–630 nm. The applied mathematical model is a result of transforming the two-temperature model to the hyperbolic heat equation, based on assumptions that the electron gas is heated up instantaneously and applying Cattaneo’s law to the phonon subsystem, agrees well with the experimental results. This model allows us to define time of electron–phonon scattering as the ratio of the heat penetration depth to the speed of sound in the bulk material that, in turn, provides an explanation of experimental results that show the dependence of the electron–phonon relaxation time on the wavelength.

Appendix

Following the solution procedure from [26], let us take the Laplace transform of (9). Taking into account that, initially, the system described by (9) is at thermal equilibrium and so $\frac{\partial\theta}{\partial \xi}|_{\xi=0}=0$ and θ| _ξ=0=0, we have

$$ \frac{d^2 \varTheta}{d \eta^2}-\bigl(2s+s^2\bigr)\varTheta +\biggl[1+\frac{1}{2}s\biggr]\tilde{Q}=0,$$

(19)

where Θ(η;s) and $\tilde{Q}(\eta;s)$ are the Laplace transforms of θ(η,ξ) and $\tilde{q}(\eta,\xi)$, respectively. The general solution of the nonhomogeneous equation (19) is

$$ Q(\eta;s)=C_1(s)e^{\lambda(s)\eta}+C_2(s)e^{-\lambda(s)\eta}+P(\eta;s),$$

(20)

where $\lambda(s)=\sqrt{2s+s^{2}}$. The two first terms on the right side of (20) are the general solution of the associated homogeneous equation with $\tilde{Q}(\eta;s)=0$, and P(η;s) is a particular solution of (19).

For the problem in question and taking into account the fact that the surface heat flux is induced by the electron gas after absorbing the laser energy, the boundary conditions become

$$ \frac{\partial\theta}{\partial \eta}\bigg|_{\eta=0}=-\tilde{q}''-\frac{1}{2}\frac{\partial \tilde{q}''}{\partial \xi},\qquad \lim_{\eta\rightarrow\infty} \theta=0,$$

(21)

where $\tilde{q}''=\frac{1}{\xi_{p}}\exp{(-a[\frac{\xi-\xi_{b}}{\xi_{p}}]^{2})}$ is the dimensionless form of the surface heat flux. Hence, the parameter C ₁(s) must be zero, and (20) is simplified into

$$ Q(\eta;s)=C(s)e^{-\lambda(s)\eta}+P(\eta;s).$$

(22)

To eliminate C(s) from (22), the derivative of Θ(η;s) with respect to η is used:

$$ \frac{d Q(\eta;s)}{d \eta}=-\lambda(s)C(s)e^{-\lambda(s)\eta}+\frac{d P(\eta;s)}{d \eta}.$$

(23)

Then, combining (22) and (23), and taking into account the relationship between the temperature gradient and the surface heat flux (21), the general solution of (20) can be written as

$$ Q(\eta;s)=\frac{1+\frac{1}{2}s}{\lambda(s)}\tilde{Q}''(s)+P(\eta;s)+\frac{1}{\lambda(s)}\frac{d P(\eta;s)}{d \eta},$$

(24)

where $\tilde{Q}''(s)$ is the Laplace transform of $\tilde{q}''(s)$. The right part of (24) consists of the sum of two terms which are responsible for the temperature responses due to the surface heat flux and volumetric heating, respectively. Taking into account that the function $\tilde{Q}(\eta;s)$ can be represented as a product of two functions, one of which depends on the complex variable s only, and the other is exp(−η/Δη), the particular solution of (20) can be written as follows:

$$ P(\eta;s)=\varDelta \eta^2\frac{1+\frac{1}{2}s}{\varDelta \eta^2s^2+2\varDelta \eta^2s-1}\tilde{Q}(\eta;s).$$

(25)