A model for collective dynamics in ant raids

Abstract

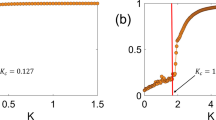
Ant raiding, the process of identifying and returning food to the nest or bivouac, is a fascinating example of collective motion in nature. During such raids ants lay pheromones to form trails for others to find a food source. In this work a coupled PDE/ODE model is introduced to study ant dynamics and pheromone concentration. The key idea is the introduction of two forms of ant dynamics: foraging and returning, each governed by different environmental and social cues. The model accounts for all aspects of the raiding cycle including local collisional interactions, the laying of pheromone along a trail, and the transition from one class of ants to another. Through analysis of an order parameter measuring the orientational order in the system, the model shows self-organization into a collective state consisting of lanes of ants moving in opposite directions as well as the transition back to the individual state once the food source is depleted matching prior experimental results. This indicates that in the absence of direct communication ants naturally form an efficient method for transporting food to the nest/bivouac. The model exhibits a continuous kinetic phase transition in the order parameter as a function of certain system parameters. The associated critical exponents are found, shedding light on the behavior of the system near the transition.

Appendices

Appendix 1: Non-dimensionalization

In order to form a dimensionless problem for the purpose of numerical computations, we must now introduce characteristic scales. A characteristic scale will be denoted by a subscript zero (e.g., $x_0$) and a non-dimensional quantity will be denoted with a hat. For example

$$\begin{aligned} x = x_0\hat{x}, \quad t = t_0\hat{t} \end{aligned}$$

where the characteristic size of an ant $x_0 = 1 \text { cm}$ and one option for the characteristic time $t_0 = 101 s$ is based on the half-life of a food source taken from Amorim (2014). The characteristic diffusion coefficient for pheromone is $\alpha _0 =x_0^2/t_0 = .01 \text {cm}^2/\text {s}$ and the characteristic concentration of pheromone deposited on a 2D surface is $c_0 = 1.1\times 10^{-4} \text {g cm}^{-2}$ (both match experimental values from Calenbuhr and Deneubourg 1992; Couzin and Franks 2003).

First, the homogeneous version of the PDE for pheromone concentration (2) becomes

$$\begin{aligned} {\left\{ \begin{array}{ll} \frac{c_0}{t_0}\partial _{\hat{t}} \hat{c} - \frac{\alpha _0 c_0\hat{\alpha }}{x_0^2}\varDelta \hat{c} + \gamma c_0 \hat{c} = 0, &{} \quad \hat{\mathbf{x}} \in {\mathbb {R}}^2, \hat{t} \in (0, \infty )\\ c_0\hat{c}(\mathbf{x}, 0) = c_0\hat{g}\left( \hat{\mathbf{x}}\right) , &{} \quad \hat{\mathbf{x}} \in {\mathbb {R}}^2 \end{array}\right. }. \end{aligned}$$

By multiplying through the first equation by $t_0/c_0$ and the second by $1/c_0$ we find a non-dimensional equation for the concentration with non-dimensional parameters $\hat{\alpha },\hat{\gamma }$, and $\hat{q}$. Once done, we replace the source term responsible for the exponential decay of the pheromone along the trail in dimensionless form

$$\begin{aligned} {\left\{ \begin{array}{ll} \partial _{\hat{t}} \hat{c} - \hat{\alpha }\varDelta \hat{c} + \hat{\gamma }\hat{c} = \sum \nolimits _{j=1}^M\hat{q}e^{-\Vert \hat{\mathbf{x}}_j(t)-\hat{\mathbf{x}}_f\Vert ^2}\delta \left( \hat{\mathbf{x}}-\hat{\mathbf{x}}_j(t)\right) , &{} \quad \hat{\mathbf{x}} \in {\mathbb {R}}^2, \hat{t} \in (0, \infty )\\ \hat{c}(\mathbf{x}, 0) = \hat{g}(\hat{\mathbf{x}}), &{} \quad \hat{\mathbf{x}} \in {\mathbb {R}}^2. \end{array}\right. } \end{aligned}$$

where $\hat{\gamma } = \gamma t_0$ ($\gamma$ has units of 1/sec, $\gamma \approx 1/300s$ in Couzin and Franks 2003). The maximal dimensionless concentration of pheromone deposited is $\hat{q} = q/c_0$. Next, we proceed to the equations for the foraging ants without the white noise term

$$\begin{aligned} {\left\{ \begin{array}{ll} \frac{x_0}{t_0}{\dot{\hat{\mathbf{x}}}_i} = \frac{x_0}{t_0}\hat{\mathbf{v}}_i\\ \frac{x_0}{t_0^2}{\dot{\hat{\mathbf{v}}}_i} = \frac{x_0^3}{t_0^3}\nu {\hat{\mathbf{v}}}_i\left( \hat{\xi }^2-|\hat{\mathbf{v}}_i|^2\right) - \frac{1}{Nx_0}\sum \nolimits _{j \ne i} \nabla _\mathbf{x} U\left( |\hat{\mathbf{x}}_i - \hat{\mathbf{x}}_j|\right) + dc_0\nabla _{\hat{\mathbf{x}}}\hat{c}\left( \hat{\mathbf{x}},\hat{t}\right) \end{array}\right. } \end{aligned}$$

By multiplying through the first equation by $t_0/x_0$ and the second by $t_0^2/x_0$ we find a non-dimensional equation and add in the dimensionless Gaussian white noise

$$\begin{aligned} {\left\{ \begin{array}{ll} {\dot{\hat{\mathbf{x}}}_i} = \hat{\mathbf{v}}_i\\ {\dot{\hat{\mathbf{v}}}_i }= \hat{\nu }\hat{\mathbf{v}}_i\left( \hat{\xi }^2-|\hat{\mathbf{v}}_i|^2\right) - \frac{1}{N}\sum \nolimits _{j \ne i} \nabla _\mathbf{x} \hat{U}\left( |\hat{\mathbf{x}}_i - \hat{\mathbf{x}}_j|\right) + \hat{d}\nabla _{\hat{\mathbf{x}}}\hat{c}\left( \hat{\mathbf{x}},\hat{t}\right) +\hat{D}\hat{W}_{\hat{t}}. \end{array}\right. } \end{aligned}$$

where $\hat{U}$ is defined in (1) with dimensionless relative distance $\hat{r}$ and the dimensionless depth of the potential well $\hat{\varepsilon } = \varepsilon _0 t_0^2/x^2_0$. Also, $\hat{\nu } = \nu x_0/t_0$ and $\hat{d} = dc_0t_0^2/x_0^2$. Similarly for returning ants we find

$$\begin{aligned} {\left\{ \begin{array}{ll} {\dot{\hat{\mathbf{x}}}_i} = \nu \hat{\varvec{\omega }}_i\\ {\dot{\hat{\mathbf{v}}}_i} = \hat{\nu }\hat{\mathbf{v}}_i\left( \hat{\xi }^2-|\hat{\mathbf{v}}_i|^2\right) - \frac{1}{N}\sum \nolimits _{j \ne i} \nabla _\mathbf{x} \hat{U}\left( |\hat{\mathbf{x}}_i - \hat{\mathbf{x}}_j|\right) + \hat{\beta }\frac{\hat{\mathbf{x}}_i - \hat{\mathbf{x}}_c}{\hat{r}} \end{array}\right. } \end{aligned}$$

where $\hat{\beta } = \beta t_0^2/x_0$ and $\hat{r} = |\hat{\mathbf{x}}_i-\hat{\mathbf{x}}_c|$. Even though the model (3)–(4) was formulated with dimensional constants, from the dimensional analysis presented in this appendix we recover the necessary dimensions of each of the original quantities if desired. Throughout this work the hats are dropped and all variables are understood as dimensionless.

Appendix 2: Pure pheromone diffusion model

As mentioned in Sect. 5, one can consider a pure diffusion model for the pheromone concentration coupled with the same equations (3)–(4) governing ant dynamics. In this setting the ants only lay pheromone at the food source the moment they become returners. The chemical gradient is formed by diffusion of pheromone in the absence of trail laying. We now introduce the following modified PDE for the pheromone concentration $c(\mathbf{x}, t)$

$$\begin{aligned} {\left\{ \begin{array}{ll} \displaystyle \partial _t c - \alpha \varDelta c + \gamma c = \sum \nolimits _{j=1}^M\delta (\mathbf{x} - \mathbf{x}_f)\delta (t - t_j), &{} \mathbf{x} \in {\mathbb {R}}^2, t >0\\ c(\mathbf{x}, 0) = g(\mathbf{x}), &{} \mathbf{x} \in {\mathbb {R}}^2. \end{array}\right. } \end{aligned}$$

(7)

Here M is the total number of visits before a food source is depleted, $g(\mathbf{x})$ is a constant uniform initial distribution of pheromone, and $t_j$ is the time that the jth quantity of food is discovered by a forager. This equation models each foraging ant depositing pheromone at the time of each visit. Once the food source is depleted the pheromone concentration naturally decays to zero resulting in the trail disappearing.

This modification results in a small change in the numerical implementation. We now have an explicit analytical solution to the PDE and need to replace (6) with

$$\begin{aligned} c(\mathbf{x},t) := e^{-\gamma t}\left[ \frac{1}{|V_L|} + \sum _{j=1}^M \chi _j \right] , \qquad \frac{\partial c}{\partial x_i} = e^{-\gamma t}\sum _{j=1}^M \frac{\partial \chi _j}{\partial x_i}. \end{aligned}$$

(8)

where

$$\begin{aligned} \chi _j := {\left\{ \begin{array}{ll} \frac{e^{\gamma t_j}}{4\pi \alpha (t-t_j)} e^{-\frac{|\mathbf{x}-\mathbf{x}_f|^2}{4\alpha (t-t_j)}}&{} \quad t > t_j,\\ 0, &{} \quad t < t_j \end{array}\right. }. \end{aligned}$$

By changing how the ants emit the chemical signal, we achieve an the added advantage of not requiring the computation of a time integral for each foraging ant. One can see from Fig. 11, that the behavior of the ants is the same as in the prior case. The greatest disadvantage is that this approximation to the main model presented is only valid for very short trails where diffusion of pheromone would be sufficient to attract all ants without trail laying.

Fig. 11

Sample ant raiding simulations with foragers (purple) and returners (blue) where $N = 200$. Each arrow represents an individual ant’s orientation ${\varvec{\omega }}_i$. The black circles denote the nest, $\mathbf{x}_c = (2,0)$, and food source, $\mathbf{x}_f = (40,0)$. a Initially ants are placed near the nest in non-overlapping positions with random orientation. b Foragers begin to discover the food source and mark it with pheromone, becoming returners. c As the pheromone diffuses more and more foragers detect the scent and begin to follow the trail to the food source. d Once the food source is depleted the trail quickly disappears and the ants return to random foraging. See Online Resource 5 (color figure online)

Fig. 12

Removal of food over the course of time for a one food source or b two food sources at equal and unequal distances from the nest. Food depleted in 4–6 h consistent with duration of raids from the experimental observations in Schneirla (1940, 1971)

The main difference in the dynamics from the main model presented (2) is seen when two food sources are present. While locally the motion of each ant may appear similar in each case, the depletion rate of each food source is different. In the case of equidistant food sources, initially both food sources are decreasing at about the same rate, but then the depletion rate of the second food source becomes lower and eventually it is no longer visited as seen by the horizontal portion of the food count function in Fig. 12b. In (2) the ants tended to all raid at the food source which was discovered first and display hardly any trail formation at the second food source until the first was depleted. For food sources at different distances the behavior of both models is similar, the closest food source is essentially depleted first and then the second food source is visited. Thus, ants will use all available foragers to completely deplete the closer quantity of food before moving on. This may provide further evidence of the efficiency in which the ants seek to carry out the raiding process.

Appendix 3: Central nest location

Some additional results are presented where the nest is located at the center of the domain. The purpose of these images is to show that the dynamics and trail formation are essentially the same as in the scenarios presented throughout this work where the nest was closer to one edge of the domain. Figure 13 illustrates the trail formation in time. The only difference is that with the nest in the center it takes longer to attract all the foragers, because some are now farther from any portion of the trail than the previous case. To see the full raid please consult Online Resource 6.

Fig. 13

Trail formation with nest in the center. Foragers (purple) and returners (blue) where $N = 400$. Each arrow represents an individual ant’s orientation ${\varvec{\omega }}_i$. The black circles denote the nest, $\mathbf{x}_c = (50,0)$, and food source, $\mathbf{x}_f = (90,0)$. a Once the food source is discovered and phermone is laid along the trail, it takes a greater amount of time for it to diffuse to the ants on the opposite end of the domain. b Eventually all ants join in the raid resulting in a trail with the same form as in Fig. 2. See Online Resource 6 (color figure online)