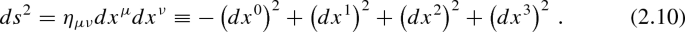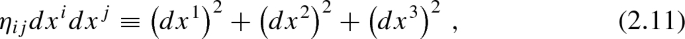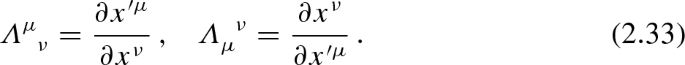Abstract
We introduce the theory of special relativity, namely the theoretical framework based on the Einstein Principle of Relativity. In Newtonian mechanics, we have space and time as two distinct entities and time is the same for all observers. Such a set-up breaks down when we impose that interactions do not propagate instantaneously with infinite velocity (an implicit assumption in the theory of Galilean relativity). In special relativity we have spacetime as the natural stage for the description of physical phenomena.
This is a preview of subscription content, log in via an institution to check access.
Access this chapter
Tax calculation will be finalised at checkout
Purchases are for personal use only
Notes
- 1.
Some authors use a different convention. For an (\(n+1\))-dimensional spacetime (n spatial dimensions \(+\) 1 temporal dimension), they write the coordinates of the spacetime as \((x^1,x^2, \ldots , x^{n+1})\), where \(x^{n+1}\) is the time coordinate. In such a case, the Minkowski metric in Eq. (2.9) becomes \(\eta _{\mu \nu } = \mathrm{diag} (1,1, \ldots , 1,-1)\).
- 2.
The convention of a metric with signature \((-+++)\) is common in the gravity community. In the particle physics community it is more common the convention of a metric with signature \((+---)\).
- 3.
Throughout the book, we use Latin letters \(i,j, k, \ldots \) for space indices (\(1,2, \ldots , n\)), where n is the number of spatial dimensions, and Greek letters \(\mu ,\nu ,\rho , \ldots \) for spacetimes indices (\(0, 1, 2, \ldots , n\)). Such a convention is also used when we sum over repeated indices. For instance, for \(n=3\) we have
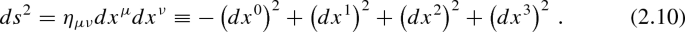
If we wrote \(\eta _{ij} dx^j dx^i\), we would mean
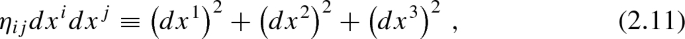
because i and j can run from 1 to n.
- 4.
With the convention \(\eta _{\mu \nu } = \mathrm{diag}(1,-1,-1,-1)\) common in particle physics, the line element along particle trajectories is \(ds^2 > 0\) (\(ds^2 < 0\)) if the particle moves at a speed lower (higher) than c. In that context, time-like curves have \(ds^2 > 0\) and space-like curves have \(ds^2 < 0\).
- 5.
Note the difference of the position of the indices \(\mu \) and \(\nu \) in \(\varLambda ^\mu _{\nu }\) and \(\varLambda _\mu ^{\nu }\). Indeed
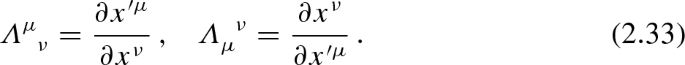
However, since the matrices of the Lorentz transformations are symmetric, sometimes the notation \(\varLambda ^\mu _\nu \) and \(\varLambda _\mu ^\nu \) is used when it is clear the initial and the final coordinate systems.
- 6.
As we will see in Sect. 6.6, there is also a contribution of opposite sign due to the difference in the gravitational field between the two points.
Author information
Authors and Affiliations
Corresponding author
Problems
Problems
2.1
The energy-momentum tensor of a perfect fluid in Cartesian coordinates and in the rest-frame of the fluid has the following form
where \(\varepsilon \) and P are, respectively, the energy density and the pressure of the fluid. Write \(T^{\mu \nu }\), \(T^{\mu }_{\nu }\), and \(T_{\mu \nu }\) in spherical coordinates.
2.2
Consider the coordinate transformation \(x^\mu \rightarrow x'^\mu \) in Eq. (2.28). Write the energy-momentum tensor of a perfect fluid in Eq. (2.60) in the new reference frame moving with velocity v along the x axis.
2.3
Let us consider three inertial reference frames with, respectively, Cartesian coordinates (ct, x, y, z), \((ct',x',y', z')\), and \((ct'',x'',y'', z'')\). The reference frame \((ct',x',y', z')\) moves with the velocity \(\mathbf{v} = (v, 0,0)\) with respect to the reference frame (ct, x, y, z), and the reference frame \((ct'',x'',y'', z'')\) moves with the velocity \(\mathbf{v}' = (v', 0,0)\) with respect to the reference frame \((ct',x',y', z')\). For \(t = t' = t'' = 0\) the three reference frames coincide. Write the Lorentz boost connecting the reference frames (ct, x, y, z) and \((ct'',x'',y'', z'')\).
2.4
Show that Lorentz transformations do not commute in general.
2.5
The GPS Navigation System consists of a network of satellites in high orbits around Earth. Each satellite has an orbital speed of about 14,000 km/hour. What is the relation between the time measured by a clock on one of these satellites and by a clock on Earth due to the orbital motion of the satellite?Footnote 6
Rights and permissions
Copyright information
© 2018 Springer Nature Singapore Pte Ltd.
About this chapter
Cite this chapter
Bambi, C. (2018). Special Relativity. In: Introduction to General Relativity. Undergraduate Lecture Notes in Physics. Springer, Singapore. https://doi.org/10.1007/978-981-13-1090-4_2
Download citation
DOI: https://doi.org/10.1007/978-981-13-1090-4_2
Published:
Publisher Name: Springer, Singapore
Print ISBN: 978-981-13-1089-8
Online ISBN: 978-981-13-1090-4
eBook Packages: Physics and AstronomyPhysics and Astronomy (R0)