Abstract
Symmetries play a fundamental role in the study of the dynamics of physical systems, because they give rise to conserved quantities. In the Hamiltonian context, these conserved quantities are encoded in what is called a momentum mapping. This mapping generalizes well-known constants of motion, like momentum or angular momentum. We start with a discussion of momentum mappings and the related Witt-Artin decomposition of the tangent space. Then, we present the classical result of Marsden, Weinstein and Meyer on symmetry reduction in the case of a free action. To generalize this result to nonfree actions, we prove the Symplectic Tubular Neighbourhood Theorem (or Symplectic Slice Theorem), derive the Marle-Guillemin-Sternberg normal form of the momentum mapping and present the theory of singular reduction in detail. Thereafter, we apply this theory to a number of examples: the geodesic flow on the three-sphere, the Kepler problem (including the Moser regularization), the Euler top, the spherical pendulum and a model of gauge theory, which can be viewed as obtained from an approximation of gauge theory on a finite lattice. Finally, we give an introduction to the study of qualitative dynamics of systems with symmetries in terms of the energy-momentum mapping.
This is a preview of subscription content, log in via an institution.
Buying options
Tax calculation will be finalised at checkout
Purchases are for personal use only
Learn about institutional subscriptionsNotes
- 1.
- 2.
Also called the Symplectic Slice Theorem.
- 3.
See Definition 6.2.6.
- 4.
- 5.
If a momentum mapping J is fixed, we may include it in the tuple, thus writing (M,ω,Ψ,J).
- 6.
If Ψ is a right action, J is a homomorphism.
- 7.
Since
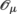 is an initial submanifold of \(\mathfrak{g}^{\ast}\), J restricts to a smooth mapping
is an initial submanifold of \(\mathfrak{g}^{\ast}\), J restricts to a smooth mapping  , denoted by the same symbol.
, denoted by the same symbol. - 8.
And δ is called the coboundary operator.
- 9.
Note that this decomposition need not be orthogonal with respect to the G m -invariant scalar product chosen above. If one wants to have an orthogonal Witt-Artin decomposition, one has to redefine the original scalar product by choosing a scalar product on each component and taking the orthogonal direct sum.
- 10.
When working with scalar products, this would require the scalar product on \({\rm T}_{\varPsi _{g}(m_{0})} M\) to be defined by \(\langle\varPsi_{g^{-1}}' \cdot, \varPsi_{g^{-1}}' \cdot \rangle\), which makes sense, because 〈⋅,⋅〉 is \(G_{m_{0}}\)-invariant.
- 11.
Alternatively, one may observe that, on Killing vector fields, \((\iota_{\mu}^{\ast}\omega)_{m}\) coincides with the pull-back of ω to the orbit G⋅m and apply Corollary 10.1.5.
- 12.
In the sequel, for convenience, we write V≡V m .
- 13.
Induced by the injection \(\mathfrak{g}_{m} \to \mathfrak{g}\).
- 14.
As before, for simplicity we denote H≡G m .
- 15.
- 16.
Note that \(\mathfrak{h}^{0}\) coincides with the subspace of H-invariant elements of the annihilator of \(\mathfrak{h}\) in \(\mathfrak{g}\).
- 17.
Which need not be equivariant, see Remark 10.5.8/ 2.
- 18.
Here, a subtlety occurs: whereas J −1(μ) can be simply viewed as a topological subspace of M,
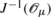 has to be endowed with the initial topology induced by the mapping J. If μ is regular and G acts freely on M, this is consistent with endowing
has to be endowed with the initial topology induced by the mapping J. If μ is regular and G acts freely on M, this is consistent with endowing 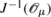 with the initial submanifold structure provided by the Transversal Mapping Theorem 1.8.2.
with the initial submanifold structure provided by the Transversal Mapping Theorem 1.8.2. - 19.
A Poisson space is a topological space together with a Poisson algebra of continuous functions.
- 20.
More precisely, we have faithful representations of these Lie algebras in the Poisson algebra of smooth functions on phase space.
- 21.
We use the simplified notation
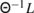 for the element of \(\mathfrak {so}(3)\) corresponding to the vector
for the element of \(\mathfrak {so}(3)\) corresponding to the vector 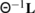 .
. - 22.
A pair (L,ω), fulfilling this differential equation, is called a Lax pair and the equation is called Lax equation, see Sect. 11.2.
- 23.
With the gravitational acceleration set equal to 1.
- 24.
A subset of ℝn defined by equations and inequalities is said to be semialgebraic.
- 25.
- 26.
See [161].
- 27.
In particular, \({\hat{P}}\) is an orbifold.
- 28.
Cf. Remark 6.6.2/5.
- 29.
Resetting \(H = \tilde{H}\) and \(J = \tilde{J}\).
References
Abraham, R., Marsden, J.E.: Foundations of Mechanics. Benjamin-Cummings, Reading (1978)
Arms, J.M., Cushman, R., Gotay, M.J.: A universal reduction procedure for Hamiltonian group actions. In: Ratiu, T.S. (ed.) The Geometry of Hamiltonian Systems, pp. 33–51. Springer, Berlin (1991)
Bates, L., Lerman, E.: Proper group actions and symplectic stratified spaces. Pac. J. Math. 181, 201–229 (1997)
Charzynski, Sz., Kijowski, J., Rudolph, G., Schmidt, M.: On the stratified classical configuration space of lattice QCD. J. Geom. Phys. 55, 137–178 (2005)
Charzynski, Sz., Rudolph, G., Schmidt, M.: On the topology of the reduced classical configuration space of lattice QCD. J. Geom. Phys. 58, 1607–1623 (2008)
Cordani, B.: The Kepler Problem. Birkhäuser, Basel (2003)
Cushman, R.H., Bates, L.M.: Global Aspects of Classical Integrable Systems. Birkhäuser, Basel (1997)
Fischer, E., Rudolph, G., Schmidt, M.: A lattice gauge model of singular Marsden-Weinstein reduction. Part I. Kinematics. J. Geom. Phys. 57, 1193–1213 (2007)
Florentino, C.A.A., Lawton, S.: The topology of moduli spaces of free group representations. Math. Ann. 345, 453–489 (2009)
Goldstein, H.: Prehistory of the Runge-Lenz vector. Am. J. Phys. 43, 737–738 (1975)
Goldstein, H.: More on the prehistory of the Runge-Lenz vector. Am. J. Phys. 44, 1123–1124 (1976)
Guillemin, V., Sternberg, S.: A normal form for the momentum map. In: Sternberg, S. (ed.) Differential Geometric Methods in Mathematical Physics. Mathematical Physics Studies, vol. 6. Reidel, Dordrecht (1984)
Guillemin, V., Sternberg, S.: Variations on a Theme by Kepler. AMS Colloquium Publications, vol. 42 (1990)
Huebschmann, J.: Kähler Spaces, Nilpotent Orbits, and Singular Reduction. Mem. Am. Math. Soc., vol. 172(814) (2004)
Huebschmann, J., Rudolph, G., Schmidt, M.: A lattice gauge model for quantum mechanics on a stratified space. Commun. Math. Phys. 286, 459–494 (2009)
Kijowski, J., Rudolph, G.: On the Gauß law and global charge for QCD. J. Math. Phys. 43, 1796–1808 (2002)
Kijowski, J., Rudolph, G.: Charge superselection sectors for QCD on the lattice. J. Math. Phys. 46, 032303 (2005)
Jarvis, P.D., Kijowski, J., Rudolph, G.: On the structure of the observable algebra of QCD on the lattice. J. Phys. A, Math. Gen. 38, 5359–5377 (2005)
Rudolph, G., Schmidt, M.: On the algebra of quantum observables for a certain gauge model. J. Math. Phys. 50, 052102 (2009)
Kogut, J., Susskind, L.: Hamiltonian formulation of Wilson’s lattice gauge theories. Phys. Rev. D 11, 395–408 (1975)
Kummer, M.: On the regularization of the Kepler problem. Commun. Math. Phys. 84, 133–152 (2002)
Kustaanheimo, P., Stiefel, E.: Perturbation theory of Kepler motion based on spinor regularization. J. Reine Angew. Math. 218, 609–636 (1965)
Libermann, P., Marle, C.-M.: Symplectic Geometry and Analytical Mechanics. Reidel, Dordrecht (1987)
Ligon, T., Schaaf, M.: On the global symmetry of the classical Kepler problem. Rep. Math. Phys. 9, 281–300 (1976)
Marle, C.-M.: Normal forms generalizing action-angle coordinates for Hamiltonian actions of Lie groups. Lett. Math. Phys., 7, 55–62 (1983)
Marle, C.-M.: Le voisinage d’une orbite d’une action hamiltonienne d’un groupe de Lie. In: Dazord, P., Desolneux-Moulis, N. (eds.) Séminaire Sud-Rhodanien de Geometrie II, pp. 19–35 (1984)
Marle, C.-M.: Modèle d’action hamiltonienne d’un groupe de Lie sur une variété symplectique. Rend. Semin. Mat. (Torino) 43(2), 227–251 (1985)
Marsden, J.E., Ratiu, T.S.: Introduction to Mechanics and Symmetry. Texts in Applied Mathematics, vol. 17. Springer, Berlin (1999)
Marsden, J.E., Weinstein, A.: Reduction of symplectic manifolds with symmetries. Rep. Math. Phys. 5, 121–130 (1974)
Marsden, J.E., Weinstein, A.: Some comments on the history, theory and applications of symplectic reduction. In: Landsman, N.P., Pflaum, M.J., Schlichenmaier, M. (eds.) Quantization of Singular Symplectic Quotients. Progress in Mathematics, vol. 198, pp. 1–19. Birkhäuser, Basel (2001)
Meyer, K.R.: Symmetries and integrals in mechanics. In: Peixoto, M.M. (ed.) Dynamical Systems, pp. 259–273. Academic Press, San Diego (1973)
Moser, J.: Regularization of Kepler’s problem and the averaging method on a manifold. Commun. Pure Appl. Math. 23, 609–636 (1970)
Ortega, J.-P., Ratiu, T.S.: Momentum Maps and Hamiltonian Reduction. Progress in Mathematics, vol. 222. Birkhäuser, Basel (2004)
Pflaum, M.J.: Analytic and Geometric Study of Stratified Spaces. Lecture Notes in Mathematics, vol. 1768. Springer, Berlin (2001)
Procesi, C.: Lie Groups. An Approach Through Invariants and Representations. Springer, Berlin (2007)
Rudolph, G., Schmidt, M., Volobuev, I.P.: Classification of gauge orbit types for SU(n)-gauge theories. Math. Phys. Anal. Geom. 5, 201–241 (2002)
Rudolph, G., Schmidt, M., Volobuev, I.P.: Partial ordering of gauge orbit types for SU(n)-gauge theories. J. Geom. Phys. 42, 106–138 (2002)
Rudolph, G., Schmidt, M., Volobuev, I.P.: On the gauge orbit space stratification: a review. J. Phys. A, Math. Gen. 35, R1–R50 (2002)
Sjamaar, R.: Singular orbit spaces in Riemannian and symplectic geometry. Ph.D. thesis, Rijksuniversiteit te Utrecht (1990)
Sjamaar, R., Lerman, E.: Stratified symplectic spaces and reduction. Ann. Math. 134, 375–422 (1991)
Smale, S.: Topology and mechanics I. Invent. Math. 10, 305–331 (1970)
Smale, S.: Topology and mechanics II. Invent. Math. 11, 45–64 (1970)
Vivarelli, M.: The KS-transformation in hypercomplex form. Celest. Mech. 29, 45–50 (1983)
Weinstein, A.: Sophus Lie and symplectic geometry. Expo. Math. 1, 95–96 (1983)
Weyl, H.: The Classical Groups. Their Invariants and Representations. Princeton University Press, Princeton (1939)
Whitehead, J.H.C.: Certain equations in the algebra of a semi-simple infinitesimal group. Quart. J. Math. Oxford 8, 220–237 (1932)
Woodhouse, N.M.J.: Geometric Quantization. Clarendon Press, Oxford (1992)
Author information
Authors and Affiliations
Rights and permissions
Copyright information
© 2013 Springer Science+Business Media Dordrecht
About this chapter
Cite this chapter
Rudolph, G., Schmidt, M. (2013). Symmetries. In: Differential Geometry and Mathematical Physics. Theoretical and Mathematical Physics. Springer, Dordrecht. https://doi.org/10.1007/978-94-007-5345-7_10
Download citation
DOI: https://doi.org/10.1007/978-94-007-5345-7_10
Publisher Name: Springer, Dordrecht
Print ISBN: 978-94-007-5344-0
Online ISBN: 978-94-007-5345-7
eBook Packages: Physics and AstronomyPhysics and Astronomy (R0)


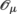 is an initial submanifold of
is an initial submanifold of  , denoted by the same symbol.
, denoted by the same symbol.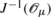 has to be endowed with the initial topology induced by the mapping J. If μ is regular and G acts freely on M, this is consistent with endowing
has to be endowed with the initial topology induced by the mapping J. If μ is regular and G acts freely on M, this is consistent with endowing 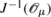 with the initial submanifold structure provided by the Transversal Mapping Theorem 1.8.2.
with the initial submanifold structure provided by the Transversal Mapping Theorem 1.8.2.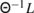 for the element of
for the element of 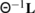 .
.